1 Introduction

Recent years have witnessed the great development of distributed cooperative control based on multi-agent systems (MASs) with the aim at solving the large variety of consensus problems commonly arising in different application fields (e.g., physics, economic sciences, biology, engineering, and robotics), such as, for example, synchronization, leader-tracking, containment, formation-containment, rendezvous [7]. The great diffusion of this control approach depends on its capability of overcoming some limits of the centralized control architectures, as the spatial distribution of devices and sensors, short-range of communication, computational burden [11].

In the above-distributed control context, it is well-known how the main challenges stem from the hypotheses that should be made on the agents model. Distributed protocols are commonly designed for dealing with homogeneous MAS, where all agents share a unique dynamical model (see for example [28, 29] and the references therein). However, as the cooperative control theory went improving, more complex and realistic scenarios have been treated bringing to the birth of the so-called heterogeneous MASs [12, 43], where each agent acts according to its own dynamics. Along this line, a major issue is that some of the tools proposed for the homogeneous framework cannot be exploited for the heterogeneous one, making this scenario harder to deal with and inducing the necessity of deriving analytical approaches able to specifically treat the agents heterogeneity [19].

To solve consensus problems in the heterogeneous framework, where agents are modeled as linear systems, different protocols have been recently proposed, ranging from the \(H_{\infty }\) for ensuring robust leader-tracking performances in the presence of external perturbation [1, 15, 22, 63], to adaptive approaches such as the ones proposed in [5, 57] for tackling the leader–follower control problem, or in [19, 20, 31] for solving containment and formation problems.

In this context, the presence of the leading behavior is usually modeled as an autonomous agent (leader) generating the reference trajectories, belonging to a prescribed family that have to be tracked by all agents (followers). For the case of heterogeneous, but linear, MASs, it is possible to prove that this goal can be reached if a set of linear matrix equations, defined as regulator equations, are verified for each agent (e.g., see [22] and references therein). To this aim, most of the approaches in the technical literature propose joining the solutions of the regulator equations to the design of distributed observers in order to estimate the leader behavior (or a convex combination of the leaders states in the multi-leader case) [22, 45]. However, this estimation funds on the precise knowledge of the leader matrix [64]. To overcome this limitation, distributed adaptive protocols, guaranteeing the online estimation of the regulator equations solution, seem to be the most promising approach, as proved in [4] for solving the leader-following problem, or in [65] for achieving the formation-tracking.

More recent approaches aim at getting over the restrictive assumption of linear agents when solving the set of regulator equations, or estimating them, in order to deal with consensus problems in heterogeneous nonlinear MASs. For example, [58] proposes a control law based on the duplex proportional and integral action for ensuring the synchronization of a nonlinear Lipschitz heterogeneous MAS. Event-triggered approaches have been also adopted as, for example, in [35, 39, 56], while the problem of unknown and nonidentical control directions has been addressed in [51] by exploiting the Nussbaum functions via a two-layer distributed hierarchical control scheme. The same problem is also dealt with in [38], where the Nussbaum functions are used by mean of a particular transformation, the so-called PI error transformation, for heterogeneous and unknown second-order nonlinear MASs. Classical diffusive protocols have been also proposed, as for example in [47], where the aim is to guarantee some leader-following performance in the case of nonlinear Lipschitz heterogeneous MASs by considering the leader as a non-autonomous system with unknown bounded input, and in [37], where the consensus is ensured in finite time. Under the assumption of boundedness of the nonlinear uncertainties dynamics, authors in [55] propose a distributed adaptive observer-based consensus protocol along with an adaptive mechanism for updating the coupling weight values. Leveraging, instead, neural networks tools, a distributed learning consensus protocol is suggested in [27, 41, 53, 59] for solving a leader tracking problem with undirected communication graph topologies. Moreover, by combining a linear and discontinuous feedback terms with neural network approximation, [62] proposes a robust adaptive distributed controller for solving consensus of uncertain MAS.

The same control problem is also addressed via distributed backstepping adaptive approaches. Along this line, [17] solves the consensus problem by assuming that the leader/followers nonlinear dynamics can be linearly parameterized with some known functions while, by relaxing this latter assumption, [21] suggests a similar approach for the solution of leader–follower and leaderless consensus problems in a unified framework. Moreover, [50] proposes a backstepping distributed adaptive control protocol based on the boundedness assumption of the nonlinear dynamics and the restrictive hypothesis of undirected communication topologies. Again, this control method is exploited in [18, 48] to address the prescribed performances consensus tracking problem in the more challenging framework of time-varying control coefficient.

Based on control theory, it is well-known that it is possible improving the steady-state and the transient performances using a Proportional-Integral-Derivative (PID) controller, with the aim to take into account also the “past” and the “future” information, beyond the “present” ones [14]. For these reasons, as well as for the robustness purpose, versatility and ease of implementation, the PID control and its variations have been widely used. However, although the well-known advantages, distributed PID-like protocols are still lightly covered in the MAS literature, and generally the approaches restrict their focus to the homogeneous framework. For example, distributed PID has been exploited in [14] where authors ensure synchronization of a homogeneous MAS in the presence of Lipschitz nonlinearities, or in [49], where the synchronization over a switching delayed topology is addressed in the case of first-order homogeneous nonlinear Lipschitz MAS leveraging the Lyapunov–Krasovskii theory.

A more tricky scenario, which deals with both communication time-delay and time-varying parameter uncertainties, has been tackled in [40], where a descriptor transformation has been exploited for enlarging the state with the derivative control action, and in [8], where a suitable derivation of the closed-loop MAS allows overcoming some of the difficulties arising from the exploitation of the descriptor approach. In addition, robust distributed PID protocols have been also proposed for solving the problem of coordinating an homogeneous linear vehicular platoon in the presence of communication delays and parameter uncertainties in smart roads scenarios [9, 10]. Distributed and adaptive PI controllers have been instead proposed in [6] with the aim of ensuring consensus in the presence of state saturation constraints, again in the context of homogeneous nonlinear Lipschitz MASs, while PI and PD protocols were designed in [46] for achieving synchronization in the case of linear homogeneous second-order MAS in the presence of external disturbances, so also providing an \(H_2\) norm metric to evaluate the coherence of the group, i.e., the variance of nodal state fluctuations. The same problem has been tackled via robust PID in [42], but in the case of high-order homogeneous linear agents under the restrictive assumption of undirected communication graph. Instead, in the context of nonlinear homogeneous Lipschitz MASs, very recently, a distributed adaptive PI control has been proposed in [13], to ensure the synchronization of dynamic agents, in the presence of stochastic coupling.

A first attempt to solve the leader-tracking control problem for heterogeneous nonlinear MAS in cooperative driving applications via distributed PID-like control can be found in [36]. However, the design is based on the QUAD assumptions of vehicle nonlinear dynamics and does not take into account agent uncertainties.

All the recent aforementioned works, suggesting PID approaches both for linear and nonlinear agents, are mainly based on the assumption of homogeneous MASs. Indeed, the heterogeneous case is usually less addressed in the current technical literature and, in general, in the heterogeneous context, the control protocols mostly require some strict constraints on the agents structure. More in detail, the mathematical tools exploited for dealing with linear heterogeneous MASs demand the fulfillment of restrictive assumptions on the agents input matrix, thus limiting the practical applicability of the control protocols. For example, a distributed adaptive PI protocol has been designed in [33], where however there is the need for a full row rank input matrix, which turns to be a very strong assumption to accomplish in practical applications. Furthermore, with respect to the model commonly assumed for the leader, further restrictions usually allow generating just constant behaviors to be tracked by the MAS. As, for example, in [34], where authors propose a distributed PI control strategy able to track only a constant leading behavior under the main hypothesis that the input matrix of each agent (follower) is structured in order to guarantee that there exists a specific control action for each state variables, limiting by this way the applicability of the approach to a specific system category. Some of these drawbacks have been very recently overcome for heterogeneous, but linear, MASs in [32], where an optimal distributed PID protocol is proposed, able to solve both leader-tracking and output containment problems (i.e., when more leaders are present), without requiring restrictive assumptions on the agents matrix structures.

Based on the above facts, in this work, we propose a fully distributed adaptive PID protocol for heterogeneous nonlinear and unknown high-order multi-agent systems, able to ensure leader-tracking in the presence of parameter uncertainties, arising from the unavoidable simplifications occurring during the modeling phase, from the not-complete knowledge of the system dynamics and from the presence of external disturbances. Specifically, the proposed Lyapunov-based approach is able to adapt the gains of the fully distributed PID-like protocol so to cope with uncertainties, to emulate the effect of an optimal control action, and to guarantee the closed-loop asymptotic stability, as well as the boundedness of the control gains. Differently from the technical literature, the proposed control strategy involves a limited amount of time-varying information for the computation of adaptive control actions. Thus, according to the metric in [30], it is able to save communication channel bandwidth and to reduce the computational burden.

Numerical simulations, involving coupled harmonic oscillators networks, confirm the theoretical derivation and disclose the ability of the adaptive approach in solving the leader tracking control problems. Most notably, to better appreciate the potential applications of our approach, we also apply our method for solving a practical problem in the engineering literature, namely the cooperative driving of autonomous connected ground vehicles. Summarizing, the main contributions are:

  • we propose a fully distributed adaptive PID control approach, able to solve the leader-tracking problem for heterogeneous, nonlinear and unknown high-order multi-agent systems sharing information on directed graph. To the best of our knowledge and according to the literature overview, there are no works dealing with this framework;

  • differently from the distributed PID approaches proposed in [13, 33, 34], the our one enlarges the protocol with a derivative action so to improve the closed-loop performance (see [10, 32] for a detailed comparison analysis w.r.t. generic diffusive protocols) and does not require any restrictive assumption on the agents model structure, hence, enabling its concrete application in a wide range of leader-tracking engineering problems such as the cooperative driving one. Note that to deal with the derivative action, we do not need the exploitation of the descriptor transformation [40];

  • concerning the heterogeneous nonlinear MAS framework, the proposed approach does not require any assumption about the leader/follower agents dynamics, e.g., boundedness/ Lipschitz nonlinear vector field [21, 50, 55, 58], QUAD assumption [36], or complex adaptive neural-network-based procedure for a specific linear parametrization of leader dynamics [17];

  • there is no need of exploiting distributed observers to estimate the leader states or obtaining the solutions of regulator equations, thus making the control design and implementation easier with respect to the current approaches proposed for dealing with heterogeneity in the linear field;

  • the proposed approach allows guaranteeing the asymptotic convergence of the tracking error differently from other adaptive approaches in the technical literature (as analyzed in [62]). In addition, for the achievement of this control purpose, differently from the aforementioned backstepping or neural network techniques, our approach requires less computational burden according to the metric defined in [30].

Finally, the paper is structured as follows. The mathematical background is given in Sect. 2. Section 3 presents the problem statement, while Sect. 4 discusses about the leader tracking framework and the proposed distributed robust adaptive PID-like control strategy, whose stability analysis is analytically carried out in Sect. 5. Numerical simulations in Sect. 6 confirm the theoretical derivation and disclose the effectiveness of the proposed approach in ensuring the leader-tracking. Conclusions are provided in Sect. 7.

2 Background

2.1 Sharing information among agents

The information exchanging among the N agents within a MAS can be modeled by a N-order directed graph \({\mathcal {G}}_{\mathcal {N}}=\left( {\mathcal {V}},{\mathcal {E}},{\mathcal {A}}\right) \), where \({\mathcal {V}}=\{ 1,\dots ,N \}\) is the set of agents sharing information and \({\mathcal {E}}\subseteq {\mathcal {V}}\times {\mathcal {V}}\) is the set of the active communication links. The graph topology is described by the Laplacian matrix \({\mathcal {L}} = {\mathcal {D}}-{\mathcal {A}}\), where \({\mathcal {A}}=\left[ a_{ij} \right] _{N\times N}\) is the adjacency matrix, whose elements are equal to 1 only if agent j sends information to the agent i, 0 otherwise, and \(D =\mathrm{diag}\lbrace {\varDelta }_1, {\varDelta }_2, . . . , {\varDelta }_N \rbrace \) is the in-degree matrix, being \({\varDelta }_i=\sum _{j\in {\mathcal {V}}} a_{ij}\). If there exist an additional agent, defined as leader and labeled with 0, which imposes the reference behavior to the whole MAS, the resulting communication structure is modeled via an augmented directed graph \(\bar{{\mathcal {G}}}={\mathcal {G}}_{{{\mathcal {N}}+1}}\) and described via the matrix \({\mathcal {H}} = {\mathcal {L}}+{\mathcal {P}} \in {\mathbb {R}}^{N \times N}\), where \({\mathcal {P}} = \mathrm{diag}\{p_1,p_2,...,p_N\}\) is the pinning matrix, defined such that \(p_i = 1\) if the leader information is directly available for the \(i-th\) agent, 0 otherwise [24].

Moreover, in what follows, we consider the following assumption to be held.

Assumption 1

([52]) The communication graph \(\bar{{\mathcal {G}}}\) contains a directed spanning tree with the leader as the root.

Remark 1

Assumption 1 is not a restrictive for MAS connected via a communication networking technology in practical applications scenarios since it only implies that information can be shared through a path from the leader to any generic agent within MAS, but it is not always assumed them to be directly linked.

Finally, we recall a useful lemma for our theoretical derivation.

Lemma 1

[50] The following inequality holds

$$\begin{aligned} 0 \le \vert z \vert - \frac{z^2}{\sqrt{z^2 + \xi ^2(t)}} \le \xi (t) \end{aligned}$$
(1)

for any \(z \in {\mathbb {R}}\) and \(\xi (t)>0\).

3 Problem statement

Consider a group of N heterogeneous uncertain nonlinear agents in the following strict-feedback form [61]:

$$\begin{aligned} \begin{aligned}&{\dot{x}}_{i,q}(t) = x_{i,q+1}(t)\\&{\dot{x}}_{i,n}(t) = f_{i}(x_i(t)) + b_i u_i(t), \\&\;\;\; q=1,\cdots ,n-1, \;\; i = 1,\cdots ,N, \end{aligned} \end{aligned}$$
(2)

where \(x_i(t)=[x_{i,1}(t),\cdots ,x_{i,n}(t)]^\top \in {\mathbb {R}}^n\) is the state vector; \(u_i(t) \in {\mathbb {R}}\) is the control input; \(f_i(x_i(t)) \in {\mathbb {R}}\) is an unknown nonlinear function vector and \(b_i \in {\mathbb {R}}\) is an unknown scalar where only the sign is known.

Remark 2

The assumption of strict-feedback form is not restrictive since it can be commonly encountered in many nonlinear control problems [60, 61]. Moreover, some diffeomorphisms exist which allow recasting more general classes of nonlinear systems in such form [2, 44].

The leader behavior is described as the following autonomous nonlinear uncertain system:

$$\begin{aligned} \begin{aligned}&{\dot{x}}_{0,q}(t) = x_{0,q+1}(t)\\&{\dot{x}}_{0,n}(t) = f_0(x_0(t)), \;\;\;q=1,\cdots ,n-1 \end{aligned} \end{aligned}$$
(3)

being \(x_0(t)=[x_{0,1}(t),\cdots ,x_{0,n}(t)]^\top \in {\mathbb {R}}^n\) the leader state vector and \(f_0(x_0(t)) \in {\mathbb {R}}\) an unknown nonlinear function. Note that this nonlinear dynamics can be used to emulate a large class of useful command trajectories [24] (e.g., unit step, sinusoidal waveform, trapezoidal signals and so on).

Now, the leader-tracking control problem for heterogeneous high-order nonlinear uncertain MAS can be stated as follows.

Problem 1

(Leader-tracking problem) Consider the heterogeneous uncertain nonlinear multi-agent system defined in (2) and (3). Then, leader-tracking consensus is achieved by designing suitable distributed control actions \(u_i(t)\) such that each follower tracks the leader dynamics as time approaches infinity, i.e., (\(i= 1,2,\cdots ,N\)):

$$\begin{aligned} \lim _{t \rightarrow \infty } \Vert x_i(t) - x_0(t) \Vert = 0. \end{aligned}$$
(4)

To deal with the leader-tracking consensus problem, we first introduce the following synchronization signal for each i-th agent (\(i = 1,\cdots ,N\)):

$$\begin{aligned} \delta _i(t)= & {} \sum _{j=1}^N a_{ij} (x_i(t)-x_j(t)) + p_i (x_i(t)-x_0(t)), \nonumber \\ \end{aligned}$$
(5)

being \(a_{ij}\) the (i, j)-element of the adjacency matrix accounting for the communication link between agents i and j according the communication topology (i.e., \(a_{ij}=1\) if this link exists, 0 otherwise), while \(p_i\) is the i-th element along the diagonal of the pinning matrix (i.e., \(p_i=1\) when the leader directly communicates to the agent i, 0 otherwise).

Furthermore, we also define for each agent i the state error w.r.t. the leader as:

$$\begin{aligned} e_i(t) = x_i(t)-x_0(t), \;\;\; i=1,2,\cdots ,N, \end{aligned}$$
(6)

and, hence, we rewrite the synchronization vector in (5) as

$$\begin{aligned} \begin{aligned} \delta _i(t)&= \sum _{j=1}^N a_{ij}(e_i(t)-e_j(t))+p_i e_i(t) \\&= \Big (p_i + \sum _{j=1}^N a_{ij}\Big ) e_i(t) - \sum _{j=1}^N a_{ij} e_j(t)\\&= c_i e_i(t) - \sum _{j=1}^N a_{ij} e_j(t), \end{aligned} \end{aligned}$$
(7)

being \(c_i = p_i + \sum _{j=1}^N a_{ij} \in {\mathbb {R}}_+\). Note that according to Assumption 1, the parameter \(c_i\) is always positive, i.e., there is no a time instant such that a single agent is isolated.

Making explicit the vector in (7), it can be rewritten as:

$$\begin{aligned} \begin{aligned} \delta _i(t)&= \begin{bmatrix} \delta _{i,1}(t)\\ \delta _{i,2}(t)\\ \vdots \\ \delta _{i,n}(t) \end{bmatrix} = c_i \begin{bmatrix} e_{i,1}(t)\\ e_{i,2}(t)\\ \vdots \\ e_{i,n}(t) \end{bmatrix} -\sum _{j=1}^N a_{ij} \begin{bmatrix} e_{j,1}(t)\\ e_{j,2}(t)\\ \vdots \\ e_{j,n}(t) \end{bmatrix}\\&= c_i \begin{bmatrix} e_{i,1}(t)\\ e_{i,2}(t)\\ \vdots \\ e_{i,n}(t) \end{bmatrix} -\begin{bmatrix} \sum _{j=1}^N a_{ij} e_{j,1}(t)\\ \sum _{j=1}^N a_{ij} e_{j,2}(t)\\ \vdots \\ \sum _{j=1}^N a_{ij} e_{j,n}(t) \end{bmatrix}, \end{aligned} \end{aligned}$$
(8)

where each generic element of the vector is expressed as

$$\begin{aligned}&\delta _{i,l}(t) = c_i e_{i,l}(t)-\sum _{j=1}^N a_{ij} e_{j,l}(t), \;\; i,j = 1,\cdots ,N, \nonumber \\&\quad l=1,\cdots ,n. \end{aligned}$$
(9)

Now, taking into account the agents and leader dynamics, in (2) and (3), respectively, we derive the dynamics of the state error vector in (6) as:

$$\begin{aligned} \begin{aligned}&{\dot{e}}_{i,q}(t) = e_{i,q+1}(t),\\&{\dot{e}}_{i,n}(t) = (f_i(x_i(t))-f_0(x_0(t))) + b_i u_i(t), \end{aligned} \end{aligned}$$
(10)

\( \forall i=1,\cdots , N;\;q=1,\cdots ,n-1\) and accordingly, from (9), we derive the dynamics of the synchronization error vector in (8) as

$$\begin{aligned} \begin{aligned} {\dot{\delta }}_{i,q}(t)&= \delta _{i,q+1}(t), \;\;\;q=1,\cdots ,n-1\\ {\dot{\delta }}_{i,n}(t)&= c_i (f_i(x_i(t))-f_0(x_0(t))) + c_i b_i u_i(t) \\&\quad - \sum _{j=1}^N a_{ij} {\dot{e}}_{j,n}(t)\\&=c_i {\tilde{f}}_i(x_i(t),x_0(t)) + c_i b_i u_i(t) + w_i(t) \end{aligned} \end{aligned}$$
(11)

where \({\tilde{f}}_i(x_i(t),x_0(t)) = f_i(x_i(t))-f_0(x_0(t))\) and \(w_i(t)=- \sum _{j=1}^N a_{ij} {\dot{e}}_{j,n}(t)\).

Given (11), the dynamics of the synchronization vector in (8) can be expressed in a more compact form as

$$\begin{aligned} {\dot{\delta }}_i(t) =&A \delta _i(t) + B_i ({\tilde{f}}_i(x_i(t),x_0(t)) \nonumber \\&+ b_i u_i(t) + c^{-1}_i w_i(t)), \end{aligned}$$
(12)

where

$$\begin{aligned} A= \left[ \begin{array}{@{}c|c@{}} 0_{n-1} &{}I_{n-1}\\ \hline 0 &{} 0^\top _{n-1} \end{array}\right] \in {\mathbb {R}}^n, \;\; B_i = \begin{bmatrix} 0_{n-1}\\ \hline c_i \end{bmatrix} \in {\mathbb {R}}^{n \times 1} \end{aligned}$$
(13)

being \(0_{n-1}\) and \(I_{n-1}\) the null and identity matrices, respectively.

Remark 3

Since \(c_i \ne 0\) \(\forall i\), each couple \(A, B_i\) is controllable (\(i=1,\cdots ,N\)).

4 Control protocol design and closed-loop system

Before designing the control action in (12) able to solve the leader-tracking problem in uncertain conditions (see Problem 1), it is worth noting that in the ideal case of perfect knowledge of the plant (12), it would be possible to design an ideal control law, say \(u_i^\star (t)\), as:

$$\begin{aligned} u_i^\star (t)= & {} \frac{1}{b_i}(-{\tilde{f}}_i(x_i(t),x_0(t))-c^{-1}_i w_i(t)\nonumber \\&-K^\star _i \delta _i(t)), \end{aligned}$$
(14)

where \(K^\star _i \in {\mathbb {R}}^{1\times n}\) is a gain vector to be optimally tuned.

Substituting the control into (12), the closed-loop dynamics can be easily derived for each agent \(i \in \mathcal {G_N}\) as

$$\begin{aligned} {\dot{\delta }}_i(t) = (A-B_i K^\star _i)\delta _i(t)= \Phi _i \delta _i(t). \end{aligned}$$
(15)

In this case, where the plant matrices in (15) are perfectly known, the asymptotic stability of the tracking error under the control action \(u_i^\star \) in (14) can be shown according to the following Lemma.

Lemma 2

The closed-loop system (15) under the action of the ideal control \(u_i^\star (t)\) (14) is asymptotically stable for each agent \(i \in {\mathcal {G}}_N\) if the control gain matrix \(K^\star _i \in {\mathbb {R}}^{1\times n}\) is selected such that \(\Phi _i\) is Hurwitz.

Proof

Consider the following Lyapunov candidate function:

$$\begin{aligned} V_{\delta _i}(t) = \sum _{i=1}^N \delta _i^\top (t) P_i \delta _i(t), \end{aligned}$$
(16)

being \(P_i\), \(\forall i\), a symmetric and positive definite matrix. Based on the Remark 3, select an optimal control gain \(K^\star _i\) in (14) such that matrix \(\Phi _i\) is Hurwitz and compute the derivative of (16) along the solutions of the closed-loop system (15) as

$$\begin{aligned} {\dot{V}}_{\delta _i}(t)= & {} \sum _{i=1}^N \delta ^\top _i(t) (P_i \Phi _i + \Phi _i^\top P_i) \delta _i(t) \nonumber \\= & {} - \sum _{i=1}^N \delta ^\top _i(t) Q_i \delta _i(t), \end{aligned}$$
(17)

where \(Q_i\) is a symmetric and positive definite matrix solution of the Lyapunov equation \(P_i \Phi _i + \Phi _i^\top P_i = - Q_i\) (\(\forall i \in {\mathcal {G}}_N\)).

This implies that \(\lim _{t \rightarrow \infty } \delta _i(t) = 0\) and, hence, \(\delta _i(t) \in L_\infty , \;\; \forall i\). In so doing, the proof is complete. \(\square \)

Remark 4

According to Remark 3, different control gains tuning procedures can be exploited for the selection of the vector \(K_i^{\star }\), such as the pole-placement technique or the LQR one [23].

Now, the uncertain leader-tracking control problem for heterogeneous nonlinear MAS in Sect. 3 is here solved via the following distributed protocol with a PID-like structure:

$$\begin{aligned} u_{i}(t)= & {} u_{{i}_{PID}}(t) + \sigma _i(t) = K_{{i}_{P}}(t) \delta _i(t) \nonumber \\&+ K_{{i}_{I}}(t) \int _{0}^t \delta _i(s)ds + K_{{i}_{D}}(t) {\dot{\delta }}_i(t) + \sigma _i(t), \end{aligned}$$
(18)

where \(K_{{i}_{P}}(t), \; K_{{i}_{I}}(t)\) and \(K_{{i}_{D}}(t) \in {\mathbb {R}}^{1 \times n}\) are adaptive control gains vectors shaping the proportional, integral and the derivative actions, respectively, while \(\sigma _i(t) \in {\mathbb {R}}\) is an auxiliary control signal that has to be properly chosen to handle the effect of uncertainties and unknown dynamics affecting the MAS.

Defining \(\theta ^\top _i(t) = [K_{{i}_{P}}(t) \;\; K_{{i}_{I}}(t) \;\; K_{{i}_{D}}(t)] \in {\mathbb {R}}^{1 \times 3n}\) and

\(\varphi _i(t) = [\delta ^\top _i(t) \;\; \int _{0}^t \delta ^\top _i(s)ds \;\;{\dot{\delta }}^\top _i(t)]^\top \in {\mathbb {R}}^{3n \times 1}\), the control protocol (18) can be rewritten in a more compact form as

$$\begin{aligned} \begin{aligned} u_{i}(t)&= u_{{i}_{PID}}(t) + \sigma _i(t) = \theta ^\top _i(t) \varphi _i(t) + \sigma _i(t). \end{aligned} \end{aligned}$$
(19)

Let \(u^\star _{{i}_{PID}}(t)\) the optimal PID protocol that uniformly approximates the optimal controller \(u^\star _i(t)\) designed according to Lemma 2. This means that there must exists an optimal parameter vector, say \(\theta ^\star _i \in {\mathbb {R}}^{1 \times 3n}\), such that the approximation between the optimal PID action \(u^\star _{{i}_{PID}}(t) = \theta ^{\star \top }_i \varphi _i(t)\) and the optimal controller \(u^\star _i(t)\) can be bounded by an unknown positive constant \({\bar{\varepsilon }}_i\) \((i = 1,\cdots ,N)\). Accordingly, we can define the following bounded approximation:

$$\begin{aligned} u^\star _{{i}_{PID}}(t)-u^\star _i(t) = \varepsilon _i(t), \end{aligned}$$
(20)

being \(\vert \varepsilon _i(t) \vert \le {\bar{\varepsilon }}_i < +\infty \), \((i=1,\cdots ,N)\).

Now, substituting the proposed control protocol (19) in (12) and adding zero sum terms according to (20), the closed-loop dynamics can be obtained as:

$$\begin{aligned}&\begin{aligned} {\dot{\delta }}_i(t)&= A \delta _i(t) + B_i({\tilde{f}}_i(x_i(t),x_0(t)) + c^{-1}_i w_i(t) \\ \quad&\quad + b_i \theta ^\top _i(t) \varphi _i(t) \\ \qquad&\quad + b_i \sigma _i(t)) +B_i(b_i \varepsilon _i(t)-b_i \theta ^{\top \star }_i \varphi _i(t) \\&\quad + b_i u^\star _i(t)). \end{aligned} \end{aligned}$$
(21)

Finally, taking into account (14)–(15), after some algebraic manipulations, the closed-loop system (21) can be recast as (\(\forall i \in {\mathcal {G}}_N\)):

$$\begin{aligned}&\begin{aligned} {\dot{\delta }}_i(t)&=\Phi _i \delta _i(t) + B_i(b_i {\tilde{\theta }}^\top _i(t) \varphi _i(t) \\&\quad + b_i \sigma _i(t) + b_i \varepsilon _i(t)), \end{aligned} \end{aligned}$$
(22)

being \({\tilde{\theta }}_i(t)\) the errors between the control parameters and their optimal value, i.e.,

$$\begin{aligned} {\tilde{\theta }}_i(t) = \theta _i(t)-\theta ^{ \star }_i. \end{aligned}$$
(23)

5 Stability analysis

In what follows, we introduce the adaptive control law updating gains \(\theta ^\top _i(t) = [K_{{i}_{P}}(t) \;\; K_{{i}_{I}}(t) \;\; K_{{i}_{D}}(t)] \in {\mathbb {R}}^{1 \times 3n}\) and the auxiliary signal \(\sigma _i(t)\) in (18) (\(i \in {\mathcal {G}}_N\)). The stability conditions for the closed-loop MAS are analytically provided according to the following Theorem.

Theorem 1

Consider the closed-loop MAS in (22). The leader-tracking consensus as in Problem 1 is solved under the action of the distributed adaptive control (19), given the auxiliary signal of the form

$$\begin{aligned} \sigma _i(t) = -sign(b_i) \frac{B_i^\top P_i \delta _i(t)}{\sqrt{\Vert B_i^\top P_i \delta _i(t) \Vert ^2 + \nu _i^2(t)}}{\hat{\varepsilon }}_i(t), \end{aligned}$$
(24)

where \({\hat{\varepsilon }}_i(t)\) is the estimation of the unknown upper-bound \({\bar{\varepsilon }}_i\) of the approximation error in (20), which is updated according to

$$\begin{aligned} \dot{{\hat{\varepsilon }}}_i(t) = \alpha _i \frac{\Vert B^\top _i P_i \delta _i(t) \Vert ^2}{\sqrt{\Vert B_i^\top P_i \delta _i(t) \Vert ^2 + \nu _i^2(t)}}, \end{aligned}$$
(25)

and adaptive laws for updating the control gains \(\theta _i\) in (19) as

$$\begin{aligned} {\dot{\theta }}_i(t) = - sign(b_i) \Gamma _i \varphi _i(t) \delta ^\top _i(t) P_i B_i, \end{aligned}$$
(26)

where \(\forall i\), \(\alpha _i \in {\mathbb {R}}_+\) are positive scalars, \(\Gamma _i\) are positive diagonal matrices which can be arbitrarily chosen to shape the adaptive rates; \(P_i \in {\mathbb {R}}^{n \times n}\) are symmetric and positive definite matrices, such that the Lyapunov equation \(P_i \Phi _i + \Phi _i^\top P_i = - Q_i\) holds for free symmetric and positive definite matrix \(Q_i\), \(\forall i\); \(\nu _i(t)\) are positive free functions chosen such that \(\nu _i(t) > 0\) and \(\int _{0}^t \nu _i(s)ds \le {\bar{\nu }}_i<+\infty \), being \({\bar{\nu }}_i\) a positive bounded constant (\( i=1,\cdots ,N\)).

Furthermore, as the tracking errors \(e_i(t)=x_i(t)-x_0(t)\) converge to zero asymptotically, the adaptive control gains \(\theta _i(t) \in {\mathbb {R}}^{3n \times 1}\) and \({\hat{\varepsilon }}_i(t) \in {\mathbb {R}} \; (i=1,\cdots ,N)\) are bounded signals over the time.

Proof

Given the closed-loop MAS in (22), consider the following candidate Lyapunov function:

$$\begin{aligned} V(t)=V_1(t) + V_2(t) + V_3(t), \end{aligned}$$
(27)

where

$$\begin{aligned} \begin{array}{l} V_1(t) = \sum _{i=1}^N \delta ^\top _i(t) P_i \delta _i(t),\\ {}\\ V_2(t) = \sum _{i=1}^N \frac{\vert b_i \vert }{\alpha _i} {\tilde{\varepsilon }}^2_i(t),\\ {}\\ V_3(t) = \sum _{i=1}^N \vert b_i \vert {\tilde{\theta }}^\top _i(t) \Gamma ^{-1}_i {\tilde{\theta }}_i(t), \end{array} \end{aligned}$$
(28)

being \(P_i\) symmetric and positive definite matrices (i.e., \(P_i = P^\top _i >0\)); \(\alpha _i\) is a positive parameters; \(\Gamma _i \in {\mathbb {R}}^{3n \times 3n}\) are positive diagonal matrices; \({\tilde{\varepsilon }}_i(t)\) is computed on the basis of the estimation of the upper bound of the approximation error in (20) and the unknown bound \({\bar{\varepsilon }}_i\) as

$$\begin{aligned} {\tilde{\varepsilon }}_i(t) = {\bar{\varepsilon }}_i-{\hat{\varepsilon }}_i(t). \end{aligned}$$
(29)

Consider the term \(V_1(t)\) of the Lyapunov function in (27). Computing its time derivative along the solutions of (22), it yields:

$$\begin{aligned} \begin{aligned} {\dot{V}}_1(t)&= \sum _{i=1}^N \delta ^\top _i(t) (P_i \Phi _i + \Phi ^\top _i P_i)\delta _i(t)\\&\quad +2 \sum _{i=1}^N b_i\delta ^\top _i(t) P_i B_i {\tilde{\theta }}^\top _i(t) \varphi _i(t)\\&+ 2 \sum _{i=1}^N b_i \delta ^\top _i(t) P_i B_i \sigma _i(t) \\&+2 \sum _{i=1}^N b_i\delta ^\top _i(t) P_i B_i \varepsilon _i(t). \end{aligned} \end{aligned}$$
(30)

Focusing on the last term of (30) and leveraging the boundedness of \(\varepsilon _i(t)\) (see (20)), we can write:

$$\begin{aligned}&2 \sum _{i=1}^N b_i\delta ^\top _i(t) P_i B_i \varepsilon _i(t) \le 2 \nonumber \\&\sum _{i=1}^N \vert b_i \vert \Vert \delta ^\top _i(t) P_i B_i \Vert {\bar{\varepsilon }}_i. \end{aligned}$$
(31)

Furthermore, consider the arbitrary auxiliary control signal in (24). Exploiting the \(sign(\cdot )\) properties, it can be proven that

$$\begin{aligned} \vert b_i \vert sign(b_i) = b_i \rightarrow b_i sign(b_i) = \vert b_i \vert . \end{aligned}$$
(32)

Thus, substituting \(\sigma _i(t)\) as in (24) in (30), we obtain:

$$\begin{aligned} \begin{aligned} {\dot{V}}_1(t)&< - \sum _{i=1}^N \delta ^\top _i(t) Q_i \delta _i(t) \\&\quad +2 \sum _{i=1}^N b_i\delta ^\top _i(t) P_i B_i {\tilde{\theta }}^\top _i(t) \varphi _i(t)\\&-\, 2 \sum _{i=1}^N \vert b_i \vert \frac{\Vert B^\top _i P_i \delta _i(t) \Vert ^2}{\sqrt{\Vert B_i^\top P_i \delta _i(t) \Vert ^2 + \nu _i^2(t)}} {\hat{\varepsilon }}_i(t) \\&\quad +\, 2 \sum _{i=1}^N \vert b_i \vert \Vert \delta ^\top _i(t) P_i B_i \Vert {\bar{\varepsilon }}_i, \end{aligned} \end{aligned}$$
(33)

where \(\nu _i(t)\) is the positive free function (\(i=1,\dots ,N\)), where we have also leveraged the fact that \(P_i \Phi _i + \Phi ^\top _i P_i = - Q_i\), with \(Q_i = Q_i^\top >0\), \(\forall i\) (see Lemma 2 and Remark 3) and that for all \(q \in {\mathbb {R}}\) it holds: \(q^\top q = \Vert q \Vert ^2\), being \(q = B^\top _i P_i \delta _i(t)\).

Finally, since \({\hat{\varepsilon }}_i(t) = {\bar{\varepsilon }}_i-{\tilde{\varepsilon }}_i(t)\) (see (29)), inequality (33) can be rewritten as

$$\begin{aligned} \begin{aligned} {\dot{V}}_1(t)&< - \sum _{i=1}^N \delta ^\top _i(t) Q_i \delta _i(t) +2 \\&\quad \sum _{i=1}^N b_i\delta ^\top _i(t) P_i B_i {\tilde{\theta }}^\top _i(t) \varphi _i(t)+2\\&\quad \sum _{i=1}^N \vert b_i \vert \Big (\Vert \delta ^\top _i(t) P_i B_i \Vert \\&\quad - \frac{\Vert B^\top _i P_i \delta _i(t) \Vert ^2}{\sqrt{\Vert B_i^\top P_i \delta _i(t) \Vert ^2 + \nu _i^2(t)}}\Big ) {\bar{\varepsilon }}_i\\&\quad +2 \sum _{i=1}^N \vert b_i \vert \frac{\Vert B^\top _i P_i \delta _i(t) \Vert ^2}{\sqrt{\Vert B_i^\top P_i \delta _i(t) \Vert ^2 + \nu _i^2(t)}} {\tilde{\varepsilon }}_i(t). \end{aligned} \end{aligned}$$
(34)

It is worth noticing that for any \(z \in {\mathbb {R}}^n\), \(\Vert z \Vert >0\) implies that \(\vert \Vert z \Vert \vert = \Vert z \Vert >0\). Thus, since \(P_i\) is a symmetric matrix \(\forall i\), \(\Vert \delta ^\top _i(t) P_i B\Vert = \Vert B_i^\top P_i \delta _i(t) \Vert \) hence, placing \(z = B_i^\top P_i \delta _i(t)\) and exploiting Lemma 1, inequality (34) can be recast as

$$\begin{aligned} \begin{aligned} {\dot{V}}_1(t)&< - \sum _{i=1}^N \delta ^\top _i(t) Q_i \delta _i(t) \\&\quad +2 \sum _{i=1}^N b_i\delta ^\top _i(t) P_i B_i {\tilde{\theta }}^\top _i(t) \varphi _i(t)\\&+2 \sum _{i=1}^N \vert b_i \vert {\bar{\varepsilon }}_i \nu _i(t)\\&\quad +2 \sum _{i=1}^N \vert b_i \vert \frac{\Vert B^\top _i P_i \delta _i(t) \Vert ^2}{\sqrt{\Vert B_i^\top P_i \delta _i(t) \Vert ^2 + \nu _i^2(t)}} {\tilde{\varepsilon }}_i(t). \end{aligned} \end{aligned}$$
(35)

Now, compute the time derivative of the function \(V_2(t)\) in (27) and summing it to (35), we obtain:

$$\begin{aligned} {\dot{V}}_1(t) + {\dot{V}}_2(t)< & {} - \sum _{i=1}^N \delta ^\top _i(t) Q_i \delta _i(t)\nonumber \\&+2 \sum _{i=1}^N b_i\delta ^\top _i(t) P_i B_i {\tilde{\theta }}^\top _i(t) \varphi _i(t) \nonumber \\&+2 \sum _{i=1}^N \vert b_i \vert {\bar{\varepsilon }}_i \nu _i(t) \nonumber \\&+ 2 \sum _{i=1}^N \vert b_i \vert \frac{\Vert B^\top _i P_i \delta _i(t) \Vert ^2}{\sqrt{\Vert B_i^\top P_i \delta _i(t) \Vert ^2 + \nu _i^2(t)}} {\tilde{\varepsilon }}_i(t) \nonumber \\&-2\sum _{i=1}^N \frac{\vert b_i \vert }{\alpha _i} {\tilde{\varepsilon }}_i(t) \dot{{\hat{\varepsilon }}}_i(t). \end{aligned}$$
(36)

Adopting the adaptation law for \({\hat{\varepsilon }}_i(t)\) in (25), inequality (36) becomes:

$$\begin{aligned} \begin{aligned} {\dot{V}}_1(t)&+ {\dot{V}}_2(t) < - \sum _{i=1}^N \delta ^\top _i(t) Q_i \delta _i(t) \\&+2 \sum _{i=1}^N b_i\delta ^\top _i(t) P_i B_i {\tilde{\theta }}^\top _i(t) \varphi _i(t)\\&+2 \sum _{i=1}^N \vert b_i \vert {\bar{\varepsilon }}_i \nu _i(t). \end{aligned} \end{aligned}$$
(37)

Consider now the third term of the Lyapunov function \(V_3(t)\) in (27). Evaluating again its time derivative and summing up to \({\dot{V}}_1(t)+{\dot{V}}_2(t)\), from (37) it yields:

$$\begin{aligned} \begin{aligned} {\dot{V}}(t)&={\dot{V}}_1(t)+{\dot{V}}_2(t)+{\dot{V}}_3(t)\\&< - \sum _{i=1}^N \delta ^\top _i(t) Q_i \delta _i(t) +2 \sum _{i=1}^N b_i\delta ^\top _i(t) P_i B_i {\tilde{\theta }}^\top _i(t) \varphi _i(t)\\&\quad +2 \sum _{i=1}^N \vert b_i \vert {\bar{\varepsilon }}_i \nu _i(t) + 2 \sum _{i=1}^N \vert b_i \vert {\tilde{\theta }}^\top _i(t) \Gamma ^{-1}_i {\dot{\theta }}(t). \end{aligned}\nonumber \\ \end{aligned}$$
(38)

Since the following relation holds for each agent \(i \in {\mathcal {G}}_N\)

$$\begin{aligned} \begin{aligned}&2 \sum _{i=1}^N b_i \delta ^\top _i(t) P_i B_i {\tilde{\theta }}^\top _i(t) \varphi _i(t) = 2 \sum _{i=1}^N b_i {\tilde{\theta }}^\top _i(t)\varphi _i(t)\delta ^\top _i(t) P_i B_i, \end{aligned}\nonumber \\ \end{aligned}$$
(39)

then, (38) becomes:

$$\begin{aligned} \begin{aligned} {\dot{V}}(t)&< - \sum _{i=1}^N \delta ^\top _i(t) Q_i \delta _i(t)+2 \sum _{i=1}^N b_i {\tilde{\theta }}^\top _i(t) \varphi _i(t) \delta ^\top _i(t) P_i B_i\\&+2 \sum _{i=1}^N \vert b_i \vert {\bar{\varepsilon }}_i \nu _i(t) + 2 \sum _{i=1}^N \vert b_i \vert {\tilde{\theta }}^\top _i(t) \Gamma ^{-1}_i {\dot{\theta }}(t). \end{aligned}\nonumber \\ \end{aligned}$$
(40)

Choosing \({\dot{\theta }}(t)\) according to the adaptive law in (26) and exploiting (32), from (40) after some algebraic manipulation it follows:

$$\begin{aligned} {\dot{V}}(t) < - \sum _{i=1}^N \delta ^\top _i(t) Q_i \delta _i(t)+2 \sum _{i=1}^N \vert b_i \vert {\bar{\varepsilon }}_i \nu _i(t). \end{aligned}$$
(41)

Finally, integrating (41) over the time interval [0, t] and applying the Rayleigh inequality [3] on symmetric matrices \(Q_i, \; i=1,\cdots ,N\), since the parameters \(\vert b_i \vert \) and \({\bar{\varepsilon }}_i\), as well as the free functions \(\nu _i(t)\), are bounded \(\forall i\), we obtain:

$$\begin{aligned} V(t)&+\sum _{i=1}^N {\underline{\lambda }}_i(Q_i) \int _{0}^t \Vert \delta _i(s) \Vert ^2ds< V(0)\nonumber \\&+2 \sum _{i=1}^N \vert b_i \vert {\bar{\varepsilon }}_i {\bar{\nu }}_i < \infty , \end{aligned}$$
(42)

where \({\underline{\lambda }}_i(Q_i)\) is the smallest eigenvalues of \(Q_i\), and \({\bar{\nu }}_i\) is the upper-bound of the integral \(\int _{0}^t \nu _i(s)ds\), i.e., \(\int _{0}^t \nu _i(s)ds \le {\bar{\nu }}_i<+\infty \).

Given (42), from (27) along with (29) and (23) we establish that \(\delta _i(t), {\hat{\varepsilon }}_i(t)\) and \(\theta _i(t)\) are bounded signals \(\forall i\) [50].

Furthermore, it is worth noticing that (42) also implies [26]:

$$\begin{aligned} \lim _{t \rightarrow +\infty }\sum _{i=1}^N {\underline{\lambda }}_i(Q_i) \int _{0}^t \Vert \delta _i(s) \Vert ^2ds \le V(0) + 2 \sum _{i=1}^N \vert b_i \vert {\bar{\varepsilon }}_i {\bar{\nu }}_i. \end{aligned}$$
(43)

Hence, since limit for \(t \rightarrow + \infty \) in (43) exists and is finite, leveraging the Barbalat Lemma and following the same mathematical steps presented in [16, 25, 26], it is possible showing that

$$\begin{aligned} \lim _{t \rightarrow + \infty } \Vert \delta _i(t) \Vert = 0,\;\;\; i=1,\cdots ,N. \end{aligned}$$

Now, introduce the following global vectors for the entire MAS:

$$\begin{aligned} \delta (t) = [\delta ^\top _1(t),\delta ^\top _2(t),\cdots ,\delta ^\top _N(t)]^\top \in {\mathbb {R}}^{Nn \times 1}, \end{aligned}$$

and

$$\begin{aligned} e(t) = [e^\top _1(t),e^\top _2(t),\cdots ,e^\top _N(t)]^\top \in {\mathbb {R}}^{Nn \times 1}. \end{aligned}$$

From the definition of \(\delta _i(t)\) in (7), it follows:

$$\begin{aligned} \delta (t) = ({\mathcal {L}}+{\mathcal {P}} \otimes I_n) e(t)=({\mathcal {H}} \otimes I_n)e(t) \end{aligned}$$
(44)

where from Assumption 1, we have that \({\mathcal {H}}={\mathcal {L}}+{\mathcal {P}}\) is a positive definite M-matrix.

Therefore, since \(\delta _i \rightarrow 0\) \(\forall i\), from (44) we also have \(e_i(t) \rightarrow 0, \; \forall i\), and hence, from (6), that also \(x_i(t) \rightarrow x_0(t)\), for \(i=1,\cdots ,N\).

In so doing, the statement is proved. \(\square \)

Remark 5

The proposed distributed PID-like control (18) leverages a double adaptive mechanism, i.e., \({\dot{\theta }}_i (t)\) as in (26) and \(\dot{{\hat{\varepsilon }}}_{i}(t)\) as in (25). The first adaptive law allows updating the values of the control gains on the basis of the value of the synchronization vectors, while the second one allows estimating the approximation error \(\varepsilon _i(t)\) in (20) so that it can be compensated via the auxiliary signal \(\sigma _i(t)\) as in (24).

Remark 6

It is worth noting how the combined action of the two adaptive mechanisms with the auxiliary control signal \(\sigma _i(t)\) guarantees the asymptotic stability of the synchronization error with a proper trade-off w.r.t. the computational burden. Indeed, according to the metric proposed in [30], since the proposed control strategy involves a limited amount of time-varying information for computing the adaptive control, our approach is able to save communication channel bandwidth and to reduce the computational burden w.r.t. the current related literature (see e.g., [21, 50, 62] and the references therein).

6 Numerical validation

6.1 Synchronization of coupled harmonic nonlinear oscillators

Consider the exemplary case of a second-order MAS composed of five nonlinear oscillators, modeled as in (2), plus a leader which imposes the oscillating reference behavior according to (3). Unknown vector fields are defined \(\forall i=1,\cdots ,5\) as

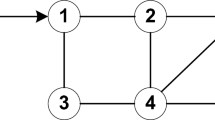
$$\begin{aligned} f_i(x_i(t))= & {} \{sin^4(x_{1,1}(t)), \; x_{2,2}^2(t), \; cos(x_{3,2}(t)),\\&x_{4,2}(t)e^{-sin(x_{4,1}(t))}, \; sin^2(x_{5,1}(t)) \} \end{aligned}$$

while \(b_i = \{0.001,\; -0.002, \; 0.005, \; 0.07, \; -0.5\}\), being \(x_{i,1}(t)\) and \(x_{i,2}(t)\) the angular position and velocity of the i-th agent, respectively. Instead, the positive free functions are selected as \(\nu _i(t) = e^{-0.1 t}\) (\(i=1,2,\cdots ,5\)). The leader behavior is modeled as \(f_0(x_0(t)) = 5 sin(1.5 t)\). The information exchanging among agents are described by the communication graph as in Fig. 1 whose Laplacian and Pinning matrices are defined as

Fig. 1
figure 1

Communication graph topology for coupled harmonic nonlinear oscillators

Full size image
Fig. 2
figure 2

Synchronization of coupled harmonic nonlinear oscillators. Leader-tracking performances under the action of the distributed adaptive PID protocol in (18). Time history of: a angular position \(x_{i,1}(t)\) (solid lines) and angular velocity \(x_{i,2}(t)\) (dashed lines) \(\forall i = 0, 1, 2, 3, 4, 5\); b angular position error w.r.t. the leader \(e_{i,1}(t) = x_{i,1}(t)-x_{0,1}(t)\) (solid lines) and angular velocity error w.r.t. the leader \(e_{i,2}(t) = x_{i,2}(t)-x_{0,2}(t)\) (dashed lines) \(\forall i = 0, 1, 2, 3, 4, 5\)

Full size image
Fig. 3
figure 3

Synchronization of coupled harmonic nonlinear oscillators. Leader-tracking performances under the action of the distributed adaptive PID protocol in (18). Time history of the adaptive control gains

Full size image
$$\begin{aligned} {\mathcal {L}}=\begin{bmatrix} 1 &{} -1 &{} 0 &{} 0 &{} 0 \\ -1 &{} 2 &{} 0 &{} -1 &{} 0 \\ -1 &{} 0 &{} 2 &{} 0 &{} -1 \\ 0 &{} -1 &{} -1 &{} 2 &{} 0 \\ 0 &{} -1 &{} 0 &{} 0 &{} 1 \end{bmatrix}, \;\; {\mathcal {P}}= \mathrm {diag}\{1, 0, 1, 0, 0 \} , \end{aligned}$$
(45)

while the optimal control gains vector \(K_i^{\star }\) in (14) is tuned by leveraging pole-placement technique. The effectiveness of the proposed distributed adaptive PID approach is disclosed in Fig. 2a, where the time histories of the agent trajectories confirm the theoretical results and prove the good performances of each agent in tracking the dynamical leader behavior. The leader-tracking errors, instead, are shown in Fig. 2b. According to the results of Theorem 1, once the consensus is reached, the adaptive proportional, integral and derivative control gain, \(K_{P,i}(t), \; K_{I,i}(t)\) and \(K_{D,i}(t) \in {\mathbb {R}}^{2 \times 1}, \; i=1,2,3,4,5\), respectively, as well as signals \({\hat{\varepsilon }}_i(t), \; i=1,2,3,4,5\), converge toward a constant steady-state value, as shown in Figs. 3–4, respectively.

6.2 Cooperative driving of nonlinear uncertain heterogeneous autonomous vehicles platoon

In order to show the effectiveness of the proposed approach in solving practical engineering problems, here we focus on the leader-tracking control problem arising in the autonomous driving field, also known as platooning. Platooning mainly consists of a cohesive fleet of cars that, connected through a communication wireless network via the Vehicle-to-Vehicle (V2V) or Vehicle-to-Infrastructure (V2I) paradigm, moves forward with a required common velocity, imposed by a leading vehicle (the first vehicle within the group) or a road infrastructure acting as a virtual leader, while keeping at the same time a prescribed safe inter-vehicular distance (see [10] and reference therein for a more detailed discussion on platooning). Traveling as a platoon formation brings very relevant benefits, such as the mitigation of traffic congestion, the reduction in the fuel consumption and the environmental pollution, an increase in the safety and the efficiency of road transportation.

Fig. 4
figure 4

Synchronization of coupled harmonic nonlinear oscillators. Leader-tracking performances under the action of the distributed adaptive PID protocol in (18). Time history of the adaptive signal \({\hat{\epsilon }}_i(t) \; i=1, 2, \cdots ,5\)

Full size image
Fig. 5
figure 5

Leader–Predecessor–Follower topology for a platoon of five heterogeneous uncertain vehicles/agents plus the leader (the first vehicle in the string formation)

Full size image

Consider a platoon composed of \(N=5\) heterogeneous uncertain vehicle (named followers) plus a leader labelled as agent 0. The behavior of each agent/follower within the platoon is described by its inherently nonlinear longitudinal motion [54] (\(i=1,\dots ,5\)):

$$\begin{aligned} \begin{aligned}&{\dot{p}}_i(t) = v_i(t)\\&{\dot{v}}_i(t) = \frac{\eta _i}{m_i R_i} u_i(t) - \frac{C_{A,i}}{m_i} v^2_i(t) - g f_{r,i}(t), \end{aligned} \end{aligned}$$
(46)

where \(p_i(t) \; [m]\) and \(v_i(t) \; [m/s]\) are the longitudinal position and velocity of the i-th vehicle, respectively, \(u_i(t) \; [N m]\) is the control input representing the vehicle propulsion torque, i.e., the driving/braking torque , \(m_i \; [kg]\) is the vehicle mass, \(\eta _i\) is the drive-train mechanical efficiency, \(R_i \; [m]\) is the wheel radius; \(C_{A,i} \; [kg/m]\) is the aerodynamic drag coefficient; \(g \; [m/s^2]\) is the gravity acceleration, while \(f_{r,i}\) is the rolling resistance coefficient.

Setting \(f_i(x_i(t))= - \frac{C_{A,i}}{m_i } v^2_i(t) - g f_{r,i} \) and \(b_i = \frac{\eta _i}{m_i R_i}\), it is possible to recast the longitudinal dynamics of the vehicles (46) as in (2). Note that as in our theoretical framework, the vector field \(f_i(x_i(t))\) are considered uncertain, since, in practice, it is very difficult to estimate or measure the effective rolling radius, the road friction information or the aerodynamic effects or to have a precise knowledge of the actual driving parameters, such as the exact drive-train efficiency. Conversely, the leader dynamics are simply modeled as a trajectories generator in order to evaluate the platoon response to different useful command trajectories, such as ramp, trapezoidal waveform and so on [24]. Moreover, all vehicles/agents are connected and share their kinematic information (position, velocity) according to the so-called leader–predecessor–follower (LPF) topology that is one of the typical communication structures in the vehicular field [10] (see Fig. 5).

The leader-tracking performances have been evaluated leveraging the MATLAB/Simulink simulation platform. Simulation parameters, as well, the initial conditions for autonomous vehicles platoon (including the ones for the leader) are given in Table 1. The positive free functions are selected as \(\nu _i(t) = e^{-0.1 t}\) (\(i=1,2,\cdots ,5\)), the desired constant distance between adjacent vehicles is set equal to \( 20 \; [m]\), while the optimal control gains vector \(K_i^{\star }\) in (14) is tuned by leveraging pole-placement technique.

Table 1 Autonomous vehicle parameters
Full size table

In order to disclose the performance of the cooperative adaptive control strategy, results presented here refer to an exemplary platoon maneuver where the leader travels with an initial velocity of \(10 \; [m/s]\) until, at time instant \(t = 15 \; [s]\), it begins to accelerate with a constant acceleration equal to \(2.35 \; [m/s^2]\), reaching the constant velocity of \(21.75 \; [m/s]\). Then, at \(t = 26.8 \; [s]\), the leader starts to decelerate with a constant deceleration of \(-1.06 \; [m/s^2]\) until it reaches the constant speed of \(18.35 \; [m/s]\). Finally, at \(t = 38.2 \; [s]\), it accelerates again with a constant acceleration equal to \(1.62 \; [m/s^2]\), reaching the final constant velocity of \(26.15 \; [m/s]\).

Fig. 6
figure 6

Cooperative driving of nonlinear uncertain heterogeneous autonomous vehicles platoon. Leader tracking performance under the adaptive distributed PID control in (18). Time history of: a inter-vehicle distances \(p_i(t)-p_{i-1}(t) \; (i=1, \dots , 5)\); b vehicles speed \(v_i(t) \; (i = 0,1,2,3,4,5)\); c position errors \(e_{i}(t)\) computed as \(p_i(t)-p_0(t)-d_{i,0}\) (\(i=1,2,3,4,5\))

Full size image
Fig. 7
figure 7

Cooperative driving of nonlinear uncertain heterogeneous autonomous vehicles platoon. Leader tracking performance under the adaptive distributed PID control in (18). Convergence of the adaptive gains. Time history of: a Proportional gains \(K_{P,i (1,2)}(t) \; i=1,2,3,4,5\); b Integral gains \(K_{I,i (1,2)}(t) \; i=1,2,3,4,5\); c Derivative gains \(K_{D,i (1,2)}(t) \; i=1,2,3,4,5\); d) Signals \({\hat{\varepsilon }}_i(t) \; i=1,2,3,4,5\)

Full size image

Results in Fig. 6 disclose the ability of the proposed distributed adaptive PID-like protocol in ensuring excellent leader-tracking performances despite the presence of uncertainties, i.e., all vehicles effectively track the leader speed, as shown in Fig. 6b), while maintaining the desired inter-vehicular distance (see Fig. 6a). Small bounded errors occur, as expected, only in the correspondence of the leader speed changes (see Fig. 6c). Furthermore, according to the theoretical derivation, the proportional, integral and derivative adaptive control gains, \(K_{{i}_{P}}(t)=[K_{{i}_{P1}} \; K_{{i}_{P2}}]^{\top }\), \( K_{{i}_{I}}(t)=[K_{{i}_{I1}} \; K_{{i}_{I2}}]^{\top }\), and \( K_{{i}_{D}}(t)=[K_{{i}_{D1}} \; K_{{i}_{D2}}]^{\top }\) (\(i=1,\dots ,5\)), respectively, as well as the adaptive estimate of \({\hat{\varepsilon }}_i(t)\) (\(i=1,\dots ,5\)) are bounded and converge to finite steady-state value as shown in Fig. 7a–d.

7 Conclusions

In this work, the leader tracking control problem for heterogeneous nonlinear high-order MAS has been addressed and solved through a fully distributed robust PID-like algorithm whose control gains are able to adapt their values so to counteract the presence of uncertainties and external disturbances acting on the agents dynamics. Exploiting the Lyapunov theory, we have provided specific adaption laws for the control parameters and we have proved the asymptotic stability of the overall closed-loop MAS under the action of the proposed control action. An illustrative MAS, composed of five harmonic nonlinear heterogeneous oscillators agents, has been used to confirm the effectiveness of the theoretical derivation. Moreover, to better appreciate the advantages and the potential applications of the proposed approach, we apply our method for solving the practical engineering problem of the cooperative driving for autonomous connected ground vehicles.