Robust fuzzy delayed sampled-data control for nonlinear active suspension systems with varying vehicle load and frequency-domain constraint

Abstract

This article studies the Takagi-Sugeno (T-S) fuzzy delayed sampled-data $\mathcal {H}_\infty$ control problem for a class of intelligent suspension systems with varying vehicle load and frequency-domain constraint. The T-S fuzzy model is utilized to characterize the varying vehicle load. Considering the transmission delay, a robust fuzzy delayed sampled-data control mechanism is newly propounded for suspension systems. According to the Lyapunov stability theory, a useful theorem is proposed based on the Wirtinger inequality to guarantee the states of the active suspension system being asymptotically stabilized with the required $\mathcal {H}_\infty$ performance by the proposed controller. Moreover, the suspension constrained requirements are also satisfied within the finite frequency domain. Finally, simulation examples are presented to attest to the usefulness and superiority of the proposed controller.

1 Introduction

In modern vehicle systems, the suspension system refers to the connecting device between the body and the tire, which acts as a bridge between the driver and the road surface. It greatly improves the overall performance of the vehicle, mainly including the riding comfort, handling stability, and safety of the driver and passengers. Generally, there are three types of vehicle suspension: passive suspension, semi-active suspension, and active suspension. Among them, the active suspension is equipped with controllable actuators to provide or dissipate the energy from the system, so as to eliminate the vibration or impact which is transmitted to the vehicle body by the irregular road surface roughness. Since the active suspension has advantages in the trade-off between ride quality and mechanical constraints, in recent years, research on the active vehicle suspension control design has attracted considerable attention, and many useful results have been accumulated [1,2,3,4,5,6].

For the vehicle suspension system control problem, improving ride comfort, i.e., minimizing the vibration from the tires to the car body and maximizing the passenger comfort, is of great significance. Note that most of the existing works consider the control of the suspension system in the entire frequency (EF) domain. However, according to ISO-2631 Standard, the human body is more sensitive to a fixed frequency band, that is, vertical vibration of $4--8$ Hz. Such a kind of resonance can cause severe damage to human organs. Moreover, typical road excitations also occur in a limited frequency range. It is proved that compared with the controller for the EF domain, the finite frequency (FF) control method can bring better system performance [7,8,9,10,11,12]. Therefore, how to apply the $\mathcal {H}_\infty$ control method to the active suspension system in the finite frequency domain is a significant problem. In recent years, the FF control design problem has achieved some significant results. Li et al. [7] developed the fuzzy wheelbase preview FF control for uncertain half-car active suspension with time delay to improve the ride comfort. With the help of the Kalman–Yakubovich–Popov theory, Fei et al. [9] investigated the reliable FF control for a cloud-aided active quarter-car vehicle suspension system with actuator failure. Zhu et al. [10] constructed three fault detection filters in different FF domains for vehicle active suspension systems to minimize the error between residuals and faults.

Due to the quality change of load and the complicated working environment, the automobile suspension system is a complex system with uncertainty. It is proved that the T-S fuzzy model is an effective method and practical tool for describing complex uncertain systems [13,14,15,16,17,18]. T-S fuzzy model method, as an excellent method to deal with the system inherent parameter uncertainty, has been widely utilized in the description of uncertain active suspension systems [11, 19,20,21]. Among them, Du et al. [19] firstly applied the T-S fuzzy model to characterize the nonlinear uncertain electrohydraulic suspension. A state feedback controller is proposed for the obtained T-S fuzzy model with optimized $\mathcal {H}_\infty$ performance by using the parallel-distributed compensation scheme. Li et al. [20] adopted an adaptive event-triggered fuzzy control mechanism for active vehicle suspension systems with uncertainties and actuator failure to ensure the desired performance. Taking the sensor failure into account, Zhang et al. [21] designed the FF T-S fuzzy $\mathcal {H}_\infty$ control for uncertain active vehicle suspension systems to strengthen ride comfort level.

With the development of digital and communication technology, the sampled-data control problem has attracted widespread attention [22,23,24,25,26]. Compared with general continuous control methods, the sampled-data control technique only needs to sample the system state in discrete time. Thus, the amount of information transmitted is greatly reduced, which makes the control more efficient. In addition, the sampled-data system based on digital technology is highly reliable and easy to implement. Four methods are commonly used to analyze and synthesize sampled-data systems: the first is the discrete design technology [27]. The second is the lifting technique [28]. Compared with the discretization method, the lifting technique can improve the performance between sampling instants. The third method is the hybrid system method [29, 30], which is a direct method based on the Riccati equation. The last method is the input delay method [22, 31], which transforms the digital controller into a time-delay system. The input delay method is popular and has been widely used in sampled-data systems. For vehicle systems, Gao et al. [32] investigated the robust sampled-data control for active vehicle suspension systems with polytopic parameter uncertainties by using an input delay technique. Meng et al. [33] considered the dual-rate hybrid sampled-data control issue for an active suspension system of an electric vehicle. Combined with the fuzzy logic technique, the fuzzy sampled-data control of automobile suspension systems is of great significance. There are only a few results [34, 35]. Li et al. [35] studied both state-feedback and output-feedback sampled-data fuzzy control method for uncertain active suspension systems to ensure the asymptotical stability, $\mathcal {H}_\infty$ disturbance attenuation level and suspension performance constraints. Li et al. [34] proposed a sampled-data asynchronous fuzzy control for half-car active suspension systems in the restricted frequency domain.

On the other hand, the time delay is an inevitable source of instability for control systems [36]. Controller communication delay always exists in the real physical systems which may lead to difficulties in realizing stability. In the sampled-data control, the update signal transmitted from the sampler to the controller and reaches the zero-order hold at the sampling instants often experiences the transmission delay [37]. Compared with the sampled-data control strategy in the existing automobile suspension system [32, 33], the fuzzy delay sampled-data control designed here is more suitable since the transmission delay and system uncertainties always occur. Even though there exist a few works on the fuzzy sampled-data control for automobile suspension systems, however, as far as the authors know, the transmission delay in the controller and the FF constraint strategy is not taken into consideration, which is the motivation of this article.

In this paper, the robust stabilization problem for nonlinear active suspension systems with varying vehicle load and frequency-domain constraint is investigated by proposing a fuzzy delayed sampled-data control scheme. The main contributions of this study include: (1) The nonlinear uncertain active suspension dynamics is approximated by the T-S fuzzy model. Based on the Wirtinger inequality, a discontinuous Lyapunov–Krasovskii functional (LKF) is employed to design the robust fuzzy delayed sampled-data controller for nonlinear active suspension systems with varying vehicle load to improve the drive comfort lever within the FF domain and ensure the active suspension constraints. (2) Compared with the existing works on fuzzy sampled-data control for active suspension systems [34, 35], the transmission delay, which plays a significant role in the data transmission, is taken into consideration. A delay-dependent stabilization criterion is proposed. (3) The frequency-domain analysis is treated in this paper. Compared with the designed controller for the EF domain in the existing works [32, 33], the FF constraint control considered here is more friendly to the drivers and passengers and can bring better system performance.

This paper is organized into six parts. In Sect. 2, the system model is formulated, and preliminaries are presented. In Sect. 3, the stability analysis and $\mathcal {H}_\infty$ performance of active suspension is addressed and the fuzzy delayed sampled-data controller design problem is discussed. Two examples are illustrated in Sect. 4. Conclusions are drawn in Sect. 5.

1.1 Notations

For any matrix P, the notations $P^T$ and $P^*$ stands for its transpose and complex conjugate transpose, respectively. $[P]_s$ means $P+P^T$. $\{P\}_m$ refers to the m-th line of a matrix P. j refers to the imaginary unit. The matrix I means an identity matrix. $\mathcal {H}_n$ denotes the set of $n \times n$ Hermitian matrix. $P>0$ means that P is positive definite and vice versa. All matrices are supposed to be compatible with the algebraic operations if their dimensions are not explicitly stated.

2 Problem formulation and preliminaries

2.1 A quarter-car model

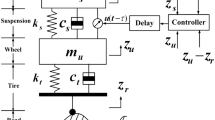
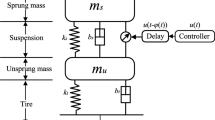
Consider the quarter-vehicle model depicted in Fig. 1 [38], according to Newton’s second law, the dynamic of the quarter suspension system can be expressed as

$$\begin{aligned} {m_s}{\ddot{z}_s}(t)= & {} - \,{c_s}({\dot{z}_s}(t) - {\dot{z}_u}(t)) - {k_s}({z_s}(t) - {z_u}(t)) \nonumber \\&+ u(t),\nonumber \\ {m_u}{\ddot{z}_u}(t)= & {} - \, {c_s}({\dot{z}_u}(t) - {\dot{z}_s}(t)) - {k_s}({z_u}(t) - {z_s}(t))\nonumber \\&- \, {k_t}({z_u}(t) - {z_r}(t)) - {c_t}({\dot{z}_u}(t) - {\dot{z}_r}(t)) \nonumber \\&- u(t), \end{aligned}$$

(1)

where $m_s$ is the sprung mass, $m_u$ is the unsprung mass. $z_s$ and $z_u$ represent the displacement of the sprung and unsprung masses, respectively. $z_r$ is the road displacement input, $c_s$ and $k_s$ is the damping and stiffness of the suspension system, respectively. u(t) is the active input of the active suspension system. $k_t$ and $c_t$ denotes the compressibility and damping of the pneumatic tire, respectively.

Define the suspension deflection ${x_1}(t) = {z_s}(t) - {z_u}(t)$, the tire deflection ${x_2}(t) = {z_u}(t) - {z_r}(t)$, the sprung mass speed ${x_3}(t) = {\dot{z}_s}(t)$, the unsprung mass speed ${x_4}(t) = {\dot{z}_u}(t)$, and the disturbance input $\omega (t) = {\dot{z}_r}(t)$. Then, the above physical dynamical equation can be described as

$$\begin{aligned} {\dot{x}(t) = A(t)x(t) + B(t)u(t) + E(t)\omega (t),} \end{aligned}$$

(2)

where $x(t) = {\left( {\begin{array}{*{20}{c}} {{x_1}(t)}&{{x_2}(t)}&{{x_3}(t)}&{{x_4}(t)} \end{array}} \right) ^T}$,

Fig. 1

The quarter-vehicle model

$A(t) = \left( {\begin{array}{*{20}{c}} 0&{}0&{}1&{}{ - 1} \\ 0&{}0&{}0&{}1 \\ { - \frac{{{k_s}}}{{{m_s}(t)}}}&{}0&{}{ - \frac{{{c_s}}}{{{m_s}(t)}}}&{}{\frac{{{c_s}}}{{{m_s}(t)}}} \\ {\frac{{{k_s}}}{{{m_u}(t)}}}&{}{ - \frac{{{k_t}}}{{{m_u}(t)}}}&{}{\frac{{{c_s}}}{{{m_u}(t)}}}&{}{\frac{{{c_s} + {c_t}}}{{{m_s}(t)}}} \end{array}} \right)$, $B(t) = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ {{1 / {{m_s(t)}}}} \\ { - {1 / {{m_u(t)}}}} \end{array}} \right)$, $E (t) = \left( {\begin{array}{*{20}{c}} 0 \\ { - 1} \\ 0 \\ {{{{c_t}} / {{m_u(t)}}}} \end{array}} \right)$,

In general, the following three key performance constraints are taken into account in suspension controller design:

• (i) Ride comfort: ride comfort is generally quantified by the vehicle body acceleration ${\ddot{z}_s}(t)$. Note that the FF range of $4-8$ Hz is the most sensitive for people. In order to improve the ride comfort, the sprung mass acceleration ${\ddot{z}_s}(t)$ needs to be minimized within the concerned frequency band.

• (ii) Suspension deflection constraint: the maximum suspension deflection should not exceed the threshold of the mechanical structure.

  $$\begin{aligned} \left| {{z_s}(t) - {z_u}(t)} \right| \leqslant {z_{\max }}, \end{aligned}$$

  (3)

  where $z_{max}$ is the maximum suspension deflection.

• (iii) Road holding ability: the dynamic tire load is required to be smaller than its static load to guarantee a firm uninterrupted contact of wheels to road,

  $$\begin{aligned} {k_t}({z_u}(t) - {z_r}(t)) < ({m_s}(t) + {m_u}(t))g, \end{aligned}$$

  (4)

  where g is the acceleration of gravity.

According to the control objects, we define the relative suspension deflection ${z_1}(t) = {\ddot{z}_s}(t)$, and the relative dynamic tire load ${\small {{z_2}(t) = {\left( {\begin{array}{*{20}{c}} {\frac{{{z_s}(t) - {z_u}(t)}}{{{z_{\max }}}}}&{\frac{{{k_t}({z_u}(t) - {z_r}(t))}}{{({m_s}(t) + {m_u}(t))g}}} \end{array}} \right) ^T}}}$. Then, the state space form of the quarter-vehicle model can be formulated:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\dot{x}(t) = A(t)x(t) + B(t)u(t) + E(t)\omega (t),} \\ {{z_1}(t) = {C_1}(t)x(t) + D(t)u(t),} \\ {{z_2}(t) = {C_2}(t)x(t),} \end{array}} \right. \end{aligned}$$

(5)

where ${C_1} = \left( {\begin{array}{*{20}{c}} { - {{{k_s}}/ {{m_s(t)}}}}&0&{ - {{{c_s}} / {{m_s(t)}}}}&{{{{c_s}}/ {{m_s(t)}}}} \end{array}} \right)$, ${C_2} = \left( {\begin{array}{*{20}{l}} {{1 / {{z_{\max }}}}}&{}0&{}0&{}0 \\ 0&{}{{{{k_t}} / {(({m_s(t)} + {m_u(t)})g)}}}&{}0&{}0 \end{array}} \right)$, $D = {1 / {{m_s(t)}}}$.

For the preparation of further analysis, as $x(t) \in \mathcal {R}^n$, we define ${e_p} = {\left( {\begin{array}{*{20}{c}} {\underbrace{0...0{} {} {} {} {} I}_p}&{0...0} \end{array}} \right) ^T}$, ${e_p} \in {\mathcal {R}^{6n \times n}}$, ${{\hat{e}}_p} = {\left( {\begin{array}{*{20}{c}} {\underbrace{0...0{} {} {} {} {} I}_p}&{0...0} \end{array}} \right) ^T}$, ${\hat{e}_p} \in {\mathcal {R}^{(6n+1) \times n}},p=1,2,...,6$, ${\hat{e}_7} \in {\mathcal {R}^{(6n+1)}}$, ${{\tilde{e}}_m} = {\left( {\begin{array}{*{20}{c}} {\underbrace{0...0{} {} {} {} {} I}_m}&{0...0} \end{array}} \right) ^T}$, ${\tilde{e}_m} \in {\mathcal {R}^{4n \times n}}$, ${\hat{\tilde{e}}_m} = {\left( {\begin{array}{*{20}{c}} {\underbrace{0...0{} {} {} {} {} I}_m}&{0...0} \end{array}} \right) ^T}$, ${\hat{\tilde{e}}_m} \in {\mathcal {R}^{(4n+1) \times n}}, m=1,2,3,4$, ${\hat{e}_5} \in {\mathcal {R}^{(4n+1)}}$.

2.2 T-S fuzzy modeling

The sprung mass and un-sprung mass are uncertain caused by the number of passengers, fuel consumption and tire wear, etc. We assume that the parameters $m_s(t)$ and $m_u(t)$ change within a certain range, ${m_s}(t) \in \left[ {{m_{s\min }},{m_{s\max }}} \right]$ and ${m_u}(t) \in \left[ {{m_{u\min }},{m_{u\max }}} \right]$.

Define

By the sector nonlinear method [20], we have

where $\frac{1}{{{m_s}(t)}}$ and $\frac{1}{{{m_u}(t)}}$ are premise variables, and membership functions $T_1$, $T_2$, $G_1$ and $G_2$ satisfy ${T_1}(\frac{1}{{{m_s}(t)}}) + {T_2}(\frac{1}{{{m_s}(t)}}) = 1$, ${G_1}(\frac{1}{{{m_u}(t)}}) + {G_2}(\frac{1}{{{m_u}(t)}}) = 1$, in which

Then, the nonlinear and uncertain active suspension system is formulated by the T-S fuzzy model:

Rule i: IF $\frac{1}{{{m_s}(t)}}$ is ${T_p}(\frac{1}{{{m_s}(t)}})$ and $\frac{1}{{{m_u}(t)}}$ is ${G_p}(\frac{1}{{{m_u}(t)}})$, then

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\dot{x}(t) = {A_i}x(t) + {B_i}u(t) + {E_i}\omega (t),} \\ {{z_1}(t) = {C_{1i}}x(t) + {D_i}u(t),} \\ {{z_2}(t) = {C_{2i}}(t)x(t),} \end{array}} \right. \end{aligned}$$

(6)

where $p=1,2$, $i=1,2,3,4$, $T_1$, $T_2$, $G_1$ and $G_2$ denotes ‘Heavy’, ‘Light’, ‘Heavy’, and ‘Light’, respectively.

By assigning and to $m_s(t)$ and $m_u(t)$, the system matrices can be calculated.

According to the fuzzy inference technique, the following overall T-S fuzzy system is employed

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\dot{x}(t) = \sum \limits _{i = 1}^4 {{h_i}(\theta (t))(} {A_i}x(t) + {B_i}u(t) + {E_i}\omega (t)),} \\ {{z_1}(t) = \sum \limits _{i = 1}^4 {{h_i}(\theta (t))(} {C_{1i}}x(t) + {D_i}u(t)),} \\ {{z_2}(t) = \sum \limits _{i = 1}^4 {{h_i}(\theta (t))} {C_{2i}}x(t),} \end{array}} \right. \end{aligned}$$

(7)

where

$$\begin{aligned} {h_1}(\theta (t)) = {T_1}\left( \frac{1}{{{m_s}(t)}}\right) \times {G_1}\left( \frac{1}{{{m_u}(t)}}\right) ,\\ {h_2}(\theta (t)) = {T_1}\left( \frac{1}{{{m_s}(t)}}\right) \times {G_2}\left( \frac{1}{{{m_u}(t)}}\right) ,\\ {h_3}(\theta (t)) = {T_2}\left( \frac{1}{{{m_s}(t)}}\right) \times {G_1}\left( \frac{1}{{{m_u}(t)}}\right) ,\\ {h_4}(\theta (t)) = {T_2}\left( \frac{1}{{{m_s}(t)}}\right) \times {G_2}\left( \frac{1}{{{m_u}(t)}}\right) , \end{aligned}$$

and it is easy to see that the fuzzy weighting functions ${h_i}(\theta (t)) \geqslant 0$, and $\sum \limits _{i = 1}^4 {{h_i}(\theta (t))} = 1$.

The following T-S fuzzy sampled-data controller mechanism with time delay is utilized by parallel-distributed compensation scheme:

Controller Rule q: IF $\frac{1}{{{m_s}(t)}}$ is ${T_p}(\frac{1}{{{m_s}(t)}})$ and $\frac{1}{{{m_u}(t)}}$ is ${G_p}(\frac{1}{{{m_u}(t)}})$,

then

$$\begin{aligned} u(t) = {K_{1q}}x({t_k}) + {K_{2q}}x({t_k} - \delta ),\nonumber \\ {t_k} \leqslant t < {t_{k + 1}}, k=0,1,2,..., \end{aligned}$$

(8)

where $q=1,2,3,4$, $p=1,2$, $\delta$ is a constant transmission delay, $K_{1q}$ and $K_{2q}$ are controller gains to be designed, and $\left\{ {{t_k}} \right\} = \left\{ {{t_0},{t_1},{t_2},...} \right\}$ is the sampling instant sequence with $0 = {t_0}< {t_1}< {t_2}< {t_3}< ...< {t_{k - 1}}< {t_k} < ...$, where ${\lim _{k \rightarrow \infty }}{t_k} = \infty$.

We assume the sampling period satisfies $t_{k+1}-t_k \buildrel \Delta \over = h_k \leqslant h, \forall k = 0,1,2,...$, where $h >0$. The controller (8) can be written as

$$\begin{aligned} u (t) = \sum \limits _{q = 1}^4 {{h_q}(\theta ({t_k}))({K_{1q}}x({t_k})} + {K_{2q}}x({t_k} - \delta )),\nonumber \\ {t_k} \leqslant t < {t_{k + 1}}, k=0,1,2, \cdots . \end{aligned}$$

(9)

Combined with system (7), the closed-loop system turns to be

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} \begin{gathered} \dot{x}(t) = \sum \limits _{i = 1}^4 {} \sum \limits _{q = 1}^4 {{h_i}(\theta (t)){h_q}(\theta ({t_k}))(} {A_i}x(t) \\ + {B_i}{K_{1q}}x({t_k}) + {B_i}{K_{2q}}x({t_k} - \delta ) + {E_i}\omega (t)), \\ \end{gathered} \\ \begin{gathered} {z_1}(t) = \sum \limits _{i = 1}^4 {} \sum \limits _{q = 1}^4 {{h_i}(\theta (t)){h_q}(\theta ({t_k}))(} {C_{1i}}x(t) \\ {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} {} + {D_i}{K_{1q}}x({t_k}) + {D_i}{K_{2q}}x({t_k} - \delta )), \\ \end{gathered} \\ {{z_2}(t) = \sum \limits _{i = 1}^4 {{h_i}(\theta (t))} {C_{2i}}(t)x(t).} \end{array}} \right. \end{aligned}$$

(10)

Remark 1

Note that the vehicle mass parameter is varying since the vehicle load is uncertain in practice. In order to characterize the nonlinear active suspension systems with varying vehicle loads, the T-S fuzzy model is effectively utilized here. Compared with the existing works on the sampled-data control for suspension systems [32, 33], the fuzzy tool can deal with the uncertainties well that it is more practical for engineering applications.

Remark 2

Considering the transmission delay, the fuzzy delayed sampled-data controller is proposed. Compared with general continuous control methods, the sampled-data control technique only needs to sample the system state in discrete time, which makes the amount of information transmitted significantly reduced. Combined with the fuzzy technique, the controller designed is efficient, highly reliable, and easy to implement. Compared with the existing on the fuzzy sampled-data controller [34, 35], the transmission delay is specially considered in the controller (8) for the active suspension system to characterize the delay when the update signal is transmitted from the sampler to the controller and reaches the zero-order hold at the sampling instants.

In what follows, we will design a robust fuzzy delayed sampled-data controller in the form of (9) for nonlinear active suspension systems with varying vehicle load and frequency-domain constraint such that

i) The closed-loop system (10) is asymptotically stable.

ii) With zero initial condition, for a given positive scalar $\gamma$, the following $\mathcal {H}_\infty$ performance inequality

$$\begin{aligned} \mathop {\sup }\limits _{{\varpi _1} \leqslant \varpi \leqslant {\varpi _2}} {\left\| {{J_{{z_1}\omega }}(j\varpi )} \right\| _\infty } < \gamma , \end{aligned}$$

(11)

holds for all nonzero $\omega (t) \in {L_2}[0,\infty )$, where ${{J_{{z_1}\omega }}(j\varpi )}$ is the transfer function from the input disturbance $\omega (t)$ to the controlled output $z_1(t)$. ${\varpi _1} \leqslant \varpi \leqslant {\varpi _2}$ is the FF band.

iii) The following control output condition needs to be ensured

$$\begin{aligned} \left| {{{\{ {z_2}(t)\} }_r}} \right| < 1,r = 1,2, \end{aligned}$$

(12)

where ${{{\{ {z_2}(t)\} }_r}}$ denotes the rth row vector of $z_2(t)$.

Remark 3

In the $\mathcal {H}_\infty$ performance inequality (11), the FF band ${\varpi _1} \leqslant \varpi \leqslant {\varpi _2}$ is taken into account. Compared with the EF band, the human body is more sensitive to a fixed frequency band, that is, the vertical vibration of $4-8$ Hz. In general, road excitations also occur in a limited frequency range. Hence, it is important and necessary to design the controller for the FF domain.

3 Main results

In this section, by constructing a Wirtinger-inequality-based Lyapunov functional, sufficient conditions are established to ensure the closed-loop active suspension system (10) possess asymptotical stability, desired $\mathcal {H}_\infty$ performance and satisfy the constraints in the FF domain.

First, some useful lemmas are given as follows.

Lemma 1

[22] For a given matrix $P>0$, the inequality

$$\begin{aligned}&- (c - b)\int _b^c {{{\dot{x}}^T}(s)P} \dot{x}(s)ds \nonumber \\&\quad \leqslant - {(x(c) - x(b))^T}P(x(c) - x(b)) \nonumber \\&\quad - 3\Bigl (x(c) + x(b) - \frac{2}{{c - b}}\int _b^c {x(s)ds} \Bigr )^T P\nonumber \\&\quad \times \Bigl ( x(c) + x(b) - \frac{2}{{c - b}}\int _b^c {x(s)ds} \Bigr ) \end{aligned}$$

(13)

holds for all continuously differentiable function x(t) in $[b,c] \in {\mathcal {R}^n}$.

Lemma 2

[39] For given a vector $l \in \mathbb {C}^n$, and matrices M, $N \in \mathcal {H}_n$, the following inequality holds

$$\begin{aligned} {l^*}Ml < 0{} {} {} {} {} {} \forall l \ne 0,{} {} {} {} {} {l^*}Nl \geqslant 0, \end{aligned}$$

(14)

if and only if

$$\begin{aligned} \exists \alpha \in \mathcal {R},\alpha \geqslant 0,M + \alpha N < 0. \end{aligned}$$

(15)

Theorem 1

Consider system (10), given positive scalars $\delta$, $\gamma$, $\alpha _l$, $\beta _m$, $l=1,2,3$, $m=1,2,3,4$ and $\vartheta$, and prescribed gain matrices $K_{1q}$ and $K_{2q}$, $q=1,2,3,4$. If there exist positive-definite matrices $P_r$, $Q_r$, $S_r$, $R_r$, $r=1,2$ and Q, symmetric matrix P, and general matrices $W_r$, $\hat{W}_r$, $r=1,2$ and H such that for $h_k \in [0,h]$,

$$\begin{aligned} {\Omega _1} + {h_k}{\Omega _2}&< 0, \end{aligned}$$

(16)

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {{\Omega _1}}&{}{{h_k}{W_1^T}}&{}{3{h_k}{W_2^T}} \\ *&{}{ - {h_k}{Q_1}}&{}0 \\ *&{}*&{}{ - 3{h_k}{Q_1}} \end{array}} \right)&< 0, \end{aligned}$$

(17)

$$\begin{aligned} \Psi _1+ {h_k}{\hat{\Omega } _2}&< 0, \end{aligned}$$

(18)

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {{\Psi _1}}&{}{{h_k}{{\hat{W}}_1^T}}&{}{3{h_k}{{\hat{W}}_2^T}} \\ *&{}{ - {h_k}{Q_2}}&{}0 \\ *&{}*&{}{ - 3{h_k}{Q_2}} \end{array}} \right)&< 0, \end{aligned}$$

(19)

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} { - I}&{}{\sqrt{\vartheta } \{ {C_{2i}}\} _r^{}} \\ *&{}{ - {P_2}} \end{array}} \right)&< 0, r=1,2, \end{aligned}$$

(20)

where

$$\begin{aligned} {\Omega _1}= & {} {[{e_2}{P_1}e_1^T]_s} - {[W_1^T{M_1}]_s} - {[3W_2^T{M_2}]_s} \\&+ {[{\phi _1}{\varphi _1}]_s} + {\delta ^2}{e_2}{R_1}e_2^T - ({e_1} - {e_5}){R_1}{({e_1} - {e_5})^T}\\&+{h^2}{e_2}{S_1}{e_2}^T - \frac{{{\pi ^2}}}{4}({e_5} - {e_6}){S_1}{({e_5} - {e_6})^T},\\ \phi _1^T= & {} \left( {\begin{array}{*{20}{l}} {{\alpha _1}{H^T}}&{{\alpha _2}{H^T}}&0&0&0&{{\alpha _3}{H^T}} \end{array}} \right) , \\ {\varphi _1}= & {} \left( {\begin{array}{*{20}{l}} {{A_i}}&{ - I}&{{B_i}{K_{1q}}}&0&0&{{B_i}{K_{2q}}} \end{array}} \right) ,\\ {\Omega _2}= & {} {e_2}{Q_1}e_2^T, {M_1} = e_1^T-e_3^T, {M_2} = e_1^T+e_3^T-2e_4^T,\\ {\hat{\Omega }} _1= & {} {[{\hat{e}_2}{P_2}\hat{e}_1^T]_s} - {[\hat{W}_1^T{\hat{M}_1}]_s} - {[3\hat{W}_2^T{\hat{M}_2}]_s} \\&+ {\delta ^2}{\hat{e}_2}{R_2}\hat{e}_2^T +{[{\phi _2}{\varphi _2}]_s}- ({\hat{e}_1} - {\hat{e}_5}){R_2}{({\hat{e}_1} - {\hat{e}_5})^T} \\&+{h^2}{\hat{e}_2}{S_2}{\hat{e}_2}^T - \frac{{{\pi ^2}}}{4}({\hat{e}_5} - {\hat{e}_6}){S_2}{({\hat{e}_5} - {\hat{e}_6})^T}, \\ {\Psi _1}= & {} {\hat{\Omega } _1} + {\eta ^T}\eta - {\hat{e}_7}{\gamma ^2}\hat{e}_7^T + \chi ,\\ {\hat{M}}_1= & {} \hat{e}_1^T-\hat{e}_3^T, {\hat{M}}_2= \hat{e}_1^T+\hat{e}_3^T-2\hat{e}_4^T, \\ {\hat{\Omega } _3}= & {} {\hat{e}_2}{Q_2}\hat{e}_2^T, \\ \phi _2^T= & {} \left( {\begin{array}{*{20}{l}} {{\beta _1}{H^T}}&{{\beta _2}{H^T}}&{{\beta _3}{H^T}}&0&0&{{\beta _4}{H^T}}&0 \end{array}} \right) ,\\ {\varphi _2}= & {} \left( {\begin{array}{*{20}{l}} {{A_i}}&{ - I}&{{B_i}{K_{1q}}}&0&0&{{B_i}{K_{2q}}}&{{E_i}} \end{array}} \right) ,\\ \eta= & {} \left( {\begin{array}{*{20}{l}} {{C_{1i}}}&0&{{D_i}{K_{1q}}}&0&0&{{D_i}{K_{2q}}}&0 \end{array}} \right) ,\\ \chi= & {} {\mathcal {F}^T}\Lambda \mathcal {F},\Lambda = \left( {\begin{array}{*{20}{c}} { - Q}&{}{P + j{\varpi _c}Q} \\ *&{}{ - {\varpi _1}{\varpi _2}Q} \end{array}} \right) ,\\ \mathcal {F}= & {} \left( {\begin{array}{*{20}{l}} 0&{}I&{}0&{}0&{}0&{}0&{}0 \\ I&{}0&{}0&{}0&{}0&{}0&{}0 \end{array}} \right) ,{\varpi _c} = \frac{{{\varpi _1} + {\varpi _2}}}{2}. \end{aligned}$$

hold, then system (10) is asymptotically stable, and has $\mathcal {H}_\infty$-gain lever $\gamma$ for the FF $\varpi \in [\varpi _1,\varpi _2 ]$. The constraint condition (12) is ensured with upper bound of the disturbance energy ${\omega _{\max }} = {{(\vartheta - \hat{V}(0))} / {{\gamma ^2}}}$.

Proof

The asymptotic stability of system (10) without the disturbance $\omega (t)$ is proved first.

Consider the following Lyapunov functional candidate:

$$\begin{aligned} V(t) = \sum \limits _{i = 1}^3 {{V_i}} , \end{aligned}$$

(21)

where

$$\begin{aligned} {V_1}(t)= & {} {x^T}(t){P_1}x(t),\\ { V_2}(t)= & {} ({h_k} - (t - {t_k}))\int _{{t_k}}^t {{{\dot{x}}^T}(s){Q_1}\dot{x}(s)} ds,\\ {V_3}(t)= & {} \delta \int _{ - \delta }^0 {} \int _{t + \theta }^t {{{\dot{x}}^T}(s){R_1}\dot{x}(s)dsd\theta } \\&+{h^2}\int _{{t_k} - \delta }^t {{{\dot{x}}^T}(s){S_1}\dot{x}(s)ds} \\&- \frac{{{\pi ^2}}}{4}\int _{{t_k} - \delta }^{t - \delta } {{(x(s) - x({t_k} - \delta ))}^T} {S_1} \\&\times (x(s) - x({t_k} - \delta ))ds \end{aligned}$$

in which matrices $P_1>0$, $Q_1>0$, $S_1>0$ and $R_1>0$ are to be determined.

Calculating the derivative of V(t), we have

$$\begin{aligned} {\dot{V}_1}(t)= & {} {\dot{x}^T}(t){P_1}x(t) + {x^T}(t){P_1}\dot{x}(t), \end{aligned}$$

(22)

$$\begin{aligned} {\dot{V}_2}(t)= & {} - \int _{{t_k}}^t {{{\dot{x}}^T}(s){Q_1}\dot{x}(s)} ds \nonumber \\&+ ({h_k} - (t - {t_k})){\dot{x}^T}(t){Q_1}\dot{x}(t), \end{aligned}$$

(23)

$$\begin{aligned} {\dot{V}_3}(t)= & {} {h^2}{\dot{x}^T}(t){S_1}\dot{x}(t) - \frac{{{\pi ^2}}}{4} (x(t - \delta ) \nonumber \\&- x({t_k} - \delta ))^T S_1 (x(t - \delta ) - x({t_k} - \delta ))\nonumber \\&+{\delta ^2}{\dot{x}^T}(t){R_1}\dot{x}(t) - \delta \int _{t - \delta }^t {{{\dot{x}}^T}(s){R_1}\dot{x}(s)ds}.\nonumber \\ \end{aligned}$$

(24)

From Lemma 1, we have

$$\begin{aligned}&- \int _{{t_k}}^t {{{\dot{x}}^T}(s){Q_1}\dot{x}(s)} ds \nonumber \\&\quad \leqslant - \frac{1}{{t - {t_k}}}({(x(t) - x({t_k}))^T}{Q_1}(x(t) - x({t_k})) \nonumber \\&\qquad + 3{(x(t) + x({t_k}) - \frac{2}{{t - {t_k}}}\int _{{t_k}}^t {x(s)ds} )^T}{Q_1}\nonumber \\&\qquad (x(t) + x({t_k}) - \frac{2}{{t - {t_k}}}\int _{{t_k}}^t {x(s)ds} )) \nonumber \\&= \quad - \frac{1}{{t - {t_k}}}{\varsigma ^T}(t)(M_1^T{Q_1}{M_1} + 3M_2^T{Q_1}{M_2})\varsigma (t) \end{aligned}$$

(25)

where ${\varsigma ^T}(t) = ({x^T}(t){} {} {} {} {} {\dot{x}^T}(t){} {} {} {} {} {x^T}(t_k){} {} {} {} {} \frac{1}{{t - {t_k}}}\int _{{t_k}}^t {{x^T}(s)ds}$ ${} {}{x^T}(t - \delta ){} {} {} {} {x^T}({t_k} - \delta ))$ and ${ M}_1 = e^T_1- e^T_3$, ${M_2} = e^T_1+e^T_3-2e^T_4$.

Here, there exist matrices $W_1$ and $W_2$ such that the following inequality holds

$$\begin{aligned}&\frac{1}{{t - {t_k}}}({Q_1}{M_1} - (t - {t_k}){W_1})^T Q_1^{ - 1} \\&\quad \;\; \times {({Q_1}{M_1} - (t - {t_k}){W_1})} \geqslant 0, \end{aligned}$$

then,

$$\begin{aligned} - \frac{1}{{t - {t_k}}}M_1^T{Q_1}{M_1}\leqslant & {} - W_1^T{M_1} - M_1^T{W_1} \nonumber \\&+ (t - {t_k})W_1^T Q_1^{ - 1}{W_1}, \end{aligned}$$

(26)

similarly, we have

$$\begin{aligned} - \frac{1}{{t - {t_k}}}M_2^T{Q_1}{M_2}\leqslant & {} - W_2^T{M_2} - M_2^T{W_2} \nonumber \\&+ (t - {t_k})W_2^T Q_1^{ - 1}{W_2}, \end{aligned}$$

(27)

thus,

$$\begin{aligned}&{{\dot{V}}_2}(t) \nonumber \\&\quad \leqslant - \frac{1}{{t - {t_k}}}{\varsigma ^T}(t)(M_1^T{Q_1}{M_1} + 3M_2^T{Q_1}{M_2})\varsigma (t) \nonumber \\&\qquad + ({h_k} - (t - {t_k})){{\dot{x}}^T}(t){Q_1}\dot{x}(t) \nonumber \\&\quad \leqslant {\varsigma ^T}(t)( - W_1^T{M_1} - M_1^T{W_1} + (t - {t_k})W_1^T Q_1^{ - 1}{W_1} \nonumber \\&\qquad - 3W_2^T{M_2} - 3M_2^T{W_2} + 3(t - {t_k})W_2^T Q_1^{ - 1}{W_2})\varsigma (t) \nonumber \\&\qquad + ({h_k} - (t - {t_k})){{\dot{x}}^T}(t){Q_1}\dot{x}(t). \end{aligned}$$

(28)

By the Jensen’s inequality, we can obtain

$$\begin{aligned}&- \delta \int _{t - \delta }^t {{{\dot{x}}^T}(s){R_1}\dot{x}(s)ds} \nonumber \\&\quad \leqslant - {(\int _{t - \delta }^t {{{\dot{x}}^T}(s)ds} )^T}{R_1}\int _{t - \delta }^t {{{\dot{x}}^T}(s)ds} \nonumber \\&\quad = - {(x(t) - x(t - \delta ))^T}{R_1}(x(t) - x(t - \delta )), \end{aligned}$$

(29)

then,

$$\begin{aligned}&{{\dot{V}}_3}(t)\leqslant {h^2}{\dot{x}^T}(t){S_1}\dot{x}(t)+{\delta ^2}{{\dot{x}}^T}(t){R_1}\dot{x}(t)\nonumber \\&\quad \; - \frac{{{\pi ^2}}}{4}{(x(t - \delta ) - x({t_k} - \delta ))^T}{S_1}(x(t - \delta ) \nonumber \\&\quad - x({t_k} - \delta )) - {(x(t) - x(t - \delta ))^T} \nonumber \\&\quad \times {R_1}(x(t) - x(t - \delta )). \end{aligned}$$

(30)

According to system (10) with $\omega (t)=0$, for a matrix $H \in \mathcal {R}^{n \times n}$, we have

$$\begin{aligned}&2\sum \limits _{i = 1}^4 {} \sum \limits _{q = 1}^4 {{h_i}(\theta (t)){h_q}(\theta ({t_k}))({\varsigma ^T}(t){\phi _1}(} - \dot{x}(t) + {A_i}x(t) \nonumber \\&\quad + {B_i}{K_{1q}}x({t_k}) + {B_i}{K_{2q}}x({t_k} - \delta )))) = 0. \end{aligned}$$

(31)

According to (22), (28), (30) and (31), we can derive

$$\begin{aligned} \dot{V} (t)\leqslant & {} {\varsigma ^T}(t){\Omega (t) }\varsigma (t) \nonumber \\= & {} {\varsigma ^T}(t)({\Omega _1} + ({h_k} - (t - {t_k})){\Omega _2} \nonumber \\&+ (t - {t_k}){\Omega _3})\varsigma (t), \end{aligned}$$

(32)

where ${\Omega _3} = W_1^T{Q_1}^{ - 1}{W_1} + 3W_2^T{Q_1}^{ - 1}{W_2}$.

Since $\Omega (t)$ is the convex combination of $t-t_k$ and $(h_k -(t - t_k))$, for $t \rightarrow {t_k}$ and $t \rightarrow h_k + t_k$, we have $\mathop {\lim }\limits _{t \rightarrow {t_k}} \Omega (t) = {\Omega _1} + {h_k}{\Omega _2}$ and $\mathop {\lim }\limits _{t \rightarrow {h_k} + {t_k}} \Omega (t) = {\Omega _1} + {h_k}{\Omega _3}$, by the Schur complement lemma, from (16) and (17), we can obtain

$$\begin{aligned} V(t) \leqslant {\varsigma ^T}(t)\Omega (t)\varsigma (t) < 0. \end{aligned}$$

(33)

Then, the asymptotic stability of the closed-loop system (10) without disturbance can be ensured.

Next, taking the disturbance into consideration, the $\mathcal {H}_\infty$-gain performance of the system (10) will be analyzed in what follows.

Consider the following Lyapunov functional candidate:

$$\begin{aligned} \hat{V}(t) = \sum \limits _{i = 1}^3 {{\hat{V}_i}} , \end{aligned}$$

(34)

where

$$\begin{aligned} {\hat{V}_1}(t)= & {} {x^T}(t){P_2}x(t),\nonumber \\ { \hat{V}_2}(t)= & {} ({h_k} - (t - {t_k}))\int _{{t_k}}^t {{{\dot{x}}^T}(s){Q_2}\dot{x}(s)} ds,\nonumber \\ {\hat{V}_3}(t)= & {} {h^2}{\dot{x}^T}(t){S_2}\dot{x}(t) - \frac{{{\pi ^2}}}{4}(x(t - \delta ) \nonumber \\&- x({t_k} - \delta ))^T S_2 (x(t - \delta ) - x({t_k} - \delta ))\nonumber \\&+\delta \int _{ - \delta }^0 {} \int _{t + \theta }^t {{{\dot{x}}^T}(s){R_2}\dot{x}(s)dsd\theta }, \end{aligned}$$

(35)

in which matrices $P_2>0$, $Q_2>0$, $S_2>0$ and $R_2>0$ are to be determined.

Similar the process from (21) to (32), we have

$$\begin{aligned} \dot{\hat{V}}(t)\leqslant & {} {\xi ^T}(t){\hat{\Omega } (t) } \xi (t) \nonumber \\ =&{\xi ^T}(t) \bigl [ {\hat{\Omega } _1} + ({h_k} - (t - {t_k})){ \hat{\Omega } _2} \nonumber \\&+(t - {t_k}){\hat{\Omega }_3} )\bigr ]\xi (t), \end{aligned}$$

(36)

where ${\xi ^T}= \left( {\begin{array}{*{20}{c}} {{\varsigma ^T}(t)}&{\omega ^T (t)} \end{array}} \right)$ and ${\hat{\Omega } _3} = {\hat{W}}_1^T{Q_2}^{ - 1}{{\hat{W}}_1} + 3{\hat{W}}_2^T{Q_2}^{ - 1}{{\hat{W}}_2}$.

From (10), we have

$$\begin{aligned}&z_1^T(t){z_1}(t) \leqslant \nonumber \\&\quad \; \sum \limits _{i = 1}^4 {} \sum \limits _{q = 1}^4 {{h_i}(\theta (t)){h_q}(\theta ({t_k})){\xi ^T}(t){\eta ^T}\eta \xi (t)} , \end{aligned}$$

(37)

where $\eta = \left( {\begin{array}{*{20}{l}} {{C_{1i}}}&0&{{D_i}{K_{1q}}}&0&0&{{D_i}{K_{2q}}}&0 \end{array}} \right)$.

Then, we have

$$\begin{aligned}&\dot{\hat{V}}(t) + z_1^T(t){z_1}(t) - {\gamma ^2}{\omega ^T}(t)\omega (t)\nonumber \\&\quad \leqslant \sum \limits _{i = 1}^4 {} \sum \limits _{q = 1}^4 {{h_i}(\theta (t)){h_q}(\theta ({t_k}))({\xi ^T}(t)\hat{\Omega } (t)\xi (t)} \nonumber \\&\qquad + {\xi ^T}(t){\eta ^T}\eta \xi (t) - {\gamma ^2}{\omega ^T}(t)\omega (t)) \nonumber \\&\quad \leqslant \sum \limits _{i = 1}^4 {} \sum \limits _{q = 1}^4 {{h_i}(\theta (t)){h_q}(\theta ({t_k})){\xi ^T}\Xi {\xi ^T}(t)} , \end{aligned}$$

(38)

where $\Xi = \hat{\Omega }t) + {\eta ^T}\eta - {\hat{e}_7}{\gamma ^2}\hat{e}_7^T$.

We define

$$\begin{aligned} \mathcal {G}&= \int _0^\infty {{\xi ^T}(t)\Xi {\xi }(t)dt}\nonumber \\&= \int _0^\infty {{\xi ^T}(t){{({\Xi ^{\frac{1}{2}}})}^*}({\Xi ^{\frac{1}{2}}}){\xi }(t)dt} \nonumber \\&= \int _0^\infty {{L^*}(t)L(t)dt}, \end{aligned}$$

(39)

where $L(t)={\Xi ^{\frac{1}{2}}}\xi (t)$.

By the Fourier transform and Parseval equality, we can obtain

$$\begin{aligned} \mathcal {G}&= \frac{1}{{2\pi }}\int _{ - \infty }^\infty {{L_s}^*(\varpi ){L_s}(\varpi )d\varpi } \nonumber \\&= \frac{1}{{2\pi }}\int _{ - \infty }^\infty {{\xi _s}^*(\varpi )\Xi {\xi _s}(\varpi )d\varpi }, \end{aligned}$$

(40)

where ${{L_s}(\varpi )}$ and ${{\xi _s}(\varpi )}$ is the spectrum of L(t) and $\xi (t)$, respectively.

Suppose that

$$\begin{aligned} \Xi + \chi < 0, \end{aligned}$$

(41)

where $\chi = {\mathcal {F}^*}\Lambda \mathcal {F}$, $\mathcal {F} = \left( {\begin{array}{*{20}{l}} 0&{}I&{}0&{}0&{}0&{}0&{}0 \\ I&{}0&{}0&{}0&{}0&{}0&{}0 \end{array}} \right)$.

By Lemma 2, we have the inequality (41) is equivalent to

$$\begin{aligned} \xi _s^*(\varpi )\Xi \xi _s^{}(\varpi ) < 0,\forall \xi _s^{}(\varpi ) \in {{\mathbf {R}}_1}, \end{aligned}$$

(42)

where ${{\mathbf {R}}_1} = \{ \xi _s^{}(\varpi ) \in \mathbb {C}\left| {\xi _s^{}(\varpi ) \ne 0,} \right. \xi _s^*(\varpi ) \chi \xi _s^{}(\varpi ) \geqslant 0\}$.

From [40], we can obtain the set ${{\mathbf {R}}_1}$ is equivalent to ${{\mathbf {R}}_2} = \{ \xi _s^{}(\varpi ) \in \mathbb {C}\left| {\xi _s^{}(\varpi ) \ne 0,} \right. {T_\varpi }\mathcal {F}\xi _s^{}(\varpi ) = 0,\varpi \in ({\varpi _1},{\varpi _2})\} ,$ where ${T_\varpi } = \left( {\begin{array}{*{20}{c}} I&{ - j\varpi I} \end{array}} \right)$.

Then, we can derive

$$\begin{aligned} \xi _s^*(\varpi )\Xi \xi _s^{}(\varpi ) < 0,\forall \varpi \in ({\varpi _1},{\varpi _2}), \end{aligned}$$

(43)

which implies $\mathcal {G}<0$.

Since $\hat{\Omega }(t)$ is the convex combination of $t-t_k$ and $(h_k -(t - t_k))$, for $t \rightarrow {t_k}$ and $t \rightarrow h_k + t_k$, we have $\mathop {\lim }\limits _{t \rightarrow {t_k}} \hat{\Omega } (t) = {\hat{\Omega } _1} + {h_k}{\hat{\Omega }_2}$, and $\mathop {\lim }\limits _{t \rightarrow {h_k} + {t_k}} \hat{\Omega } (t) = {\hat{\Omega } _1} + {h_k}{\hat{\Omega }_3}$, by the Schur complement lemma, from (18) and (19), we can ensure (41) holds. Thus, by (38), (40) and (43), we have

$$\begin{aligned}&\dot{\hat{V}}(t) + z_1^T(t){z_1}(t) - {\gamma ^2}{\omega ^T}(t)\omega (t) \nonumber \\&\;\; \leqslant {{\xi ^T}}(t)\Xi {\xi } (t) < 0, \end{aligned}$$

(44)

which yields that ${\left\| {{z_1}(j\varpi )} \right\| _2} < \gamma {\left\| {\omega (j\varpi )} \right\| _2}$, $\varpi \in ({\varpi _1},{\varpi _2})$.

In the following, we will discuss the constraint output condition iii). From (44), we have

$$\begin{aligned} {\dot{\hat{V}}}(t) < \gamma ^2 {\omega ^T}(t)\omega (t). \end{aligned}$$

(45)

Integrating the above inequality on both sides from 0 to t, we can obtain

$$\begin{aligned} {\hat{V}}(t) - {\hat{V}}(0)&< {\gamma ^2}\int _0^t {{\omega ^T}(t)\omega (t)} dt \nonumber \\&\leqslant {\gamma ^2}\left\| {\omega (t)} \right\| _2^2 = {\gamma ^2}{\omega _{\max }}, \end{aligned}$$

(46)

since $\hat{V}_2(t)$ and $\hat{V}_3(t)$ are positive, then $x^T(t)P_2x(t) <\vartheta$ with $\vartheta ={\hat{V}}(0) + {\gamma ^2}{\omega _{\max }}$.

Consider the constraint output,

$$\begin{aligned}&\mathop {\max }\limits _{t \geqslant 0} {\left\| {{{\{ {z_2}(t)\} }_r}} \right\| ^2} \\&\quad \leqslant \mathop {\max }\limits _{t0} {\left\| {\sum \limits _{i = 1}^4 {{h_i}(\theta (t)){x^T}(t)} \{ {C_{2i}}\} _r^T\{ {C_{2i}}\} _r^{}x(t)} \right\| _2}\\&=\mathop {\max }\limits _{t \geqslant 0} \Biggl \Vert {\sum \limits _{i = 1}^4 {h_i}(\theta (t)) x^T}(t) P_2^{\frac{1}{2}} P_2^{ - \frac{1}{2}} \{ {C_{2i}}\}_r^T \{ {C_{2i}}\}_r^{} \\&\;\; P_2^{- \frac{1}{2}} P_2^{\frac{1}{2}}x(t) \Biggr \Vert _2 \\ \leqslant&\vartheta {\lambda _{\max }} \biggl ( \sum \limits _{i = 1}^4 {{h_i}(\theta (t))} P_2^{\frac{1}{2}} P_2^{ - \frac{1}{2}}\{ {C_{2i}}\} _r^T\{ {C_{2i}}\} _r^{} \\&\;\; \times P_2^{ - \frac{1}{2}}P_2^{\frac{1}{2}} \biggr ),\; r = 1,2, \end{aligned}$$

where ${\lambda _{\max }}( \cdot )$ denotes the maximum eigenvalue.

From (20), by the Schur complement, we have

$$\begin{aligned} \vartheta P_2^{ - \frac{1}{2}}\{ {C_{2i}}\} _r^T\{ {C_{2i}}\} _r^{}P_2^{ - \frac{1}{2}} < I,r = 1,2, \end{aligned}$$

(47)

then,

$$\begin{aligned} \left| {{{\{ {z_2}(t)\} }_r}} \right| \leqslant 1,r=1,2, \end{aligned}$$

(48)

thus, $\mathop {\max }\limits _{t \geqslant 0} {\left\| {{{\{ {z_2}(t)\} }_r}} \right\| ^2} <1$ holds. Therefore, for the FF bound $\varpi \in [\varpi _1,\varpi _2 ]$, the closed-loop system (10) is asymptotically stable with $\mathcal {H}_\infty$ lever $\gamma$ and satisfies the constraint condition (12). The proof is completed. $\square$

Next, based on the result in Theorem 1, the fuzzy delayed sampled-data controller is designed as follows. In order to conduct the synthesis theorem, we define some notations first:

$$\begin{aligned} \mathcal {J}_1= & {} diag\{ {H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}}\},\\ \mathcal {J}_2= & {} diag\{ {H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}}\},\\ \mathcal {J}_3= & {} diag\{ {H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}}, \\&\;\; {H^{ - 1}}\},\\ \mathcal {J}_4= & {} diag\{ {H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},I,I\},\\ \mathcal {J}_5= & {} diag\{ {H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},{H^{ - 1}},I,{H^{ - 1}}, \\&\;\; {H^{ - 1}},I\},\\ \mathcal {J}_6= & {} diag\{I, {H^{ - 1}}\},\\ \bar{P}_1= & {} H^{-1}P_1H^{-T}, \bar{W}_1=\mathcal {J}_1{W_1}{H^{ - T}}, \\ \bar{W}_2= & {} \mathcal {J}_1{W_2}{H^{ - T}}, \bar{R}_1 =H^{-1}R_1H^{-T}, \\ \bar{Q}_1= & {} H^{-1}Q_1H^{-T},\bar{P}_2=H^{-1}P_2H^{-T},\\ \bar{Q}_2= & {} H^{-1}P_2H^{-T},\bar{\hat{W}}_1= \mathcal {J}_2{\hat{W}_1}{H^{ - T}}, \\ \bar{\hat{W}}_2= & {} \mathcal {J}_2{\hat{W}_2}{H^{ - T}}, \bar{R}_2 =H^{-1}R_2H^{-T}, \\ \bar{P}= & {} H^{-1}PH^{-T}, \bar{Q}=H^{-1}QH^{-T}, \bar{H} =H^{-1}. \end{aligned}$$

Theorem 2

Consider system (10), given positive scalars $\delta$, $\gamma$, $\alpha _l$, $\beta _m$, $l=1,2,3$, $m=1,2,3,4$ and $\vartheta$. If there exist positive-definite matrices $\bar{P}_r$, $\bar{Q}_r$, $\bar{S}_r$, $\bar{R}_r$, $r=1,2$ and $\bar{Q}$, symmetric matrix $\bar{P}$, and general matrices $\bar{W}_r$, ${\hat{\bar{W}}}_r$, $r=1,2$, $\bar{K}_{1q}$, $\bar{K}_{2q}$, $q=1,2,3,4$, and $\bar{H}$, such that

$$\begin{aligned}&{\bar{\Omega } _1} + {h_k}{\bar{\Omega } _2} < 0, \end{aligned}$$

(49)

$$\begin{aligned}&\left( {\begin{array}{*{20}{c}} {{{\bar{\Omega } }_1}}&{}{{h_k}{{\bar{W}}_1^T}}&{}{3{h_k}{{\bar{W}}_2^T}} \\ *&{}{ - {h_k}{{\bar{Q}}_1}}&{}0 \\ *&{}*&{}{ - 3{h_k}{{\bar{Q}}_1}} \end{array}} \right) < 0, \end{aligned}$$

(50)

$$\begin{aligned}&\left( {\begin{array}{*{20}{c}} {{{\bar{\Psi } }_1} + {h_k}{{\bar{\hat{\Omega }} }_2}}&{}{{{\bar{\eta } }^T}} \\ *&{}{ - I} \end{array}} \right) < 0, \end{aligned}$$

(51)

$$\begin{aligned}&\left( {\begin{array}{*{20}{c}} {{{\bar{\Psi } }_1}}&{}{{h_k}{{\bar{\hat{W}}}_1^T}}&{}{3{h_k}{{\bar{\hat{W}}}_2^T}}&{}{{{\bar{\eta } }^T}} \\ *&{}{ - {h_k}{{\bar{Q}}_2}}&{}0&{}0 \\ *&{}*&{}{ - 3{h_k}{{\bar{Q}}_2}}&{}0 \\ *&{}*&{}*&{}{ - I} \end{array}} \right) < 0, \end{aligned}$$

(52)

$$\begin{aligned}&\left( {\begin{array}{*{20}{c}} { - I}&{}{\sqrt{\vartheta } \{ {C_{2i}}\} _r^{}{{\bar{H}}^T}} \\ *&{}{ - {{\bar{P}}_2}} \end{array}} \right) < 0,r = 1,2, \end{aligned}$$

(53)

where

$$\begin{aligned} {\bar{\Omega } _1}= & {} {[{e_2}{\bar{P}_1}e_1^T]_s} - {[\bar{W}_1^T{ M_1}]_s} - {[3\bar{W}_2^T{ M_2}]_s} \\&+ {[{\bar{\phi } _1}{\bar{\varphi } _1}]_s}+ {\delta ^2}{e_2}{{\bar{R}}_1}{e_2}^T - ({e_1} - {e_5}){{\bar{R}}_1}{({e_1} - {e_5})^T},\\&+{h^2}{e_2}{\bar{S}_1}{e_2}^T - \frac{{{\pi ^2}}}{4}({e_5} - {e_6}){\bar{S}_1}{({e_5} - {e_6})^T},\\ \bar{\phi } _1^T= & {} \left( {\begin{array}{*{20}{l}} {\alpha _1 }&{\alpha _2 }&{0}&{0}&{0}&{\alpha _3} \end{array}} \right) , \\ {\bar{\varphi } _1}= & {} \left( {\begin{array}{*{20}{l}} {{A_i}\bar{H}^T}&{ - \bar{H}^T}&{{B_i}{\bar{K}_{1q}}}&0&0&{{B_i}{\bar{K}_{2q}}} \end{array}} \right) ,\\ {\bar{\Omega }_2}= & {} {e_2}{\bar{Q}_1}e_2^T, {M_1}= e_1^T-e_3^T, {M_2}= e_1^T+e_3^T-2e_4^T,\\ {\bar{\hat{\Omega }} _1}= & {} {[{\hat{e}_2}{\bar{P}_2}\hat{e}_1^T]_s} - {[{\bar{\hat{W}}}_1^T{{{\hat{ M}}_1}}]_s} - {[3{\bar{\hat{ W}}}_2^T{ {\hat{ M}}}_2}]_s \\&+ {[{\bar{\phi } _2}{\bar{\varphi }_2}]_s}+ {\delta ^2}{{\hat{e}}_2}{{\bar{R}}_2}{{\hat{e}}_2}^T - ({{\hat{e}}_1} - {{\hat{e}}_5}){{\bar{R}}_2}{({{\hat{e}}_1} - {{\hat{e}}_5})^T}, \\&+{h^2}{\hat{e}_2}{\bar{S}_2}{\hat{e}_2}^T - \frac{{{\pi ^2}}}{4}({\hat{e}_5} - {\hat{e}_6}){\bar{S}_2}{({\hat{e}_5} - {\hat{e}_6})^T},\\ {\bar{\Psi } _1}= & {} {\bar{\hat{\Omega }} _1} - {\hat{e}_7}{\gamma ^2}\hat{e}_7^T + \bar{\chi } \\ {\hat{M}}_1= & {} \hat{e}_1^T-\hat{e}_3^T, {\hat{M}}_2= \hat{e}_1^T+\hat{e}_3^T-2\hat{e}_4^T, {\bar{\hat{\Omega }} _2}={\hat{e}_2}{\bar{Q}_2}\hat{e}_2^T,\\ \bar{\phi } _2^T= & {} \left( {\begin{array}{*{20}{l}} {\beta _1 }&{\beta _2 }&{\beta _3}&{0}&{0}&{\beta _4}&{0} \end{array}} \right) ,\\ {\bar{\varphi } _2}= & {} \left( {\begin{array}{*{20}{l}} {{A_i\bar{H}^T}}&{ - \bar{H}^T}&{{B_i}{\bar{K}_{1q}}}&0&0&{{B_i}{\bar{K}_{2q}}}&{{E_i}} \end{array}} \right) ,\\ \bar{\eta }= & {} \left( {\begin{array}{*{20}{l}} {{C_{1i}}\bar{H}^T}&0&{{D_i}{\bar{K}_{1q}}}&0&0&{{D_i}{\bar{K}_{2q}}}&0 \end{array}} \right) ,\\ \bar{\chi }= & {} {\mathcal {F}^T}\bar{\Lambda }\mathcal {F},\bar{\Lambda }= \left( {\begin{array}{*{20}{c}} { - \bar{Q}}&{}{\bar{P} + j{\varpi _c}\bar{Q}} \\ *&{}{ - {\varpi _1}{\varpi _2}\bar{Q}} \end{array}} \right) ,\\ \mathcal {F}= & {} \left( {\begin{array}{*{20}{l}} 0&{}I&{}0&{}0&{}0&{}0&{}0 \\ I&{}0&{}0&{}0&{}0&{}0&{}0 \end{array}} \right) ,{\varpi _c}= \frac{{{{\varpi _1}} + {\varpi _2}}}{2} \end{aligned}$$

hold, then system (10) is asymptotically stable, and has $\mathcal {H}_\infty$-gain lever $\gamma$ for the FF $\varpi \in [{\varpi _1},{\varpi _2}]$. The constraint condition (12) is ensured with upper bound of the disturbance energy ${\omega _{\max }} = {{(\vartheta - \hat{V}(0))} / {{\gamma ^2}}}$. The controller gain matrices are $K_{1q}=\bar{K}_{1q} \bar{H}^{-T}$, $K_{2q}=\bar{K}_{2q} \bar{H}^{-T}$.

Proof

By using a congruence transformation to (16)–(20) by the full rank matrix $\mathcal {J}_1$, $\mathcal {J}_3$, $\mathcal {J}_4$, $\mathcal {J}_5$ and $\mathcal {J}_6$ on the left, $\mathcal {J}_1^T$, $\mathcal {J}_3^T$, $\mathcal {J}_4^T$, $\mathcal {J}_5^T$ and $\mathcal {J}_6^T$ on the right, respectively, we can obtain conditions (49)–(53). $\square$

Remark 4

According to the Parseval’s theorem, a signal from time domain is converted to frequency domain. Based on the frequency-domain analysis from the signal viewpoint, the proposed controller is with FF domain constraint. Compared with the designed controller for the EF domain, the FF constraint controller is more friendly to the drivers and passengers and can bring better system performance. The superior of the FF controller is also illustrated in the simulation part.

Remark 5

The transmission delay is considered in the controller (8) for the active suspension system. When the delay $\delta$ is set as 0, Theorem 2 can be degenerate to the case of fuzzy sampled-data control scheme, which is formulated as follows.

Corollary 1

Consider system (10), given positive scalars $\gamma$, $\alpha _l$, $\beta _m$, $l=1,2$, $m=1,2,3$ and $\vartheta$. If there exist positive-definite matrices $\bar{P}_r$, $\bar{Q}_r$, $r=1,2$ and $\bar{Q}$, symmetric matrix $\bar{P}$, and general matrices $\bar{W}_r$, ${\hat{\bar{W}}}_r$, $r=1,2$, $\bar{K}_{1q}$, $q=1,2,3,4$, and $\bar{H}$, such that for $h_k \in [0,h]$, (49)–(53) hold, where

$$\begin{aligned} {\bar{\Omega }_1}= & {} {[{{\tilde{e}}_2}{\bar{P}_1}{\tilde{e}}_1^T]_s} - {[\bar{W}_1^T{ M_1}]_s} - {[3\bar{W}_2^T{ M_2}]_s} + {[{\bar{\phi } _1}{\bar{\varphi }_1}]_s},\\ \bar{\phi }_1^T= & {} \left( {\begin{array}{*{20}{l}} {\alpha _1 }&{\alpha _2 }&{0}&{0} \end{array}} \right) , \\ {\bar{\varphi }_1}= & {} \left( {\begin{array}{*{20}{l}} {{A_i}\bar{H}^T}&{ - \bar{H}^T}&{{B_i}{\bar{K}_{1q}}}&0 \end{array}} \right) ,\\ {\bar{\Omega }_2}= & {} {{\tilde{e}}_2}{\bar{Q}_1}{\tilde{e}}_2^T, {M_1}= {\tilde{e}}_1^T-{\tilde{e}}_3^T, {M_2}= {\tilde{e}}_1^T+{\tilde{e}}_3^T-2{\tilde{e}}_4^T,\\ {\bar{\hat{\Omega }} _1}= & {} {[{\hat{\tilde{e}}_2}{\bar{P}_2}\hat{\tilde{e}}_1^T]_s} - {[{\bar{\hat{W}}}_1^T{{{\hat{ M}}_1}}]_s} - {[3{\bar{\hat{ W}}}_2^T{ {\hat{ M}}}_2}]_s + {[{\bar{\phi } _2}{\bar{\varphi } _2}]_s},\\ {\bar{\Psi } _1}= & {} {\bar{\hat{\Omega }} _1} - {\hat{\tilde{e}}_5}{\gamma ^2}\hat{\tilde{e}}_5^T + \bar{\chi }\\ {\hat{M}}_1= & {} \hat{\tilde{e}}_1^T-\hat{\tilde{e}}_3^T, {\hat{M}}_2= \hat{\tilde{e}}_1^T+\hat{\tilde{e}}_3^T-2\hat{\tilde{e}}_4^T, {\bar{\hat{\Omega }} _2}={\hat{\tilde{e}}_2}{\bar{Q}_2}\hat{\tilde{e}}_2^T,\\ \bar{\phi } _2^T= & {} \left( {\begin{array}{*{20}{l}} {\beta _1 }&{\beta _2 }&{\beta _3}&{0}&{0} \end{array}} \right) ,\\ {\bar{\varphi } _2}= & {} \left( {\begin{array}{*{20}{l}} {{A_i\bar{H}^T}}&{ - \bar{H}^T}&{{B_i}{\bar{K}_{1q}}}&0&{{E_i}} \end{array}} \right) ,\\ \bar{\eta }= & {} \left( {\begin{array}{*{20}{l}} {{C_{1i}}\bar{H}^T}&0&{{D_i}{\bar{K}_{1q}}}&0&0&{{D_i}{\bar{K}_{2q}}}&0 \end{array}} \right) ,\\ \bar{\chi }= & {} {\mathcal {F}^T}\bar{\Lambda } \mathcal {F},\bar{\Lambda }= \left( {\begin{array}{*{20}{c}} { - \bar{Q}}&{}{\bar{P} + j{\varpi _c}\bar{Q}} \\ *&{}{ - {\varpi _1}{\varpi _2}\bar{Q}} \end{array}} \right) ,\\ \mathcal {F}= & {} \left( {\begin{array}{*{20}{l}} 0&{}I&{}0&{}0&{}0 \\ I&{}0&{}0&{}0&{}0 \end{array}} \right) ,{\varpi _c}= \frac{{{{\varpi _1}} + {\varpi _2}}}{2} \end{aligned}$$

then system (10) without transmission delay $\delta$ is asymptotically stable, and has $\mathcal {H}_\infty$-gain lever $\gamma$ for the FF $\varpi \in [{\varpi _1},{\varpi _2}]$. The constraint condition (12) is ensured. The controller gain matrix is $K_{1q}=\bar{K}_{1q} \bar{H}^{-T}$.

Table 1 The minimum admissible $\gamma$ with different upper bounds of sampled-data periods

Remark 6

Note that the robust fuzzy delayed sampled-data control mechanism proposed in this paper is general and can also be applied to other practical system models, such as underwater fish tracking systems, robotics systems, power systems, and so on. The active vehicle suspension system investigated here is one possible real system in engineering.

4 Numerical examples

In this section, two examples are presented to testify the validity and superiority of the designed fuzzy sampled-data $\mathcal {H}_\infty$ control with transmission delay for an active quarter-suspension system. First, the performance of the proposed controller is illustrated, and both the EF constraint controller case and FF constraint controller case are shown for comparisons. Further, when the transmission delay is not considered in the controller (9), the system performance is demonstrated and compared the existing work.

Example 1

Consider the quarter-vehicle model shown in Fig. 1. Some vehicle parameters are given as follows: The sprung mass $m_s (t)$ is assumed to change within [300kg, 340kg], the unsprung mass $m_u (t)$ varies within [38kg, $42{}{}kg]$, the maximum admissible suspension stroke is chosen as $z_{max} = 80{}{} mm$, others are given as $\vartheta = 1$, $k_s=18000{}{}N/m$, $k_t=200000{}{}N/m$, ${c_s} = 1000 {}{}N \cdot s/m$ and $c_t=10 {}{}N \cdot s/m$.

First, select the upper bound of sampling intervals as $h=0.01{}{}s$, the considered transmission delay in the controller $\delta =0.05{}{}s$. Choose scalars $\alpha _1=1$, $\alpha _2=1$, $\alpha _3=1$, $\beta _1=1$, $\beta _2=1$, $\beta _3=2$ and $\beta _4=1$. By solving the matrix inequalities (49)–(53) in Theorem 2 with the constraint frequency band $[{\varpi _1},{\varpi _2}]$, where ${\varpi _1}=4{}{}Hz$ and ${\varpi _1}=8{}{}Hz$, we can calculate the minimum admissible $\mathcal {H}_\infty$ performance lever $\gamma ^{*}$ is 6.6381, and the designed controller gain matrices are

$$\begin{aligned} {K_{11}}&=[{ 17417.17127038}\ \ \ {5445.57510198}\\&\quad {399.35574708}\ \ \ {-314.13655779}],\\ {K_{21}}&= [{0.43273529}\ \ \ {245.47509305}\\&\quad {-29.05139338}\ \ \ { 3.24753998}],\\ {K_{12}}&= [{17417.17144684}\ \ \ {5445.57551073}\\&\quad { 399.35576533}\ \ \ {-314.13656878}],\\ {K_{22}}&= [{0.43258271}\ \ \ {245.47523874}\\&\quad {-29.05142152}\ \ \ { 3.24753733}],\\ {K_{13}}&= [{17417.17178006}\ \ \ {5445.57627825}\\&\quad {399.35579998}\ \ \ {-314.13658952}],\\ {K_{23}}&= [{0.43229452}\ \ \ {245.47550999}\\&\quad {-29.05147473}\ \ \ { 3.24753231}],\\ {K_{14}}&= [{17417.17169872}\ \ \ {5445.57609331}\\&\quad {399.35579138}\ \ \ { -314.13658447}],\\ {K_{24}}&= [{0.43236490}\ \ \ {245.47544587}\\&\quad {-29.05146170}\ \ \ { 3.24753353}]. \end{aligned}$$

By choosing different upper bounds of sampled-data periods h and solving the criteria of Theorem 2, based on the convex optimal method, we can obtain the minimum $\mathcal {H}_\infty$-gain performance levers $\gamma ^*$ for two cases, namely, the EF band constraint controller, the FF band constraint controller, which are shown in Table 1. It can be observed that a smaller h will lead to a smaller $\gamma ^*$, which means that stronger robustness can be achieved when the sampling frequency of the controller increases. Moreover, with the same h, the minimum admissible $\mathcal {H}_\infty$-gain performance lever under FF band constraint $\gamma ^*(FF)$ is smaller than that under EF band constraint $\gamma ^*(EF)$, which implies that the controller designed with the FF band constraint possesses a better $\mathcal {H}_\infty$ performance. Hence, Table 1 concludes that the FF band constraint controller proposed in this paper could reduce the conservatism effectively compared with the case of EE controller.

Next, we will show the effectiveness of the robust fuzzy delayed sampled-data controller designed in this paper. Consider the case of a periodic road bump input which is expressed as follows:

$$\begin{aligned} \omega (t) = \left\{ {\begin{array}{*{20}{l}} {0.4\sin (5\pi t),{} {} {} {} if0 \leqslant t \leqslant {0.2},} \\ {0,{} {} {} if{} {} {} t > \mathrm{0.2}.} \end{array}} \right. \end{aligned}$$

By Theorem 2, we can obtain the EF band constraint controller gain matrices as

$$\begin{aligned} {K_{11}}= & {} [{16876.21717184}{} {14703.58119733}\\&{-152.04983199}{} { 227.47910632}],\\ {K_{21}}= & {} [{68.05040263}{} {624.14684765}\\&{31.81403432}{} {37.37333087}],\\ {K_{12}}= & {} [{ 16876.21727042}{} {14703.58087411}\\&{-152.04972210}{} { 227.47911652}],\\ {K_{22}}= & {} [{68.05032668}{} {624.14718936}\\&{31.81391217}{} {37.37332877}],\\ {K_{13}}= & {} [{16876.21734521}{} {14703.58068785}\\&{-152.04964909}{} { 227.47912280}],\\ {K_{23}}= & {} [{68.05026489}{} {624.14742134}\\&{31.81383042}{} {37.37332751}],\\ {K_{14}}= & {} [{16876.21732861}{} {14703.58070819}\\&{-152.04966149}{} { 227.47912192}],\\ {K_{24}}= & {} [{68.05027968}{} {624.14738016}\\&{31.81384442}{} {37.37332768}]. \end{aligned}$$

Fig. 2

The dynamics of the passive system and closed-loop system of Example 1

Fig. 3

Body acceleration

The bump response results are shown in Figs. 2, 3, 4, 5 and 6. Figure 2 shows the system states of the passive system and closed-loop system with FF band constrain controller, including the curves of suspension deflection, tire deflection, sprung mass speed, and unsprung mass speed. It can be seen that the closed-loop system can converge asymptotically with the proposed controller. Figure 3 provides the curve of body vertical acceleration for passive systems and closed-loop systems with FF and EF band constraint controllers, respectively. It can be found from Fig. 3 that the body acceleration of closed-loop systems is more stable than that of the open-loop systems, which illustrates the usefulness of the proposed controller strategy. The change of the body acceleration with FF band constraint controller is smoother than that with EF band constraint controller, which implies that a better riding comfort can be achieved by the proposed controller. The suspension deflection constraint response is shown in Fig. 4 and the tire deflection constraint response is shown in Fig. 5. It can be observed that the suspension deflection is below the maximum allowable suspension stroke, and the rate of tire deflection and the maximum restriction is less than 1, which means that the suspension deflection constraint and the road holding performance for both EF controller and FF controller can be ensured. The control input is shown in Fig. 6. Hence, the proposed FF band constraint controller is effective to ensure the stability of the suspension system with $\mathcal {H}_\infty$ performance, and compared with the EF controller, the FF one significantly has a better performance.

Fig. 4

Suspension deflection constraint response

Fig. 5

Tire deflection constraint response

Fig. 6

The control input of Example 1

Fig. 7

The dynamics of the passive system and closed-loop system of Example 2

Fig. 8

Body acceleration

Fig. 9

Suspension deflection constraint response

Fig. 10

Tire deflection constraint response

Fig. 11

The control input of Example 2

Furthermore, in order to illustrate the superiority of this study, when the transmission delay in the controller is not considered, the fuzzy sampled-data controller performance is compared with the one in [35].

Example 2

The system data are set as those in [35]. The sprung mass $m_s (t)$ is change within [950kg, 996kg], the unsprung mass $m_u (t)$ is within [110kg, $118{}{}kg]$, others are given as $z_{max} = 100{}{} mm$, $\vartheta = 1$, $k_s=42720{}{}N/m$, $k_t=101115{}{}N/m$, ${c_s} = 1095 {}{}N \cdot s/m$ and $c_t=14.6 {}{}N \cdot s/m$. The upper bound of sampling intervals as $h=0.01{}{}s$. Choose scalars $\alpha _1=1$, $\alpha _2=1$, $\beta _1=1$, $\beta _2=1$ and $\beta _3=1$. By Corollary 1, we can obtain the fuzzy sampled-data controller with FF domain constraint as

$$\begin{aligned} {K_{11}}= & {} [{41886.9909505453}{} {2851.1096147340}\\&{-329.8605565996}{} { -669.1244889522}],\\ {K_{12}}= & {} [{41886.9909505474}{} {2851.1096147342}\\&{-329.8605565928}{} {-669.1244889520}],\\ {K_{13}}= & {} [{41886.9909505433}{} {2851.1096147325}\\&{-329.8605565964}{} { -669.1244889519}],\\ {K_{14}}= & {} [{ 41886.9909505445}{} {2851.1096147344}\\&{-329.8605565990}{} { -669.1244889520}], \end{aligned}$$

the minimum allowable $\mathcal {H}_\infty$ performance lever $\gamma ^{*}$ is 2.2199, which is much smaller than that in [35] ($\gamma ^{*}=6.5700$). Figs. 7, 8, 9, 10 and 11 demonstrate bump response results. Figure 7 shows the dynamics of the passive system and closed-loop system with FF band constrain controller, which confirms the closed-loop system can converge asymptotically with the proposed controller. It can be observed from Fig. 8 that an improved ride comfort can be achieved via the designed controller in this paper than that in [35]. Figures 9 and 10 show that the relative suspension travel and the tire deflection are simultaneously satisfied. The control input is shown in Fig. 11. Hence, compared with the controller in [35], the proposed controller in this paper possesses an improved performance obviously.

Based on the above simulation results, it can be concluded that the robust fuzzy delayed sampled-data control with the FF domain can ensure the asymptotical stability and $\mathcal {H}_\infty$ performance, and satisfies the suspension constrained requirements effectively. Compared with the existing controller for active suspension systems, better performance can be achieved. Hence, the effectiveness and superiority of the proposed controller scheme are validated.

5 Conclusion

This article studies the T-S fuzzy delayed sampled-data $\mathcal {H}_\infty$ control problem for a class of intelligent suspension systems with varying vehicle load and frequency-domain constraints. The T-S fuzzy model is utilized to characterize the varying vehicle load. Considering the transmission delay, a robust fuzzy delayed sampled-data control mechanism is newly propounded for suspension systems. According to the Lyapunov stability theory, a useful theorem is proposed to guarantee the states of the active suspension system being asymptotically stabilized with the required $\mathcal {H}_\infty$ performance by the proposed controller. Moreover, the suspension constrained requirements are also satisfied within the FF domain. Finally, simulation examples are presented to attest to the usefulness of the proposed controller. For future study, inspired by [5, 41, 42], finite-time sampled-data T-S fuzzy control or sliding mode control of nonlinear systems and its applications to the wind energy conversion systems and chaotic systems would be further addressed.