Dynamic analysis of 1-dof and 2-dof nonlinear energy sink with geometrically nonlinear damping and combined stiffness

Abstract

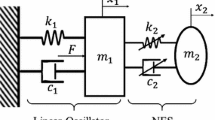
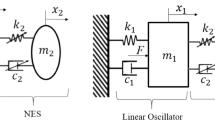
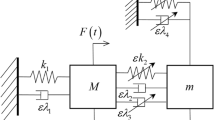
Nonlinear energy sink (NES) refers to a typical passive vibration device connected to linear or weakly nonlinear structures for vibration absorption and mitigation. This study investigates the dynamics of 1-dof and 2-dof NES with nonlinear damping and combined stiffness connected to a linear oscillator. For the system of 1-dof NES, a truncation damping and failure frequency are revealed through bifurcation analysis using the complex variable averaging method. The frequency detuning interval for the existence of the strongly modulated response (SMR) is also reported. For the system of 2-dof NES, it is reported in a similar bifurcation analysis that the mass distribution between NES affects the maximum value of saddle-node bifurcation. To obtain the periodic solution of the 2-dof NES system with the consideration of frequency detuning, the incremental harmonic balance method (IHB) and Floquet theory are employed. The corresponding response regime is obtained by Poincare mapping, it shows that the responses of the linear oscillator and 2-dof NES are not always consistent, and 2-dof NES can generate extra SMR than 1-dof NES. Finally, the vibration suppression effect of the proposed NES with nonlinear damping, and combined stiffness is analyzed and verified by the energy spectrum, and it also shows that the 2-dof NES system demonstrates better performance.

Appendix: Derivation of simplified system equations

The system equation is expressed as

$$\begin{aligned} \begin{aligned}&{{m}_{1}}{{{\ddot{x}}}_{1}}+{{k}_{1}}{{x}_{1}}+{{c}_{1}}{{{\dot{x}}}_{1}}+{{k}_{21}}({{x}_{1}}-{{x}_{2}}) \\&\quad +{{k}_{23}}{{({{x}_{1}}-{{x}_{2}})}^{3}}+{{c}_{2}}{{({{{\dot{x}}}_{1}}-{{{\dot{x}}}_{2}})}^{3}}={{F}_{0}}\cos (wt) \\&{{m}_{2}}{{{\ddot{x}}}_{2}}+{{k}_{21}}({{x}_{2}}-{{x}_{1}})+{{k}_{23}}{{({{x}_{2}}-{{x}_{1}})}^{3}}\\&\quad +{{c}_{2}}{{({{{\dot{x}}}_{2}}-{{{\dot{x}}}_{1}})}^{3}}=0 \end{aligned} \end{aligned}$$

(A.1)

To transform Eq. (A.1) into a dimensionless form, the following coordinate transformations are introduced

$$\begin{aligned} \bar{t}=\sqrt{\frac{{{k}_{1}}}{{{m}_{1}}}}\text { }t,\text { }{{\bar{x}}_{i}}={{x}_{i}},\text { }\bar{w}=w\sqrt{\frac{{{m}_{1}}}{{{k}_{1}}}} \end{aligned}$$

(A.2)

Letting $c_1 = 0$, by defining the following variables

$$\begin{aligned} \begin{aligned}&\frac{{{k}_{21}}}{{{k}_{1}}}=\varepsilon {{k}_{221}},\quad \frac{{{k}_{23}}}{{{k}_{1}}}=\varepsilon {{k}_{223}},\quad \frac{{{c}_{2}}}{{{m}_{1}}}\sqrt{\frac{{{k}_{1}}}{{{m}_{1}}}}=\varepsilon \lambda \\&\frac{{{m}_{2}}}{{{m}_{1}}}=\varepsilon ,\quad \qquad \frac{{{F}_{0}}}{{{k}_{1}}}=\varepsilon A \end{aligned} \end{aligned}$$

(A.3)

and substituting Eqs. (A.2) and (A.3) into Eq. (A.1), we have

$$\begin{aligned} \begin{aligned}&{{{\ddot{x}}}_{1}}+{{x}_{1}}+\varepsilon {{k}_{221}}({{x}_{1}}-{{x}_{2}})+\varepsilon {{k}_{223}}{{({{x}_{1}}-{{x}_{2}})}^{3}} \\&\quad +\varepsilon \lambda {{({{{\dot{x}}}_{1}}-{{{\dot{x}}}_{2}})}^{3}}=\varepsilon A\cos (wt) \\&{{{\ddot{x}}}_{2}}+{{k}_{221}}({{x}_{2}}-{{x}_{1}})+{{k}_{223}}{{({{x}_{2}}-{{x}_{1}})}^{3}}+\lambda {{({{{\dot{x}}}_{2}}-{{{\dot{x}}}_{1}})}^{3}}=0 \\ \end{aligned} \end{aligned}$$

(A.4)