Order and chaos around resonant motion in librating spring–mass–spherical pendulum

Abstract

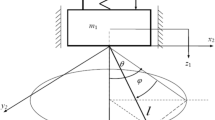
Using both analytical and numerical techniques, we investigate the 3-degree-of-freedom, autonomous, autoparametric, Hamiltonian spring–mass–pendulum system in libration and reveal the order–chaos–order transition with the change in the ratio of frequencies of corresponding independent normal modes. In the process, we also present an integrable limit of it and find all the three independent constants of motion. Furthermore, we study the possibility of the precession of the swing plane of the constituent spherical pendulum and the related energy exchanges between the modes at the autoparametric resonance. We use the method of the fast Lyapunov indicators to characterise and distinguish the order and the chaos in the system.

Appendix: Comparison with the numerical solutions of exact system

To ascertain the robustness of the perturbative techniques and various other approximations made in Sect. 5, we must compare the unmodulated and modulated solutions with the numerical integration of the exact equations of motion of the SMSP. Comparing these two solutions, we see that the perturbative solutions of the unmodulated and modulated cases closely match the solutions of the exact system. To this end, we present Fig. 9 similar to Fig. 3, except for the fact that here we use exact equations of motion (Eqs. 2a–2c) instead of the approximated equations of motion (Eqs. 26a–26c). We use the same initial conditions as used in Fig. 3.

Fig. 9

Precession of the swing plane about the z- axis is observed. Here, we compare the unmodulated and the modulated solutions with the numerical solutions of the exact system (Eqs. 2a–2c). The first column depicts the results for the unmodulated solutions (subplots (a)–(e)), while the second column shows the results for the modulated solution (subplots (f)–(g)). Subplot (a) and subplot (f) depict the precession about the z-axis in the unmodulated case and the modulated case, respectively. In subplots (b) and (g), we, respectively, plot $\rho \equiv \sqrt{x^2+y^2}$ versus t for the unmodulated and the modulated solutions in dark red; the amplitudes A (black solid line) and B (black dashed line) closely follow the extrema of $\rho$. Similarly, in subplots (e) and (j), we plot z versus t for both the cases in dark red. Here also, the amplitude C (green solid line) closely follows the extremum of z. Here, $\alpha$ is fixed at 0.3

In Fig. 9a, we observe a precession of $90^\circ$ in the x-y plane, on integrating up to $t=836$ units, as observed in Fig. 3a. Additionally, it may be noted (as shown in Fig. 9b) that similar to Fig. 3b, here also, A and B closely follow, respectively, the maxima and the minima of $\rho \equiv \sqrt{x^2+y^2}$,the radial distance from the z-axis. In Fig. 9c–e, we plot the time series for x, y and z of exact system. Also, C follows the extrema of z as can be seen in Fig. 9e.

In Fig. 9f, we observe a precession of the swing plane in the clockwise sense for the exact system. Additionally, in Fig. 9g, j, respectively, we see that analytically calculated (using Eqs. (33a)–(33f)) A and B closely follow the extrema of the numerically found $\rho$ using the equations of motion of the exact system and the solution for C obtained from the modulated equations also closely follows the extrema of z for the exact system.