Locating order-chaos-order transition in elastic pendulum

Abstract

An undamped elastic pendulum being a nonintegrable Hamiltonian system always has some chaotic trajectories observable on choosing appropriate initial conditions. This is true even if the pendulum is in libration with small amplitude; in this situation, the pendulum may be seen as a nearly integrable system. Since the measure of the set of the local chaotic trajectories in the phase space may be very small, the trajectories are hard to locate. However, the emergence of widespread chaos when the elastic pendulum is at autoparametric resonance is well-documented. The transition from the local and the widespread chaos is typically established through the Chirikov overlap criterion that approximates the phase portrait around a resonance using a one degree-of-freedom pendulum Hamiltonian. We argue in this paper that the aforementioned transition in the elastic pendulum is due to interaction between two resonances of same kind and their coexistence can be analytically located using perturbation methods, like the method of averaging, whereas the technique of the pendulum Hamiltonian is inapplicable. Furthermore, in the course of validating the result numerically, we also showcase the order-chaos-order transition in the elastic pendulum using the fast Lyapunov indicator.

Appendices

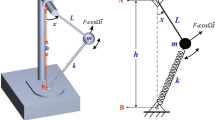
A Pendulum model in planar elastic pendulum

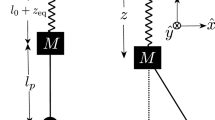
Let $l+\delta r$ and $\theta$ denote the radial and the polar coordinates respectively, and $p_r$ and $p_{\theta }$ denote the corresponding conjugate momenta. Under the small amplitude approximation (i.e., $\delta r\ll l$ and $\theta \rightarrow 0$), the Hamiltonian of the planar elastic pendulum [7, 33, 56] in the plane polar coordinates—up to the cubic-order terms—can be written as,

$$\begin{aligned}&H(\delta r,\theta ,p_r,p_{\theta })\nonumber \\&\quad = \frac{p_{\theta }^2}{2ml^2}+ \frac{p_r^2}{2m}+ mgl(1-\cos \theta ) \nonumber \\&\qquad + \frac{1}{2}k_s \delta r^2 + H_{\text {pert}}(\delta r,\theta ,p_r,p_{\theta })+E_{\text {min}}, \end{aligned}$$

(30)

where $H_{\text {pert}} \equiv -{p_{\theta }^2\delta r}/{ml^3}+m g \delta r(1-\cos \theta )$.

Let the action-angle variables [38, 39, 41] for the unperturbed Hamiltonian be $(J_p^0,\phi _p^0,J_s^0,\phi _s^0)$ so that in the libration regime, the perturbative part of Hamiltonian, $H_{\text {pert}}$, becomes [7, 39, 40],

$$\begin{aligned} H_{\text {pert}}= & {} \frac{\pi ^2}{K(k)^{2}}6mgA_s \sum _{n=1}^{\infty } C_n \left[ \sin (2n\phi _p^0-\phi _s^0)\right. \nonumber \\&\left. -\sin (2n\phi _p^0+\phi _s^0)\right] \nonumber \\&-4mgA_s \frac{E(k)-{k^\prime }^2K(k)}{K(k)} \sin \phi _s^0\nonumber \\&+2mg A_s \frac{K(k) - E(k)}{K(k)} \sin \phi _s^0 \end{aligned}$$

(31)

here, $k^2 \equiv [{p_{\theta }^2}/{2ml^2}+ mgl(1-\cos \theta )]/2mgl$, K(k) is the complete elliptic integral [57, 58] of first kind, E(k) is the complete elliptic integral of second kind, $C_n\equiv nq^n/(1-q^{2n})$ with $q \equiv \exp (-\pi K(\sqrt{1-k^2})/K(k))$, and $A_s\equiv \sqrt{2 J_s^0/m \omega _s^0}$ with $J_s^0 = [{p_r^2}/{2m}+ k_s \delta r^2/2]/\omega _s^{0}$ where $\omega _s^0=\sqrt{k_s/m}$. Furthermore,

$$\begin{aligned}&J_p^0 = \frac{8ml^2\omega _p^{0}}{\pi }\left[ E(k)-(1-k^2)K(k) \right] , \end{aligned}$$

(32a)

$$\begin{aligned}&\phi _s^0 = \sin ^{-1}\left( \sqrt{\frac{m \omega _s^0}{2 J_s^0}}\delta r\right) , \end{aligned}$$

(32b)

$$\begin{aligned}&\phi _p^0 = \frac{\pi }{2K(k)}F\left( \frac{1}{k}\sin \frac{\theta }{2};k \right) , \end{aligned}$$

(32c)

where $\omega _p^0=\sqrt{g/l}$ and F(k) is incomplete elliptic integral of the first kind [57, 58]. The frequency, $\varOmega _p^0(k)$, corresponding to the unperturbed pendulum is given by $\varOmega _p^0(k) = \pi \omega _p^0/2K(k)$.

Now we look for the resonances in the planar elastic pendulum. The resonance condition [7, 59, 60] in the planar elastic pendulum is given by,

$$\begin{aligned}&n_p\dot{\phi }_p^0-n_s\dot{\phi }_s^0=0\, \end{aligned}$$

(33)

To locate the approximated position of an $n_p:n_s$ resonance in the planar elastic pendulum in the phase space using the pendulum model, one needs to keep the corresponding isolated resonance term in the perturbative part of the Hamiltonian (Eq. 31). To find dominating 2:1 resonance, we work with the following truncated Hamiltonian, obtained using Eq. (30),

$$\begin{aligned} H= & {} J_s^0\omega _s^0+2 (m g k)^2 \frac{\mu }{k_s} + 6 m g \frac{q}{1-q^2}\sqrt{\frac{2 J_s^0}{m \omega _s^0}}\nonumber \quad \\&\times \frac{\pi ^2}{K(k)^2}\sin (2\phi _p^0-\phi _s^0)+E_{\text {min}}\, \end{aligned}$$

(34)

The positions of the two centers and the two saddles of the 2:1 resonance can be found using Eqs. (33) and (34) together. In $\theta$-$p_{\theta }$ plane ($\phi _s^0=0$), their location is specified by $\phi _p^0=(2j+1)\pi /4$ (mod $2\pi$), where $j\in \lbrace 0,1,2,\dots \rbrace$. The fixed points at $j=0$ and $j=2$ correspond to the two centers of the 2:1 resonance, and that at $j=1$ and $j=3$ correspond to the saddle points of the same 2:1 resonance. However, numerically it has been observed  [7] that there actually are two 2:1 resonances: Only one of the resonances matches with the above analytical prediction. This issue is expected to persist even for the elastic pendulum even if one manages to go through the involved algebra.

B Method of averaging: planar elastic pendulum

For the sake of completeness of the paper’s narrative, we present here the analogous study of the 2:1 resonance in the planar elastic pendulum using the method of averaging.

We start with the approximated Hamiltonian of the planar elastic pendulum [5, 7, 8] constrained to librate in x-z plane:

$$\begin{aligned}&H_\mathrm{PEP}\approx \frac{p_x^2}{2m}+\frac{p_z^2}{2m}+\frac{1}{2}m\left( \omega _{10}^2x^2+\omega _{20}^2z^2\right) \nonumber \\&\qquad + m\nu _1x^2z+E_{\text {min}}\,. \end{aligned}$$

(35)

The corresponding equations of motion are:

$$\begin{aligned}&\ddot{x}+\omega _{10}^2x+2\nu _1 x z=0\,, \end{aligned}$$

(36a)

$$\begin{aligned}&\ddot{z}+\mu \omega _{10}^2 z+2\nu _1 x^2=0\, \end{aligned}$$

(36b)

We can import the calculation steps done in the context of the elastic pendulum to the analogous ones for the planar elastic pendulum by substituting $a_y=0$ in Eqs. (18a)–(18c) and obtain,

$$\begin{aligned}&\dot{a}_x\sin (t+\beta _x)+\dot{\beta }_xa_x\cos (t+\beta _x)\nonumber \\&\qquad =2\epsilon \nu _1a_xa_z\cos (t+\beta _x)\cos (2t+\beta _z)\,, \end{aligned}$$

(37a)

$$\begin{aligned}&\dot{a}_z\sin (2t+\beta _z)+\dot{\beta }_za_z\cos (2t+\beta _z)\nonumber \\&\qquad =\epsilon \frac{\varDelta }{2}a_z\cos (2t+\beta _z)\nonumber \\&\quad \qquad +\epsilon \nu _1a_x^2\cos ^2(t+\beta _x)\,. \end{aligned}$$

(37b)

On repeating the similar steps done in Sect. 4, we arrive at,

$$\begin{aligned}&\dot{a}_x=-\frac{\nu _1}{2}a_xa_z \sin \chi , \end{aligned}$$

(38a)

$$\begin{aligned}&\dot{a}_z=\frac{\nu _1}{8}a_x^2\sin \chi ,\end{aligned}$$

(38b)

$$\begin{aligned}&\dot{\chi }\equiv \dot{\beta }_z-2\dot{\beta }_x=\frac{\varDelta }{4}+\frac{\nu _1}{8}\frac{a_x^2}{a_z}\cos \chi -\nu _1a_z\cos \chi .\nonumber \\ \end{aligned}$$

(38c)

Now we note that $\chi ^{\star }=j\pi$ ($j\in \mathbb {Z}$) is must for the non-trivial (non-zero) values of the amplitudes $(a_x^\star ,a_z^\star )$ at the fixed points of Eqs. (38a)–(38c). To ascertain what $(a_x^\star ,a_z^\star )$ should be, it is convenient to do the following transformation: $a_x \equiv \rho \sin \psi$ and $a_z\equiv \left( \rho /2\right) \cos \psi$; and use them to rewrite Eqs. (38a)–(38c) as follows:

$$\begin{aligned}&\dot{\rho }=0\,,\end{aligned}$$

(39a)

$$\begin{aligned}&\dot{\psi }=-\frac{\nu _1}{2}\rho \sin \chi \sin \psi \,,\end{aligned}$$

(39b)

$$\begin{aligned}&\dot{\chi }=\frac{\varDelta }{4}+\frac{\nu _1}{4}\frac{\rho \sin ^2\psi }{\cos \psi }\cos \chi -\frac{\nu _1 \rho }{2}\cos \psi \cos \chi \,.\nonumber \\ \end{aligned}$$

(39c)

By equating Eqs. (39a)–(39c) to zero for the equilibrium solutions, we notice that the following condition must be fulfilled for the existence of $(a_x^\star ,a_z^\star )$:

$$\begin{aligned}&\cos \psi ^{\star }=\frac{\pm \varDelta + \sqrt{\varDelta ^2 + 12 {\rho ^\star }^2 \nu _1^2}}{6 \rho ^\star \nu _1}\,, \end{aligned}$$

(40)

with the upper sign when $j=2\tilde{j}$ ($\tilde{j}\in \mathbb {Z}$) and with the lower sign when $j=2\tilde{j}+1$ ($\tilde{j}\in \mathbb {Z}$). The star in the superscript indicates a fixed point.

For amplitudes to be positive, the value of $\psi ^\star _z$ varies between 0 and $\pi /2$ which gives condition, $\varDelta /(2 \rho ^\star \nu _1)\le 1$, for the upper sign and condition, $-1\le \varDelta /(2 \rho ^\star \nu _1)$, for the lower sign in Eq. (40) to make sense. Consequently, the condition for coexistence of two distinct 2:1 resonant solutions is:

$$\begin{aligned}&-1\le \frac{\varDelta }{2 \rho ^\star \nu _1}\le 1. \end{aligned}$$

(41)

Fig. 6

Coexistence of two 2:1 resonances in planar elastic pendulum. The curves represent the values of amplitudes, $a_x$ and $a_y$, obtained as the fixed points analysis up to the first order using method of averaging. The cyan and the magenta colours respectively correspond to the resonant solutions for the upper and the lower signs in Eq. (40). The stars and the triangles are the numerically extracted values of resonance centers from the corresponding Poincaré sections at some randomly chosen $\mu$-values. The left and the right vertical grey dashed lines respectively represent the lower and the upper bounds of the coexistence condition given in inequality (41). Here, $R=-0.9$

Fig. 7

Order-chaos-order in the planar elastic pendulum. We exhibit the Poincaré sections in x-$p_x$ plane. Going from subplots (a)–(e), we vary $\mu$ from 3 to 5 in the steps of 0.5, while keeping R fixed at -0.9. The blue and the red colours denote the regular and the chaotic trajectories respectively

In the light of the discussion above, we now plot these two resonant solutions in $a_x$-$\mu$ space. We use Eq. (40) in $a^{\star }_x \equiv \rho ^\star \sin \psi ^{\star }$, where $\rho ^\star \equiv \sqrt{{a^\star _x}^2+{a^\star _z}^2}=\sqrt{-2(R+1)E_{\text {min}}}$, and plot $a^{\star }_x$ with varying $\mu$ at $R=-0.9$ in Fig. 6. We also compare it with the $a^{\star }_x$ calculated numerically at different values of $\mu$. The numerical values of $a^{\star }_x\equiv \sqrt{(x^2+p_x^2)}$ at a given $\mu$ may be calculated by extracting the resonance centers from Poincaré sections in x-$p_x$ plane. We observe that the resonance centers—extracted numerically from some randomly chosen Poincaré sections—are quite close to the analytically predicted values. For the Poincaré sections in x-$p_x$ plane, we solve the corresponding equations of motion of the planar elastic pendulum [Eqs. (36a)–(36b)] using various initial conditions at different fixed values of R and $\mu$, and take the section of trajectories in x-$p_x$ plane while fixing $z = 0$ and $p_z > 0$.

We also look for the order-chaos-order transition in the planar elastic pendulum with the help of the Poincaré section technique. In Fig. 7, we show the Poincaré sections at $R=-0.9$ for $\mu$ varying from 3 to 5. In Fig. 7a, at $\mu =3$ we only observe the presence of a single resonance in x-$p_x$ plane and hence, we do not find any noticeable chaotic region. Beyond, $\mu >3$, we observe the presence of another resonance [Fig. 7(b)–(e)]. We immediately witness the transition to chaos around $\mu =4$, in Figs. 7c, due to the overlap of both the resonances. The blue region in Fig. 7 shows the regular loci of phase points in x-$p_x$ plane and represents the regular region. The red-coloured region represents the scattered points (which can be observed by zooming into the plot), and hence, it represents the chaotic region. Similar to the elastic pendulum, with further increase in the value of $\mu$ beyond 4, we find the transition from chaotic state to ordered state. In Fig. 7e, we observe that the planar elastic pendulum is in a predominantly order state at $\mu =5$, thereby completing the order-chaos-order transition in the planar elastic pendulum.