Dynamics of a mass–spring–pendulum system with vastly different frequencies

Abstract

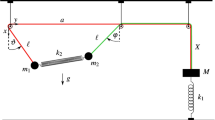
We investigate the dynamics of a simple pendulum coupled to a horizontal mass–spring system. The spring is assumed to have a very large stiffness value such that the natural frequency of the mass–spring oscillator, when uncoupled from the pendulum, is an order of magnitude larger than that of the oscillations of the pendulum. The leading order dynamics of the autonomous coupled system is studied using the method of Direct Partition of Motion (DPM), in conjunction with a rescaling of fast time in a manner that is inspired by the WKB method. We particularly study the motions in which the amplitude of the motion of the harmonic oscillator is an order of magnitude smaller than that of the pendulum. In this regime, a pitchfork bifurcation of periodic orbits is found to occur for energy values larger that a critical value. The bifurcation gives rise to nonlocal periodic and quasi-periodic orbits in which the pendulum oscillates about an angle between zero and π/2 from the down right position. The bifurcating periodic orbits are nonlinear normal modes of the coupled system and correspond to fixed points of a Poincare map. An approximate expression for the value of the new fixed points of the map is obtained. These formal analytic results are confirmed by comparison with numerical integration.

Appendices

Appendix A: Motivation for the assumed form of solution

The considered mass–spring–pendulum system is governed by the following system of equations:

$$\ddot{\theta}+ \sin\theta= - \varepsilon\ddot{\chi}\cos\theta, $$

$$\ddot{\chi}+ \frac{1}{{\varepsilon^2 }} \chi= - \frac{\mu }{\varepsilon} \bigl( {\ddot{\theta}\cos\theta- \dot{\theta}^2 \sin\theta} \bigr). $$

In its present form, each of the equations contains the second derivative of both χ and θ. We can rewrite the system of equations so that each second derivative appears in only one of the equations, as follows:

In this latter form, the θ equation appears as that of a nonlinear oscillator parametrically forced by χ, which we expect to be a fast oscillation. Hence this suggests the partitioning of the θ motion into a slow component overlaid by a fast component, as in the DPM ansatz. Also, we can see that the χ equation appears as that of a fast oscillator with a frequency whose magnitude is modulated by θ which we expect to be a slow oscillation, that is, it appears as an equation of a fast oscillator with a slowly changing frequency, similar to that which the WKB method is well suited for. This suggests rescaling fast time in the following manner:

$$\frac{{dT}}{{dt}} = \frac{{\omega ( t )}}{\varepsilon} \quad \mathrm{or}\quad T = \int_0^t {\frac{{\omega ( {t'} )}}{\varepsilon}dt'}, $$

and the assumed solution becomes:

$$\left \{\begin{array}{l} \chi=\chi ( {t,T} ),\\ \noalign {\vspace {3pt}} \theta ( {t,T} ) = \theta_0 ( t ) + \varepsilon\theta_1 ( {t,T} ). \\ \end{array} \right . $$

Here, ω(t) is to be chosen such that the fast oscillation is a perturbation of a harmonic oscillation on the new timescale T. That is, we will choose ω(t) so as the χ equation has the form:

$$\frac{{\partial^2 \chi}}{{\partial T^2 }} + \chi+ O ( \varepsilon) = 0, $$

then, an approximate expression for χ can be found using regular perturbations.

Appendix B: Details of the method of direct partition of motion

The method of direct partition of motion is based on the following three main assumptions:

• The motion of the slow oscillator, which is subject to fast parametric forcing, is partitioned as a sum of a leading order purely slow motion and an overlaid fast component.

• All functions of fast time are periodic with a zero average over a period of fast oscillation.

• Purely slow motions are treated as constants when averaging over a period of fast oscillation.

We start by substituting the form of solution presented in Appendix A into the following equations of motion:

$$ \everymath{\displaystyle }\begin{array}{@{}l} \ddot{\theta}+ \sin\theta= - \varepsilon\ddot{\chi}\cos\theta, \\ \noalign {\vspace {6pt}} \ddot{\chi}+ \frac{1}{{\varepsilon^2 }} \chi= - \frac{\mu }{\varepsilon} \bigl( {\ddot{\theta}\cos\theta- \dot{\theta}^2 \sin\theta} \bigr). \end{array} $$

(21)

The θ equation becomes:

(22)

We proceed to apply the standard DPM procedure [2] to this equation:

• 1. We average Eq. (22) over a period of fast timescale, while making use of the second and third assumption of DPM. The resulting averaged equation is:

  $$ \frac{{d^2 \theta_0 }}{{dt^2 }} + \sin\theta_0 - \omega^2 \sin\theta_0 \biggl\langle{\frac{{\partial^2 \chi}}{{\partial T^2 }}\theta_1 } \biggr\rangle_T = 0, $$

  (23)

  where 〈•〉 _T denotes averaging with respect to the fast timescale, T, over a period of fast oscillation which is equal to 2π:

  $$\langle\bullet\rangle_T = \frac{1}{{2\pi}} \int_0^{2\pi} ( \bullet)\,dT. $$

• 2. We subtract Eq. (23) from Eq. (22), then retaining the leading order terms only gives:

  $$ \frac{{\partial^2 \theta_1 }}{{\partial T^2 }} + \frac {{\partial^2 \chi}}{{\partial T^2 }}\cos\theta_0 =0. $$

  (24)

• 3. We integrate the latter equation twice with respect to T:

  $$\theta_1 = - \chi\cos\theta_0 + c_1 T +c_2. $$

• 4. In order to satisfy the second assumption of DPM, we set c ₁=c ₂=0, and obtain the following expression for θ ₁:

  $$ \theta_1 = - \chi\cos\theta_0. $$

  (25)

Substituting the latter into Eq. (23), we get:

$$ \frac{{d^2 \theta_0 }}{{dt^2 }} + \sin\theta_0 +\omega^2 \biggl\langle{\frac{{\partial^2 \chi}}{{\partial T^2 }}\chi} \biggr\rangle_T \cos \theta_0 \sin\theta_0 = 0. $$

(26)

From Appendix C, we have:

$$\chi\approx C\sqrt{\omega( t )} \cos T $$

with

$$\omega( t ) = \frac{1}{{\sqrt{1 - \mu\cos^2 \theta_0 } }}. $$

So the averaged term in Eq. (26) becomes:

We substitute this into Eq. (26) along with the expression for ω(t). Then the equation governing θ ₀, to leading order, reduces to:

Appendix C: Solving for χ

For convenience, we restate here the assumed form of solution:

$$\left \{\begin{array}{l} \chi=\chi ( t,T ), \\ \noalign {\vspace {3pt}} \theta ( t,T ) = \theta_0 ( t ) + \varepsilon\theta_1 ( t,T ), \\ \end{array} \right . $$

where

$$\frac{{dT}}{{dt}} = \frac{\omega ( t)}{\varepsilon} \quad \mathrm{or}\quad T = \int_0^t {\frac{{\omega ( {t'} )}}{\varepsilon}dt'} . $$

We substitute this into the following equations of motion:

$$\ddot{\theta}+ \sin\theta= - \varepsilon\ddot{\chi}\cos\theta, $$

$$\ddot{\chi}+ \frac{1}{{\varepsilon^2 }} \chi= -\frac{\mu }{\varepsilon} \bigl( {\ddot{\theta}\cos\theta- \dot{\theta}^2 \sin\theta} \bigr). $$

The χ equation becomes:

(27)

In order to eliminate the second derivative of θ ₀ from the above equation, we substitute the expression for θ ₁ from Eq. (25) into Eq. (22) in Appendix B. Then, the θ equation becomes:

We substitute this expression into Eq. (27), along with the expression for θ ₁ from Eq. (25). Then, multiplying by ε ², the χ equation becomes:

(28)

For the above equation to be of the form:

$$\frac{\partial^2 \chi}{\partial T^2 } + \chi+ O ( \varepsilon ) = 0, $$

we choose

$$ \omega( t ) = \frac{1}{{\sqrt{1 - \mu \cos^2 \theta_0 } }}. $$

(29)

The χ equation becomes:

(30)

Now, we are ready to expand χ in an asymptotic series:

$$\chi( {t,T} ) = \chi_0 ( {t,T} ) + \varepsilon \chi_1 ( {t,T} ) + \cdots. $$

Substituting this into Eq. (30), and collecting terms of the same order, we get:

O(1): 

$$\frac{{\partial^2 \chi_0 }}{{\partial T^2 }} +\chi_0 =0, $$

O(ε): 

The first equation gives:

$$\chi_0 = X ( t )\cos T. $$

Then, killing secular terms from the χ ₁ equation results in the following equation relating the amplitude X and θ ₀:

$$\frac{1}{{\omega^2 }}\frac{{d\omega}}{{dt}}X + \frac{2}{\omega}\frac {{dX}}{{dt}} + 2 \omega\mu\sin\theta_0 \cos\theta_0 \frac{{d\theta_0 }}{{dt}}X = 0, $$

which we rearrange into

$$\frac{1}{\omega}\frac{{d\omega}}{{dt}} + \frac{2}{X}\frac{{dX}}{{dt}} + 2 \omega^2 \mu\sin\theta_0 \cos\theta_0 \frac{{d\theta_0 }}{{dt}} = 0. $$

Integrating with respect to t, we get

$$ \everymath{\displaystyle }\begin{array}[b]{@{}l} \int{\frac{1}{\omega}d\omega} + \int{\frac{2}{X}dX} + \int{2 \omega^2 \mu\sin\theta_0 \cos\theta_0 \,d\theta_0 } = 0 \\ \noalign {\vspace {6pt}} \quad \Rightarrow\quad \ln\omega+ 2\ln X + \int 2\omega^2\mu\sin\theta_0 \cos\theta_0 \,d\theta_0 = k, \\ \noalign {\vspace {6pt}} \end{array} $$

(31)

where k is an arbitrary constant.

But

So Eq. (31) becomes

(32)

As a result, to leading order, χ is given by

$$ \chi\approx C\sqrt{\omega( t )} \cos T $$

(33)

with

$$\omega( t ) = \frac{1}{{\sqrt{1 - \mu\cos^2 \theta_0 } }}, $$

where C is an arbitrary constant that depends on initial conditions.

Appendix D: The bifurcation in the slow dynamics

θ ₀ is governed by the following equation:

(34)

We rewrite this as a system of two first order equations:

$$ \everymath{\displaystyle }\begin{array}{@{}l} \dot{\theta}_0 = \phi,\\ \noalign {\vspace {6pt}} \dot{\phi}= - \sin\theta_0 + \frac{{C^2 }}{2} \frac{{ \sin\theta_0 \cos\theta_0 }}{{ (1-\mu\cos^2\theta_0 )\sqrt {1 - \mu\cos^2 \theta_0 } }}. \end{array} $$

(35)

Looking for the value of θ ₀ that corresponds to equilibrium points of this equation (with ϕ=0):

$$\everymath{\displaystyle }\begin{array}{@{}l} \sin\theta_0 = 0, \quad \mathrm{or} \\ \noalign {\vspace {5pt}} 1 - \frac{{C^2 }}{2}\frac{\cos\theta_0}{ (1-\mu\cos^2\theta_0 ) \sqrt{1 - \mu\cos^2 \theta_0 } } = 0. \end{array} $$

So the first condition gives θ ₀=0,π,−π, while the second condition allows two additional equilibrium points θ ₀=E such that

(36)

To know when a root to this equation actually exists,

$$\mathrm{let} \alpha= \cos^2 E, \quad \mathrm{so} \ 0 \le\alpha\le1. $$

Consider the two functions f and g, illustrated in Fig. 12:

$$f ( \alpha) = ( {1 - \mu\alpha} )^3,\qquad g ( \alpha) = \frac{{C^4 }}{4}\alpha. $$

f is a decreasing function of α with

$$f ( 0 ) = 1 \quad \mathrm{and} \quad f ( 1 ) = ( {1 - \mu} )^3. $$

The function g is the line through the origin, with a slope of C ⁴/4. So, the two functions will intersect for some α∈[0,1] when the following condition is met:

$$ \frac{{C^4 }}{4} \ge( {1 - \mu} )^3. $$

(37)

Hence, when C satisfies this above condition, two new equilibrium points will exist at θ ₀=±E , ϕ=0, such that cosE satisfies Eq. (36).

Fig. 12

Schematic of the two functions f(α)&g(α)

The Jacobian for the system in Eq. (35) has a zero trace while the determinant is given by the following expression:

looking at the value of this determinant for θ ₀=0:

$$\Delta_{\theta_0 = 0} = 1 - \frac{{C^2}}{2}\frac{1}{ ( {1 - \mu})^{3/2}} $$

$$\Delta_{\theta_0 = 0} > 0 \quad \Rightarrow\quad \frac{{C^4 }}{4} \le( {1 - \mu})^3. $$

So the origin goes from being a center to a saddle as the two new equilibrium points are born, hence, a pitchfork bifurcation takes place. To check the determinant for θ ₀=±E, we solve for C ² from Eq. (36):

$$ C^2 =\frac{2 ( {1 - \mu\cos^2 E} )^{3/2}}{\cos E}; $$

(38)

substituting this into the expression for the determinant, we get:

$$\Delta_{\theta_0 = E} = \frac{{\mu\sin^2 ( {2E} ) + 2\sin^2 ( E )}}{{2\cos E ( {1 - \mu\cos^2 E} )}} > 0, $$

where we have used Eq. (38) to judge that cosE>0. This confirms that the two new equilibrium points are centers.

To summarize, when the following condition is met:

$$ C^2 > 4 ( {1 - \mu} )^{\frac{3}{2}}, $$

(39)

the approximate equation governing θ ₀ undergoes a pitchfork bifurcation where two new equilibrium points are born (θ ₀=±E, ϕ=0) such that

$$\bigl( {1 - \mu\cos^2 E} \bigr)^3 = \frac{{C^4}}{4} \cos^2 E. $$

The arbitrary constant C that appears in the equation can be expressed in terms of the initial conditions. As mentioned in Sect. 4, for initial zero velocities, the initial conditions take the form:

with

$$\omega( 0 ) = \frac{1}{\sqrt{1 - \mu\cos^2 A} }. $$

Then C can be expressed as follows:

$$\quad \Rightarrow \quad C = B \bigl( {1 - \mu\cos^2 A} \bigr)^{\frac{1}{4}} . $$

The bifurcation condition in Eq. (39) becomes

$$ B^4 \bigl(1 - \mu\cos^2 A \bigr) > 4 ( {1 - \mu} )^3. $$

(40)

Also, for such initial conditions, the energy function h that corresponds to the full system (1) is

$$h = \frac{1}{2}B^2 + \mu( {1 - \cos A} ); $$

solving for B ² in terms of h and substituting the resulting expression into Eq. (40), we can derive a minimum required value of h so that the bifurcation occurs:

which leads to the following condition on h:

$$h \ge\mu( {1 - \cos A} ) + \sqrt{\frac{{ ( {1 - \mu} )^3 }}{{1 - \mu\cos^2 A}}} . $$

The expression on the right hand side of the equality increases as A increases. For A=0, it takes the value 1−μ. This leads to the following minimum requirement for the pitchfork bifurcation to happen:

$$h > 1 - \mu. $$

Now, going back to the full system (1), we recall from Eq. (12) that the approximate θ motion took the form:

$$\theta\approx\theta_0 -x \cos\theta_0, $$

where θ ₀ is governed by Eq. (34).

So, when the condition for the existence of the two new equilibrium points is met, we expect certain solutions that obey approximately the following relation:

$$\theta\approx E - x \cos E. $$

That is, if we start with an initial condition $\theta (0 )=\theta_{0} (0 )=E, \dot{\theta}= \phi=0$, then the approximate equation for θ ₀ predicts that θ ₀ will remain equal to E for all time, since θ ₀=E,ϕ=0 is a neutrally stable fixed point (center) of Eq. (35).

Now we look for the initial amplitude of θ that corresponds to such solutions. That is, for each constant value of h that allows the mentioned bifurcation to occur, we look for θ ₀(0)=A, such that E=A. From Eq. (38), we have:

$$ C^2 = \frac{{2 ( {1 - \mu\cos^2 E} ) ^{3/2} }}{{\cos E}}, $$

(41)

but the expression for C in terms of the initial conditions is:

(42)

We substitute Eq. (41) into Eq. (42), and require

$$ E=A=\theta_0 (0). $$

(43)

We get

$$B^2 = \frac{{2 ( {1 - \mu\cos^2 A} )}}{{\cos A}}. $$

Now, we can substitute this relation into the expression for h, in order to solve for A:

We rewrite this as

(44)

For such a solution to exist, we need

which coincides with the condition for the existence of the pitchfork bifurcation.

To summarize, for a fixed value of μ, we expect to see a fixed point in the map (x=0 and $\dot{x}>0$) if we choose a value for h that meets h>1−μ, and integrate the system in Eq. (1), with the following initial conditions:

$$\everymath{\displaystyle }\left \{\begin{array}{@{}l} \theta ( 0 ) = \pm A^* \\ \noalign {\vspace {5pt}} \qquad = \pm\cos^{ - 1} \biggl( {\frac{{\mu - h \pm\sqrt{ ( {h - \mu} )^2 + 8\mu} }}{{4\mu}}} \biggr), \\ \noalign {\vspace {5pt}} \dot{\theta}( 0 ) = 0, \\ \noalign {\vspace {5pt}} x ( 0 ) = \varepsilon B^* = \varepsilon \sqrt{2 \bigl( h - \mu ( {1 - \cos A} ) \bigr) }, \\ \noalign {\vspace {5pt}} \dot{x} ( 0 ) = 0. \end{array} \right . $$

Figure 13 shows the pendulum oscillation for the special ICs for which θ is predicted to be θ≈A ^∗−xcosA ^∗, that is, θ is predicted to undergo no slow oscillation and instead the motion of the pendulum will consist of a fast oscillation about the θ=A ^∗. Due to the error in the approximate solution and numerical integration, θ undergoes a small amplitude slow oscillation instead of no slow oscillation. Figure 14 shows that this slow oscillation gets smaller in amplitude as energy is increased farther from the bifurcation value. This can be explained by the fact that the value of A ^∗ increases as energy increases and thus the relative error decreases. The solution also gets closer to the predicted one as ε is decreased, as illustrated in Fig. 15.

Fig. 13

θ vs. time for the initial condition corresponding to θ(0)=A ^∗ for h=0.7, ε=0.02

Fig. 14

θ vs. time for the initial condition corresponding to θ(0)=A ^∗ for h=2 with ε=0.02

Fig. 15

θ vs. time for the initial condition corresponding to θ(0)=A ^∗ for h=2 with ε=0.01

Appendix E: Relating the curves of the Poincare map to θ ₀

The Poincare map considered in the body of this paper corresponds to a plot of $\dot{\theta}$ vs. θ with x=0 and $\dot{x}>0$. If we could relate $\dot{\theta}$ to $\dot{\theta}_{0}$, and θ to θ ₀, then we can approximately generate the Poincare map of the full system (1) from the solution to the θ ₀ equation.

θ was found to be expressed as

$$\theta\approx\theta_0 -x \cos\theta_0. $$

With x assumed to be O(ε), we can say

$$\theta\approx\theta_0 +O (\varepsilon). $$

To find an expression for $\dot{\theta}$ in terms of $\dot{\theta}_{0}$, we differentiate both sides of the expression for θ with respect to time:

(45)

Note that since x is O(ε), we ignore the term multiplied by x, however, we retain the term containing the derivative of x since x oscillates with a frequency of O(1/ε) and so $\dot{x}$ is of O(1).

In order to eliminate $\dot{x}$ from the expression for $\dot{\theta}$, we observe that

where we have used the fact that

$$\frac{{dT}}{{dt}} = \frac{{\omega ( t )}}{\varepsilon}. $$

Now, for the Poincare map, we have

$$\left \{\begin{array}{l} \noalign {\vspace {-1pt}} x = 0 \quad \Rightarrow \quad\cos T = 0 \\ \noalign {\vspace {3pt}} \dot{x} > 0 \quad \Rightarrow \quad\sin T < 0 \\ \noalign {\vspace {-1pt}} \end{array} \right . \quad \Rightarrow \quad \sin T = - 1, $$

then

$$\frac{{dx}}{{dt}} \approx C\omega\sqrt{\omega}+ O ( \varepsilon). $$

Substituting this into Eq. (45), we get

$$\frac{{d\theta}}{{dt}} = \frac{{d\theta_0 }}{{dt}} - C\omega\sqrt{\omega}\cos \theta_0 + O ( \varepsilon). $$

Substituting the following expression for ω(t) yields

$$\omega( t ) = \frac{1}{{\sqrt{1 - \mu\cos^2 \theta_0 } }} = \bigl( {1 - \mu\cos^2 \theta_0 } \bigr)^{ - \frac{1}{2}} . $$

We obtain the following expression for the $\dot{\theta}$ values, corresponding to points in the Poincare map, in terms of $\dot{\theta}_{0}$ and θ ₀:

$$\frac{{d\theta}}{{dt}} \approx\frac{{d\theta_0 }}{{dt}} - C \bigl( {1 - \mu \cos^2 \theta_0 } \bigr)^{ - \frac{3}{4}} \cos \theta_0. $$