Skip to main content
SpringerLink
Log in

Chaos and hyperchaos via secondary Neimark–Sacker bifurcation in a model of radiophysical generator

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

Using an example of a radiophysical generator model, scenarios for the formation of various chaotic attractors are described, including chaos and hyperchaos. It is shown that as a result of a secondary Neimark–Sacker bifurcation, a hyperchaos with two positive Lyapunov exponents can occur in the system. A comparative analysis of chaotic attractors born as a result of loss of smoothness of an invariant curve, as a result of period-doubling bifurcations, and as a result of secondary Neimark–Sacker bifurcation was carried out.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Notes

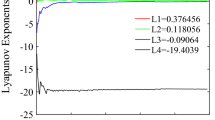
  1. System (1) is four-dimensional and in fact it has four Lyapunov exponents, but the fourth exponent is always negative, and we did not add it to the plots.

  2. In accordance with [40, 41], if for a flow dynamical system at variation of the parameter, the largest Lyapunov exponent is equal zero and two of the following are negative and equal to each other before bifurcation, and if two of the largest Lyapunov exponents are equal zero and the third is negative after bifurcation, it indicates the Neimark–Sacker bifurcation.

  3. Also sometimes it is called adiabatic initial conditions, i.e., for each new value of the parameter, the initial conditions were chosen as the final state attained for the previous value of the parameter.

References

  1. Schuster, H.G.: Deterministic chaos: an introduction, p. 220. Physik-Verlag, Weinheim (1984)

    MATH  Google Scholar 

  2. Mosekilde, E., Maistrenko, Y., Postnov, D.: Chaotic Synchronization: Applications to Living Systems, vol. 42. World Scientific, Singapore (2002)

    Book  MATH  Google Scholar 

  3. Strogatz, S.H.: Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Westview Press, Boulder (2014)

    MATH  Google Scholar 

  4. Benettin, G., Galgani, L., Giorgilli, A., Strelcyn, J.-M.: Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems: a method for computing all of them. Meccanica 15, 9–30 (1980)

    Article  MATH  Google Scholar 

  5. Pikovsky, A., Politi, A.: Lyapunov Exponents: A Tool to Explore Complex Dynamics. Cambridge University Press, Cambridge (2016)

    Book  MATH  Google Scholar 

  6. Rossler, O.E.: An equation for hyperchaos. Phys. Lett. A 71, 155–157 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  7. Tamasevicius, A., Namajunas, A., Cenys, A.: Simple 4D chaotic oscillator. Electron. Lett. 32, 957–958 (1996)

    Article  Google Scholar 

  8. Blokhina, E.V., Kuznetsov, S.P., Rozhnev, A.G.: High-dimensional chaos in a gyrotron. IEEE Trans. Electron Dev. 54, 188–193 (2007)

    Article  Google Scholar 

  9. Rozental’, R.M., Isaeva, O.B., Ginzburg, N.S., Zotova, I.V., Sergeev, A.S., Rozhnev, A.G.: Characteristics of chaotic regimes in a space-distributed gyroklystron model with delayed feedback. Russ. J. Nonlinear Dyn. 14, 155–168 (2018)

    MathSciNet  MATH  Google Scholar 

  10. Chen, Z., Yang, Y., Qi, G., Yuan, Z.: A novel hyperchaos system only with one equilibrium. Phys. Lett. A 360, 696–701 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  11. Wu, W., Chen, Z., Yuan, Z.: The evolution of a novel fourdimensional autonomous system: among 3-torus, limit cycle, 2-torus, chaos and hyperchaos. Chaos Solitons Fractals 39, 2340–2356 (2009)

    Article  Google Scholar 

  12. Li, Q., Tang, S., Zeng, H., Zhou, T.: On hyperchaos in a small memristive neural network. Nonlinear Dyn. 78, 1087–1099 (2014)

    Article  MATH  Google Scholar 

  13. Li, Q., Zeng, H., Li, J.: Hyperchaos in a 4D memristive circuit with infinitely many stable equilibria. Nonlinear Dyn. 79, 2295–2308 (2015)

    Article  MathSciNet  Google Scholar 

  14. Biswas, D., Banerjee, T.: A simple chaotic and hyperchaotic time-delay system: design and electronic circuit implementation. Nonlinear Dyn. 83, 2331–2347 (2016)

    Article  MathSciNet  Google Scholar 

  15. Fonzin, T.F., Kengne, J., Pelap, F.B.: Dynamical analysis and multistability in autonomous hyperchaotic oscillator with experimental verification. Nonlinear Dyn. 93, 653–669 (2018)

    Article  Google Scholar 

  16. Kapitaniak, T., Thylwe, K.E., Cohen, I., Wojewoda, J.: Chaos-hyperchaos transition. Chaos Solitons Fractals 5, 2003–2011 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  17. Harrison, M.A., Lai, Y.C.: Route to high-dimensional chaos. Phys. Rev. E 59, R3799 (1999)

    Article  Google Scholar 

  18. Kapitaniak, T., Maistrenko, Y., Popovych, S.: Chaos–hyperchaos transition. Phys. Rev. E 62, 1972 (2000)

    Article  Google Scholar 

  19. Yanchuk, S., Kapitaniak, T.: Symmetry-increasing bifurcation as a predictor of a chaos–hyperchaos transition in coupled systems. Phys. Rev. E 64, 056235 (2001)

    Article  Google Scholar 

  20. Nikolov, S., Clodong, S.: Hyperchaos–chaos–hyperchaos transition in modified Rössler systems. Chaos Solitons Fractals 28, 252–263 (2006)

    Article  MATH  Google Scholar 

  21. Harikrishnan, K.P., Misra, R., Ambika, G.: On the transition to hyperchaos and the structure of hyperchaotic attractors. Eur. Phys. J. B 86, 1–12 (2013)

    Article  MathSciNet  Google Scholar 

  22. Li, Q., Tang, S., Yang, X.S.: Hyperchaotic set in continuous chaos–hyperchaos transition. Commun. Nonlinear Sci. Numer. Simul. 19, 3718–3734 (2014)

    Article  MathSciNet  Google Scholar 

  23. Munteanu, L., Brian, C., Chiroiu, V., Dumitriu, D., Ioan, R.: Chaos–hyperchaos transition in a class of models governed by Sommerfeld effect. Nonlinear Dyn. 78, 1877–1889 (2014)

    Article  MathSciNet  Google Scholar 

  24. Gonchenko, S.V., Ovsyannikov, I.I., Simò, C., Turaev, D.: Three-dimensional Hénon-like maps and wild Lorenz-like attractors. Int. J. Bifurc. Chaos 15, 3493–3508 (2005)

    Article  MATH  Google Scholar 

  25. Gonchenko, A.S., Gonchenko, S.V., Shilnikov, L.P.: Towards scenarios of chaos appearance in three-dimensional maps. Russ. J. Nonlinear Dyn. 8, 3–28 (2012). (Russian)

    Google Scholar 

  26. Gonchenko, A., Gonchenko, S., Kazakov, A., Turaev, D.: Simple scenarios of onset of chaos in three-dimensional maps. Int. J. Bifurc. Chaos 24, 1440005 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  27. Stankevich, N.V., Dvorak, A., Astakhov, V., Jaros, P., Kapitaniak, M., Perlikowski, P., Kapitaniak, T.: Chaos and hyperchaos in coupled antiphase driven toda oscillators. Regul. Chaotic Dyn. 23, 120–126 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  28. Kuznetsov, A.P., Sedova, Y.V.: Coupled systems with hyperchaos and quasiperiodicity. J. Appl. Nonlinear Dyn. 5, 161–167 (2016)

    Article  MathSciNet  Google Scholar 

  29. Rech, P.C.: Hyperchaos and quasiperiodicity from a four-dimensional system based on the Lorenz system. Eur. Phys. J. B 90, 251 (2017)

    Article  MathSciNet  Google Scholar 

  30. Amabili, M., Karagiozis, K., Païdoussis, M.P.: Hyperchaotic behaviour of shells subjected to flow and external force. In: ASME 2010 3rd Joint US-European Fluids Engineering Summer Meeting collocated with 8th International Conference on Nanochannels, Microchannels, and Minichannels, American Society of Mechanical Engineers, pp. 1209–1217 (2010)

  31. Kuznetsov, A.P., Migunova, N.A., Sataev, I.R., Sedova, YuV, Turukina, L.V.: From chaos to quasi-periodicity. Regul. Chaotic Dyn. 20, 189–204 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  32. Stankevich, N.V., Astakhov, O.V., Kuznetsov, A.P., Seleznev, E.P.: Exciting chaotic and quasi-periodic oscillations in a multicircuit oscillator with a common control scheme. Tech. Phys. Lett. 44, 428–431 (2018)

    Article  Google Scholar 

  33. Anishchenko, V.S., Nikolaev, S.M.: Generator of quasi-periodic oscillations featuring two-dimensional torus doubling bifurcations. Tech. Phys. Lett. 31, 853–855 (2005)

    Article  Google Scholar 

  34. Anishchenko, V.S., Nikolaev, S.M., Kurths, J.: Peculiarities of synchronization of a resonant limit cycle on a two-dimensional torus. Phys. Rev. E 76, 046216 (2007)

    Article  Google Scholar 

  35. Kuznetsov, A.P., Stankevich, N.V.: Autonomous systems with quasiperiodic dynamics. Examples and their properties: review. Izv. VUZ Appl. Nonlinear Dyn. 23, 71–93 (2015). (in Russia)

    Google Scholar 

  36. Kuznetsov, N.V.: The Lyapunov dimension and its estimation via the Leonov method. Phys. Lett. A 380, 2142–2149 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  37. Kuznetsov, N.V., Leonov, G.A., Mokaev, T.N., Prasad, A., Shrimali, M.D.: Finite-time Lyapunov dimension and hidden attractor of the Rabinovich system. Nonlinear Dyn. 92, 267–285 (2018)

    Article  MATH  Google Scholar 

  38. Zhusubaliyev, Z.T., Mosekilde, E.: Formation and destruction of multilayered tori in coupled map systems. Chaos 18, 037124 (2008)

    Article  MathSciNet  Google Scholar 

  39. Zhusubaliyev, Z.T., Laugesen, J.L., Mosekilde, E.: From multi-layered resonance tori to period-doubled ergodic tori. Phys. Lett. A 374, 2534–2538 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  40. Vitolo, R., Broer, H., Simó, C.: Routes to chaos in the Hopf-saddle-node bifurcation for fixed points of 3D-diffeomorphisms. Nonlinearity 23, 1919–1947 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  41. Broer, H., Simó, C., Vitolo, R.: Quasi-periodic bifurcations of invariant circles in low-dimensional dissipative dynamical systems. Regul. Chaotic Dyn. 16, 154–184 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  42. Komuro, M., Kamiyama, K., Endo, T., Aihara, K.: Quasi-periodic bifurcations of higher-dimensional tori. Int. J. Bifurc. Chaos 26, 1630016 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  43. Wieczorek, S., Krauskopf, B., Lenstra, D.: Mechanisms for multistability in a semiconductor laser with optical injection. Opt. Commun. 183, 215–226 (2000)

    Article  Google Scholar 

  44. Stankevich, N.V., Volkov, E.I.: Multistability in a three-dimensional oscillator: tori, resonant cycles and chaos. Nonlinear Dyn. 94, 2455–2467 (2018)

    Article  Google Scholar 

Download references

Acknowledgements

Authors thank Igor Sataev, Alexey Kazakov and Serhiy Yanchuk for fruitful discussion of this problem.

Funding

The work was carried out with the financial support of the Russian Foundation of Basic Research, Grant No. 18-32-00285 (Introduction, Sects. 2, 3, 4.1) and Russian Science Foundation, Grant No. 17-12-01008 (Sect. 4.2). Analysis of multistability was carried out in the frame of project of the Russian Foundation of Basic Research, Grant No. 19-02-00610.

Author information

Authors and Affiliations

  1. Department of Radio-Electronics and Telecommunication, Yuri Gagarin State Technical University of Saratov, Saratov, Russia

    Nataliya Stankevich

  2. Saratov Branch, Kotel’nikov’s Institute of Radio-Engineering and Electronics of RAS, Saratov, Russia

    Nataliya Stankevich, Alexander Kuznetsov, Elena Popova & Evgeniy Seleznev

  3. Department of Applied Cybernetics, Saint-Petersburg State University, Saint-Petersburg, Russia

    Nataliya Stankevich

Authors
  1. Nataliya Stankevich
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alexander Kuznetsov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Elena Popova
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Evgeniy Seleznev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nataliya Stankevich.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Stankevich, N., Kuznetsov, A., Popova, E. et al. Chaos and hyperchaos via secondary Neimark–Sacker bifurcation in a model of radiophysical generator. Nonlinear Dyn 97, 2355–2370 (2019). https://doi.org/10.1007/s11071-019-05132-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05132-0

Keywords

Mathematics Subject Classification

Search

Navigation