Skip to main content
SpringerLink
Log in

Rational and semi-rational solutions of the Kadomtsev–Petviashvili-based system

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

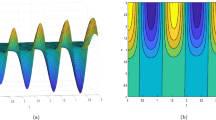
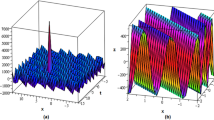
We investigate the rational and semi-rational solutions of the integrable Kadomtsev–Petviashvili (KP)-based system, which appears in fluid mechanics, plasma physics, and gas dynamics. Various types of solutions, including soliton, breather, and a mixture of breather and soliton, of the KP-based system are derived by applying the Hirota’s bilinear method and the perturbation expansion. By taking a long-wave limit of the soliton solutions and particular parameter constraints, the rational and semi-rational solutions are generated. The rational solutions have two different dynamical behaviors: lump and line rogue wave; the first-order lump and line rogue wave are classified into three patterns: bright state, mixed state, and dark state. The semi-rational solutions reveal the following dynamic features: (1) Elastic interactions between lumps and bound-state dark solitons; (2) Elastic interactions between line rogue waves and bound-state dark solitons; (3) Inelastic collisions of breathers and rogue waves. Compared to the rational solutions, the semi-rational solutions have more interesting patterns.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Garrett, C., Gemmrich, J.: Rogue waves. Phys. Today 15, 3210 (2009)

    Google Scholar 

  2. Kharif, C., Pelinovsky, E., Slunyaev, A.: Rogue Waves in the Ocean. Springer, Berlin, Heidelberg (2009)

    MATH  Google Scholar 

  3. Osborne, A.R.: Nonlinear Ocean Waves and the Inverse Scattering Transform. Academic Press, New York (2010)

    MATH  Google Scholar 

  4. Kibler, B., Fatome, J., Finot, C., Millot, G., Dias, F., Genty, G., Akhmediev, N., Dudley, J.: The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 6, 790 (2010)

    Article  Google Scholar 

  5. Solli, D., Ropers, C., Koonath, P., Jalali, B.: Optical rogue waves. Nature 450, 1054 (2007)

    Article  Google Scholar 

  6. Chabchoub, A., Hoffmann, N., Akhmediev, N.: Rogue wave observation in a water wave tank. Phys. Rev. Lett. 106, 204502 (2011)

    Article  Google Scholar 

  7. Bailung, H., Sharma, S., Nakamura, Y.: Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett. 107, 255005 (2011)

    Article  Google Scholar 

  8. Ganshin, A., Efimov, V., Kolmakov, G., Mezhov-Deglin, L., McClintock, P.: Observation of an inverse energy cascade in developed acoustic turbulence in superfluid helium. Phys. Rev. Lett. 101, 065303 (2008)

    Article  Google Scholar 

  9. Moslem, W.M., Shukla, P.K., Eliasson, B.: Surface plasma rogue waves. EPL 96, 25002 (2011)

    Article  Google Scholar 

  10. Shats, M., Punzmann, H., Xia, H.: Capillary rogue waves. Phys. Rev. Lett. 104, 104503 (2010)

    Article  Google Scholar 

  11. Stenflo, L., Marklund, M.: Rogue waves in the atmosphere. J. Plasma Phys. 76, 293 (2010)

    Article  Google Scholar 

  12. Peregrine, D.: Water waves, nonlinear Schrödinger equations and their solutions. J. Austral. Math. Soc. Ser. B 25, 16 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kibler, B., Fatome, J., Finot, C., Millot, G., Genty, G., Wetzel, B., Akhmediev, N., Dias, F., Dudley, J.M.: Observation of Kuznetsov–Ma soliton dynamics in optical fibre. Sci. Rep 2, 463 (2012)

    Article  Google Scholar 

  14. Akhmediev, N., Ankiewicz, A., Soto-Crespo, J.M.: Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E 80, 026601 (2009)

    Article  Google Scholar 

  15. Ankiewicz, A., Wang, Y., Wabnitz, S., Akhmediev, N.: Extended nonlinear Schrödinger equation with higher-order odd and even terms and its rogue wave solutions. Phys. Rev. E 89, 012907 (2014)

    Article  Google Scholar 

  16. He, J., Zhang, H., Wang, L., Porsezian, K., Fokas, A.: Generating mechanism for higher-order rogue waves. Phys. Rev. E 87, 052914 (2013)

    Article  Google Scholar 

  17. Guo, B., Ling, L., Liu, Q.: High-order solutions and generalized Darboux transformations of derivative nonlinear Schrödinger equations. Stud. Appl. Math. 130, 317 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  18. Xu, S., He, J.: The rogue wave and breather solution of the Gerdjikov–Ivanov equation. J. Math. Phys. 53, 063507 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  19. Xu, S., He, J., Wang, L.: The Darboux transformation of the derivative nonlinear Schrödinger equation. J. Phys. A Math. Theor. 44, 305203 (2011)

    Article  MATH  Google Scholar 

  20. Zhang, Y., Guo, L., He, J., Zhou, Z.: Darboux transformation of the second-type derivative nonlinear Schrödinger equation. Lett. Math. Phys. 105, 853 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  21. Zhang, Y., Guo, L., Xu, S., Wu, Z., He, J.: The hierarchy of higher order solutions of the derivative nonlinear Schrödinger equation. Commun. Nonlinear Sci. Numer. Simulat. 19, 1706 (2014)

    Article  Google Scholar 

  22. Ankiewicz, A., Soto-Crespo, J.M., Akhmediev, N.: Rogue waves and rational solutions of the Hirota equation. Phys. Rev. E 81, 046602 (2010)

    Article  MathSciNet  Google Scholar 

  23. Tao, Y., He, J.: Multisolitons, breathers, and rogue waves for the Hirota equation generated by the Darboux transformation. Phys. Rev. E 85, 026601 (2012)

    Article  Google Scholar 

  24. Chen, S., Soto-Crespo, J.M., Baronio, F., Grelu, P., Mihalache, D.: Rogue-wave bullets in a composite (2+1) D nonlinear medium. Opt. Express 24, 15251 (2016)

    Article  Google Scholar 

  25. Ohta, Y., Yang, J.: Rogue waves in the Davey–Stewartson I equation. Phys. Rev. E 86, 036604 (2012)

    Article  Google Scholar 

  26. Ohta, Y., Yang, J.: Dynamics of rogue waves in the Davey–Stewartson II equation. J. Phys. A Math. Theor. 46, 105202 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  27. Maccari, A.: The Kadomtsev–Petviashvili equation as a source of integrable model equations. J. Math. Phys. 37, 6207 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  28. Ablowitz, M.J., Clarkson, P.A.: Soliton, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1991)

    Book  MATH  Google Scholar 

  29. Kadomtsev, B.B., Petviashvili, V.I.: On the stability of solitary waves in weakly dispersing media. Sov. Phys. Dokl. 192, 539 (1970)

    MATH  Google Scholar 

  30. Ablowitz, M.J., Segur, H.: On the evolution of packets of water waves. J. Fluid Mech. 92, 691 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  31. Infeld, E., Rowlands, G.: Nonlinear Waves, Solitons and Chaos. Cambridge University Press, Cambridge (2000)

    Book  MATH  Google Scholar 

  32. Pelinovsky, D.E., Stepanyants, Y.A., Kivshar, Y.S.: Self-focusing of plane dark solitons in nonlinear defocusing media. Phys. Rev. E 51, 5016 (1995)

    Article  MathSciNet  Google Scholar 

  33. Tsuchiya, S., Dalfovo, F., Pitaevskii, L.: Solitons in two-dimensional Bose–Einstein condensates. Phys. Rev. A 77, 045601 (2008)

    Article  Google Scholar 

  34. Dubard, P., Matveev, V.: Multi-rogue waves solutions to the focusing NLS equation and the KP-I equation. Nat. Hazards Earth Syst. 11, 667–672 (2011)

    Article  Google Scholar 

  35. Dubard, P., Matveev, V.: Multi-rogue waves solutions: from the NLS to the KP-I equation. Nonlinearity 26, R93 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  36. Manakov, S., Zakharov, V.E., Bordag, L., Its, A., Matveev, V.: Two-dimensional solitons of the Kadomtsev–Petviashvili equation and their interaction. Phys. Lett. A 63, 205 (1977)

    Article  Google Scholar 

  37. Satsuma, J., Ablowitz, M.: Two-dimensional lumps in nonlinear dispersive systems. J. Math. Phys. 20, 1496 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  38. Porzesain, K.: Painlevé analysis of new higher-dimensional soliton equation. J. Math. Phys. 38, 4675 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  39. Yan, Z.: Extended Jacobian elliptic function algorithm with symbolic computation to construct new doubly-periodic solutions of nonlinear differential equations. Comput. Phys. Commun. 148, 30 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  40. Yu, G., Xu, Z.: Dynamics of a differential-difference integrable (2+1)-dimensional system. Phys. Rev. E 91, 062902 (2015)

    Article  MathSciNet  Google Scholar 

  41. Bekir, A.: New exact travelling wave solutions of some complex nonlinear equations. Commun. Nonlinear Sci. Numer. Simul. 14, 1069 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  42. Meng, G.Q., Gao, Y.T., Yu, X., Shen, Y.J., Qin, Y.: Painlevé analysis, Lax pair, Bäcklund transformation and multi-soliton solutions for a generalized variable-coefficient KdV-mKdV equation in fluids and plasmas. Phys. Scr. 85, 055010 (2012)

    Article  MATH  Google Scholar 

  43. Wang, C., Dai, Z., Liu, C.: The breather-like and rational solutions for the integrable Kadomtsev–Petviashvili-based system. Adv. Math. Phys. 2015, 861069 (2015)

    MathSciNet  MATH  Google Scholar 

  44. Yu, X., Gao, Y.T., Sun, Z.Y., Liu, Y.: Solitonic propagation and interaction for a generalized variable-coefficient forced Korteweg–de Vries equation in fluids. Phys. Rev. E 83, 056601 (2011)

    Article  Google Scholar 

  45. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  46. Chan, H.N., Ding, E., Kedziora, D.J., Grimshaw, R., Chow, K.W.: Rogue waves for a long-wave-short wave resonance model with multiple short waves. Nonlinear Dyn. 85, 2827 (2016)

    Article  MathSciNet  Google Scholar 

  47. Tajiri, M., Arai, T.: Growing-and-decaying mode solution to the Davey–Stewartson equation. Phys. Rev. E 60, 2297 (1999)

    Article  MathSciNet  Google Scholar 

  48. Tajiri, M., Watanabe, Y.: Breather solutions to the focusing nonlinear Schrödinger equation. Phys. Rev. E 57, 3510 (1998)

    Article  MathSciNet  Google Scholar 

  49. Wazwaz, A., El-Tantawy, S.: A new integrable (3+1)-dimensional KdV-like model with its multiple-soliton solutions. Nonlinear Dyn. 83, 1529 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  50. Wazwaz, A., El-Tantawy, S.: Solving the (3+1)-dimensional KP-Boussinesq and BKP-Boussinesq equations by the simplified Hirota’s method. Nonlinear Dyn. 88, 3017 (2017)

    Article  MathSciNet  Google Scholar 

  51. Cao, Y., He, J., Mihalache, D.: Families of exact solutions of a new extended (2+1)-dimensional Boussinesq equation. Nonlinear Dyn. 91, 2593 (2018)

    Article  Google Scholar 

  52. Liu, Y., Mihalache, D., He, J.: Families of rational solutions of the \(y\)-nonlocal Davey–Stewartson II equation. Nonlinear Dyn. 90, 2445 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  53. Sun, B.: General soliton solutions to a nonlocal long-wave-short-wave resonance interaction equation with nonzero boundary condition. Nonlinear Dyn. 92, 1369 (2018)

    Article  MATH  Google Scholar 

  54. Liu, Y.K., Li, B., An, H.: General high-order breathers, lumps in the (2+1)-dimensional Boussinesq equations. Nonlinear Dyn. 92, 2061 (2018)

    Article  Google Scholar 

  55. Chen, J., Chen, Y., Feng, B.F., Maruno, K.I.: Rational solutions to two- and one-dimensional multicomponent Yajima–Oikawa systems. Phys. Lett. A 379, 1510 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  56. Rao, J., Wang, L., Zhang, Y., He, J.: Rational solutions for the Fokas system. Commun. Theor. Phys. 64, 605 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  57. Rao, J., Cheng, Y., He, J.: Rational and semi-rational solutions of the nonlocal Davey–Stewartson equations. Stud. Appl. Math. 139, 568 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  58. Rao, J., Porsezain, K., He, J.: Semi-rational solutions of third-type nonlocal Davey–Stewartson equation. Chaos 27, 083115 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  59. Wazwaz, A.M.: Negative-order integrable modified KdV equations of higher orders. Nonlinear Dyn. 93, 1371 (2018)

    Article  MATH  Google Scholar 

  60. Ankiewicz, A., Akhmediev, N.: Rogue wave-type solutions of the mKdV equation and their relation to known NLSE rogue wave solutions. Nonlinear Dyn. 91, 1931 (2018)

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by the NSF of China under Grant Nos. 11671219, 11801510 and the K.C. Wong Magna Fund in Ningbo University. K. Porsezian acknowledges DST-SERB, NBHM, IFCPAR and CSIR, the Government of India, for financial support through major projects.

Author information

Authors and Affiliations

  1. College of Science, Zhejiang University of Science and Technology, Hangzhou, Zhejiang Province, People’s Republic of China

    Yongshuai Zhang

  2. School of Mathematical Sciences, University of Science and Technology of China, Hefei, 230026, Anhui, People’s Republic of China

    Jiguang Rao

  3. Department of Physics, Pondicherry University, Kalapet, Pondicherry, 605014, India

    K. Porsezian

  4. Department of Mathematics, Ningbo University, Ningbo, 315211, Zhejiang, People’s Republic of China

    Jingsong He

Authors
  1. Yongshuai Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiguang Rao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. Porsezian
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jingsong He
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jingsong He.

Ethics declarations

Conflict of interest

We declare we have no conflict of interests.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Y., Rao, J., Porsezian, K. et al. Rational and semi-rational solutions of the Kadomtsev–Petviashvili-based system. Nonlinear Dyn 95, 1133–1146 (2019). https://doi.org/10.1007/s11071-018-4620-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4620-4

Keywords

Search

Navigation