Skip to main content
SpringerLink
Log in

Darboux Transformation of the Second-Type Derivative Nonlinear Schrödinger Equation

  • Published:
Letters in Mathematical Physics Aims and scope Submit manuscript

Abstract

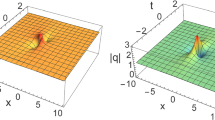
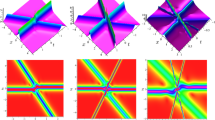
The second-type derivative nonlinear Schrödinger (DNLSII) equation was introduced as an integrable model in 1979. Very recently, the DNLSII equation has been shown by an experiment to be a model of the evolution of optical pulses involving self-steepening without concomitant self-phase-modulation. In this paper, the n-fold Darboux transformation (DT) T n of the coupled DNLSII equations is constructed in terms of determinants. Comparing with the usual DT of the soliton equations, this kind of DT is unusual because T n includes complicated integrals of seed solutions in the process of iteration. By a tedious analysis, these integrals are eliminated in T n except the integral of the seed solution. Moreover, this T n is reduced to the DT of the DNLSII equation under a reduction condition. As applications of T n , the explicit expressions of soliton, rational soliton, breather, rogue wave and multi-rogue wave solutions for the DNLSII equation are displayed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Chen H.H., Lee Y.C., Liu C.S.: Integrability of nonlinear Hamiltonian systems by inverse scattering method. Phys. Scr. 20, 490–492 (1979)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  2. Nakamura A., Chen H.H.: Multi-soliton solutions of a derivative nonlinear Schrödinger equation. J. Phys. Soc. Jpn. 49, 813–816 (1980)

    Article  ADS  MathSciNet  Google Scholar 

  3. Kakei S., Sasa N., Satsuma J.: Bilinearization of a generalized derivative nonlinear Schrödinger equation. J. Phys. Soc. Jpn. 64, 1519–1523 (1995)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  4. Tsuchida T., Wadati M.: New integrable systems of derivative nonlinear Schrödinger equations with multiple components. Phys. Lett. A 257, 53–64 (1999)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  5. Lee J.H., Lin C.K.: The behaviour of solutions of NLS equation of derivative type in the semiclassical limit. Chaos Solitons Fractals 13, 1475–1492 (2002)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  6. Kaup D.J., Newell A.C.: An exact solution for a derivative nonlinear Schrödingere quation. J. Math. Phys. 19, 798–801 (1978)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  7. Wadati M., Sogo K.: Gauge transformations in soliton theory. J. Phys. Soc. Jpn. 52, 394–398 (1983)

    Article  ADS  MathSciNet  Google Scholar 

  8. Kundu A.: Landau–Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrödinger-type equations. J. Math. Phys. 25, 3433–3438 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  9. Ablowitz M.J., Clarkson P.A.: Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1991)

    Book  MATH  Google Scholar 

  10. Rogister A.: Parallel propagation of nonlinear low frequency waves in high β plasma. Phys. Fluids 14, 2733–2739 (1971)

    Article  ADS  Google Scholar 

  11. MjØlhus E.: On the modulational instability of hydromagnetic waves parallel to the magnetic field. J. Plasma Phys. 16, 321–334 (1976)

    Article  ADS  Google Scholar 

  12. Mio K., Ogino T., Minami K., Takeda S.: Modified nonlinear Schrödinger equation for Alfvén waves propagating along the magnetic field in cold plasmas. J. Phys. Soc. Jpn. 41, 265–271 (1976)

    Article  ADS  MathSciNet  Google Scholar 

  13. Johnson R.S.: On the modulation of water waves in the neighbourhood of kh ≈ 1.363. Proc. R. Soc. Lond. A 357, 131–141 (1977)

    Article  ADS  MATH  Google Scholar 

  14. Tzoar N., Jain M.: Self-phase modulation in long-geometry optical waveguides. Phys. Rev. A 23, 1266–1270 (1981)

    Article  ADS  Google Scholar 

  15. Anderson D., Lisak M.: Nonlinear asymmetric self-phase modulation and self-steepening of pulses in long optical waveguides. Phys. Rev. A 17, 1393–1398 (1983)

    Article  ADS  Google Scholar 

  16. Verheest F., Buti B.: Parallel solitary Alfvén waves in warm multispecies beam-plasma systems. Part 1. J. Plasma Phys. 47, 15–24 (1992)

    Article  ADS  Google Scholar 

  17. Moses, J., Malomed, B.A., Wise, F.W.: Self-steepening of ultrashort optical pulses without self-phase-modulation. Phys. Rev. A 76, 021802(R) (2007)

  18. Kawata T., Kobayashi N., Inoue H.: Soliton solution of the derivative nolinear Schrödinger equation. J. Phys. Soc. Jpn. 46, 1008–1015 (1979)

    Article  ADS  MathSciNet  Google Scholar 

  19. Zhou, G.Q., Huang, N.N.: An N-soliton solution to the DNLS equation based on revised inverse scattering transform. J. Phys. A Math. Theor. 40, 13607–13623 (2010). doi:10.1088/1751-8113/40/45/008

  20. Chen X.J., Lam W.K.: Inverse scattering transform for the derivative nonlinear Schrödinger equation with nonvanishing boundary conditions. Phys. Rev. E 69, 066604 (2004)

    Article  ADS  MathSciNet  Google Scholar 

  21. Imai K.: Generlization of Kaup–Newell inverse scattering formulation and Darboux transformation. J. Phys. Soc. Jpn. 68, 355–359 (1999)

    Article  ADS  MATH  Google Scholar 

  22. Steudel H.: The hierarchy of multi-soliton solutions of the derivative nonlinear Schrödinger equation. J. Phys. A Math. Gen. 36, 1931–1946 (2003)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  23. Xu, S.W., He, J.S., Wang, L.H.: The Darboux transformation of the derivative nonlinear Schrödinger equation. J. Phys. A Math. Theor. 44, 305203 (2011)

  24. Guo B.L., Ling L.M., Liu Q.P.: High-order solutions and generalized Darboux transformations of derivative nonlinear Schrödinger equations. Stud. Appl. Math. 130, 317–344 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  25. DeMartini F., Townes C.H., Gustafson T.K., Kelley P.L.: Self-steepening of light pulses. Phys. Rev. 164, 312–323 (1967)

    Article  ADS  Google Scholar 

  26. Grischkowsky D., Courtens E., Armstrong J.A.: Observation of self-steepening of optical pulses with possible shock formation. Phys. Rev. Lett. 31, 422–425 (1973)

    Article  ADS  Google Scholar 

  27. Moses, J., Wise F.W.: Controllable self-steepening of ultrashort pulses in quadratic nonlinear media. Phys. Rev. Lett. 97, 073903 (2006)

  28. Akhmediev N., Ankiewicz A., Taki M.: Waves that appear from nowhere and disappear without a trace. Phys. Lett. A 373, 675–678 (2009)

    Article  ADS  MATH  Google Scholar 

  29. He, J.S., Zhang, H.R., Wang, L.H., Porsezian, K., Fokas, A.S.: A generating mechanism for higher order rogue waves. Phys. Rev. E 87, 052914 (2013)

  30. Solli D.R., Ropers C., Koonath P., Jalali B.: Optical rogue waves. Nature 450, 1054–1057 (2007)

    Article  ADS  Google Scholar 

  31. Kibler B., Fatome J., Finot C., Millot G., Dias F., Genty G., Akhmediev N., Dudley J.M.: The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 6, 790–795 (2010)

    Article  Google Scholar 

  32. Chabchoub, A., Hoffmann, N.P., Akhmediev, N.: Rogue wave observation in a water wave tank. Phys. Rev. Lett. 106, 204502 (2011)

  33. Bailung, H., Sharma, S.K., Nakamura, Y.: Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett. 107, 255005 (2011)

  34. Matveev V.B.: Darboux transformation and explicit solutions of the Kadomtcev–Petviaschvily equation, depending on functional parameters. Lett. Math. Phys. 3, 213–216 (1979)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  35. Matveev V.B.: Darboux transformation and the explicit solutions of differential–difference and difference–difference evolution equations I. Lett. Math. Phys. 3, 217–222 (1979)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  36. Matveev V.B., Salle M.A.: Differential–difference evolution equations. II (Darboux transformation for the Toda lattice). Lett. Math. Phys. 3, 425–429 (1979)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  37. Matveev V.B.: Some comments on the rational solutions of the Zakharov–Schabat equations. Lett. Math. Phys. 3, 503–512 (1979)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  38. Darboux, G.: Sur une proposition relative aux equations lineaires. C. R. Acad. Sci. 94, 1456–1459 (1882)

  39. Peregrine D.H.: Water waves, nonlinear Schrödinger equations and their solutions. J. Aust. Math. Soc. Ser. B 25, 16–43 (1983)

    Article  MATH  MathSciNet  Google Scholar 

  40. Akhmediev N., Eleonsky V., Kulagin N.: Generation of periodic trains of picosecond pulses in an optical fiber: exact solutions. Sov. Phys. JETP 62, 894–899 (1985)

    Google Scholar 

  41. Akhmediev, N., Ankiewicz, A., Soto-Crespo, J.M.: Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E 80, 026601 (2009)

  42. Ankiewicz, A., Clarkson, P., Akhmediev, N.: Rogue waves, rational solutions, the patterns of their zeros and integral relations. J. Phys. A Math. Theor. 43, 122002 (2010)

  43. Kedziora, D.J., Ankiewicz, A., Akhmediev, N.: Circular rogue wave clusters. Phys. Rev. E 84, 056611 (2011)

  44. Ankiewicz, A., Soto-Crespo, J.M., Akhmediev, N.: Rogue waves and rational solutions of the Hirota equation. Phys. Rev. E 81, 046602 (2010)

  45. Tao, Y.S., He, J.S.: Multisolitons, breathers, and rogue waves for the Hirota equation generated by the Darboux transformation. Phys. Rev. E 85, 026601 (2012)

  46. Bandelow, U., Akhmediev, N.: Sasa–Satsuma equation: soliton on a background and its limiting cases. Phys. Rev. E 86, 026606 (2012)

  47. He, J.S., Xu, S.W., Porsezian, K.: Rogue waves of the Fokas–Lenells equation. J. Phys. Soc. Jpn. 81, 124007 (2012)

  48. Dubard P., Gaillard P., Klein C., Matveev V.B.: On multi-rogue wave solutions of the NLS equation and positon solutions of the KdV equation. Eur. Phys. J. Spec. Top. 185, 247–258 (2010)

    Article  Google Scholar 

  49. Dubard, P.: Multi-rogue solutions of to the focusing NLS equation. PhD thesis, Université de Bourgogne, Dijon (2010). https://tel.archives-ouverts.fr/tel-00625446/document

  50. Dubard P., Matveev V.B.: Multi-rogue waves solutions to the focusing NLS equation and the KP-I equation. Nat. Hazards Earth Syst. Sci. 11, 667–672 (2011)

    Article  ADS  Google Scholar 

  51. Gaillard, P.: Families of quasi-rational solutions of the NLS equation and multi-rogue waves. J. Phys. A Math. Theor, 44, 435204 (2011)

  52. Gaillard, P.: Degenerate determinant representation of solutions of the nonlinear Schrödinger equation, higher order Peregrine breathers and multi-rogue waves. J. Math. Phys, 54, 013504 (2013)

  53. Dubard P., Matveev V.B.: Multi-rogue waves solutions: from NLS to KP-I equation. Nonlinearity 26, R93–R125 (2013)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  54. Ohta, Y., Yang, J.K.: Rogue waves in the Davey–Stewartson I equation. Phys. Rev. E 86, 036604 (2012)

  55. Gui, M., Yun, Q.Z.: Rogue waves for the coupled Schrödinger–Boussinesq equation and the coupled Higgs equation. J. Phys. Soc. Jpn. 81, 084001 (2012)

  56. Matveev V.B., Salle M.A.: Darboux Transformations and Solitons. Springer, Berlin (1991)

    Book  MATH  Google Scholar 

  57. Gu C.H., Hu H.S., Zhou Z.X.: Darboux Trasformations in Integrable Systems. Springer, Dortrecht (2006)

    Google Scholar 

  58. Salle M.A.: Darboux transformations for non-Abelian and nonlocal equations of the Toda chain type. Teoret. Mat. Fiz. 53, 227–237 (1982)

    MathSciNet  Google Scholar 

  59. Neugebauer G., Meinel R.: General N-soliton solution of the AKNS class on arbitrary background. Phys. Lett. A 100, 467–470 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  60. Li Y.S., Gu X.S., Zou M.R.: Three kinds of Darboux transformation for the evolution equation which connect with AKNS eigenvalue problem. Acta Math. Sin. (New Ser.) 3, 143–151 (1985)

    MathSciNet  Google Scholar 

  61. Gu C.H., Zhou Z.X.: On the Darboux matrix of Backlund transformations of the AKNS system. Lett. Math. Phys. 13, 179–187 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  62. He J.S., Zhang L., Cheng Y., Li Y.S.: Determinant representation of Darboux transformation for the AKNS system. Sci. China Ser. A Math. 12, 1867–1878 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  63. Xu, S.W., He, J.S.: The rogue wave and breather solution of the Gerdjikov–Ivanov equation. J. Math. Phys. 53, 063507 (2012)

  64. Kuznetsov E.A.: Solitons in a parametrically unstable plasma. Sov. Phys. Dokl. 22, 507–508 (1977)

    ADS  Google Scholar 

  65. Ma Y.C.: The perturbed plane-wave solutions of the cubic Schrödinger equation. Stud. Appl. Math. 60, 43–58 (1979)

    ADS  MathSciNet  Google Scholar 

  66. Guo, B.L., Ling, L.M., Liu, Q.P.: Nonlinear Schrödinger equation: generalized Darboux transformation and rogue wave solutions. Phys. Rev. E 85, 026607 (2012)

  67. He, J.S., Xu, S.W., Porseizan, K.: N-order bright and dark rogue waves in a resonant erbium-doped fiber system. Phys. Rev. E 86, 066603 (2012)

  68. Li L.J., Wu Z.W., Wang L.H., He J.S.: High-order rogue waves for the Hirota equation. Ann. Phys. 334, 198–211 (2013)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  69. Wang, L.H., Porsezian, K., He, J.S.: Breather and rogue wave solutions of a generalized nonlinear Schrödinger equation. Phys. Rev. E 87, 053202 (2013)

  70. Xu, S.W., He, J.S., Cheng, Y., Porsezian, K.: The N-order rogue waves of Fokas–Lenells equation. Math. Meth. Appl. Sci. (2014). doi:10.1002/mma.3133

  71. Zhang Y.S., Guo L.J., Xu S.W., Wu Z.W., He J.S.: The hierarchy of higher order solutions of the derivative nonlinear Schrödinger equation. Commun. Nonlinear Sci. Numer. Simul. 19, 1706–1722 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  72. Guo, L.J., Zhang, Y.S., Xu, S.W., Wu, Z.W., He, J.S.: The higher order rogue wave solutions of the Gerdjikov–Ivanov equation. Phys. Scr. 89, 035501 (2014)

  73. Zakharov, V.E., Gelash, A.A.: Nonlinear stage of modulation instability. Phys. Rev. Lett. 111, 054101 (2013)

  74. Shrira V.I., Geogjaey V.V.: What makes the Peregrine soliton so special as a prototype of freak waves?. J. Eng. Math. 67, 11–22 (2010)

    Article  MATH  Google Scholar 

  75. Calini A., Schober C.M.: Numerical investigation of stability of breather-type solutions of the nonlinear Schrödinger equation. Nat. Hazards Earth Syst. Sci. 14, 1431–1440 (2014)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Ningbo University, Ningbo, 315211, Zhejiang, People’s Republic of China

    Yongshuai Zhang, Lijuan Guo & Jingsong He

  2. School of Mathematical Sciences, Fudan University, Shanghai, 200433, People’s Republic of China

    Zixiang Zhou

Authors
  1. Yongshuai Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lijuan Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jingsong He
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zixiang Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jingsong He.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Y., Guo, L., He, J. et al. Darboux Transformation of the Second-Type Derivative Nonlinear Schrödinger Equation. Lett Math Phys 105, 853–891 (2015). https://doi.org/10.1007/s11005-015-0758-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11005-015-0758-x

Mathematics Subject Classification

Keywords

Search

Navigation