Coherent neural oscillations induced by weak synaptic noise

Abstract

We analyze the effect of synaptic noise on the dynamics of the FitzHugh–Nagumo (FHN) neuron model. In our deterministic parameter regime, a limit cycle solution cannot emerge through a singular Hopf bifurcation, but such a limit cycle can nevertheless arise as a stochastic effect, as a consequence of weak synaptic noise in a regime of strong timescale separation ($\varepsilon \rightarrow 0$) between the slow and fast variables of the model. We investigate the mechanism behind this phenomenon, known as self-induced stochastic resonance (SISR) (Muratov et al. in Physica D 210:227–240, 2005), by using multiple-time perturbation techniques and by analyzing the escape mechanism of the random trajectories from the stable manifolds of the model equation. Even though SISR occurs only in the limit as the singular parameter $\varepsilon \rightarrow 0$, decreasing $\varepsilon$ does not increase the coherence of the oscillations in the FHN model, but rather increases the interval of the noise amplitude $\sigma$ for which coherence occurs. This is in contrast to the dynamical system studied in Muratov et al. (2005). Moreover, the phenomenon is robust under parameter tuning. Numerical simulations exhibit the results predicted by the theoretical analysis. In fact, our analysis together with that in Yamakou and Jost (Weak noise-induced transitions with inhibition and modulation of neural oscillations, 2017) reveals that the FHN model can support different stochastic resonance phenomena. While it had been known (Pikovsky and Kurths in Phys Rev Lett 78:775–778, 1997) that coherence resonance can occur when the slow variable is subjected to noise, we show that, when noise is added to the fast variable, two other types, inverse stochastic resonance and SISR, may emerge in the same weak noise limit and that the transition between these phenomena can be induced by varying a simple parameter.

1 Introduction

Since electrical information in the nervous system is encoded, processed, and transmitted by trains of neuronal action potentials [4, 5], a major goal in neuroscience is to understand how neurons generate action potentials both spontaneously and in response to possibly random synaptic and ion channel inputs. It is a standard electrophysiological observation that neurons with nearly identical physiological features and external stimuli may react differently and therefore exhibit different neurocomputational properties. Conversely, neurons having different physiological features and external stimuli may show nearly identical activities. It is generally believed that these variances in neuronal behavior are caused by differences in the neurons’ bifurcation dynamics. The latter, however, can only be understood with the help of sophisticated tools from nonlinear dynamics.

Noise is ubiquitous in neural systems. It may arise from many different sources, and it may have different effects. In fact, depending on the deterministic parameter regime of a neuron model, the addition of noise to either the membrane potential variable and/or the recovery current variable can induce different dynamical effects. Some of these effects can be somewhat counterintuitive, as noise, instead of being a nuisance, in some settings actually plays a constructive role in signal detection.

The sources of neuronal noise include synaptic noise, that is, the quasi-random release of neurotransmitters by synapses or random synaptic input from other neurons, and channel noise, that is, the random switching of ion channels. Since contributions of the inherently stochastic nature of voltage-gated ion channels to neuronal noise levels are widely assumed to be minimal, because typically a large number of ion channels are involved and fluctuations should therefore average out, the channel noise is frequently ignored in the mathematical modeling. Synaptic noise on the other hand is believed to be the dominant source of membrane potential fluctuations in neurons, and it can have a strong influence on their integrative properties [6]. In this paper, we shall investigate the effects of synaptic noise on the fast membrane potential variable of the FHN neuron model. Here, we do not consider channel noise, which, however, could be included by simply adding it to the slow current recovery variable equation of this neuron model.

Of course, we are not the first to study noise-induced phenomena in the context of computational neuroscience. Let us therefore briefly discuss four such phenomena treated in the literature. The oldest such phenomenon is stochastic resonance (SR). It was first proposed in 1981 by Benzi et al. [7] in order to explain the periodic recurrence of ice ages. The idea behind SR is that a system in a noisy environment becomes more sensitive to a subthreshold periodic perturbation at some optimal finite level of noise intensity. In 1993, Douglass et al. [8] reported the first experimental demonstration of SR in crayfish sensory neurons. This, coupled with the development of a more general characterization of SR as a threshold phenomenon independent of dynamics, led to a widespread interest in applications of the idea in biological systems, in general, and in computational neuroscience in particular [9, 10].

In 1993, Longtin [11] demonstrated the occurrence of SR in a computational neuron model. Here, the 2-dimensional FHN neuron model is considered and perturbed by a subthreshold external periodic stimulus and a noisy stimulus governed by an Ornstein–Uhlenbeck process. As predicted by the SR scheme (see also [12]), it was shown that the oscillation of the FHN neuron becomes more closely correlated with the subthreshold periodic input current at some optimal level of noise intensity. The stochastic analysis of the FHN neuron and other neuron models has been extensively studied in recent years with various types of noises, multi-stability, and even how SR can be controlled; see, for example, [13,14,15,16,17,18,19,20,21,22,23].

In 1997, Pikovsky and Kurths [3] reported on another noise-induced phenomenon in an excitable system. They considered the FHN neuron model with the noise term added to the slow recovery variable equation containing the Hopf bifurcation parameter. For this neuron model, they then showed that, even in the absence of an external periodic stimulus (unlike SR), the noise could activate the neuron by producing a sequence of pulses that could achieve a maximal degree of coherence for an optimal noise amplitude, provided the bifurcation parameter is in the neighborhood of its Hopf bifurcation value. They called this phenomenon coherence resonance (CR). Following [3], many research papers have investigated CR in a variety of systems ranging from multiple timescale systems [24,25,26] to systems with no multiple timescales [27, 28]. CR has also been extensively studied [29,30,31,32,33,34,35,36] and the relation between CR and chimeras states in network of excitable systems has also been recently reported [37].

In 2005, Muratov et al. discovered and developed the fundamental theory (based on large deviation theory [38, 39]) of a new form of coherence behavior. They called this new phenomenon self-induced stochastic resonance (SISR); here, a weak noise amplitude could induce coherent oscillations (a limit cycle behavior) that the deterministic model equation cannot exhibit [1]. SISR has been investigated theoretically and numerical in different systems including Brownian ratchets and cancer model [40,41,42,43]. A natural question is: in what ways is SISR different from SR and CR? First, unlike SR and CR, which do not necessarily require a system to evolve on a multiple timescale [27, 44], SISR requires the system to possess fast and slow timescales. Moreover, in the complete absence of a deterministic perturbation or in the presence of a subthreshold deterministic perturbation, SISR may occur. This contrasts with SR, which always requires a subthreshold periodic perturbation (in fact, SR is precisely the enhancement of this weak low-frequency harmonic signal by some optimal noise strength). Also, in contrast to CR, SISR does not require the model parameter to be in the immediate neighborhood of its bifurcation value. Thus SISR, unlike CR, is robust to parameter tuning.

In the FHN neuron model, coherent spike trains emerge through very different mechanisms depending on whether the noise term is added to the fast variable (SISR) or to the slow variable (CR); the former is analyzed in the present paper, and for the latter, see [3, 24, 25, 45]. There are, however, examples of multiple timescale systems in which CR occurs when the noise term is added to the fast variable equation, which contains the bifurcation parameter (see, e.g., [26]). What is crucial for CR is the proximity of the parameter to the bifurcations (Hopf or saddle-node bifurcations on a limit cycle).

In all of these phenomena (SR, CR, and SISR), noise has a facilitating effect on the oscillations and increases coherent responses. Noise can, however, also have the opposite effect and turn-off repetitive neuronal activity, as was discovered both experimentally [46] and theoretically [47]. In fact, Gutkin et al. [47,48,49] used neural model equations with a mean input current consisting of both a constant deterministic and a random input component, to computationally confirm the inhibitory and modulation effects of noise on the neuron’s spiking activity. They found that there is a tuning effect of noise that has a character opposite to SR, CR, and SISR. They called this other noise-induced phenomenon inverse stochastic resonance (ISR). During ISR, when the intensity of the (weak) noise amplitude is increased, it will first strongly inhibit the spiking activity and decrease the mean number of spikes to a minimal value, but a further increase in the noise amplitude will increase the mean number of spikes again, even above what is observed in the noise-free case. Mathematically, ISR has not been extensively studied as compared to other resonance phenomena; see [50,51,52,53], and it was recently confirmed experimentally in [54].

In the current paper, we analyze the mechanism behind SISR in the FHN neuron model under the influence of synaptic noise. We clarify the different conditions leading to either SISR or ISR (analyzed in our previous paper [2]) in the weak synaptic noise limit. For the FHN model, we obtain the interval in which the noise amplitude $\sigma$ has to lie in order to induce a coherent spike train (SISR) in the limit as $\varepsilon \rightarrow 0$. We also determine another very small interval for $\sigma$ in which the FHN neuron generates only a Poisson sequence of spikes in the limit as $\varepsilon \rightarrow 0$. One of the most important findings of our paper is that, even though SISR occurs only in the limit as the singular parameter $\varepsilon \rightarrow 0$, decreasing $\varepsilon$ does not increase the coherence of the oscillations due SISR in the FHN model, but rather increases the interval of $\sigma$ for which coherence occurs. That is, making $\varepsilon \rightarrow 0$ does not improve the coherence of the oscillations (the coefficient of variation, CV, does not turn to 0; it stays low and constant) when the conditions required for SISR are satisfied. This is in contrast to the excitable model considered in [1], where theoretical and numerical analyses show that when the conditions required for SISR are satisfied (which are essentially the same conditions as required for SISR in the FHN model), the coherence of the oscillations becomes perfect ($\hbox {CV}\rightarrow 0$) in the limit as the singular parameter turns to 0 (see Fig. 3(b) in [1]). Therefore, the coherence of the oscillations as the singular parameter turns to 0 depends on the excitable model under consideration, and this might be worth to be investigated in more detail.

Furthermore, our analysis also clarifies the crucial difference between the deterministic parameter setting required for SISR to occur and those required for the occurrence ISR (analyzed in [2]) in the FHN model. We find that it depends on the stability of the (unique) fixed point and whether it is located to either the left or right of the fold point of the critical manifold, whether SISR or ISR can emerge in the same weak noise limit. We thereby produce a unified mathematical setting to analyze both ISR and SISR. This allows us to understand how a neuron could effectively switch from one phenomenon to the other (thus encoding different information) without changing the weak synaptic noise limit required for both phenomena to occur.

The rest of the paper is organized as follows: Sect. 2 introduces the version of the neuron model used for our investigation. Section 3 analyzes the deterministic dynamics of the model equation: The singular Hopf bifurcation scenario of the fixed point considered is investigated. We define the critical manifold of the model equation on which we determine the reduced equation of the fast variable together with its evolution timescale. In Sect. 4, we analyze the stochastic dynamics: For the model equation, we obtain the order of the stochastic timescale at which random trajectories escape from the basins of attraction of the stable parts of the critical manifold. In Sect. 5, we analyze the scaling asymptotic limit of the deterministic and stochastic timescales and the consequences on resonance. In Sect. 6, we characterize the limit cycle behavior induced by noise. In Sect. 7, we present and discuss numerical results. We have concluding remarks in Sect. 8.

2 Model equation

The FHN neuron model (for biophysical details, see [55]) has been extensively used to investigate many complex dynamical behaviors occurring in neuroscience [56,57,58,59,60]. For our investigation of SISR, we consider the following version of the FHN neuron model written on the slow timescale $\tau$ as

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} \hbox {d}v_{\tau }&{}=&{}\varepsilon ^{-1}f(v_{\tau },w_{\tau })\hbox {d}\tau +\frac{\sigma }{\sqrt{\varepsilon }}\hbox {d}W_{\tau },\\ \hbox {d}w_{\tau }&{}=&{}g(v_{\tau },w_{\tau })\hbox {d}\tau , \end{array}\right. \end{aligned} \end{aligned}$$

(1)

with the deterministic velocity vector fields given by

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} f(v,w)&{}=&{}v-\frac{v^3}{3}-w,\\ g(v,w)&{}=&{}v+d-c w, \end{array}\right. \end{aligned} \end{aligned}$$

(2)

where $0<\varepsilon :=\tau /t\ll 1$ is the timescale separation parameter between the slow timescale $\tau$ and the fast timescale t; the fast variable $v\in \mathbb {R}$ represents the membrane potential (or action potential) variable and the slow variable $w\in \mathbb {R}$ represents the recovery current (or sodium gating) variable which restores the resting state of the neuron model. Biologically, $\varepsilon$ accounts for the slow kinetics of the sodium channel in the nerve cell and controls the main morphology of the action potential generated [61]. $d\in (0,1)$ is a constant parameter, and $c>0$ is a co-dimension-one Hopf bifurcation parameter. d and c influence the generation of the action potential, and their ranges have been chosen such that the FHN model best captures some excitable–oscillatory behaviors of the biophysically more realistic Hodgkin–Huxley neuron model [55, 61,62,63].

$\hbox {d}W_\tau$ is standard white noise, the formal derivative of Brownian motion with mean zero and unit variance. This term which is added to the membrane potential variable (v) equation mimics the influence of synaptic noise on the dynamics of the neuron [64]. We note that because of the scaling law of Brownian motion, the scaling $\frac{\sigma }{\sqrt{\varepsilon }}$ of the noise term will guarantee that the amplitude of the noise ($\sigma$) measures the relative strength of the noise term compared to the deterministic term f(v, w) irrespective of the value of $\varepsilon$, when we transform Eq. (1) to its equivalent fast timescale equation [see Eq. (22)].

To analyze SISR, we notice that in Eq. (1), the random term is added to the membrane potential variable equation to mimic the effect of synaptic noise. This is different for CR in the FHN model, where the random term is added instead to the recovery variable to mimic the effect of channel noise (see [3, 24, 25]). We further note that, just as for the phenomenon of CR, our model equation in Eq. (1) has no periodic perturbation, in contrast to the phenomenon of SR [11].

3 Deterministic dynamics and its timescale on stable manifolds

The deterministic dynamics and the emergence of a limit cycle solution (relaxation oscillation) in the FHN neuron model equation have been studied extensively [65,66,67,68,69,70], and various types of behavior were detected or confirmed. In this section, we shall establish the deterministic setting in which we want our neuron model to be before a random perturbation is introduced into the equation. In particular, we shall clarify the role played by the relative positioning of the fixed point and the local minimum of the cubic nullcline in the occurrence of either SISR or ISR (analyzed in [2]) in the FHN neuron. It seems to be a new discovery that just (carefully) changing the position of the fixed point with respect to the minimum of the cubic nullcline of the FHN neuron model can lead to very different noise-induced phenomena (in particular SISR and ISR) in the same weak noise limit. We shall also determine the timescale of the slow dynamics of the fast variable v on the stable parts of the critical manifold.

We thus consider the deterministic dynamics corresponding to the behavior of Eq. (1) when $\sigma =0$. At the fixed (or equilibrium) points $(v_e,w_e)$ (rest states of the neuron), the variables $v(\tau )$ and $w(\tau )$ reach a stationary state, while the set of equilibrium points defined by the intersection of nullclines as

$$\begin{aligned} (v_e,w_e):=\Big \{(v,w)\in \mathbb {R}^2:f(v,w)=g(v,w)=0\Big \} \end{aligned}$$

(3)

depends on the parameters $d\in (0,1)$ and $c>0$. The sign of

$$\begin{aligned} \Delta =\displaystyle {\left( \frac{1}{c}-1\right) ^3+9\frac{d^2}{4c^2}} \end{aligned}$$

(4)

determines the number of fixed points. If $\Delta >0$, we have a unique fixed point given by

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} \displaystyle {v_e=-\frac{\root 3 \of {2}\big (-9+\frac{9}{c}\big )}{3I(c,d)}+\frac{I(c,d)}{3\root 3 \of {2}}},\\ \displaystyle {w_{e}=\frac{1}{c}(v_{e}+d)},\\ \displaystyle {I(c,d)=\root 3 \of {-\,81\frac{d}{c}+\sqrt{4\Big (-\,9+\frac{9}{c}\Big )^3+6561\frac{d^2}{c^2}}}}. \end{array}\right. \end{aligned} \end{aligned}$$

(5)

If $\Delta < 0$, three real and distinct solutions (fixed points) exist. For this, we need $c>1$ or $c<0$. The three fixed points are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {v_{e_1}=2\sqrt{1-\frac{1}{c}}\sin \phi }, \,\,\ \displaystyle {w_{e_1}=\frac{1}{c}(v_{e_1}+d)}. \\ \displaystyle {v_{e_2}=-\,2\sqrt{1-\frac{1}{c}}\sin \left( \phi +\frac{\pi }{3}\right) }, \,\,\ \displaystyle {w_{e_2}=\frac{1}{c}(v_{e_2}+d)}. \\ \displaystyle {v_{e_3}=2\sqrt{1-\frac{1}{c}}\sin \left( -\,\phi +\frac{\pi }{3}\right) }, \,\,\ \displaystyle {w_{e_3}=\frac{1}{c}(v_{e_3}+d)}. \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} \displaystyle {\phi =\frac{1}{3}\arcsin \left[ \frac{3d}{2c\sqrt{(1-\frac{1}{c})^3}}\right] }. \end{aligned}$$

As $\Delta < 0$ if and only if $\phi \in (-\,\frac{\pi }{6},\frac{\pi }{6})$, we have $v_{e_2}<v_{e_1}<v_{e_3}$.

If $\Delta =0$, we have two fixed points. This happens if and only if $\phi =\pm \,\frac{\pi }{6}$. These limiting cases correspond to saddle-node-type bifurcations during which two fixed points in the case $\Delta < 0$ coincide. If $\phi =\frac{\pi }{6}$, then $v_{e_1}$ and $v_{e_3}$ will coincide and the two fixed points are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {v_{e_1}=v_{e_3}=2\sqrt{1-\frac{1}{c}}}, \,\,\ \displaystyle {w_{e_1}=\frac{1}{c}(v_{e_1}+d)}. \\ \displaystyle {v_{e_2}=-\,2\sqrt{1-\frac{1}{c}}}, \,\,\ \displaystyle {w_{e_2}=\frac{1}{c}(v_{e_2}+d)}. \end{array}\right. } \end{aligned}$$

If $\phi =-\frac{\pi }{6}$, then $v_{e_1}$ and $v_{e_2}$ will coincide and the two fixed points are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {v_{e_1}=v_{e_2}=-\sqrt{1-\frac{1}{c}}}, \,\,\ \displaystyle {w_{e_1}=\frac{1}{c}(v_{e_1}+d)}. \\ \displaystyle {v_{e_3}=2\sqrt{1-\frac{1}{c}}}, \,\,\ \displaystyle {w_{e_3}=\frac{1}{c}(v_{e_3}+d)}. \end{array}\right. } \end{aligned}$$

We denote such a fixed point by $(v_\star ,w_{\star })$ and study its stability from the linearization of Eq. (1) at the fixed point chosen. The linearization at $(v_\star ,w_{\star })$ is given by

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} \varepsilon \dfrac{\hbox {d}\varphi }{\hbox {d}\tau }&{}=&{} \varphi -v_{\star }^2\varphi -\eta ,\\ \dfrac{\hbox {d}\eta }{\hbox {d}\tau }&{}=&{} \varphi -c \eta , \end{array}\right. \end{aligned} \end{aligned}$$

(6)

with the Jacobian matrix

$$\begin{aligned} J_{ij}(v_\star ,w_{\star })=\left( \begin{array}{cc} \frac{1}{\varepsilon }(1-v_\star ^2 )&{} \,\,\,\,-\frac{1}{\varepsilon }\\ \\ 1&{}\,\,\,\,-c \end{array} \right) . \end{aligned}$$

(7)

The stability of a fixed point $(v_\star ,w_{\star })$ depends on the signs of the trace ($\mathrm {tr}J_{ij}$) and the determinant ($\mathrm {det} J_{ij}$) of the Jacobian matrix in Eq. (7). For a fixed point $(v_\star ,w_{\star })$ to be stable, we need $\mathrm {tr}J_{ij}<0$ and $\mathrm {det} J_{ij}>0$. Since $\varepsilon ,c >0$, we have $\mathrm {tr}J_{ij}<0$ and $\mathrm {det} J_{ij}>0$ only if

$$\begin{aligned} 1-v_\star ^2<0. \end{aligned}$$

(8)

It is important to note here that the condition in Eq. (8) is sufficient, but not necessary for the stability of a fixed point $(v_\star ,w_{\star })$. In [2], this was crucial for the analysis of ISR, via the consequences that the stability of a fixed point has on the dynamics of the slow–fast neuron model when the condition in Eq. (8) is violated.

In the present paper, we shall choose c and d such that $\Delta$ in Eq. (4) is greater than 0, in which case we have a unique fixed point at $(v_e,w_e)$ given by Eq. (5). We also choose c and d such that $1-v_e^2<0$, so that we have a unique and stable fixed point located at $(v_e,w_e)$. For the FHN neuron model with a unique and stable fixed point, in the absence of any perturbation as in Eq. (1) with $\sigma =0$ (or in general in the presence of a subthreshold perturbation), the neuron cannot maintain a self-sustained oscillation (i.e., no limit cycle solution). One says in this case that the neuron is in the excitable regime [71]. In this regime, choosing an initial condition in the basin of attraction of $(v_e,w_e)$ will result in at most one large non-monotonic excursion into the phase space after which the trajectory returns exponentially fast to this fixed point and stays there until the initial conditions are changed again.

However, as we saw in [2], the existence of a unique and stable fixed point in the FHN model with no perturbation (or even with a subthreshold perturbation) by itself does not necessarily mean that the neuron is in an excitable regime, as in some cases it might have just one stable fixed point coexisting with a stable limit cycle. We consider here the case of a bistable regime (a crucial requirement for the occurrence ISR) consisting of a stable fixed point and a stable limit cycle (see also [72, 73]) in which the dynamical behavior is globally different from the one in the excitable regime.

With parameters c and d chosen such that condition Eq. (8) holds for the fixed point $(v_e,w_e)$ in Eq. (5), a Hopf bifurcation is the only way through which Eq. (1) (with $\sigma =0$) can exhibit a limit cycle solution. As we shall see later why this should be so, the noise-induced phenomenon of SISR requires that the timescale parameter $\varepsilon \rightarrow 0$. For the deterministic system in Eq. (1), we shall, for $\varepsilon \rightarrow 0$, calculate a special value of $c=c_\mathrm{H}$ that will give us the location of the so-called singular Hopf bifurcation of the fixed point $(v_e,w_e)$. A singular Hopf bifurcation in Eq. (1) with $\sigma =0$ (and in planar slow–fast dynamical systems in general) is said to occur if the linearized center manifold system has a pair of singular eigenvalues $\lambda (\varepsilon ;c)$ at the Hopf bifurcation point $c=c_\mathrm{H}$ [74], that is,

$$\begin{aligned} \lambda (\varepsilon ;c)=\mu (\varepsilon ;c)+i\beta (\varepsilon ;c), \end{aligned}$$

so that $\mu (\varepsilon ;c)=0$, $\displaystyle {\frac{d}{dc}\mu (\varepsilon ;c)\ne 0}$, with

$$\begin{aligned} \begin{aligned}&\lim \limits _{\varepsilon \rightarrow 0}|\beta (\varepsilon ;c)|=\infty \,\,\, \text {on the slow timescale}~ \tau ,~\text {and}\\&\lim \limits _{\varepsilon \rightarrow 0}\beta (\varepsilon ;c)=0\,\,\, \text {on the fast timescale}~t. \\ \end{aligned} \end{aligned}$$

Clearly, for the fixed point $(v_e,w_e)$ in Eq. (5), with the associated linearization in the slow timescale $\tau$ given by the matrix $J_{ij}$ in Eq. (7), the Hopf bifurcation occurs at $\mathrm {tr}J_{ij}=0$, that is, at $c=\frac{1}{\varepsilon }(1-v_e^2)$. The eigenvalues of $J_{ij}(v_e,w_e)$ at the Hopf bifurcation are $\lambda _{\pm }=\pm \, i\sqrt{\frac{1}{\varepsilon }-c(1-v_e^2)}$ which tend to infinity as $\varepsilon \rightarrow 0$. Alternatively, we can also look at Eq. (1) on the fast timescale $t=\tau /\varepsilon$ [see Eq. (17)] with linearization $\varepsilon J_{ij}(v_e,w_e)$ and eigenvalues at the Hopf bifurcation given by $\lambda _{\pm }=\pm \, i\sqrt{\varepsilon [1-c(1-v_e^2)]}$ which tend to 0 as $\varepsilon \rightarrow 0$. On both timescales, the eigenvalues at the Hopf bifurcation are “singular.” In short, a singular Hopf bifurcation occurs when the eigenvalues become singular as $\varepsilon \rightarrow 0$. We shall return to the singular Hopf bifurcation later.

We now need to define the critical manifold of Eq. (1), to determine its stability properties and to obtain the reduced equation describing the evolution of the fast variable v and the deterministic timescale at which v evolves on this manifold. The deterministic critical manifold $\mathcal {M}_0$ defining the phase space of the slow sub-system associated with Eq. (1) [that is, the system we obtain from Eq. (1) in the singular limit $\varepsilon =0$] is, by solving $f(v,w)=0$ for the slow variable w, given by

$$\begin{aligned} \mathcal {M}_0:=\left\{ (v,w)\in \mathbb {R}^2: w=\displaystyle {v-\frac{v^3}{3}}\right\} . \end{aligned}$$

(9)

We note that $\mathcal {M}_0$ coincides with the v-nullcline of the neuron model; see the red cubic curve in Fig. 1a, b. This manifold is normally hyperbolic away from the fold points at $v=\pm \,1$ satisfying $\displaystyle {\frac{\mathrm{d}w}{\mathrm{d}v}(\pm \,1)=0}$ and naturally splits into three sub-manifolds:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} v_{-}^*(w)&{}=&{}\mathcal {M}_0\cap \{v<-1\},\\ v_{0}^*(w)&{}=&{}\mathcal {M}_0\cap \{-1\le v \le 1\},\\ v_{+}^*(w)&{}=&{}\mathcal {M}_0\cap \{v>1\}. \end{array}\right. \end{aligned} \end{aligned}$$

(10)

The linearized stability of points on $\mathcal {M}_0$ as steady states of the fast sub-system [that is, the system we obtain in the singular limit $\varepsilon =0$ of Eq. (1) when it is written on the fast timescale t, that is, Eq. (17)], is determined by the Jacobian scalar $(D_vf)(v,w)=1-v^2$. This shows that points with $|v|>1$ are stable, while points with $|v|<1$ are unstable. It follows that the branch $v_{-}^*(w)\in (-\,\infty ,-\,1)$ is stable, $v_0^*(w)\in [-\,1,1]$ is unstable, and $v_+^*(w)\in (1,+\infty )$ is stable. A trajectory will therefore be attracted to $v_{-}^*(w)$ or $v_{+}^*(w)$ (depending on initial conditions) and move along these stable manifolds toward the stable fixed point or fold points. Along $v_{0}^*(w)$, motion is not possible as it is a repulsive branch of $\mathcal {M}_0$. Motion is however possible on $v_{0}^*(w)$ when conditions for the so-called canard explosion [75] are satisfied. This situation is not of interest in the context of this work.

For simplicity, we shall denote the basins of attraction of the stable parts of the critical manifold $v_{-}^*(w)$ and $v_{+}^*(w)$ [that is, the sets of initial conditions that asymptotically lead to $v_{-}^*(w)$ or $v_{+}^*(w)$] by $\mathcal {B}(v_{-}^*(w))$ and $\mathcal {B}(v_{+}^*(w))$, respectively. $v_{0}^*(w)$ plays the role of the separatrix between these basins of attraction.

From Fenichel’s invariant manifold theorem [76], we know that, while the dynamics of the slow sub-system takes place on the critical manifold $\mathcal {M}_0$, the dynamics of the full system [the dynamics of Eq. (1) when $\varepsilon \ne 0$, i.e., $\varepsilon$ strictly different from 0] takes place not on $\mathcal {M}_0$ itself, but on a perturbed $\mathcal {M}_0$, the so-called slow manifold denoted by $\mathcal {M}_{\varepsilon }$. The theorem states that $\mathcal {M}_{\varepsilon }$ is at a distance of $\mathcal {O}(\varepsilon )$ from $\mathcal {M}_0$ and the flow on $\mathcal {M}_{\varepsilon }$ converges to the flow of the slow sub-system on $\mathcal {M}_0$ as $\varepsilon \rightarrow 0$. This can be seen in Fig. 1. Here, the black trajectories (with arrows) of the slow sub-system in Fig. 1a evolve on $\mathcal {M}_0$ with fast jumps (indicated by the horizontal double arrows) at the fold points of $\mathcal {M}_0$. In Fig. 1b, we see the trajectories of the full system for 3 different values of the singular parameter $\varepsilon$. We see that with $\varepsilon \ne 0$, the trajectories of the full system do not move on $\mathcal {M}_0$, but instead move at a distance from $\mathcal {M}_0$, that is, on the slow manifold $\mathcal {M}_{\varepsilon }$ (not shown). In Fig. 1b, trajectories get closer and closer to $\mathcal {M}_0$ and eventually will coincide with the trajectories of the slow sub-system in Fig. 1a in the limit as $\varepsilon \rightarrow 0$.

Therefore, because the noise-induced phenomenon under investigation in this paper occurs only in the limit as $\varepsilon \rightarrow 0$, this suggests to consider the approximation where the full dynamics of Eq. (1) (with $\varepsilon \rightarrow 0$) takes place on the critical manifold $\mathcal {M}_0$, which, as just explained, is very close to $\mathcal {M}_{\varepsilon }$ in the limit $\varepsilon \rightarrow 0$. In other words, the full dynamics of Eq. (1) (with $\varepsilon \rightarrow 0$) will coincide with the dynamics of the slow sub-system whose equation is given by Eq. (11), itself obtained in the singular limit $\varepsilon =0$. Moreover, with this approximation, the basins of attraction of the stable parts of $\mathcal {M}_{\varepsilon }$ can be assumed to coincide with $\mathcal {B}(v_{-}^*(w))$ and $\mathcal {B}(v_{+}^*(w))$.

Fig. 1

In a, black trajectories moving on the critical manifold $\mathcal {M}_{0}$ (red cubic curve) represent the singular solution of Eq. (11) (which coincides with the solution of Eq. (1) in the limit as $\varepsilon \rightarrow 0$). The single arrows indicate slow motion, and the double arrows indicate fast motion (horizontal jumps at the fold point). In b, trajectories of the full system with $\varepsilon >0$ move on $\mathcal {M}_{\varepsilon }$ (not shown but at a distance of $\mathcal {O}(\varepsilon )$ from $\mathcal {M}_{0}$) into the stable fixed point located at the intersection of $\mathcal {M}_{0}$ and the w-nullcline, represented by the green line. As $\varepsilon$ becomes smaller and smaller, the dynamics of the full system get closer and closer and eventually coincide with the dynamics of Eq. (11) on the stable parts of $\mathcal {M}_{0}$

The reduced dynamics along $v_{-}^*(w)$ and $v_{+}^*(w)$ for the fast variable v is governed by Eq. (11). This reduced equation is obtained by implicitly differentiating $w=\displaystyle {v-\frac{v^3}{3}}$ with respect to $\tau$:

$$\begin{aligned} \displaystyle {\frac{\mathrm{d}w}{\mathrm{d}\tau }=\frac{\mathrm{d}v}{\mathrm{d}\tau }(1-v^2)}. \end{aligned}$$

Combining this with the equation for w in Eq. (1), we eliminate the slow variable to get

$$\begin{aligned} \displaystyle {\frac{\mathrm{d}v}{\mathrm{d}\tau }=\frac{d+(1-c)v+\frac{c}{3}v^3}{1-v^2}}. \end{aligned}$$

(11)

Equation (11) is an ODE with an algebraic constraint $w=v-\frac{v^3}{3}$. Therefore, we have a differential-algebraic equation whose initial conditions must satisfy this constraint for solutions to exist. In other words, the dynamics on the slow timescale is described by the reduced equation [in Eq. (11)] defined by the projection of the slow dynamics onto the tangent space of the critical manifold. We note that Eq. (11) becomes singular at $v=\pm \,1$ (the fold points) where $\mathcal {M}_0$ loses its normal hyperbolicity. In particular, the existence and uniqueness theorems for ODEs do not apply at these points. This is the reason why a trajectory moving along $v_{-}^*(w)$ and $v_{+}^*(w)$ jumps away horizontally when it reaches the fold points located at $(\pm \,1,\pm \,\frac{2}{3})$. See the black trajectory with arrows in Fig. 1a.

Fig. 2

a, c are the time series of the spiking activity of the neuron. v in blue and w in black; this legend is maintained through out this paper. A limit cycle is present for $c=0.745<c_\mathrm{H}$ in (a) and absent for $c=0.756>c_\mathrm{H}$ in (c). b, d are the phase portraits of the time series (a) and (c), respectively. In b, the limit cycle (in blue) made up of relaxation oscillations with jumps at the fold points located at $(\pm \,1,\pm \,\frac{2}{3})$ and initial conditions at $(v_0,w_0)=(-\,2.0,0.25)$. In d, just a transient solution (in blue) with initial conditions at $(v_0,w_0)=(-\,2.0,0.25)$ moves and stops at $(v_e,w_e)$ and another transient solution (in black) with initial conditions now at $(v_0,w_0)=(2.0,-\,0.25)$ through a jump at $p_2=(1,\frac{2}{3})$ also moves and stops at $(v_e,w_e)$ which is stable. e, f are the magnifications of the immediate neighborhood of the fold point $p_1=(-\,1,-\,\frac{2}{3})$ in (b) and (d), respectively. One clearly sees the relative position of the fixed point and the fold point at $p_1$. The critical manifold (red curve) and w-nullcline (green line) intersecting at the unique fixed point at $(v_e,w_e)=(-\,1.003988,-\,0.666651)$ for $c=0.756$ and $\varepsilon =0.0001$

In view of the properties of this approximation, we shall henceforth talk of the dynamics of the full system on the critical manifold $\mathcal {M}_0$. Thus, in the limit $\varepsilon \rightarrow 0$, the dynamics of the full system in Eq. (1) is described by Eq. (11). For concreteness, we shall choose $\varepsilon =0.0001$ in the numerical plots, except in Figs. 5 and 8, where we vary $\varepsilon$ to see how it affect the phenomenon.

With $\sigma =0$, $\Delta >0$ and $1-v_e^2<0$, a trajectory with initial conditions in $\mathcal {B}(v_{-}^*(w))$ will be attracted to $v_{-}^*(w)$ and slowly (as $\varepsilon \rightarrow 0$) move along it downwards toward the unique and stable fixed point $(v_e,w_e)$ in Eq. (5), where it stops. This behavior is shown in Fig. 2d for the blue trajectory with the initial conditions at $(v_0,w_0)=(-\,2.0,0.25)$. If the initial conditions are now chosen in $\mathcal {B}(v_{+}^*(w))$, as in Fig. 2d for the black trajectory with the initial conditions at $(v_0,w_0)=(2.0,-\,0.25)$, then this trajectory is also attracted to $v_{+}^*(w)$ and moves slowly (as $\varepsilon \rightarrow 0$) along it upwards toward the fold point at $\left( 1,\frac{2}{3}\right)$, where it is forced to jump to $v_{-}^*(w)$ and then moves again down toward the stable fixed point $(v_e,w_e)$, where it stops.

We note that as a trajectory moves along on $v_{-}^*(w)$, and when the unique fixed point $(v_e,w_e)$ satisfies the condition in Eq. (8), then it will stop at this fixed point and not move onto the fold point at $(-\,1,-\,\frac{2}{3})$, from where it will have jumped to the other stable manifold $v_{+}^*(w)$. This is observed again in Fig. 2d with the blue and black trajectories. There, the trajectories stop at the stable fixed point located at $(v_e,w_e)=(-\,1.003988,-\,0.666651)$ and do not move on to the jump point $(-\,1,-\,\frac{2}{3})$, which is located to the right of $(v_e,w_e)$; notice $1-v_e^2<0$. Thus, the fold point $(-\,1,-\,\frac{2}{3})$ will not be reached by the trajectories of the full system.

Equation (11) together with the equations of the stable manifolds $v=v_{-}^*(w)$ and $v=v_{+}^*(w)$ specifies the dynamics of the fast variable v arising on the deterministic slow timescale of $\mathcal {O}(\varepsilon ^{-1})$. We note that this timescale becomes slower and slower as $\varepsilon \rightarrow 0$.

We now return to our discussion of the singular Hopf bifurcation. We state and use the theorem by Krupa and Szmolyan [75] to determine the value of the singular Hopf bifurcation $c_\mathrm{H}$ for Eq. (1) together with its criticality. Consider a general slow–fast dynamical system on the fast timescale t given in the normal form:

$$\begin{aligned} \left\{ \begin{array}{lcl} \displaystyle {\frac{\mathrm{d}x}{\mathrm{d}t}}=&{}-&{}yh_1(x,y,\alpha ,\varepsilon )+x^2h_2(x,y,\alpha ,\varepsilon )\\ &{}+&{}\varepsilon h_3(x,y,\alpha ,\varepsilon ),\\ \displaystyle {\frac{\mathrm{d}y}{\mathrm{d}t}}=&{}\varepsilon &{}\Big (xh_4(x,y,\alpha ,\varepsilon )-\alpha h_5(x,y,\alpha ,\varepsilon )\\ &{}+&{}y h_6(x,y,\alpha ,\varepsilon )\Big ), \end{array}\right. \end{aligned}$$

(12)

where $\varepsilon$ is the timescale separation parameter, $\alpha$ is the Hopf bifurcation parameter, and the functions $h_i$ are given by

$$\begin{aligned} \left\{ \begin{array}{lcl} h_3(x,y,\alpha ,\varepsilon )&{}=&{}\mathcal {O}(x,y,\alpha ,\varepsilon ),\\ h_j(x,y,\alpha ,\varepsilon )&{}=&{}1+\mathcal {O}(x,y,\alpha ,\varepsilon ),\\ j=1,2,4,5. \end{array}\right. \end{aligned}$$

(13)

We define several computable constants, abbreviating $(0,0,0,0)=(0)$ in the definitions:

$$\begin{aligned} \left\{ \begin{array}{lcl} a_1=\frac{\partial h_3(0)}{\partial x}, a_2=\frac{\partial h_1(0)}{\partial x}, a_3=\frac{\partial h_2(0)}{\partial x},\\ a_4=\frac{\partial h_4(0)}{\partial x}, a_5=h_6(0). \end{array}\right. \end{aligned}$$

(14)

Note that all $a_1$ to $a_4$ only depend on the partial derivatives with respect to x. Next we define another constant:

$$\begin{aligned} A=-\,a_2+3a_3-2a_4+2a_5. \end{aligned}$$

(15)

Theorem

Suppose $(x,y)=(0,0)$ is a generic folded singularity for $\alpha =0$ with normal form Eq. (12). Then there exist $\varepsilon _0>0$ and $\alpha _0>0$ such that for $0< \varepsilon <\varepsilon _0$ and $|\alpha |<\alpha _0$ , in a suitable neighborhood of the origin, system Eq. (12) has precisely one equilibrium point $(x_e,y_e)$ with $(x_e,y_e)\rightarrow (0,0)$ as $(\alpha ,\varepsilon )\rightarrow (0,0)$. Furthermore, the equilibrium point $(x_e,y_e)$ undergoes a Hopf bifurcation at $\alpha _\mathrm{H}$ with:

$$\begin{aligned} \alpha _\mathrm{H}=-\frac{a_1+a_5}{2}\varepsilon +\mathcal {O}(\varepsilon ^{3/2}). \end{aligned}$$

(16)

The Hopf bifurcation is non-degenerate for $A\ne 0$, supercritical for $A<0$, and subcritical for $A>0$.

To apply the theorem, we write Eq. (1) with $\sigma =0$ on the fast timescale $t=\tau /\varepsilon$ as

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} \hbox {d}v&{}=&{}(-w+v-\frac{v^3}{3})\mathrm{d}t,\\ \hbox {d}w&{}=&{}\varepsilon (v+d-c w)\mathrm{d}t. \end{array}\right. \end{aligned} \end{aligned}$$

(17)

The fold points of $\mathcal {M}_0$ are at its extrema: $p_1=(-\,1,-\,\frac{2}{3})$ and $p_2=(1,\frac{2}{3})$. Since we want our unique fixed point $(v_e,w_e)$ in Eq. (5) to be stable, we again choose c and d such that Eq. (8) holds. It is useful to see that this will imply that our unique fixed point $(v_e,w_e)$ will be located on a decreasing part of the critical manifold $\mathcal {M}_0$, that is, either on $v_{-}^*(w)$ or on $v_{+}^*(w)$.

It is easy to check that the fold point $p_1$ satisfies the conditions necessary for a generic folded singularity [77]. We therefore direct our interest to the fold point $p_1$. Locating the fixed point $(v_e,w_e)$ to the left of $p_1$ [that is, locating it on $v_{-}^*(w)$] is sufficient to make it stable. We shall consider this deterministic setting for our analysis of SISR.

It is important to point out that, even though the fold point $p_1=(-\,1,-\,\frac{2}{3})$ is very close to the fixed point $(v_e,w_e)=(-\,1.003988,-\,0.666651)$, the relative position of these points is crucial for the occurrence of either SISR or ISR as analyzed in [2]. To see why this relative positioning (positioning the fixed point $(v_e,w_e)$ either to the left or right of the fold point $p_1=(-\,1,-\,\frac{2}{3})$) is important for SISR, consider the opposite situation, that is, assume that the fixed point $(v_e,w_e)$ lies to the right of the fold point $p_1=(-\,1,-\,\frac{2}{3})$ [that is, $(v_e,w_e)$ is now lying on the unstable branch $v_{0}^*(w)$ of $\mathcal {M}_0$]. With the fixed point $(v_e,w_e)$ lying on $v_{0}^*(w)$, it can be either stable or unstable (recall that Eq. (8) is only a sufficient but not a necessary condition for stability of a fixed point). If $(v_e,w_e)$ is unstable (after losing stability through a Hopf bifurcation), then even in the complete absence of noise, a trajectory with initial conditions in $\mathcal {B}(v_{-}^*(w))$ will be attracted to $v_{-}^*(w)$ along which it moves toward the fold point $p_1=(-\,1,-\,\frac{2}{3})$, at which point it jumps horizontally and avoids the unstable fixed point $(v_e,w_e)$ located on the unstable branch $v_{0}^*(w)$ as it finally drops on the stable branch $v_{+}^*(w)$. Along $v_{+}^*(w)$, it moves toward the fold point $p_2=(1,\frac{2}{3})$, where it again jumps horizontally to drop back on the stable branch $v_{-}^*(w)$, from where the whole cycle repeats again. This behavior is shown in Fig. 2b where the blue closed trajectory with initial conditions located at $(v_0,w_0)=(-\,2.0,0.25)$ jumps at the fold points located at the extrema $(\pm \,1,\pm \,\frac{2}{3})$ of $\mathcal {M}_0$. This will lead to a deterministic limit cycle (relaxation oscillation) around the unstable fixed point. This is precisely the deterministic setting we do not want to have, as the phenomenon of SISR requires the emergence of a limit cycle behavior due only to the introduction of noise into the system and not because of the presence of a Hopf bifurcation.

On the contrary, as we have shown in [2], the phenomenon of ISR requires that the fixed point $(v_e,w_e)$ is located to the right of the fold point $p_1$ [that is, on the unstable manifold $v_{0}^*(w)$] and, most importantly, has to be stable. This deterministic setting requires that $\varepsilon >0$, a condition which, as we shall see, does not allow SISR to occur, but which is crucial for the occurrence of ISR. Therefore, for SISR to occur in Eq. (1), the unique fixed point $(v_e,w_e)$ should be located to the left of the fold point $p_1=(-\,1,-\,\frac{2}{3})$, which by the condition in Eq. (8) makes it already stable.

We now return to the computation of the singular Hopf bifurcation value $c_\mathrm{H}$ and its criticality given by the sign of A in Eq. (15). After translating the generic folded singularity $p_1=(-\,1,-\,\frac{2}{3})$ to the origin by using the transformations $v\rightarrow v-1$ and $w\rightarrow w-\frac{2}{3}$, we write Eq. (17) in the normal form of Eq. (12) as

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} \hbox {d}v&{}=&{}(-\,w+v^2(1+\frac{v}{3}))\hbox {d}t,\\ \hbox {d}w&{}=&{}\varepsilon (v-\alpha -c w)\hbox {d}t, \end{array}\right. \end{aligned} \end{aligned}$$

(18)

where $\alpha :=1-d-\frac{2c}{3}$. We compare Eq. (18) and the standard form in Eq. (12), and we compute the relevant parameters $a_i$ defined in Eq. (14) to get

$$\begin{aligned} a_1= & {} 0,\,\,\,a_2=0,\,\,\,a_3=-\frac{1}{3},\,\,\,a_4=0,\nonumber \\ a_5= & {} -\,c,\,\,\,A=-\,1-2c_\mathrm{H}. \end{aligned}$$

(19)

We use Eq. (16) to get the singular Hopf bifurcation value $c_\mathrm{H}$ of our neuron model equation as

$$\begin{aligned} \alpha _\mathrm{H}&=1-d-\frac{2c_\mathrm{H}}{3}=-\frac{a_1+a_5}{2}\varepsilon +\mathcal {O}(\varepsilon ^{3/2})\nonumber \\&\Rightarrow c_\mathrm{H}=\frac{6(1-d-\mathcal {O}(\varepsilon ^{3/2}))}{4+3\varepsilon }. \end{aligned}$$

(20)

It is important to note that Eq. (20) gives the location of the Hopf bifurcation only in the limit as $\varepsilon \rightarrow 0$. We choose $d=0.5$ (this value is maintained through out the paper), and we choose $\varepsilon$ very small, for example $\varepsilon =0.0001$, to have

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} c_\mathrm{H}=0.749942,\\ A=-\,2.499885. \end{array}\right. \end{aligned} \end{aligned}$$

(21)

Therefore, with $\sigma =0$, Eq. (1) [or Eq. (17) which is equivalent to Eq. (1) with $\sigma =0$] exhibits a supercritical $(A<0)$ Hopf bifurcation near ($\varepsilon \rightarrow 0$) $c_\mathrm{H}=0.749942$. For values of c such that $c\le c_\mathrm{H}$, Eq. (1) [or Eq. (17)] exhibits a continuous spiking activity (a limit cycle solution), while for $c>c_\mathrm{H}$ there is no spiking (no limit cycle solution). These deterministic behaviors are shown in the time series in Fig. 2a, c and in their respective phase portraits in (b) and (d).

Figure 2e is a zoom into the neighborhood of the fold point $p_1=(-\,1,-\,\frac{2}{3})$ in Fig. 2b, that is, when $c=0.745<c_\mathrm{H}$. Here, the fixed point is located to the right of the $p_1$ and it is unstable. We recall that the situation where $c<c_\mathrm{H}$ is not of interest to us because in this regime, we already have a limit cycle due to a supercritical singular Hopf bifurcation at $c_\mathrm{H}$.

Figure 2f is a zoom into the neighborhood of the fold point $p_1=(-\,1,-\,\frac{2}{3})$ in Fig. 2d. We clearly see that for $\varepsilon =0.0001$, $c=0.756>c_\mathrm{H}$, and $d=0.5$, the fixed point in Eq. (5) is located at $(v_e,w_e)=(-\,1.003988,-\,0.666651)$, that is, to the left of the fold point at $p_1$. This makes the fixed point $(v_e,w_e)$ stable by the condition in Eq. (8). This is precisely the state in which we want our deterministic neuron in Eq. (17) to be before a random perturbation is added to its fast variable (v) equation, and we want to see how this noise can induce a limit cycle behavior (coherent spike train) that the deterministic model cannot exhibit, that is, the phenomenon of SISR.

4 Stochastic dynamics and timescale of escape processes from the stable manifolds

So far, we have considered the dynamics of Eq. (1) when there is no noise, i.e., when $\sigma =0$. Now we switch on the noise. In order to use the corresponding theory [78, 79], we shall derive the necessary formulae for the FHN neuron model in detail. Due to the diffusion that results from the presence of noise, random trajectories may then eventually escape from $\mathcal {B}(v_{-}^*(w))$ or $\mathcal {B}(v_{+}^*(w))$ before the fixed point or fold points are reached. To understand the escape processes from the basins of attraction and to quantify the stochastic timescale of these escape processes, we transform Eq. (1) to its equivalent fast timescale equation [which evolves on a timescale of $\mathcal {O}(1)$] by rescaling the time as $t=\tau /\varepsilon$. We note that the noise term (and not only the variables $v_{\tau }$ and $w_{\tau }$) has to be taken into consideration during the rescaling. The noise term is rescaled according to the scaling law of Brownian motion. That is, if $W_{\tau }$ is a standard Brownian motion, then, for every $\lambda >0$, $\lambda ^{-1/2}W_{\lambda \tau }$ is also a standard Brownian motion (i.e., the two processes have the same distribution [80]). We therefore have Eq. (1) written on the fast timescale as follows:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} \hbox {d}v_{t}&{}=&{}(-w_{t}+v_{t}-\frac{v_{t}^3}{3})\mathrm{d}t+\sigma \mathrm{d}W_{t},\\ \mathrm{d}w_{t}&{}=&{}\varepsilon (v_{t}+d-c w_{t})\mathrm{d}t. \end{array}\right. \end{aligned} \end{aligned}$$

(22)

We also notice that the noise term is now independent of $\varepsilon$, and hence, $\sigma$ will measure the relative strength of the noise term compared to the deterministic term irrespective of the value of $\varepsilon$. Furthermore, the form of Eq. (22), unlike Eq. (1), will avoid singularity problems when we are in the limit $\varepsilon \rightarrow 0$.

In the singular limit $\varepsilon \rightarrow 0$, the timescale separation between $v_t$ and $w_t$ becomes larger and Eq. (22) becomes a singularly perturbed ODE, with the equation for $w_{t}$ reducing to $dw_{t}=0$. This indicates that $w_{t}$ is frozen on the $\mathcal {O}(1)$ fast timescale and, on this timescale, the dynamics is governed by the fast equation in Eq. (22), where $w_{t}$ enters merely as a fixed parameter. Thus, Eq. (22) in this limit becomes a 1-D stochastic differential equation of the form

$$\begin{aligned} \hbox {d}v_{t}=-\frac{\partial U(v_{t},w_{t})}{\partial v_{t}}\hbox {d}t+\sigma \hbox {d}W_{t}, \end{aligned}$$

(23)

where

$$\begin{aligned} U(v,w)=\frac{1}{12}v^4-\frac{1}{2}v^2+vw, \end{aligned}$$

(24)

viewed as a function of v with w nearly constant, is a double-well potential. The two local minima are located at the value of v where $v_{-}^*(w)$ and $v_{+}^*(w)$ intersect the horizontal line $w=k$ with $k\in \big (-\frac{2}{3},\frac{2}{3}\big )$, and a local maximum at the intersection with the unstable branch $v_{0}^*(w)$; see Fig. 3. We now define the quantities

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} \triangle U_{-}(w)&{}=&{}U\big (v_{0}^*(w),w\big )-U\big (v_{-}^*(w),w\big ),\\ \triangle U_{+}(w)&{}=&{}U\big (v_{0}^*(w),w\big )-U(v_{+}^*(w),w\big ), \end{array}\right. \end{aligned} \end{aligned}$$

(25)

where from Eq. (9), we use Viète’s trigonometric expressions of the roots in the three-real-roots case ($w^2\le 2/3$) to get

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} v_{-}^*(w)&{}=&{}2\cos \left( \frac{2}{3}\pi +\frac{1}{3}\arccos (-\frac{3}{2}w)\right) ,\\ v_{0}^*(w)&{}=&{}2\cos \left( -\frac{2}{3}\pi +\frac{1}{3}\arccos (-\frac{3}{2}w)\right) ,\\ v_{+}^*(w)&{}=&{}2\cos \left( \frac{1}{3}\arccos (-\frac{3}{2}w)\right) . \end{array}\right. \end{aligned} \end{aligned}$$

(26)

The graphs of $v_{-}^*(w)$ and $v_{+}^*(w)$ in Eq. (26) are strictly monotonically decreasing for values of $w\in \big [-\frac{2}{3},\frac{2}{3}\big ]$. In each case, $\triangle U_{\pm }(w)$ is the potential difference (energy barrier function) between the local maximum $v_{0}^*(w)$ and a local minimum $v_{\pm }^*(w)$, respectively. See Fig. 4.

Fig. 3

Landscapes of the potential in Eq. (24) with the energy barriers $\triangle U_{\pm }(w)$ indicated in the asymmetric ($w\ne 0$) cases (a) and (b) and in the symmetric ($w=0$) case (c). The saddle point and the left and right minima of the potential are located at $v=v_{0}^*(w)$, $v=v_{-}^*(w)$, and $v=v_{+}^*(w)$, respectively

Fig. 4

Graphs of the energy barriers $\triangle U_{-}(w)$ (in red) and $\triangle U_{+}(w)$ (in black) as a function of w. $\triangle U_{-}(w)$ and $\triangle U_{+}(w)$ are monotone in the intervals $\big (-\frac{2}{3},0\big )$ and $\big (0,\frac{2}{3}\big )$, respectively. $\triangle U_{-}(w)=\triangle U_{+}(w)=0.75$ at $w=0$. $\triangle U_{-}(w(c))\rightarrow 0$ because $w(c)\rightarrow w_e=-\frac{2}{3}$ as $c\rightarrow c_\mathrm{H}^+$

In order to understand the escape processes of the trajectories of Eq. (23) from the basins of attraction $\mathcal {B}(v_{\pm }^*(w))$, and to estimate the stochastic timescale at which these escape processes take place, one may picture these escape processes as the motion of a particle in a double-well potential under the influence of a stochastic perturbation. That is, one could view the escape of a trajectory of Eq. (23) from the basin of attraction $\mathcal {B}(v_{-}^*(w))$ into $\mathcal {B}(v_{+}^*(w))$ as the escape of a particle from the minimum of the left well at $v_{-}^*(w)$ into the minimum of the right well at $v_{+}^*(w)$ of the double-well potential U(v, w) and vice versa. For the neuron model equation under consideration, there is a perfect analogy between the escape process of a trajectory from the basins of attraction $\mathcal {B}(v_{\pm }^*(w))$ and the escape process of a particle from those minima of the double-well potential U(v, w).

With this picture in mind, we can conveniently estimate the escape rate $E_{r_-}$ of a trajectory from $\mathcal {B}(v_{-}^*(w))$ into $\mathcal {B}(v_{+}^*(w))$ and hence the stochastic timescale $1/E_{r_-}$ at which the trajectory escapes. The escape rate $E_{r_+}$ of a trajectory from $\mathcal {B}(v_{+}^*(w))$ back into $\mathcal {B}(v_{-}^*(w))$ and the stochastic timescale $1/E_{r_+}$ at which it occurs can be estimated analogously to $E_{r_-}$ because of the symmetry between the two escape processes.

To estimate $E_{r_-}$, we consider our particle obeying the dynamics of Eq. (23), initially at the minimum $v_{-}^*(w)$ of the left well and wanting to escape to the minimum $v_{+}^*(w)$ of the right well of the potential U(v, w). This setting corresponds to the situation in Fig. 3a. For this escape event to occur, the particle should be able to go over the potential barrier $\triangle U_{-}(w)$ given in Eq. (25).

With $\sigma \ne 0$, the probability density p(v, t) of finding the particle at position v at time t in the double-well potential U(v, w) obeys the Fokker–Planck equation (FPE) [81] corresponding to the Langevin equation in Eq. (23); that is,

$$\begin{aligned} \frac{\partial }{\partial t}p(v,t)=\displaystyle {-\frac{\partial }{\partial v}\Big [U(v,w)p(v,t)\Big ]+\frac{\sigma ^2}{2}\frac{\partial ^2 }{\partial v^2}}p(v,t), \end{aligned}$$

(27)

with initial and natural boundary conditions chosen, respectively, as

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} \lim \limits _{t \rightarrow t_0}p(v,t|v_0,t_0)=\delta (v-v_0),\\ \lim \limits _{v \rightarrow \pm \,\infty }p(v,t)=\lim \limits _{v \rightarrow \pm \,\infty }\frac{\partial }{\partial v}p(v,t)=0, \end{array}\right. \end{aligned} \end{aligned}$$

(28)

where $v_0$ and $t_0$ are the initial position and starting time, respectively.

We write Eq. (27) in the form of the continuity equation [81] as

$$\begin{aligned} \frac{\partial }{\partial t}p(v,t)=-\frac{\partial }{\partial v}j(v,t), \end{aligned}$$

(29)

where the so-called current or probability flux j(v, t) is given by

$$\begin{aligned} j(v,t)= & {} \displaystyle {-\frac{\partial }{\partial v}U(v,w)p(v,t)-\frac{\sigma ^2}{2}\frac{\partial }{\partial v}p(v,t)}\nonumber \\= & {} -\frac{\sigma ^2}{2}\exp {\Bigg (-\frac{2U(v)}{\sigma ^2}\Bigg )}\frac{\partial }{\partial v}\nonumber \\&\times \,\left[ p(v,t)\exp {\Bigg (\frac{2U(v)}{\sigma ^2}\Bigg )} \right] \end{aligned}$$

(30)

as w is merely a constant here.

With our particle at the left minimum $v_{-}^*(w)$ of the potential U(v, w), an escape event into the right minimum at $v_{+}^*(w)$ occurs if the noise is strong enough to push the particle over the potential barrier $\triangle U_{-}(w)$. If the particle is initially ($t=0$) at position $v_{-}^*(w)$, then from the initial boundary condition in Eq. (28), we have the probability density given by

$$\begin{aligned} p(v,0)=\delta (v-v_{-}^*(w)). \end{aligned}$$

(31)

When the quantity $\displaystyle {\frac{U(v)}{\sigma ^2}}$ in Eq. (30) is large (e.g., in the limit as $\sigma \rightarrow 0$), we expect p(v, t) to be concentrated around the minimum $v_{-}^*(w)$ of the left potential well. This implies that the escape over the potential barrier $\triangle U_{-}(w)$ becomes a rare event. We are precisely interested in the probability of this rare event.

However, if we allow the particle to interact with the noise for a sufficiently long time (in other words, if we integrate Eq. (23) in a sufficiently large time interval), then this weak noise may eventually push the particle far away from $v_{-}^*(w)$ into the right minimum at $v_{+}^*(w)$ by going over $\triangle U_{-}(w)$. Thus, making $\displaystyle {\frac{U(v)}{\sigma ^2}\rightarrow \infty }$, we make the probability flux j in Eq. (30) infinitely small and the probability density p(v, t) becomes almost time-independent. In this case, we obtain a stationary probability density $\displaystyle {\frac{\partial }{\partial t}p(v,t)\approx 0}$ and the continuity equation in Eq. (29) then implies that $\displaystyle {\frac{\partial j}{\partial v}\approx 0}$. Hence, j is approximately some constant $j_0$ and Eq. (30) is simply rewritten as

$$\begin{aligned} j_0= & {} -\frac{\sigma ^2}{2}\exp {\Bigg (-\frac{2U(v)}{\sigma ^2}\Bigg )}\frac{\partial }{\partial v}\nonumber \\&\times \left[ p(v,t)\exp {\Bigg (\frac{2U(v)}{\sigma ^2}\Bigg )} \right] . \end{aligned}$$

(32)

To obtain the escape rate of the particle, we therefore have to integrate Eq. (32) from the initial position of the particle [that is, at the minimum $v_{-}^*(w)$] to some point $\beta _1$ beyond the maximum $v_{0}^*(w)$ ($\beta _1>v_{0}^*(w)$) of the potential U(v, w), i.e.,

$$\begin{aligned}&j_0\int \limits _{v_{-}^*(w)}^{\beta _1}\exp {\Bigg (\frac{2U(v)}{\sigma ^2}\Bigg )}\hbox {d}v\nonumber \\&\quad =\frac{\sigma ^2}{2}\Bigg [-p(\beta _1,t)\exp {\Bigg (\frac{2U(\beta _1)}{\sigma ^2}\Bigg )}\nonumber \\&\qquad +p(v_{-}^*(w),t)\exp {\Bigg (\frac{2U(v_{-}^*(w))}{\sigma ^2}\Bigg )}\Bigg ]. \end{aligned}$$

(33)

From the natural boundary condition in Eq. (28), we have that $p(\beta _1,t)\approx 0$ and we obtain the constant probability flux $j_0$ from Eq.(33) as

$$\begin{aligned} j_0=&\frac{\sigma ^2/2}{\displaystyle \int \nolimits _{v_{-}^*(w)}^{\beta _1}\exp {\Big (\frac{2U(v)}{\sigma ^2}\Big )}\hbox {d}v}p(v_{-}^*(w),t)\exp {\Bigg (\frac{2U(v_{-}^*(w))}{\sigma ^2}\Bigg )}. \end{aligned}$$

(34)

When the particle is at the minimum $v_{-}^*(w)$, and the quantity $\displaystyle {\frac{U(v)}{\sigma ^2}\rightarrow \infty }$ as $\sigma \rightarrow 0$, and in Eq. (30), we have $j\approx 0$ which means that $p(v,t)\exp {\Big (\frac{2U(v)}{\sigma ^2}\Big )}=\beta _2$, where $\beta _2$ is a constant. We then obtain the invariant probability distribution as

$$\begin{aligned} p_i(v,t)=\beta _2\exp {\Bigg (-\frac{2U(v)}{\sigma ^2}\Bigg )}. \end{aligned}$$

(35)

The constant $\beta _2$ can be given a convenient arbitrary value; we choose $\beta _2=p(v_{-}^*(w),t)\exp {\Big (\frac{2U(v_{-}^*(w))}{\sigma ^2}\Big )}$, so that the invariant probability density of the particle when it is at the minimum $v_{-}^*(w)$ is now given by

$$\begin{aligned} p_i(v,t)=p(v_{-}^*(w),t)\exp {\Bigg (-\frac{2\big (U(v)-U(v_{-}^*(w)\big )}{\sigma ^2}\Bigg )}. \end{aligned}$$

(36)

We now consider two points $\beta _3<v_{-}^*(w)<\beta _4$ in the immediate neighborhood of the minimum at $v_{-}^*(w)$. The probability $p_0$ of finding the particle in the interval $\big [\beta _3,\beta _4\big ]$ is calculated by integrating over the invariant probability density $p_i(v,t)$, i.e.,

$$\begin{aligned} p_0&=p(v_{-}^*(w),t)\exp {\Bigg (\frac{2U(v_{-}^*(w))}{\sigma ^2}\Bigg )}\nonumber \\&\quad \times \int \limits _{\beta _3}^{\beta _4} \exp {\Bigg (-\frac{2U(v)}{\sigma ^2}\Bigg )}\hbox {d}v. \end{aligned}$$

(37)

As the value of the invariant density $p_i(v,t)$ in Eq. (36) becomes small away from the minimum at $v_{-}^*(w)$ for $\sigma \rightarrow 0$ since $\exp {\Big (-\frac{2\big (U(v)-U(v_{-}^*(w)\big )}{\sigma ^2}\Big )}$ is very small, then we do not need to know the values of $\beta _3$ and $\beta _4$ to evaluate the integral in Eq. (37).

The escape rate $E_{r_-}$ can then be obtained by noting that Eq. (34) gives the conditional probability of escape per unit time, given that the escaping particle is initially at the minimum $v_{-}^*(w)$ of the potential. With

$$\begin{aligned} E_{r_-}=\frac{j_0}{p_0}, \end{aligned}$$

(38)

and Eqs. (34) and (37), we obtain

$$\begin{aligned} \frac{1}{E_{r_-}}= & {} \frac{1}{\sigma ^2}\int \limits _{\beta _3}^{\beta _4}\exp {\Bigg (-\frac{2U(v)}{\sigma ^2}\Bigg )}\hbox {d}v\nonumber \\&\times \int \limits _{v_{-}^*(w)}^{\beta _1} \exp {\Bigg (\frac{2U(v)}{\sigma ^2}\Bigg )}\hbox {d}v. \end{aligned}$$

(39)

Since the integrands in the first and second integral of Eq. (39) are peaking at the minimum $v_{-}^*(w)$ and the maximum $v_{0}^*(w)$, respectively, the next approximation consists in Taylor expanding U(v) to second order about these peak values while noting that at the local extrema of the potential U(v), we have $U''(v_{-}^*(w))=U''(v_{0}^*(w))=0$. We have

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} 2U(v)\approx 2U(v_{-}^*(w))+U''(v_{-}^*(w))(v-v_{-}^*(w))^2,\\ 2U(v)\approx 2U(v_{0}^*(w))-\left| U''(v_{0}^*(w))\right| (v-v_{-}^*(w))^2. \end{array}\right. \end{aligned} \end{aligned}$$

(40)

Noting that $U(v_{-}^*(w))$ and $U(v_{0}^*(w))$ are, respectively, the dominant terms in the two integrals in Eq. (39), we insert the Taylor expansions into Eq. (39) and use the fact that $\int \nolimits _{-\infty }^{\infty }\exp {(-\alpha x^2)}\mathrm{d}x=\sqrt{\frac{\pi }{\alpha }}$ to obtain the escape rate $E_{r_-}$ as

$$\begin{aligned} E_{r_-}=\mu _-\exp {\Bigg (-\frac{2\triangle U_{-}(w)}{\sigma ^2}\Bigg )}. \end{aligned}$$

(41)

By the same analysis, we get the escape rate $E_{r_+}$ in the reverse direction as

$$\begin{aligned} E_{r_+}=\mu _+\exp {\Bigg (-\frac{2\triangle U_{+}(w)}{\sigma ^2}\Bigg )}, \end{aligned}$$

(42)

where the prefactors $\mu _{\pm }$ are given, respectively, by the square roots of the product of the curvatures of the potential at its local extrema as

$$\begin{aligned} \mu _{\pm }=\frac{1}{2\pi }\Big (U''(v_{\pm }^*(w))\left| U''(v_{0}^*(w))\right| \Big )^{1/2}. \end{aligned}$$

(43)

Here, we could extend the domain of the integration in Eq. (39) to the real line because the contributions of points away from the minimum point $v_{-}^*(w)$ and the maximum point $v_{0}^*(w)$ are exponentially small. For this step, it is important that the original domain of integration extended to some point $\beta _1$ beyond the maximum $v_{0}^*(w)$, so that we integrate over some interval containing $v_{0}^*(w)$ in its interior.

For bistable systems, the inverse of the escape rate from a basin of attraction is the escape time from this basin of attraction [78, 82]. The stochastic timescales at which trajectories escape from the basins of attraction $\mathcal {B}(v_{\pm }^*(w))$ are therefore of $\mathcal {O}\Big (\frac{1}{E_{r_-}}\Big )$ and $\mathcal {O}\Big (\frac{1}{E_{r_+}}\Big )$, respectively.

5 Asymptotic matching of timescales and resonance

We still need to do some work, as even though in the previous section we derived for Eq. (22) the stochastic timescale of the escape processes in 1-D by neglecting the slow equation in the limit $\varepsilon =0$, $\varepsilon$ is only very small, but not exactly 0 in the full dynamics of the neuron [that is, the dynamics of Eq. (22) when $\varepsilon \ne 0$]. However, as we already pointed out in Sect. 3, from Fenichel’s invariant manifold theorem, the limit $\varepsilon \rightarrow 0$ used to obtain the stochastic timescales in the previous section is a sufficiently good approximation because under this limit, the basins of attraction of the stable parts of the slow manifold $\mathcal {M}_{\varepsilon }$ coincide with $\mathcal {B}(v_{\pm }^*(w))$. In this section, where we consider the full dynamics, this approximation will continue to be valid.

Now consider $0<\varepsilon \ll 1$ (positive but very small), that is, we allow w in Eq. (22) to move as well. We choose $c>c_\mathrm{H}$ so that no limit cycle can appear due to a singular Hopf bifurcation. If the stochastic timescales of the escape processes are much longer (this can happen with extremely weak noise) than the deterministic timescale of the reduced equation in Eq. (11) on the manifolds $v_{\pm }^*(w)$, then the trajectory has no time to escape and is most likely to stay in the basins of attraction $\mathcal {B}(v_{\pm }^*(w))$ for a very long time with no or very rare transitions between $\mathcal {B}(v_{-}^*(w))$ and $\mathcal {B}(v_{+}^*(w))$. In this case, the trajectory is forced to move “almost” deterministically on $v_{\pm }^*(w)$ toward the stable fixed point $(v_e,w_e)$ where it sticks.

On the other hand, when the stochastic timescales are much shorter (this can happen when the noise is strong) than the deterministic timescale, the noise-induced transitions are very frequent and incoherent. In this case, the neuron’s dynamics can only be captured by its invariant density. This is an immediate consequence of a strong noise with which no coherent structure can emerge.

An interesting case occurs when the escape events from $\mathcal {B}(v_{\pm }^*(w))$ and motions along $v_{\pm }^*(w)$ have comparable timescales. With the stochastic timescales given by the inverse of Eqs. (41) and (42), a trajectory with initial conditions in $\mathcal {B}(v_{-}^*(w))$ may escape into $\mathcal {B}(v_{+}^*(w))$ and conversely at some specific points of w with probabilities close to 1 if some suitable scaling limit conditions are imposed. With these conditions, the reduced equation in Eq. (11) may not be valid along $v_{-}^*(w)$ all the way down to the fixed point $(v_e,w_e)$ and may neither be valid along $v_{+}^*(w)$ all the way up to the fold point $p_2=(1,\frac{2}{3})$. This equation will only govern the motions on these stable manifolds until some well-defined points, $w_{-}\in v_{-}^*(w)$ and $w_{+}\in v_{+}^*(w)$ where the trajectory, respectively, escapes from $\mathcal {B}(v_{-}^*(w))$ and $\mathcal {B}(v_{+}^*(w))$. Indeed, as soon as $w_{-}$ is reached, the stochastic timescale becomes comparable to the deterministic timescale of the motion along $v_{-}^*(w)$ and an escape event instantaneously happens at $w_{-}$ and likewise for $w_{+}$. Therefore, we can only expect a coherent spike train with a weak noise when the neuron can match the deterministic timescale to the stochastic timescale only when $w=w_{\pm }$, but not at other points. Thus, we need

$$\begin{aligned} \varepsilon ^{-1}\approx {\left\{ \begin{array}{ll} \frac{1}{\mu _{-}}\exp {\Big (\frac{2\triangle U_{-}(w_-)}{\sigma ^2}\Big )}, &{} w<0\\ \frac{1}{\mu _{+}}\exp {\Big (\frac{2\triangle U_{+}(w_+)}{\sigma ^2}\Big )}, &{} w>0\\ \end{array}\right. } \end{aligned}$$

(44)

For this, we must therefore choose a suitable double scaling limit: $(\sigma ,\varepsilon )\rightarrow (0,0)$, such that

$$\begin{aligned} \varPhi =\frac{1}{2}\sigma ^2\log _e(\varepsilon ^{-1})\rightarrow {\left\{ \begin{array}{ll} \triangle U_{-}(w_{-}), &{} w<0 \\ \triangle U_{+}(w_{+}), &{} w>0 \\ \end{array}\right. } \end{aligned}$$

(45)

for some finite $\varPhi \in (\varPhi _{\min },\varPhi _{\max })$, with $\varPhi _{\min }$ and $\varPhi _{\max }$ to be specified later. Eq. (45) implies that $\triangle U_{-}(w_{-})\rightarrow \triangle U_{+}(w_{+})$, and therefore, if a trajectory escapes from $\mathcal {B}(v_{-}^*(w))$ at $w_{-}$, then at $w_{+}=-\,w_{-}$, we should expect an escape from $\mathcal {B}(v_{+}^*(w))$.

Provided that the equations in Eq. (46) have solutions on the accessible parts of the stable manifolds $v_{\pm }^*(w)$, the jump points $w_{\pm }$ are the unique solutions of

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} \triangle U_{-}(w_{-})=\varPhi ,\\ \triangle U_{+}(w_{+})=\varPhi . \end{array}\right. \end{aligned} \end{aligned}$$

(46)

The uniqueness follows from the monotonicity of the energy barrier functions $\triangle U_{-}(w)$ for $w\in (-\frac{2}{3},0)$ and $\triangle U_{+}(w)$ for $w\in (0,\frac{2}{3})$; see Fig. 4. The matching of these timescales implied in Eq. (45) is precisely the resonance mechanism in standard stochastic resonance [12].

We note that we must have $w_e<w_-$, that is, when the point $w=w_-$ can be reached by the slow flow of Eq. (11) along $v_{-}^*(w)$. Otherwise, the trajectory of Eq. (11) will stick to the stable fixed point at $w_e$. Since $\triangle U_{-}(w)$ is monotone, this will occur when $\varPhi >\varPhi _{\min }=\triangle U_{-}(w_e)$ (since $w_e$ is the lowest attainable point on $v_{-}^*(w)$).

On the other hand, we should also have $w_-<w_+$, which is violated when $\varPhi \ge \varPhi _{\max }=\frac{3}{4}$ ($w_-=w_+=0$ at $\varPhi =\varPhi _{\max }$); see Fig. 4. The limit cycle behavior (coherent spike train) emerges only if we choose $\sigma$ and $\varepsilon$ sufficiently small such that $\varPhi \in (\varPhi _{\min },\varPhi _{\max })=\left( \triangle U_{-}(w_e),\frac{3}{4}\right)$. This interval is not empty because $w_e=-\,0.666651<0$.

With the asymptotic limits in Eq. (45), that is, $\varPhi \in \big (\triangle U_{-}(w_e),\frac{3}{4}\big )$, a truly deterministic limit cycle behavior could emerge even though $c>c_\mathrm{H}$ (a regime in which the zero-noise dynamics cannot display a limit cycle). The phase portrait of this noise-induced limit cycle behavior is composed of the two portions of the critical manifolds $v_{\pm }^*(w)$ between the jump points $w=w_-$ and $w=w_+$, together with the horizontal lines joining these manifolds at $w_-$ and $w_+$. See the phase portraits in Fig. 7; they are different from the one in Fig. 2b, where the jumps from the stable manifolds can only occur at the fold points $(\pm \,1,\pm \,\frac{2}{3})$. We note also that on $v_{-}^*(w)$, $w_-$ is a jump point, while $w_+$ is a drop point. On $v_{+}^*(w)$, $w_-$ is a drop point, while $w_+$ is a jump point.

6 Characterization of the limit cycle

First, we note that while the deterministic characteristics (e.g., the period) of the limit cycle behavior obtained are controlled by the value of $\varPhi$, the degree of its coherence is controlled by $\sigma$ and $\varepsilon$. It can thus be made as high as desired by choosing $\sigma$ and $\varepsilon$ very small, provided that $\varPhi \in \big (\triangle U_{-}(w_e),\frac{3}{4}\big )$.

Since a trajectory spends most of the time on the stable manifolds $v_{-}^*(w)$ and $v_{+}^*(w)$ (due to the slow motion on the timescale of $\mathcal {O}(\varepsilon ^{-1})$ with $\varepsilon \rightarrow 0$), asymptotically, the period of the limit cycle will be the sum of the time it spends on these manifolds. That is, it is the sum of the time it takes to go from the drop point $w_+$ to the jump point $w_-$ on $v_{-}^*(w)$ and from the drop point $w_-$ to the jump point $w_+$ on $v_{+}^*(w)$. This period, $T(d,c,\sigma ,\varepsilon )$, can be obtained explicitly as the sum of the integrals over the reduced equation in Eq. (11) from $v_{-}^*(w_+)$ to $v_{-}^*(w_-)$ and from $v_{+}^*(w_-)$ to $v_{+}^*(w_+)$, that is,

$$\begin{aligned} T(d,c,\sigma ,\varepsilon )= & {} \int \limits _{v_{-}^*(w_+)}^{v_{-}^*(w_-)}\frac{1-v^2}{d+(1-c)v+\frac{c}{3}v^3}\hbox {d}v\nonumber \\+ & {} \quad \int \limits _{v_{+}^*(w_-)}^{v_{+}^*(w_+)}\frac{1-v^2}{d+(1-c)v+\frac{c}{3}v^3}\hbox {d}v. \end{aligned}$$

(47)

The integrals in Eq.(47) certainly exist for any $w_{\pm }\in \big (-\frac{2}{3},\frac{2}{3}\big )$, thanks to the boundedness of the graphs of $v_{-}^*(w)$ and $v_{+}^*(w)$ for $w\in \big [-\frac{2}{3},\frac{2}{3}\big ]$ and thanks to the boundedness and continuity of the integrand $\frac{1-v^2}{d+(1-c)v+\frac{c}{3}v^3}$ in the compact intervals given by

$\Big [v_{-}^*\big (\frac{2}{3}\big ), v_{-}^*\big (-\frac{2}{3}\big )\Big ]$= $\big [-2,-1\big ]$ and $\Big [v_{+}^*\big (\frac{2}{3}\big ), v_{+}^*\big (-\frac{2}{3}\big )\Big ]$= $\big [1,2\big ]$ in the first and second integral, respectively.

From the boundaries of integration in Eq. (47), one can see that the period of the limit cycle created by noise has a non-trivial dependence on $\sigma$ and $\varepsilon$ through its dependence on the points $w_{\pm }$, themselves connected to $\sigma$ and $\varepsilon$ as in Eqs. (45) or (46). Thus, the period of the limit cycle can be controlled by $\sigma$ for a fixed $\varepsilon$ without significantly affecting its coherence, provided Eq. (44) holds. From the asymptotic theory above, it is determined [from Eq. (46)] that a trajectory escapes at $w_-=-\,w_+=-\,0.432$ for $\varepsilon =0.0001$ and $\sigma =0.005$, which gives a period of $T\approx 1.6396$ for $c=0.760>c_\mathrm{H}$.

We now investigate what happens in the neighborhood of the singular Hopf bifurcation value, more precisely how the emergence of the limit cycle behavior is affected as c approaches $c_\mathrm{H}$ from above ($c\rightarrow c_\mathrm{H}^+$). The case in which $c_\mathrm{H}$ is approached from below ($c\rightarrow c_\mathrm{H}^-$) is not interesting because in this case, a limit cycle already exists due to a supercritical singular Hopf bifurcation, while we are interested in a limit cycle behavior due only to the presence of noise. As before, we take the double limit $(\sigma ,\varepsilon )\rightarrow (0,0)$ such that

$$\begin{aligned} \frac{1}{2}\sigma ^2\log _e(\varepsilon ^{-1})=\varPhi \in \Big (\triangle U_{-}(w_e),\frac{3}{4}\Big ). \end{aligned}$$

(48)

The upper bound of this open interval is fixed and does not depend on the choice of the parameter c. But the lower bound depends on $w_e$ which in turn depends on the parameter c as in Eq. (5). Therefore, the effect of $c\rightarrow c_\mathrm{H}^+$ on the emergence of the limit cycle behavior could be “observed” just by looking at the behavior of the following limit:

$$\begin{aligned} \lim _{c\rightarrow c_\mathrm{H}^+}\triangle U_{-}\big (w_e(c)\big ). \end{aligned}$$

(49)

If this limit decreases as we get closer and closer to $c_\mathrm{H}$, thus increasing the length of the open interval in Eq. (48), then the emergence of the limit cycle behavior is facilitated in the sense that for a fixed $\varepsilon$, weaker and weaker noise could trigger the limit cycle behavior.

On the other hand, if this limit continuously increases, thus decreasing the length of this open interval, then the emergence of the limit cycle behavior is inhibited in the sense that for a fixed $\varepsilon$, we are now having a thinner and thinner interval of the noise amplitude for which the behavior can occur. And if this interval length shrinks to zero, then the limit cycle behavior simply disappears regardless of the value of $\sigma$ we choose for a fixed $\varepsilon$.

With $d=0.5$, we see [from Eq. (5)] that $v_e\rightarrow -1$ as $c\rightarrow c_\mathrm{H}^+$, making $w_e\rightarrow -\frac{2}{3}$. Then, in Eq. (49), $\triangle U_{-}(w_e(c))\rightarrow 0$ as $w_e\rightarrow -\frac{2}{3}$; this limiting behavior is readily seen in the red curve in Fig. 4. Thus, as we approach the singular Hopf bifurcation value, the limit cycle behavior due to noise is facilitated; see Fig. 9 and compare with Fig. 6.

7 Numerical simulations and discussion

For the purpose of numerical computations, the term $\frac{1}{2}\sigma ^2$ in $\frac{1}{2}\sigma ^2\log _e(\varepsilon ^{-1})$ will be absorbed into $\sigma$ so that the matching of the timescales in Eq. (45) leading to the emergence of a coherent spike train will require that

$$\begin{aligned} \lim \limits _{(\varepsilon ,\sigma )\rightarrow (0,0)}\sigma \log _e(\varepsilon ^{-1})\in \Big (\triangle U_{-}(w_e),\frac{3}{4}\Big ). \end{aligned}$$

(50)

With Eq. (50), we easily calculate the minimum ($\sigma _{\min }$) and the maximum ($\sigma _{\max }$) of the noise amplitude required to induce a coherent spike train in the neuron’s activity when $\varepsilon \rightarrow 0$ as

$$\begin{aligned} \sigma _{\min }=\frac{\triangle U_{-}(w_e)}{\log _e(\varepsilon ^{-1})},\,\,\,\sigma _{\max }=\frac{3}{4\log _e(\varepsilon ^{-1})}. \end{aligned}$$

(51)

With the fixed point $(v_e,w_e)=(-\,1.003988,-\,0.666651)$ located to the left of the fold point $p_1=(-\,1,-\,\frac{2}{3})$, we therefore must have $w_e>-\,\frac{2}{3}$ (even though $w_e$ is very close to $-\,\frac{2}{3}$, the inequality has to be strict). Moreover, the energy barrier function $\triangle U_-(w)$ at the fold point $p_1$ is $\triangle U_-(w=-\,\frac{2}{3})=0$ (again seen from the red curve in Fig. 4). These facts imply that $\triangle U_-(w_e)>\triangle U_-(-\,\frac{2}{3})=0$. Therefore, in the double limit $(\varepsilon ,\sigma )\rightarrow (0,0)$ we have an incoherent spike train if

$$\begin{aligned} \sigma \log _e(\varepsilon ^{-1})\in \Bigg (\triangle U_{-}\big (-\,\frac{2}{3}\big ),\triangle U_{-}(w_e)\Bigg ), \end{aligned}$$

(52)

a very small but non-empty interval, since $w_e>-\,\frac{2}{3}$ and $\triangle U_{-}(w)$ is a monotonically increasing function of $w\in (-\,\frac{2}{3},0)$. Inserting the value of $w_e$ in $\triangle U_{-}(w_e)$, we get the interval in Eq. (52) for which only a rare and incoherent spike train emerges in the limit $(\varepsilon ,\sigma )\rightarrow (0,0)$ as $\big (\triangle U_{-}(-\,\frac{2}{3}),\triangle U_{-}(w_e)\big )=(0,1.46667\times 10^{-5})$. It follows from Eq. (51) that choosing the noise amplitude $\sigma$ such that $\sigma \le \sigma _{\min }=1.46667\times 10^{-5}/\log _e(\varepsilon ^{-1})$ for a fixed $\varepsilon \rightarrow 0$ will lead only to incoherent spike trains. For $\sigma \ge \sigma _{\max }$, we of course have incoherent spike trains as the noise amplitude is already too strong.

Fig. 5

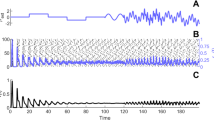
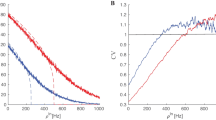
The mean interspike interval $\langle \hbox {ISI}\rangle$ in (a) and the coefficient of variation ($\hbox {CV}$) in (b), as a function of the noise amplitude $\sigma$. In (a), the standard deviation is also shown as error bars. In all cases, $c=0.760>c_\mathrm{H}$. Note the high degree of coherence that can be achieved when $\varepsilon$ is small, while at the same time $\langle \hbox {ISI}\rangle$ shows significant dependence on the noise amplitude $\sigma$. In b, $\hbox {CV}\approx 0.2$ for all values of $\varepsilon$ with a larger interval of $\sigma$ for which CV remains that low for $\varepsilon =0.0001$

Now we present and discuss the numerical simulations carried out to illustrate the theoretical analysis. To numerically generate the Gaussian white noise $W_t$, we start from two random numbers $b_1$ and $b_2$ which are uniformly distributed on the unit interval [0, 1] and, with the Box–Muller algorithm [83], we generate a standardized Gaussian distributed sequence. We use the Euler algorithm [84] to integrate Eq. (22) with initial conditions at $(v_0,w_0)=(-\,2.0,0.25)$; the numerical scheme is

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} W|_{\Delta t}&{}=&{}\sqrt{-4\sigma \Delta t\log (b_1)}\cos (2\pi b_2),\\ v|_{\Delta t}&{}=&{}v+(-w+v-\frac{v^3}{3})\Delta t+W|_{\Delta t},\\ w|_{\Delta t}&{}=&{}w+\varepsilon (v+d-c w)\Delta t. \end{array}\right. \end{aligned} \end{aligned}$$

(53)

To quantify the regularity of the spiking activity of the neuron, we use the first two moments of the interval between excitations [the interspike interval (ISI)] of [3]. We determine the spike occurrence times by the upward crossing of the membrane potential variable v past the spike detection threshold of $v_\mathrm{th}=0$. Then, we calculate the regularity of the spike train using the coefficient of variation (CV) defined as

$$\begin{aligned} \hbox {CV}=\frac{\sqrt{\langle \hbox {ISI}^2\rangle -\langle \hbox {ISI}\rangle ^2}}{\langle \hbox {ISI}\rangle }, \end{aligned}$$

(54)

where $\langle \hbox {ISI}\rangle$ and $\langle \hbox {ISI}^2\rangle$ represent the mean and the mean squared interspike intervals, respectively. Biologically, CV is important because it is related to the timing precision of the information processing in neural systems [85].

For a Poissonian spike train (rare and incoherent spiking), $\hbox {CV}=1$. If $\hbox {CV}<1$, the sequence becomes more coherent and CV vanishes for periodic deterministic spikes, for example in the deterministic limit cycle regime of Eq. (17); see the perfect coherence of the spike train in Fig. 2a. In the case $\hbox {CV}<1$, large excursions of trajectories in the phase space can be interpreted as motion on a “stochastic limit cycle” [86]. $\hbox {CV}$ values $>\,1$ correspond to a point process that is more variable than a Poisson process.

Fig. 6

Time series in (a) and corresponding phase portrait in (b) showing a rare and incoherent (Poissonian) spike train. $\varepsilon =0.0001$, $c=0.76>c_\mathrm{H}$. Compare this with Fig. 9 having a frequent and coherent spike train with the same noise strength and same integration time interval but with $c=0.756$ which is closer to $c_\mathrm{H}$ than in Fig. 6

In Fig. 5a, we have the mean interspike interval $\langle \hbox {ISI}\rangle$ and its standard deviation shown as error bars as a function of the noise amplitude $\sigma$ for 4 different values of the timescale parameter $\varepsilon$. The mean interspike interval decreases with increase in the noise if $\sigma \notin \big (\sigma _{\min },\sigma _{\max }\big )$ and stays almost unchanged if $\sigma \in \big (\sigma _{\min },\sigma _{\max }\big )$, for each value of $\varepsilon$.

In Fig. 5b, we show the $\hbox {CV}$ as a function of $\sigma$ for the same 4 values of $\varepsilon$ as in Fig. 5a. For very small values of $\sigma$ (i.e., $\sigma \sim 10^{-7}<\sigma _{\min }$ for $\varepsilon =0.0001$, $\sigma \sim 10^{-6}<\sigma _{\min }$ for $\varepsilon =0.0005$, $\sigma \sim 10^{-5}<\sigma _{\min }$ for $\varepsilon =0.001$, and $\sigma \sim 10^{-4}<\sigma _{\min }$ for $\varepsilon =0.01$, with each $\sigma _{\min }(\varepsilon )$ given by Eq. (51)), the firing has the character of a Poisson process since $\hbox {CV}$ is close to 1 (see also the large error bars). The activity in these cases represent rare and incoherent spike trains. For $\sigma \sim 10^{-7}$ and $\varepsilon =0.0001$ for example, the noise is just too weak to induce any oscillation, and because $c=0.76>c_\mathrm{H}$, the trajectory just evolves and stops at the stable fixed point at $(v_e,w_e)$.

On the other hand, when $\sigma$ begins to be large, i.e., when $\sigma \sim 10^{-2}>\sigma _{\max }$ for all 4 values of $\varepsilon$, with $\sigma _{\max }(\varepsilon )$ given by Eq. (51), the spike train also starts losing coherence as $\hbox {CV}$ starts to increase rapidly.

When $10^{-6}<\sigma <10^{-2}$ for $\varepsilon =0.0001$, $10^{-5}<\sigma <10^{-2}$ for $\varepsilon =0.0005$, $10^{-4}<\sigma <10^{-2}$ for $\varepsilon =0.001$, and $10^{-3}<\sigma <10^{-2}$ for $\varepsilon =0.01$, we have $\hbox {CV}\approx 0.2$, indicating a high level of coherence of the spike train consistent with theory. In the value range of $\varepsilon$ satisfying Eq. (50), a smaller value does not increase the coherence of the spike train, but instead increases the interval in which the noise amplitude must lie to be able to induce SISR. This is not the case in [1], where $\hbox {CV}\rightarrow 0$ as the singular parameter turns to 0 and the interval of the noise for which SISR occurs stays almost unchanged. We can also see in Fig. 5a that in these intervals of $\sigma$, for each $\varepsilon$, the short error bars do not almost change in height indicating that the high coherence of the spike train is not affected by noise when $\sigma$ lies in these intervals for each value of $\varepsilon$.

Figure 6a, b shows the time series and its corresponding phase portrait for $\varepsilon =0.0001$, $c=0.76>c_\mathrm{H}$, $\sigma =1.55\times 10^{-7}<\sigma _{\min }=\frac{1.46667\times 10^{-5}}{\log _e(1/0.0001)} =1.59242\times 10^{-6}$. As predicted, we have a rare and incoherent spike train. Recall that the emergence of a coherent spike train requires the matching of the timescales such that Eq. (50) holds. One easily checks that this is not the case for Fig. 6, where Eq. (52) holds instead. Therefore, even though $\sigma$ and $\varepsilon$ are small, we have only a rare and incoherent spike train for a very large integration time interval.

In the double limit $\sigma \rightarrow 0$ and $\varepsilon \rightarrow 0$ such that $\sigma \log _e(\varepsilon ^{-1})\in \big (\triangle U_{-}(w_e),\frac{3}{4}\big )$, the spike train abruptly changes to a frequent and coherent one (limit cycle behavior; see Fig. 7), consistent with the theoretical analysis. We further note that the simulations in Fig. 7 run for a time interval 5 times shorter than those in Fig. 6. But because of SISR in Fig. 7, we have a more frequent and coherent spiking than in Fig. 6. In Fig. 7a, b, with $\sigma =0.005$, the jump points are at $w_-\approx -0.585\pm 0.075$ and $w_+\approx 0.591\pm 0.025$, with $\langle \hbox {ISI}\rangle \approx 1.9348$. These jump points are a little later than those predicted by the theory and $\langle \hbox {ISI}\rangle$ is within $\sim 18\%$ of the period from the theory.

The simulations in Fig. 7 show that the stronger the noise is (of course the noise amplitude always has to satisfy Eq. (50) for a given $\varepsilon$), the further away are the jump points $w_-$ from the fixed point $(v_e,w_e)$ and $w_+$ from the fold point $p_2=(1,\frac{2}{3})$. The trajectories never succeed in attaining $(v_e,w_e)$ and $(1,\frac{2}{3})$ as they are systematically kicked out of $\mathcal {B}(v_{-}^*(w))$ and $\mathcal {B}(v_{+}^*(w))$ before these points are reached. Moreover, increasing the noise amplitude has the effect of decreasing the period of the oscillations while remarkably keeping the high degree of coherence of the spike train.

Fig. 7

The time series in (a), (c), (e) and their phase portraits in (b), (d), (f), respectively. The effect of varying the noise amplitude on the period of the coherent structure. Increasing the noise amplitude reduces the period of oscillations without considerably affecting its coherence. $\varepsilon =0.0001$, $c=0.76>c_\mathrm{H}$

The simulations in Fig. 8 show how the spiking frequency for a fixed weak noise amplitude varies with the singular parameter $\varepsilon$. As the value of $\varepsilon$ increases, the spiking frequency also increases. The reason for this lies in the fact that the deterministic timescale on which trajectories move on the stable manifolds $v_{-}^*(w)$ and $v_{+}^*(w)$ is of the order of $\varepsilon ^{-1}$. Therefore, as $\varepsilon$ becomes larger and larger (for example, 0.0005, 0.001, 0.002), the time spent by the trajectories on these stable manifolds becomes shorter and shorter, thus decreasing the period of oscillations for a given integration time interval.

Fig. 8

a–c show the time series for a fixed time interval with the corresponding value of the singular parameter $\varepsilon$. We observe the effect of varying $\varepsilon$ on the period of the coherent structure for a weak noise amplitude; increasing $\varepsilon$ (but remaining in the limit $\varepsilon \rightarrow 0$) decreases the period (increases the frequency) of oscillations without affecting its coherence. $\sigma =0.01$, $c=0.76>c_\mathrm{H}$

In Fig. 9, we verify that as $c\rightarrow c_\mathrm{H}^+$ the limit cycle behavior can be induced by a weaker noise. We choose $c=0.756>c_\mathrm{H}$, a value at which the deterministic neuron cannot display a limit cycle as in Fig. 2c and at the same time is closer to $c_\mathrm{H}$ than in the case of Fig. 6, where the same weak noise amplitude ($\sigma =1.55\times 10^{-7}$) cannot induce a coherent spike train. At $c=0.756$, this noise intensity produces a coherent spike train; see Fig. 9. This has been predicted theoretically above by Eq. (49) where $\triangle U_{-}(w_e(c))\rightarrow 0$ as $c\rightarrow c_\mathrm{H}^+$. This increases the length of the open interval in Eq. (50) which means that weaker and weaker noise amplitudes have enough strength to induce a coherent spike train. The limit cycle behavior in this case is much closer to that in Fig. 2a due to proximity to $c_\mathrm{H}$.

Finally, we verify the robustness of SISR to parameter tuning. We show that the effect does not require tuning of the bifurcation parameter and can be realized for any value c even much farther away from $c_\mathrm{H}$. In contrast, for CR to occur in the FHN model, the bifurcation parameter has to be in the immediate neighborhood of the Hopf bifurcation [3, 24].

To check the robustness of SISR, we take $c=1.5$, which is two times larger than $c_\mathrm{H}$. The result is shown in Fig. 10. Note that for this value of c one needs a stronger noise intensity to induce the oscillations. We see a coherent almost periodic spike train, with clearly defined jump points which are significantly higher than the fixed point $(v_e,w_e)$ on the left branch of the critical manifold $\mathcal {M}_0$ and lower than the fold point at $p_2=(1,\frac{2}{3})$ on the right branch of $\mathcal {M}_0$.

Fig. 9

Here, we have $\varepsilon =0.0001$ and $c=0.756$ which is closer to $c_\mathrm{H}$ than in Fig. 6. We observe that the same noise amplitude producing only rare and incoherent spike train in Fig. 6 produces rather a frequent and coherent spike train in Fig. 9 for the same integration time interval. Thus, closeness to the singular Hopf bifurcation value facilitates SISR by extending the interval of $\sigma$ for which a coherent spike train emerges

Fig. 10

Parameter tuning is not required for the effect. Coherence is preserved for the bifurcation parameter tuned at $c=1.5\approx 2c_\mathrm{H}$, $\varepsilon =0.0001$

8 Concluding remarks

In this paper, we have analyzed the effects of synaptic noise on the dynamics of a spiking neuron model with a strong timescale separation ($\varepsilon \rightarrow 0$) between its dynamical variables. First, we analyzed the deterministic dynamics ($\sigma =0$) and determined the locations of the unique and stable fixed point and the singular Hopf bifurcation value $c_\mathrm{H}$. From the slow–fast structure of the neuron model, we obtained the deterministic timescale at which the slow trajectories move on the stable parts of the critical manifold.

We set our neuron model in a regime where deterministic dynamics cannot display a limit cycle ($c>c_\mathrm{H}$) and added white noise ($\sigma >0$) to the fast membrane potential variable (to model the effect of synaptic noise). By considering the singular limit on the fast timescale, we obtained the stochastic timescales of the escape processes from the basins of attraction of the stable manifolds of the model equation.

If the deterministic timescale of the motion of a trajectory on the stable parts of the critical manifold is always matched to the stochastic timescale of the escaping trajectory at specific points on these stable manifolds, then weak noise can induce a transition to a coherent spike train (limit cycle behavior) which has no deterministic counterpart, that is, the following conditions should be satisfied:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} \sigma \rightarrow 0,\\ \varepsilon \rightarrow 0,\\ c>c_\mathrm{H}, \end{array}\right. \end{aligned} \end{aligned}$$

(55)

such that

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{lcl} \sigma \log _e(\varepsilon ^{-1})\in \big (\triangle U_{-}(w_e),\frac{3}{4}\big ),\\ \sigma \log _e(\varepsilon ^{-1})=\mathcal {O}(1). \end{array}\right. \end{aligned} \end{aligned}$$

(56)

We saw that, within the range of values of $\varepsilon$ for which Eqs. (55) and (56) hold, a smaller value does not significantly increase the coherence of the spike train, but instead increases the interval of the noise amplitude which could induce SISR.

Moreover, the coherent spiking activity due to noise is shown to be robust to parameter tuning as it persists for values of $c\gg c_\mathrm{H}$. This effect is quite different from CR, where the bifurcation parameter has to be in the immediate neighborhood of the Hopf bifurcation threshold, making it sensitive to parameter tuning. SISR could therefore, from a biological point of view, provide a mechanism through which real neurons may convert irregular signals into a frequency-encoded periodic output irrespective of the state of other parameters.

Summarizing and comparing the findings of [2] and the present paper, we first used Fenichel’s theorem to approximate the dynamics for a small timescale separation $\varepsilon$ by the dynamics on the stable part of the slow manifold, with jumps to the other stable branch occurring at those points where the slow manifold loses its stability. These fold points are given by the local extrema of the cubic polynomial that defines the slow manifold. The crucial point then is whether the trajectory on the slow manifold first reaches the stable fixed point or the fold point. In the first case, introducing noise can have the effect of causing an escape before the stable fixed point (located to the left of the fold point) is reached. That is self-induced stochastic resonance requires $\varepsilon \rightarrow 0$ as investigated in this paper. In contrast, in the second case, noise can induce a transition to the basin of attraction of the fixed point (now located to the right of the fold point) before the fold point is reached. This is inverse stochastic resonance, which requires $\varepsilon >0$, as studied in [2]. In both phenomena, the fold point corresponds to the minimum of the slow manifold.

However, both SISR and ISR require a weak synaptic noise limit to occur. This could mean that in a weak synaptic noise limit, a neuron could spontaneously switch from encoding information generated during SISR to encoding information generated during ISR, just by changing the membrane voltage of its quiescent state (i.e., by changing the position of the fixed point). Our results could explain experimental observations where very distinct spiking behaviors in physiologically identical neurons may emerge even when these neurons are excited by the same strength and type of stimulus.

Finally, it is worth noting that the type of bifurcation leading to deterministic spiking (Hopf bifurcation for a type II neuron or saddle-node bifurcation for a type I neuron) does not affect the mechanisms behind SISR. We see that SISR occurs if an excitable system is driven by small noise, the escape times of the trajectories from some part of the phase space are exponentially distributed, and their transition rate is governed by an activation energy. If the system is placed out of equilibrium, the parameters are chosen such that the system relaxes slowly to the equilibrium, and the activation energy function monotonically decreases as the system relaxes, then at a specific time during the relaxation period, the timescale for escape events matches the relaxation timescale, and the system jumps at this point almost surely. If the jump brings the system back out of equilibrium, the relaxation stage can start over again, and then the scenario repeats itself indefinitely, leading to a rather regular behavior (i.e., coherent spiking) which cannot occur in the noise-free system. This coherent spiking (due to SISR) cannot occur in the noise-free system simply because the system parameters are chosen such that a Hopf or Saddle-node bifurcation leading to deterministic spiking activity cannot occur. What is crucial for SISR is the interplay between different timescales, and not the type of bifurcation leading to deterministic spiking.