Introduction

There have been numerous investigations of the effects of noise in neurobiological dynamical systems, for both single neurons and neural networks. A large number of interesting noise-related phenomena have been analyzed, including synchronization, stochastic resonance, and coherence resonance (reviewed in Lindner et al. 2004). Most often, noise leads to increased responses (Stein et al. 2005) and sometimes to the phenomenon of stochastic resonance in which a maximum occurs in a response variable at a particular noise strength (Wiesenfeld and Moss 1995; Gammaitoni et al. 1998; Badzey and Mohanty 2005). This phenomenon has been demonstrated in neuronal systems, particularly, but not exclusively, in the case of periodic inputs (Gang et al. 1993; Collins et al. 1996; Longtin 1993; Nozaki et al. 1999). However, recently, it has been discovered experimentally (Paydarfar et al. 2006; Sim and Forger 2007) and in neuronal models (Gutkin et al. 2008) that noise can subdue or turn off repetitive neuronal activity. In this article, we report further investigations of such properties in Hodgkin–Huxley single neurons. We find that there is a tuning effect of noise that has the opposite character to stochastic resonance, and thus, it might be called inverse stochastic resonance. We argue that these phenomena will occur generically in neural and other dynamical systems that exhibit a specific kind of bistability between a stable limit cycle and a stable focus.

In the central nervous system, neurons are embedded in complex neuronal and glial networks (Silberberg et al. 2005). The responses of many types of neurons to input currents, whether injected or synaptic, have been much investigated experimentally and theoretically (McCormick et al. 1985; Tuckwell 1988; Chen et al. 1996; Jolivet et al. 2008). They receive input signals from many other neurons through thousands of excitatory and inhibitory synapses at unpredictable or random times (Destexhe et al. 2001). In order for a neuron to send out a signal, called an action potential (Bean 2007), it must receive sufficient net excitation (over inhibition) in a small enough time interval so that the current or voltage distribution in the cell passes through some threshold condition. Once the threshold is reached, self-exciting processes lead to the emission of an action potential.

Methods

To study neuronal response to signals with noise, we use the classical Hodgkin–Huxley model (Hodgkin and Huxley 1952), which is capable of reproducing spiking behavior similar to those of many real neurons and has often been employed in investigations of the effects of noise on neuronal dynamics (Brown et al. 1999; Schmid et al., 2004; Tuckwell 2005; Torcini et al. 2007). We employ two commonly used different models for the input to the cell, which are described as “current-driven” and “conductance-driven” (Destexhe et al. 2001; Tiesinga et al. 2000). In the first of these, the input current is additive, being of the form I(t) = µ + σw(t), where t is time, µ and σ are constant, and w(t) is standard Gaussian white noise. Such an input may represent somatic current injection by microelectrode in the laboratory. In the second model, which is closer to the nature of synaptic stimulation as it occurs in the nervous system, the driving current is of the form I(t) = g(t)(V E − V(t)), where V(t) is the membrane depolarization, V E  > 0 is the reversal potential for synaptic excitation (Tuckwell 1988), and g(t) satisfies a first-order differential equation containing a noise amplitude σ E and a conductance parameter g E, along with a time constant (Destexhe et al. 2001; Tiesinga et al. 2000). If there is inhibition, there is a similar term involving the inhibitory reversal potential, but here, we consider excitation only. All the model equations for both kinds of input current and the relevant parameter values are given in the Appendix.

Results

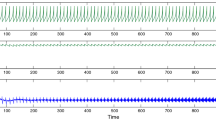
We first demonstrate the unusual inhibitory effect of noise in the case of a Hodgkin–Huxley neuron with a current-based input when the mean current is just greater than the critical value for repetitive firing. Figure 1a shows the voltage responses of the model neuron in such a case with various noise levels. Initially, the neuron is taken to be at rest, which, by definition (see Hodgkin and Huxley 1952), implies that the depolarization is zero. The applied signal has a mean of strength µ and a noisy component of amplitude σ. Without noise (top left record), there is, for this value of the steady input, µ  =  6.6, a repetitive stream of output spikes, there being eight in the time period duration of 150 ms shown. Adding noise makes the output sequence of spikes irregular. Extremely weak noise naturally has little effect, but slightly larger amounts can have a significant effect on the neuron’s spiking activity. Moreover, moderate amounts of noise can actually arrest the spiking for a long time. In the examples shown, a noise level of σ  =  0.2 can halt the firing of action potentials after three spikes, and a somewhat larger noise level of σ  =  0.5 here stops the spiking after just one spike. When the noise level is turned up to σ  =  2, more spikes are emitted, there being 9 in the trial shown. In Fig. 1b, plots of voltage vs the potassium conductance auxiliary variable, n (Hodgkin and Huxley 1952), are shown. These phase-space diagrams are useful in understanding the effects of noise of various levels, as discussed below.

Fig. 1
figure 1

a Showing voltage trajectories with spikes for a “current-driven” Hodgkin–Huxley model neuron. The mean input current density is 6.6 µA/cm2 and the effects of noise of various magnitudes, σ, are shown. b Orbits of voltage vs potassium activation variable corresponding to the plots of a. The limit cycle is clearly seen in the noise-free case and the manner in which small noise, σ  =  0.2, and intermediate noise, σ  =  0.5 may switch the orbit away from the limit cycle. When σ  =  2, the orbits are close to the noise-free case

Full size image

We further explored the effects of noise on the spiking activity of varying the mean of the input and its noise level in both the current-driven and conductance-driven cases. In Fig. 2a, results are shown for the current-driven neuron. The mean number of action potentials, N, emitted over a 1,000-ms period, is plotted for various values of the mean current µ against the noise level σ. It should be noted that, in characterizing most central nervous system activity, except for example some brain stem neurons, 1,000 ms is a very long time, as the natural scale is milliseconds. For each data point with noise, 200 trials were performed.

Fig. 2
figure 2

a Inverse stochastic resonance in the “current-driven” Hodgkin–Huxley model. The mean number of spikes N over a 1,000 ms period is shown as the noise intensity increases for three values of the mean input current µ. A minimum in the output is clearly seen as σ increases when µ is near the critical value µ c. b Inverse stochastic resonance in the “conductance-driven” Hodgkin–Huxley model. The mean number of spikes N over a 1,000-ms period is shown as the noise intensity increases for three values of the mean input signal strength g E (mS/cm2). A minimum in the output is clearly seen as σ E increases when g E is near the critical value at 0.112 and also when g E  =  0.1318 mS/cm2

Full size image

Without noise (σ  =  0), there is a critical value of µ = µ c, which is about 6.44, at which a stable and unstable limit cycle appear and co-exist with a stable focus. For values of µ > µ c up to a second critical value \( \mu_{\text{c}}^{*} \) with approximate value 9.8 (Hassard 1978), at which a subcritical Hopf bifurcation occurs, the system is bistable, and repetitive periodic firing may persist without noise. For \( \mu > \mu_{\text{c}}^{*} \), the focus becomes unstable, and only the stable limit cycle exists (until a further critical value is reached). For values of µ between µ c and \( \mu_{\text{c}}^{*} \), perturbations, which may be stochastic or deterministic, can drive the system from near the stable limit cycle or spiking state to near the rest point, or vice-versa. In this article, we are mainly concerned with the effects of noise for values of µ between µ c and \( \mu_{\text{c}}^{*} \).

When µ  =  5.5, below the critical value µ c, there is only one spike without noise. As the noise level increases beyond σ  =  0.2, so does the mean number of spikes. However, when µ  =  6.8, not far above the critical value and when there are 57 spikes without noise, increasing the noise level makes the mean number N of spikes at first drop dramatically. There is a pronounced minimum of six spikes at about σ  =  0.5, representing a drop in mean spike count of 89%, and thereafter, the mean number of spikes increases at first quite sharply and then more slowly as the noise level increases. For the larger value of the mean input current, µ  =  8, there are 62 spikes without noise and a noticeable, yet less pronounced, minimum value of 48 in the mean number of spikes when σ is just less than one.

In order to examine what role the initial conditions might have played in these results, the values of V, n, m, and h at t  =  0 were all chosen randomly. For V, the initial value was uniformly distributed from the minimum to the maximum voltage obtained in rhythmic spiking without noise. For n, m, and h, their values at t  =  0 were uniformly distributed on (0,1). The effects of additive noise were qualitatively the same as for the case of initial resting conditions. For example, with µ  =  6.8 at a time interval of 500 ms, the mean number of spikes dropped from 20.3 without noise to 3.08 as σ increased to 0.5. Thereafter, as σ increased, the mean number of spikes increased monotonically to about 31 at σ  =  4. With µ  =  8, there is a small decline in mean spike count from 29.9 to 24.9 as σ increases from 0 to 0.7, and then a slow increase to N  =  32.4 as σ increased further to four. The results for µ  =  5.5 also paralleled those for resting initial conditions. It is pointed out that, with some of the randomly chosen initial conditions, some of the solutions would, in the absence of noise, evolve to the rest point, whereas others would tend to the limit cycle.

As a further test of the robustness of the results we have described, we performed simulations in which the initial conditions were fixed at the resting values given in the Appendix, but the noise was switched on at a random time T R. The latter was uniformly distributed over the period of rhythmic spiking, which is about 20 ms. Thus, the neuron is set spiking with a given value of µ > µ c, and then at T R  =  100 + 20U, where U is a uniform (0,1) random variable, the noise is switched on. We recorded the mean number N* of spikes for T R < t < 500 ms, that is, after the noise is switched on until t  =  500. The dependence of N* on σ for the two values of µ previously employed (6.8 and 8) again paralleled those shown in Fig. 2a. For example, with µ  =  6.8, the mean spike count N* declined sharply from 21.5 with no noise to a minimum of 4.2 with σ  =  0.5. Thereafter, N* increased with increasing noise amplitude. It may be concluded that the observed inhibitory effect of noise for certain values of the mean input current and the occurrence of a minimum as the noise level increases are robust phenomena for the Hodgkin–Huxley system.

In further support of this latter claim, Fig. 2b shows corresponding results obtained for the case of a conductance-driven neuron, for which the equations are also given in the Appendix. We have focused on the case of excitatory synaptic input. Here, when there is no noise, there is a critical conductance value just less than g E  =  0.112 mS/cm2, below which there is no sustained firing. The bottom curve shows the effects of increasing noise when g E  =  0.0906 mS/cm2, which is below the critical value. With increasing noise levels, the average number of spikes gradually increases from one to about 50. When g E  =  0.112 mS/cm2 and there is no noise, there are 55 spikes in a 1,000-ms period. A small amount of noise causes a very large decrease in spike rate, and as the noise level increases, there is a well-defined minimum at about σ E  =  0.005. For a stronger mean stimulus level, g E  =  0.1318 mS/cm2, there are 63 spikes without noise. As the noise level increases, a distinct minimum occurs at about σ E  =  0.0075. Thus, for both kinds of input current, current-driven and conductance-driven, a noise-induced decrease in firing rate occurs for inputs with means near the critical value for periodic spiking, and this inhibitory effect occurs even if the neuron is driven by a purely excitatory synaptic input.

Discussion

In this article, we reported new and interesting findings on the effects of noise on the behavior of certain dynamical systems relevant to neuronal activity. These arose from our investigations of the properties of pairs of coupled type 1 (Gutkin and Ermentrout 1998) neurons with noisy inputs (Gutkin et al. 2008). The results presented here on the silencing effects of noise on single Hodgkin–Huxley neurons, which are of type 2 excitability, came from our studies of pairs of such coupled neurons, to be reported elsewhere. Our main observation is that, contrary to what is generally accepted, noise does not always have an excitatory or positive effect (Cope and Tuckwell 1979; Yu and Lewis 1989; Stein et al. 2005), but it can lead to inhibitory or negative effects, which are also amenable to tuning.

The occurrence of a minimum in the response as the noise level increases through a certain value might be called inverse stochastic resonance, a term which derives from its having the opposite character to stochastic resonance, in which a maximum in a response variable occurs as the noise level increases (Collins et al. 1996). We obtained similar results when the initial values of the four Hodgkin–Huxley variables were chosen randomly or when the noise was switched on at a random time, thus lending support to the robustness of the findings. Preliminary simulations of more complex nerve models and larger networks have yielded the same kind of behavior, both in regard to silencing and the occurrence of a minimum in the firing rate, indicating that these phenomenona are quite general in neural systems.

The effects of noise reported above are explainable in terms of the behavior of the voltage and other variables on what are called stable limit cycles (Murray 1993), which occur when, for example, a neuron fires repetitively at the same frequency (see Fig. 1b) or a heart pacemaker beats continually (Panfilov and Holden 1997). Such a stable limit cycle in a dynamical system often appears by a bifurcation mechanism when a parameter, like the mean input current strength in the Hodgkin–Huxley model, varies continuously and crosses some critical value. Just above that critical value, the basin of attraction of the limit cycle, that is, the region from which it is approached, is rather narrow. The stable limit cycle then coexists with one or more other attractors, which is the key to the occurrence of the phenomena we have reported. In the Hodgkin–Huxley model, for \( \mu_{\text{c}} < \mu < \mu_{\text{c}}^{*} \), the only other attractor is a stable quiescent or resting state. Noise can make the solutions leave the basin of attraction of the limit cycle for that of the quiescent state so that spiking ceases. A minimum in the spike count as noise increases is likely to occur for values of µ not far above µ c. The transitions to and from the attractors can be explored technically using classical stochastic process theory, as we will report with mathematical detail elsewhere.

When the noise is small, the solution will then typically stay near the rest state for a very long time, but for larger noise, there is a considerable probability that the solutions will get kicked back up to threshold so that spiking may resume. This may be followed by a period of relative silence, and so on. This is illustrated in detail in Fig. 1b, where the voltage variable V is plotted against the potassium conductance variable n for µ  =  6.6, with no noise, σ  =  0, (top left), and values of the noise parameter σ  =  0.2, 0.5, and 2. It is seen that weak noise can act to switch off the activity and induce a long period without spikes, whereas stronger noise tends to make the system switch back and forth between spiking and non-spiking states. The rate at which transitions then occur between spiking and non-spiking can be so rapid that the activity seems almost uninterrupted.

The switching behavior for small noise has been observed in recent experiments (Paydarfar et al. 2006). Thus, the functional significance of these effects of noise on rhythmic activity is that a very small disturbance can lead to a drastic change in behavior. In the brain, electrical activity is often broadly rhythmic, involving limit-cycles in both normal and epileptic activity (Steriade 2000; Buzsáki and Draguhn 2004). If such oscillations arise near a bifurcation point, then a small noisy signal could lead to the cessation of, or a sharp modification of, rhythmic activity. It is feasible that this could be the basis of a therapeutic approach to alleviate symptoms in the case of pathological oscillatory activity. Also, in a population of cells, for example, with functionally tuned receptive fields, those which are weakly responding and operating near a bifurcation point akin to µ c could be silenced easily by noisy inputs, whereas cells firing at higher levels would have their activity augmented by noise, giving noise-induced tuning to the population responses. This may represent a new noise-induced mechanism for the sharpening of neural responses. Note that the perturbing inputs (noise) do not have to be smooth but could be just as effective if they had an impulsive nature.

Since dynamical systems in diverse fields exhibit stable limit cycles coexisting with a stable focus, we expect to find that the phenomena of inhibition of cyclic, repetitive, or rhythmic activity by noise and inverse stochastic resonance will have widespread occurrence. Examples of fields or systems where a stable limit cycle coexists with a stable rest state occur in circadian rhythms (Jewett and Kronauer 1998), cardiology (Panfilov and Holden 1997), cell kinetics and tumor growth (Lahav et al. 2004; Goldbeter 1991), and oscillating neural networks (Steriade 2000; Buzsáki and Draguhn 2004), as well as in climatology, ecology, and astrophysics. The underlying mathematical bifurcation pattern suggests that the phenomena we have detected are of a general nature and not restricted to the Hodgkin–Huxley model. Although the phenomena we have described are of interest in themselves, as indeed is stochastic resonance, their functional significance in neurobiological and other dynamical systems remains to be fully explored. A related finding was reported in a heuristic nonlinear stochastic model of affective disorders (Huber et al., 2004).