Local coordinates on Lie groups for half-explicit time integration of Cosserat-rod models with constraints

Abstract

Explicit Runge–Kutta methods are the gold standard of time-integration methods for nonstiff problems in system dynamics since they combine a small numerical effort per time step with high accuracy, error control, and straightforward implementation. For the analysis of beam dynamics, we couple them with a local coordinates approach in a Lie group setting to address large rotations. Stiff shear forces and inextensibility conditions are enforced by internal constraints in a coarse-grid discretization of a geometrically exact beam model. The resulting nonstiff constrained systems are handled by a half-explicit approach that relies on the constraints at velocity level and avoids all kinds of Newton–Raphson iteration. We construct half-explicit Runge–Kutta Lie group methods of order up to five that are equipped with an adaptive step-size strategy using embedded Runge–Kutta pairs for error estimation. The methods are tested successfully for a roll-up maneuver of a flexible beam and for the classical flying-spaghetti benchmark.

1 Introduction

Geometric numerical methods preserve the essential properties of the flow of differential equation models [13]. Such strategies are important for the robust, efficient, and numerically stable dynamical simulations of highly flexible structures. In space, they are used to obtain coarse-grid discretizations that reflect the characteristic behavior of geometrically exact beam models. In the time domain, geometric integration is tailored to nonlinear configuration spaces that are typical of mechanical systems with large rotations.

In the present paper, we address the latter aspect and present a novel Runge–Kutta Lie group integrator for constrained mechanical systems and its application to beam dynamics. The method is half-explicit and avoids all kinds of Newton–Raphson iterations that are a bottleneck for the efficiency of classical implicit integrators in beam analysis. Stiff shear forces are represented by internal constraints [19, 20] that may be used as well to enforce a beam’s inextensibility. These internal constraints are combined with a coarse-grid space discretization and result finally in a constrained system that is for typical application scenarios nonstiff in its differential part.

The equations of motion of constrained mechanical systems form differential-algebraic equations (DAEs) with Lagrange multipliers as algebraic variables that couple the constraints to the equilibrium equations for forces and moments [12, 13]. Following the approach of Brasey and Hairer [6], the equations of motion are transformed analytically before half-explicit time discretization, resulting in the index-2 formulation with constraint equations at the level of velocity coordinates. In that way, the velocity vector is constrained to the null space of the constraint Jacobian that is known from null-space approaches like the one of Betsch [4]. In the context of Lie group time integration, these velocity constraints have been used before in the RATTLie integrator [16] and in the application of generalized-$\alpha$ methods to the stabilized index-2 formulation of the equations of motion [2].

The successful application of generalized-$\alpha$ and other Newmark-type Lie group integrators in flexible multibody dynamics [7, 8, 12] relies on the specific Lie group structure of the configuration space for mechanical systems with large rotations [22, 23]. The Lie group setting is attractive in this context since it allows us to describe large rotations and the orientation of bodies and flexible structures without any singularities [27]. The spaces one comes across are the space of Special Orthogonal matrices $SO(3)$ or the space of unit quaternions $\mathbb{S}^{3}$, their direct or semidirect product with $\mathbb{R}^{3}$, and tensor products thereof.

The half-explicit Runge–Kutta Lie group integrator is tested for a geometrically exact beam model that goes back to Lang and Linn [19, 20]. The space discretization follows the variational integration approach of Hante [15, 17] with nodal variables $(q_{i},x_{i})\in \mathbb{S}^{3} \ltimes \mathbb{R}^{3}$. The semidirect product of $\mathbb{S}^{3}$ and $\mathbb{R}^{3}$ may be considered to be isomorphic to the Special Euclidean group $SE(3)$, taking into account that $\mathbb{S}^{3}$ is a double covering of the Special Orthogonal group $SO(3)$, i.e., $q,-q\in \mathbb{S}^{3}$ represent the same rotation matrix $R\in SO(3)$.

In the work of Munthe-Kaas [24], see also Iserles et al. [18], classical Runge–Kutta methods are generalized to Lie group integrators with the help of the exponential map that defines local coordinates on the Lie group by a tangent space parametrization. The possibility to work locally in the tangent space, which is a linear space with the well-known operations among its elements, simplifies substantially the numerical solution of a system set in a Lie group. The use of the exponential map assures that the numerical solution remains in the Lie group, given that we work with local coordinates.

In a general Lie group setting, the construction and implementation of higher-order Runge–Kutta Munthe-Kaas methods is challenging since they involve frequent evaluations of matrix exponentials [21] and the approximation of its derivatives [24]. There are no such problems in the application to $SO(3)$ since Rodrigues’ formula allows us to evaluate the exponential map in closed form and a similar expression may be found for its derivative [18]. Park and Chung generalized this approach to the Special Euclidean group $SE(3)$ and pointed out that any classical explicit Runge–Kutta method may be generalized in that way to a Lie group integrator on $SE(3)$ with the same order of convergence [26]. Several recent studies focus on the closed-form expression of the exponential map and its derivatives, as well as their efficient evaluation [15, 30, 32]. Additionally, one may be concerned with singularities occurring at the origin, which are solved by extended investigation of the approximation of the closed form by a Taylor polynomial [15, Appendix B].

The present paper considers nonstiff integrators that are a quasistandard in nonlinear system dynamics, such as the default integrator ode45 in MATLAB’s ODE suite [28], addressing two main challenges: Nonlinear configuration spaces and constraints. We aim to solve the former by introducing Lie group integrators and the latter by adapting the existing numerical method of half-explicit Runge–Kutta type [6].

2 Half-explicit Runge–Kutta Lie group integrators

In the present section, we elaborate the definition of the method. In the early 1990s, Brasey and Hairer introduced the half-explicit Runge–Kutta methods for semiexplicit index-2 DAEs in Hessenberg form [6]. Some years later, Murua [25] and Arnold [1] proposed a modification, which simplifies the order conditions of higher order methods and makes the approach more efficient. In each time step, the methods start with an explicit stage and evaluate in all later stages velocity vectors in the null space of the corresponding constraint Jacobians.

2.1 Equations of motion and local coordinates

First, we consider a flexible multibody system in the Lie group $G:=(\mathbb{S}^{3}\ltimes \mathbb{R}^{3})^{N+1}$, with $N$ denoting the number of beam edges after space discretization [15]. The elements $q\in G$ have $7(N+1)$ components: 4 for the orientation and 3 for the position of each frame that is attached to one of the $N+1$ nodes of this discretization. Let $e$ be the identity element of the Lie group $G$. We introduce the elements of the tangent space $\tilde{\mathbf{v}}\in T_{e}G$, that summarize both angular and translational velocity. The tangent space $T_{e}G$ at the identity element has been identified with $\mathbb{R}^{6(N+1)}$ through an isomorphism called the tilde operator $\tilde{\bullet}:\mathbb{R}^{6(N+1)}\to T_{e}G$.

By the use of the previous elements, we set the equations of motion for a constrained flexible multibody system as expressed in [7]:

$$\begin{aligned} \dot{q} &= D\textrm{L}_{q}(e)\cdot \tilde{\mathbf{v}} \end{aligned}$$

(1a)

$$\begin{aligned} \mathbf{M}(q)\dot{\mathbf{v}} &= -\mathbf{g}(t, q, \mathbf{v})- \mathbf{B}^{\top}(q)\boldsymbol{\lambda} \end{aligned}$$

(1b)

$$\begin{aligned} \boldsymbol{0} &= \boldsymbol{\Phi}(q), \end{aligned}$$

(1c)

where $\mathbf{M}(q)$ is the mass and inertia matrix, $\mathbf{g}(t, q, \mathbf{v})$ is the vector of external and internal forces, and $\mathbf{B}(q)$ is the gradient of the constraint function at the position level $\boldsymbol{\Phi}(q)$ in the sense of [7, Eq. (9)]:

$$ D\boldsymbol{\Phi}(q)\cdot \left (D\textrm{L}_{q}(e)\cdot \tilde{\mathbf{w}}\right )=\mathbf{B}(q)\mathbf{w},\quad \mathbf{w} \in \mathbb{R}^{6(N+1)}. $$

(2)

Equations (1a)–(1c) are the index-3 formulation of the equations of motion. The right-hand side $D\textrm{L}_{q}(e)\cdot \tilde{\mathbf{v}}$ of the kinematic equation (1a) evaluates at $y=e$ the directional derivative of the left translation $L_{q}(y)=q\circ y$ in the direction of $\tilde{\mathbf{v}}\in T_{q}G$:

$$ \dot{q}(t)=\lim _{\epsilon \to 0} \frac{q(t)\circ \exp{\left (\epsilon \tilde{\mathbf{v}}(t)\right )}-q(t)}{\epsilon}. $$

(3)

We can perform an index reduction by differentiating in time the constraints in Equation (1c):

$$ \boldsymbol{0}=\frac{\textrm{d}\boldsymbol{\Phi}}{\textrm{d}t}(q(t))=D \boldsymbol{\Phi}(q(t))\cdot \dot{q}(t)=D\boldsymbol{\Phi}(q(t)) \cdot (D\textrm{L}_{q(t)}(e)\cdot \tilde{\mathbf{v}}(t))=\mathbf{B}(q(t)) \mathbf{v}(t). $$

(4)

The index-2 formulation of the equations of motion is

$$\begin{aligned} \dot{q} &= D\textrm{L}_{q}(e)\cdot \tilde{\mathbf{v}} \end{aligned}$$

(5a)

$$\begin{aligned} \mathbf{M}(q)\dot{\mathbf{v}} &= -\mathbf{g}(t, q, \mathbf{v})- \mathbf{B}^{\top}(q)\boldsymbol{\lambda} \end{aligned}$$

(5b)

$$\begin{aligned} \boldsymbol{0} &= \mathbf{B}(q) \mathbf{v}. \end{aligned}$$

(5c)

It is analytically equivalent to (1a)–(1c) and avoids the time-consuming evaluation of curvature terms in the index-1 formulation of the equations of motion [31, 33].

Given the equations of motion, the solution in local coordinates, in the neighborhood of $t=t_{n}$, is

$$ q(t) = q(t_{n})\circ \exp{\left (\tilde{\boldsymbol{\theta}}_{n}(t) \right )}, $$

(6)

where ${\boldsymbol{\theta}}_{n}(t)$ denotes a local parametrization of the Lie group with ${\boldsymbol{\theta}}_{n}(t_{n})=\boldsymbol{0}$. Differentiating (6) in time, the time derivative of $q(t)$ is given by

$$ \dot{q}(t)=\lim _{\epsilon \to 0}\frac{q(t+\epsilon )-q(t)}{\epsilon}= \lim _{\epsilon \to 0} \frac{q(t_{n})\circ \exp{\left (\tilde{\boldsymbol{\theta}}_{n}(t+\epsilon )\right )}-q(t)}{\epsilon}. $$

(7)

Comparing this equation with (3), they have to coincide for finite $\epsilon$ up to higher-order terms:

$$ q(t)\circ \exp{\left (\epsilon \tilde{\mathbf{v}}\right )}=q(t_{n}) \circ \exp{\left (\tilde{\boldsymbol{\theta}}_{n}(t)+\epsilon \dot{\tilde{\boldsymbol{\theta}}}_{n}(t)\right )}+o(\epsilon ). $$

(8)

Given that

$$ \frac{\textrm{d}}{\textrm{d}\epsilon}\exp{\left ( \tilde{\boldsymbol{\theta}}_{n}(t)+\epsilon \dot{\tilde{\boldsymbol{\theta}}}_{n}(t)\right )}\Big\vert _{ \epsilon =0}=\exp{\left (\tilde{\boldsymbol{\theta}}_{n}(t)\right )} \textrm{dexp}_{-\tilde{\boldsymbol{\theta}}_{n}(t)} \dot{\tilde{\boldsymbol{\theta}}}_{n}(t) $$

(9)

with $\textrm{dexp}_{-\tilde{\boldsymbol{\theta}}_{n}(t)}$ denoting the right trivialized differential of exp, see [18, Definition 2.18], we obtain

$$ q(t_{n})\circ \exp{\left (\tilde{\boldsymbol{\theta}}_{n}(t)+ \epsilon \dot{\tilde{\boldsymbol{\theta}}}_{n}(t)\right )}=q(t_{n}) \circ \exp{\left (\tilde{\boldsymbol{\theta}}_{n}(t)\right )}\circ \exp{\left (\epsilon \,\textrm{dexp}_{-\tilde{\boldsymbol{\theta}}_{n}(t)} \dot{\tilde{\boldsymbol{\theta}}}_{n}(t)\right )}+o(\epsilon ) $$

and (8) results in

$$ \tilde{\mathbf{v}}(t)=\textrm{dexp}_{-\tilde{\boldsymbol{\theta}}_{n}(t)} \dot{\tilde{\boldsymbol{\theta}}}_{n}(t). $$

(10)

For practical computations, the equivalent representation in terms of the tangent operator [7, 8] proves to be favorable:

$$ \mathbf{v}(t)=\mathbf{T}({\boldsymbol{\theta}}_{n}(t)) \dot{\boldsymbol{\theta}}_{n}(t). $$

(11)

The $\textrm{dexp}$ operator may be evaluated in terms of iterations of the adjoint operator [18, Equation (2.44)] resulting in a series expansion of the tangent operator $\mathbf{T}$, see [8], that may be summarized to closed-form expressions for all Lie groups of practical relevance in multibody dynamics, see [18, 26] and the more detailed discussion in Sect. 2.3.

2.2 Half-explicit Runge–Kutta Lie group methods

In classical Runge–Kutta methods, we use parameters $a_{ij},\ b_{j},\ c_{i},\ (i,j=1,\dots ,s)$ to build stage vectors and numerical solution. In particular, we evaluate $s$ stage vectors using $a_{ij}$, $c_{i}$ and we compute the numerical solution as a linear combination of the $s$ stage vectors weighted by the $b_{j}$ parameters. When using the half-explicit Runge–Kutta methods, we may introduce more stage vectors $(\bar{s}\geq s)$, and use the notation $b_{j}=a_{s+1,j}$, $(j=1,\dots ,s)$. In the Lie group integrator, the stage vectors are

$$\begin{aligned} Q_{ni}=q_{n}\circ \exp{\left (\tilde{\boldsymbol{\Theta}}_{ni}\right )}, \ \boldsymbol{\Theta}_{ni}=h\sum ^{i-1}_{j=1}a_{ij} \dot{\boldsymbol{\Theta}}_{nj},\ \mathbf{V}_{ni}=\mathbf{v}_{n}+h \sum _{j=1}^{i-1}a_{ij}\dot{\mathbf{V}}_{nj},& \\ (i=1,\dots ,\bar{s}+1),& \end{aligned}$$

(12)

with

$${\dot{\mathbf{\Theta }}}_{ni}={\mathbf{T}}^{-1}({\mathbf{\Theta }}_{ni}){\mathbf{V}}_{ni},(i=1,\dots ,\overline{s}),$$

(13a)

$$\mathbf{M}(Q_{ni}){\dot{\mathbf{V}}}_{ni}=-\mathbf{g}(t_n+c_{i}h,Q_{ni},{\mathbf{V}}_{ni})-{\mathbf{B}}^{\mathrm{\top }}(Q_{ni}){\mathbf{\Lambda }}_{ni},(i=1,\dots ,\overline{s}).$$

(13b)

The first stage $(i=1)$ is explicit with

$$ Q_{n1}=q_{n},\quad \boldsymbol{\Theta}_{n1}=\boldsymbol{0},\quad \mathbf{V}_{n1}=\mathbf{v}_{n},\quad \boldsymbol{\Lambda}_{n1}= \boldsymbol{\lambda}_{n}. $$

For $i=2,\dots ,\bar{s}$, we enforce the hidden constraints at velocity level (5c) for stage vectors $Q_{n,i+1}$, $\mathbf{V}_{n,i+1}$ resulting in

$$\begin{aligned} \boldsymbol{0}=\mathbf{B}(Q_{n,i+1})\mathbf{V}_{n,i+1}=\mathbf{B}(Q_{n,i+1})( \mathbf{v}_{n}+h\sum _{j=1}^{i-1}a_{i+1,j}\dot{\mathbf{V}}_{nj}+ha_{i+1,i} \dot{\mathbf{V}}_{ni}),& \\ (i=2,\dots ,\bar{s}).& \end{aligned}$$

(13c)

Equations (13b) and (13c) form a system of linear equations in terms of $\boldsymbol{\Lambda}_{ni}$, $\dot{\mathbf{V}}_{ni}$, $(i=2,\dots ,\bar{s})$, that motivate the notation half-explicit for this class of time-integration methods [6]:

$$\begin{array}{rrr}\left(\begin{array}{cc}\mathbf{M}(Q_{ni})& {\mathbf{B}}^{\mathrm{\top }}(Q_{ni})\\ h{a}_{i+1,i}\mathbf{B}(Q_{n,i+1})& \mathbf{0}\end{array}\right)\left(\begin{array}{c}{\dot{\mathbf{V}}}_{ni}\\ {\mathbf{\Lambda }}_{ni}\end{array}\right)=\left(\begin{array}{c}-\mathbf{g}(t_n+c_{i}h,Q_{ni},{\mathbf{V}}_{ni})\\ -\mathbf{B}(Q_{n,i+1})({\mathbf{v}}_n+h\sum _{j=1}^{i-1}{a}_{i+1,j}{\dot{\mathbf{V}}}_{nj})\end{array}\right)& & \\ (i=2,\dots ,\overline{s}).& & \end{array}$$

(14)

The total number of linear systems to be solved in each time step is $\bar{s}-1$. Note that the half-explicit approach avoids all iterations and does not rely on some kind of Newton–Raphson method.

The updated solution at time step $t = t_{n+1}$ is

$$ q_{n+1}=Q_{n,s+1}=q_{n}\circ \exp{\left (\tilde{\boldsymbol{\Theta}}_{n,s+1} \right )},\ \mathbf{v}_{n+1}=\mathbf{V}_{n,s+1},\ \boldsymbol{\lambda}_{n+1}=\sum _{i=1}^{\bar{s}}d_{i} \boldsymbol{\Lambda}_{ni}, $$

(15)

where $d_{j}$ are additional parameters for the computation of the Lagrange multipliers. Their value, as for the other parameters, is set by order conditions and by a contractivity condition to ensure zero stability. The method has been tested up to order five. We list in Table 1 the Butcher tableaux with parameters $a_{ij},\,(i=1,\dots ,\bar{s}+1,j< i)$ for the implemented methods [1].

Table 1 Parameters of half-explicit methods up to order $p=5$

In a local coordinates approach, the order analysis in [1], valid for linear spaces, appears to be applicable also for nonlinear configuration spaces. In our case, the tests are performed for the Lie groups $SE(3)$ and $SO(3)\times \mathbb{R}^{3}$ in Sect. 2.4 and for Lie group $(\mathbb{S}^{3}\ltimes \mathbb{R}^{3})^{N+1}$ for the applications to beam dynamics.

2.3 Implementation issues

As stated in the previous subsection, the Lie groups of interest are $SO(3)$, $\mathbb{S}^{3}$, their direct or semidirect product with $\mathbb{R}^{3}$, and tensor products thereof. Inspired by Rodrigues’ formula [18]

$$ \exp _{SO(3)}{(\tilde{\boldsymbol{\Omega}})}=\mathbf{I}_{3} + \frac{\sin{\omega}}{\omega}\tilde{\boldsymbol{\Omega}}+ \frac{1-\cos{\omega}}{\omega ^{2}}\tilde{\boldsymbol{\Omega}}^{2}, $$

(16)

we consider the closed-form expression, see, e.g., [5]

$$ \exp _{\mathbb{S}^{3}}{(\tilde{\boldsymbol{\Omega}})}= \begin{bmatrix} \cos{(\frac{\omega}{2})} \\ \frac{\boldsymbol{\Omega}}{\omega}\sin{(\frac{\omega}{2})} \end{bmatrix} . $$

(17)

Here and later in the current section, we set $\omega =\Vert \boldsymbol{\Omega}\Vert _{2}$.

Following the approach of Hante [15], we consider the semidirect product $\mathbb{S}^{3}\ltimes \mathbb{R}^{3}$ that introduces a coupling between the orientation and the position variables, which results in the appearance of the tangent operator in the exponential map as it is known from $SE(3)$. Given $\mathbf{v}=[\boldsymbol{\Omega}^{\top},\mathbf{U}^{\top}]^{\top}$

$$\begin{aligned} \exp _{\mathbb{S}^{3}\ltimes \mathbb{R}^{3}}{(\tilde{\mathbf{v}})}&= \left ( \exp _{\mathbb{S}^{3}}{(\tilde{\boldsymbol{\Omega}})}, \mathbf{T}^{\top}_{\mathbb{S}^{3}}(\boldsymbol{\Omega})\cdot \mathbf{U}\right ), \end{aligned}$$

(18)

where the tangent operator $\mathbf{T}_{\mathbb{S}^{3}}(\boldsymbol{\Omega})$ is

$$ \mathbf{T}_{\mathbb{S}^{3}}(\boldsymbol{\Omega})=\mathbf{I}_{3} + \frac{\cos{\omega}-1}{\omega ^{2}}\tilde{\boldsymbol{\Omega}}+ \frac{\omega -\sin{\omega}}{\omega ^{3}}\tilde{\boldsymbol{\Omega}}^{2} . $$

(19)

At the same time, we need to specify the tangent operator on $\mathbb{S}^{3}\ltimes \mathbb{R}^{3}$

$$ \mathbf{T}_{\mathbb{S}^{3}\ltimes \mathbb{R}^{3}}(\mathbf{v})= \begin{pmatrix} \mathbf{T}_{\mathbb{S}^{3}}(\boldsymbol{\Omega}) & \boldsymbol{0} \\ \mathbf{C}_{1}(\boldsymbol{\Omega},\mathbf{U}) &\mathbf{T}_{ \mathbb{S}^{3}}(\boldsymbol{\Omega}) \end{pmatrix} , $$

(20)

where the function $\mathbf{C}_{1}(\boldsymbol{\Omega},\mathbf{U})$ is

$$\begin{aligned} \mathbf{C}_{1}(\boldsymbol{\Omega},\mathbf{U})&= \frac{\cos{\omega}-1}{\omega ^{2}}\tilde{\mathbf{U}} + \frac{\omega -\sin{\omega}}{\omega ^{3}}\left (\tilde{\mathbf{U}} \tilde{\boldsymbol{\Omega}}+\tilde{\boldsymbol{\Omega}} \tilde{\mathbf{U}}\right )+ \\ & \hspace{8mm} +\frac{2-2\cos{\omega}-\omega \sin{\omega}}{\omega ^{4}}\left ( \boldsymbol{\Omega}^{\top}\mathbf{U}\right ) \tilde{\boldsymbol{\Omega}}+ \\ & \hspace{8mm} -\frac{\omega (2+\cos{\omega})-3\sin{\omega}}{\omega ^{5}}\left ( \boldsymbol{\Omega}^{\top}\mathbf{U}\right ) \tilde{\boldsymbol{\Omega}}^{2}. \end{aligned}$$

In the space of interest for beam analysis $G=\left (\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\right )^{N+1}$, the exponential map and the tangent operator are diagonal block matrices, where each block is of the form (18) and (20), respectively.

We would like to remark that due to the form of the expression of the operators, one has to consider alternatives for the singularities at $\boldsymbol{\Omega}\approx \boldsymbol{0}$. In [15, Appendix B], a deep investigation is performed to obtain the expression needed to have the numerical method without loss of accuracy. In Table 2, we present a limited output of this study, focusing on the functions that are needed in the group $\mathbb{S}^{3}\ltimes \mathbb{R}^{3}$.

Table 2 Singular functions and their Taylor polynomials [15, Appendix B]

2.4 Case study

As a proof of concept, we refer to the classical benchmark of the heavy top. We use the model as described in [3], where the orientation of the top is parameterized by rotation matrices in $SO(3)$.

The heavy top has a fixed point in the origin of the inertial frame and it is free to rotate about that point. The motion under the influence of gravity is described via the position of the center of mass in the inertial frame $\mathbf{x}\in \mathbb{R}^{3}$ and the orientation of the body using a rotation matrix $\mathbf{R}\in SO(3)$, i.e., the variable $q$ in Eq. (5a)–(5c) is $q(t)=(\mathbf{R}(t),\mathbf{x}(t))$. The data, omitting physical units, include the center of mass in the body-attached frame $\mathbf{X}=(0,1,0)^{\top}$, the mass $m = 15.0$, the inertia tensor w.r.t. the center of mass $\mathbf{J}=\text{diag}(0.234375,0.46875,0.234375)$, and the constant gravitational acceleration vector $\gamma =(0,0,-9.81)^{\top}$. The constraints at position level refer to the rotation about a fixed point, which can be modeled with the constraint $\boldsymbol{\Phi}(q)=\mathbf{R}^{\top}\mathbf{x}-\mathbf{X}$. As an initial configuration, we set the rotation $\mathbf{R}(0)=\mathbf{I}_{3}$ and the angular velocity $\boldsymbol{\Omega}(0)=(0, 150, -4.61538)^{\top}$ with initial position and translational velocity consistent with the holonomic constraints at position level and corresponding hidden constraints at velocity level. In Fig. 1 and Fig. 2, the proposed numerical methods are applied to the heavy-top benchmark. In the plots, one may observe that the expected order of convergence is preserved for the test cases in the Lie group setting. Moreover, the same order of convergence applies also to the Lagrange multipliers $\lambda$, right plots in Figs. 1 and 2. The experiment solves the system in its index-2 formulation, where the constraints are at the velocity level. A known limitation is the risk of linear growth of the residual in the holonomic constraints (drift-off) and it appears to be group dependent. One may observe in Fig. 3 that the choice of the Lie group determines the presence of the drift-off. When using a direct product $SO(3)\times \mathbb{R}^{3}$, the constraints at position level are not completely satisfied and the numerical solution diverges systematically from the manifold of constraints. On the contrary, for the semidirect product $SE(3):=SO(3)\ltimes \mathbb{R}^{3}$ the solution maintains the constraints both at position and velocity levels. This is in line with a detailed theoretical analysis for other Lie group integrators [3, Sect. 3.6]. The drift-off effect will be further investigated in future research. It does not appear in the specific applications to beam dynamics we are going to show later in the paper. In a direct comparison with the Lie group DAE integrators that rely on the index-1 formulation of the equations of motion [31, 33], the reduced risk of drift in the index-2 formulation (5a)–(5c) is a clear benefit of the proposed method (12)–(14), see also [13, Theorem VII.2.1]. In the literature, the heavy-top benchmark is set in the direct or semidirect product of $SO(3)$ and $\mathbb{R}^{3}$. For the setting presented in the current paper and for homogeneity with the following tests, we repeated the tests with unit quaternions, i.e., in the spaces $\mathbb{S}^{3}\times \mathbb{R}^{3}$ and $\mathbb{S}^{3}\ltimes \mathbb{R}^{3}$. In Figs. 4 to 6, we obtained qualitatively the same results, with a slightly larger error constant.

Fig. 1

Heavy top modeled in $SO(3)\times \mathbb{R}^{3}$. Convergence study for the variable at position level $q$ (left plot) and for the Lagrange multipliers $\lambda$ (right plot). (Color figure online)

Fig. 2

Heavy top modeled in $SE(3)$. Convergence study for the variable at position level $q$ (left plot) and for the Lagrange multipliers $\lambda$ (right plot). (Color figure online)

Fig. 3

Drift-off effect of the residual of the constraint at position level: $SO(3)\times \mathbb{R}^{3}$ (left plot) and $SE(3)$ (right plot)

Fig. 4

Heavy top modeled in $\mathbb{S}^{3}\times \mathbb{R}^{3}$. Convergence study for the variable at position level $q$ (left plot) and for the Lagrange multipliers $\lambda$ (right plot). (Color figure online)

Fig. 5

Heavy top modeled in $\mathbb{S}^{3}\ltimes \mathbb{R}^{3}$. Convergence study for the variable at position level $q$ (left plot) and for the Lagrange multipliers $\lambda$ (right plot). (Color figure online)

Fig. 6

Drift-off effect of the residual of the constraint at position level: $\mathbb{S}^{3}\times \mathbb{R}^{3}$ (left plot) and $\mathbb{S}^{3}\ltimes \mathbb{R}^{3}$ (right plot)

3 Error-controlled variable time step-size

In Sect. 2, we introduced a modified half-explicit Runge–Kutta method for Lie group settings. In the current section, we are going to expand the study to variable time step-sizes. The advantages of using an error-controlled variable time step-size are the reduction of the computational time, obtaining at the same time a control over the error. In particular, when solving the equations with fixed time steps, we do not know how well the simulation is performing while it is running. For variable step sizes, we have to estimate the local error to establish a new time step-size. The theory behind the approach used here can be found in [14].

3.1 Methodology

The main challenge is the estimation of the local error for the position variable. Since we are working in a Lie group setting, the position variable, indicated before by $q(t)$, cannot be used in sums and differences as an element of a linear space. The decision we make is to estimate the local error of the local parametrization $\boldsymbol{\theta}_{n}(t)$. In this way, we are able to use the established theory of embedded Runge–Kutta formulas [14]. To implement it, we need to introduce a new variable, which does not lie in the Lie group, and for which we can perform operations of sums and difference: $\mathbf{y}=(\boldsymbol{\theta}^{\top},\mathbf{v}^{\top})$. Here, $\boldsymbol{\theta}$ and $\mathbf{v}$, as before, are the local parametrization of the Lie group and the velocities, respectively.

Local error estimate

First, we introduce the embedded Runge–Kutta formulas. At the same time step, we are going to evaluate two numerical solutions obtained with two Runge–Kutta methods with the same stage vectors $Q_{ni}$, $\boldsymbol{\Theta}_{ni}$, $\mathbf{V}_{ni}$ but different weights $b_{i}$, such that we obtain a first numerical approximation $\mathbf{y}_{1}$ of order $p$ and a second numerical approximation $\hat{\mathbf{y}}_{1}$ of order $\hat{p}$. Usually, we have $\hat{p}=p-1$ or $\hat{p}=p+1$. The approximation $\mathbf{y}_{1}$ is used to continue the integration, while the approximation $\hat{\mathbf{y}}_{1}$ is used to evaluate the estimate of the local error. Given user-defined tolerances, the error indicator at time $t=t_{n}$ is

$$ err=\sqrt{\frac{1}{m}\sum _{i=1}^{m}\left ( \frac{y_{n,i}-\hat{y}_{n,i}}{Atol_{i}+\max{(\vert y_{n-1,i}\vert ,\vert{y}_{n,i}\vert )}\cdot Rtol_{i}} \right )^{2}}, $$

(21)

where $m=6(N+1)$ is the number of components of the solution vectors, $Atol_{i}$, $Rtol_{i}$, $(i=1,\dots ,m)$ are vector-valued user-defined tolerances.

In the present paper, we implement the variable time step-size for embedded half-explicit Runge–Kutta Lie group methods of the fifth order, using the scheme previously reported with $s=6$, $\bar{s}=7$. The coefficients for the embedded method are those that are known from the seminal work of Dormand and Prince [10]:

$$\begin{gathered} \hat{a}_{81}=5179/57600,\, \hat{a}_{82}=0,\, \hat{a}_{83}=7571/16695, \, \hat{a}_{84}=393/640, \\ \hat{a}_{85}=-92097/339200,\, \hat{a}_{86}=187/2100,\, \hat{a}_{87}=1/40. \end{gathered}$$

New time step-size

After the local error estimate is evaluated, the value of the error indicator $err$ is compared with 1. If $err\leq 1$, the computed step is accepted and the computation will continue for the time step $t_{n+2}=t_{n+1}+h_{\text{new}}$. On the contrary, if $err>1$, the computed step is rejected and a new computation for the time step $t_{n}\to t_{n+1}$ will be performed using a new time step-size, i.e., $t_{n+1}=t_{n}+h_{\text{new}}$. As one may observe, in both cases we need to compute a new value for the time step-size. We are going to evaluate the new time step-size in terms of the local error estimate, but we are going to use some multiplicative factors to avoid too large a change in the step size from one step to the next. In particular, given the previous time step-size $h$, the new one will be [14]

$$ h_{\text{new}}=h\cdot \min{\left (facmax,\max{\left (facmin,fac\cdot (1/err)^{1/( \mu +1)}\right )}\right )}, $$

(22)

where $\mu =\min{(p,\hat{p})}$. We observe that for $err>1$, $(1/err)<1$ and the time step-size will surely diminish, while for $err\leq 1$ the new time step-size could still be smaller than the previous one due to the role of the multiplicative factor $fac$, which is set to be smaller than one. Typical values of these factors are $fac=0.8$, $facmin=0.2$, and $facmax=5.0$, see [14].

4 Applications to geometrically exact beam model

4.1 Roll-up and flying spaghetti

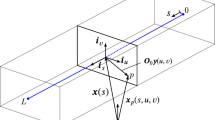
The numerical experiments in the present section are performed for Cosserat beams with internal constraints. In detail, the geometrically exact model of a rod describes the rod as a curve, the centerline $\mathcal{C}(s)$, parameterized by the curvilinear abscissa $s$, along which we position the cross sections with a specific orientation dictated by the rotation matrix $R(s)$ or the unit quaternion $p(s)$ [17, 19], which indicates the rotation of a body-fixed reference system $\{e_{1},e_{2},e_{3}\}$ with respect to the inertial system $\{E_{1},E_{2},E_{3}\}$. In Fig. 7a, we may observe the model previously stated and in Fig. 7b the discretization in space is depicted. The discretization of the beam is motivated by the staggered grid in [19], but only from a computational point of view. In our practical applications, both the quaternions, indicating the orientation of the cross section, and the position coordinates are set on the nodes of the discretization. The methodology goes back to the work of Hante [15] and has been introduced in [17]. We evaluate in the midpoints of the edges the spatial derivatives of the configuration variables

$$ \mathbf{w}_{i-1/2}(t) = \frac{1}{\Delta s_{i-1/2}}\widetilde{\log}{ \left (q^{-1}_{i-1}(t)\circ q_{i}(t)\right )},\qquad i=1,\dots ,N, $$

(23)

where $N$ is the total number of discretization edges in which the beam is divided, $s\in [0,L]$ is the curvilinear abscissa, $q_{i}=(p_{i},x_{i})\in \mathbb{S}^{3}\ltimes \mathbb{R}^{3}$ and $\widetilde{\log}$ denotes the inverse of the exponential map with image in $\mathbb{R}^{6(N+1)}$. Finally, the trapezoidal and midpoint rule are used, respectively, to discretize the kinetic and the potential energy.

Fig. 7

Cosserat rod

The validation of the numerical method through numerical experiments is performed with two test cases: the roll-up maneuver and the flying spaghetti. Both tests involve a constrained Cosserat rod as presented in [19], see also [17]. They go back to previous work of Géradin and Cardona [11] and Simo and Vu-Quoc [29], respectively, and are fully described in [15]. The roll-up maneuver was first introduced as a static benchmark problem [11] and later its dynamics were studied [9].

The physical parameters involve the use of material parameters such as Young’s modulus and geometric parameters such as the area of the cross section or inertia values in different directions. In Table 3, we summarize these parameters, the initial conditions and the boundary conditions for both experiments. We define $\mathbf{d}$ and a time-dependent input $g(t)$ as

$$ \mathbf{d} = \begin{bmatrix} -6 \\ 8 \\ 0 \end{bmatrix} ,\qquad g(t) = \textstyle\begin{cases} 200t/2.5, &t\in [0,2.5] \\ 200(5-t)/2.5,&t\in [2.5,5] \\ 0,&t>5. \end{cases} $$

(24)

The roll-up maneuver experiment considers a rod, fixed at one of the ends and subject to a moment on the other one, see Fig. 8a. The flying spaghetti, already introduced by [29], on the contrary, does not have any Dirichlet boundary conditions, having both ends free, but it has both a force and a momentum applied to one of its ends, see Fig. 8b. For both test cases, the constraints arise from the use of the Kirchhoff model [19]. In particular, the model avoids shear deformations of the cross sections, which remain perpendicular to the centerline. The constraint at position level is

$$ \begin{bmatrix} \mathbf{e}_{1}^{\top} \\ \mathbf{e}_{2}^{\top }\end{bmatrix} \cdot \boldsymbol{\Gamma}(s,t)=\boldsymbol{0}, $$

(25)

where $\boldsymbol{\Gamma}$ is the material strain vector. Since we require (25), the first two components of $\boldsymbol{\Gamma}$ need to vanish.

Fig. 8

Cosserat-rod test cases

Table 3 Physical parameters in dimensionless form, see [15]

For the experiments, we apply the half-explicit Runge–Kutta Lie group methods described in the sections above with coefficients that allow the methods to perform up to order five, see Table 1. In Fig. 9, we observe the expected order of convergence for the method applied to the roll-up maneuver test case with $N=8$ edges and for the flying-spaghetti test case with $N=16$ edges. Here, the reference solutions for the two sets of tests are evaluated with a finer time grid ($h_{\text{ref}}=10^{-6}$), but maintaining the space grid fixed. We note that the convergence properties of the method in the classical setting are maintained in the Lie group setting. We now consider the solution of the two problems when using an algorithm for variable time step-size. Here, we first observe the behavior of the local error for fixed time step-size. In Fig. 10, the local error estimate $\Vert \hat{\mathbf{y}}-\mathbf{y}\Vert$ is plotted vs. time for various values of a fixed time step-size $h$. The left plot shows the local error estimate for the roll-up maneuver test and we note that it decreases while reaching a more stable configuration. On the other side, the flying-spaghetti plot shows more variations due to the nature of the movement of the rod in this experiment. What we observe is how the local error estimates change as a function of the fixed time step-size. In particular, given a fixed time step-size $h$, the simulation is then performed two more times, once with time step-size $2h$ and once with time step-size $h/2$. One may note that the local error estimate for the solution with time step-size $h$ is about $2^{4+1}$ times larger than the local error for the solution with time step-size $h/2$, similarly when computing the quotient between the local error for $2h$ and $h$. In fact, the method we use to estimate the local error is of order four, and we know that

$$ err=\mathcal{O}(h^{p+1}), $$

(26)

where $p$ is the order of the method.

Fig. 9

Order of convergence (relative global error in the position variable vs. time step-size) for the roll-up maneuver test case (left) and the flying spaghetti (right) solved with half-explicit Runge–Kutta Lie group methods of order $p\leq 5$. (Color figure online)

Fig. 10

Estimate of the local error indicator for fixed time step-size. On the $x$-axis there is the time $t$, on the $y$-axis the variable $err$ in logarithmic scale. (Color figure online)

We implemented the fifth-order method with variable step size and in Fig. 11 we observe the results for both the roll-up maneuver and the flying-spaghetti example. In Fig. 11, the simulations run in the time interval $t\in [0,5]$ and we note that after a first time interval in which the time step-size is comparable in size between the two test experiments, for $t>1\text{ s}$ the step size increases substantially for the roll-up maneuver and remains bounded for the flying spaghetti. The difference in the size of the time step could be explained by the nature of the test case itself: In the flying spaghetti there is no equilibrium state that could be reached, while for the roll-up maneuver the closed-ring position is an equilibrium point of the motion. The increase in the time step-size could then be associated with the achieved equilibrium status. Other observations may regard the behavior in the change of time step-size as a function of the variable err. When err decreases we note a spike in the step-size sequence, since the error reaches lower values.

Fig. 11

The blue lines represent the test data for the roll-up test with $N=8$ edges, the red lines for the flying spaghetti with $N=16$ edges. The upper plot represents the trend in the variable $err$ that is the estimate of the local error against the user-defined tolerance $Atol = 10^{-8}$ and $Rtol = 10^{-6}$, the lower plot is the new time step-size after each accepted step. (Color figure online)

Figure 12 shows the difference in step-size history when increasing the bending stiffness for the roll-up maneuver test setup. As expected, the step size increases towards the end of the simulation, since the solution approaches a stationary state. The blue line correspond to a value of the stiffness $\mathbf{C}^{\mathbf{K}}=$diag($5\cdot 10^{2}$,$5 \cdot 10^{2}$,$5\cdot 10^{2}$), while the orange line corresponds to $\mathbf{C}^{\mathbf{K}}=$diag($5\cdot 10^{4}$,$5\cdot 10^{4}$,$5 \cdot 10^{4}$). We observe that a smaller value of the stiffness will make the numerical integration smoother, in the sense that the local error will have fewer oscillations and the time step-size will have less variation. We note that when increasing the stiffness, spikes in the local error will increase, which will require the decreasing of the time step by quite a large factor. Those differences are not unexpected, on the contrary, we know that stiffer systems may require smaller time step-sizes for their resolution if explicit integrators are used.

Fig. 12

The blue line represents the solution for the roll-up test with bending stiffness $\mathbf{C}^{\mathbf{K}}=5\cdot 10^{2}$, the orange line represents the solution with bending stiffness $\mathbf{C}^{\mathbf{K}}=5\cdot 10^{4}$. (Color figure online)

5 Conclusion

The time integrator we introduced in the present paper shows favorable properties: Having the structure of a half-explicit integrator, it does not need the use of a Newton–Raphson method to solve possible nonlinear systems of equations, and being designed to maintain the solution on the Lie group, it is advantageous for the evaluation of the solution of mechanical systems subject to large rotations. We observed that the application of the Lie group does not influence the stability behavior and the classical orders of convergence are preserved in the corresponding Lie group integrator.

On the other hand, we extended the study to the control of the local error. The implementation of a variable time step-size is not only helpful to reduce the computing time, but also to control the local error. The classical fifth-order explicit Runge–Kutta method of Dormand and Prince [10] has been made available to a constrained system on Lie groups.