Skip to main content
SpringerLink
Log in

Runge-Kutta methods on Lie groups

  • Published:
BIT Numerical Mathematics Aims and scope Submit manuscript

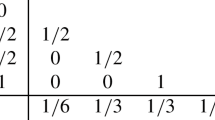
Abstract

We construct generalized Runge-Kutta methods for integration of differential equations evolving on a Lie group. The methods are using intrinsic operations on the group, and we are hence guaranteed that the numerical solution will evolve on the correct manifold. Our methods must satisfy two different criteria to achieve a given order.

  • • CoefficientsA i,j andb j must satisfy the classical order conditions. This is done by picking the coefficients of any classical RK scheme of the given order.

  • • We must construct functions to correct for certain non-commutative effects to the given order.

These tasks are completely independent, so once correction functions are found to the given order, we can turn any classical RK scheme into an RK method of the same order on any Lie group.

The theory in this paper shows the tight connections between the algebraic structure of the order conditions of RK methods and the algebraic structure of the so called ‘universal enveloping algebra’ of Lie algebras. This may give important insight also into the classical RK theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R. Abraham, J. E. Marsden, and T. Ratiu,Manifolds, Tensor Analysis, and Applications. AMS 75, Springer-Verlag, second edition, 1988.

  2. R. L. Bryant,An introduction to Lie groups and symplectic geometry, in Geometry and Quantum Field Theory, D. S. Freed and K. K. Uhlenbeck, editors., Volume 1 of IAS/Park City Mathematics Series, AMS, second edition, 1995.

  3. J. C. Butcher,Coefficients for the study of Runge-Kutta integration processes, J. Austral. Math. Soc., 3 (1963), pp. 185–201.

    Article  MATH  MathSciNet  Google Scholar 

  4. J. C. Butcher,An algebraic theory of integration methods, Math. Comput., 26 (1972), pp. 79–106.

    Article  MATH  MathSciNet  Google Scholar 

  5. M. P. Calvo, A. Iserles, and A. Zanna,Runge-Kutta methods on manifolds, in A. R. Mitchell's 75th Birthday Volume, D. F. Griffiths and G. A. Watson, editors, World Scientific, Singapore pp. 57–70, 1996.

    Google Scholar 

  6. P. E. Crouch and R. Grossman,Numerical integration of ordinay differential equations on manifolds, J. Nonlinear Sci., 3 (1993), pp. 1–33.

    Article  MATH  MathSciNet  Google Scholar 

  7. E. Hairer, S. P. Nørsett, and G. Wanner,Solving Ordinary Differential Equations I, Volume 8 of SCM. Springer-Verlag, Berlin, 1987.

    MATH  Google Scholar 

  8. A. Iserles,Solving linear ordinary differential equations by exponentials of iterated commutators, Numer. Math., 45:183–199, 1984.

    Article  MATH  MathSciNet  Google Scholar 

  9. A. Iserles,Numerical methods on (and off) manifolds, in F. Cucker, editor, Foundation of Computational Mathematics, pp. 180–189. Springer-Verlag, 1997.

  10. A. Iserles and S. P. Nørsett,On the solution of linear differential equations in Lie groups, Technical Report 1997/NA3, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, England, 1997.

    Google Scholar 

  11. A. Iserles,Multistep methods on manifolds, Technical Report 1997/NA13, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, England, 1997.

    Google Scholar 

  12. A. Marthinsen, H. Munthe-Kaas, and B. Owren,Simulation of ordinary differential equations on manifolds—some numerical experiments and verifications, Modeling, Identification and Control, 18 (1997), pp. 75–88.

    Article  MATH  Google Scholar 

  13. H. Munthe-Kaas,Lie-Butcher theory for Runge-Kutta methods, BIT, 35 (1995), pp. 572–587.

    Article  MATH  MathSciNet  Google Scholar 

  14. H. Munthe-Kaas,High order Runge-Kutta methods on manifolds, Technical Report 1997/NA14, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, England, 1997.

    Google Scholar 

  15. H. Munthe-Kaas and A. Zanna,Numerical integration of differential equations on homogeneous manifolds, in Foundations of Computational Mathematics, F. Cucker, ed., Springer Verlag, pp. 305–315, 1997.

  16. B. Owren and A. Marthinsen,Integration methods based on rigid frames, Technical Report Numerics No. 1/1997, Department of Mathematical Sciences, The Norwegian University of Science and Technology, 1997.

  17. R. D. Russel, L. Dieci, and E. S. van Vleck,Unitary integrators and applications to continuous orthonormalization techniques, SIAM J. Numer. Anal., 31:1 (1994), pp. 261–281.

    Article  MathSciNet  Google Scholar 

  18. J. M. Sanz-Serna and M. P. Calvo,Numerical Hamiltonian Problems, AMMC 7, Chapman & Hall, 1994.

  19. V. S. Varadarajan,Lie Groups, Lie Algebras, and Their Representation. GTM 102, Springer-Verlag, 1984.

  20. F. W. Warner,Foundations of Differentiable Manifolds and Lie Groups, GTM 94, Springer-Verlag, 1983.

  21. A. Zanna,The method of iterated commutators for ordinary differential equations on Lie groups, Technical Report 1996/NA12, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, England, 1996.

    Google Scholar 

  22. A. Zanna and H. Munthe-Kaas,Iterated commutators, Lie's reduction method and ordinary differential equations on matrix Lie groups, in Foundation of Computational Mathematics, F. Cucker, ed., Springer-Verlag, pp. 434–441, 1997.

Download references

Author information

Authors and Affiliations

  1. Department of Informatics, University of Bergen, Thormøhlensgt. 55, N-5020, Bergen, Norway

    Hans Munthe-Kaas

Authors
  1. Hans Munthe-Kaas
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by Gustaf Söderlind.

This work is sponsored by NFR under contract no. 111038/410, through the SYNODE project. WWW:http://www.math.ntnu.no/num/synode.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Munthe-Kaas, H. Runge-Kutta methods on Lie groups. Bit Numer Math 38, 92–111 (1998). https://doi.org/10.1007/BF02510919

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02510919

Keywords

Search

Navigation