1 Introduction

The present work aims to study a geometrically exact Cosserat rod model using a structure preserving variational integrator for constrained systems on Lie groups. This model of a Cosserat rod goes back to the seminal work of Simo on the geometrically exact modeling of beams [31] that is one of the standard references in this field. Following the approach of Linn, Lang, and others [16, 23], we aim at numerically efficient methods that have the potential to be used in real-time applications [16] as well as in system simulation [29].

Internal constraints may be introduced to enforce the rigid cross sections to remain perpendicular to the center line. In that way, some of the high-frequency solution components are eliminated and the full Cosserat beam model is reduced to a Kirchhoff beam model [17]. Space discretization results in equations of motion that form differential-algebraic equations (DAEs) of index 3 and may be solved efficiently by standard methods in this field [15]. The parametrization of rotations by unit quaternions helps to avoid singularities in simulation scenarios with large rotations and reduces the number of arithmetic operations per function evaluation (compared to mathematically equivalent approaches) [15]. On the contrary, the corresponding configuration space is nonlinear and normalization conditions need to be enforced during time integration at each time step if the equations of motion are embedded in higher dimensional linear spaces [30]. As an alternative to this brute force approach, the nonlinear structure of the configuration space may be addressed directly using Lie group integrators [9, 19, 33]. The performance of Lie group integrators may depend strongly on the specific Lie group formulation [5] with clear benefits for formulations that are based on the special Euclidean group [26, 34]. For rotations being parametrized by unit quaternions, the corresponding Lie groups are multiples of the semi-direct product \(\mathbb{S}^{3} \ltimes \mathbb{R}^{3}\), see [11, 19]. This semi-direct product (as well as the special Euclidean group) refers to rigid body motions in space and its application in beam theory helps to reduce the risk of locking phenomena [21, 34], see also the last part of the present paper. Recently published paper [21] follows a very similar approach, while using higher order integration schemes but being restricted to the unconstrained case. In the present paper, however, the straightforward incorporation of internal and external constraints allows, e.g., enforcing the cross sections to remain normal to the centerline tangent such that transverse shearing is inhibited, see also [15, 17] as well as Sect. 3.5 below.

Our research was inspired by industrial challenges that are studied in the Horizon 2020 Marie Skłodowska-Curie Innovative training network “THREAD” [10]. Twelve European research groups aim at new modeling and simulation techniques for highly flexible structures in system dynamics [3]. In fact, the applications of rod model simulation in the industries are numerous and various, ranging from cable harnesses in automotive applications and endoscopes in biomedical engineering via yarns in braiding machines to ropeway systems [10]. In industrial applications, static and quasistatic solution techniques are still dominating, but the THREAD project will also result in efficient and numerically stable methods for dynamic problems.

To this end, we consider coarse grid discretizations that preserve certain geometrical properties of the equations of motion and achieve numerical stability in that way [9]. Following the framework of variational integration in space and time [8, 19], we discretize the action integral before solving the variational problem, which proves to be favorable in long-term simulation [24]. Internal or external constraints introduce extra terms in the Lagrangian that finally result in constraint equations and constraint forces in the fully discretized model that may be considered, e.g., by (nearly) energy preserving methods from molecular dynamics [1, 12]. Restricting the analysis to low order methods, we get discrete equations of rather simple structure that are tailored to low or moderate accuracy requirements. Constraints are enforced in a stable way using a discontinuous approximation of the Lagrange multipliers [11] that allows enforcing the constraints and hidden constraints at the level of position and at the level of velocity coordinates simultaneously.

In this paper, we will use the well-known ingredients of Lie group structured configuration spaces, variational integrators, and numerical treatment of DAEs, to find a way of simulating thin beams efficiently and accurately at the same time. Following the approaches of Cardona, Zupan, Brüls, and others [4, 6, 37, 38], we try to provide this investigation in a language that is close to the implementation with entities that bear a physical meaning.

The remaining part of the paper is organized as follows: In Sect. 2, we present the configuration space. We define in detail the Lie group and its operations. In particular, we explain how to use unit quaternions to describe rotation and which operations we can perform with them. The tools needed in the following study are mentioned. In Sect. 3, we derive the continuous equations of motion for the Cosserat beam model. We evaluate the expression for the kinetic and potential energy and we also consider the constraint as a different kind of energy, such that we are able to write the action integral. Using the action integral, we can apply the variational principle to obtain the continuous equations of motion. In Sect. 4, we are able to fully discretize the equations both in space and in time. We directly discretize the equations after applying the Hamilton’s principle. Finally, in Sect. 5 we present our numerical experiments. We analyze how the steps in arc length and the time step sizes influence the errors.

2 A Lie group structured configuration space

In this section, we will discuss configuration spaces with Lie group structure in general, the configuration space \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\) in particular, and how we can find a Lie group structure of a configuration space. Lie groups are well researched theoretically [36]. They also have been applied in numerical integrations [14], and especially in the description of mechanical systems [4, 18, 26] and beams in particular [7, 8, 20, 33]. Note that for Lie groups, we will use the notations of Brüls et al. [4–6]. This notation, as well as the notation for unit quaternions, is intentionally implementation oriented avoiding notational shortcuts such that it becomes very clear how formulae must be or should be implemented.

Position

Let us first consider the position of a mass point in space. Usually, the set \(\mathbb{R}^{3}\) is used as a configuration space, where any \({\boldsymbol{x}}\in \mathbb{R}^{3}\) is a possible position of the mass point. Now let us instead consider \({\boldsymbol{x}}\in \mathbb{R}^{3}\) as a translation of the mass point from some reference position. Now we can apply two of these translations \({\boldsymbol{x}},{\boldsymbol{y}}\in \mathbb{R}^{3}\), leading us to the concatenation \({\boldsymbol{x}}+{\boldsymbol{y}}\in \mathbb{R}^{3}\). It can be seen that with this operation +, the configuration space \(\mathbb{R}^{3}\) actually becomes a linear Lie group \((\mathbb{R}^{3},+)\) with identity element \({\boldsymbol{0}}\in \mathbb{R}^{3}\) and inversion \({\boldsymbol{x}}\mapsto -{\boldsymbol{x}}\).

Orientation

Now we consider the orientation of a rigid body in space. Here, we will use unit quaternions

$$ \mathbb{S}^{3} = \{p\in \mathbb{R}^{4}\colon \|p\|_{2} = 1 \} $$

in order to represent orientation, where \(\|\bullet \|_{2}\) is the Euclidean norm. As before, we consider any \(p\in \mathbb{S}^{3}\) to represent a rotation from some reference configuration of the rigid body. Concatenation of two unit quaternions \(p,q\in \mathbb{S}^{3}\) leads to the quaternion multiplication

$$ p*q = \begin{bmatrix} p_{0} q_{0} - {\boldsymbol{p}}^{\top }\cdot {\boldsymbol{q}} \\ p_{0} {\boldsymbol{q}}+ q_{0}{\boldsymbol{p}}+ {\boldsymbol{p}}\times {\boldsymbol{q}}\end{bmatrix} \in \mathbb{S}^{3}, $$

where each of the quaternions \(p,q\in \mathbb{S}^{3}\) are decomposed into their scalar (or real) parts \(p_{0},q_{0}\in \mathbb{R}\) and their vector (or imaginary) parts \({\boldsymbol{p}},{\boldsymbol{q}}\in \mathbb{R}^{3}\) with

$$ p = \begin{bmatrix} p_{0} \\ {\boldsymbol{p}}\end{bmatrix} ,\qquad q = \begin{bmatrix} q_{0} \\ {\boldsymbol{q}}\end{bmatrix} . $$

Note that the quaternion multiplication is also defined for non-unit quaternions in \(\mathbb{R}^{4}\). Again, we end up with a Lie group \((\mathbb{S}^{3},*)\) with identity element \(e=[1,0,0,0]^{\top }\) and inversion \(p=[p_{0},{\boldsymbol{p}}^{\top }]^{\top }\mapsto p^{-}=[p_{0},-{\boldsymbol{p}} ^{\top }]^{\top }\).Footnote 1 This Lie group, in contrast to the linear Lie group, is not commutative. Further, we define the rotation \(R(p)\;{\boldsymbol{a}}\) of a vector \({\boldsymbol{a}}\in \mathbb{R}^{3}\) with respect to a unit quaternion \(p\in \mathbb{S}^{3}\) as

$$ \begin{bmatrix} 0 \\ R(p)\;{\boldsymbol{a}}\end{bmatrix} = p* \begin{bmatrix} 0 \\ {\boldsymbol{a}}\end{bmatrix} *p^{-}. $$

Note that antipodal unit quaternions \(p,-p\in \mathbb{S}^{3}\) represent the same rotation:

$$ R(p)\;{\boldsymbol{a}}= R(-p)\;{\boldsymbol{a}} $$

for all \(p\in \mathbb{S}^{3}\) and \({\boldsymbol{a}}\in \mathbb{R}^{3}\).Footnote 2

Rigid bodies

Now we repeat the above process with a rigid body in space, that has an orientation \(p\in \mathbb{S}^{3}\) and a position \({\boldsymbol{x}}\in \mathbb{R}^{3}\). Now we consider \((p,{\boldsymbol{x}})\) with \(p\in \mathbb{S}^{3}\), \({\boldsymbol{x}}\in \mathbb{R}^{3}\) to be a rigid body motion

$$ M_{(p,{\boldsymbol{x}})}\colon \mathbb{R}^{3} \to \mathbb{R}^{3},\qquad { \boldsymbol{a}}\mapsto {\boldsymbol{x}}+ R(p)\;{\boldsymbol{a}}. $$

The concatenation of two of these rigid body motions associated with the tuples \((p_{1},{\boldsymbol{x}}_{1})\) and \((p_{2},{\boldsymbol{x}}_{2})\), where \(p_{1},p_{2}\in \mathbb{S}^{3}\), \({\boldsymbol{x}}_{1},{\boldsymbol{x}}_{2}\in \mathbb{R}^{3}\), leads us to an operation

$$ (p_{1},{\boldsymbol{x}}_{1})\circ (p_{2},{\boldsymbol{x}}_{2}) = \bigl(p_{1}*p_{2}, \; {\boldsymbol{x}}_{1} + R(p_{1})\;{\boldsymbol{x}}_{2}\bigr), $$

since the rotation \(R\) is linear in its vector argument and it holds \(R(p_{1})\;R(p_{2})\;{\boldsymbol{a}}= R(p_{1}*p_{2})\;{\boldsymbol{a}}\). It can be easily seen that the operation ∘ is smooth and has an identity element \(e=([1,0,0,0]^{\top },{\boldsymbol{0}})\), each element having an inverse and the inversion is also smooth. Since \(\mathbb{S}^{3}\) and \(\mathbb{R}^{3}\) are clearly smooth manifolds, \((\mathbb{S}^{3}\ltimes \mathbb{R}^{3},\circ )\) is a Lie group. We will call the Lie group \((\mathbb{S}^{3}\ltimes \mathbb{R}^{3},\circ )\) or, by abuse of notation \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\), because it is not a direct product of the Lie groups \((\mathbb{S}^{3},*)\) and \((\mathbb{R}^{3},+)\) but rather a semi-direct product [11]. The dimension of \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\) is \(n=6\), since it has dimension six as a smooth manifold. If we would have used rotation matrices \(\mathrm{SO}(3)\) instead of unit quaternions to characterize rotation or orientation respectively, we would have arrived at the special Euclidean Lie group \((\mathrm{SE}(3),\cdot )\).

Derivative vectors

We consider now configuration spaces \(G\) with dimension \(n\) that have a Lie group structure \((G,\circ )\) with an identity element \(e\in G\). If we consider a differentiable curve \(q(t)\in G\), each derivative is an element of the corresponding tangent space: \(\dot{q}(t)\in T_{q(t)}G\). The Lie group structure now gives us the possibility to express \(\dot{q}(t)\) as

$$ \dot{q}(t) = \mathrm {d}L_{q(t)}(e)\; v(t), $$

where \(v(t)\in T_{e}G\) is an element of the tangent space at \(e\) for all \(t\) and \(\mathrm {d}L_{q(t)}(e)\) is the differential of the left translation defined by \(L_{q_{1}}(q_{2})=q_{1}\circ q_{2}\). The tangent space \(T_{e}G=\mathfrak{g}\) is called the Lie algebra of \(G\). Instead of handling elements \(v(t)\in \mathfrak{g}\) of an abstract tangent space, we will express \(v(t)\) as the velocity vector \({\boldsymbol{v}}(t)\in \mathbb{R}^{n}\), which bears a physical meaning [4, 37]. The identification of \(\mathfrak{g}\) and \(\mathbb{R}^{n}\) is done by choosing a linear vector space isomorphism \(\widetilde{\bullet }\colon \mathbb{R}^{n}\to T_{e}G\). This concept can be applied to arbitrary real variables other than time \(t\) in which case we speak of a derivative vector.

In the case of \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\), we have

$$ \mathrm {d}L_{(p,{\boldsymbol{x}})}\; \widetilde{\begin{bmatrix}{\boldsymbol{\varOmega }}\\{\boldsymbol{U}}\end{bmatrix}} = \biggl(\frac{1}{2} p* \begin{bmatrix} 0 \\ {\boldsymbol{\varOmega }}\end{bmatrix} ,\; R(p)\;{\boldsymbol{U}}\biggr) $$

and the physical meaning is that \({\boldsymbol{\varOmega }}\in \mathbb{R}^{3}\) is the angular velocity and \({\boldsymbol{U}}\in \mathbb{R}^{3}\) is the velocity of a rigid body described by the configuration \((p,{\boldsymbol{x}})\). Note that both \({\boldsymbol{\varOmega }}\) and \({\boldsymbol{U}}\) are expressed with respect to the body-fixed frame \(\{R(p)\;{\boldsymbol{e}}_{1},R(p)\;{\boldsymbol{e}}_{2},R(p)\;{\boldsymbol{e}}_{3}\}\).

Exponential map

Now we will define the exponential map \(\widetilde{\exp }\colon \mathbb{R}^{n}\to G\). For a \({\boldsymbol{v}}\in \mathbb{R}^{n}\), \(\widetilde{\exp }({\boldsymbol{v}})\in G\) is defined by the solution \(q_{\boldsymbol{v}}(1) = \widetilde{\exp }({\boldsymbol{v}})\) of the initial value problem [36]

$$ \dot{q}_{\boldsymbol{v}}(t) = \mathrm {d}L_{q_{\boldsymbol{v}}(t)}(e)\; \widetilde{{\boldsymbol{v}}},\qquad q_{\boldsymbol{v}}(0) = e. $$

Usually, the exponential map \(\exp \colon T_{e}G\to G\) is used, but since we are using the concept of velocity vectors, \(\widetilde{\exp }\) as the concatenation of exp and the tilde operator is easier to handle. If we consider a differentiable curve \({\boldsymbol{v}}(t)\in \mathbb{R}^{n}\), then the derivative of \(\widetilde{\exp }\bigl ({\boldsymbol{v}}(t)\bigr )\) is given by

$$ \frac{\mathrm {d}}{\mathrm {d}t}\widetilde{\exp }\bigl({\boldsymbol{v}}(t)\bigr) = \mathrm {d}L_{\widetilde{\exp }\bigl({\boldsymbol{v}}(t)\bigr)}\; \widetilde{\Bigl({\mathbf{T}}\bigl({\boldsymbol{v}}(t)\bigr){\boldsymbol{\dot{v}}}(t)\Bigr)}, $$
(1)

where \({\mathbf{T}}\colon \mathbb{R}^{n}\to \mathbb{R}^{n\times n}\) is called the tangent operator.Footnote 3 In the Lie group \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\), the exponential map is given by

$$ \widetilde{\exp }\biggl( \begin{bmatrix} {\boldsymbol{\varOmega }} \\ {\boldsymbol{U}}\end{bmatrix} \biggr) = \Biggl( \begin{bmatrix} \cos \frac{\|{\boldsymbol{\varOmega }}\|_{2}}{2} \\ \frac{{\boldsymbol{\varOmega }}}{\|{\boldsymbol{\varOmega }}\|_{2}}\sin \frac{\|{\boldsymbol{\varOmega }}\|_{2}}{2}\end{bmatrix} ,\; {\mathbf{T}}_{\mathbb{S}^{3}}(-{\boldsymbol{\varOmega }})\cdot { \boldsymbol{U}}\Biggr) $$

for \([{\boldsymbol{\varOmega }}^{\top },{\boldsymbol{U}}^{\top }]^{\top }\neq {\boldsymbol{0}}\) and \(\widetilde{\exp }({\boldsymbol{0}}) = ([1,0,0,0]^{\top },{\boldsymbol{0}})\). Here, \({\mathbf{T}}_{\mathbb{S}^{3}}\) is the tangent operator that is associated with the Lie group \((\mathbb{S}^{3},*)\) as well as with the Lie group of rotation matrices \((\mathrm{SO}(3),\cdot )\). The tangent operator for \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\) actually coincides with the tangent operator for the Lie group \((\mathrm{SE}(3),\cdot )\), which can be found in [5]. Further, we will also need the inverse \({\mathbf{T}}^{-}({\boldsymbol{x}}) = \bigl ({\mathbf{T}}({\boldsymbol{x}})\bigr ) ^{-}\) of the tangent operator. The tangent operators that are not already defined here and their inverses are given in the Appendix.

Logarithm

The exponential map \(\widetilde{\exp }\) is injective in a neighborhood of the origin.Footnote 4 We call the inverse function the logarithm \(\widetilde{\log }\) which maps Lie group elements \(g\in G\) that are sufficiently close to the identity element \(e\in G\) back to \(\mathbb{R}^{n}\) such that \(\widetilde{\exp }\bigl (\widetilde{\log }(g)\bigr ) = g\). For the Lie group \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\), the logarithm is given by

$$ \widetilde{\log }\bigl((p,{\boldsymbol{x}})\bigr) = \begin{bmatrix} \widetilde{\log }_{\mathbb{S}^{3}}(p) \\ {\mathbf{T}}^{-}\bigl(-\widetilde{\log }_{\mathbb{S}^{3}}(p) \bigr)\cdot {\boldsymbol{x}}\end{bmatrix} $$

for \((p,{\boldsymbol{x}})\in \mathbb{S}^{3}\ltimes \mathbb{R}^{3}\) sufficiently close to the identity element, where \(\widetilde{\log }_{\mathbb{S}^{3}}\) is the logarithm of the Lie group \((\mathbb{S}^{3},*)\) and is given in the Appendix.

Hat operator

We will now introduce the hat operator \(\widehat{\bullet }\colon \mathbb{R}^{n}\to \mathbb{R}^{n\times n}\) by the relation

$$ \widetilde{\widehat{{\boldsymbol{a}}}\cdot {\boldsymbol{b}}} = \frac{\mathrm {d}^{2}}{\mathrm {d}s \mathrm {d}t}\sigma _{\boldsymbol{a}}(s)\circ \sigma _{ \boldsymbol{b}}(t)\circ \sigma _{\boldsymbol{a}}(-s)\big|_{s=t=0}, $$

where \(\sigma _{\boldsymbol{a}}\) and \(\sigma _{\boldsymbol{b}}\) are differentiable curves in \(G\) with \(\sigma _{\boldsymbol{a}}(0)=\sigma _{\boldsymbol{b}}(0)=e\) and velocity vectors \({\boldsymbol{a}}\) and \({\boldsymbol{b}}\) at the origin, respectively. We can see that the hat operator is actually the adjoint operator formulated in the language of velocity vectors with the relationFootnote 5

$$ \operatorname{ad}_{\widetilde{{\boldsymbol{a}}}}(\widetilde{{\boldsymbol{b}}}) = \widetilde{\widehat{{\boldsymbol{a}}}\cdot {\boldsymbol{b}}}. $$

In fact, the hat operator is used to write down the tangent operator as well as its inverse in a series from which the closed expressions can be derived:

$$ {\mathbf{T}}({\boldsymbol{w}}) = \sum _{k=0}^{\infty }\frac{(-1)^{k}}{(k+1)!} \widehat{{\boldsymbol{w}}}^{k},\qquad {\mathbf{T}}^{-}({\boldsymbol{w}}) = \sum _{k=0}^{\infty }\frac{(-1)^{k} B_{k}}{k!}\widehat{{\boldsymbol{w}}}^{k}, $$

where \(B_{k}\) are the Bernoulli numbers with \(B_{1} = -1/2\), see [25]. In the case of the Lie group \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\), we have

$$ \widehat{\begin{bmatrix}{\boldsymbol{\varOmega }}\\{\boldsymbol{U}}\end{bmatrix}} = \begin{bmatrix} \operatorname{skw}({\boldsymbol{\varOmega }}) & {\mathbf{0}} \\ \operatorname{skw}({\boldsymbol{U}}) & \operatorname{skw}({\boldsymbol{\varOmega }})\end{bmatrix} $$

for \({\boldsymbol{\varOmega }},{\boldsymbol{U}}\in \mathbb{R}^{3}\). Like the tangent operator, the hat operator of \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\) coincides with the hat operator of \(\mathrm{SE}(3)\), [33].

Derivative vectors of bivariate functions

Let us now consider a function \(q\colon \mathbb{R}^{2}\to G\) that is differentiable and has derivative vectors \({\boldsymbol{x}}(x,y),{\boldsymbol{y}}(x,y)\in \mathbb{R}^{n}\) with respect to \(x\) and \(y\), respectively. Then there is this very nice relationship between the partial derivatives of the derivative vectors:

$$ \widehat{{\boldsymbol{x}}(x,y)}\cdot {\boldsymbol{y}}(x,y) = \frac{\mathrm {d}}{\mathrm {d}y}{ \boldsymbol{x}}(x,y) - \frac{\mathrm {d}}{\mathrm {d}x}{\boldsymbol{y}}(x,y), $$
(2)

see, e.g., [5], where this was used with \(\mathrm {d}/\mathrm {d}y\) being the variation and \(x=t\).

A differential operator

Now we will consider functions \({\boldsymbol{\varPsi }}\colon G \to \mathbb{R}^{k}\) whose arguments are elements of a Lie group. The derivative \(\mathrm {d}{\boldsymbol{\varPsi }}(g)\colon T_{g} G \to \mathbb{R}^{k}\) for \(g\in G\) is then a linear function on the tangent space \(T_{g} G\). We can formulate \(\mathrm {d}{\boldsymbol{\varPsi }}(g)\) in the language of velocity vectors and introduce the differential operator \(\mathbf {D}\), where \(\mathbf {D}{\boldsymbol{\varPsi }}(g)\) is defined by

$$ \mathbf {D}{\boldsymbol{\varPsi }}(g)\cdot {\boldsymbol{w}}= \mathrm {d}{\boldsymbol{\varPsi }}(g)\; \mathrm {d}L_{g}(e)\;\widetilde{{\boldsymbol{w}}} $$

for all \({\boldsymbol{w}}\in \mathbb{R}^{k}\). The actual expression for \(\mathbf {D}{\boldsymbol{\varPsi }}(g)\) can often be calculated easily by considering a differentiable curve \(q(t)\in G\) with velocity vectors \({\boldsymbol{v}}(t)\) and considering

$$ \frac{\mathrm {d}}{\mathrm {d}t}{\boldsymbol{\varPsi }}\bigl(q(t)\bigr) = \mathbf {D}{ \boldsymbol{\varPsi }}\bigl(q(t)\bigr)\cdot {\boldsymbol{v}}(t). $$

We can use the differential operator \(\mathbf {D}\) in order to calculate the derivative of the logarithm:

$$ \mathbf {D}\widetilde{\log }(q) = {\mathbf{T}}^{-}\bigl( \widetilde{\log }(q)\bigr) $$
(3)

for all \(q\in G\) close enough to the identity. This can be shown by differentiating \(\widetilde{\exp }\bigl (\widetilde{\log }(q)\bigr ) = q\) and using (1). Furthermore, we can calculate the derivative of nonlinear differences by

$$\begin{aligned} \mathbf {D}_{q_{0}}\widetilde{\log }(q_{0}^{-}\circ q_{1}) = -{ \mathbf{T}}^{-}\bigl(-\widetilde{\log }(q_{0}^{-}\circ q_{1}) \bigr), \end{aligned}$$
(4a)
$$\begin{aligned} \mathbf {D}_{q_{1}}\widetilde{\log }(q_{0}^{-}\circ q_{1}) = { \mathbf{T}}^{-}\bigl(\widetilde{\log }(q_{0}^{-}\circ q_{1}) \bigr). \end{aligned}$$
(4b)

Interpolation

Lastly, we will introduce an interpolation function

$$ \operatorname{Ip}(\xi ;a,b) = a\circ \widetilde{\exp }\bigl(\xi \widetilde{\log }(a^{-}\circ b)\bigr),\qquad \xi \in \mathbb{R},\; a,b \in G, $$
(5)

that is a smooth mapping in \(\xi \) with constant derivative vectors \(\widetilde{\log }(a^{-}\circ b)\):

$$ \frac{\mathrm {d}}{\mathrm {d}\xi }\operatorname{Ip}(\xi ;a,b) = \mathrm {d}L_{\operatorname{Ip}(\xi ;a,b)} \; \widetilde{\widetilde{\log }(a^{-}\circ b)} $$
(6)

and it holds \(\operatorname{Ip}(0;a,b) = a\) and \(\operatorname{Ip}(1;a,b)= b\). In the context of the linear Lie group \((\mathbb{R}^{n},+)\), where \(\widetilde{\exp }\) and \(\widetilde{\log }\) are the identity maps, \(\operatorname{Ip}\) is just the regular linear interpolation, making \(\operatorname{Ip}\) a generalization of linear interpolation to Lie groups. For more information on Lie group interpolation see, e.g., [34].

3 The continuous equations of motion

In this section, we consider the continuous equations of motions of a constrained Cosserat beam. This model was originally formulated by Simo [31] and then reformulated by Lang and Linn [15, 17]. A similar approach to our was followed in [9, 33], where the authors had used rotation matrices instead of unit quaternions. Celledoni et al. [7] had used quaternions but not semi-directly linked with the positions in order to describe an unconstrained Cosserat beam model.

3.1 Geometrically exact beams

We consider the Cosserat beam to be a framed curve or, in the context of our Lie group, a curve \(q(\bullet ,t)\in \mathbb{S}^{3}\ltimes \mathbb{R}^{3}\) at each time instant \(t\). The configuration \(q(s,t)=\bigl (p(s,t), {\boldsymbol{x}}(s,t)\bigr )\) then describes the position \({\boldsymbol{x}}(s,t)\in \mathbb{R}^{3}\) and the orientation \(p(s,t)\in \mathbb{S}^{3}\) of the cross section at \(s\). We assume that \(s\) represents the arc-length of the undeformed beam and that deformation of the cross section is negligible, such that it can be considered rigid.

The velocity vectors \({\boldsymbol{v}}(s,t)\in \mathbb{R}^{6}\) then contain the velocity \({\boldsymbol{U}}(s,t)\in \mathbb{R}^{3}\) and the angular velocity \({\boldsymbol{\varOmega }}(s,t)\in \mathbb{R}^{3}\) of the rigid cross section expressed with respect to the body-fixed frame:

$$ {\boldsymbol{v}}(s,t) = \begin{bmatrix} {\boldsymbol{\varOmega }}(s,t) \\ {\boldsymbol{U}}(s,t)\end{bmatrix} . $$

In the same way, we can consider the derivative vectors \({\boldsymbol{w}}(s,t)\) with respect to the spatial parameter \(s\):

$$ q'(s,t) = \frac{\mathrm {d}}{\mathrm {d}s} q(s,t) = \mathrm {d}L_{q(s,t)}\; \widetilde{{\boldsymbol{w}}(s,t)}. $$

In a similar way as before, \({\boldsymbol{w}}(s,t)\) contains the stress \({\boldsymbol{\varGamma }}(s,t)\in \mathbb{R}^{3}\) and material curvature \({\boldsymbol{K}}(s,t)\in \mathbb{R}^{3}\) expressed with respect to the body-fixed frame:

$$ {\boldsymbol{w}}(s,t) = \begin{bmatrix} {\boldsymbol{K}}(s,t) + {\boldsymbol{K}}^{*}(s) \\ {\boldsymbol{\varGamma }}(s,t) + {\boldsymbol{\varGamma }}^{*}(s)\end{bmatrix} . $$

Here, \({\boldsymbol{K}}^{*}(s)\in \mathbb{R}^{3}\) and \({\boldsymbol{\varGamma }}^{*}(s)\in \mathbb{R}^{3}\) are the material curvature and stress of the undeformed beam. We will summarize those two quantities to

$$ {\boldsymbol{w}}^{*}(s) = \begin{bmatrix} {\boldsymbol{K}}^{*}(s) \\ {\boldsymbol{\varGamma }}^{*}(s)\end{bmatrix} . $$

3.2 Energies

We will now give expressions for kinetic and potential energy of the Cosserat beam model. The kinetic energy \(\mathscr {T}\) at each time instance \(t\) is given by the integral of a kinetic energy density

$$\begin{aligned} T\bigl({\boldsymbol{v}}(s,t)\bigr) &= \frac{1}{2} {\boldsymbol{v}}^{\top }(s,t)\cdot { \mathbf{M}}\cdot {\boldsymbol{v}}(s,t) \\ &= \frac{\rho }{2} {\boldsymbol{\varOmega }} ^{\top }(s,t)\cdot \begin{bmatrix} I_{1}&&\\ &I_{2}&\\ &&J\end{bmatrix} \cdot {\boldsymbol{\varOmega }}(s,t) + \frac{A\rho }{2}{\boldsymbol{U}}^{\top }(s,t) \cdot {\boldsymbol{U}}(s,t), \end{aligned}$$

where \({\mathbf{M}}\in \mathbb{R}^{6\times 6}\) is a mass matrix given by

$$ {\mathbf{M}}= \operatorname{diag}(\rho I_{1},\rho I_{2},\rho J,\; \rho A,\rho A,\rho A), $$

where \(\rho >0\) is the material density, \(A>0\) is the area of the cross section, \(I_{1},I_{2},J>0\) are the principal moments of inertia of the infinitely thin cross section. Of course, this assumes that the material is homogeneous and the shape of the cross section does not change. The kinetic energy is then given by

$$ \mathscr {T}\bigl({\boldsymbol{v}}(\bullet ,t)\bigr) = \int _{0}^{L} T\bigl({ \boldsymbol{v}}(s,t)\bigr)\mathrm {d}s = \frac{1}{2} \int _{0}^{L} {\boldsymbol{v}}^{\top }(s,t) \cdot {\mathbf{M}}\cdot {\boldsymbol{v}}(s,t)\mathrm {d}s. $$

Now we give the potential energy \(\mathscr {U}\) under the assumption of linear material behaviour. As before, the potential energy is given by the integral over the whole beam of the potential energy density

$$\begin{aligned} U\bigl({\boldsymbol{w}}(s,t)\bigr) &= \frac{1}{2} \bigl({\boldsymbol{w}}(s,t)-{\boldsymbol{w}}^{*}(s) \bigr)^{\top }\cdot {\mathbf{C}}\cdot \bigl({\boldsymbol{w}}(s,t)-{\boldsymbol{w}}^{*}(s) \bigr) \\ &= \frac{1}{2} {\boldsymbol{K}}^{\top }(s,t)\cdot \begin{bmatrix} \mathit{EI}_{1}&&\\ &\mathit{EI}_{2}&\\ &&\mathit{GJ} \end{bmatrix}\cdot {\boldsymbol{K}}(s,t) \\ &\quad {}+ \frac{1}{2} {\boldsymbol{\varGamma }} ^{\top }(s,t)\cdot \begin{bmatrix} \mathit{GA}_{1}&&\\ &\mathit{GA}_{2}&\\ &&\mathit{EA} \end{bmatrix}\cdot {\boldsymbol{\varGamma }}(s,t). \end{aligned}$$

Here, the matrix \({\mathbf{C}}\in \mathbb{R}^{6\times 6}\) is a diagonal matrix

$$ {\mathbf{C}}= \operatorname{diag}(\mathit{EI}_{1},\mathit{EI}_{2},\mathit{GJ},\;\mathit{GA}_{1},\mathit{GA}_{2},\mathit{EA}), $$

that contains the moduli \(E,G>0\) as well as the moments of inertia \(I_{1},I_{2},J>0\) and the area \(A>0\) of the cross section. The quantities \(A_{1}>0\) and \(A_{2}>0\) are often identified with the product of the area \(A\) with some Timoshenko shear correction factors. In practice, the products \(\mathit{EI}_{1}\), \(\mathit{EI}_{2}\), \(\mathit{GJ}\), \(\mathit{GA}_{1}\), \(\mathit{GA}_{2}\) and \(\mathit{EA}\) are determined experimentally instead of calculated from \(I_{1},I_{2},J,A\) and the experimentally obtained moduli and Timoshenko shear correction factors. The potential energy is given by

$$ \mathscr {U}\bigl({\boldsymbol{w}}(\bullet ,t)\bigr) = \int _{0}^{L} U\bigl({ \boldsymbol{w}}(s,t)\bigr)\mathrm {d}s = \frac{1}{2} \int _{0}^{L} \bigl({\boldsymbol{w}}(s,t)-{ \boldsymbol{w}}^{*}(s)\bigr)^{\top }\cdot {\mathbf{C}}\cdot \bigl({\boldsymbol{w}}(s,t)-{ \boldsymbol{w}}^{*}(s)\bigr)\mathrm {d}s. $$

3.3 Derivation of the equations of motion

We want to derive a constrained Cosserat beam model that can be used to reduce the full Cosserat model, e.g., to a Kirchhoff beam model. In case that the quantities \(\mathit{GA}_{1}\) and \(\mathit{GA}_{2}\) are very large, the problem becomes very stiff. By reducing the full Cosserat model to a Kirchhoff model, we neglect the shearing and therefore remove the stiffness resulting from these large parameters. In order to introduce such constraints, we will require \({\boldsymbol{\varPsi }}\bigl ({\boldsymbol{w}}(s,t)\bigr )={\boldsymbol{0}}\in \mathbb{R}^{k}\) for all admissible \(s,t\) with some function \({\boldsymbol{\varPsi }}\).Footnote 6 We will later derive the equations of motion of the beam by a variational principle with an augmented Lagrangian. In order to simplify the notation, we introduce the quantity

$$ \mathscr {C}\bigl({\boldsymbol{w}}(\bullet ,t),{\boldsymbol{\lambda }}(\bullet ,t) \bigr) = \int _{0}^{L} {\boldsymbol{\varPsi }}^{\top }\bigl({\boldsymbol{w}}(s,t) \bigr)\cdot {\boldsymbol{\lambda }}(s,t)\mathrm {d}s $$

that contains the constraint-related terms. Here \({\boldsymbol{\lambda }}(s,t)\in \mathbb{R}^{k}\) are Lagrange multipliers.

Now we can define the action integral

$$ \mathscr {S}(q,\lambda ) = \int _{t_{0}}^{t_{\mathrm {e}}} \mathscr {T} \bigl({\boldsymbol{v}}(\bullet ,t)\bigr) - \mathscr {U}\bigl({\boldsymbol{w}}( \bullet ,t)\bigr) - \mathscr {C}\bigl({\boldsymbol{w}}(\bullet ,t),{ \boldsymbol{\lambda }}(\bullet ,t)\bigr)\mathrm {d}t $$

with augmented Lagrangian.

We introduce the generalized internal force densities

$$ {\boldsymbol{G}}(s,t) = {\mathbf{C}}\cdot \bigl({\boldsymbol{w}}(s,t) - {\boldsymbol{w}}^{*}(s) \bigr) + \mathbf {D}{\boldsymbol{\varPsi }}^{\top }\bigl({\boldsymbol{w}}(s,t)\bigr) \cdot {\boldsymbol{\lambda }}(s,t). $$

The first term characterizes general internal force densities arising from bending, torsion, extension, as well as shearing and the second term characterizes generalized internal constraint force densities.

Since we are considering a beam that is free on both ends, we assume that the generalized internal force densities vanish at both ends of the beam:

$$ {\boldsymbol{G}}(0,t) = {\boldsymbol{G}}(L,t) = {\boldsymbol{0}},\qquad t\in [t_{0}, t_{\mathrm {e}}]. $$

We call these natural boundary conditions. Now we can derive the equations of motion by Hamilton’s principle [24], see also [15, 18, 22]

$$ 0 = \delta \!\mathscr {S}(q,{\boldsymbol{\lambda }}) $$
(7)

with an augmented Lagrangian. As before, we use the concept of derivative vectors for the variation:

$$ \delta \!q(s,t) = \mathrm {d}L_{q(s,t)}(e)\; \widetilde{{\boldsymbol{\delta \!{}q}}(s,t)}. $$

The boundary conditions for the derivative vectors with respect to the variation are assumed to be

$$ {\boldsymbol{\delta \!{}q}}(s,t_{0}) = {\boldsymbol{\delta \!{}q}}(s,t_{\mathrm {e}}) = {\boldsymbol{0}},\qquad s\in [0,L]. $$
(8)

Now we can interchange variation and double integration, use (2) with respect to time and space, apply partial integration and end up with, by omitting the arguments \(s\) and \(t\),

$$\begin{aligned} 0 &= \int _{t_{0}}^{t_{\mathrm {e}}}\!\!\int _{0}^{L} {\boldsymbol{v}}^{\top }\cdot {\mathbf{M}}\cdot \delta \!{\boldsymbol{v}}- \bigl(({\boldsymbol{w}}-{ \boldsymbol{w}}^{*})^{\top }\cdot {\mathbf{C}}+ {\boldsymbol{\lambda }}^{\top }\cdot \mathbf {D}{\boldsymbol{\varPsi }}({\boldsymbol{w}})\bigr)\cdot \delta \!{\boldsymbol{w}}- {\boldsymbol{\varPsi }}^{\top }({\boldsymbol{w}})\cdot \delta \!{\boldsymbol{\lambda }} \mathrm {d}s \mathrm {d}t \\ &= \int _{t_{0}}^{t_{\mathrm {e}}}\!\!\int _{0}^{L} \bigl[{\boldsymbol{v}} ^{\top }\cdot {\mathbf{M}}\cdot \widehat{{\boldsymbol{v}}} - { \boldsymbol{\dot{v}}}^{\top }\cdot {\mathbf{M}}- {\boldsymbol{G}}\cdot \widehat{{\boldsymbol{w}}} + {\boldsymbol{G}}'\bigr]\cdot {\boldsymbol{\delta \!{}q}}- { \boldsymbol{\varPsi }}^{\top }({\boldsymbol{w}})\cdot \delta \!{\boldsymbol{\lambda }} \mathrm {d}s \mathrm {d}t, \end{aligned}$$

since the boundary terms of the partial integrations vanish due to the natural boundary conditions of the beam and (8). The term \(\delta \!{\boldsymbol{w}}\) can be expressed by \({\boldsymbol{w}}\) and \({\boldsymbol{\delta \!{}q}}\) by using (2). The above equation has to hold for all variations \({\boldsymbol{\delta \!{}q}}(s,t)\) and \(\delta \!{\boldsymbol{\lambda }}(s,t)\), and, therefore, the factors of those variations have to vanish, leading us to the continuous equations of motion

$$\begin{aligned} {\mathbf{M}}\cdot {\boldsymbol{\dot{v}}}(s,t) &= \widehat{{\boldsymbol{v}}(s,t)} ^{\top }\cdot {\mathbf{M}}\cdot {\boldsymbol{v}}(s,t) + {\boldsymbol{G}}'(s,t) - \widehat{{\boldsymbol{w}}(s,t)}^{\top }\cdot {\boldsymbol{G}}(s,t), \end{aligned}$$
(9a)
$$\begin{aligned} {\boldsymbol{0}}&= {\boldsymbol{\varPsi }}\bigl({\boldsymbol{w}}(s,t)\bigr) \end{aligned}$$
(9b)

for all \(s\in (0,L)\) and \(t\in (t_{0},t_{\mathrm {e}})\).

3.4 Generalizations

As in [17], external forces are added by

$$ 0 = \delta \!\mathscr {S}(q,{\boldsymbol{\lambda }}) + \int _{t_{0}}^{t_{\mathrm {e}}}\int _{0}^{L} \mathscr {F}^{\top }(s,t,q)\cdot { \boldsymbol{\delta \!{}q}}(s,t)\mathrm {d}s \mathrm {d}t, $$
(10)

where \(\mathscr {F}(s,t,q)\) is a density of external generalized forces that may depend on \(s\), \(t\), \(q\) as well as any derivatives of \(q\). Applying the same technique as before, we end up with the equations of motion

$$\begin{aligned} {\mathbf{M}}\cdot {\boldsymbol{\dot{v}}}(s,t) &= \widehat{{\boldsymbol{v}}(s,t)} ^{\top }\cdot {\mathbf{M}}\cdot {\boldsymbol{v}}(s,t) + {\boldsymbol{G}}'(s,t) - \widehat{{\boldsymbol{w}}(s,t)}^{\top }\cdot {\boldsymbol{G}}(s,t) + \mathscr {F}(s,t,q), \\ {\boldsymbol{0}}&= {\boldsymbol{\varPsi }}\bigl({\boldsymbol{w}}(s,t)\bigr), \end{aligned}$$

where we have just added the term \(\mathscr {F}(s,t,q)\) to the right hand side of the dynamic equations (9a).

A viscoelastic beam could be simulated by adding damping. This can be incorporated by

$$ 0 = \delta \!\mathscr {S}(q,{\boldsymbol{\lambda }}) - 2\int _{t_{0}}^{t_{\mathrm {e}}}\int _{0}^{L} {\boldsymbol{\dot{w}}}^{\top }(s,t)\cdot { \mathbf{D}}\cdot \delta \!{\boldsymbol{w}}(s,t)\mathrm {d}s \mathrm {d}t $$
(11)

with a diagonal matrix \({\mathbf{D}}\in \mathbb{R}^{6\times 6}\), containing dissipative material constants [15, 17]. Here, the term \(2{\mathbf{D}}\cdot {\boldsymbol{\dot{w}}}(s,t)\) could also be interpreted as the derivative of a dissipative power density

$$ {\boldsymbol{\dot{w}}}^{\top }(s,t)\cdot {\mathbf{D}}\cdot {\boldsymbol{\dot{w}}}(s,t) $$

with respect to \({\boldsymbol{\dot{w}}}(s,t)\). Treating the additional integral in the same way as before, we arrive at the same equations of motion (9a), (9b), but with generalized internal forces

$$ {\boldsymbol{G}}(s,t) = {\mathbf{C}}\cdot \bigl({\boldsymbol{w}}(s,t) - {\boldsymbol{w}}^{*}(s) \bigr) + 2{\mathbf{D}}\cdot {\boldsymbol{\dot{w}}}(s,t) + \mathbf {D}{ \boldsymbol{\varPsi }}^{\top }\bigl({\boldsymbol{w}}(s,t)\bigr)\cdot { \boldsymbol{\lambda }}(s,t). $$

3.5 Internal constraints

In the case of a Kirchhoff beam model, we require the cross sections to be perpendicular to the center line, so the first two components of the material stress vector \({\boldsymbol{\varGamma }}(s,t)\) have to vanish. This is equivalent to

$$ {\boldsymbol{0}}= {\boldsymbol{\varPsi }}\bigl({\boldsymbol{w}}(s,t)\bigr) := \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0\end{bmatrix} \cdot {\boldsymbol{\varGamma }}(s,t) = \begin{bmatrix} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0\end{bmatrix} \cdot \bigl({\boldsymbol{w}}(s,t) - {\boldsymbol{w}}^{*}(s)\bigr). $$

In the case of an inextensible Kirchhoff beam model, we also require that the beam remains parametrized by arc-length and therefore \({\boldsymbol{\varGamma }}(s,t) = {\boldsymbol{0}}\), which is equivalent to

$$ {\boldsymbol{0}}= {\boldsymbol{\varPsi }}\bigl({\boldsymbol{w}}(s,t)\bigr) := { \boldsymbol{\varGamma }}(s,t) = \begin{bmatrix} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1\end{bmatrix} \cdot \bigl({\boldsymbol{w}}(s,t) - {\boldsymbol{w}}^{*}(s)\bigr). $$

3.6 Equations of motion in the inertial frame

The equations of motion (9a), (9b) may not look familiar to the reader. If, however, we consider an unconstrained beam, separate equation (9a), into two equations in \(\mathbb{R}^{3}\) and formulate them with respect to the inertial frame by applying the rotation \(p(s,t)\) from \(q(s,t)=\bigl (p(s,t),{\boldsymbol{x}}(s,t)\bigr )\), we end up with the familiar equations

$$\begin{aligned} \rho A {\boldsymbol{\dot{u}}}&= \partial _{s}{\boldsymbol{f}}, \\ \rho ({\mathbf{i}}\cdot {\boldsymbol{\dot{\omega }}}+ {\boldsymbol{\omega }} \times ({\mathbf{i}}\cdot {\boldsymbol{\omega }})\bigr) &= \partial _{s}{ \boldsymbol{m}}+ \partial _{s}{\boldsymbol{x}}\times {\boldsymbol{f}}, \end{aligned}$$

with internal moments \({\boldsymbol{m}}(s,t)\in \mathbb{R}^{3}\) and forces \({\boldsymbol{f}}(s,t)\in \mathbb{R}^{3}\), the velocity \({\boldsymbol{u}}(s,t)={\boldsymbol{\dot{x}}}(s,t)\in \mathbb{R}^{3}\), the angular velocity \({\boldsymbol{\omega }}(s,t)\in \mathbb{R}^{3}\) as well as the inertia tensor \({\mathbf{i}}(s,t)\in \mathbb{R}^{3\times 3}\) with respect to the inertial frame:

$$\begin{gathered} \begin{bmatrix} R\bigl(p^{-}(s,t)\bigr)\;{\boldsymbol{m}}(s,t) \\ R\bigl(p^{-}(s,t)\bigr)\;{\boldsymbol{f}}(s,t) \end{bmatrix} = {\boldsymbol{G}}(s,t),\qquad \begin{bmatrix} R\bigl(p^{-}(s,t)\bigr)\;{\boldsymbol{\omega }}(s,t) \\ R\bigl(p^{-}(s,t)\bigr)\;{\boldsymbol{u}}(s,t) \end{bmatrix} = \begin{bmatrix} {\boldsymbol{\varOmega }}(s,t) \\ {\boldsymbol{U}}(s,t) \end{bmatrix}={\boldsymbol{v}}(s,t), \\ \Bigl(R\bigl(p^{-}(s,t)\bigr)\;{\boldsymbol{a}}\Bigr)^{\top }\cdot \begin{bmatrix} I_{1}&0&0 \\ 0&I_{2}&0 \\ 0&0&J \end{bmatrix}\cdot R\bigl(p^{-}(s,t)\bigr)\;{\boldsymbol{b}}= {\boldsymbol{a}} ^{\top }\cdot {\mathbf{i}}(s,t)\cdot {\boldsymbol{b}} \end{gathered}$$

for all \({\boldsymbol{a}},{\boldsymbol{b}}\in \mathbb{R}^{3}\). We prefer, however, to look at the equations of motion in slightly more complicated form (9a), (9b) because it agrees well with our choice of configuration space and, more importantly, the mass matrix \({\mathbf{M}}\) is constant unlike the inertia tensor \({\mathbf{i}}(s,t)\).

4 The fully discretized equations of motion

In this section, we will concentrate on the discretization of the Cosserat beam. In order to do this, we will heavily rely on the toolbox of variational integrators [24]. A similar approach was used in [8, 9, 20].

4.1 Discretization of the functional space

In order to obtain fully discrete equations of motion of the constrained beam, we will reduce the number of functions that we consider in the variational principle (7). First, we consider a spatial grid

$$\begin{gathered} 0=s_{0}< s_{1}< \cdots < s_{K}=L \end{gathered}$$

as well as a time grid

$$\begin{gathered} t^{(0)}< t^{(1)}< \cdots < t^{(N)}=t^{(\mathrm {e})} \end{gathered}$$

with step sizes

Δ s k = s k + 1 − s k ,andΔ t ( n ) = t ( n + 1 ) − t ( n ) .

Furthermore, we define the midpoints of the spatial grid

as well as the interior of the space-time grid cells

$$ C_{k}^{(n)} = (s_{k},s_{k+1})\times (t^{(n)},t^{(n+1)}). $$

We consider only trajectories \(q^{\mathrm {d}}\) that take the form

$$ q^{\mathrm {d}}(s,t) = \operatorname{Ip}\biggl(\frac{t-t^{(n)}}{\Delta t^{(n)}}; \operatorname{Ip}\Bigl(\frac{s-s_{k}}{\Delta s_{k}}; q_{k}^{(n)}, q_{k+1}^{(n)} \Bigr), \operatorname{Ip}\Bigl(\frac{s-s_{k}}{\Delta s_{k}}; q_{k}^{(n+1)}, q_{k+1}^{(n+1)} \Bigr)\biggr) $$

for \(s\in [s_{k},s_{k+1}]\), \(t\in [t^{(n)},t^{(n+1)}]\), which are interpolations of the data \((s_{k},t^{(n)},q_{k}^{(n)})\) in the Lie group [34]. The trajectory \(q^{\mathrm {d}}\) is of course continuous everywhere on \([0,L]\times [t^{(0)},t^{(\mathrm {e})}]\) and its degrees of freedom are its values at the grid points \(q^{\mathrm {d}}(s_{k},t^{(n)})=q^{(n)}_{k}\in G\) for \(k=0,\dots ,K\) and \(n=0,\dots ,N\). Notice, however, that \(q^{\mathrm {d}}\) is only almost everywhere differentiable: The spatial derivative does not have to exist at all spatial grid points \(s=s_{k}\) and the time derivative does likewise not have to exist at all time grid point \(t=t^{(n)}\). On the contrary, inside a grid cell \(C_{k}^{(n)}\), the spatial derivatives are constant along a fixed time \(t^{*}\) and the time derivatives are constant along a fixed arc length \(s^{*}\). More importantly, we give names to the spatial derivative along the spatial grid points and to the time derivative along the time grid points, again using the concept of derivative and velocity vectors:

with using (6),

(12a)
(12b)

Furthermore, we define the derivative vectors with respect to space of the undeformed configuration of the beam

We do not need to assume a special kind of function for the Lagrange multipliers \({\boldsymbol{\lambda }}\), but we allow the Lagrange multipliers \({\boldsymbol{\lambda }}^{\mathrm {d}} (s,t)\), corresponding to the trajectories \(q^{\mathrm {d}} (s,t)\), to be discontinuous in time at all time grid points \(t=t^{(n)}\). We give the following names to their one-sided limits around \(t^{(n)}\) in the middle of the spatial grid points:

We will later see that both limits are required to respect the hidden constraints.

4.2 Derivation of the discrete equations of motion

Now we split up the action integral

$$\begin{aligned} \mathscr {S}(q^{\mathrm {d}} ,{\boldsymbol{\lambda }}^{\mathrm {d}} ) = \sum _{k=0}^{K-1} \sum _{n=0}^{N-1} \iint _{C_{k}^{(n)}} \mathscr {L}(q^{\mathrm {d}} ,{ \boldsymbol{\lambda }}^{d}) \mathrm {d}s \mathrm {d}t \end{aligned}$$

in order to approximate the integral of the Lagrange function over a space-time grid cell

$$\begin{aligned} \iint _{C_{k}^{(n)}} \mathscr {L}(q^{\mathrm {d}} ,{\boldsymbol{\lambda }}^{d}) \mathrm {d}s \mathrm {d}t &= \int _{t^{(n)}}^{t^{(n+1)}}\int _{s_{k}}^{s_{k+1}} T\bigl({\boldsymbol{v}}^{\mathrm {d}} (s,t)\bigr) \mathrm {d}s\mathrm {d}t - \int _{s_{k}}^{s_{k+1}} \int _{t^{(n)}}^{t^{(n+1)}} U\bigl({\boldsymbol{w}}^{\mathrm {d}} (s,t) \bigr) \mathrm {d}t \mathrm {d}s \\ &\qquad \qquad {} - \int _{s_{k}}^{s_{k+1}}\int _{t^{(n)}}^{t^{(n+1)}} {\boldsymbol{\varPsi }}^{\top }({\boldsymbol{w}}^{\mathrm {d}} )\cdot {\boldsymbol{\lambda }}^{\mathrm {d}} \mathrm {d}t\mathrm {d}s. \end{aligned}$$

Here we have used the linearity of the integral and interchanged the order of integration in one of the terms. In order to do this we have chosen to apply the trapezoidal rule to the inner integrals and the midpoint rule to the outer integrals:

Using these second-order accurate approximations, we can now define a discrete Lagrangian

Further, we will use the abbreviation

in order to keep the notation easier to read. Due to the earlier second-order approximations, we now know that

$$\begin{aligned} \iint _{C_{k}^{(n)}}\mathscr {L}(q^{\mathrm {d}} ,{\boldsymbol{\lambda }}^{\mathrm {d}})\mathrm {d}s\mathrm {d}t &\approx \mathscr {L}_{k,k+1}^{(n,n+1)} \end{aligned}$$

as well as

$$\begin{aligned} \mathscr {S}(q^{\mathrm {d}} ,{\boldsymbol{\lambda }}^{\mathrm {d}}) \approx \sum _{k=0}^{K-1}\sum _{n=0}^{N-1} \mathscr {L}_{k,k+1}^{(n,n+1)}. \end{aligned}$$

We call the sum over all discrete Lagrangians the discrete action

which depends on all discrete configurations \(q_{k}^{(n)}\) as well as on all one-sided limits of the Lagrange multipliers .

Now we continue along the lines of variational integrators and derive the discretized equations of motion by finding a stationary point of the discrete action with

$$ {\boldsymbol{\delta \!{}q}}_{k}^{(0)} = {\boldsymbol{\delta \!{}q}}_{k}^{(N)} = { \boldsymbol{0}}, $$

the standard assumption for the variation of the endpoints in time:

Here, \(\mathbf {D}_{j}\mathscr {L}_{k,k+1}^{(n,n+1)}\) and \(\mathrm {d}_{j}\mathscr {L}_{k,k+1}^{(n,n+1)}\) refer to the derivative with respect to the \(j\)-th argument of the function . Now we will use the linearity of the sum, shift the indices and use the assumption on the variation of endpoints in time and end up with

by defining the missing discrete Lagrangian derivatives as zero in order to facilitate the notation:

$$ \mathbf {D}_{1}\mathscr {L}_{K,K+1}^{(n,n+1)} = \mathbf {D}_{2}\mathscr {L}_{-1,0}^{(n,n+1)} = \mathbf {D}_{3}\mathscr {L}_{K,K+1}^{(n-1,n)} = \mathbf {D}_{4}\mathscr {L}_{-1,0}^{(n-1,n)} = 0. $$

Since the above equation has to hold for all variations, we obtain the discrete equations of motion in the form

$$\begin{aligned} \mathbf {D}_{1}\mathscr {L}_{k,k+1}^{(n,n+1)} + \mathbf {D}_{2}\mathscr {L}_{k-1,k}^{(n,n+1)} + \mathbf {D}_{3}\mathscr {L}_{k,k+1}^{(n-1,n)} + \mathbf {D}_{4}\mathscr {L}_{k-1,k}^{(n-1,n)} &= {\boldsymbol{0}}, \end{aligned}$$
(13a)
d 5 L k , k + 1 ( n , n + 1 ) =0,(k≠K)
(13b)
d 6 L k , k + 1 ( n , n + 1 ) =0,(k≠K)
(13c)

for \(k=0,\dots ,K\) and \(n=1,\dots ,N-1\). We can now rearrange the first equation to

$$ -\mathbf {D}_{1}\mathscr {L}_{k,k+1}^{(n,n+1)} - \mathbf {D}_{2}\mathscr {L}_{k-1,k}^{(n,n+1)} = \mathbf {D}_{3}\mathscr {L}_{k,k+1}^{(n-1,n)} + \mathbf {D}_{4}\mathscr {L}_{k-1,k}^{(n-1,n)}. $$

The left and right hand side of the equation define two canonical momenta \({\boldsymbol{p}}_{k}^{(n,+)}\) and \({\boldsymbol{p}}_{k}^{(n,-)}\), respectively. The equation can thus be interpreted as an instance of momentum matching [24], leading to well-defined values of the momenta at the node. Here, we identify the moments by using mass matrix \({\mathbf{M}}\) multiplied with velocities \({\boldsymbol{v}}_{k}^{(n)}\) instead: This means we have

$$ -\mathbf {D}_{1}\mathscr {L}_{k,k+1}^{(n,n+1)} - \mathbf {D}_{2}\mathscr {L}_{k-1,k}^{(n,n+1)} = \bigl({\mathbf{M}}\cdot {\boldsymbol{v}}_{k}^{(n)}\bigr)^{\top }= \mathbf {D}_{3} \mathscr {L}_{k,k+1}^{(n-1,n)} + \mathbf {D}_{4}\mathscr {L}_{k-1,k}^{(n-1,n)}. $$
(14)

This approach is called a discrete Legendre transform [24] and the transformation from momenta to velocities can be considered the application of the inverse continuous Legendre transform.

Now we can consider the left hand equation and the right hand equation of (14) independently and get, by shifting \(n\) by one in the right hand equation

$$\begin{aligned} \bigl({\mathbf{M}}\cdot {\boldsymbol{v}}_{k}^{(n)}\bigr)^{\top }&= -\mathbf {D}_{1} \mathscr {L}_{k,k+1}^{(n,n+1)} - \mathbf {D}_{2}\mathscr {L}_{k-1,k}^{(n,n+1)}, \end{aligned}$$
(15a)
$$\begin{aligned} \bigl({\mathbf{M}}\cdot {\boldsymbol{v}}_{k}^{(n+1)}\bigr)^{\top }&= \mathbf {D}_{3} \mathscr {L}_{k,k+1}^{(n,n+1)} + \mathbf {D}_{4}\mathscr {L}_{k-1,k}^{(n,n+1)}. \end{aligned}$$
(15b)

Note, that we extend the validity of the equation (15a) to \(n=0\) and (15b) to \(n=N-1\) by arguing that we could have started already at \(t^{(-1)}=t^{(0)}-\varepsilon \) and ended at \(t^{(n+1)}=t^{(n)}+\varepsilon \) with some \(0<\varepsilon \ll 1\).

In order to obtain the derivatives of the Lagrangian, we will need the derivatives of the velocity vectors and with respect to the \(q_{k}^{(n)}\) by which they are defined, see (4a), (4b) and (12a), (12b):

Now, the derivatives of the discrete Lagrangian can be written as

We can see that the derivatives of the discrete Lagrangian with respect to the two different Lagrange multipliers, and , both give us the same constraint equation only with shifted index \(n\). We will drop one of the redundant equations and instead replace it by the constraint equation on velocity level

(16)

This constraint (16) is often called the hidden constraint, because it can be revealed by differentiating the constraint equation on position level with respect to time. Assuming that \({\boldsymbol{v}}_{k}^{(n)}\) actually approximates the velocity vector of \(q_{k}^{(n)}\) with respect to time, we define

Now, we can put equations (15a), (15b), (13c), (16), (12a), as well as (12b) together and obtain – by using the derivatives of the discrete Lagrangian – the full discrete equations of motion

(17a)
(17b)
(17c)
(17d)
(17e)

for \(k=0,\dots ,K\) and \(n=0,\dots ,N-1\). Here are internal generalized forces given by

for \(n=0,\dots ,N\) and \(k=1,\dots ,K-1\). All quantities in (17a)–(17e) with lower index −1, , or \(K+1\) are defined to vanish in order to facilitate notation; e.g., equation (17b) for \(k=0\) takes the form

4.3 Generalizations

External forces

Now using the variational principle (10) instead of Hamilton’s one (7), we will consider external forces. Since we already know how to treat \(\delta \!\mathscr {S}\), we will focus on the second term. We insert the trajectories \(q^{\mathrm {d}} \), split the integration interval, approximate \(\mathscr {F}(q^{\mathrm {d}} ,s,t)\) on \(C_{k}^{(n)}\) by \(\int _{s_{k}}^{s_{k+1}}\mathscr {F}(q^{\mathrm {d}} ,s,t)\mathrm {d}s/\Delta s_{k}\), use the trapezoidal rule for the remaining integral and finally shift indices:

where

for \(k=1,\dots ,K-1\) and \(n=0,\dots ,N\) and the terms vanish for lower indices less than 0 or greater than \(K\). Now the term \(\mathscr {F}_{k}^{(n)}\) will appear on the left hand side of (13a) and when this equation gets rearranged, we make sure that the products with \(\Delta t^{(n)}\) come to the left side and the products with \(\Delta t^{(n-1)}\) to the right side of (14). This will lead to the extra term

(18a)

on the right hand side of (17b), as well as

(18b)

on the right hand side of (17d).

Internal damping

Now we will consider internal damping of the beam. In order to do this, we will use the variational principle (11). Again, we insert \(q^{d}\) and approximate the remaining integral, since we already dealt with \(\delta \!\mathscr {S}(q^{\mathrm {d}} ,{\boldsymbol{\lambda }}^{\mathrm {d}} )\). We know that the derivative vectors of \(q^{\mathrm {d}} (s,t^{(n)})\) are constant for \(s\in (s_{k},s_{k+1})\) and that . We split the integration range and subsequently apply the midpoint rule in space and the trapezoidal rule in time:

Now we can calculate the variations of using (4a), (4b) and end up, by shifting indices, with

where all quantities with lower index less than 0 or more than \(K\) vanish. As in the case of external forces, we make sure that the extra terms that have the factor \(\Delta t^{(n)}\) get written on the left hand side of (14) and the terms with factor \(\Delta t^{(n-1)}\) on the right hand side of (14). We notice, however, that in the equations of motion, the transposed inverse of the tangent operator can be factored, leading to the exact same equations of motion (17a)–(17e), where the generalized internal forces now include the damping term:

where all quantities with lower index less than 0 or more than \(K\) vanish.

Implementation

We have formulated a high-level Algorithm 1 to solve the equations of motion (17a)–(17e). Note that the system in line 5 is linear if there are no external forces that depend on time-derivatives of \(q\). In that case, the Newton-Raphson iteration requires exactly one step. The starting values can be chosen by quantities that are already known from the previous time step or the current time step. It is noteworthy that the Jacobians of the systems in lines 3 and 5 have band structure [2, 15] if the equations and unknowns are ordered with ascending spatial index \(k\) including the constraint equations and Lagrange multipliers. Therefore, the linear systems that appear in the Newton-Raphson method can be solved very efficiently.

Algorithm 1
figure 1

Solution of the discrete equations of motion

Full size image

5 Numerical experiments

In this section, we will consider two different numerical benchmark problems. The first one will be a heavily damped beam that is rolled up to form a circle. The computations of the benchmark problem often give faulty results if locking is present in the numerical approximation [28]. We will see that in our case, no locking can be observed. The second benchmark will be the so-called flying spaghetti [32], where we will study the influence of the spatial step size as well as the time step size on the overall accuracy of the approximate solution obtained by the numerical scheme.

We have implemented the equations of motion derived in Sect. 4 by applying the existing numerical scheme RATTLie [12] to the spatially discretized beam model in a method of lines approach [13].

5.1 Roll-up

We consider an unconstrained Cosserat beam of length \(L=10\) and material properties \(\mathit{GA}_{1}=\mathit{GA}_{2}=\mathit{EA}=10^{4}\), \(\mathit{EI}_{1}=\mathit{EI}_{2}=\mathit{GI}=500\), \(A\rho = 1\), \(I_{1}=I_{2}=J=10\) as well as viscoelastic parameters \({\mathbf{D}}=\operatorname{diag}(100,100,100,100,100,100)\). The beam is clamped at \(s=0\), where we prescribe \({\boldsymbol{x}}(0,t)={\boldsymbol{0}}\) and \(p(0,t) = [1,0,1,0]^{\top }/\sqrt{2}\) for all times \(t\geq 0\). To the initially straight beam \({\boldsymbol{x}}(s,0) = sL\) and \(p(s,0) = [1,0,1,0]^{\top }/\sqrt{2}\), we apply a constant external torque \({\boldsymbol{M}}=[0,2\pi \mathit{EI}_{1}/L,0]^{\top }\) to the free end \(s=L\). The discretization is done with an equidistant spatial grid with \(K=8\) and constant time steps of \(\Delta t = 2^{-10} \approx 9.7{\times }10^{-4}\). In Fig. 1, we have shown snapshots of the center line; and, in Fig. 2, we have shown the norm of the distance between the two endpoints \((p_{0}^{(n)},{\boldsymbol{x}}_{0}^{(n)})\) and \((p_{K}^{(n)},{\boldsymbol{x}}_{K}^{(n)})\) as well as the norm of the velocity vectors \([({\boldsymbol{\varOmega }}_{K}^{(n)})^{\top },({\boldsymbol{U}}_{K}^{(n)}) ^{\top }]^{\top }\). It can be seen that after a few seconds, the beam is almost at rest due to the relatively high internal damping. We observe an equilibrium where the cross sections of both ends are almost in the same position and orientation. It is known that if a beam model has shear locking, the bending stiffness is largely overestimated and the beam would not complete the ring [28]. Since this behavior cannot be observed here even for this very coarse spatial discretization, we can conclude that shear locking is not present in our beam model. The recently published paper [21] describes a similar experiment. Furthermore, the authors of [21] prove that there is no locking in their model because of the semi-direct product structure of the unit dual quaternions used in [21], similar to the structure of \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\) used in the present paper.Footnote 7

Fig. 1
figure 2

Roll-up of viscoelastic beam: Snapshots of the calculated configuration of the beam at \(t=0,0.5,1,1.5, 2, 3, 30\)

Full size image
Fig. 2
figure 3

Roll-up of viscoelastic beam: The left plot shows the distance \(\|{\boldsymbol{x}}_{0}^{(n)} - {\boldsymbol{x}}_{K}^{(n)}\|_{2}+\|p_{0}^{(n)} + p_{K}^{(n)} \|_{2}\) of the configurations of the left and right end of the beam over time \(t^{(n)}\). Notice that due to the 360° rotation of the right end, the unit quaternion \(p_{K}^{(n)}\) approaches the antipodal \(-p_{0}^{(n)}\) which encode the same orientation. The right plot shows the norm \(\|{\boldsymbol{v}}_{K}^{(n)}\|_{2}\) of the velocity vector of the right end of the beam over time \(t^{(n)}\)

Full size image

5.2 Flying spaghetti

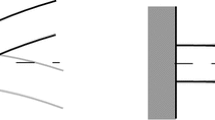
Now we will apply our discretization to the flying spaghetti benchmark [32], in order to numerically observe the order of convergence in space and time. The flying spaghetti benchmark consists of an initially straight beam of length \(L=10\) with material parameters: \(\mathit{GA}_{1}=\mathit{GA}_{2}=\mathit{EA}=10^{4}\), \(\mathit{EI}_{1}=\mathit{EI}_{2}=\mathit{GJ}=50\), \(A\rho =1\), and \(\rho I_{1} = \rho I_{2} = \rho J = 10\). Both ends of the beam are free, and at the end, where \(s=0\), forces and moments are applied, ramping up from \(t=0\) to \(t=2.5\) and then decreasing from \(t=2.5\) to \(t=5\). A schematic description of the initial configuration and the applied moments can be found in Fig. 3. In Fig. 4, we have provided snapshots of the configuration of the beam. In this paper, we used a Kirchhoff beam model for the flying spaghetti by constraining the full Cosserat beam model as described in the above sections.

Fig. 3
figure 4

Description of the flying spaghetti benchmark [32]: Initial position as well as applied forces and moments on the left and the magnitude of the forces and moments on the right

Full size image
Fig. 4
figure 5

Flying spaghetti: Snapshots of the configuration with \(N=8\) beam segments at \(t=0,2,3,4,\dots ,15\) and the trajectory of the end points

Full size image

In Fig. 5, we have considered the benchmark problem with equidistant spatial grid with \(K=8\) and varied step size \(\Delta t\) of the equidistant time grid. The maximal absolute discrete \(L^{2}\) error in \(q\) is defined by

$$ \max _{n=0,\dots ,N}\sqrt{\frac{1}{7(K+1)}\sum _{k=0}^{K} \|q_{k}^{(n)} - Q_{k}^{(n)}\|_{2}^{2}}, $$

where \(Q_{k}^{(n)}\approx q(s_{k},t^{(n)})\) is the reference solution. Accordingly, the maximal absolute discrete \(L^{2}\) error in \({\boldsymbol{v}}\) can be defined. Note that we are using here differences of Lie group elements, but only for getting a grasp of the magnitude of the errors not for computing any values of the numerical solution! We can see in Fig. 5 that the slope of the errors in \(q\) and \({\boldsymbol{v}}\) over the time step size \(\Delta t\) is approximately two. This means that we can observe second order convergence behaviour numerically.

Fig. 5
figure 6

Flying spaghetti: Maximum of absolute error over time step size \(\Delta t\) with \(K=8\) beam segments. The reference solution was calculated with \(\Delta t\approx 3.8{\times }10^{-6}\)

Full size image

In Fig. 6, we have considered the flying spaghetti with equidistant time grid with \(\Delta t=2^{-12}\approx 2.5{\times }10^{-4}\) and varied the number of equidistant spatial grid points \(K\). This time, we have interpolated the beam in space [34] by using piecewise Lie group interpolation (5) in \(q\) and piecewise linear interpolation in \({\boldsymbol{v}}\). Then we have plotted the maximal absolute discrete \(L^{2}\) error of the interpolated beam at \(s=0,L/8,\dots ,8L/8\). Here, we can observe that the slope of the errors over \(K\) is approximately −2, which means that we can observe second order convergence in space. The error in the velocity vectors \({\boldsymbol{v}}\), however, starts to saturate for larger \(K\). This could have two reasons: All solutions were calculated with a rather coarse time step, and, so, this error saturation could indicate that the solutions can not become a lot more precise without reducing the time step size. The second reason could be that piecewise linearly interpolating the velocity vectors \({\boldsymbol{v}}\) could be incompatible with the way the discretization scheme was derived, where the velocity vectors of the discretized configuration \(q^{\mathrm {d}}\) with respect to time had jumps at the time grid points and were constant in between them.

Fig. 6
figure 7

Flying spaghetti: Maximum of absolute error over number of beam segments \(K\) with time step \(\Delta t\approx 2.4{\times }10^{-4}\). The reference solution was calculated with \(K=265\) beam segments

Full size image

All in all, we can observe that our discretization scheme is convergent of second order in space and time. This is what could have been expected, since we have only used approximations of second order in the derivation of the scheme, namely Lie group interpolation of first order (which is a generalization of linear interpolation) and the trapezoidal and midpoint rule for approximating integrals. A rigorous mathematical analysis is, however, needed in order to prove the claim of second order convergence.

Lastly, we have depicted the change of mechanical energy of the flying spaghetti in Fig. 7 in the conservative realm \(t\in [5,110]\). As we expect from a variational discretization, there is no systematic energy drift, see, e.g., [24], where the discrete Noether theorem is shown, stating that a variational integrator has to conserve a perturbed energy.

Fig. 7
figure 8

Flying spaghetti: Change \(\Delta E\) in mechanical energy for \(t\in [5,110]\), where no forces and moments are applied. Results were calculated with \(\Delta t\approx 4.9{\times }10^{-4}\) and \(\Delta s = 0.625\)

Full size image

6 Conclusion

We have shortly introduced the toolbox of Lie group structured configuration spaces and the concept of velocity and derivative vectors with special attention to the Lie group of rigid body motions \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\), where rotations are parametrized using unit quaternions \(\mathbb{S}^{3}\). Then we have described a constrained Cosserat beam model, where the configuration space \(\mathbb{S}^{3}\ltimes \mathbb{R}^{3}\) was used to describe the orientation and position of each cross section of the beam. The constraints can be used to reduce the Cosserat beam model to a Kirchhoff beam model by requiring the cross sections to remain perpendicular to the center line. The continuous equations of the beam were then derived using variational principles like Hamilton’s principle with an augmented Lagrangian. Furthermore, we have discretized the infinite-dimensional space of functions by only considering trajectories, which are given by a piecewise first order Lie group interpolation. Applying again the variational principles, we arrived at the fully discrete equations of motion. The derived discrete scheme was then tested on two benchmark problems. We could observe that no shear locking was present in the scheme and that it can be numerically seen to converge with second order both in space and in time.