Co-simulation with variable approximation order: order control algorithm for solver coupling approaches

Abstract

Considering co-simulation and solver coupling approaches, the coupling variables have to be approximated within a macro-time step (communication-time step), e.g., by using extrapolation/interpolation polynomials. Usually, the approximation order is assumed to be fixed. The efficiency and accuracy of a co-simulation may, however, be increased by using a variable approximation order. Therefore, a technique to control the integration order is required. Here, an order control algorithm for co-simulation and solver coupling methods is presented. The order controller is incorporated into the control algorithm for the macro-step size so that co-simulations with variable integration order and variable macro-step size can be carried out. Different numerical examples are presented, which illustrate the applicability and benefit of the proposed order control strategy. This contribution mainly focuses on mechanical systems. The presented techniques may, however, also be applied to nonmechanical dynamical systems.

1 Introduction

Co-simulation terms a variety of numerical techniques, which can be applied to couple different solvers in time domain. A classical field of application for co-simulation methods concerns the simulation of multiphysical systems, see, e.g., [13, 16, 20, 49, 69]. In this case, each physical subdomain is modeled and simulated with its own (specialized) subsystem solver, whereas each subsystem may be considered as a black-box system. The subsystem solvers are numerically coupled by an appropriate co-simulation method. In literature, many interesting multidisciplinary problems have been solved incorporating co-simulation techniques, e.g., fluid/structure interaction problems [1, 43], analysis of coupled finite-element/multibody models [2, 3, 48], multidisciplinary simulations in the framework of vehicle dynamics [11, 36, 45] or coupled problems including particle models [14, 33, 70, 76].

Besides this classical area of application, co-simulation may also be applied advantageously to parallelize monodisciplinary dynamical systems, see, for instance, [4, 10, 31, 32, 38, 44, 46, 63, 74]. Therefore, the global system is split into a certain number of subsystems, which are connected and simulated by a proper co-simulation approach. As a consequence, the overall computation time may be reduced massively.

A very straightforward consideration can be useful to demonstrate the possible computational benefit, which may be achieved by a co-simulation-based parallelization approach. We consider therefore a multibody system with $n$ degrees of freedom, which is decomposed into $r$ equally sized subsystems. The decomposed system is assumed to be integrated with an implicit predictor/corrector co-simulation method, see Sect. 3. Note that for implicit co-simulation approaches, an interface-Jacobian is required, which may, however, be calculated very easily in parallel with the predictor/corrector subsystem integrations so that the computation of the interface-Jacobian will not (markedly) increase the overall co-simulation time. Regarding an implicit co-simulation approach, the main computational effort is produced by the repetition of the macro-step for carrying out the corrector iteration over the macro-interval. Now, we assume that an $\mathcal{O} \left ( n^{\alpha } \right )$-algorithm is used for solving the equations of motion, where $\alpha$ is usually a value between 1 and 3. Consequently, the simulation time for the monolithic model is given by $T_{\mathit{Mono}} =\mathit{constant} \cdot n^{\alpha }$. Applying an implicit co-simulation scheme and assuming an average number of $l$ corrector iterations within each macro-step, the simulation time of the co-simulation may roughly be estimated by $T_{\mathit{Cosim}} =(1+l) \cdot \mathit{constant} \cdot \left ( \frac{n}{r} \right )^{\alpha } +\mathit{Overhead}$ (one predictor-step and $l$ corrector-steps). Practical simulations show (see [40]) that the number of corrector steps $l$ is frequently rather small ($l=2$ or $l=3$). Hence, if the overall model is decomposed into a sufficiently large number of subsystems, the reduction of computation time may become very significant. It should be noted that the estimation formula for $T_{\mathit{Cosim}}$ will only yield reasonable results if the (average) integration step-size of the monolithic model equals the (average) integration step-size of the subsystems, see Sect. 6.6. The possible speed-up compared to a monolithic simulation may be improved even more, if the co-simulation is accomplished with a variable macro-step size (macro-step size controller). A further improvement may be achieved if a variable integration order is used (i.e., variable approximation order for the coupling variables). Applying an explicit co-simulation method, the possible speed-up may become even larger, since $l=0$ for explicit co-simulations. It should be pointed out that for the case that $r$ is chosen too large, the overhead will become the dominant part of the computation time so that the co-simulation will get inefficient [29, 40].

Besides the directly obvious speed-up due to the decomposition into subsystems, which can be solved independently and in parallel within each macro-step, an improvement with respect to the simulation time may also be achieved due to the multi-rate effect. If the global model can be split into a small-sized stiff subsystem and a large-scaled non-stiff subsystem, only the smaller stiff subsystem has to be integrated with small subsystem integration-step sizes, while the larger non-stiff subsystem can be integrated very efficiently and stable with larger subsystem integration-step sizes.

Remark 1

Parallelization of a dynamical system can be realized in different ways. Considering a monolithic dynamical model, which is discretized by an (implicit) time-integration scheme (e.g., BDF method, Runge–Kutta method), an algebraic system of equations has to be solved in each time step. Usually, parallelization is accomplished by solving the algebraic system of equations in parallel, i.e., the equation solver is parallelized. In contrast to this classical type of parallelization, a further parallelization can be achieved by making use of a co-simulation approach, as mentioned above. Hence, parallelization may be realized on two levels, namely

• i) by a decomposition of the overall model into subsystems, which are integrated in parallel within each macro-time step and

• ii) by applying the classical type of parallelization, i.e., by using parallelized subsystem solvers for solving the algebraic subsystem equations.

Here, we omit a detailed literature review on co-simulation and solver coupling techniques. The interested reader is referred to literature, see, e.g., [17, 18, 22, 56].

Within a co-simulation approach, a macro-time grid (also called communication-time grid) has to be defined, i.e., macro-time points $T_{i}$ $(i=0,1,2,\ldots)$ have to be specified, where the subsystems exchange the coupling variables. Between the macro-time points, the coupling variables are approximated, e.g., by means of extrapolation/interpolation polynomials of degree $k$. In the simplest case, an equidistant macro-time grid is used and the order of the approximation polynomials for the coupling variables is assumed to be constant. Using a co-simulation with constant order and constant macro-step size may, however, be rather inefficient. It has been shown in literature that the efficiency, accuracy, and stability of a co-simulation implementation may significantly be improved by incorporating a macro-step size controller, see [6, 40, 51, 53, 54].

In the current manuscript, the possible improvement of a co-simulation with variable integration order is investigated. For realizing a variable integration order, a strategy is required, which determines the optimal integration order. Therefore, the local truncation error within the macro-step from $T_{N}$ to $T_{N+1} = T_{N} + H_{N}$ ($H_{N}$ denotes the current macro-step size) is estimated for different polynomial degrees $k$. The optimal polynomial order minimizes the estimated local error. Applying an appropriate order control algorithm, co-simulations with variable integration order can be realized. In this work, only co-simulation implementations with variable macro-step size are considered. It should therefore be stressed that the control algorithm for the integration order and the macro-step size control algorithm cannot be considered independently, since both influence each other. As a consequence, order and step-size have to be controlled simultaneously.

In the paper at hand, mechanical co-simulation models with an arbitrary number of subsystems are investigated. The developed order control algorithm may, however, also be used for nonmechanical systems. Considering mechanical systems, the coupling of the subsystems can be realized either by constitutive laws (coupling by applied-forces) [1, 3, 9, 19, 21, 48, 58, 60] or by algebraic constraint equations (coupling by reaction forces) [5, 23, 30, 39, 55, 57, 59, 61, 62, 72, 73, 75]. In this work, we restrict ourselves to the case of applied-force coupling approaches (explicit and implicit). Furthermore, we only consider parallel co-simulation implementations of Jacobi type. Sequential integration techniques (Gauss–Seidel type) [26, 27] are not applied, since we focus on fully parallelizable models. To approximate the coupling variables between two macro-time points, Lagrange polynomials are used here. Other approximation approaches – acceleration based techniques [34, 35], interface-model-based approaches [47], context-based approximation polynomials [7], methods applying a least square fit [42], etc. – are not considered in the current manuscript.

The new contributions of this manuscript can be summarized as follows:

• An algorithm for controlling the order of the approximation polynomials for co-simulation and solver coupling methods is presented.

• The developed order controller is imbedded into the macro-step size control algorithm.

• Efficiency, accuracy, and stability of a co-simulation implementation with variable integration order and variable macro-step size is analyzed with different numerical examples.

• The large potential of parallelizing dynamical models with the help of co-simulation is demonstrated.

The manuscript is organized as follows: In Sect. 2, the basic idea of co-simulation and the relevant definitions are briefly summarized. The classical explicit and implicit co-simulation methods are shortly recapitulated in Sect. 3. The different error estimators, which are used in the current work for controlling the macro-step size, are collected in Sect. 4. The order control strategy and the combined algorithm for controlling the integration order and the macro-step size simultaneously are presented in Sect. 5. Numerical examples are given in Sect. 6. The paper is concluded in Sect. 7. Calculation of the interface-Jacobian, which is required for the implicit co-simulation approach, is treated in Appendix A. Some additional simulation results for Example 3 in Sect. 6.3 are collected in Appendix B.

2 Co-simulation model

2.1 General case: arbitrary mechanical system decomposed into subsystems

To demonstrate the basic strategy behind a co-simulation approach, a general mechanical system is considered, which is mathematically defined by the following first-order DAE system (differential-algebraic system of equations)

$$ \boldsymbol{B} ( t,\boldsymbol{z} ) \dot{\boldsymbol{z}} = \boldsymbol{f} ( t, \boldsymbol{z} ). $$

(1)

The vector $\boldsymbol{z}$ contains the position variables $\boldsymbol{q}$, the velocity variables $\boldsymbol{v}$, and also the Lagrange multipliers $\boldsymbol{\lambda }$; $\boldsymbol{B}$ represents a symmetric square matrix, which is not invertible in the general case, where Eq. (1) represents a DAE. For classical constrained multibody systems [12], for instance, the matrix $\boldsymbol{B}$ is given by $\left ( \begin{array}{c@{\quad }c@{\quad }c} \boldsymbol{I} & \boldsymbol{0} & \boldsymbol{0}\\ \boldsymbol{0} & \boldsymbol{M} & \boldsymbol{0}\\ \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} \end{array} \right )$, where $\boldsymbol{I}$ denotes the identity matrix and $\boldsymbol{M}$ the mass matrix. In the ODE case, $\boldsymbol{B}$ is invertible.

Next, the overall system is decomposed into $r$ subsystems. To describe the coupling between the subsystems, appropriate coupling variables $\boldsymbol{u}$ have to be defined. Throughout this manuscript, we assume that the subsystems are connected by applied forces/torques (applied-force coupling) so that the coupling between the subsystems is described by constitutive laws. Constraint coupling, where the subsystems are connected by algebraic constraint equations and corresponding reaction forces (Lagrange multipliers) is not considered here. In the framework of a co-simulation approach, macro-time points $T_{i} \ (i=0,1,2,\dots )$ have to be defined. Macro-time points are discrete, not necessarily equidistant time points. With the macro-time points, the macro-step size $H_{N} = T_{N+1} - T_{N}$ is defined. If a constant macro-step size $H= T_{N+1} - T_{N} =\mathit{const}$. is used, $H$ has to be specified by the user so that the co-simulation runs stable and provides accurate results. Applying an appropriate error estimator, the current macro-step size $H_{N}$ is determined by the macro-step size controller so that a user-defined error criterion is fulfilled. Between the macro-time points, the subsystems are integrated independently, since the subsystems only exchange information at the macro-time points. To carry out the subsystem integrations between the macro-time points, the coupling variables have to be approximated. In this work, Lagrange polynomials are used for approximating the coupling variables.

The states and multipliers of an arbitrary subsystem $s\in \left \{ 1,\dots ,r \right \}$ are arranged in the vector $\boldsymbol{z}^{s} = ( \boldsymbol{q}^{s^{T}}, \boldsymbol{v}^{s^{T}}, \boldsymbol{\lambda }^{s^{T}} )^{T}$. Note that the number of the subsystem is indicated by the superscript $s$. The equations of motion of subsystem $s$ read

$$ \boldsymbol{B}^{s} \bigl( t, \boldsymbol{z}^{s} \bigr) \dot{\boldsymbol{z}}^{s} = \boldsymbol{f}^{s} ( t, \boldsymbol{z} ). $$

(2)

The coupling variables $\boldsymbol{u}$, which here represent input variables of the subsystems, can be defined implicitly by the coupling functions $\boldsymbol{g}_{c}:=\boldsymbol{u}-\boldsymbol{\varphi } \left ( t, \boldsymbol{z},\boldsymbol{u} \right ) = \boldsymbol{0}$. It should be mentioned that the subsystem coupling is, one the one hand, defined by the constitutive laws of the coupling forces/torques and, on the other hand, by the decomposition technique. Note that basically three different decomposition techniques may be distinguished, namely force/force-decomposition, force/displacement-decomposition, and displacement/displacement-decomposition, see [58, 61, 75] for more details. It should further be stressed that for applied-force coupling approaches, the coupling variables are only functions of $\boldsymbol{q}$ and $\boldsymbol{v}$, i.e., the coupling functions may be expressed as $\boldsymbol{g}_{c}:=\boldsymbol{u}-\boldsymbol{\varphi } \left ( t, \boldsymbol{q},\boldsymbol{v},\boldsymbol{u} \right ) = \boldsymbol{0}$. Making use of the coupling variables, the equations of motion of subsystem $s$ can be rewritten as

$$ \boldsymbol{B}^{s} \bigl( t, \boldsymbol{z}^{s} \bigr) \dot{\boldsymbol{z}}^{s} = \boldsymbol{f}^{\mathit{co},s} \bigl( t, \boldsymbol{z}^{s},\boldsymbol{u} \bigr). $$

(3)

Collecting the right-hand sides of all subsystem equations into the vector $\boldsymbol{f}^{\mathit{co}} \left ( t, \boldsymbol{z},\boldsymbol{u} \right ) = ( \boldsymbol{f}^{\mathit{co},1} \left ( t, \boldsymbol{z}^{1},\boldsymbol{u} \right )^{T},\dots , \boldsymbol{f}^{\mathit{co},r} \left ( t, \boldsymbol{z}^{r},\boldsymbol{u} \right )^{T} )^{T}$, the decomposed co-simulation system can be formulated as

$$ \textstyle\begin{array} {l} \boldsymbol{B} ( t,\boldsymbol{z} ) \dot{ \boldsymbol{z}} = \boldsymbol{f}^{\mathit{co}} ( t, \boldsymbol{z}, \boldsymbol{u} ), \\ \boldsymbol{g}_{c} ( t, \boldsymbol{z},\boldsymbol{u} ) = \boldsymbol{0} \end{array} $$

(4)

with $\boldsymbol{z}= ( \boldsymbol{z}^{1^{T}},\dots , \boldsymbol{z}^{r^{T}} )^{T}$. Note that in the framework of a co-simulation approach, the coupling conditions are only enforced at the macro-time points $T_{N}$. Between the macro-time points, approximated coupling variables are used. Further details and examples concerning the decomposition of an overall system into subsystems can, for instance, be found in [29, 40]. It should be emphasized again that co-simulation and the here investigated strategies for controlling the macro-step size and approximation order are not limited to mechanical systems.

2.2 Special case: system of coupled multibody models

In the subsequent sections, we focus on the special case that the subsystems are general constrained multibody systems. Then, the equations of motion (3) for an arbitrary subsystem $s$ can be written as

$$ \begin{aligned} \dot{\boldsymbol{x}}^{s} &= \boldsymbol{H}^{s} \bigl( \boldsymbol{x}^{s} \bigr) \boldsymbol{v}^{s}, \\ \boldsymbol{M}^{s} \bigl( t, \boldsymbol{x}^{s} \bigr) \dot{\boldsymbol{v}}^{s}& = \boldsymbol{f}^{s} \bigl( t, \boldsymbol{x}^{s}, \boldsymbol{v}^{s} \bigr) - \boldsymbol{H}^{s^{\mathrm{T}}} \bigl( \boldsymbol{x}^{s} \bigr) \boldsymbol{G}^{s ^{\mathrm{T}}} \bigl( t, \boldsymbol{x}^{s} \bigr) \boldsymbol{\lambda }^{s} + \boldsymbol{f}^{\mathrm{c},\mathrm{s}} \bigl( t, \boldsymbol{x}^{s}, \boldsymbol{v}^{s},\boldsymbol{u} \bigr), \\ \boldsymbol{0}& = \boldsymbol{g}^{s} \bigl( t, \boldsymbol{x}^{s} \bigr). \end{aligned} $$

(5)

The matrix $\boldsymbol{H}^{s}$ defines the relationship between the (generalized) velocity variables $\boldsymbol{v}^{s}$ and the (generalized) position variables $\boldsymbol{x}^{s}$; $\boldsymbol{M}^{s}$ denotes the symmetric mass matrix, and $\boldsymbol{f}^{s}$ the vector of the applied and Coriolis forces. The algebraic constraint equations of the subsystem are collected in the vector $\boldsymbol{g}^{\boldsymbol{s}} \left ( t, \boldsymbol{x}^{s} \right ) =\boldsymbol{0}$. The term $\boldsymbol{H}^{s^{\mathrm{T}}} \left ( \boldsymbol{x}^{s} \right ) \boldsymbol{G}^{s ^{\mathrm{T}}} \left ( t, \boldsymbol{x}^{s} \right ) \boldsymbol{\lambda }^{s}$ with the constraint Jacobian $\boldsymbol{G}^{s} = \frac{\partial \boldsymbol{g}^{\boldsymbol{s}}}{\partial \boldsymbol{x}}$ and the vector of Lagrange multipliers $\boldsymbol{\lambda }^{s}$ represents the constraint forces/torques generated by the subsystem constraint equations. The coupling forces/torques of subsystem $s$ are arranged in the vector $\boldsymbol{f}^{c,\mathrm{s}}$. A comparison with the general case of Sect. 2.1 shows that one gets for the special case of a system of coupled multibody models the relationships $\boldsymbol{B}^{s} \left ( t,\boldsymbol{z} \right ) = \mathrm{blockdiag} ( \boldsymbol{I}, \boldsymbol{M}^{s},\boldsymbol{0})$ and $\boldsymbol{f}^{\mathit{co},s} = \left ( \begin{array}{c} \boldsymbol{H}^{s} \boldsymbol{v}^{s}\\ \boldsymbol{f}^{s} - \boldsymbol{H}^{s^{\mathrm{T}}} \boldsymbol{G}^{s^{\mathrm{T}}} \boldsymbol{\lambda }^{s} + \boldsymbol{f}^{\mathrm{c},\mathrm{s}}\\ \boldsymbol{g}^{s} \end{array} \right )$.

2.2.1 Example: two multibody systems coupled by a flexible bushing element

As an example, two arbitrary unconstrained mechanical subsystems are considered. It is assumed that the subsystems are mechanically coupled by a linear viscoelastic bushing element (flexible atpoint joint) [58], see Fig. 1. More precisely, point $C_{i}$ of body $i$ (center of mass $S_{i}$, mass $m_{i}$, inertia tensor $\boldsymbol{J}_{i}$) belonging to subsystem 1 is connected to marker $C_{j}$ of body $j$ (center of mass $S_{j}$, mass $m_{j}$, inertia tensor $\boldsymbol{J}_{j}$) related to subsystem 2 by a linear three-dimensional spring/damper element.

Fig. 1

Body ${i}$ of subsystem 1 coupled to body ${j}$ of subsystem 2 (coupling points ${C}_{{i}}$ and ${C}_{{j}}$)

The coupling points $C_{i}$, $C_{j}$ are represented by the body fixed vectors $\boldsymbol{r}_{C_{i}}$, $\boldsymbol{r}_{C_{j}}$. Applying absolute coordinates, position and orientation of an arbitrary rigid body $q$ is defined by the 3 coordinates of the center of mass $\boldsymbol{r}_{S_{q}}$ and by 3 rotation parameters arranged in the vector $\boldsymbol{\gamma }_{q} \in \mathbb{R}^{3}$ (e.g., 3 Bryant angles). The coordinates of the angular velocity $\boldsymbol{\omega }_{q}$ are associated with the time derivative of the rotation parameters by the general expression $\dot{\boldsymbol{\gamma }}_{q} = \boldsymbol{H} \left ( \boldsymbol{\gamma }_{q} \right ) \boldsymbol{\omega }_{q}$ with $\boldsymbol{H} \in \mathbb{R}^{3\times 3}$. The equations of motion (Newton–Euler equations) for the coupling bodies $i$ and $j$ are given by

Coupling body $i$ (subsystem 1):

$$ \begin{aligned} \dot{\boldsymbol{r}}_{S_{i}} &=\boldsymbol{v}_{S_{i}}, \\ m_{i}\dot{\boldsymbol{v}}_{S_{i}} &= \boldsymbol{f}_{i} \bigl( t, \boldsymbol{x}^{1}, \boldsymbol{v}^{1} \bigr) + \boldsymbol{f}_{i}^{c,1}, \\ \dot{\boldsymbol{\gamma }}_{i} &= \boldsymbol{H} ( \boldsymbol{ \gamma }_{i} ) \boldsymbol{\omega }_{i}, \\ \boldsymbol{J}_{i} \dot{\boldsymbol{\omega }}_{i} + \boldsymbol{\omega }_{i} \times \boldsymbol{J}_{i} \boldsymbol{\omega }_{i}& = \boldsymbol{\tau }_{i} \bigl( t, \boldsymbol{x}^{1}, \boldsymbol{v}^{1} \bigr) + \boldsymbol{\tau }_{i}^{c,1}. \end{aligned} $$

(6)

Coupling body $j$ (subsystem 2):

$$ \begin{aligned} \dot{\boldsymbol{r}}_{S_{j}} &= \boldsymbol{v}_{S_{j}}, \\ m_{j}\dot{\boldsymbol{v}}_{S_{j}} &= \boldsymbol{f}_{j} \bigl( t, \boldsymbol{x}^{2}, \boldsymbol{v}^{2} \bigr) + \boldsymbol{f}_{j}^{c,2}, \\ \dot{\boldsymbol{\gamma }}_{j} &= \boldsymbol{H} ( \boldsymbol{ \gamma }_{j} ) \boldsymbol{\omega }_{j}, \\ \boldsymbol{J}_{j} \dot{\boldsymbol{\omega }}_{j} + \boldsymbol{\omega }_{j} \times \boldsymbol{J}_{j} \boldsymbol{\omega }_{j} &= \boldsymbol{\tau }_{j} \bigl( t, \boldsymbol{x}^{2}, \boldsymbol{v}^{2} \bigr) + \boldsymbol{\tau }_{j}^{c,2}. \end{aligned} $$

(7)

In the above equations, $\boldsymbol{f}_{i}$ and $\boldsymbol{f}_{j}$ represent the resultant applied forces, which are acting on the two coupling bodies. The resultant applied torques are denoted by $\boldsymbol{\tau }_{i}$ and $\boldsymbol{\tau }_{j}$.

The coupling force $\boldsymbol{f}^{{c}}$ represents a spring/damper force, which is proportional to the relative displacement and to the relative velocity of the coupling points $C_{i}$ and $C_{j}$; $\boldsymbol{f}^{{c}}$ can implicitly be described by the three coupling conditions

$$\begin{aligned} \boldsymbol{g}_{c} :=& \boldsymbol{f}^{{c}} + \boldsymbol{C} \cdot \bigl[ ( \boldsymbol{r}_{S_{i}} + \boldsymbol{r}_{C_{i}} ) - ( \boldsymbol{r}_{S_{j}} + \boldsymbol{r}_{C_{j}} ) \bigr] \\ &{}+ \boldsymbol{D} \cdot \frac{\mathrm{d}}{\mathrm{d} t} \bigl\{ \bigl[( \boldsymbol{r}_{S_{i}} + \boldsymbol{r}_{C_{i}} )-( \boldsymbol{r}_{S_{j}} + \boldsymbol{r}_{C_{j}} ) \bigr] \bigr\} = \boldsymbol{0}, \end{aligned}$$

(8)

where the diagonal matrix $\boldsymbol{C} = \mathrm{diag} \,\left ( c_{x}, c_{y}, c_{z} \right )$ collects the three spring constants and the diagonal matrix $\boldsymbol{D} = \mathrm{diag}\, \left ( d_{x}, d_{y}, d_{z} \right )$ the three damping coefficients. Note that the total time derivative with respect to the inertial system $K_{0}$ is denoted by $\frac{d}{dt}$. Hence, the coupling forces and torques, which are acting on the two coupling bodies, read

$$ \begin{aligned} \boldsymbol{f}_{i}^{c,1} &= \boldsymbol{f}^{\mathrm{c}},\qquad \boldsymbol{\tau }_{i}^{c,1} = \boldsymbol{r}_{C_{i}} \times \boldsymbol{f}^{\mathrm{c}}, \\ \boldsymbol{f}_{j}^{c,2} &=- \boldsymbol{f}^{\mathrm{c}}, \qquad \boldsymbol{\tau }_{j}^{c,2} =- \boldsymbol{r}_{C_{j}} \times \boldsymbol{f}^{\mathrm{c}} . \end{aligned} $$

(9)

3 Classical explicit and implicit co-simulation schemes

For approximating the coupling variables $\boldsymbol{u}$ within the macro-step $T_{N} \rightarrow T_{N+1}$, extrapolation/interpolation polynomials $\boldsymbol{p}_{N+1} \left ( t \right )$ of degree $k$ (local approximation order $k+1$, i.e., $\mathcal{O} \left ( H^{k+1} \right )$) are used. Since the subsystems only exchange information at the macro-time points, the coupling conditions are only enforced at the macro-time points $T_{N}$, i.e., $\boldsymbol{g}_{c} \left ( t, \boldsymbol{z},\boldsymbol{u} \right ) = \boldsymbol{0}$ is only fulfilled at the macro-time points. Between the macro-time points, the subsystems can be integrated independently.

Applying a co-simulation approach, system (1) is replaced by the weakly coupled co-simulation system

$$ \boldsymbol{B} ( t,\boldsymbol{z} ) \dot{\boldsymbol{z}} = \boldsymbol{f}^{\mathit{co}} \bigl( t, \boldsymbol{z}, \boldsymbol{p}_{N+1} (t) \bigr). $$

(10)

The new variables $\boldsymbol{z}_{N+1}$ are obtained by integrating Eq. (10) from $T_{N}$ to $T_{N+1}$ with the initial conditions $\boldsymbol{z}_{N}$.

It should be noted that for an explicit co-simulation method, the extrapolated coupling variables $\boldsymbol{p}_{N+1} ( T_{N+1} )$ will usually not satisfy the coupling equations at the new macro-time point $T_{N+1}$ so that $\boldsymbol{p}_{N+1} \left ( T_{N+1} \right ) -\boldsymbol{\varphi } \left ( T_{N+1}, \boldsymbol{z}_{N+1}, \boldsymbol{p}_{N+1} ( T_{N+1} ) \right ) \neq \boldsymbol{0}$. Consistent coupling variables $\boldsymbol{u}_{N+1}$ can, however, simply be calculated by an update step. Therefore, the coupling equations $\boldsymbol{u}_{N+1} =\boldsymbol{\varphi } \left ( T_{N+1}, \boldsymbol{z}_{N+1}, \boldsymbol{u}_{N+1} \right )$ have just to be solved for $\boldsymbol{u}_{N+1}$. The update step will produce (small) jumps in the coupling variables, because $\boldsymbol{p}_{N+1} \left ( T_{N+1} \right )$ is usually not equivalent with the updated coupling variables $\boldsymbol{u}_{N+1}$.

3.1 Explicit co-simulation scheme

The classical explicit co-simulation approach can be described very easily by considering the general macro-time step from $T_{N} \rightarrow T_{N+1}$ [52, 60, 64, 69]. We assume that at the beginning of the macro-time step, the variables of the subsystems (subsystem states and subsystem multipliers) as well as the coupling variables are known.

• In a first step, the vector collecting the extrapolation polynomials $\boldsymbol{p}_{N+1}^{\mathit{ext}} \left ( t \right )$ for the coupling variables $\boldsymbol{u} (t )$ in the time interval [$T_{N}$,$T_{N+1}$] is generated by making use of the $k+1$ sampling points $\left ( T_{N}, \boldsymbol{u}_{N} \right ), \left ( T_{N-1}, \boldsymbol{u}_{N-1} \right ), \dots , \left ( T_{N-k}, \boldsymbol{u}_{N-k} \right )$.

• In a second step, Eq. (10) is integrated from $T_{N} \rightarrow T_{N+1}$ using the extrapolation polynomials $\boldsymbol{p}_{N+1}^{\mathit{ext}} \left ( t \right )$. This yields the variables $\boldsymbol{z}_{N+1}^{\mathit{ext}}$. In case of the explicit co-simulation scheme, the new variables at $T_{N+1}$ are simply given by $\boldsymbol{z}_{N+1}:= \boldsymbol{z}_{N+1}^{\mathit{ext}}$.

• In a final step, updated coupling variables $\boldsymbol{u}_{N+1}$ are computed. Therefore, the variables $\boldsymbol{z}_{N+1}$ are inserted into the coupling equations and $\boldsymbol{u}_{N+1} =\boldsymbol{\varphi } \left ( T_{N+1}, \boldsymbol{z}_{N+1}, \boldsymbol{u}_{N+1} \right )$ is solved for $\boldsymbol{u}_{N+1}$.

Now, the next macro-time step $T_{N+1} \rightarrow T_{N+2}$ can be accomplished. The integration scheme is sketched in Fig. 2.

Fig. 2

Explicit co-simulation scheme (${k}={1}$): (a) approximation of coupling variable ${u}_{{i}}$ with linear extrapolation polynomial; (b) update step

Note that for practical reasons, problems may occur in conjunction with feed-through systems. From the practical point of view, it may be complicated to perform the update step, e.g., if commercial simulation tools are used with reduced solver access. In this case, $\boldsymbol{u}_{N+1} =\boldsymbol{\varphi } \left ( T_{N+1}, \boldsymbol{z}_{N+1}, \boldsymbol{u}_{N+1} \right )$ is just replaced by $\boldsymbol{u}_{N+1} =\boldsymbol{\varphi } \left ( T_{N+1}, \boldsymbol{z}_{N+1}, \boldsymbol{p}_{N+1} \left ( T_{N+1} \right ) \right )$. As a result, problems with the error estimator may arise (see [40] for more details). In the following, we therefore assume that updated coupling variables $\boldsymbol{u}_{N+1}$ are calculated.

3.2 Implicit co-simulation scheme

The classical implicit co-simulation scheme is based on a predictor/corrector approach, see, e.g., [58, 60]. Again, the general macro-time step from $T_{N}$ to $T_{N+1}$ is considered to explain the approach. The coupling variables $\boldsymbol{u} \left ( t \right )$ are approximated by Lagrange polynomials of degree $k$. At the beginning of the macro-time step, the subsystem variables and the coupling variables are assumed to be known.

Predictor step:

• Firstly, predictor polynomials $\boldsymbol{p}_{N+1}^{\mathit{pre}} \left ( t \right )$ for the coupling variables $\boldsymbol{u} (t )$ in the time interval [$T_{N}$,$T_{N+1}$] are generated by making use of the $k+1$ sampling points $\left ( T_{N}, \boldsymbol{u}_{N} \right ), \left ( T_{N-1}, \boldsymbol{u}_{N-1} \right ), \dots , \left ( T_{N-k}, \boldsymbol{u}_{N-k} \right )$.

• Secondly, Eq. (10) is integrated from $T_{N} \rightarrow T_{N+1}$ with $\boldsymbol{p}_{N+1}^{\mathit{pre}} \left ( t \right )$. This yields the variables $\boldsymbol{z}_{N+1}^{\mathit{pre}}$. It should be mentioned that the predictor step is identical with the explicit co-simulation step of Sect. 3.1 (except for the update step).

Corrector iteration:

• Let $\boldsymbol{u}_{N+1}^{*}$ denote arbitrary (initially unknown) coupling variables at the macro-time point $T_{N+1}$. Using $\boldsymbol{u}_{N+1}^{*}$, interpolation polynomials $\boldsymbol{p}_{N+1}^{*} \left ( t \right )$ for the coupling variables $\boldsymbol{u} (t )$ in the time interval [$T_{N}$,$T_{N+1}$] can formally be generated with the help of the $k+1$ sampling points $\left ( T_{N+1}, \boldsymbol{u}_{N+1}^{*} \right ), \left ( T_{N}, \boldsymbol{u}_{N} \right ),\ \dots , \left ( T_{N-k+1}, \boldsymbol{u}_{N-k+1} \right )$. Note that $\boldsymbol{u}_{N}$,…,$\boldsymbol{u}_{N-k+1}$ term the coupling variables at the previous macro-time points, which are assumed to be known.

• A formal integration of the subsystems with the polynomials $\boldsymbol{p}_{N+1}^{*} \left ( t \right )$ will yield a relationship of the form $\boldsymbol{z}_{N+1}^{*}$($\boldsymbol{u}_{N+1}^{*}$).

• By inserting $\boldsymbol{z}_{N+1}^{*}$($\boldsymbol{u}_{N+1}^{*}$) into the coupling equations $\boldsymbol{g}_{c}$, one formally gets the relationship $\boldsymbol{g}_{c} \left ( T_{N+1}, \boldsymbol{z}_{N+1}^{*} ( \boldsymbol{u}_{N+1}^{*} ), \boldsymbol{u}_{N+1}^{*} \right )$. Considering arbitrary coupling variables $\boldsymbol{u}_{N+1}^{*}$, the coupling equations are not fulfilled, i.e., $\boldsymbol{g}_{c} \left ( T_{N+1}, \boldsymbol{z}_{N+1}^{*} ( \boldsymbol{u}_{N+1}^{*} ), \boldsymbol{u}_{N+1}^{*} \right ) \neq \boldsymbol{0}$.

  To compute corrected coupling variables $\boldsymbol{u}_{N+1}$, which fulfill the coupling equations $\boldsymbol{g}_{c} \left ( T_{N+1}, \boldsymbol{z}_{N+1}, \boldsymbol{u}_{N+1} \right ) = \boldsymbol{0}$, a Newton iteration has to be carried out. Therefore, the relationship $\boldsymbol{g}_{c} \left ( T_{N+1}, \boldsymbol{z}_{N+1}, \boldsymbol{u}_{N+1} \right ) = \boldsymbol{0}$ is linearized by a Taylor series expansion.

• In the first corrector iteration step, the predictor point $\left ( T_{N+1}, \boldsymbol{z}_{N+1}^{\mathit{pre}} ( \boldsymbol{u}_{N+1}^{\mathit{pre}} ), \boldsymbol{u}_{N+1}^{\mathit{pre}} \right )$ is used as expansion point for the Taylor series expansion. Note that the predictor point may also be denoted as zeroth corrector point, i.e., $\left ( T_{N+1}, \boldsymbol{z}_{N+1}^{\mathit{cor},0} ( \boldsymbol{u}_{N+1}^{\mathit{cor},0} ), \boldsymbol{u}_{N+1}^{\mathit{cor},0} \right )$. The Taylor series expansion yields the linearized coupling equations

  $$\begin{aligned} &\boldsymbol{g}_{c}^{\mathit{linear}} \bigl( T_{N+1}, \boldsymbol{z}_{N+1} ( \boldsymbol{u}_{N+1} ), \boldsymbol{u}_{N+1} \bigr) \\ &\quad := \boldsymbol{g}_{c} \bigl( T_{N+1}, \boldsymbol{z}_{N+1}^{\mathit{pre}} \bigl( \boldsymbol{u}_{N+1}^{\mathit{pre}} \bigr), \boldsymbol{u}_{N+1}^{\mathit{pre}} \bigr) + \left . \frac{d \boldsymbol{g}_{c}}{d \boldsymbol{u}_{N+1}^{*}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{pre}}} \cdot \bigl( \boldsymbol{u}_{N+1} - \boldsymbol{u}_{N+1}^{\mathit{pre}} \bigr) = \mathbf{0}\, . \end{aligned}$$

  (11)

  By solving the linear system (11) for $\boldsymbol{u}_{N+1}$, corrected coupling variables $\boldsymbol{u}_{N+1}^{\mathit{cor},1}$ are obtained.

  To compute corrected subsystem variables $\boldsymbol{z}_{N +1}^{\mathit{cor},1}$, interpolation polynomials $\boldsymbol{p}_{N +1}^{\mathit{cor},1} \left ( t \right )$ for the coupling variables $\boldsymbol{u} (t )$ are generated by using the $k+1$ sampling points $\left ( T_{N+1}, \boldsymbol{u}_{N +1}^{\mathit{cor},1} \right ), \left ( T_{N}, \boldsymbol{u}_{N} \right ), \ldots , \left ( T_{N- k +1}, \boldsymbol{u}_{N - k +1} \right )$. Now, the subsystem integration from $T_{N}\rightarrow T_{N+1}$ is repeated with the polynomials $\boldsymbol{p}_{N +1}^{\mathit{cor},1} \left ( t \right )$, which yields the corrected subsystem variables $\boldsymbol{z}_{N +1}^{\mathit{cor},1}$.

• Considering the $\alpha$th corrector step, the ($\alpha -$1)th corrector point $\left ( T_{N+1}, \boldsymbol{z}_{N +1}^{\mathit{cor}, \alpha -1} \left ( \boldsymbol{u}_{N +1}^{\mathit{cor}, \alpha -1} \right ), \boldsymbol{u}_{N +1}^{\mathit{cor}, \alpha -1} \right )$ is used as expansion point for the Taylor series expansion and the above procedure is repeated.

• The procedure is repeated $l$ times, until a convergence criterion is fulfilled. The final variables $\boldsymbol{u}_{N +1}:= \boldsymbol{u}_{N +1}^{\mathit{cor}, l}$ are the corrected variables.

• By setting $\boldsymbol{z}_{N+1}:= \boldsymbol{z}_{N+1}^{\mathit{cor},l}$, the next macro-step from $T_{N+1} \rightarrow T_{N+2}$ is accomplished.

The implicit co-simulation scheme is illustrated in Fig. 3.

Fig. 3

Implicit co-simulation approach (linear approximation polynomials, ${k}={1}$): (a) predictor step; (b) corrector iteration

Some remarks on the different possibilities to calculate/approximate the interface-Jacobian $\frac{d \boldsymbol{g}_{c}}{d \boldsymbol{u}_{N+1}^{*}}$ can be found in Appendix A. In the following sections, basically two methods are used and compared, namely the calculation of the interface-Jacobian by a finite difference approach (Appendix A.1) and the approximate computation of the interface-Jacobian based on a low-order expansion technique (Appendix A.2).

4 Error estimators for the classical explicit and implicit co-simulation schemes

The efficiency and accuracy of a co-simulation may significantly be improved by using a macro-step size controller so that a nonequidistant communication-time grid can be realized. Therefore, error estimators are required, which can be used to estimate the numerical error produced by the co-simulation approach, i.e., the error introduced by the polynomial approximation of the coupling variables. In [40], three different error estimators for the classical explicit co-simulation approach (called ExLocal, ExMilne, ExSLocal) and two error estimators for the classical implicit co-simulation approach (called ImMilne, ImSLocal) have been derived. The basic idea for the construction of an error estimator, which estimates the local error generated in the macro-step $T_{N} \rightarrow T_{N+1}$, is to compare two different solutions at $T_{N+1}$: the state variables $\boldsymbol{q}_{N+1}$, $\boldsymbol{v}_{N+1}$ (or, alternatively, the coupling variables $\boldsymbol{u}_{N+1}$) of the actual co-simulation generated with the classical explicit/implicit approach are compared with reference variables $\hat{\boldsymbol{q}}_{N+1}$, $\hat{\boldsymbol{v}}_{N+1}$ (or alternatively $\boldsymbol{u}_{N+1}^{\mathit{ext}}$, $\boldsymbol{u}_{N+1}^{\mathit{pre}}$). The differences $\boldsymbol{q}_{N+1} - \hat{\boldsymbol{q}}_{N+1}$, $\boldsymbol{v}_{N+1} - \hat{\boldsymbol{v}}_{N+1}$ (or, alternatively, $\boldsymbol{u}_{N+1} - \boldsymbol{u}_{N+1}^{\mathit{ext}}$ for the explicit and $\boldsymbol{u}_{N+1} - \boldsymbol{u}_{N+1}^{\mathit{pre}}$ for the implicit co-simulation) can be used to construct an error estimator. In this section, the main formulas for the five error estimators are shortly recapitulated. For a detailed description, we refer to [40]. It should be pointed out that the error estimators used here are only valid for continuous co-simulation systems. Considering discontinuous systems, systems with switches, etc., a modified error estimation strategy has to be applied.

In this work, the classical explicit and implicit co-simulation schemes are considered, see Sect. 3. Using extrapolation/interpolation polynomials of degree $k$ (i.e., polynomial order $k+1$), the coupling variables are approximated with $\mathcal{O} \left ( H^{k+1} \right )$. Since the coupling variables and therefore the accelerations are approximated with $\mathcal{O} \left ( H^{k+1} \right )$, the velocities $\boldsymbol{v}_{N+1}$ will converge with $\mathcal{O} \left ( H^{k+2} \right )$ and the position variables $\boldsymbol{q}_{N+1}$ with order $\mathcal{O} \left ( H^{k+3} \right )$ for both the explicit and implicit scheme. Hence, the following estimates hold:

$$ \begin{aligned} \boldsymbol{q}_{N+1} &= \boldsymbol{q} ( T_{N+1} ) + \mathcal{O} \bigl( H^{k+3} \bigr), \\ \boldsymbol{v}_{N+1} &= \boldsymbol{v} ( T_{N+1} ) + \mathcal{O} \bigl( H^{k+2} \bigr), \end{aligned} $$

(12)

where $\boldsymbol{q} \left ( T_{N+1} \right )$ and $\boldsymbol{v} \left ( T_{N+1} \right )$ denote the analytical solutions with $\boldsymbol{q} \left ( T_{N} \right ) = \boldsymbol{q}_{N}$ and $\boldsymbol{v} \left ( T_{N} \right ) = \boldsymbol{v}_{N}$. As can be seen, the integration order of the co-simulation may directly be controlled by controlling the polynomial degree of the approximation polynomials (see Sect. 5.2). Note that the error bounds of Eq. (12) are only valid for the case that the errors resulting from the numerical subsystem integrations can be neglected, i.e., strictly speaking for the case that the subsystems are integrated analytically.

4.1 Error estimator 1 for explicit co-simulation (ExLocal)

The first error estimator for the classical explicit co-simulation is based on a local extrapolation technique [65, 71] and is denoted by ExLocal. In order to calculate an error estimator for $\boldsymbol{q}_{N+1}$ and $\boldsymbol{v}_{N+1}$, comparative solutions $\hat{\boldsymbol{q}}_{N+1}$ and $\hat{\boldsymbol{v}}_{N+1}$ are needed. If a local extrapolation technique is applied for deriving an error estimator, two solutions with different convergence orders are compared. For this purpose, two parallel co-simulations are carried out from $T_{N}$ to $T_{N+1}$, whereby the comparative solution is calculated with the same initial conditions ($\hat{\boldsymbol{z}}_{N} = \boldsymbol{z}_{N}$):

• The firstsimulation (actual co-simulation) is accomplished with the extrapolation polynomials $\boldsymbol{p}_{N+1}^{\mathit{ext}} \left ( t \right ) = \boldsymbol{P}_{N+1}^{k} \left ( t; \left ( T_{N}, \boldsymbol{u}_{N} \right ), \dots , \left ( T_{N-k}, \boldsymbol{u}_{N-k} \right ) \right )$ of degree $k$ (approximation order $k+1$). This integration yields the variables $\boldsymbol{q}_{N+1}$ and $\boldsymbol{v}_{N+1}$.

• The second simulation (comparative solution) is carried out with the extrapolation polynomials $\hat{\boldsymbol{p}}_{N+1}^{\mathit{ext}} \left ( t \right ) = \boldsymbol{P}_{N+1}^{k+1} \left ( t; \left ( T_{N}, \boldsymbol{u}_{N} \right ), \dots , \left ( T_{N-k}, \boldsymbol{u}_{N-k} \right ), \left ( T_{N-k-1}, \boldsymbol{u}_{N-k-1} \right ) \right )$ of degree $k+1$. The second integration provides the variables $\hat{\boldsymbol{q}}_{N+1}$ and $\hat{\boldsymbol{v}}_{N+1}$.

The two co-simulations are illustrated in Fig. 4. Within the local extrapolation technique, the local error of the co-simulation in the macro-step from $T_{N} \rightarrow T_{N+1}$ can very easily be estimated by the difference of the two solutions. Considering the first simulation, the local errors of the position variable $q_{i}$ and the velocity variable $v_{i}$ are defined by

$$ \textstyle\begin{array} {l} e_{i,N+1}^{\mathit{pos}} = \bigl\vert q_{i,N+1} - q_{i} ( T_{N+1} ) \bigr\vert , \\ e_{i,N+1}^{\mathit{vel}} = \bigl\vert v_{i,N+1} - v_{i} ( T_{N+1} ) \bigr\vert . \end{array} $$

(13)

Substituting the analytical solutions $q_{i} \left ( T_{N+1} \right )$ and $v_{i} \left ( T_{N+1} \right )$ by $\hat{q}_{i,N+1} = q_{i} \left ( T_{N+1} \right ) + \mathcal{O} \left ( H^{k+4} \right )$ and $\hat{v}_{i,N+1} = v_{i} \left ( T_{N+1} \right ) + \mathcal{O} \left ( H^{k+3} \right )$, one gets

$$ \begin{aligned} e_{i,N+1}^{\mathit{pos}} &= \bigl\vert q_{i,N+1} - \bigl( \hat{q}_{i,N+1} + \mathcal{O} \bigl( H^{k+4} \bigr) \bigr) \bigr\vert \\ &= \vert q_{i,N+1} - \hat{q}_{i,N+1} \vert + \mathcal{O} \bigl( H^{k+4} \bigr), \\ e_{i,N+1}^{\mathit{vel}} &= \bigl\vert v_{i,N+1} - \bigl( \hat{v}_{i,N+1} + \mathcal{O} \bigl( H^{k+3} \bigr) \bigr) \bigr\vert \\ &= \vert v_{i,N+1} - \hat{v}_{i,N+1} \vert + \mathcal{O} \bigl( H^{k+3} \bigr). \end{aligned} $$

(14)

Therefore, it is possible to use the expressions

$$ \begin{aligned} \varepsilon _{i,N+1}^{\mathit{pos}} &= \vert q_{i,N+1} - \hat{q}_{i,N+1} \vert , \\ \varepsilon _{i,N+1}^{\mathit{vel}} &= \vert v_{i,N+1} - \hat{v}_{i,N+1} \vert \end{aligned} $$

(15)

as error estimators for the actual co-simulation. The estimators converge to the local errors $e_{i,N+1}^{\mathit{pos}}$ and $e_{i,N+1}^{\mathit{vel}}$ with order $\mathcal{O} \left ( H^{k+4} \right )$ and $\mathcal{O} \left ( H^{k+3} \right )$, respectively [40].

Fig. 4

Extrapolation polynomials for the coupling variable ${u}_{{i}}$ using the ExLocal error estimator (case ${k}={1}$)

With the error estimators $\varepsilon _{i,N+1}^{\mathit{pos}}$ and $\varepsilon _{i,N+1}^{\mathit{vel}}$ according to Eq. (15), it is possible to monitor the local error of all state variables. To simplify the implementation, it would be possible to only monitor the state variables of the coupling bodies.

4.2 Error estimator 2 for explicit co-simulation (ExMilne)

The second error estimator for the classical explicit co-simulation approach is indicated by ExMilne and based on a Milne device approach [41]. Within this approach, two different solutions with the same convergence order but different leading error terms are compared. Again, two parallel co-simulations from $T_{N}$ to $T_{N+1}$ are executed with the same initial conditions ($\hat{\boldsymbol{z}}_{N} = \boldsymbol{z}_{N}$):

• The first simulation (actual co-simulation) is carried out with the extrapolation polynomials $\boldsymbol{p}_{N+1}^{\mathit{ext}} \left ( t \right ) = \boldsymbol{P}_{N+1}^{k} \left ( t; \left ( T_{N}, \boldsymbol{u}_{N} \right ), \dots , \left ( T_{N-k}, \boldsymbol{u}_{N-k} \right ) \right )$, which yields the variables $\boldsymbol{q}_{N+1}$ and $\boldsymbol{v}_{N+1}$.

• The second simulation (comparative solution) with the interpolation polynomials $\hat{\boldsymbol{p}}_{N+1}^{\mathit{int}} \left ( t \right ) = \boldsymbol{P}_{N+1}^{k} \left ( t; \left ( T_{N+1}, \hat{\boldsymbol{u}}_{N +1} \right ), \left ( T_{N}, \boldsymbol{u}_{N} \right ), \dots , \left ( T_{N-k+1}, \boldsymbol{u}_{N-k+1} \right ) \right )$ provides the variables $\hat{\boldsymbol{q}}_{N+1}$ and $\hat{\boldsymbol{v}}_{N+1}$, where $\hat{\boldsymbol{u}}_{N +1} = \hat{\boldsymbol{p}}_{N+1}^{\mathit{ext}} \left ( T_{N+1} \right )$ represent extrapolated coupling variables generated with the extrapolation polynomials $\hat{\boldsymbol{p}}_{N+1}^{\mathit{ext}} \left ( t \right ) = \boldsymbol{P}_{N+1}^{k+1} ( t; ( T_{N}, \boldsymbol{u}_{N} ), \dots , ( T_{N-k}, \boldsymbol{u}_{N-k} ), ( T_{N-k-1}, \boldsymbol{u}_{N-k-1} ) )$ of degree $k +1$.

The two co-simulations are illustrated in Fig. 5 for the case $k=1$. Note that $\boldsymbol{q}_{N+1}$ and $\hat{\boldsymbol{q}}_{N+1}$ are calculated with polynomials of degree $k$ and locally convergence with $\mathcal{O} \left ( H^{k+3} \right )$. In [40] (Appendix A.2), it is shown that the local errors of $\boldsymbol{q}_{N+1}$ and $\hat{\boldsymbol{q}}_{N+1}$ may be written as

$$ \begin{aligned} \boldsymbol{q}_{N+1} - \boldsymbol{q} ( T_{N+1} ) &= H_{N}^{2} C_{\mathit{pos},N+1}^{k+1} \boldsymbol{A}_{N}^{\mathit{co}} \Delta \boldsymbol{p}_{N+1} + \mathcal{O} \bigl( H^{k+4} \bigr), \\ \hat{\boldsymbol{q}}_{N+1} - \boldsymbol{q} ( T_{N+1} ) &= H_{N}^{2} \bigl( C_{\mathit{pos},N+1}^{k+1} - C_{\mathit{pos},N+1}^{k} \bigr) \boldsymbol{A}_{N}^{\mathit{co}} \Delta \boldsymbol{p}_{N+1} + \mathcal{O} \bigl( H^{k+4} \bigr), \end{aligned} $$

(16)

where $H_{N} = T_{N+1} - T_{N}$ represents the current macro-step size. The error constants $C_{\mathit{pos},N+1}^{k}$ and $C_{\mathit{pos},N+1}^{k+1}$ can be expressed as special integrals of the Lagrange basis polynomials $L^{k} \left ( t \right )$, namely

$$ C_{\mathit{pos},N+1}^{k} = \frac{1}{H_{N}^{2}} \int _{T_{N}}^{T_{N +1}} \int _{T_{N}}^{\tau } L^{k} ( t ) dt d\tau \quad \text{with}\quad L^{k} ( t ) = \prod _{j =0}^{k -1} \frac{t - T_{N - j}}{T_{N +1} - T_{N - j}}. $$

(17)

The matrix $\boldsymbol{A}_{N}^{\mathit{co}}$ represents a special Jacobian matrix, which does not explicitly depend on the macro-step size $H_{N}$. The vector $\Delta \boldsymbol{p}_{N+1}$ is also not explicitly depending on $H_{N}$ and may be calculated by the difference of two polynomials. A direct calculation of the leading error term $H_{N}^{2} C_{\mathit{pos},N+1}^{k+1} \boldsymbol{A}_{N}^{\mathit{co}} \Delta \boldsymbol{p}_{N+1}$ in Eq. (16) is not possible. The leading error term may, however, be determined in a straightforward manner with the help of the two solutions $\boldsymbol{q}_{N+1}$ and $\hat{\boldsymbol{q}}_{N+1}$. Subtracting Eq. (16a) from Eq. (16b) and multiplying by $C_{\mathit{pos},N+1}^{k+1} / C_{\mathit{pos},N+1}^{k}$ gives

$$\begin{aligned} &\boldsymbol{q}_{N+1} - \boldsymbol{q} ( T_{N+1} ) - \bigl( \hat{\boldsymbol{q}}_{N+1} - \boldsymbol{q} ( T_{N+1} ) \bigr) = H_{N}^{2} C_{\mathit{pos},N+1}^{k} \boldsymbol{A}_{N}^{\mathit{co}} \Delta \boldsymbol{p}_{N+1} \\ &\quad \Rightarrow \frac{C_{\mathit{pos},N+1}^{k+1}}{C_{\mathit{pos},N+1}^{k}} ( \boldsymbol{q}_{N+1} - \hat{\boldsymbol{q}}_{N+1} ) = H_{N}^{2} C_{\mathit{pos},N+1}^{k+1} \boldsymbol{A}_{N}^{\mathit{co}} \Delta \boldsymbol{p}_{N+1} + \mathcal{O} \bigl( H^{k+4} \bigr). \end{aligned}$$

(18)

Obviously, the local error $e_{i,N+1}^{\mathit{pos}} = \left \vert q_{i,N+1} - q_{i} \left ( T_{N+1} \right ) \right \vert$ of the actual co-simulation can be estimated by the error estimator

$$ \varepsilon _{i,N+1}^{\mathit{pos}} = \frac{C_{\mathit{pos},N+1}^{k+1}}{C_{\mathit{pos},N+1}^{k}} \vert q_{i,N+1} - \hat{q}_{i,N+1} \vert , $$

(19)

which converges to the local error $e_{i,N+1}^{\mathit{pos}}$ with order $\mathcal{O} \left ( H^{k+4} \right )$.

Fig. 5

Extrapolation polynomials for the coupling variable ${u}_{{i}}$ using the ExMilne error estimator (case ${k}={1}$)

Also, an error estimator $\varepsilon _{i,N+1}^{\mathit{vel}}$ for the velocity variables can be derived, namely

$$ \begin{aligned} &\varepsilon _{i,N+1}^{\mathit{vel}} = \frac{C_{\mathit{vel},N+1}^{k+1}}{C_{\mathit{vel},N+1}^{k}} \vert v_{i,N+1} - \hat{v}_{i,N+1} \vert , \\ &\quad \text{with}\quad C_{\mathit{vel},N+1}^{k} = \frac{1}{H_{N}} \int _{T_{N}}^{T_{N +1}} L^{k} ( t ) dt \quad \text{and}\quad L^{k} ( t ) = \prod _{j =0}^{k -1} \frac{t - T_{N - j}}{T_{N +1} - T_{N - j}}, \end{aligned} $$

(20)

which approximates the local error $e_{i,N+1}^{\mathit{vel}} = \left \vert v_{i,N+1} - v_{i} \left ( T_{N+1} \right ) \right \vert$ of the actual co-simulation with order $\mathcal{O} \left ( H^{k+3} \right )$.

4.3 Error estimator 3 for the explicit co-simulation (ExSLocal)

The third error estimator for the classical explicit co-simulation approach is also constructed with the help of the local extrapolation technique and termed by ExSLocal. With the error estimators of Sects. 4.1 and 4.2, the local errors $e_{i,N+1}^{\mathit{pos}} = \left \vert q_{i,N+1} - q_{i} \left ( T_{N+1} \right ) \right \vert$ and $e_{i,N+1}^{\mathit{vel}} = \left \vert v_{i,N+1} - v_{i} \left ( T_{N+1} \right ) \right \vert$ of the state variables $\boldsymbol{q}$ and $\boldsymbol{v}$ can be estimated. In an alternative approach, the quality of the co-simulation is not directly measured by considering the local error of the state variables, but by regarding the local error of the coupling variables $\boldsymbol{u}$. The coupling variables are generally defined by the implicit coupling conditions $\boldsymbol{u}-\boldsymbol{\varphi } \left ( t, \boldsymbol{q},\boldsymbol{v},\boldsymbol{u} \right ) = \boldsymbol{0}$ and may therefore simply be considered as a nonlinear function of $\boldsymbol{q}$ and $\boldsymbol{v}$. Instead of using $e_{i,N+1}^{\mathit{pos}}$ and $e_{i,N+1}^{\mathit{vel}}$ for measuring the quality of the co-simulation, the local error $\left \vert u_{i,N+1} - u_{i} \left ( T_{N+1} \right ) \right \vert$ of the coupling variables may be considered.

Applying the classical explicit co-simulation scheme, the extrapolated coupling variables $\boldsymbol{p}_{N+1}^{\mathit{ext}} \left ( t \right ) = \boldsymbol{P}_{N+1}^{k} \left ( t; \left ( T_{N}, \boldsymbol{u}_{N} \right ),\ \dots , \left ( T_{N-k}, \boldsymbol{u}_{N-k} \right ) \right )$ are used for integrating the subsystems. After the subsystem integration from $T_{N}$ to $T_{N+1}$ has been accomplished, updated coupling variables $\boldsymbol{u}_{N+1}$ are computed at the new time point $T_{N+1}$. Therefore, the new state variables $\boldsymbol{q}_{N+1}$, $\boldsymbol{v}_{N+1}$ are inserted into the coupling equations and the relationship $\boldsymbol{u}_{N+1} -\boldsymbol{\varphi } \left ( T_{N+1}, \boldsymbol{q}_{N+1}, \boldsymbol{v}_{N+1}, \boldsymbol{u}_{N+1} \right ) = \boldsymbol{0}$ is solved for $\boldsymbol{u}_{N+1}$.

The predicted coupling variables $\boldsymbol{u}_{N+1}^{\mathit{ext}} = \boldsymbol{P}_{N+1}^{k} \left ( T_{N+1}; \left ( T_{N}, \boldsymbol{u}_{N} \right ), \dots , \left ( T_{N-k}, \boldsymbol{u}_{N-k} \right ) \right )$ are usually different from the updated coupling variables $\boldsymbol{u}_{N+1}$. The difference $\boldsymbol{u}_{N+1}^{\mathit{ext}} - \boldsymbol{u}_{N+1}$ may therefore be used to construct an error estimator based on the local extrapolation technique. It has been shown in [40] that the local error $e_{i,N+1}^{u} = \left \vert u_{i,N+1}^{\mathit{ext}} - u_{i} \left ( T_{N+1} \right ) \right \vert$ of the predicted coupling variable $u_{i,N+1}^{\mathit{ext}}$ can be estimated with the help of the updated coupling variable $u_{i,N+1}$ according to

$$ \varepsilon _{i,N+1}^{u} = \bigl\vert u_{i,N+1}^{\mathit{ext}} - u_{i,N+1} \bigr\vert . $$

(21)

The estimator $\varepsilon _{i,N+1}^{u}$ converges with order $\mathcal{O} \left ( H^{k+2} \right )$ to the local error $e_{i,N+1}^{u}$ if consistent coupling variables $u_{i,N+1}$ are used. Hence, this estimator can only be applied, if updated coupling variables are calculated at $T_{N+1}$ by solving $\boldsymbol{u}_{N+1} -\boldsymbol{\varphi } \left ( T_{N+1}, \boldsymbol{q}_{N+1}, \boldsymbol{v}_{N+1}, \boldsymbol{u}_{N+1} \right ) = \boldsymbol{0}$ for $\boldsymbol{u}_{N+1}$. Note that $e_{i,N+1}^{u}$ does not monitor the local error $\left \vert u_{i,N+1} - u_{i} \left ( T_{N+1} \right ) \right \vert$ of the updated coupling variables, but the local error $\left \vert u_{i,N+1}^{\mathit{ext}} - u_{i} \left ( T_{N+1} \right ) \right \vert$ of the predicted coupling variables.

It should be mentioned that for systems without feed-through, consistent coupling variables can be calculated explicitly in a very straightforward manner with the help of the new variables $\boldsymbol{q}_{N+1}$ and $\boldsymbol{v}_{N+1}$ by simply evaluating $\boldsymbol{u}_{N+1} =\boldsymbol{\varphi } \left ( T_{N+1}, \boldsymbol{q}_{N+1}, \boldsymbol{v}_{N+1} \right )$. For systems with feed-though, the update relationship $\boldsymbol{u}_{N+1} =\boldsymbol{\varphi } \left ( T_{N+1}, \boldsymbol{z}_{N+1}, \boldsymbol{u}_{N+1} \right )$ is – for practical reasons – sometimes replaced by the simplified update $\boldsymbol{u}_{N+1} =\boldsymbol{\varphi } \left ( T_{N+1}, \boldsymbol{z}_{N+1}, \boldsymbol{p}_{N+1} \left ( T_{N+1} \right ) \right )$. In this case, $\varepsilon _{i,N+1}^{u}$ will in general not converge with $\mathcal{O} \left ( H^{k+2} \right )$ to the local error $e_{i,N+1}^{u}$. As a consequence, Eq. (21) will not represent a mathematically sound error estimator for the predicted coupling variables.

4.4 Error estimator 4 for the implicit co-simulation (ImMilne)

The implicit co-simulation scheme according to Sect. 3.2 is based on a predictor/corrector approach. With the help of the Milne device technique, the difference between the predicted and corrected state variables can be used to construct an error estimator [40]. The local error of the corrected position variables $q_{i,N+1}$ can be estimated by

$$ \varepsilon _{i,N+1}^{\mathit{pos}} = \biggl( 1- \frac{C_{\mathit{pos},N+1}^{k+1}}{C_{\mathit{pos},N+1}^{k}} \biggr) \bigl\vert q_{i,N+1}^{\mathit{pre}} - q_{i,N+1} \bigr\vert , $$

(22)

where $C_{\mathit{pos},N+1}^{k}$ are the error constants defined in Eq. (17). The estimator $\varepsilon _{i,N+1}^{\mathit{pos}}$ converges to the local error $e_{i,N+1}^{\mathit{pos}} = \left \vert q_{i,N+1} - q_{i} \left ( T_{N+1} \right ) \right \vert$ with order $\mathcal{O} \left ( H^{k+4} \right )$.

A similar approach for the velocity variables yields the error estimator

$$ \varepsilon _{i,N+1}^{\mathit{vel}} = \biggl( 1- \frac{C_{\mathit{vel},N+1}^{k+1}}{C_{\mathit{vel},N+1}^{k}} \biggr) \bigl\vert v_{i,N+1}^{\mathit{pre}} - v_{i,N+1} \bigr\vert , $$

(23)

where $C_{\mathit{vel},N+1}^{k}$ denote the error constants of Eq. (20). The estimator $\varepsilon _{i,N+1}^{\mathit{vel}}$ approximates the local error $e_{i,N+1}^{\mathit{vel}} = \left \vert v_{i,N+1} - v_{i} \left ( T_{N+1} \right ) \right \vert$ of the corrected velocity variables with order $\mathcal{O} \left ( H^{k+3} \right )$.

4.5 Error estimator 5 for the implicit co-simulation (ImSLocal)

This error estimator, which is based on a local extrapolation approach, can be used to monitor the error of the predicted coupling variables $\boldsymbol{u}_{N+1}^{\mathit{pre}}$, i.e., to estimate the local error $e_{i,N+1}^{u} = \left \vert u_{i,N+1}^{\mathit{pre}} - u_{i} \left ( T_{N+1} \right ) \right \vert$. As shown in [40], the difference between the predicted and corrected coupling variables, i.e.,

$$ \varepsilon _{i,N+1}^{u} = \bigl\vert u_{i,N+1}^{\mathit{pre}} - u_{i,N+1} \bigr\vert , $$

(24)

converges with order $\mathcal{O} \left ( H^{k+2} \right )$ to the local error $e_{i,N+1}^{u}$.

5 Macro-step size and order control algorithm

The here proposed algorithm for controlling the macro-step size and the integration order (i.e., the polynomial degree $k$ of the approximation polynomials for the coupling variables) is carried out in three steps. The suggested approach may be interpreted as a straightforward generalization of step size and order control strategies well-established in the field of classical time integration [8, 15, 67, 68]. In the first step, it is checked, whether the macro-step can be accepted or has to be repeated since the estimated error is too large (Sect. 5.1). For that purpose, the error estimators for the local error of Sect. 4 are used. The second step contains the algorithm for the selection of the optimal integration order (Sect. 5.2). In the third step, the optimal step size for the next macro-step is determined (Sect. 5.3).

5.1 Step 1: Local error test

After the macro-step $T_{N} \rightarrow T_{N+1}$ with $T_{N+1} = T_{N} + H_{N}$ has been accomplished, the local error is estimated with the help of one of the entire five methods suggested in Sect. 4. The estimated error $\boldsymbol{\varepsilon }_{N+1}$ – more precisely the weighted root mean square norm of $\boldsymbol{\varepsilon }_{N+1}$ – has to pass the subsequent local error test

$$ \Vert \boldsymbol{\varepsilon }_{N+1} \Vert _{\mathit{WRMS}} = \sqrt[2]{\frac{1}{n^{*}} \sum _{i=1}^{n^{*}} \biggl( \frac{\varepsilon _{i,N+1}}{W_{i,N+1}} \biggr)^{2}} \leq 1. $$

(25)

Note that $n^{*}$ designates the number of variables, which are used for controlling the macro-step size. Basically, three alternatives exist. First, all state variables of all subsystems may be considered in the sum of Eq. (25). Second, only the state variables of the coupling bodies are taken into account in the summation. Third, in connection with the error estimators of Sect. 4.2 and Sect. 4.5, the summation is carried out over the $n_{c}$ coupling variables (i.e., $n^{*} = n_{c}$). The weights $W_{i,N+1}$ depend on the user-defined relative and absolute error tolerances $\mathit{rtol}$ and $\mathit{ato} l_{i}$ and also on the magnitude of the variables, which are used for the error estimation. Hence, essentially two cases have to be distinguished:

• i) The error of the state variables is estimated (ExLocal, ExMilne, ImMilne);

• ii) The error of the coupling variables is estimated (ExSLocal, ImSLocal).

In case i), the error analysis is carried out separately on position level and on velocity level. This is reasonable, since the position and velocity variables exhibit a different convergence behavior, see Sect. 4. Hence, in case i) the local error test

$$ \max \bigl( \bigl\Vert \boldsymbol{\varepsilon }_{N+1}^{\mathit{pos}} \bigr\Vert _{\mathit{WRMS}}, \bigl\Vert \boldsymbol{\varepsilon }_{N+1}^{\mathit{vel}} \bigr\Vert _{\mathit{WRMS}} \bigr) \leq 1 $$

(26)

with the weights $W_{i,N+1}^{\mathit{pos}} =\mathit{ato} l_{i}^{\mathit{pos}} +\mathit{rtol}\cdot \left \vert q_{i,N+1} \right \vert$ and $W_{i,N+1}^{\mathit{vel}} =\mathit{ato} l_{i}^{\mathit{vel}} +\mathit{rtol}\cdot \left \vert v_{i,N+1} \right \vert$ is applied. Principally, all subsystem state variables can be used for the error estimation, i.e., the index $i$ in Eq. (25) runs over all bodies. Alternatively, only the states of the coupling bodies are considered for the error estimation so that the index $i$ only runs over the coupling bodies. It should be mentioned that the value $\mathit{ato} l_{i}$ can be chosen individually for each component, while $\mathit{rtol}$ is identical for all components. It is clear that the proper choice of $\mathit{ato} l_{i}$ and $\mathit{rtol}$ is problem-dependent and strongly affects the accuracy and the efficiency of the co-simulation.

In case ii), the local error test reads

$$ \bigl\Vert \boldsymbol{\varepsilon }_{N+1}^{u} \bigr\Vert _{\mathit{WRMS}} \leq 1, $$

(27)

with the weights $W_{i,N+1}^{u} =\mathit{ato} l_{i}^{u} +\mathit{rtol}\cdot \left \vert u_{i,N+1} \right \vert$. The index $i$ in Eq. (25) runs over all coupling variables.

Now, two possibilities have to be considered:

• a) The local error test is passed, i.e., condition (26) or condition (27) is fulfilled. Then, the next macro-step $T_{N+1} \rightarrow T_{N+2}$ with $T_{N+2} = T_{N+1} + H_{N+1}$ can be carried out.

• b) The local error test is not passed. In this case, a repetition of the current macro-step $T_{N} \rightarrow \tilde{T}_{N+1}$ ($\tilde{T}_{N+1} = T_{N} + \tilde{H}_{N}$) with a reduced step size $\tilde{H}_{N}$ has to be accomplished.

For a concise notation, both possibilities are combined. Therefore, the macro-step carried out next is denoted by $T_{M} \rightarrow T_{M+1}$ ($T_{M+1} = T_{M} + H_{M}$), where

$$ T_{M} \rightarrow T_{M+1}:= \left \{ \textstyle\begin{array} {l} T_{N+1} \rightarrow T_{N+2} \quad \mbox{for} \quad \Vert \boldsymbol{\varepsilon }_{N+1} \Vert _{\mathit{WRMS}} \leq 1, \\ T_{N} \rightarrow \tilde{T}_{N+1} \quad \mbox{for}\quad \Vert \boldsymbol{\varepsilon }_{N+1} \Vert _{\mathit{WRMS}} >1. \end{array}\displaystyle \right . $$

(28)

In short, the index $M$ is set to $M:=N+1$ if the local error test is passed. If the local error test has failed, the index $M$ is set to $M:=N$.

5.2 Step 2: optimal integration order and order control algorithm

The task consists of the selection of the optimal polynomial degree $k$ for the approximation polynomials for the next macro-step $T_{M} \rightarrow T_{M+1}$. Note again that the next macro-step is either a new macro-step (case a)) or a repetition of the current macro-step (case b)).

5.2.1 Order control algorithms for BDF solvers

a) Basic idea:

The order control algorithm applied here for calculating the optimal polynomial degree $k$ for the approximation polynomials is inspired by well-established order control approaches used in connection with BDF solvers. Regarding variable-order BDF solvers, the optimal integration order is determined by considering the leading error term in the remainder of a Taylor series expansion. The remainder of the Taylor series is used for estimating the local truncation error (LTE). The local truncation error of an arbitrary time integration method of order $k$ depends on the ($k+1$)th derivative of the solution vector $\boldsymbol{z}$ and on the solver step size $h$ [15, 67] and reads

$$ \boldsymbol{LTE} ( k ) = c_{k+1} h^{k+1} \boldsymbol{z}^{(k+1)} + \mathcal{O} \bigl( h^{k+2} \bigr) . $$

(29)

Note that $c_{k+1}$ terms the leading error constant, which generally depends on the numerical integration method. Considering concretely the time step from $t_{N}$ to $t_{N+1} = t_{N} +h$ carried out with a BDF integrator of order $k$, the local truncation error reads $\boldsymbol{LTE} \left ( k \right ) = \frac{1}{k +1} h^{k +1} \boldsymbol{z}^{\left ( k +1 \right )} \left ( t_{i +1} \right ) + {\mathcal{O}} \left ( h^{k +2} \right )$. Since $\boldsymbol{z}^{\left ( k +1 \right )} \left ( t_{i +1} \right )$ is unknown at the beginning of the time step, the term $\boldsymbol{z}^{\left ( k +1 \right )} \left ( t_{i +1} \right )$ is replaced by the $(k+ 1)^{\mathrm{st}}$ derivative of a predictor polynomial $\boldsymbol{P}_{k +1}^{\mathit{pre}} \left ( t \right )$, i.e., $\boldsymbol{z}^{\left ( k +1 \right )} \left ( t_{i +1} \right ) \approx \left . \frac{d^{k +1}}{dt^{k +1}} \boldsymbol{P}_{k +1}^{\mathit{pre}} \left ( t \right ) \right \vert _{t_{i +1}}$.

The integration order for the next solver step is determined with the aim to maximize the integration step size. Therefore, the local truncation error norms $\left \Vert \boldsymbol{LTE} \left ( k-1 \right ) \right \Vert \approx \left \Vert c_{k} h^{k} \boldsymbol{z}^{(k)} \right \Vert$, $\left \Vert \boldsymbol{LTE} \left ( k \right ) \right \Vert \approx \left \Vert c_{k+1} h^{k+1} \boldsymbol{z}^{\left ( k+1 \right )} \right \Vert$, and $\left \Vert \boldsymbol{LTE} \left ( k+1 \right ) \right \Vert \approx \left \Vert c_{k+2} h^{k+2} \boldsymbol{z}^{(k+2)} \right \Vert$ are considered. The integration order, which provides the lowest estimated truncation error and consequently allows the largest step size, is used for the next step [50].

If higher order integration methods are used ($k>2$), the order selection algorithm is usually extended by a heuristic approach to detect numerical instabilities. The heuristic approach suggested in [68] is based on the idea that oscillations with high frequencies and growing amplitudes will arise, if the simulation gets unstable. As a consequence, the local truncation error will oscillate rapidly with increasing magnitudes, when solver instabilities occur.

b) Modified approach:

A slightly modified approach for controlling the integration order, which is, for instance, implemented in the IDA solver of the SUNDIALS package [25], has been suggested in [8]. Note that IDA is a variable-order, variable-coefficient BDF solver for the solution of implicit differential-algebraic equation systems. The modified approach also considers the leading error term of the remainder of a Taylor series expansion. However, the leading error term is scaled to be independent of the error constant. Within the control algorithm proposed in [8], the three terms $\left \Vert h^{k-1} \boldsymbol{z}^{(k-1)} \right \Vert$, $\left \Vert h^{k} \boldsymbol{z}^{(k)} \right \Vert$, and $\left \Vert h^{k+1} \boldsymbol{z}^{(k+1)} \right \Vert$ are compared. If these three terms do not form a decreasing sequence, i.e., if the condition $\left \Vert h^{k-1} \boldsymbol{z}^{(k-1)} \right \Vert > \left \Vert h^{k} \boldsymbol{z}^{(k)} \right \Vert > \left \Vert h^{k+1} \boldsymbol{z}^{(k+1)} \right \Vert$ is not fulfilled, the integration order is decreased to $k-1$. If the condition is fulfilled and if also $\left \Vert h^{k+1} \boldsymbol{z}^{(k+1)} \right \Vert > \left \Vert h^{k+2} \boldsymbol{z}^{(k+2)} \right \Vert$ is satisfied, the order may be increased to $k+1$. Numerical studies have shown that applying the modified approach, the integration order is reduced sooner in case of numerical instabilities compared to the approach described in a).

5.2.2 Order control algorithm for co-simulation

The order control algorithm implemented here for controlling the integration order of the co-simulation may be regarded as a straightforward adaption of the order control strategy suggested in [8] for BDF solvers. Within each macro-step, extrapolation polynomials $\boldsymbol{P}_{M+1}^{j} = \boldsymbol{P}_{M+1}^{j} \left ( t; \left ( T_{M}, \boldsymbol{u}_{M} \right ), \dots , \left ( T_{M-j}, \boldsymbol{u}_{M-j} \right ) \right )$ of different degrees $j=1,\dots ,k+1$ are considered. Then, corresponding scaled derivative norms according to $\mathit{SDN} \left ( j \right ):= \left \Vert H_{N}^{j} \boldsymbol{P}_{M+1}^{j,(j)} \right \Vert$ are computed for the different polynomials, where $H_{N}$ is the current macro-step size. Note that the upper index in brackets denotes the differentiation with respect to time $t$, i.e., $\boldsymbol{P}_{M+1}^{j,(j)} = \frac{d^{j} \boldsymbol{P}_{M+1}^{j}}{d t^{j}}$. If the condition

$$ \bigl\Vert H_{N}^{1} \boldsymbol{P}_{M+1}^{1,(1)} \bigr\Vert >\cdots > \bigl\Vert H_{N}^{k-1} \boldsymbol{P}_{M+1}^{k-1, ( k-1 )} \bigr\Vert > \bigl\Vert H_{N}^{k} \boldsymbol{P}_{M+1}^{k, ( k )} \bigr\Vert > \bigl\Vert H_{N}^{k+1} \boldsymbol{P}_{M+1}^{k+1,(k+1)} \bigr\Vert $$

(30)

is fulfilled, the co-simulation is continued with the current polynomial degree $k$. If the condition is not fulfilled, the polynomial degree is reduced to $k-1$. If the condition (30) is fulfilled and if $k+1$ consecutive macro-time steps have been carried out successfully with degree $k$, also the term $\bigl \Vert H_{N}^{k+2} \boldsymbol{P}_{M+1}^{k+2,(k+2)} \bigr \Vert$ is computed. The polynomial degree will be increased to $k+1$, if $\bigl \Vert H_{N}^{k+1} \boldsymbol{P}_{M+1}^{k+1,(k+1)} \bigr \Vert > \bigl \Vert H_{N}^{k+2} \boldsymbol{P}_{M+1}^{k+2,(k+2)} \bigr \Vert$ is fulfilled.

The complete order control algorithm implemented here is summarized in the subsequent scheme and in the flowchart of Fig. 6 and is mainly based on the order controller of the IDA solver [25]:

• Check, if polynomial order has to be decreased:

  • If $k=1$ and $\mathit{SDN} \left ( 1 \right ) \leq \frac{1}{2} \mathit{SDN} \left ( 2 \right )$:

    • ⁎ $k_{\mathit{new}}:= 0$

    Fig. 6

    

    Flowchart of the order control algorithm

  • Else if $k>1$ and $\max \left ( \mathit{SDN} \left ( k \right ),\mathit{SDN}(k-1) \right ) \leq \mathit{SDN}(k+1)$:

    • ⁎ $k_{\mathit{new}}:=k-1$

  • Else:

    • ⁎ $k_{\mathit{new}}:=k$

• Additional condition based on the number of consecutive failed macro-steps $N_{\mathit{fail}}$:

  • If $N_{\mathit{fail}} >5$:

    • ⁎ $k_{\mathit{new}}:=0$

  • Else if $N_{\mathit{fail}} >3$:

    • ⁎ $k_{\mathit{new}}:= \min \left ( k_{\mathit{new}},1 \right )$

  • Else:

    • ⁎ $k_{\mathit{new}}$ is not adjusted

• If the number of consecutive successful macro-steps with constant order $k$ and without reducing the macro-step size fulfills $N_{\mathit{succ}} >k$, then $\mathit{SDN} \left ( k+2 \right )$ is computed and an adjustment of the order is considered:

  • If $k=0$ and $\mathit{SDN} \left ( 2 \right ) < \frac{1}{2} \mathit{SDN} \left ( 1 \right )$:

    • ⁎ $k_{\mathit{new}}:=1$

  • Else if $k>0$ and $\mathit{SDN} \left ( k \right ) \leq \min \left ( \mathit{SDN} \left ( k+1 \right ),\mathit{SDN} \left ( k+2 \right ) \right )$:

    • ⁎ $k_{\mathit{new}}:=k-1$

  • Else if $k>0$ and $\mathit{SDN} \left ( k+2 \right ) <\mathit{SDN} \left ( k+1 \right )$:

    • ⁎ $k_{\mathit{new}}:=k+1$

  • Else:

    • ⁎ $k_{\mathit{new}}$ is not adjusted

5.3 Macro-step size controller

After the polynomial degree $k:= k_{\mathit{new}}$ for the next macro-step has been determined, the algorithm for the macro-step size selection is executed. The macro-step size controller computes a positive, real-valued scaling factor $r^{\rho }$. This factor is used for calculating the new macro-step size $H_{M}$ for the next macro-step $T_{M} \rightarrow T_{M+1}$ (see Eq. (28)) by means of the simple relationship $H_{M} = r^{\rho } \ \cdot H_{N}$. The calculation of the new macro-step size $H_{M}$ is based on the estimated error $\boldsymbol{\varepsilon }_{N+1}$. The idea is to select the new macro-step size $H_{M}$ in such a way that the resulting estimated error exactly fulfills the local error condition (25), i.e., $\left \Vert \boldsymbol{\varepsilon }_{M+1} \right \Vert _{\mathit{WRMS}} =1$.

The determination of $H_{M}$ for the next macro-step $T_{M} \rightarrow T_{M+1}$ on the basis of the estimated error $\boldsymbol{\varepsilon }_{N+1}$ is only possible, if the next macro-step $T_{M} \rightarrow T_{M+1}$ is carried out with the same polynomial degree $k$ as the current macro-step $T_{N} \rightarrow T_{N+1}$. Therefore, two cases have to be distinguished:

• 1) The two consecutive macro-steps $T_{N} \rightarrow T_{N+1}$ and $T_{M} \rightarrow T_{M+1}$ are carried out with the same polynomial degree. In this case, the error estimator $\boldsymbol{\varepsilon }_{N+1}$ according to Sect. 4, which has been used for the local error test in Eq. (25), is also applied for calculating the new macro-step size $H_{M}$.

• 2) After the macro-step $T_{N} \rightarrow T_{N+1}$ has been accomplished, the polynomial degree is changed by the order control algorithm. In this second case, the error estimator $\boldsymbol{\varepsilon }_{N+1}$ cannot be used to calculate the step size for the next macro-step. Hence, the alternative a priori error estimator

$$\begin{aligned} \tilde{\boldsymbol{\varepsilon }}_{M+1}^{u} =& \boldsymbol{P}_{M+1}^{k+1} ( T_{M+1} ) - \boldsymbol{P}_{M+1}^{k} ( T_{M+1} ) \\ =& \frac{1}{ ( k+1 ) !} \prod_{j=1}^{k+1} ( T_{M+1} - T_{M+1-j} ) \boldsymbol{P}_{M+1}^{k+1, ( k+1 )} \end{aligned}$$

(31)

is used for the next macro-step $T_{M} \rightarrow T_{M+1}$. The two vectors $\boldsymbol{P}_{M+1}^{k+1}(t) = \boldsymbol{P}_{M+1}^{k+1} ( t; ( T_{M}, \boldsymbol{u}_{M} ), \dots , ( T_{M-k-1}, \boldsymbol{u}_{M-k-1} ) )$ and $\boldsymbol{P}_{M+1}^{k}(t) = \boldsymbol{P}_{M+1}^{k} ( t; ( T_{M}, \boldsymbol{u}_{M} ), \dots , ( T_{M-k}, \boldsymbol{u}_{M-k} ) )$ collect approximation polynomials of degree $k$ and $k+1$, respectively. Note again that the upper index in brackets denotes the differentiation with respect to the time, i.e., $\boldsymbol{P}_{M+1}^{k+1, \left ( k+1 \right )} = \frac{d^{k+1} \boldsymbol{P}_{M+1}^{k+1}}{d t^{k+1}}$. It should be mentioned that $\tilde{\boldsymbol{\varepsilon }}_{M+1}^{u}$ simply estimates the local error of the predicted coupling variables.

Remark 1

The a priori error estimator $\tilde{\boldsymbol{\varepsilon }}_{M+1}^{u}$ is only used to determine the new macro-step size $H_{M}$. After the macro-step $T_{M} \rightarrow T_{M+1}$ has been accomplished with $H_{M}$, the error is again checked with the a posteriori error estimator $\boldsymbol{\varepsilon }_{M+1}$ according to Sect. 4. Hence, acceptance of a macro-step, see Eq. (25), is always based on the a posteriori error estimator.

Remark 2

The a priori estimator only monitors the error of the coupling variables. Using the error estimators ExLocal, ExMilne, ImMilne, however, the error of the state variables is monitored. As a consequence, the a priori estimator and the a posteriori estimator may be based on different variables.

Considering case 1), the scaling factor $r^{\rho }$ for the new (optimal) macro-step size $H_{M}$ is calculated by one of the following two relations:

$$ \begin{aligned} &(\alpha ) \quad r^{\mathit{pos}} = \bigl( \mathit{SF}\cdot \bigl\Vert \boldsymbol{\varepsilon }_{N+1}^{\mathit{pos}} \bigr\Vert _{\mathit{WRMS}} \bigr)^{\frac{-1}{k+3}}, \qquad r^{\mathit{vel}} = \bigl( \mathit{SF}\cdot \bigl\Vert \boldsymbol{\varepsilon }_{N+1}^{\mathit{vel}} \bigr\Vert _{\mathit{WRMS}} \bigr)^{\frac{-1}{k+2}} \\ & (\beta ) \quad r^{u} = \bigl( \mathit{SF}\cdot \bigl\Vert \boldsymbol{\varepsilon }_{N+1}^{u} \bigr\Vert _{\mathit{WRMS}} \bigr)^{\frac{-1}{k+1}},\qquad \tilde{r}^{u} = \bigl( \mathit{SF}\cdot \bigl\Vert \tilde{\boldsymbol{\varepsilon }}_{M+1}^{u} \bigr\Vert _{\mathit{WRMS}} \bigr)^{\frac{-1}{k+1}}. \end{aligned} $$

(32)

Relation ($\alpha$) is used for the error estimators ExLocal, ExMilne and ImMilne, which are based on state variables; ($\beta$) is applied in connection with the error estimators ExSLocal and ImSLocal, which are based on coupling variables.

Regarding case 2), the scaling factor $r^{\rho }$ for the new macro-step size $H_{M}$ is computed by

$$ \tilde{r}^{u} = \bigl( \mathit{SF}\cdot \bigl\Vert \tilde{\boldsymbol{\varepsilon }}_{M+1}^{u} \bigr\Vert _{\mathit{WRMS}} \bigr)^{\frac{-1}{k+1}}. $$

(33)

The exponents in Eqs. (32) and (33) refer to the convergence order of the co-simulation method, which is $k+3$ on position level and $k+2$ on velocity level for the here considered explicit and implicit co-simulation approaches. The coupling variables converge with order $k+1$. A detailed derivation of Eqs. (32) and (33) can be found in [40]; $\mathit{SF}$ is a user-defined safety factor, e.g., $\mathit{SF}\in [2, 6]$. The safety factor has to be chosen carefully. If the safety factor $\mathit{SF}$ is chosen too small, the number of macro-step repetitions may increase significantly due to the increased number of failed local error tests. Choosing $\mathit{SF}$ too large may entail too small macro-step sizes. If both the error of the position variables and the error of the velocity variables are estimated (ExLocal, ExMilne, ImMilne), the scaling factor is here chosen conservatively by means of $r^{\rho } = \min \left ( r^{\mathit{pos}}, r^{\mathit{vel}} \right )$.

Summarizing, the scaling factor $r^{\rho }$ is determined according to

$$ r^{\rho } = \left \{ \textstyle\begin{array}{l@{\quad }l} \min ( r^{\mathit{pos}}, r^{\mathit{vel}} ) & \mathrm{error}\ \mathrm{estimator}\ \mbox{for} \ \mathrm{state}\ \mathrm{variables}\ ( \mathit{ExLocal}, \mathit{ExMilne}, \mathit{ImMilne} ),\\ r^{u} & \mathrm{error}\ \mathrm{estimator}\ \mbox{for} \ \mathrm{coupling}\ \mathrm{variables}\ ( \mathit{ExSLocal}, \mathit{ImSLocal} ),\\ \tilde{r}^{u} & \mathrm{change}\ \mathrm{of}\ \mathrm{the}\ \mathrm{order}\ \mathrm{of}\ \mathrm{the}\ \mathrm{approximation}\ \mathrm{polynomials}. \end{array}\displaystyle \right . $$

(34)

Finally, the macro-step size control algorithm is explained. Depending on the number $N_{\mathit{fail}}$ of consecutively failed macro-steps within the current step $T_{N} \rightarrow T_{N+1}$, the following limitations for the scaling factor $r^{\rho }$ are used (see also the flowchart in Fig. 7):

• $N_{\mathit{fail}} =0$:

  • (a) If $r^{\rho } \geq r_{\max }^{\rho }$:

    perform next macro-step with $H_{M}:= r_{\max }^{\rho } \cdot \ H_{N}$ (e.g., $r_{\max }^{\rho } =2.0$) (restriction for maximum step-size increase).

  • (b) If $r^{\rho } <1$:

    perform next macro-step with $H_{M}:= \min \left \{ 0.9, \max ( r_{\min }^{\rho }, \ r^{\rho } ) \right \} \cdot \ H_{N}$ (e.g., $r_{\min }^{\rho } =0.5$).

  • (c) If $1\leq r^{\rho } < r_{\max }^{\rho }$:

    perform next macro-step with $H_{M}:= H_{N}$.

• $N_{\mathit{fail}} =1$:

  repeat current macro-step with reduced step size $H_{M}:= \min \left \{ 0.9, \max (0.25, \ 0.9 \cdot r^{\rho } ) \right \} \cdot \ H_{N}$.

• $N_{\mathit{fail}} >1$ or corrector failed to converge (implicit co-simulation):

  repeat current macro-step with reduced step size $H_{M}:= 0.25 \cdot \ H_{N}$.

• If $H_{M} \leq H_{M,\min } = 10^{-12}$:

  simulation is aborted and an error message is printed.

Fig. 7

Flowchart of the macro-step size controller

It should be noted that the error tolerances $\mathit{atol}_{i}$ and $r \mathit{tol}$ for the co-simulation as well as the safety factor $\mathit{SF}$ have to be specified by the user. Generally, they are problem-dependent.

The macro-step size control algorithm described above may be interpreted as an I-controller. Alternatively, a PI-controller may be used by incorporating the previous errors $\varepsilon _{i,N}^{\mathit{pos}}$ and $\varepsilon _{i,N}^{\mathit{vel}}$ [24].

6 Numerical examples

The co-simulation models considered here consist of the subsystems and the co-simulation interface. The communication between the co-simulation interface and the subsystems is managed over the Message Passing Interface v3.1 (Intel MPI Library). Each subsystem is executed by an individual MPI-rank. If multiple integrations of the same subsystem within a macro-time step are required, e.g., to numerically compute the interface Jacobian by a finite difference approach or in connection with the calculation of the error estimator, the additional subsystem integrations are parallelized via OpenMP. The parallel threads are synchronized at the macro-time points.

A flowchart of the parallel implementation of the explicit co-simulation method with the macro-step size and order control algorithm is shown in Fig. 8. A corresponding flowchart of the implicit co-simulation approach is depicted in Fig. 9.

Fig. 8

Flowchart of the explicit co-simulation approach with the macro-step size controller ExMilne

Fig. 9

Flowchart of the implicit co-simulation approach with the macro-step size controller ImMilne (interface Jacobian computed by a finite difference approach requiring additional subsystem integrations with perturbed approximation polynomials)

It should be mentioned that the co-simulations have been executed fully parallelized on a high-performance supercomputer [37] with Intel Xeon Platinum 9242 processors. Each subsystem integration has been accomplished on an individual core; the different cores are connected over an InfiniBand interconnect. Note that the computation times shown in the subsequent figures reflect the wall-clock time (including communication latency).

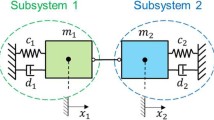
6.1 Example 1: Nonlinear two-mass oscillator

As a first example, we consider the nonlinear two-mass oscillator shown in Fig. 10 (masses $m_{1}$, $m_{2}$; spring constants $c_{1}$, $c_{2}$; damping coefficients $d_{1}$, $d_{2}$). The two masses are coupled by the nonlinear force $f^{\mathrm{c}} = c_{c} \cdot \left ( x_{2} - x_{1} \right ) + d_{c} \cdot \left ( v_{2} - v_{1} \right ) + C_{c} \cdot \left ( x_{2} - x_{1} \right )^{3} + D_{c} \cdot \left ( v_{2} - v_{1} \right )^{3}$. Furthermore, a penalty-based contact force $F_{C} =- 10^{-2} \ \mathrm{N} \cdot e^{( 10^{7} m^{-1} \cdot x_{1} )}$ is assumed to act at $m_{1}$.

Fig. 10

Two coupled single-mass oscillators

Applying a force/force-decomposition approach, the coupled co-simulation system is defined by the following semi-explicit index-1 DAE system

Subsystem 1:

$$ \begin{aligned} &\dot{x}_{1} = v_{1},\\ &\dot{v}_{1} =- \frac{c_{1}}{m_{1}} x_{1} - \frac{d_{1}}{m_{1}} v_{1} + \frac{F_{C}}{m_{1}} + \frac{f^{\mathrm{c}}}{m_{1}} \end{aligned} \quad (a) $$

Subsystem 2:

$$ \begin{aligned} \dot{x}_{2} &= v_{2},\\ \dot{v}_{2} &=- \frac{c_{2}}{m_{2}} x_{2} - \frac{d_{2}}{m_{2}} v_{2} - \frac{f^{\mathrm{c}}}{m_{2}} \end{aligned}\quad (b) $$

(35)

Coupling condition:

$$\begin{aligned} g_{c} :=& f^{\mathrm{c}} - c_{c} \cdot ( x_{2} - x_{1} ) - d_{c} \cdot ( v_{2} - v_{1} ) \\ &{} - C_{c} \cdot ( x_{2} - x_{1} )^{3} - D_{c} \cdot ( v_{2} - v_{1} )^{3} =0\, . \quad (c) \end{aligned}$$

The simulations have been carried out with the subsequent parameters: $m_{1} =50\ \mathrm{kg}$, $m_{2} =1\ \mathrm{kg}$, $c_{1} =1.0E5\ \frac{\mathrm{N}}{\mathrm{m}}$, $c_{2} =1.0E3\ \frac{\mathrm{N}}{\mathrm{m}}$, $c_{c} =1.0E5\ \frac{\mathrm{N}}{\mathrm{m}}$, $d_{1} = d_{2} = d_{c} =0$, $C_{c} =1.0E5\ \frac{\mathrm{N}}{\mathrm{m}^{3}}$, and $D_{c} =1.0E-2\ \frac{\mathrm{Ns}^{3}}{\mathrm{m}^{3}}$. The initial conditions are: $x_{1,0} =-2.0\ \mathrm{m}$, $x_{2,0} =0\ \mathrm{m}$, $v_{1,0} =100\ \frac{\mathrm{m}}{\mathrm{s}}$, and $v_{2,0} =-200\ \frac{\mathrm{m}}{\mathrm{s}}$. Subsystem integration has been accomplished with a BDF integrator [25] (variable step-size, relative and absolute error tolerances $\mathit{ato} l_{x}^{\mathit{BDF}} = 10^{-9}$, $\mathit{ato} l_{v}^{\mathit{BDF}} = 10^{-6}$, $\mathit{rto} l^{\mathit{BDF}} = 10^{-6}$). The following parameters have been used for the macro-step size controller: $\mathit{SF} =6.0$, $\mathit{atol}_{x} = 10^{-8}$, $\mathit{ato} l_{v} = 10^{-5}$, $\mathit{rtol} = 10^{-5}$, $\mathit{atol}_{f_{c}} = 10^{-1}$, $\mathit{rto} l_{f_{c}} = 10^{-3}$, $r_{\min }^{\rho } =0.5$, and $r_{\max }^{\rho } =2.0$.

Figure 11 depicts the displacement $x_{1} (t)$ and the corresponding velocity $v_{1} (t)$ for the different error estimators of Sect. 4 in combination with the order control algorithm of Sect. 5. The reference solution has been generated with a monolithic model, which has been integrated with very small error tolerances. The macro-step sizes for the different error estimators are shown in Fig. 12; the degree $k$ of the approximation polynomials is depicted in Fig. 13. It can clearly be seen that the macro-step size and also the polynomial degree are reduced at the time points where the contacts occur. The macro-step size is reduced very strongly with the simplified error estimators (ExSLocal and ImSLocal), since these two error estimators are based on the coupling force, which is large at the time points where the contacts occur. The total number of macro-steps and the resulting global error are illustrated in Fig. 14. Note that the scalar error norm used in Fig. 14(a) is based on the normalized root mean square error $e$ according to

$$ \begin{aligned} e_{i} &= \sqrt{\frac{\sum_{j=1}^{N} ( z_{i,j}^{\mathit{ref}} - z_{i,j} )^{2}}{\sum_{j=1}^{N} ( z_{i,j}^{\mathit{ref}} - \overline{z}_{i}^{\mathit{ref}} )^{2}}} \quad \mbox{with} \quad \overline{z}_{i}^{\mathit{ref}} = \frac{1}{N} \sum_{j=1}^{N} z_{i,j}^{\mathit{ref}} \\ \Rightarrow \quad e &= \Vert \boldsymbol{e} \Vert _{2} \quad \mbox{with} \quad \boldsymbol{e} = ( e_{1},\dots , e_{i},\dots , e_{N_{z}} )^{T}, \end{aligned} $$

(36)

where $\boldsymbol{z}^{\mathit{ref}} \in \mathbb{R}^{N\times N_{z}}$ denotes the reference solution; $N_{z}$ terms the number of state variables, and $N$ is the number of output points.

Fig. 11

Nonlinear two-mass oscillator: displacement ${x}_{{1}}$ and velocity ${v}_{{1}}$ of mass ${m}_{{1}}$

Fig. 12

Nonlinear two-mass oscillator: macro-step size ${H}$ for the different error estimators

Fig. 13

Nonlinear two-mass oscillator: polynomial degree ${k}$ of the approximation polynomials for the different error estimators

Fig. 14

Nonlinear two-mass oscillator: global errors and number of macro-steps for the error and order controlled co-simulations

6.2 Example 2: Comparative study between explicit and implicit co-simulation approaches

A chain of $n_{K}$ masses is considered, see Fig. 15. The masses, described by the displacement coordinates $x_{i}$ and the velocities $v_{i} = \dot{x}_{i}$, are connected by nonlinear spring/damper elements. The spring/damper element depicted in Fig. 16, which connects the two masses $m_{i -1}$ and $m_{i}$, is defined by the constitutive equation

$$ F_{\mathit{SD},i} = c_{i} ( x_{i} - x_{i -1} ) + d_{i} ( v_{i} - v_{i -1} ) + C_{i} ( x_{i} - x_{i -1} )^{3} + D_{i} ( v_{i} - v_{i -1} )^{3}, $$

(37)

where $c_{i}$, $d_{i}$, $C_{i}$, $D_{i}$ characterize the linear and nonlinear stiffness and damping parameters. The chain model is used here because it is simple to scale with respect to the number of degrees of freedom. Also, the number of subsystems can be changed very easily. Therefore, the model is well suited to carry out reliable numerical studies in order to compare efficiency and accuracy of different co-simulation methods.

Fig. 15

(a) Nonlinear oscillator chain; (b) decomposition into subsystems using force/force-decomposition

Fig. 16

Coupling force ${\lambda }_{{s}}$ between the last body of subsystem ${s}$ and the first body of subsystem ${s} +{1}$

The model is separated into $r$ subsystems via force/force-decompositions. The $n_{c} = r -1$ coupling conditions are defined by the constitutive equations of the coupling spring/damper elements. Regarding the two adjacent subsystems $s$ and $s +1$, the coupling condition $g_{s}$ is given by

$$\begin{aligned} g_{s} :=& \lambda _{s} - c_{c} \bigl( {}^{s +1} x_{1} - {}^{s} x_{n_{K}, s} \bigr) - d_{c} \bigl( {}^{s +1} v_{1} - {}^{s} v_{n_{K}, s} \bigr) - C_{c} \bigl( {}^{s +1} x_{1} - {}^{s} x_{n_{K}, s} \bigr)^{3} \\ &{} - D_{c} \bigl( {}^{s +1} v_{1} - {}^{s} v_{n_{K}, s} \bigr)^{3} =0 \quad ( s =1, \dots , n_{c} ). \end{aligned}$$

(38)

At special time points $t_{\alpha }$ ($t_{\alpha } =0, 0.05~\mathrm{s}, 0.1~\mathrm{s}, \dots$), impulse-shaped external forces $F_{\mathit{Imp},j} = \frac{1}{2} \Delta F_{j} \left [ \tanh \left ( \frac{t- t_{\alpha }}{\delta } \right ) - \tanh \left ( \frac{t- \left ( t_{\alpha } + \Delta t \right )}{\delta } \right ) \right ]$ with $\delta =1.0E-5\ \mathrm{s}$ and $\Delta t=2.5E-3\ \mathrm{s}$ are applied at 30% of the masses (randomly selected). The force amplitude $\Delta F_{j}$ is chosen randomly in the interval $\pm [1.0E6,\ 5.0E6]\ \mathrm{N}$. Moreover, at 10% of the masses (randomly chosen), contact forces are applied by means of the penalty approach $F_{\mathit{Con},i} =A\ e^{B x_{i}}$ with $A=-1.0E-2\ \mathrm{N}$ and $B=5.0E5\ \mathrm{m}^{-1}$.

A chain with 10,000 masses is considered here, which is decomposed into 191 subsystems. The simulations have been carried out with the subsequent parameters: $m_{i} =1.0E-1\ \mathrm{kg}$ (varied in case study 3), $c_{i} =1.0E7\ \frac{\mathrm{N}}{\mathrm{m}}$ (varied in case study 2), $d_{i} =1.0E4\ \mathrm{Ns} / \mathrm{m}$ (varied in case study 1), $C_{i} =1.0E14\ \frac{\mathrm{N}}{\mathrm{m}^{3}}$, $D_{i} =1.0E2\ \frac{\mathrm{Ns}^{3}}{\mathrm{m}^{3}}$, simulation time $t_{\mathit{sim}} =0.5\ \mathrm{s}$. Random initial conditions have been used ($x_{0,i} = \left [ -1.0E-3,\ 1.0E-3 \right ] \ \mathrm{m}$ and $v_{0,i} = \left [ -1.0E1,1.0E1 \right ]\ \frac{\mathrm{m}}{\mathrm{s}}$). The subsystem integrations have been accomplished with a variable step-size BDF integrator [25] with the solver settings $\mathit{rto} l^{\mathit{BDF}} =1.0E-6$, $\mathit{ato} l_{x}^{\mathit{BDF}} =1.0E-9$, and $\mathit{ato} l_{v}^{\mathit{BDF}} =1.0E-6$. The co-simulations have been carried out with the macro-step size and order control algorithm described in Sect. 5. Simulation results are presented for the two error estimators ExSLocal and ImSLocal, see Sect. 4, with the subsequent macro-step size controller parameters: $\mathit{SF} =6.0$, $\mathit{atol}_{\lambda _{c}} = 10^{-1}$, $\mathit{rto} l_{\lambda _{c}} = 10^{-3}$, $r_{\min }^{\rho } =0.5$, and $r_{\max }^{\rho } =2.0$.

6.2.1 Case study 1

The main intention of Example 2 is to compare the numerical performance of the explicit with the implicit co-simulation approach. Giving general statements is, of course, not possible since the performance of a co-simulation approach strongly depends on the system and the model parameters. For the considered model, our simulations have, however, shown that the damping coefficients are crucial and important parameters for comparing the efficiency of explicit and implicit methods. Within a first numerical study, the damping parameter $d_{i}$ of the spring/damper elements is therefore varied in the range $\left [ 1.0E3,\ 1.0E6 \right ] \ \mathrm{Ns} / \mathrm{m}$, see Figs. 17–21.

Fig. 17

Explicit co-simulation (ExSLocal) of the nonlinear oscillator chain with ${d}_{{i}} =1.0 E 4\ \mathrm{Ns} / \mathrm{m}$ and ${c}_{{i}} =1.0 E 7~\mathrm{N}/\mathrm{m}$: displacement and velocity of mass ${m}_{{6891}}$

Figure 17 shows displacement and velocity of mass 6891 for $d_{i} =1.0E4\ \mathrm{Ns} / \mathrm{m}$ simulated with the explicit co-simulation approach (variable co-simulation order; variable macro-step size with error estimator ExSLocal). Although the system is rather stiff and although steep gradients occur due to the impulse-shaped excitation, the co-simulation is stable and the results are accurate and close to the reference solution.

Figure 18 collects simulation results accomplished with the implicit co-simulation method (variable co-simulation order; variable macro-step size with error estimator ImSLocal). The same model parameters have been used as for the explicit co-simulations depicted in Fig. 17; only the damping parameter has been increased to $d_{i} =5.0E5\ \mathrm{Ns} / \mathrm{m}$. Again, a good agreement between the co-simulation and the reference solution can be observed.

Fig. 18

Implicit co-simulation (ImSLocal) of the nonlinear oscillator chain with ${d}_{{i}} =5.0 E 5~{\mathrm{Ns}} / {\mathrm{m}}$ and ${c}_{{i}} ={1.0 E 7}\ \mathrm{N}/\mathrm{m}$: displacement and velocity of mass ${m}_{{6891}}$

Figure 19 shows a direct comparison between the explicit (ExSLocal) and the implicit (ImSLocal) co-simulation approach for the case $d_{i} =1.0E4\ \mathrm{Ns} / \mathrm{m}$. The plots illustrate the macro-step size as well as the polynomial degree of the approximation polynomials over the simulation time $t$. As can be seen, the (average) macro-step size is (slightly) smaller for the explicit approach. The order controller works well for both methods; the variation of the integration order is little larger for the explicit approach.

Fig. 19

Explicit (ExSLocal) and implicit (ImSLocal) co-simulation of the nonlinear oscillator chain with ${d}_{{i}} ={1.0 E 4}\ {\mathrm{Ns}} / {\mathrm{m}}$ and ${c}_{{i}} ={1.0 E 7}\ \mathrm{N}/\mathrm{m}$: macro-step size ${H}$ and polynomial degree ${k}$ of the approximation polynomials

The same study for the case $d_{i} =5.0E5\ \mathrm{Ns} / \mathrm{m}$ is collected in Fig. 20. Here, the (average) macro-step size is markedly smaller for the explicit approach indicating that the implicit co-simulation approach is more efficient for the higher-damped case with $d_{i} =5.0E5\ \mathrm{Ns} / \mathrm{m}$. Again, the order control algorithm works well for both co-simulation methods.

Fig. 20

Explicit (ExSLocal) and implicit (ImSLocal) co-simulation of the nonlinear oscillator chain with ${d}_{{i}} ={5.0 E 5}\ {\mathrm{Ns}} / {\mathrm{m}}$ and ${c}_{{i}} ={1.0 E 7}\ \mathrm{N}/\mathrm{m}$: macro-step size ${H}$ and polynomial degree ${k}$ of the approximation polynomials

Figure 21 exhibits the computation time, the number of macro-steps and the global error of the explicit and implicit co-simulation approach as a function of the damping coefficient $d_{i}$. It can clearly be observed that the implicit co-simulation approach becomes more efficient for increasing values of $d_{i}$. The explicit co-simulation is faster for $d_{i} \leq 1.0E5\ \mathrm{Ns} / \mathrm{m}$ (Fig. 21(a)), although smaller macro-step sizes are needed in connection with the explicit approach (Fig. 21(b)). Note that the implicit approach requires a computationally expensive corrector iteration. As a consequence, the implicit approach will only be more efficient than the explicit approach, if the macro-step sizes for implicit method are significantly larger than for the explicit method. The resulting global error of the state variables of the coupling bodies is depicted in Fig. 21(c). As can be detected, the error of the implicit approach is usually little smaller, although both methods have been simulated with the same error tolerances for the macro-step size controller.

Fig. 21

Comparison between the explicit and the implicit co-simulation approach: computation time, number of macro steps, and global error as functions of the linear damping parameter ${d}_{{i}}$

6.2.2 Case study 2

In a second numerical study, the performance of the explicit approach is compared with the performance of the implicit co-simulation method for different values of the stiffness coefficient $c_{i}$, see Fig. 22. The simulations have been carried out with the same parameters that have been used in the first case study. The damping coefficient has been set to $d_{i} =1.0E4\ \mathrm{Ns} / \mathrm{m}$. As can be seen, the explicit approach is always faster than the implicit method.

Fig. 22

Comparison of the explicit and the implicit co-simulation approach: computation time, number of macro steps, and global error as functions of the linear stiffness parameter ${c}_{{i}}$

6.2.3 Case study 3

Within the third study, the explicit and implicit co-simulation methods are compared for different values of $m_{i}$, see Fig. 23. The same parameters have been used as in the first case study. The damping and stiffness coefficients have been set to $d_{i} =1.0E4\ \mathrm{Ns} / \mathrm{m}$ and $c_{i} =1.0E7\ \mathrm{N} / \mathrm{m}$. The plots clearly indicate that the implicit approach is more efficient than the explicit method for small values of $m_{i}$ ($m_{i} \leq 8.0E-3\ \mathrm{kg}$).

Fig. 23

Comparison of the explicit and the implicit co-simulation approach: computation time, number of macro steps and global error as a function of the mass ${m}_{{i}}$

6.3 Example 3: comparative study between co-simulations with constant and variable integration order

Next, the performance of co-simulations including the order controller ($k=\mathit{var}$.) is compared with the performance of co-simulations using a fixed polynomial degree for the approximation polynomials ($k=\mathit{const}$.). The chain model of Example 2 is considered again and basically the same parameters are used. In Sect. 6.3, all explicit co-simulations are carried out with $d_{i} =1.0E4\ \frac{\mathrm{Ns}}{\mathrm{m}}$ and all implicit co-simulations with $d_{i} =5.0E5\ \frac{\mathrm{Ns}}{\mathrm{m}}$. The following macro-step size controller parameters have been used: $\mathit{SF} =6$, $\mathit{atol}_{{x}} = 10^{-3} \cdot \mathit{rtol}$, $\mathit{atol}_{{v}} =\mathit{rtol}$, $\mathit{atol}_{\lambda _{c}} = 10^{2} \cdot \mathit{rtol}$, $r_{\min }^{\rho } =0.5$, $r_{\max }^{\rho } =2.0$. In the subsequent simulations, $\mathit{rtol}$ is varied in order to show the influence of $\mathit{rtol}$ on the global error and on the number of macro-steps.

Simulation results with the five different error estimators of Sect. 4 are depicted in Figs. 24–28. The plots show the total number of macro-steps and the resulting global error of the state variables of the coupling bodies. The following observations can be made:

• The order controller reduces the number of macro-steps for all considered co-simulation approaches and for all chosen error tolerances. An exception is only observed for the ImMilne error estimator, where simulations with a fixed polynomial degree of $k=1$ and $k=2$ show a slightly better performance for certain error tolerances $\mathit{rtol}$.

• The simplified error estimators (ExSLocal and ImSLocal) do not perform very well in combination with constant approximation polynomials ($k=0$), because of the rather large discontinuities in the coupling variables at the macro-time points. Note that the corresponding curves are missing in the plots of Figs. 26 and 28.

• Considering the plots (a) of Figs. 24, 25, 26, it can be seen that for $k\geq 2$ the number of macro-steps is almost constant and not influenced by the error tolerance. Usually, one would expect that the number of macro-steps will decrease with increasing $\mathit{rtol}$. This unexpected behavior might be traced back to a stability problem [60]. Most likely, the co-simulations for $k\geq 2$ will get unstable for larger macro-step sizes. Therefore, the macro-step size controller reduces the macro-step size, until the system reaches a numerically stable region.

  Fig. 24

  

  ExLocal approach: number of macro-steps and global error of the state variables of the coupling bodies for different error tolerances and different approximation orders

  Fig. 25

  

  ExMilne approach: number of macro-steps and global error of the state variables of the coupling bodies for different error tolerances and different approximation orders

  Fig. 26

  

  ExSLocal approach: number of macro-steps and global error of the state variables of the coupling bodies for different error tolerances and different approximation orders

• Regarding the plots a) of Fig. 27 and Fig. 28, it can be observed that for $k\geq 3$ the number of macro-steps will not be reduced if the error tolerance $\mathit{rtol}$ is increased. This unexpected behavior might also be explained by the fact that the stability limit of the co-simulation is reached for $k\geq 3$.

  Fig. 27

  

  ImMilne approach: number of macro-steps and global error of the state variables of the coupling bodies for different error tolerances and different approximation orders

  Fig. 28

  

  ImSLocal approach: number of macro-steps and global error of the state variables of the coupling bodies for different error tolerances and different approximation orders

The resulting computation time (wall-clock time) of the considered co-simulation approaches are depicted in Figs. 29–33. The overall computation time of the fully parallelized co-simulation basically consists of four parts:

• i) Subsystem integration time (the slowest subsystem integration process is relevant);

• ii) Additional subsystem computations resulting from the co-simulation (save/reload of subsystem workspace in connection with macro-step repetitions);

• iii) Special computations of the co-simulation interface, specific for the different co-simulation methods (e.g., macro-step size controller, computation of corrected coupling variables);

• iv) Synchronization and data exchange between the subsystems and the co-simulation interface (MPI data traffic).

The four parts of the overall computation time are represented with different colors in Figs. 29–33.

Fig. 29

ExLocal approach: computation time for different error tolerances and different approximation orders

Fig. 30

ExMilne approach: computation time for different error tolerances and different approximation orders

Fig. 31

ExSLocal approach: computation time for different error tolerances and different approximation orders

Fig. 32

ImMilne approach in connection with finite differences: computation time for different error tolerances and different approximation orders

Fig. 33

ImSLocal approach in connection with finite differences: computation time for different error tolerances and different approximation orders

6.4 Example 4: comparative study between finite difference gradients and low-order sensitivities

Next, the system size is increased by adding further masses to the chain. The model is decomposed into $r=2399$ subsystems and simulated by the fully controlled, i.e., order and macro-step size controlled, ExSLocal and ImSLocal co-simulation approaches. The subsequent macro-step size controller parameters have been used: $\mathit{SF} =6$, $\mathit{atol}_{\lambda _{c}} = 10^{-1}$, $\mathit{rto} l_{\lambda _{c}} = 10^{-3}$, $r_{\min }^{\rho } =0.5$, $r_{\max }^{\rho } =2$. Due to the increased number of subsystems, the number of coupling variables will also increase.

Basically, the interface-Jacobian required for implicit co-simulation approaches, see Eq. (11), can always be calculated numerically using a finite difference approach (FD), see Appendix A.1. The additional subsystem integrations with perturbed coupling variables, which are required for the finite difference approach, can be executed in parallel with the main subsystem integration (predictor/corrector integration). Due to the parallel integration, the overall computation time of the co-simulation will therefore not be (markedly) increased. However, additional cores are required for carrying out the subsystem integrations with the perturbed approximation polynomials. The larger the number of coupling variables becomes, the larger the number of additional cores will be. Hence, for models with a large number of coupling variables, the FD approach for calculation the interface-Jacobian will get problematic or even impossible. In this case, the gradients can very easily be approximated by making use of a low-order approximation approach (low-order sensitivities, LOS), see [29]. For the considered model, for instance, $3\cdot r-2+1=7196$ cores are required in total if an FD approach is used to calculate the interface-Jacobian. With the low-order approximation approach, only $r+1=2400$ cores are needed, which equals the number of required cores for a fully parallelized explicit co-simulation approach (ExSLocal). A description of the FD approach and a short summary of the LOS approach are collected in Appendix A.

In Example 4, the interface-Jacobian required for the implicit co-simulation approach (ImSLocal) is therefore calculated with the LOS approach. It should be mentioned that the interface-Jacobian for the examples in Sects. 6.1–6.3 have been calculated with the FD approach. For the example in Sect. 6.3, simulation results generated with the LOS technique are arranged in Appendix B so that implementations with FD and LOS may directly be compared.

Co-simulation results using the chain model of Sect. 6.2 with $n_{K} = \left \{ 5E4,\! 1E5,\! 5E5,\! 1E6 \right \}$ masses are depicted in Fig. 34. The simulations have shown that the average macro-step size is slightly increased compared to the case $n_{K} =1E4$ of Sect. 6.2. As a consequence, the computational overhead caused by the co-simulation interface (green) and also the overhead caused by the data traffic between the co-simulation interface and the subsystems (yellow) is slightly decreased compared to the case $n_{K} =1E4$ in Sect. 6.2. The solver time per subsystem (blue) is increased, because the number of masses per subsystem is increased. Regarding the efficiency of the implementation, it can clearly be seen from Fig. 34 that a decomposition of the model into 2399 subsystems is inefficient for a model size with $n_{K} =5E4$ and $n_{K} =1E5$ masses, since the overhead is rather large compared to the overall computation time. If the number of masses increases, the overhead becomes lower compared to the subsystem integration time. This clearly indicates that a parallelization of a dynamical model by means of a co-simulation technique can very significantly reduce the overall simulation time. Increasing the number of masses even more ($n_{K} >1E6$), the improvement would even be more apparent.

Fig. 34

ExSLocal approach (for ${d}_{{i}} ={1.0 E 4}\ \mathrm{Ns} / \mathrm{m}$) and ImSLocal approach (for ${d}_{{i}} ={5.0 E 5}\ \mathrm{Ns} / \mathrm{m}$) in connection with low-order sensitivities: number of macro-steps and computation time for different model sizes

6.5 Example 5: Study on the safety factor

The safety factor $\mathit{SF}$, see Eq. (32), is a parameter to tune the ratio between the total number of macro-steps and the number of failed macro-steps (failed local error tests). Again, the chain model of Sect. 6.2 is considered with the following parameters: $n_{K} = 10^{5}$ masses, $r=100$ subsystems, $m_{i} =5.0E-2\ \mathrm{kg}$, $c_{i} =2.5E6\ \frac{\mathrm{N}}{\mathrm{m}}$, $d_{i} =2.5E1\ \frac{\mathrm{Ns}}{\mathrm{m}}$, $C_{i} =1.0E10\ \frac{\mathrm{N}}{\mathrm{m}^{3}}$, $D_{i} =1.0E-4\ \frac{\mathrm{Ns}^{3}}{\mathrm{m}^{3}}$. External forces $F_{S,j} = \Delta F_{S,j} \left ( \sin \Omega _{S,j} \right )^{A_{S}}$ with the amplitudes $\Delta F_{S,j}$ (randomly chosen in the interval $\pm \left [ 1.0E6, 1.0E7 \right ] \ \mathrm{N}$) and the frequencies $\Omega _{S,j}$ (randomly distributed in the interval $\left [ 5.0E2, 5.0E3 \right ] \ \mathrm{s}^{-1}$) and the parameter $A_{S} =95$ are applied at 50% of the masses (randomly selected).

The model is computed by the explicit and the implicit co-simulation approach with quadratic approximation polynomials ($k=2$). The macro-step size is controlled by the error estimators ExMilne and ImMilne. The limits for the scaling factor $r^{\rho }$ between two consecutive macro-steps are chosen by $r_{\min }^{\rho } =0.5$, $r_{\max }^{\rho } =1.5$. The error tolerances for the macro-step size controller are set to $\mathit{atol}_{x} = 10^{-8}$, $\mathit{atol}_{v} = 10^{-4}$, and $\mathit{rtol}= 10^{-4}$. The resulting computation time as a function of the safety factor $\mathit{SF}$ is illustrated in Fig. 35.

Fig. 35

Computation time of the explicit (blue) and the implicit (red) co-simulation approach depending on the safety factor ${SF}$. (Color figures online)

For the chosen model parameters, the explicit co-simulation approach is more efficient than the implicit method: the ExMilne approach (left y-axis, blue bars) is almost twice as fast as the ImMilne method (right y-axis, red bars). The computation time of both co-simulation approaches can be reduced significantly by selecting an appropriate value for the safety factor $\mathit{SF}$. Choosing the safety factor in the range $\mathit{SF}\in \left [ 4{,}6 \right ]$ instead of using $\mathit{SF}=1$, the computation time can approximately be reduced by 30%. The plot further indicates that the simulation time only slightly changes if the safety factor is varied in the range $\mathit{SF}\in \left [ 3{,}8 \right ]$. It should be emphasized that these findings are model dependent. Further studies, not presented here, indicate that a safety factor in the range $\mathit{SF}\in \left [ 2{,}6 \right ]$ might generally be an appropriate choice [28].

6.6 Example 6: Diverse case studies

6.6.1 Case study 1: monolithic simulation versus co-simulations with fixed/variable macro-step size

To compare the computation time of a co-simulation with the simulation time of the corresponding monolithic model, the oscillator chain of Sect. 6.2 is reconsidered. Therefore, the chain model with $n_{K} = 10^{5}$ masses is split into $r =100$ equally-sized subsystems. The model parameters are: $m_{i} =5.0E-5\ \frac{\mathrm{Ns}^{2}}{\mathrm{mm}}$, $c_{i} =2.5E6\ \frac{\mathrm{N}}{\mathrm{mm}}$, $d_{i} =2.5E-1\ \frac{\mathrm{Ns}}{\mathrm{mm}}$, $C_{i} =1.0E10\ \frac{\mathrm{N}}{\mathrm{mm}^{3}}$, $D_{i} =5.0E-5\ \frac{\mathrm{Ns}^{3}}{\mathrm{mm}^{3}}$. Impulse-shaped forces $F_{\mathit{Imp},j} = \frac{1}{2} \Delta F_{j} \bigl [ \tanh \left ( \frac{t- t_{\alpha }}{\delta } \right ) - \tanh \left ( \frac{t- \left ( t_{\alpha } + \Delta t \right )}{\delta } \right ) \bigr]$ with an amplitude of $\Delta F_{j} = \left ( -1 \right )^{j+1} \cdot 1.0E6\ \mathrm{N}$ and the parameters $\delta =1.0E-6\ \mathrm{s}$ and $\Delta t=1.0E-3\ \mathrm{s}$ are applied to the coupling bodies at the time points $t_{\alpha }$ ($t_{\alpha } =1.0E-4\ \mathrm{s},\ 0.1\ \mathrm{s},\ 0.2\ \mathrm{s},\ \dots ,\ 0.9 \ \mathrm{s}$). Note that contact forces $F_{\mathit{Con},i}$ are not considered in the simulations of Sects. 6.6.1 and 6.6.2; however, in Sect. 6.6.3 they are considered. The subsequent macro-step size controller parameters have been used: $\mathit{SF} =6$, $\mathit{atol}_{x} = 10^{-3} \cdot \mathit{rtol}$, $\mathit{a to l}_{v} = \mathit{rtol}$, $\mathit{a to l}_{\lambda _{c}} = 10^{2} \cdot \mathit{rtol}$, $r_{\min }^{\rho } =0.5$, $r_{\max }^{\rho } =2.0$.

The model is computed with the explicit and implicit co-simulation approaches, whereby three different cases are considered:

• a) fixed order ($k=\mathit{const}$.) and fixed macro-step size ($H=\mathit{const}$.),

• b) fixed order ($k=\mathit{const}$.) and variable macro-step size ($H=\mathit{var}$.),

• c) variable order ($k=\mathit{var}$.) and variable macro-step size ($H=\mathit{var}$.).

The simulation results are compared with the results of a reference simulation (monolithic simulation with very tight error tolerances). In order to compare the simulation results, the global error $e^{\mathit{glob}}$ (normalized root mean square error) of the state variables of the coupling bodies is computed. To obtain a reasonable comparison, the simulation parameters have been chosen in such a way that the accuracy condition $e^{\mathit{glob}} \leq 2.50E-3$ will be satisfied.

To achieve a global error of $e_{\mathit{mono}}^{\mathit{glob}} \approx 2.34E-3$, a simulation time of $2.69E4\ \mathrm{s}$ is required for the monolithic model (mean solver-step size: $\overline{h} =1.34E-6\ \mathrm{s}$).

Case a): $k=\mathit{const}$., $H=\mathit{const}$.

• To obtain results of the required accuracy with the implicit co-simulation method, a simulation with $k=2$ and $H=1.0E-7\ \mathrm{s}$ (Im2H) exhibits the best performance. With these parameters, the implicit co-simulation takes $2.0E4\ \mathrm{s}$ with a global error of $e_{\mathit{impl}}^{\mathit{glob}} \approx 1.07E-3$.

• Using the explicit co-simulation approach, best results are achieved with the parameters $k=1$ and $H=2.5E-8\ \mathrm{s}$ (Ex1H). The computation time with the explicit approach is $1.89E4\ \mathrm{s}$ yielding a global error of $e_{\mathit{expl}}^{\mathit{glob}} \approx 7.94E-4$.

• Remark. A comparison between the monolithic simulation (Mono) and the explicit co-simulation (Ex1H) shows that the simulation time is only slightly reduced ($\approx 30\%$) due to the co-simulation. The poor performance of the co-simulation can be explained as follows. The model contains a few impulse-shaped external forces, which require a small macro-step size in order to obtain a stable co-simulation. The monolithic model is, however, solved with a variable step-size solver so that the integration step-size is only reduced at the time points, where the impulse-shaped forces act. Hence, the mean integration step-size of the monolithic model is significantly larger than the mean integration step-size of the subsystem solvers. As a consequence, the formula in the introduction for estimating the possible speed-up by a co-simulation cannot be applied.

Case b): $k=\mathit{const}$., $H=\mathit{var}$.

• The best performance for the implicit approach has been achieved with $k=5$ and $\mathit{rtol} = 10^{-4}$ (Im5Milne). With these parameters, the computation time is $3925\ \mathrm{s}$, the average macro-step size is $\overline{H} =2.99E-6\ \mathrm{s}$ and the global error becomes $e_{\mathit{impl}}^{\mathit{glob}} \approx 1.86E-3$.

• The explicit approach performs best for $k=4$ and $\mathit{rtol} = 10^{-6}$ (computation time $1014\ \mathrm{s}$, average macro-step size $\overline{H} =9.594E-7\ \mathrm{s}$, global error $e_{\mathit{expl}}^{\mathit{glob}} \approx 3.95E-5$).

• Remark. The formula for estimating the co-simulation time will now provide a more realistic estimation, since both the monolithic simulation and the co-simulation have similar integration step-sizes. The real speed-up factor is ≈26.5; the estimation formula provides $T_{\mathit{Mono}} =100 \cdot ( T_{\mathit{Cosim}} - \mathit{Overhead})$. Note that the scaling factor $r$ is approximately 1 for the considered model.

Case c): $k=\mathit{var}$., $H=\mathit{var}$.

• The fully controlled implicit co-simulation ImMilne with $\mathit{rtol} = 10^{-4}$ takes $4154\ \mathrm{s}$ to obtain a resulting error of $e_{\mathit{impl}}^{\mathit{glob}} \approx 9.00E-4$ (average macro-step size $\overline{H} =3.03E-6\ \mathrm{s}$).

• Applying the simplified error estimator in combination with the implicit co-simulation method (ImSLocal) with $\mathit{rtol} = 10^{-4}$, the computation is $3356\ \mathrm{s}$ with a global error of $e_{\mathit{impl}}^{\mathit{glob}} \approx 9.36E-4$ (average macro-step size $\overline{H} =5.08E-6\ \mathrm{s}$).

• The fully controlled explicit co-simulation ExMilne shows that the computation time decreases if the macro-step size is decreased. Best results with regard to the computation time are achieved with the rather tight error tolerances $\mathit{rtol} = 10^{-6}$ (computation time $1187\ \mathrm{s}$, global error $e_{\mathit{expl}}^{\mathit{glob}} \approx 6.81E-5$, average macro-step size $\overline{H} =1.10E-6\ \mathrm{s}$).

• For the fully controlled explicit co-simulation ExLocal with $\mathit{rtol} = 10^{-6}$, similar results are obtained (computation time $1207\ \mathrm{s}$, global error $e_{\mathit{expl}}^{\mathit{glob}} \approx 7.49E-5$, average macro-step size $\overline{H} =1.10E-6\ \mathrm{s}$).

• The fully controlled explicit co-simulation in combination with the simplified error estimator (ExSLocal) and an error tolerance of $\mathit{rtol} = 10^{-6}$ takes $1265\ \mathrm{s}$ to obtain a global error of $e_{\mathit{impl}}^{\mathit{glob}} \approx 3.43E-4$. The average macro-step size is $\overline{H} =1.68E-6\ \mathrm{s}$.

The resulting computation times of the different approaches are summarized in Fig. 36.

Fig. 36

Comparison of different co-simulation approaches (accuracy condition ${e}^{{glob}} {\leq 2.50 E}-{3}$)

Based on the above results, the following conclusions can be drawn:

• Co-simulations with a fixed macro-step size are rather inefficient for the considered model. Compared to the monolithic simulation, the computation time is only reduced by $\approx 30\%$.

• Applying the macro-step size controller, efficiency of all co-simulation approaches may significantly be increased. A speed-up factor of ≈26.5 compared to the monolithic computation may be achieved.

• For the considered model, the order control algorithm does not significantly reduce the computation time since the impulse-shaped forces only act at very few time points. At the time points, where the impulse-shaped forces act, the approximation order is – as expected – reduced. Between these time points, the order controller selects a larger integration order ($k=3-5$). Therefore, the benefit of the order controller is rather low for the considered problem.

• The three error estimators for the explicit co-simulation approach exhibit a similar behavior.

• The two error estimators for the implicit co-simulation method yield comparable results.

6.6.2 Case study 2: Modified decomposition

The decomposition of the chain model used above may not be ideal because the coupling masses are directly affected by impulse-shaped forces. To reduce the computation time, it might be useful to apply a modified decomposition. Therefore, the chain model is repartitioned into 101 subsystems in such a way that the first and the last subsystem contain 500 masses; the remaining 99 subsystems are assumed to be equally sized containing 1000 masses. The influence of the increased number of subsystems (101 instead of 100) on the simulation time is negligible. The essential point is that the impulse-shaped forces will not longer act directly at the coupling bodies, but inside the subsystems 2-100.

The results of the computations with the modified decomposition are collected in Fig. 37 (red bars). A comparison with the original decomposition of Sect. 6.6.1 shows that the computation time is (slightly) reduced with the modified decomposition. For the ExSLocal approach, for instance, the computation time is reduced by 14%.

Fig. 37

Monolithic simulation and different co-simulations of the chain model of Sect. 6.6.2 without contacts (red) and for the extended chain model of Sect. 6.6.3 with contacts (yellow). (Color figures online)

6.6.3 Case study 3: Extended model and multirate effect

Finally, the oscillator chain is modified to demonstrate the multirate effect. Small subsystems with 25 masses are added at both ends of the oscillator chain. In the newly added small subsystems (subsystems 1 and 103), contact forces $F_{\mathit{Con},i} =A\ e^{B x_{i}}$ with $A=-1.0E-2\ \mathrm{N}$ and $B=5.0E5\ \mathrm{mm}^{-1}$ are assumed to act at three masses so that these two subsystems become very stiff. Subsystems 2-102 are identical with the model of Sect. 6.6.2 (modified decomposition).

Considering the monolithic simulation of the extended model, the stiff contacts strongly affect the computation time, since the solver-step size is reduced for the complete model. However, applying a co-simulation approach, the integration-step size is selected individually by the step-size controllers of the subsystem solvers. Therefore, the solver-step sizes of subsystems 1 and 103 will be reduced due to the stiff contacts. The remaining subsystems 2-102 will be integrated with larger step sizes. Since the subsystems 1 and 103 are very small, the overall computation time of the co-simulation will not be increased significantly compared to the non-extended model.

Simulation results with the extended model (containing contacts in subsystems 1 and 103) are shown in Fig. 37 (yellow bars). As expected, the computation time of the monolithic simulation is significantly increased, while the computation time of the co-simulation approaches are not changed markedly. The number of macro-steps and the resulting global error are only slightly increased.

The speed-up factor of the explicit co-simulation (ExMilne) compared to the monolithic simulation is ≈400 for the extended model with contacts (simulation time of the monolithic model: $5 \frac{1}{2}$ days; simulation time of the co-simulation model: 30 minutes). This very high speed-up factor has mainly two reasons: (i) dynamical parallelization of the model by means of the co-simulation and (ii) exploiting the multirate effect by an appropriate model decomposition.

7 Conclusions

An algorithm for controlling the degree of the polynomials, which are used for approximating the coupling variables within co-simulation and solver coupling approaches, has been presented. The order controller has been incorporated into the algorithm for controlling the macro-step size so that co-simulations with variable order and variable macro-step size could be realized. Different numerical examples have been presented, which confirm the functionality and the accurate operation of the combined order and step-size control algorithm. The numerical tests also clearly demonstrated the benefit, which can be achieved with a combined order and macro-step size control algorithm.

Using a constant (i.e., fixed) integration order, the question on the proper choice of the integration order arises. As a matter of fact, the optimal integration order is problem-dependent and may change during the co-simulation. Using a constant integration order can cause different difficulties:

• If the integration order is chosen too high, the co-simulation may get unstable or the macro-step size may be reduced significantly by the macro-step size controller.

• Choosing the integration order too small, the co-simulation may become inefficient and less accurate.

• Especially for highly nonlinear systems, for systems with impacts or for models where steep gradients occur, a simulation with a fixed integration order may be rather inefficient.

The main problems associated with the usage of a constant integration order – namely a trade-off between stability/accuracy and efficiency – will disappear, if an order controller is used.

The different numerical examples presented in Sect. 6 have shown that in most cases the efficiency and accuracy of a co-simulation could be (markedly) improved by incorporating an order control algorithm.

In our tests, failures of the order controller have not been detected, although rather stiff systems, systems with contacts and systems with steep, impulse-shaped external forces have been considered. A rather stable and robust performance has been observed, which clearly recommends the usage of a variable integration order.

Considering implicit co-simulation methods, an interface-Jacobian is required for the corrector iteration, which is usually calculated by a finite difference (FD) approach. Applying an FD approach, a large number of additional cores might be necessary in order to calculate the interface-Jacobian in parallel with the predictor/corrector subsystem integrations. Alternatively, approximation formulas for the interface-Jacobian might be used (low-order sensitivities, LOS), which can be implemented in a very straightforward manner. Using the LOS approach, the additional parallel subsystem integrations required in connection with the FD approach can be omitted without a significant increase of the computation time. Depending on the problem, the usage of low-order sensitivities can (slightly) increase the co-simulation time, since the number of corrector iterations may (slightly) increase compared to the FD approach. Accuracy of the co-simulation is, however, not affected. In contrast, problems with ill-conditioning and numerical cancellation, which are often observed in association with FD approaches, will not occur if low-order sensitivities are applied.

Summarizing, the innovation of this work concerns the realization of variable-order co-simulations and the incorporation of the order control algorithm into the macro-step size controller. Using a combined order and macro-step size controller may significantly increase the numerical efficiency and accuracy of a coupled simulation. While co-simulation is frequently used to carry out multi-physical or multi-disciplinary simulations, co-simulation methods may also be applied to parallelize a mono-disciplinary system in time domain. To exploit the full potential of a co-simulation-based parallelized dynamical model, controlling the integration order and the macro-step size may be an essential point.

Concerning the future work, the subsequent topics may – amongst others – be interesting:

• Application of the presented approaches to co-simulation methods based on constraint coupling.

• Usage of co-simulation techniques to parallelize large-scaled finite element models in time domain.

• Development of error estimators for alternative explicit and implicit co-simulation methods.

• Error estimation and macro-step size control for systems with discontinuities.

Appendices

Appendix A

This appendix contains additional information on the calculation of the interface-Jacobian, which is required for the implicit co-simulation scheme, see Sect. 3.2. Basically, the interface-Jacobian $\frac{d \boldsymbol{g}_{c}}{d \boldsymbol{u}_{N+1}^{*}}$ can be computed in different ways, e.g., by using:

• analytical gradients,

• numerically calculated gradients based on a finite difference approach,

• approximated gradients,

• gradients computed with the help of automatic differentiation.

Here, the gradients are calculated either by a finite difference approach (Appendix A.1) or with the help of a low-order approximation technique (Appendix A.2).

To explain the two approaches, we consider the equations of motion of an arbitrary subsystem $s$. For a concise representation, the subsystem is assumed to be a multibody system. For other mechanical or nonmechanical subsystems, a very similar strategy may be applied. The equations of motion of the multibody subsystem $s$ are given by

$$ \begin{aligned} \dot{\boldsymbol{x}}^{s} & = \boldsymbol{B}^{s} \bigl( \boldsymbol{x}^{s} \bigr) \boldsymbol{v}^{s}, \\ \boldsymbol{M}^{s} \bigl( t, \boldsymbol{x}^{s} \bigr) \dot{\boldsymbol{v}}^{s} &= \boldsymbol{f}^{s} \bigl( t, \boldsymbol{x}^{s}, \boldsymbol{v}^{s} \bigr) - \boldsymbol{B}^{s \mathrm{T}} \bigl( \boldsymbol{x}^{s} \bigr) \boldsymbol{G}^{s \mathrm{T}} \bigl( t, \boldsymbol{x}^{s} \bigr) \boldsymbol{\lambda }^{s} \\ &\quad + \boldsymbol{f}^{\mathrm{c},\mathrm{s}} \bigl( t, \boldsymbol{x}^{s}, \boldsymbol{v}^{s}, \boldsymbol{p}_{N+1}^{*} ( t ) \bigr), \\ \boldsymbol{g}^{s} \bigl( t, \boldsymbol{x}^{s} \bigr) &=\boldsymbol{0} \end{aligned} $$

(39)

with $\left \{ \boldsymbol{x}^{s}, \boldsymbol{v}^{s} \right \} \in \mathbb{R}^{n}$, $\boldsymbol{\lambda }^{s} \in \mathbb{R}^{m}$, see Sect. 2.2. To keep the notation simple, the subsystem index $s$ is omitted in the following (i.e., $\boldsymbol{x}^{s} \boldsymbol{\rightarrow x}$, etc.). The coupling variables are approximated with the polynomials $\boldsymbol{p}_{N+1}^{*} \left ( t \right ) = \boldsymbol{P}_{N+1}^{k} \left ( t; \left ( T_{N+1}, \boldsymbol{u}_{N+1}^{{*}} \right ), \left ( T_{N}, \boldsymbol{u}_{N} \right ), \dots , \left ( T_{N-k+1}, \boldsymbol{u}_{N-k+1} \right ) \right ) = \sum _{i=N-k+1}^{N} \boldsymbol{u}_{i} L_{i} \left ( t \right ) + \boldsymbol{u}_{N+1}^{{*}} L_{N+1} \left ( t \right )$, where $L_{i} \left ( t \right )$ represent the Lagrange basis polynomials.

The two approaches for calculating the interface-Jacobian are explained by regarding the $\alpha$th corrector step, i.e., the calculation of the interface-Jacobian $\left . \frac{d \boldsymbol{g}_{c}}{d \boldsymbol{u}_{N+1}^{*}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}}$ is considered. To compute the interface-Jacobian, it is useful to rewrite the term $\frac{d \boldsymbol{g}_{c}}{d \boldsymbol{u}_{N+1}^{*}}$. The total derivative of $\boldsymbol{g}_{c} \left ( T_{N+1}, \boldsymbol{z}_{N+1}^{*} ( \boldsymbol{u}_{N+1}^{*} ), \boldsymbol{u}_{N+1}^{*} \right ) = \boldsymbol{u}_{N+1}^{*} -\boldsymbol{\varphi } \left ( T_{N+1}, \boldsymbol{z}_{N+1}^{*} ( \boldsymbol{u}_{N+1}^{*} ), \boldsymbol{u}_{N+1}^{*} \right )$ with respect to $\boldsymbol{u}_{N+1}^{*}$ can be written as

$$ \begin{aligned} \left . \frac{d \boldsymbol{g}_{c}}{d \boldsymbol{u}_{N+1}^{*}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} &= \left . \biggl( \frac{\partial \boldsymbol{g}_{c}}{\partial \boldsymbol{u}_{N+1}^{*}} + \frac{\partial \boldsymbol{g}_{c}}{\partial \boldsymbol{z}_{N+1}^{*}} \cdot \frac{\partial \boldsymbol{z}_{N+1}^{*}}{\partial \boldsymbol{u}_{N+1}^{*}} \biggr) \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}, \boldsymbol{z}_{N+1}^{\mathit{cor}, \alpha -1}} \\ & = \left . \biggl( \boldsymbol{I} - \frac{\partial \boldsymbol{\varphi }}{\partial \boldsymbol{u}_{N+1}^{*}} - \frac{\partial \boldsymbol{\varphi }}{\partial \boldsymbol{z}_{N+1}^{*}} \cdot \frac{\partial \boldsymbol{z}_{N+1}^{*}}{\partial \boldsymbol{u}_{N+1}^{*}} \biggr) \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}, \boldsymbol{z}_{N+1}^{\mathit{cor}, \alpha -1}}, \end{aligned} $$

(40)

where $\boldsymbol{I}$ is the identity matrix. Since the coupling functions $\boldsymbol{g}_{c}:=\boldsymbol{u}-\boldsymbol{\varphi } \left ( t, \boldsymbol{z},\boldsymbol{u} \right ) = \boldsymbol{0}$ or, more precisely, the functions $\boldsymbol{g}_{c}:=\boldsymbol{u}-\boldsymbol{\varphi } \left ( t, \boldsymbol{x},\boldsymbol{v},\boldsymbol{u} \right ) = \boldsymbol{0}$ are assumed to be explicitly known, the terms $\frac{\partial \boldsymbol{\varphi }}{\partial \boldsymbol{u}_{N+1}^{*}}$ and $\frac{\partial \boldsymbol{\varphi }}{\partial \boldsymbol{z}_{N+1}^{*}}$ can be expressed analytically. Note that for systems without feed-through, the coupling equations simply read $\boldsymbol{g}_{c}:=\boldsymbol{u}-\boldsymbol{\varphi } \left ( t, \boldsymbol{x},\boldsymbol{v} \right ) = \boldsymbol{0}$ so that the term $\frac{\partial \boldsymbol{\varphi }}{\partial \boldsymbol{u}_{N+1}^{*}}$ equals zero. The main task to compute the interface-Jacobian is therefore the calculation of the term $\left . \frac{\partial \boldsymbol{z}_{N+1}^{*}}{\partial \boldsymbol{u}_{N+1}^{*}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}}$. More precisely, the two expressions

$$ \left . \frac{\partial \boldsymbol{x}_{N+1}^{*}}{\partial \boldsymbol{u}_{N+1}^{*}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} \quad \mbox{and}\quad \left . \frac{\partial \boldsymbol{v}_{N+1}^{*}}{\partial \boldsymbol{u}_{N+1}^{*}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}}, $$

(41)

which describe the sensitivities of the subsystem states with respect to the coupling variables, have to be determined.

1.1 A.1 Numerical calculation of the interface-Jacobian using a finite difference approach (FD sensitivities/gradients)

To numerically calculate the partial derivatives of Eq. (41) with the help of a finite difference approximation, additional subsystem integrations have to be carried out in parallel with the $( \alpha -1)\mathrm{th}$ corrector step. For a concise representation, we simply consider the calculation of the gradients $\left . \frac{\partial \boldsymbol{x}_{N+1}^{*}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}}$ and $\left . \frac{\partial \boldsymbol{v}_{N+1}^{*}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}}$, where $u_{i,N+1}^{{*}} = \boldsymbol{u}_{N+1}^{{*}} \cdot \boldsymbol{e}_{i}$ represents an arbitrary input variable.

The $(\alpha - 1)\mathrm{th}$ corrector step is accomplished with the interpolation polynomials $\boldsymbol{p}_{N+1}^{\mathit{cor}, \alpha -1} \left ( t \right ) = \boldsymbol{P}_{N+1}^{k} \left ( t; \left ( T_{N+1}, \boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1} \right ), \left ( T_{N}, \boldsymbol{u}_{N} \right ), \dots , \left ( T_{N-k+1}, \boldsymbol{u}_{N-k+1} \right ) \right )$, which yields the corrected variables $\boldsymbol{z}_{N+1}^{\mathit{cor}, \alpha -1}$. To calculate the partial derivatives $\left . \frac{\partial \boldsymbol{x}_{N+1}^{*}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}}$ and $\left . \frac{\partial \boldsymbol{v}_{N+1}^{*}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}}$, additional subsystem integrations have to be carried out with perturbed interpolation polynomials. The perturbed corrector polynomials are given by $\boldsymbol{p}_{N+1}^{\mathit{cor}, \alpha -1,\mathit{per}} \left ( t \right ) = \boldsymbol{P}_{N+1}^{k} \left ( t; \left ( T_{N+1}, \boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1} + \Delta u_{i,N+1}^{{*}} \boldsymbol{e}_{i} \right ), \left ( T_{N}, \boldsymbol{u}_{N} \right ), \dots , \left ( T_{N-k+1}, \boldsymbol{u}_{N-k+1} \right ) \right )$, where $\Delta u_{i,N+1}^{{*}}$ denotes a small user-defined increment. Integrating the subsystem with the perturbed interpolation polynomials $\boldsymbol{p}_{N+1}^{\mathit{cor}, \alpha -1,\mathit{per}} \left ( t \right )$ provides the perturbed subsystem variables $\boldsymbol{z}_{N+1}^{\mathit{cor}, \alpha -1,\mathit{per}}$. The gradients may then simply be approximated by

$$ \begin{aligned} &\left . \frac{\partial \boldsymbol{x}_{N+1}^{*}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} \approx \frac{\boldsymbol{x}_{N+1}^{\mathit{cor}, \alpha -1,\mathit{per}} - \boldsymbol{x}_{N+1}^{\mathit{cor}, \alpha -1}}{\Delta u_{i,N+1}^{{*}}},\\ &\left . \frac{\partial \boldsymbol{v}_{N+1}^{*}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} \approx \frac{\boldsymbol{v}_{N+1}^{\mathit{cor}, \alpha -1,\mathit{per}} - \boldsymbol{v}_{N+1}^{\mathit{cor}, \alpha -1}}{\Delta u_{i,N+1}^{{*}}}. \end{aligned} $$

(42)

The interface-Jacobians $\left . \frac{d \boldsymbol{g}_{c}}{d \boldsymbol{u}_{N+1}^{*}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor},\alpha }}$ for the next corrector step is calculated in the same way.

The perturbation increment $\Delta u_{i,N+1}^{{*}}$ has to be chosen very carefully. For the simulations in Sect. 6, the subsequent perturbation increments have been used

$$ \textstyle\begin{array} {l@{\quad }l} \Delta u_{i,N+1}^{{*}} = \max \bigl( \bigl\vert u_{i,N}^{\mathit{pre}} - u_{i,N}^{\mathit{cor},l} \bigr\vert ,\Delta u_{i}^{\min } \bigr) & \mbox{for} \ \mathrm{the}\ \mathrm{predictor}\ \mathrm{step}, \\ \Delta u_{i,N+1}^{{*}} = \max \bigl( \bigl\vert u_{i,N+1}^{\mathit{cor},\alpha } - u_{i,N+1}^{\mathit{cor},\alpha -1} \bigr\vert ,\Delta u_{i}^{\min } \bigr) & \mbox{for} \ \mathrm{the}\ \alpha \mathrm{th} \ \mathrm{corrector}\ \mathrm{step}, \end{array} $$

(43)

where $\Delta u_{i}^{\min }$ is a user-defined (small) value; $\Delta u_{i}^{\min }$ has to be chosen appropriately with respect to the type of the coupling variable (position, velocity or force variable).

The corrector iteration is terminated if a convergence criterion is fulfilled. For this purpose, the scalar weighted root-mean-square norm

$$ \bigl\Vert u_{i,N+1}^{\mathit{cor},\alpha } - u_{i,N+1}^{\mathit{cor},\alpha -1} \bigr\Vert _{\mathit{WRMS}} = \sqrt[2]{ \frac{1}{n_{c}} \sum_{i=1}^{n_{c}} \biggl( \frac{u_{i,N+1}^{\mathit{cor},\alpha } - u_{i,N+1}^{\mathit{cor},\alpha -1}}{\mathit{atol}_{i} + \mathit{rtol} \cdot \vert u_{i,N+1}^{\mathit{cor},\alpha } \vert } \biggr)^{2}} $$

(44)

is applied; $\mathit{atol}_{i}$ and $\mathit{rtol}$ term user-defined absolute and relative error tolerances, respectively. The corrector iteration is terminated if the following criterion is fulfilled:

$$ \bigl\Vert u_{i,N+1}^{\mathit{cor},\alpha } - u_{i,N+1}^{\mathit{cor},\alpha -1} \bigr\Vert _{\mathit{WRMS}} \cdot \frac{R_{\alpha }}{1- R_{\alpha }} < \tau . $$

(45)

The factor $R_{\alpha } = \frac{\left \Vert u_{i,N+1}^{\mathit{cor},\alpha } - u_{i,N+1}^{\mathit{cor},\alpha -1} \right \Vert _{\mathit{WRMS}}}{\left \Vert u_{i,N+1}^{\mathit{cor},\alpha -1} - u_{i,N+1}^{\mathit{cor},\alpha -2} \right \Vert _{\mathit{WRMS}}}$ is a measure for the convergence rate [66] and $\tau$ denotes a user-defined value (e.g., $\tau =0.3$).

1.2 A.2 Approximate calculation of the interface-Jacobian using low-order sensitivities

A straightforward approach for approximately calculating the coupling sensitivities $\left . \frac{\partial \boldsymbol{x}_{N+1}^{*}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}}$ and $\left . \frac{\partial \boldsymbol{v}_{N+1}^{*}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}}$ has been presented in [29]. These approximations, called low-order sensitivities (LOS) in the following, converge to the exact sensitivities for $H\rightarrow 0$. Concretely, the low-order sensitivities for the velocity variables converge with $\mathcal{O} \left ( H^{1} \right )$ to the exact sensitivities and the low-order sensitivities for the position variables with $\mathcal{O} \left ( H^{2} \right )$. Calculation of low-order sensitivities is rather straightforward and basically only requires the solution of a system of linear equations of the dimension of the subsystem. If the subsystems are ODEs – or, more precisely, if the coupling bodies are not connected by constraint equations to the rest of the subsystem – even closed analytical formulas may be derived for the low-order sensitivities.

Here, we just explain the application of the low-order sensitivity approach. For details, the reader is referred to [29]. In a first step, low-order sensitivities for the subsystem accelerations $\dot{\boldsymbol{v}}$ (i.e., $\dot{\boldsymbol{v}}^{s}$) and for the subsystem multipliers $\boldsymbol{\lambda }$ (i.e., $\boldsymbol{\lambda }^{s}$) are computed for the time-point $T_{N+1}$. Therefore, the linear system of equations

$$\begin{aligned} & \underbrace{\left ( \textstyle\begin{array}{c@{\quad }c} \boldsymbol{M} \left ( T_{N+1}, \boldsymbol{x}^{\mathit{cor}, \alpha -1} \left ( T_{N+1} \right ) \right ) & \boldsymbol{B}^{\mathrm{T}} \left ( \boldsymbol{x}^{\mathit{cor}, \alpha -1} \left ( T_{N+1} \right ) \right ) \cdot \boldsymbol{G}^{\mathrm{T}} \left ( T_{N+1}, \boldsymbol{x}^{\mathit{cor}, \alpha -1} \left ( T_{N+1} \right ) \right )\\[3pt] \boldsymbol{G} \left ( T_{N+1}, \boldsymbol{x}^{\mathit{cor}, \alpha -1} \left ( T_{N+1} \right ) \right ) \cdot \boldsymbol{B} \left ( \boldsymbol{x}^{\mathit{cor}, \alpha -1} \left ( T_{N+1} \right ) \right ) & \boldsymbol{0} \end{array}\displaystyle \right )} _{\boldsymbol{A}} \\ &\quad \cdot \left ( \textstyle\begin{array}{c} \left . \frac{\partial \dot{\boldsymbol{v}}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} \left ( T_{N+1} \right )\\ \left . \frac{\partial \boldsymbol{\lambda }}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} \left ( T_{N+1} \right ) \end{array}\displaystyle \right ) = \underbrace{\left ( \textstyle\begin{array}{c} \left . \frac{\partial \boldsymbol{f}^{\mathrm{c}}}{\partial \boldsymbol{p}_{N+1}^{*}} \right \vert _{\boldsymbol{z}^{\mathit{cor},\alpha -1} \left ( T_{N+1} \right ), \boldsymbol{p}_{N+1}^{\mathit{cor},\alpha -1} \left ( T_{N+1} \right )} \cdot \boldsymbol{e}_{i}\\[3pt] \boldsymbol{0} \end{array}\displaystyle \right )} _{\boldsymbol{b}} \end{aligned}$$

(46)

has to be solved for the expressions $\left . \frac{\partial \dot{\boldsymbol{v}}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} \left ( T_{N+1} \right )$ and $\left . \frac{\partial \boldsymbol{\lambda }}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} \left ( T_{N+1} \right )$. Note that $\boldsymbol{M} \left ( T_{N+1}, \boldsymbol{x}^{\mathit{cor}, \alpha -1} \left ( T_{N+1} \right ) \right )$, $\boldsymbol{B} \left ( \boldsymbol{x}^{\mathit{cor}, \alpha -1} \left ( T_{N+1} \right ) \right )$ and $\boldsymbol{G} \left ( T_{N+1}, \boldsymbol{x}^{\mathit{cor}, \alpha } \left ( T_{N+1} \right ) \right )$ denote subsystem matrices according to Eq. (39) to be evaluated at the macro-time point $T_{N+1}$ with the known variables $\boldsymbol{x}^{\mathit{cor}, \alpha -1} \left ( T_{N+1} \right )$ from the ($\alpha -1$)th corrector step. The matrix $\left . \frac{\partial \boldsymbol{f}^{\mathrm{c}}}{\partial \boldsymbol{p}_{N+1}^{*}} \right \vert _{\boldsymbol{z}^{\mathit{cor},\alpha -1} \left ( t \right ), \boldsymbol{p}_{N+1}^{\mathit{cor},\alpha -1} \left ( t \right )}$ can simply be calculated with the help of the constitutive equations of the coupling forces/torques and the known variables $\boldsymbol{z}^{\mathit{cor}, \alpha -1} \left ( T_{N+1} \right )$. Hence, after the $( \alpha -1 ) \mathrm{th}$ corrector step has been carried out, $\boldsymbol{A}$ and $\boldsymbol{b}$ can be computed and Eq. (46) can be solved for the required sensitivities, i.e.,

$$ \left ( \textstyle\begin{array}{c} \left . \frac{\partial \dot{\boldsymbol{v}}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} \left ( T_{N+1} \right )\\ \left . \frac{\partial \boldsymbol{\lambda }}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} \left ( T_{N+1} \right ) \end{array}\displaystyle \right ) = \boldsymbol{A}^{-1} \cdot \boldsymbol{b}. $$

(47)

With this result, the sensitivities for the accelerations can very easily be calculated in the complete macro-time interval [$T_{N}$, $T_{N+1}$], namely

$$ \left . \frac{\partial \dot{\boldsymbol{v}}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} ( t ) = \left . \frac{\partial \dot{\boldsymbol{v}}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} ( T_{N+1} ) \cdot L_{N+1} ( t ). $$

(48)

Integration of the acceleration sensitivities yields the velocity sensitivities

$$ \left . \frac{\partial \boldsymbol{v}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} ( t ) = \left . \frac{\partial \dot{\boldsymbol{v}}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} ( T_{N+1} ) \cdot \int _{T_{N}}^{t} L_{N+1} ( \overline{t} ) d \overline{t}. $$

(49)

A further integration will then provide the sensitivities on position level

$$ \begin{aligned} & \left .\frac{\partial \boldsymbol{x}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} ( t ) = \boldsymbol{B} \bigl( \boldsymbol{x}^{\mathit{cor}, \alpha -1} ( T_{N+1} ) \bigr) \int _{T_{N}}^{t} \left . \frac{\partial \boldsymbol{v}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} ( \overline{t} ) d \overline{t} \quad ( \boldsymbol{B}\neq \boldsymbol{I} ), \\ &\left . \frac{\partial \boldsymbol{x}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} ( t ) = \int _{T_{N}}^{t} \left . \frac{\partial \boldsymbol{v}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} ( \overline{t} ) d \overline{t} \quad ( \boldsymbol{B}=\boldsymbol{I} ). \end{aligned} $$

(50)

Evaluation of Eqs. (49) and (50) at $T_{N+1}$ yields the sensitivities $\left . \frac{\partial \boldsymbol{v}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} \left ( T_{N+1} \right )$ and $\left . \frac{\partial \boldsymbol{x}}{\partial u_{i,N+1}^{{*}}} \right \vert _{\boldsymbol{u}_{N+1}^{\mathit{cor}, \alpha -1}} \left ( T_{N+1} \right )$ required in Eq. (40). Note that instead of $\boldsymbol{M} \left ( T_{N+1}, \boldsymbol{x}^{\mathit{cor},\! \alpha -1} \!\left ( \!T_{N+1} \!\right ) \right )$, $\boldsymbol{B} \left ( \boldsymbol{x}^{\mathit{cor}, \alpha -1} \left ( T_{N+1} \right ) \right )$, and $\boldsymbol{G} \left ( T_{N+1}, \boldsymbol{x}^{\mathit{cor}, \alpha -1} \left ( T_{N+1} \right ) \right )$, in a simplified approach also the matrices $\boldsymbol{M} \left ( T_{N}, \boldsymbol{x}^{\mathit{cor}, \alpha -2} \left ( T_{N} \right ) \right )$, $\boldsymbol{B} \left ( \boldsymbol{x}^{\mathit{cor}, \alpha -2} \left ( T_{N} \right ) \right )$, and $\boldsymbol{G} \left ( T_{N}, \boldsymbol{x}^{\mathit{cor}, \alpha -2} \left ( T_{N} \right ) \right )$ might be used so that the sensitivities can be calculated in parallel with the $( \alpha -1 ) \mathrm{th}$ corrector step.

Appendix B

In Sect. 6.3, the interface-Jacobian for the implicit co-simulation approaches (ImMilne and ImSLocal) has been calculated with a finite difference (FD) approach. In this appendix, the same simulations are considered; the interface-Jacobian is, however, generated with the low-order sensitivities (LOS) of Appendix A.2. As can be seen in Figs. 38, 39, 40, 41, the basic behavior with the low-order sensitivities is quite similar to the simulation results with FD gradients. For the considered model and parameters, the performance with the FD gradients is little better. Applying the LOS approach, the number of corrector iterations is usually little larger compared with the FD implementation so that the co-simulation time may slightly be increased in association with the LOS approximation. Using FD gradients, numerical problems (ill-conditioning, numerical cancellation) may be observed if the perturbation increments are chosen inappropriately or if the macro-step size becomes very small. Then, the usage of LOS may even be more efficient than applying FD gradients [29].

Fig. 38

ImMilne approach: number of macro-steps and global error of the state variables of the coupling bodies for different error tolerances and different approximation orders

Fig. 39

ImSLocal approach: number of macro-steps and global error of the state variables of the coupling bodies for different error tolerances and different approximation orders

Fig. 40

ImMilne approach: computation time for different error tolerances and different approximation orders

Fig. 41

ImSLocal approach: computation time for different error tolerances and different approximation orders

Nomenclature

atol	absolute error tolerance of the macro-step size controller
$\mathit{atol}^{\mathit{BDF}}$	absolute error tolerance of the subsystem solver
B	symmetric square matrix (DAE-system)
$C^{k}$	error constant
$C_{i}$	nonlinear stiffness coefficient of spring/damper element i
$c_{i}$	linear stiffness coefficient of spring/damper element i
$D_{i}$	nonlinear damping coefficient of spring/damper element i
$d_{i}$	linear damping coefficient of spring/damper element i
e	local error
$f^{c}$	coupling force
G	constraint Jacobian
$\boldsymbol{g}_{c}$	vector of coupling conditions
h	solver-step size
$H_{N}$	macro-step size
$\boldsymbol{J}_{i}$	inertia tensor of body i
k	polynomial degree of approximation polynomials
l	number of corrector iterations
$L^{k}$	Lagrange basis polynomial of degree k
M	mass matrix
$m_{i}$	mass of body i
$n_{c}$	number of coupling variables
$n_{K}$	number of coupling bodies
$\boldsymbol{p}_{N+1}$	approximation polynomials
$\boldsymbol{P}^{k}$	vector of interpolation polynomials of degree k
q	vector of position variables
r	number of subsystems
$r^{\rho }$	scaling factor for the macro-step size
rtol	relative error tolerance of the macro-step size controller
$\mathit{rto} l^{\mathit{BDF}}$	relative error tolerance of the subsystem solver
$S_{i}$	center of mass of body i
SF	safety factor of the macro-step size controller
s	subsystem index
SDN	scaled derivative norm
$T_{\mathit{Cosim}}$	computation time of the co-simulation model
$T_{\mathit{Mono}}$	computation time of the monolithic simulation
$T_{N}$	macro-time point N
u	vector of coupling variables
v	vector of velocity variables
$W_{i}$	weighting factor
z	vector of state variables
α	index of corrector iteration
ε	estimated local error
$\lambda _{c}$	coupling force
$\boldsymbol{\varphi } \left ( t, \boldsymbol{z},\boldsymbol{u} \right )$	vector of coupling functions
	vector of angular velocities