Implicit co-simulation method for constraint coupling with improved stability behavior

Abstract

This paper deals with a novel co-simulation approach for coupling mechanical subsystems in time domain. The submodels are assumed to be coupled by algebraic constraint equations. In contrast to well-known coupling techniques from the literature, the here presented index-1 approach uses a special technique for approximating the coupling variables so that the constraint equations together with the hidden constraints on velocity and acceleration level can be enforced simultaneously at the communication time points. The method discussed here uses second- and third-order approximation polynomials. Because of the high approximation order, the numerical errors are very small, and a good convergence behavior is achieved. A stability analysis is carried out, and it is shown that—despite the fact that higher-order approximation polynomials are applied—also a good numerical stability behavior is observed. Different numerical examples are presented, which illustrate the practical application of the approach.

Appendix A: Numerical stability of the index-1 co-simulation approach

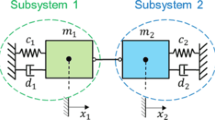
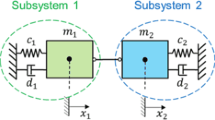
The numerical stability of time integration schemes is defined by Dahlquist´s test equation $\dot{y} (t)= \varLambda \cdot y(t)$ with complex constant $\varLambda = \varLambda_{r} +i \varLambda_{i}$. This test equation can be interpreted as the complex representation of the homogenous linear single-mass oscillator. Dahlquist´s test equation cannot directly be used for analyzing the stability of co-simulation methods. For analyzing the stability of co-simulation methods, a proper test model is therefore required. The straightforward generalization of Dahlquist´s test model for analyzing the stability of co-simulation methods is the two-mass oscillator of Sect. 2, which represents two algebraically coupled Dahlquist equations. The two-mass oscillator is described by five independent parameters and may be considered as a general (complete) linear test model for analyzing the numerical stability of coupling methods with algebraic constraints.

For the stability analysis, we introduce dimensionless variables. The dimensionless time is denoted by $\overline{t} = \frac{t}{H}$. The derivative with respect to the dimensionless time $\overline{t}$ is represented by $( \cdot ) ' = \frac{d( \cdot )}{d \overline{t}}$. We assume that $\overline{x}_{1}, \overline{x}_{2}$ are properly chosen dimensionless position coordinates. The dimensionless velocities are characterized by $\overline{v}_{1} =H \cdot v_{1}$ and $\overline{v}_{2} =H \cdot v_{2}$. The dimensionless coupling force is termed by $\overline{\lambda}_{c} = \frac{\lambda_{c} \cdot H^{2}}{m_{1}}$ and represented by the polynomial $\overline{\lambda}_{c} ( \overline{t} ) = \overline{\lambda}_{c,N+1} ( \overline{\boldsymbol{\beta}}_{N+1}; \overline{t} )$ with $\overline{\boldsymbol{\beta}}_{N+1} = \frac{\boldsymbol{\beta}_{N+1} \cdot H^{2}}{m_{1}}$. We additionally introduce the following five parameters

$$\begin{aligned} \overline{c}_{1} = \frac{c_{1} \cdot H^{2}}{m_{1}}, \quad \quad \overline{d}_{1} = \frac{d_{1} \cdot H}{m_{1}}, \quad \quad \alpha_{m} = \frac{m_{2}}{m_{1}}, \quad \quad \alpha_{c} = \frac{c_{2}}{c_{1}}, \quad \quad \alpha_{d} = \frac{d_{2}}{d_{1}}. \end{aligned}$$

(39)

The dimensionless form of the equations of motion for the two-mass oscillator of Sect. 2 then reads as

$$\begin{aligned} & \overline{x}_{1} ' = \overline{v}_{1}, \\ & \overline{v}_{1} ' =- \overline{c}_{1} \cdot \overline{x}_{1} - \overline{d}_{1} \cdot \overline{v}_{1} + \overline{\lambda}_{c}, \\ & \overline{x}_{2} ' = \overline{v}_{2}, \\ & \overline{v}_{2} ' =- \frac{\alpha_{c}}{\alpha_{m}} \cdot \overline{c}_{1} \cdot \overline{x}_{2} - \frac{\alpha_{d}}{\alpha_{m}} \cdot \overline{d}_{1} \cdot \overline{v}_{2} - \frac{1}{\alpha_{m}} \cdot \overline{\lambda}_{c}, \\ & 0= \overline{x}_{2} - \overline{x}_{1}. \end{aligned}$$

(40)

If $m_{1}, m_{2}, c_{1}, c_{2}, d_{1}, d_{2} >0$, then the two-mass oscillator is physically stable. In terms of a co-simulation approach, the two-mass oscillator is decomposed into two subsystems, and a homogenous linear system of recurrence equations can be derived, which describes the discrete-time co-simulation results. The co-simulation is called numerically stable if all eigenvalues of the recurrence system are inside the unit circle. The eigenvalues depend on five independent test model parameters specified in Eq. (39).

We analyze the stability of time integration algorithms by discretizing Dahlquist´s test equation with a time integration scheme. This yields a linear recurrence equation. The spectral radius $\rho$ of this recurrence equation determines the stability of the time integration method and depends on two parameters $h \varLambda_{r}$ and $h \varLambda_{i}$. Hence, we can generate 2D-stability plots, which illustrate the complete stability behavior of the integration scheme. Discretizing the co-simulation test model with a co-simulation scheme yields a linear system of recurrence equations. The spectral radius of this recurrence system depends on five independent test model parameters defined in Eq. (39). Consequently, it is impossible to depict the complete stability behavior with 2D-stability plots. Therefore one possibility is to fix three of the entire five test model parameters and to depict the spectral radius of the recurrence system as a function of two properly chosen parameters.

Bearing in mind the stability definition for numerical time integration schemes, where the two parameters $h \varLambda_{r}$ and $h \varLambda_{i}$ are used to characterize the stability behavior, it seems to be advantageous not to use the five co-simulation test model parameters introduced in Eq. (39), but to employ five different parameters. The following five parameters might be more convenient to be used as independent test model parameters:

$$\begin{aligned} \begin{aligned} &\overline{\varLambda}_{r1} =- \frac{\overline{d}_{1}}{2}, \quad \quad \overline{\varLambda}_{i1} = \frac{1}{2} \sqrt{4 \cdot \overline{c}_{1} - \overline{d}_{1}^{2}}, \\ & \alpha_{m} = \frac{m_{2}}{m_{1}}, \quad \quad \alpha_{\varLambda_{r}} = \frac{\overline{\varLambda}_{r2}}{\overline{\varLambda}_{r1}} = \frac{\alpha_{d}}{\alpha_{m}}, \\ & \alpha_{\varLambda_{i}} = \frac{\overline{\varLambda}_{i2}}{\overline{\varLambda}_{i1}} = \frac{1}{\alpha_{m}} \frac{\sqrt{4 \cdot \alpha_{m} \cdot \alpha_{c} \cdot \overline{c}_{1} - \alpha_{d}^{2} \cdot \overline{d}_{1}^{2}}}{\sqrt{4 \cdot \overline{c}_{1} - \overline{d}_{1}^{2}}}. \end{aligned} \end{aligned}$$

(41)

The physical interpretation of the new parameters is straightforward: $\overline{\varLambda}_{r1}$ and $\overline{\varLambda}_{i1}$ define subsystem 1 and represent the real and imaginary parts of the eigenvalue of subsystem 1; the mass-ratio is characterized by the coefficient $\alpha_{m}$; The parameters $\alpha_{\varLambda_{r}}$ and $\alpha_{\varLambda_{i}}$ denote the ratio of the real and imaginary part of subsystem 2 with respect to subsystem 1; they describe the asymmetry of the co-simulation test model and characterize the damping and the frequency ratio of subsystem 2 with respect to subsystem 1. Regarding the stability plots for numerical time integration schemes, it seems to be convenient to use the parameters $\overline{\varLambda}_{r1}$ and $\overline{\varLambda}_{i1}$ as axes for 2D-stability plots and to fix the remaining three parameters. In the subsequent stability analysis, the three parameters $\alpha_{m}, \alpha_{\varLambda r}$, and $\alpha_{\varLambda i}$ are therefore assumed to be constant, and the spectral radius is computed as a function of $\overline{\varLambda}_{r1}$ and $\overline{\varLambda}_{i1}$.

With the dimensionless variables and parameters introduced before, the decomposed system reads as

$$\begin{aligned} \textstyle\begin{array}{l@{\qquad}l} \mbox{Subsystem 1:} \\ \qquad \textstyle\begin{array}{l} \overline{x}_{1} ' = \overline{v}_{1},\\ \overline{v}_{1} ' = ( \overline{\varLambda}_{r1}^{2} + \overline{\varLambda}_{i1}^{2} ) \cdot \overline{x}_{1} + 2\cdot \overline{\varLambda}_{r1} \cdot \overline{v}_{1} + \overline{\lambda}_{c} \end{array}\displaystyle & \mbox{(a)}, \\ \mbox{Subsystem 2:} \\ \qquad \textstyle\begin{array}{l} \overline{x}_{2} ' = \overline{v}_{2},\\ \overline{v}_{2} ' = ( \overline{\varLambda}_{r1}^{2} \alpha_{\varLambda r}^{2} + \overline{\varLambda}_{i1}^{2} \alpha_{\varLambda i}^{2} ) \cdot \overline{x}_{2} + 2\cdot \overline{\varLambda}_{r1} \cdot \alpha_{\varLambda r} \cdot \overline{v}_{2} - \frac{1}{\alpha_{m}} \overline{\lambda}_{c} \end{array}\displaystyle & \mbox{(b)}, \\ \mbox{Coupling condition:} \\ \qquad 0= \overline{x}_{2} - \overline{x}_{1}& \mbox{(c)}. \end{array}\displaystyle \end{aligned}$$

(42)

We denote the dimensionless macro time point by $\overline{T}_{N} = \frac{T_{N}}{H}$. At the beginning of the macro time step, the state variables and the coupling variable are assumed to be known:

$$\begin{aligned} \textstyle\begin{array}{l@{\quad }l} \textstyle\begin{array}{l} \overline{x}_{1} ( \overline{t} = \overline{T}_{N} ) = \overline{x}_{1,N},\quad \quad \overline{v}_{1} ( \overline{t} = \overline{T}_{N} ) = \overline{v}_{1,N}, \\ \overline{x}_{2} ( \overline{t} = \overline{T}_{N} ) = \overline{x}_{2,N},\quad \quad \overline{v}_{2} ( \overline{t} = \overline{T}_{N} ) = \overline{v}_{2,N}, \end{array}\displaystyle &\quad (\mbox{a}) \\ \overline{\lambda}_{c} ( \overline{t} = \overline{T}_{N} ) = \overline{\lambda}_{c,N}&\quad \mbox{(b)}. \end{array}\displaystyle \end{aligned}$$

(43)

We define the auxiliary vector $\overline{\boldsymbol{z}}_{N} = ( \overline{x}_{1,N}, \overline{v}_{1,N}, \overline{x}_{2,N}, \overline{v}_{2,N}, \overline{\lambda}_{c} )^{T}$, which contains the dimensionless variables of the two subsystems and the dimensionless coupling force at the macro time point $\overline{T}_{N}$. Using the general coupling force

$$\begin{aligned} \overline{\lambda}_{c}^{*} ( \overline{t} ) = \overline{\lambda}_{c,N+1} \bigl( \overline{\boldsymbol{ \beta}}_{N+1}^{*}; \overline{t} \bigr), \end{aligned}$$

(44)

an integration of the two subsystems from $\overline{T}_{N}$ to $\overline{T}_{N+1}$ with the initial conditions (43)(a) yields the general dimensionless variables

$$\begin{aligned} \overline{x}_{1,N+1}^{*}, \ \overline{v}_{1,N+1}^{*},\ \overline{x}_{2,N+1}^{*},\ \overline{v}_{2,N+1}^{*},\ \overline{\lambda}_{c,N+1}^{*} = \overline{\lambda}_{c}^{*} \quad ( \overline{t} = \overline{T}_{N+1} ) \end{aligned}$$

(45)

at the communication time point $\overline{T}_{N+1}$, which are functions of $\overline{\boldsymbol{\beta}}_{N+1}^{*}$ and $\overline{\boldsymbol{z}}_{N}$. Then the accelerations at the communication time point $\overline{T}_{N+1}$ are computed, i.e.,

$$\begin{aligned} \overline{v}_{1,N+1}^{*'}, \quad \overline{v}_{2,N+1}^{*'}. \end{aligned}$$

(46)

Since the dimensionless variables depend linearly on the coefficient vector $\overline{\boldsymbol{\beta}}_{N+1}^{*}$, three constraint equations

$$\begin{aligned} \begin{aligned} & 0= \overline{x}_{2,N+1}^{*} \bigl( \overline{\boldsymbol{\beta}}_{N+1}^{*}; \overline{ \boldsymbol{z}}_{N} \bigr) - \overline{x}_{1,N+1}^{*} \bigl( \overline{\boldsymbol{\beta}}_{N+1}^{*}; \overline{ \boldsymbol{z}}_{N} \bigr), \\ & 0= \overline{v}_{2,N+1}^{*} \bigl( \overline{\boldsymbol{ \beta}}_{N+1}^{*}; \overline{\boldsymbol{z}}_{N} \bigr) - \overline{v}_{1,N+1}^{*} \bigl( \overline{\boldsymbol{ \beta}}_{N+1}^{*}; \overline{\boldsymbol{z}}_{N} \bigr), \\ & 0= \overline{v}_{2,N+1}^{*'} \bigl( \overline{\boldsymbol{ \beta}}_{N+1}^{*}; \overline{\boldsymbol{z}}_{N} \bigr) - \overline{v}_{1,N+1}^{*\,\prime} \bigl( \overline{\boldsymbol{ \beta}}_{N+1}^{*}; \overline{\boldsymbol{z}}_{N} \bigr) \end{aligned} \end{aligned}$$

(47)

can be solved by one Newton iteration step. Hence the corrected polynomial coefficients are independent of the predicted coupling force. With the corrected coefficient vector $\overline{\boldsymbol{\beta}}_{N+1}$, we finally calculate the corrected variables

$$\begin{aligned} \textstyle\begin{array}{l} \overline{x}_{1,N+1} = \overline{x}_{1,N+1} ( \overline{\boldsymbol{z}}_{N} ),\quad \quad \overline{v}_{1,N+1} = \overline{v}_{1,N+1} ( \overline{\boldsymbol{z}}_{N} ),\\ \overline{x}_{2,N+1} = \overline{x}_{2,N+1} ( \overline{\boldsymbol{z}}_{N} ),\quad \quad \overline{v}_{2,N+1} = \overline{v}_{2,N+1} ( \overline{\boldsymbol{z}}_{N} ),\\ \overline{\lambda}_{c,N+1} = \overline{\lambda}_{c} \quad ( \overline{t} = \overline{T}_{N+1}; \overline{\boldsymbol{z}}_{N} ). \end{array}\displaystyle \end{aligned}$$

(48)

Note that the vector $\overline{\boldsymbol{z}}_{N+1}$ depends linearly on the initial values $\boldsymbol{z}_{N}$. Hence we obtain a system of five coupled linear recurrence equations of the form

$$\begin{aligned} \boldsymbol{A}_{N+1} \cdot \overline{ \boldsymbol{z}}_{N+1} + \boldsymbol{A}_{N} \cdot \overline{ \boldsymbol{z}}_{N} =\boldsymbol{0} . \end{aligned}$$

(49)

We study the stability of the homogenous system (49) by an eigenvalue analysis. With the exponential approach $\overline{\boldsymbol{z}}_{N} = \hat{\boldsymbol{z}}_{j} \cdot \varLambda_{j}^{N}$, we can calculate the eigenvalues $\varLambda_{j}$ and the corresponding eigenvectors $\hat{\boldsymbol{z}}_{j}$ ($j=1, \dots, 5$). The stability of the recurrence system depends on the magnitude of the largest eigenvalue, which terms the spectral radius $\rho= \max \{ \vert \varLambda_{j} \vert \}$. For $\rho\leq1$, the underlying co-simulation approach is stable, and otherwise unstable.

We should stress that the spectral radius can only be calculated numerically. Hence the three parameters $\alpha_{m}$, $\alpha_{\varLambda r}$, $\alpha_{\varLambda i}$ are fixed, and $\rho$ is plotted for different values of $\overline{\varLambda}_{r1}$ and $\overline{\varLambda}_{i1}$. If $\rho\leq1$ for a certain parameter combination, then we mark the corresponding point as a green point in the ($\overline{\varLambda}_{r1}$, $\overline{\varLambda}_{i1}$)-plane. If $\rho>1$, then we plot no point in the stability diagram. Since we can calculate $\rho$ only for discrete parameter combinations, stability information is available only at discrete grid points.

For the case of a symmetrical test model ($\alpha_{m} = \alpha_{\varLambda r} = \alpha_{\varLambda i} =1$), we collect stability plots in Fig. 14. To get information over a larger parameter region, we use two different scales, namely $[ -10,10 ]$ and $[ -1000,1000 ]$. For the symmetrical test model, only stable points are observed, also for the case of large damping values $\overline{\varLambda}_{r1}$ and large stiffnesses $\overline{\varLambda}_{i1}$, both for quadratic ($k=2$) and cubic $( k=3 )$ interpolation polynomials. Further calculations, not shown here, for even larger values of $\overline{\varLambda}_{i1}$ and $\overline{\varLambda}_{r1}$ also yielded only stable points. Hence the numerical stability analysis seems to indicate that the symmetrical test model is stable in the complete left half-plane (comparable with an A-stable time integration scheme). We should however stress again that stability in the left half-plane cannot be shown analytically, since the spectral radius can only be evaluated numerically.

Fig. 14

Stability plots for the symmetrical co-simulation test model: left column for quadratic approximation polynomials (${k}=2$); right column for cubic approximation polynomials (${k}=3$)

We discuss the influence of asymmetry with the help of Fig. 15. Firstly, only the mass ratio coefficient $\alpha_{m}$ is changed from 1 to $1E3$. No change in the stability plots is observed, neither for $k=2$ nor for $k=3$. Next, the damping ratio coefficient $\alpha_{\varLambda r}$ is increased to $1E3$. Again, we detect only stable points in the diagrams. Since both cases—($\alpha_{m} =1E3, \alpha_{\varLambda r} =1, \alpha_{\varLambda i} =1$) and ($\alpha_{m} =1, \alpha_{\varLambda r} =1E3, \alpha_{\varLambda i} =1$)—only yield stable points, the corresponding plots are not shown in Fig. 15. Then, we examine the influence of the frequency ratio. Here a significant reduction of the numerical stability can be seen for the case $k=2$, and an unstable region can clearly be observed close to the vertical axes, i.e., for systems with low damping. Interesting, and somewhat surprising, is that, for $k=3$, no unstable points occur. Finally, we change all three parameters simultaneously ($\alpha_{m} = \alpha_{\varLambda r} = \alpha_{\varLambda i} =1E3$). Using cubic polynomials ($k=3$), all points in the considered parameter range are stable. For $k=2$, again unstable points are detected close to the $\overline{\varLambda}_{i1}$-axis. The region of instability is a little bit smaller compared to the case $\alpha_{m} =1, \alpha_{\varLambda r} =1, \alpha_{\varLambda i} =1E3$, most probably due to the increased damping introduced by the parameter $\alpha_{\varLambda r} =1E3$.

Fig. 15

Stability plots for the asymmetrical co-simulation test model: left column for quadratic approximation polynomials (${k}=2$); right column for cubic approximation polynomials (${k}=3$)

Summary: Using cubic approximation polynomials, the proposed co-simulation approach exhibits a very stable stability behavior. In the case where the subsystems are very different ($\alpha_{m} \neq1, \alpha_{\varLambda r} \neq1, \alpha_{\varLambda i} \neq1$), we are often faced with severe numerical stability problems, especially if higher-order approximation polynomials are used [5, 11, 15, 17, 34, 35]. The method discussed here provides stable results, even for critical parameter values and for the practically interesting case where the subsystems are integrated in parallel (Jacobi-type).