1 Introduction

The use of multibody-based simulation tools has enabled engineers to iteratively design, validate, and re-design new products with reduced prototyping costs. This approach has also been extended to real-time environments [23]. Growing product complexity and the increasing importance of system-level simulation have resulted in renewed research interest in the efficient and accurate coupling of dynamical system solver tools.

A straightforward way to couple the simulation of multiple dynamical systems is the strongly coupled or monolithic approach [22, 27, 29] that yields a single set of equations to be integrated. The benefits of simple and accurate coupling, however, are often overshadowed in practical applications by the loss of modularity. For this reason, co-simulation approaches [2, 3, 15, 35] are used in a large number of multidisciplinary simulations. In co-simulation setups the application under study is divided into several subsystems and a different numerical solver is assigned to each of them. This makes it possible to select simulation tools that specifically fit the nature of each subsystem and allows one to tune their parameters independently. The information exchanged between solver tools is limited to a reduced set of input and output quantities, i.e., coupling variables, and takes place at discrete instants in time. In the macro-step between these communication points the integration of each subsystem proceeds independently, without knowledge of the internals of other system components. This is an attractive feature when coupling solvers and models from different vendors in industrial applications, as the implementation details of each software tool remain unknown to other system components, and so intellectual property is protected.

Following a co-simulation approach, however, poses multiple challenges regarding the stability of the numerical integration and the accuracy of the results. Coupling errors inherently occur as a consequence of discrete-time information exchange and, for that reason, accuracy and stability cannot always be guaranteed. Iterative approaches have been proposed to alleviate this problem [20, 32], but in some cases, such as demanding real-time environments, this may not be a feasible option and, thus, non-iterative schemes need to be used. Moreover, some simulation packages and models do not permit to retake an integration step once it has been completed, which prevents the use of iterative co-simulation schemes if such tools are to be used. When computational efficiency is an issue, the execution of the numerical integration of the subsystems should take place in parallel, following the well-known Jacobi scheme. This means that in each macro-step \([t_{0}, t_{0}+H]\) all the subsystems should perform their numerical integration only with the input variables available at \(t_{0}\), without knowledge of the results delivered by other subsystems at time \(t_{0}+H\).

The use of non-iterative schemes demands additional effort to guarantee the accuracy and stability of the results. This often requires some numerical treatment of the coupling variables. In some cases, a simple polynomial extrapolation of the input values of a subsystem may increase the accuracy of the results and allow the use of larger communication step-sizes. However, as shown in [18], an optimal solution valid for any system at all times cannot be found, in general.

The topic of enhancing the stability of non-iterative co-simulation schemes in a systematic way has been addressed several times in the literature. It is possible to deal with this issue from different points of view. Extrapolation of the coupling variables can be used to make the integration process more stable [9], especially in multi-rate co-simulation environments [14]. As noted in [18], the selection of the extrapolation method often has a critical and strongly case-dependent impact on the accuracy and robustness of the co-simulation process. The performance of extrapolation methods for co-simulation has often been assessed using linear test problems [1, 10]; it is not straightforward, however, to generalize the conclusions obtained with linear systems to more complex applications of industrial interest, whose behavior is frequently highly nonlinear. The methodology introduced in [4] represents a practical way to choose an extrapolation method when simulating complex systems: the degree of the extrapolation polynomial is selected online during the numerical integration process, as a function of the previously known system behavior and a prediction of its immediate evolution. System energy can also be used as a relevant source of information about the stability and accuracy of a co-simulation process [16]. Maintaining the energy balance at the co-simulation interface is the basis for the nearly energy-preserving coupling element introduced in [7]. In [28], in turn, the concepts of power bond and energy residual were used to adaptively select the communication step-size in non-iterative co-simulation schemes. The online selection of macro step-size was also addressed in [6], using frequency-domain analysis instead of energy residuals. Moreover, if one or more of the components of the co-simulation environment are mechanical systems, and some information is available about their internal configuration, other methods can be used as well to achieve a more stable integration procedure. These include using the partial derivatives of the subsystem states with respect to the coupling variables to model more accurately the behavior of mechanical constraints [21, 31] and building reduced-order interface models of the mechanical subsystems to provide more accurate estimations of their evolution between communication points [25].

Despite recent developments and the wide variety of available coupling techniques, polynomial extrapolation is likely to remain a relevant method in the information exchange in co-simulation setups due to its generality and simple implementation. Polynomial extrapolation can be used even when information about the internals of the subsystems is completely unavailable, and lends itself well to multi-rate co-simulation setups and subsystems with nonmatching time-grids. On the other hand, selecting an adequate extrapolation method for a particular co-simulation task is still a challenging and time-consuming endeavor in many cases. Relevant settings in the co-simulation environment, such as the integrator method used in the subsystems, may not be tunable, because their implementation can be hidden from third-party software. Even if they are, their selection is often conducted by trial and error, with little or no information about their effect on the overall accuracy of the simulation. Either way, it is difficult to predict from a theoretical standpoint which extrapolation methods would suit best the co-simulation problem at hand. This is even more challenging if some of the simulation inputs come from external sources, which is the case in Human/Hardware-in-the-Loop (HiL) and System-in-the-Loop (SiTL) applications, where the co-simulation environment interacts with physical components or human operators. Such inputs cannot be anticipated in many cases, and they have a critical effect on simulation stability. For this reason, an automated methodology to select a functional co-simulation configuration, based on a set of pre-determined tests, can represent a valuable tool to co-simulation analysts [5].

In this paper we put forward a methodology to determine a stable and efficient configuration for non-iterative Jacobi scheme co-simulation setups, especially aimed at multiphysics problems in the context of simulation of machinery. The models used in this field often receive inputs that are difficult to predict and feature frequent discontinuities in their dynamics, e.g., the above-mentioned HiL/SiTL simulators and test benches. The subsystems in such applications are commonly solved using relatively simple integration formulas and constant step-sizes, in order to keep the elapsed time in computations short and predictable. A major concern when using these setups is preventing the numerical integration from becoming unstable during execution [33]. Because co-simulation can be used to deal with a very wide range of applications, these conditions may differ from the ones encountered in other co-simulation environments, where it is possible to theoretically determine acceptable error bounds for a given problem, or to modify the integration step-size to match the changing system dynamics [30]. In some cases, the introduction of errors at the coupling interface will give rise to latency instead of instability, which requires a different treatment [34].

The method described in this paper relies on the evaluation of energy residuals at the co-simulation interface, which are used as indicators of the stability of the numerical integration. Subsystem inputs are replaced during the initialization phase with a series of standard test functions and the communication step-size \(H\) is gradually increased until the stability limit is reached. Determining a priori an optimal set of integration parameters and configuration settings for each particular co-simulation application is not feasible in most cases [18], partly because the actual inputs of the numerical simulation are often unknown and the system behavior is highly dependent on these. However, the proposed method provides information to determine a stable co-simulation configuration in a simple manner with little additional effort for the user. The viability of the algorithm was verified in the co-simulation of benchmark problems composed of mechanical and hydraulic subsystems.

2 Methods

This section introduces the co-simulation methodology used in this research and the error estimation via conservation laws, and its application in non-iterative co-simulation. For the sake of clarity the coupling of only two subsystems is considered in this section, although the presented methods could be applied, as it is shown with a case-example, to co-simulation environments with more than two co-simulation units.

2.1 Co-simulation setup

A non-iterative, parallelizable Jacobi-scheme co-simulation approach was selected for the purposes of this work. This scheme is often found in applications that require computational effort to be kept to a minimum, such as real-time environments like heavy machinery simulators, and HiL and SiTL platforms. A generic co-simulation manager tool, intended to couple several subsystems in multi-rate co-simulation applications, was implemented to test the methods described in this paper. The scope of this research is limited to subsystems with fixed integration step-sizes and matching communication time grids, although with multi-rate integration. The proposed method, however, could also be used with variable-step integrators.

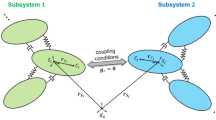
Figure 1 shows the model used in this research, namely two subsystems, 1 and 2, coupled in a co-simulation setup through a co-simulation manager. Each subsystem has its own set of internal states, not disclosed to the rest of the simulation environment. The integration of these internal states is carried out with integrator \(\int _{1} \) and step-size \(h_{1} \) for subsystem 1, and \(\int _{2} \) and \(h_{2} \) for subsystem 2. The communication between 1 and 2 takes place only at discrete points in time, separated by macro time steps of duration \(H \). At communication points, the subsystems provide their outputs \(\mathbf{y}_{1} \) and \(\mathbf{y}_{2} \) to the co-simulation manager and receive their inputs \(\mathbf{u}_{1} \) and \(\mathbf{u} _{2} \). Subsystem 2, moreover, receives a set of external inputs \(\mathbf{w}_{2} \). These may represent interactions with elements that are not contained in the computational environment, e.g., inputs provided by a human operator.

Fig. 1
figure 1

Two subsystems in a co-simulation setup with external inputs \(\mathbf{w}_{2}\)

Full size image

2.2 Power bonds

Multiple error estimation methods have been applied to co-simulation setups [15]. In practice, however, the available options are limited by the application requirements, such as no rollback and fixed step-sizes in real-time cases. A possible solution for this problem was recently introduced by Sadjina et al. in [28], where a conservation law based approach was proposed for a non-iterative adaptive step-size control and error estimation. The method is based on the concept of power bonds and it allows one to monitor the spurious energy created or lost in the signal extrapolation at the co-simulation interface, and requires only little domain knowledge about the co-simulation units. As the underlying theory of power bonds, and bond graphs in general, has been extensively presented in the literature [8, 24], only the topics relevant to this work are presented here.

A power bond is defined by a pair of variables such as velocity and force, often referred to as flow and effort in the literature, whose product is a physical power, and it connects two systems via their power ports, i.e., parts of the system where power flows in and out. In the context of co-simulation, this pair of variables corresponds to the inputs and outputs exchanged between the subsystems, i.e., the coupling variables. To illustrate this, consider the progress of Jacobi-scheme co-simulation between two communication time steps shown in Fig. 2. At communication point \(i-1 \) subsystems 1 and 2 receive inputs \(u_{k_{1}}(t_{i-1}) \) and \(u_{k_{2}}(t_{i-1}) \), respectively. As explained previously, both subsystems then integrate their internal states independently until the next communication point \(i \), when they send outputs \(y_{k_{1}}(t _{i}) \) and \(y_{k_{2}}(t_{i}) \), computed based on their previous inputs \(u_{k}(t_{i-1}) \). Here, the subscript \(k \) refers to power bond \(k \), and, in general, \(u \) and \(y \) can be vectors of power bond variables, as will be explained in Sect. 2.3.

Fig. 2
figure 2

Power bonds in a Jacobi-scheme co-simulation

Full size image

As inputs \(u \) are only known at the communication points, subsystems that use shorter internal time steps \(h < H \) need to extrapolate their inputs until the next update instant. In the case shown in Fig. 2, subsystem 1 needs extrapolated inputs \(u_{k_{1}} \) at every internal micro time step. If only the input value \(u \) is known, but not its derivatives, Lagrange polynomials or least squares fitting can be used to carry out this extrapolation. If the input derivatives \(\dot{u}\), \(\ddot{u}\), …, etc. are also available, the inputs can also be integrated over the communication time step. Both input extrapolation and integration can be carried out either by subsystem 1 or by the co-simulation manager; in the latter case, the subsystem needs to establish a communication with the manager every time that it takes a new internal time step.

In any case, the concept of power bonds can be used to monitor the flow of energy between the systems. Subsystems 1 and 2 exchange energy via power ports \(k_{1} \) and \(k_{2} \), correspondingly, and thus create a power bond \(k \) between the systems. From the Subsystem 1 point of view, the total transmitted power \(P_{k_{1}} \) at a communication time \(t \) can be computed as

$$ P_{k_{1}}(t) = \tilde{u}_{k_{1}}(t) y_{k_{1}}(t)\text{,} $$
(1)

where \(\tilde{u}_{k_{1}}(t) \) is the extrapolated value of the input \({u}_{k_{1}}(t) \) at the end of the communication time step, and \(y_{k_{1}}(t) \) is the output. Correspondingly, the power transmitted by Subsystem 2, \(P_{k_{2}} \) takes the form

$$ P_{k_{2}}(t) = \tilde{u}_{k_{2}}(t) y_{k_{2}}(t)\text{,} $$
(2)

where \(\tilde{u}_{k_{2}}(t) \) and \(y_{k_{2}}(t) \) are, again, the inputs and outputs, respectively.

Ideally, no power should be lost at the coupling interface between the subsystems. Thus, the following balance should hold at any communication point:

$$ -(P_{k_{1}} + P_{k_{2}}) = 0\text{.} $$
(3)

However, as the extrapolation error is an inherent issue in non-iterative co-simulation due to the independent integration of the subsystems, Eq. (3) will be violated during the simulation, and, therefore

$$ -(P_{k_{1}} + P_{k_{2}}) \neq 0 \text{.} $$
(4)

Since the transmitted energy is the power integrated over time, this violation of power leads to the accumulation of errors in the system energy.

2.3 Energy residuals

The violation of energy conservation that unavoidably occurs in non-iterative co-simulation interfaces can be exploited to monitor the simulation accuracy. As presented in [28], a residual power \(\delta P \) can be defined for the power bond \(k \) as

$$ \delta P_{k} = -(P_{k_{1}} + P_{k_{2}})\text{.} $$
(5)

The dot product can be utilized to conveniently compute the residual power for the whole system. For power bonds \([k \ l \ \dots] \), the inputs can be grouped into a vector \(\tilde{\mathbf{u}} = [ \tilde{u}_{k_{1}} \ \tilde{u}_{k_{2}} \ \tilde{u}_{l_{1}} \ \tilde{u} _{l_{2}} \ \dots] ^{\mathrm{T}} \), and the outputs, similarly, \(\mathbf{y} = [ y_{k_{1}} \ y_{k_{2}} \ y_{l_{1}} \ y_{l_{2}} \ \dots ] ^{\mathrm{T}} \). Then the residual power for the whole system can be expressed as

$$ \delta P = -\tilde{\mathbf{u}} \cdot \mathbf{y} $$
(6)

where ⋅ stands for a dot product between two vectors.

In [28], zero-order hold extrapolation was assumed for the input values \(\mathbf{u} \), and, thus, following the notation used in Fig. 2, the residual power \(\delta P _{k} \) at communication time step \(i \) can be written as

$$ \delta P_{k}(t_{i}) = - \mathbf{u}_{k}(t_{i-1}) \cdot \mathbf{y}_{k} (t _{i})\text{.} $$
(7)

On the other hand, if we assume that an extrapolated input is available or can be computed in the co-simulation interface, a more accurate value for the residual power at communication time step \(i \) can obtained:

$$ \delta P_{k}(t_{i}) = -\tilde{ \mathbf{u}}_{k}(t_{i}) \cdot \mathbf{y} _{k} (t_{i})\text{.} $$
(8)

The corresponding energy residual can now be defined [28] by an integral

$$ \delta E_{k} (t_{i}) = \int _{t_{i-1}}^{t_{i}} \delta P_{k} (t) \, dt, $$
(9)

which gives the energy incorrectly added to the coupled system as a result of the extrapolation errors during the time step \(t_{i-1} \rightarrow t_{i} \). These local energy fluxes will inevitably alter the energy balance of the coupled system, and, therefore, deteriorate the co-simulation accuracy.

Numerical approximation can be used to evaluate the integral in Eq. (9). For a constant extrapolation \(\tilde{\mathbf{u}}_{k} (t_{i}) = \mathbf{u}_{k} (t_{i-1}) \) the rectangle quadrature rule can be used, resulting in

$$ \delta E_{k}(t_{i}) \approx \delta P_{k}(t_{i}) H (t_{i}) \text{,} $$
(10)

where \(H(t_{i}) \) is the communication step-size. For higher-order extrapolation, higher-order quadrature rules should be used, to prevent integration errors from becoming of the same order as the accumulated residuals. In the case of linear extrapolation, the energy residual can be approximated with the trapezoidal rule

$$ \delta E_{k} (t_{i}) \approx - \frac{H}{2} \bigl( \delta P_{k} (t_{i-1}) + \delta P_{k} (t_{i}) \bigr) . $$
(11)

For \(m = 2 \), in turn, Simpson’s rule might be appropriate. However, since this formula would require one to know the outputs \(\mathbf{y}_{k} (t_{i-1} + 0.5H) \), which may not be available, in this work trapezoidal rule is used for the extrapolation orders \(m>1 \).

2.4 Co-simulation configuration search

The above presented concept of energy residual [28] allows us now to monitor the co-simulation accuracy. The energy residual is, however, only a scalar value that is not normalized, thus, it may be difficult to interpret on its own. While it is obvious that a relatively low amount of spurious energy with respect to the total transmitted energy accumulated or dissipated at the coupling process indicates stable and accurate co-simulation, the exact point at which the co-simulation accuracy degrades to insufficient or the stability is lost is much less clear. In addition, the residual energy is dependent on the extrapolation method used in the information exchange, which further complicates the accuracy estimation. For this reason, in [28] the energy residual was utilized to develop a scalar error indicator, which requires tuning for each power bond, and an adaptive step-size control for non-iterative co-simulation. Here, a different direction is taken to methodologically evaluate the co-simulation accuracy under different configurations, based on the energy residual.

The definition of co-simulation accuracy, however, also needs to be discussed in this context. The energy residuals do measure the accuracy of the simulation, but only at the co-simulation interface. Assuming that the internal integrators of the subsystems do not introduce any additional errors, the energy residuals directly define the system-level energy error. However, in practice this will not be the case, since the subsystem integrators will introduce their own error into the system-level solution. In this work, it is assumed that the internal integrators are accurate enough for the purposes of the analyst, and therefore the accuracy depends only on the co-simulation configuration. Since the scope of the work is in the area of HiL/SiTL simulators, it is assumed that numerically stable solutions also have sufficient accuracy.

The basis of the proposed approach is illustrated in Fig. 3, where the dependency between energy residual and communication step-size for a nonlinear case example described in Sect. 3.1.1 is presented. In the figure, the energy residual is plotted for polynomial extrapolations of orders 0 to 4 (\(m=0\) to \(m=4\)) and integration of the system inputs (\(I2\)). As can be seen, when the communication step-size is reduced, the residuals appear to approach zero. In the figure, the extrapolation methods other than \(m=0\) yield practically the same value for the linear approximation of the residual by the trapezoidal rule of Eq. (11) at small communication step-sizes, and, thus only one line is visible. In theory, the depicted errors in the energy residuals should be \(\mathcal{O}(H^{m+1})\) [28]. As the figure indicates, this property is lost when the simulation goes unstable, i.e., \(\sum_{i} |\delta E_{k}(t_{i})| \gg \mathcal{O} (H^{m+1})\). When \(H \) is increased the energy residuals are approximately linearly dependent on the communication step-size at first, until either exponential growth is seen, i.e., the accuracy gradually degrades, or the residual suddenly rises to a high value, i.e., the simulation goes unstable. This behavior is further demonstrated in Sect. 4.

Fig. 3
figure 3

Relation between energy residual \(E_{k}\) and communication step-size \(H\)

Full size image

In this work, the observed relation between the communication step-size and the accumulated energy residual over all the macro time steps is taken as an indicator of a stable and accurate co-simulation; it is assumed that the co-simulation is stable and accurate as long as the relation between the accumulated energy residual and communication step-size is approximately linear. This criterion allows us to methodologically evaluate the accuracy of co-simulation under different configurations in a simple manner, with modifications to the co-simulation scheme only implemented in the co-simulation manager. As the number of possible configurations can be too large to experiment manually, an automated procedure, which is described in Sect. 2.4.1, is used to parse through the possible set of configurations. The produced information can be used by an analyst to find a suitable compromise between accuracy and efficiency for the case under study.

However, for practical reasons it would be useful or even required, e.g., when the external inputs \(\mathbf{w} \) are not known, to perform the evaluation in advance without performing the full simulation for each possible configuration. For this reason, and to provide an example of use-case for the method, an application for the methodology is put forward to find a suitable configuration for a co-simulation case in which the external inputs are not know. In practice, the automated procedure uses a set of pre-defined tests for the external inputs \(\mathbf{w} \) when they are unknown.

2.4.1 Automated accuracy evaluation

The entire process of testing the different configurations with several communication step-sizes can be easily automated. In this section an algorithm for the automatic testing procedure, illustrated in Fig. 4, is proposed. Since the external inputs \(\mathbf{w} \) are not, in general, known in advance, they are here replaced with a series of pre-defined tests, described in Sect. 2.4.2 in detail, to examine the system response under different excitations. To make the overall process efficient, the simulation time for each test is defined to be relatively short, i.e., only long enough to verify the response of each test. In the presented example that will follow, a simulation time of 1 s is used for step, ramp, and impulse test, and for the sinusoidal tests the length of one period is used. As information exchange at communication points adds overhead to the co-simulation process, the configuration that achieves the largest communication step-size can often be considered the most efficient for the system. While it would also be possible to tune the internal step-sizes of the co-simulation units, in this work the subsystem with the largest internal step-size is assumed to share the communication step-size, i.e., \(h = H \), and in subsystems with \(h < H \), the internal step-size is kept constant.

Fig. 4
figure 4

Flowchart of the automated accuracy evaluation

Full size image

Admittedly, the assumption of \(h = H \) in the slow subsystem leads to internal integration errors being scaled with \(H \). While the use of smaller internal step-sizes would better decouple the errors that occur in the co-simulation interface and in the subsystem integrators, in practical co-simulation environments this would decrease the overall efficiency of the simulation, as the higher number of integration steps of slow subsystems would increase the total computational load of the problem. As the proposed test methodology aims to reproduce actual operating conditions, the assumption \(h = H\) in the slow subsystem can be justified. Note that the procedure itself is valid for any value of \(h \) inside the subsystems.

In the first step, an initial communication step size \(H_{\text{ini}} \) and an increment \(H_{\text{inc}} \) are selected for the system. The initial communication step size should be selected small enough for a stable solution to be found, i.e., for the energy residual to be in the linear region. It may take more than one attempt to find suitable \(H_{\text{ini}} \) and \(H_{\text{inc}} \) for the system, if no knowledge about the system behavior is available. Secondly, a configuration for the co-simulation is selected and applied. In this paper, this includes the selection of extrapolation methods and options that are available for the co-simulation manager and the integrator methods used in the subsystems; other configuration environments can have different tunable options as part of their configuration space. The selection of the test input \(\mathbf{w} \) for the system takes place at this point as well. In the third step, a simulation is run with the given configuration. Upon completion, if the simulation had been run for the first time with the current configuration, i.e., \(H = H_{ \text{ini}} \), the communication step-size is incremented and the simulation is run again. If the second simulation run succeeds, the linear relation between communication step-size and energy residual is checked. If the latest simulation is still in the linear region, the communication step-size is incremented, \(H = H + H_{\mathrm{inc}}\) and the simulation is run again. If not, or if the simulation failed, the configuration and the largest successful communication step-size are saved, a new configuration set is selected and the process starts again. Finally, after the configuration set space is exhausted, the obtained results are parsed for the user.

2.4.2 External input tests

To assess the system behavior under different inputs, four typical functions, namely step, ramp, impulse, and sinusoidal are used.

In the following, \(v_{0} \) is the initial value of the input, and \(v_{\text{min}} \) and \(v_{\text{max}} \) are the minimum and maximum values that it can take. In addition, the tests are assumed to have a length of 1 second. The step function, here denoted by \(w_{1} \), is defined piece-wise as follows:

$$ w_{1}(t) = \textstyle\begin{cases} v_{0} \text{,} & t < 0.5 \text{,} \\ v_{\text{max}} \text{,} & t \geq 0.5 \text{,} \end{cases} $$
(12)

where \(t \) is the simulation time. It is assumed that the subsystem inputs can be discontinuous, which is often the case if discretely sampled digital controllers are used to feed inputs to the system. The function in Eq. (12) can easily be modified to obtain a continuous approximation of a step function if required.

A ramp function, \(w_{2} \) is also defined piece-wise, as follows:

$$ w_{2}(t) = \textstyle\begin{cases} v_{0} \text{,} & t < 0.5 \text{,} \\ v_{0} + 2(t - 0.5)v_{\text{max}} \text{,} & t \geq 0.5 \text{,} \end{cases} $$
(13)

where the input reaches its maximum value at the end of the simulation time of 1 second. An impulse function is defined as follows:

$$ w_{3}(t) = \textstyle\begin{cases} v_{\text{max}} \text{,} & 0.5-\frac{d}{2} \leq t < 0.5 + \frac{d}{2} \text{,} \\ v_{0} \text{,} & \text{otherwise}\text{,} \end{cases} $$
(14)

where \(d \) is the width of the signal determined by user. Determining the pulse width requires some knowledge of the system, but it is not unreasonable to assume that the analyst responsible for the co-simulation has enough information for an educated guess.

Finally, a sinusoidal function is defined as

$$ w_{4}(t) = v_{0} + a \sin (\omega t) \text{,} $$
(15)

where \(a \) is the user-defined amplitude of the signal and \(\omega \) is the input frequency. Again, a reasonable level of system knowledge is required to set suitable values for these parameters, but it can be assumed that, for instance, the maximum and minimum values and the frequency limits of the input signals are known.

3 Examples

Two case examples were implemented to evaluate the proposed method. A 2-D model of a single-actuator crane was used first to test the method in single-input co-simulation scenarios. A second actuator was later added to this model to evaluate cases with multiple inputs. In this section, both examples are presented together with the hydraulics model used in this research. The different co-simulation configurations tested are subsequently described.

3.1 Multibody models and algorithms

The mechanical systems used as test problems were modeled as multibody systems composed of rigid links, using a set of generalized coordinates \(\mathbf{q}\) subjected to a set of kinematic constraints \({\boldsymbol{\varPhi }}= \mathbf{0}\).

3.1.1 Single-actuator model

A 2-D model of a hydraulically actuated crane is shown in Fig. 5. A similar model was described in [22] and used as test problem in [25].

Fig. 5
figure 5

Single-actuated planar model of a hydraulic crane

Full size image

Link 1 is a rod of length \(L\) and distributed mass \(m\). Link 2 has length \(L_{\text{h}}\) and is considered to be massless. Two point masses \(m_{\text{p}}\) and \(m_{\text{h}}\) are placed at points \(\mathsf{ Q } \) and \(\mathsf{ R } \). The system moves under gravity effects and is actuated with a hydraulic piston that connects points \(\mathsf{ B } \) and \(\mathsf{ P } \). The values of the system properties used in the numerical experiments are summarized in Table 1. The generalized coordinates used to model this system are the \(x\) and \(y\) global coordinates of points \(\mathsf{ P } \) and \(\mathsf{ R } \), and angle \(\theta _{1}\): \(\mathbf{q}= [ x_{ \mathsf{ P } },y_{ \mathsf{ P } },\theta _{1},x _{ \mathsf{ R } },y_{ \mathsf{ R } } ] {^{\mathrm{T}}}\). The system has two degrees of freedom; accordingly, three kinematic constraints are imposed on coordinates \(\mathbf{q}\)

$$ {\boldsymbol{\varPhi }}= \left [ \textstyle\begin{array}{c} L\cos {\theta _{1}} - 2 x_{ \mathsf{ P } } \\ L\sin {\theta _{1}} - 2 y_{ \mathsf{ P } } \\ ( x_{ \mathsf{ R } }-L\cos {\theta _{1}} ) ^{2} + ( y_{ \mathsf{ R } }-L\sin {\theta _{1}} ) ^{2} - L_{\text{h}} ^{2} \end{array}\displaystyle \right ] = \mathbf{0}\text{.} $$
(16)
Table 1 Mechanical parameters of the single-actuated model
Full size table

3.1.2 Two-actuator model

Adding a second hydraulic actuator to the mechanical system in Sect. 3.1.1 we obtain the system in Fig. 6. The mechanical properties of the system are those reported in Table 1. Both actuators are identical; the second one acts between point \(\mathsf{ P } \) and the middle point of link 2. The generalized coordinates \(\mathbf{q}\) and kinematic constraints \({\boldsymbol{\varPhi }}=\mathbf{0}\) used to model this example are the same ones used in Sect. 3.1.1 for the single actuator model.

Fig. 6
figure 6

Double-actuated planar model of a hydraulic crane

Full size image

3.1.3 Multibody system dynamics algorithms

The dynamics of the examples in Sects. 3.1.1 and 3.1.2 was solved by means of two augmented Lagrangian algorithms described in [11]. The trapezoidal rule (TR) was used as integration formula. The first algorithm is an index-1 algorithm (I1AL), in which the system accelerations \(\ddot{\mathbf{q}}\) are used as primary integration variables. The dynamics is solved via the following iterative process:

$$\begin{aligned} & \bigl(\mathbf{M}+ {\boldsymbol{\varPhi }}_{\mathbf{q}}{^{\mathrm{T}}}\alpha { \boldsymbol{\varPhi }}_{\mathbf{q}} \bigr)\ddot{\mathbf{q}}_{j} + {\boldsymbol{ \varPhi }} _{\mathbf{q}}{^{\mathrm{T}}} {\boldsymbol{\lambda }}^{*}_{j} \\ & \quad = \mathbf{Q}- {\boldsymbol{\varPhi }}_{\mathbf{q}}{^{\mathrm{T}}}\alpha \bigl( \dot{\boldsymbol{\varPhi }}_{\mathbf{q}}\dot{\mathbf{q}}+ \dot{\boldsymbol{\varPhi }}_{t}+ 2 \xi \omega \dot{\boldsymbol{\varPhi }}+ \omega ^{2} { \boldsymbol{\varPhi }} \bigr)\text{,} \end{aligned}$$
(17a)
$$\begin{aligned} &{\boldsymbol{\lambda }}^{*}_{j+1} = {\boldsymbol{\lambda }}^{*}_{j} + \alpha \bigl( \ddot{\boldsymbol{\varPhi }}+ 2 \xi \omega \dot{\boldsymbol{\varPhi }}+ \omega ^{2} {\boldsymbol{\varPhi }} \bigr) \text{,} \end{aligned}$$
(17b)

where \(j\) stands for the iteration number. In a problem with \(n\) generalized coordinates and \(m\) kinematic constraints, term \(\mathbf{M}\) is the \(n \times n\) system mass matrix, \(\mathbf{Q}\) stands for the \(n\times 1\) generalized applied forces term, \({\boldsymbol{\varPhi }} _{\mathbf{q}}\) is the \(m \times n\) Jacobian matrix of the constraints, \({\boldsymbol{\varPhi }}_{t}= \partial {\boldsymbol{\varPhi }}/\partial t\), and \({\boldsymbol{\lambda }} ^{*}\) represents the \(m\) Lagrange multipliers of the method. Term \(\alpha \) is a scalar penalty factor, and \(\xi \) and \(\omega \) are scalar parameters that play a role similar to those used in Baumgarte stabilization.

The second method is an index-3 augmented Lagrangian algorithm (I3AL) that uses the generalized coordinates \(\mathbf{q}\) as primary variables. The dynamics equations (17a), (17b) are combined with the trapezoidal rule expressions

$$\begin{aligned} \begin{aligned} &\dot{\mathbf{q}}_{i+1} = \frac{2}{h} { \mathbf{q}}_{i+1} - \widehat{\dot{\mathbf{q}}}_{i}; \quad \mathrm{where}\ \widehat{\dot{\mathbf{q}}}_{i} = \frac{2}{h} {\mathbf{q}}_{i} + \dot{\mathbf{q}}_{i} \text{,} \\ &\ddot{\mathbf{q}}_{i+1} = \frac{4}{h^{2}} { \mathbf{q}}_{i+1} - \widehat{\ddot{\mathbf{q}}}_{i}; \quad \mathrm{where}\ \widehat{\ddot{\mathbf{q}}}_{i} = \frac{4}{h ^{2}} {\mathbf{q}}_{i} + \frac{4}{h} \dot{\mathbf{q}}_{i} + \ddot{\mathbf{q}}_{i}, \end{aligned} \end{aligned}$$
(18)

where \(h\) is the integration step-size, and subscript \(i\) stands for the integration time step, to obtain a system of nonlinear equations at time step \(i+1\) in the form

$$ \mathbf{g} ( \mathbf{q}, \dot{\mathbf{q}} ) = \mathbf{0}, $$
(19)

which is solved by means of Newton–Raphson iteration. Upon convergence of the generalized coordinates \(\mathbf{q}\), the generalized velocities and accelerations \(\dot{\mathbf{q}}\) and \(\ddot{\mathbf{q}}\) are projected upon the constraint manifold to ensure the satisfaction of the derivatives of the kinematic constraints. The method is described in detail in [12] and [13]. Both I1AL and I3AL methods have displayed a robust and efficient performance in the simulation of challenging multibody dynamics problems, e.g., [17].

3.2 Hydraulic model

The hydraulic circuit used to command the actuators was represented using a simple model. The schematics of the circuit are presented in Fig. 7 and its physical parameters can be found in Table 2. The cylinder is connected to a pump and a tank, both of which are simplified as constant pressure sources, and the flow is controlled by a 4/3 directional valve. In addition, at the piston side the flow is restricted with a throttle valve. This model was originally described in [27] and later used with minor modifications in [26]; it is used in this research with different parameters and with the addition of end dampers to the cylinder. The modeling approaches have not been altered for this work. In the case study, the cylinder is connected to the manipulators described at Sects. 3.1.1 and 3.1.2 such that the piston side is attached to point \(\mathsf{ B } \), and the rod side to point \(\mathsf{ P } \).

Fig. 7
figure 7

A hydraulic circuit with three volumes

Full size image
Table 2 Parameters of the example circuit
Full size table

Lumped fluid theory [36] is applied to compute the pressure rates in the hydraulic volumes. This approach splits the circuit into volumes, in which the pressures can be assumed to be equally distributed, i.e., phenomena such as pressure waves are ignored. For the pressure rates in the volumes \(V_{1} \), \(V_{2} \), and \(V_{3} \), this approach yields the following expressions:

$$\begin{aligned} \dot{p}_{1} =& \frac{B_{e1}}{V_{1}}(Q_{31} - A_{1} \dot{s}), \end{aligned}$$
(20)
$$\begin{aligned} \dot{p}_{2} =& \frac{B_{e2}}{V_{2}}(A_{2} \dot{s} - Q_{2V}), \end{aligned}$$
(21)
$$\begin{aligned} \dot{p}_{3} =& \frac{B_{e3}}{V_{3}}(Q_{V3} - Q_{31}), \end{aligned}$$
(22)

where \(B_{e1} \), \(B_{e2} \), and \(B_{e3} \) are the effective bulk moduli of the volumes, \(A_{1} \) and \(A_{2} \) are the piston-side and rod-side areas, respectively, of the cylinder, \(\dot{s} \) is the cylinder velocity, and, finally, \(Q_{31} \), \(Q_{2V} \), and \(Q_{V3} \) are the volume flows over valves. The positive directions of the volume flows are depicted in Fig. 7. The pump and tank pressures, \(p_{P} \) and \(p_{T} \), correspondingly, are assumed to be constant.

The effective bulk moduli take the oil and chamber compressibility into account, and can be expressed for the volumes as

$$\begin{aligned} B_{e1} =& \biggl(B_{o}^{-1} + \biggl(\frac{V_{1} B_{c}}{A_{1} l_{1}} \biggr) ^{-1} + \biggl( \frac{V_{1} B_{h}}{V_{h1}} \biggr)^{-1} \biggr)^{-1} , \end{aligned}$$
(23)
$$\begin{aligned} B_{e2} =& \biggl(B_{o}^{-1} + \biggl(\frac{V_{2} B_{c}}{A_{2} l_{1}} \biggr) ^{-1} + \biggl( \frac{V_{2} B_{h}}{V_{h2}} \biggr)^{-1} \biggr)^{-1} , \end{aligned}$$
(24)
$$\begin{aligned} B_{e3} =& \bigl(B_{o}^{-1} + B_{h}^{-1} \bigr)^{-1}, \end{aligned}$$
(25)

where \(B_{o} \), \(B_{c} \), and \(B_{h} \) are the bulk moduli of the oil, the cylinder, and the hoses, correspondingly.

3.2.1 Valve models

The system valves are modeled following a semi-empirical approach [19], which allows for a simple and accurate model to be built even if all the internal details are not known. For a simple throttle valve the volume flows can be written as follows:

$$ Q = \textstyle\begin{cases} C_{t} \sqrt{ \vert \Delta p \vert }, & \Delta p > 0 , \\ 0 , & \Delta p = 0, \\ -C_{t} \sqrt{ \vert \Delta p \vert }, & \Delta p < 0 , \\ \end{cases} $$
(26)

where \(C_{t} \) is the semi-empirical flow rate coefficient and \(\Delta p\) is pressure difference over the valve. While the semi-empirical coefficient is usually computed from empirical data, here we obtain it from \(C_{t} = C_{d} A_{t} \sqrt{\frac{2}{\rho }} \), an equation for valves with simple geometry where \(C_{d} \) is the flow discharge coefficient and \(A_{t} \) is the throttle area.

For the directional valve the following equations can be used:

$$ Q = \textstyle\begin{cases} C_{v} U \sqrt{ \vert \Delta p \vert }, & \Delta p > 0 , \\ 0 , & \Delta p = 0, \\ -C_{v} U \sqrt{ \vert \Delta p \vert }, & \Delta p < 0 , \end{cases} $$
(27)

where \(C_{v} \) is the semi-empirical coefficient of the directional valve and \(U \) is the feedback signal that corresponds to spool position. The coefficient \(C_{v} \) can be determined from empirical data with \(C_{v} = \frac{Q}{U\sqrt{\Delta p}} \) when the volume flow is known at one operational point. To avoid numerical problems with the solution of Eqs. (26) and (27) near zero pressure difference, these models are replaced with a linear model when \(|\Delta p| < 2~\mbox{bar} \).

To take the valve dynamics into account, the spool position is obtained from the solution of a first-order differential equation

$$ \dot{U} = \frac{U_{\text{ref}} - U}{\tau }, $$
(28)

where the time constant of the valve, \(\tau \), is computed as

$$ \tau = \frac{1}{2 \pi f_{-45}}, $$
(29)

and \(U_{\mathit{ref}} \) is the user-defined reference signal fed to the valve and, here, it can take values from −10 V to 10 V, zero being the closed position. In Eq. (29), \(f_{-45} \) is the frequency at \(-45^{\circ}\) phase shift, read from the Bode diagram of the valve.

3.2.2 Cylinder force

The cylinder force can be computed based on the pressure difference over the piston, and the velocity-dependent friction term. In addition, the end dampers can be taken into account in the force computation. Thus, the force can be expressed as

$$ F = p_{1} A_{1} - p_{2} A_{2} - c \dot{s} + F_{d}, $$
(30)

where \(c \) is the viscous coefficient and \(F_{d} \) is the end damper force. In this case, the end dampers are modeled as a spring–damper system:

$$ F_{d} = \textstyle\begin{cases} k_{d}(l_{d} - l_{1}) - c_{d} \dot{s} & l_{1} \leq l_{d}, \\ -k_{d}(l_{d} - l_{2}) - c_{d} \dot{s} & l_{2} \leq l_{d}, \\ 0 & \text{otherwise,} \end{cases} $$
(31)

where \(l_{d} \) is length of the end damper, and \(k_{d} \) and \(c_{d} \) are the spring and damping coefficients of the damper, respectively.

3.3 Co-simulation configuration

The implemented co-simulation manager is used to couple the above described models by means of a Jacobi-scheme, and also to compute the energy residuals at the interface. The available variables for the information exchange are, in the current implementation, the cylinder length, rate, and acceleration, \(s \), \(\dot{s} \), and \(\ddot{s} \), from the mechanical subsystem, and the actuator force \(F \) from the hydraulics. In addition, the co-simulation manager is responsible for evaluating the extrapolated values of these values, thus allowing use of Eq. (8) in the process of energy residual computation.

Table 3 shows the different co-simulation configuration options used in this study. The mechanical subsystem shares the communication step-size of the co-simulation, i.e., \(h_{m} = H \). The hydraulic subsystem, in turn, has a shorter internal step-size of \(h_{\text{h}} = 0.1~\mbox{ms} \) and therefore requires the input variables, in this case the cylinder length \(s \) and velocity \(\dot{s} \), to be extrapolated. Polynomial extrapolation of orders 0–4, i.e., \(m = 0 \) to \(m = 4\), and also integration of the variables based on their derivatives, i.e., \(I2 \) for the integration of \(s \) and \(\dot{s} \), were implemented to this end. The extrapolation and integration are done on the basis of the variables exchanged at the communication points, extrapolation being performed by the means of Lagrange polynomials within the co-simulation manager.

Table 3 Parameter space
Full size table

The dynamics of the multibody systems was solved using the I1AL and I3AL augmented Lagrangian algorithms described in Sect. 3.1.3, in combination with the trapezoidal rule (TR) integration formula, the integrated variables being, correspondingly, either the accelerations \(\ddot{\mathbf{q}} \) or positions \(\mathbf{q} \). The hydraulics equations were integrated using either the trapezoidal rule or the forward Euler (FWE) formula, and the integrated variables, in turn, were the pressures \(\dot{p}_{1} \), \(\dot{p}_{2} \), and \(\dot{p}_{3} \) from Equations (20)–(22). However, it must be noted that in this study the step-size for the integration of the hydraulics was kept constant and set to 0.1 ms, which was small enough to keep the integration stable with both integrators. Accordingly, changing the hydraulics integration formula had little impact on the co-simulation performance.

3.4 Configuration of the test functions

As the external input of the described hydraulic circuit takes values from −10 V to 10 V, 0 V being the initial position, configuration of the inputs is a rather straightforward process. The step and ramp functions defined in Sect. 2.4.2 can be directly used. As the coupled system can be expected to be quite slow, the width of the impulse is set to 0.4 s to give time for the system to react.

Regarding the sinusoidal input, its amplitude in this case can be set according to minimum and maximum values of the input voltage. Frequencies, in turn, are, in this case, set according to the time constant of the valve. Thus, 35 Hz and 70 Hz, i.e., the frequency at \(-45^{\circ}\) phase shift and its second order, correspondingly, are used, as well as 17.5 Hz.

4 Results

The validity of the co-simulation accuracy and stability criteria discussed in Sect. 2.4 was confirmed comparing the results delivered by a series of simulations, in which some configurations complied with the criteria and others were outside the region assumed to be stable in Fig. 3. In addition, the use of test functions for the external inputs was evaluated. The single actuator model, which contains one external input, was first used for both cases, and, secondly, the double actuator model with multiple external inputs was examined. A user-generated joystick input was introduced in each case as reference signal \(U_{\text{ref}} \) to the directional valve in order to evaluate the criteria and the use of the test functions. Results are compared, when applicable, to a reference solution obtained with a monolithic scheme.

4.1 Single actuator model

Figure 8 shows the actuator length of the single-actuator model with the user-generated input. This input is used to examine the dependency between the accumulation of \(E_{k} \) and \(H \), and it is generated such that the end dampers, which are represented by a contact model, are hit during the simulation. The figure is obtained with \(H=0.2\) ms and second-order extrapolation with I1AL and forward Euler integrators, which, as will be shown next, can be considered a stable and accurate configuration for the system. For this model and input the graph of \(E_{k} \) as a function of \(H \) is already presented in Fig. 3.

Fig. 8
figure 8

The joystick input applied to the directional valve, and the resultant actuator length

Full size image

Figure 9 compares the co-simulation traces between the simulations that are in the approximately linear region and the non-linear region, according to Fig. 3. In the figures, the actuator length \(s \), as obtained from the mechanical system, is depicted for different values of \(H\) during the first half of the simulation cycle. As can be seen, after a certain limit, depending on the extrapolation order, an increase in the communication step-size quickly yields incorrect results, and, thus in Fig. 9f, only \(m = 2 \) remains stable. Compared to Fig. 3 in Sect. 2.4, it is evident that the unstable solutions lie in the highly nonlinear region. As Figs. 9d and 9e demonstrate, however, the increase in error shown for \(m = 1 \) in Fig. 3 is barely evident in the position-level solution. This is better illustrated in Fig. 10, where the corresponding velocity-level solutions are depicted.

Fig. 9
figure 9

Stability and accuracy issues associated with the increase of the communication step-size

Full size image
Fig. 10
figure 10

A detail of the velocity-level solution

Full size image

Figures 9 and 10 support the statement that an approximately linear relation, demonstrated in Sect. 2 with Fig. 3, between the energy residual accumulation and the communication step-size indicates an accurate and stable co-simulation.

Next, the external input of the hydraulic subsystem was replaced with the pre-defined test inputs to determine a stable configuration a priori. The results obtained for the single-actuator model with the algorithm described in Sect. 2.4.1 are given in Table 4. In the table, the subscript of \(H \) refers to the communication step-size increment of the search algorithm; in all cases \(H_{\text{ini}} \) was set to 1 ms. As can be seen, the selected given integrator for the hydraulics and algorithm for the multibody dynamics were the same in all cases. The extrapolation method and communication step-size, in turn, were dependent on the external input.

Table 4 Results of the pre-defined test for the single-actuator model
Full size table

Regarding the obtained communication step-sizes and extrapolation methods, a comparison to the behavior depicted in Figs. 3 and 9 suggests that a stable and accurate configuration can be found with the method, given that the most pessimistic result of those shown in the table, i.e., the configuration with the smallest \(H\), is taken as a final solution. In more detail, the table shows for the ramp and 70 Hz sinusoidal input test communication step-sizes of 5.0 ms and 4.4 ms, correspondingly, with \(m = 2 \). Figure 3, in turn, demonstrates unstable behavior at these communication step-sizes. A possible explanation for this result is that while the user-defined input hit the end-dampers of the cylinder, and thus created a demanding operation point for the simulation, these points were not reached during the short pre-defined tests. Alternatively, it is also possible that these tests, i.e., ramp and 70 Hz sinusoidal inputs, are not demanding enough for the step-size limits to be found.

Table 4 also shows that the step-size \(H\) and the extrapolation method selected by the configuration algorithm differ depending on the input signal used. This result agrees with [18], where it was shown that even for a simple model no all-encompassing optimal co-simulation method can be found, whereas here it is shown that even for exactly the same model a single optimal solution may not exist.

4.2 Double actuator model

In Sect. 4.1, a single subsystem with a single external input was considered. To evaluate the use of the criteria and the automated procedure with more than one subsystem, the double-actuator model is studied here. As described in Sect. 3.1.2, both hydraulic subsystems take one external input, and again, these inputs, resultant actuator lengths of which are depicted in Fig. 11, are defined by user. The figure is obtained with \(H = 1~\mbox{ms} \) and second-order extrapolation, which, as will be show next, is inside the stable region.

Fig. 11
figure 11

Actuator lengths obtained with the joystick input

Full size image

The dependency between the energy residual and the communication step-size with different extrapolation methods for the work cycle of Fig. 11 is depicted in Fig. 12. A behavior similar to the single-actuator model can be seen, although in this case the achieved step-sizes are smaller due to the indirect coupling between the hydraulic subsystems via the mechanical system. Again, the extrapolation methods other than \(m = 0 \) yield almost identical results at small communication step-sizes, and, thus only one line can be seen. The first-order extrapolation and integration of \(s \) and \(\dot{s} \) also yield almost the same residuals. In all cases the energy residual grows at first almost linearly with respect to the communication step-size, until the simulation becomes unstable. In Fig. 13 the actuator positions and velocities for the two cylinders with zeroth-order hold and integration of \(s\) and \(\dot{s}\) are illustrated. As can be seen, at certain point, depending on the used configuration, the simulation quickly becomes unstable. It is noteworthy that the error may not be clearly visible in the position-level solution, whereas the velocity-level solution shows discrepancies, as shown in the figure. Since the energy residual is computed from the velocities and forces, the erroneous behavior is, however, visible in \(\sum_{i} |\delta E_{k}(t_{i}) |\).

Fig. 12
figure 12

Dependency between the energy residual and communication step-size with the double-actuator model

Full size image
Fig. 13
figure 13

Positions and elongation rates of the actuators

Full size image

Again, the external inputs, i.e., the control signals \(U_{\text{ref}} \) of the hydraulic subsystems were replaced with the pre-defined tests. To limit the number of possible configurations, the same input functions were used for both subsystems. Results of the procedure are displayed in Table 5. In this case, the \(H_{\text{ini}} \) was set to 0.5 ms, and the increment also to 0.5 ms. Similar to the single-actuator model, the integrators for hydraulic systems and the formulation for the mechanical system yielded by the configuration algorithm were found to be the same for all test cases. Regarding the extrapolation methods and communication step-sizes, in this case it also seems that a stable configuration can be found, the most pessimistic result from the table being taken as the configuration for the system. While this result may not be the most efficient possible configuration, it seems to be, as Fig. 12 shows, in a stable region also for a more demanding simulation.

Table 5 Co-simulation options delivered by the configuration algorithm for each test case for the double-actuator model
Full size table

5 Discussion

The proposed configuration method discussed in this paper intends to provide a stable initial configuration for a Jacobi-scheme co-simulation in which some external inputs are unknown beforehand. Discontinuities in system dynamics need to be addressed, as they are often detrimental to system stability. In the demonstrated examples, the hydraulic circuit contains multiple potential sources of discontinuities, the end dampers being the most obvious as they represent a contact model. Should the spring and damping coefficients not be properly tuned, an otherwise stable simulation might fail, since the maximum communication step-size in this region might be significantly shorter than in other operation points. In addition to the end dampers, the valve model may become numerically problematic if the linearization of the volume flows is neglected, or if the valve dynamics given in Eq. (28) are not included.

The need for careful modeling of the potentially discontinuous operating points holds true also in the context of the proposed algorithm, since, as is the case with the demonstrated examples, these discontinuities may not be encountered when using test functions as inputs. In these cases the algorithm might fail to provide a useful configuration, if a smooth solution cannot be obtained. This, however, is not a fault of the algorithm itself, but a consequence of the fixed communication step-size and the blind evaluation of states in Jacobi-scheme co-simulation.

In addition to the modeling aspects, attention must be paid to the internal solvers of the subsystems. Regarding this, an interesting observation about the integrators can be made from Tables 4 and 5, as the integrators chosen by the algorithm were the same in all cases. The hydraulic system is numerically stiff, and therefore a small internal integration step-size is required for the forward Euler formula to provide correct simulation results. In this work, it was assumed that the step-size used for the hydraulics was small enough to guarantee that the integration proceeded in an accurate and stable way.

6 Conclusions

In this paper a method for the automatic configuration of Jacobi-scheme co-simulation setups in which some inputs are provided by external sources has been put forward. The method is based on the relation between energy residuals of a stable simulation and the communication step-size at the co-simulation interface; this relation is here exploited to monitor co-simulation accuracy and stability. During the initialization phase of the co-simulation setup, the proposed method replaces the external inputs with standard test functions. A battery of short tests is run during this initialization stage to determine a combination of co-simulation parameters, such as extrapolation method, subsystem integrators, and communication step-size, that can be used to conduct the actual simulation of the system. The energy residual is employed as an indicator to achieve an efficient and stable set of parameters.

The initialization method was tested in the simulation of two mechanical systems with hydraulic actuation. The results indicate that the approximately linear region in the relation between communication step-size and energy residual is the region in which a stable and accurate solution can be found. Thus, the algorithm put forward in this paper seems to be able to provide a stable initial configuration for co-simulation environments in an automated fashion. The use of standardized test functions as a replacement for unknown external system inputs during the initialization phase enables the selection of a set of co-simulation parameters, such as the communication step-size and extrapolation method, to keep the numerical integration stable in an efficient way. As it is the case with co-simulation in general, carefully constructed subsystem models are required for reliable results to be obtained.