Introduction

With landscapes seeing increasing rates of fragmentation and land-use changes, understanding the effects of intervening landscapes on the functional connectivity among populations is gaining importance in species conservation and spatial planning (Collinge 1996; Brennan et al. 2022). Landscape connectivity refers to the degree to which landscape composition facilitates or impedes movement among resource patches (Taylor 1993). In meta-population theory, high connectivity among populations reduces the risk of local extinction (Hanski 1991). Barriers to dispersal, whether complete or incomplete, may hinder the (re)colonisation of suitable habitat and increase population isolation (Haddad et al. 2015). The degree to which organisms actually succeed in moving through the landscape, i.e. the functional connectivity, can therefore alter the distribution of genetic variation by modulating the importance of gene flow and genetic drift (Manel et al. 2003).

Landscape genetics aims to quantify the effects of the landscape matrix on gene flow and the distribution of genetic variation by integrating data and analytical methods of both landscape ecology and population genetics (Storfer et al. 2007; Balkenhol et al. 2016). Since its formal definition in 2003 (Manel et al. 2003), the field of landscape genetics has grown persistently with the development of numerous new methods and wide-ranging applications (Storfer et al. 2010, 2018; Manel & Holderegger 2013). Inferences drawn from landscape genetic analyses have facilitated the implementation of targeted management plans and generated new ecological and evolutionary insights (Segelbacher et al. 2010; Keller et al. 2015). However, the rapid evolution of the field also poses a challenge to ensure that methods yield robust results, i.e. results that are accurate, precise, and reproducible (Richardson et al. 2016). Failure to acknowledge and treat sources of uncertainty in landscape genetics can lead to poor management decisions in the design of wildlife corridors or protected area networks (Beier et al. 2008; Keller et al. 2015). However, landscape genetics is complex and uncertainty can arise from a variety of sources related to sampling design and analytical approaches. Inferences were shown to be affected by sample size (Landguth et al. 2012; Winiarski et al. 2020a, b), sampling design (Oyler-McCance et al. 2013; Seaborn et al. 2019), regression models (Landguth et al. 2012; Shirk et al. 2018; Peterman & Pope 2021), genetic distances (Shirk et al. 2017), unsampled populations (Shirk et al. 2021), spatial scales (Cushman & Landguth 2010a; Galpern et al. 2012; Bauder et al. 2021), and time lags (Cushman & Landguth 2010b; Epps & Keyghobadi 2015).

One method that is gaining popularity is the optimisation of resistance surfaces using the genetic algorithm as implemented in ResistanceGA (Peterman et al. 2019; Winiarski et al. 2020a, b). ResistanceGA provides a model selection framework without requiring a priori assumptions on resistance effects (Peterman et al. 2019). Pairwise genetic distance data enter the linear mixed effects models as a response variable and drive the optimisation of resistance surfaces (Shirk et al. 2018). Researchers have free choice over which genetic distance metric they deem suitable to represent the distribution of genetic variation in their study and both population-based (i.e. where pairwise genetic distance are estimated between subpopulations) and individual-based (i.e. where pairwise genetic distances are estimated between individuals) approaches are possible (Winiarski et al. 2020a, b). The biology and distribution of the study species can inform the sampling design. While a population-based study design is advantageous when individuals form discrete subpopulations, individual-based approaches may be more appropriate in the case of small subpopulation sample sizes or more continuously distributed individuals (Landguth et al. 2010; Shirk et al. 2017; Seaborn et al. 2019). The extent to which such analytical decisions affect resistance surface optimisations has not been fully quantified thus far.

The present study assessed the robustness of results generated by ResistanceGA when using different genetic distance measures for both population- and individual-based approaches with empirical and simulated data. We used the case study of the northern crested newt (Triturus cristatus) in Luxembourg to assess the effect of different sampling and analytical approaches on the identification of the most influential landscape features in defining population genetic structuring. We hypothesised that individual-based models would result in more robust inferences for this study species because additional data points from sparsely sampled ponds could be included, compared to the population-based approach. Simulated datasets were used to evaluate the performance of different genetic distance metrics in their ability to correctly identify the landscape features leading to population structure.

The study species is a pond-breeding amphibian with limited dispersal capacities (Baker & Halliday 1999; Kupfer & Kneitz 2000). During the terrestrial phase, T. cristatus generally shows strong philopatry to its breeding pond by staying within a 100 m radius (Jehle 2000; Jarvis 2016). Long-distance dispersal events, by both females and males, are rare but play an important role in maintaining connectivity among populations and establishing new colonies (Kupfer 1998). Owing to the intensification of agricultural practices, habitat loss and degradation, and landscape fragmentation, populations of T. cristatus have declined across its range (Clemons 1997; Thiesmeier et al. 2009). Around two-thirds of crested newt populations in known breeding ponds had disappeared in Luxembourg by the 1980’s (Gerend 1994). Triturus cristatus is listed on Annexes II and IV of the EU Habitats Directive (Council of the European Communities, 1992) and EU member states must therefore ensure the maintenance or, where appropriate, the re-establishment of a favourable state of conservation of the species and its habitats. In Luxembourg, one of the countries with the most fragmented landscapes in Europe (Babí Almenar et al. 2019), conservation efforts led to the creation and restoration of more than 500 artificial freshwater bodies since 1993. Owing to these habitat restoration projects, in combination with improved monitoring techniques, T. cristatus populations were reported to have expanded their range over the past 20 years (Proess 2016; Glesener et al. 2022). Notably, 14% of created ponds have thus far been successfully colonised by the target species (Glesener et al. 2022). However, an evidence-based understanding of the movement ecology of crested newts could significantly improve the rate of successful colonisations by guiding the optimal location of habitat restoration efforts. As a first step towards using landscape genetics to inform conservation actions of the great crested newt in Luxembourg, this study aimed to assess the limitations and uncertainty of resistance surface optimisations.

Methodology

Sample collection

In spring 2019 and 2020, Laar newt traps were set in 85 ponds in southwestern Luxembourg. Three to four overnight traps were deployed per pond and the presence of any trapped animals was verified the following day. Tissue samples were collected from captured newts by taking non-lethal tail clips, i.e. 3–5 mm of the tail tip, which were stored in 96% ethanol. All fieldwork was performed under permits issued by the Ministry of the Environment, Climate and Sustainable Development Luxembourg (92,671 CD/gp, 95,227 & 95,827 CD/ne).

Laboratory work

DNA extractions from tissue samples were performed with an ammonium acetate salting-out procedure (Miller et al. 1988). Samples were genotyped at 15 microsatellite loci (Krupa et al. 2002; Sotiropoulos et al. 2008; Drechsler et al. 2013) using three multiplex reactions. Multiplex 1 (annealing temperature of 60 °C) contained loci Tcri13, Trci29, Tcri35, and Tcri36. Multiplex 2 (annealing temperature of 62 °C) included Tc50, Tc52, Tc66, Tc68, and Tc81. The third multiplex (annealing temperature of 62 °C) consisted of loci TC58, Tc69, Tc70, and Tc74. Tcri27 and TCM96 were used in individual reactions at an annealing temperature of 60 °C. A reaction volume of 4 µl was used with 1 × GoTaq (Promega) and primer mix at 0.2 µg/µl. PCR reactions were carried out on a S1000 Thermal Cycler (BioRad Inc.) or MasterCycler Nexus (Eppendorf). The PCR products were separated by capillary electrophoresis using an 3730xl DNA Analyzer (Applied Biosystems Inc.). The size of amplification products was estimated using the Genescan ROX-500 size standard (Applied Biosystems Inc.) and GENEMAPPER™ (v.4.0, Applied Biosystems Inc.). PCR reactions were all run in duplicate to verify multilocus genotypes and estimate laboratory inconsistency rates. If genotypes differed, a third run was performed to ascertain the correct allele for the given individual. An allele was accepted when it appeared at least twice. If no consensus was found the individual genotype was removed. Negative controls were included on each plate.

Dataset preparation

Deviations from the expected Hardy–Weinberg genotype proportions were assessed using Fisher’s exact tests based on 1,000 permutations as implemented in the PEGAS R package (v.0.10; Paradis 2010). The cumulative binomial distribution was used to evaluate whether the observed fraction of (unadjusted) significant tests differed significantly from α = 0.05 (Waples 2015). For multiple-testing corrections, the false discovery rate (Benjamini & Hochberg, 1995) was applied. Deviation from linkage equilibrium was tested using a standardised index of association \({\overline{r}}_{d}\) (Agapow & Burt 2001) as implemented in the POPPR R package (v. 2.5.0; Kamvar et al. 2014) with 999 genotype permutations. Incidences of duplicate sampling of the same individual were identified using CERVUS (v. 3.0.7; Kalinowski et al. 2007). One sample was removed at random from pairs with an exact match of genotypes if both samples originated from the same pond.

The inclusion of highly-related samples (e.g. full-siblings) can increase the signal of genetic differentiation among populations and affect population clustering solutions (Goldberg & Waits 2010; Whiteley et al. 2014; Peterman et al. 2016; O’Connell et al. 2019). However, there is an ongoing debate on best-practices regarding the purging of putative siblings from datasets (Peterman et al. 2016; Waples & Anderson 2017). Here, we estimated departure from Hardy–Weinberg proportions within local subpopulations (same pond samples) as \({F}_{IS}\) using the R package HIERFSTAT (v. 0.04–22; Goudet 2005). Subpopulations with a significantly positive \({F}_{IS}\) (confidence interval based on 10,000 bootstrap iterations did not include zero) were inferred to include an excessive amount of highly related individuals and were considered for filtering based on relatedness. Highly-related samples were identified employing Milligan's (2003) dyadic likelihood estimator as implemented in the R package RELATED (v.1; Pew et al. 2015). One individual was removed at random from dyads with an estimated relatedness \(r\) value ≥ 0.5. This threshold value represented the highest \(r\) estimate of unrelated dyads as determined from 400 simulated dyads of known relatedness (i.e. unrelated, half-siblings, full-siblings, parent-offspring) from the observed allele frequencies (Pew et al. 2015).

Genetic differentiation estimation

Observed heterozygosity (\({H}_{O}\)), expected heterozygosity (\({H}_{E}\)), and rarefied allelic richness (\({A}_{R}\)) were estimated in the DIVERSITY R package (v.1.9.90; Keenan et al. 2013) for ponds with sample sizes N ≥ 14 (Suppl. Information; Figures S1-3). Population-specific \({F}_{ST}\) (mode) with 95% highest posterior density interval was estimated in GESTE (v.2; Gaggiotti & Foll 2010). The population-specific \({F}_{ST}\) can be interpreted as the degree of differentiation between the allele frequency of a population and that of the whole metapopulation, where a large \({F}_{ST}\) indicates that the genetic composition of the population differs from that of the metapopulation (Gaggiotti & Foll 2010).

The Bayesian clustering approach as implemented in STRUCTURE (v.2.3.4; Pritchard et al. 2000) was used to estimate the number of distinct genetic clusters \(K\) with the highest support. An admixture model with correlated allele frequencies was assumed. The population-specific ancestry prior and \(\alpha =1/K\) were applied as recommended by Wang (2017). The model was run with a burn-in period of 150,000 Markov-Chain Monte-Carlo (MCMC) iterations, followed by 400,000 MCMC for each \(K\), ranging from one to 15. Three independent runs of fifteen replicates were performed for each value of K to assess consistency among runs. The most likely number of clusters was inferred from the estimated posterior probability for the data \(LnP(D|K)\) and the rate of change in the log probability (\(\Delta K\); Evanno et al. 2005).

The presence of an isolation-by-distance pattern among populations was assessed using Mantel tests, implemented in the ADE4 R package (v.1.7–13; Dray & Dufour 2007), with linearised \({F}_{ST}\), i.e. \({F}_{ST}/(1-{F}_{ST})\), as genetic distance and log transformed Euclidean distances among ponds as geographic distance (Rousset 1997). We employed Weir & Cockerham's (1984) formulation of \({F}_{ST}\) as implemented in the HIERFSTAT R package (v. 0.5–10; Goudet 2005). The probability of the slope estimate of the regression was estimated from 9,999 permutations.

Landscape genetics

Resistance surfaces were optimised using a genetic algorithm, as implemented in the ResistanceGA R package (v.4.1.0.45; Peterman 2018). ResistanceGA does not require a priori assumptions on the effect of landscape surfaces on genetic distance measures and therefore allows for true optimisation without relying on expert opinion. Briefly, ResistanceGA applies a nonlinear functional transformation to one or more resistance surfaces and calculates pairwise effective distances across the transformed surface using the spatial location of genetic samples. A linear mixed-effects model using maximum likelihood population effects (MLPE) parameterisation is fit to the data, with pairwise genetic distance as the response and pairwise effective cost distance as the predictor variables (Clarke et al. 2002). This type of regression model accounts for non-independence of pairwise data. The genetic optimisation algorithm explores parameter space to maximise the statistical relationship between pairwise genetic and cost distances using log-likelihood as objective function.

Environmental resistance surfaces

Candidate landscape resistance surfaces were chosen based on known effects of topology, climate, human structures, land use, and aquatic bodies on gene flow in amphibians (e.g. Hels & Buchwald 2001; Murphy et al. 2010; Gutiérrez-Rodríguez et al. 2017; Homola et al. 2019; Haugen et al. 2020). A full list of candidate surfaces is provided in Table 1 (see Fig. 1 for examples). Landscape features were summarised in a 200 m-by-200 m grid as presence/absence, average grid cell value (Zonal Statistics plugin), coverage percentage in grid cell (overlap analysis tool), or distance from grid cell to a given feature (NNjoin plugin). The 200 m grid cell size was chosen as a compromise between spatial resolution and total number of grid cells to ensure reasonable computation times. ASCII landscape files were all generated using QGIS (v. 3.10.11; QGIS Development Team 2016) with the Luxembourg 1930 (EPSG: 2169) projection.

Table 1 Candidate landscape surfaces considered in resistance surface optimisation models
Full size table
Fig. 1
figure 1

Examples of candidate environmental variables included in the landscape genetic analysis. Black triangles indicate newt sample locations

Full size image

Genetic distance measures

To compare the effect of different genetic measures, we employed both population-based and individual-based genetic measures. In the population-based approach, measures of genetic distance were estimated among sampling sites rather than individuals, thereby drastically decreasing the number of pairwise genetic distances, which reduces the computational power, and concomitantly time, required to carry out optimisations. The disadvantage of this approach is that a minimum number of representative samples is required for an accurate estimation of population-based genetic distances. In our dataset, we sampled population-based metrics for sample sizes of 2, 4, 6, 8, 10, 12, 14, 16, and 18. Fourteen samples were found to be the minimum number of samples that still gave accurate estimates (within 5% of true median) without sacrificing too much data (Suppl. Information, Figures S1-3).

For all ponds with 14 or more samples, 13 different pairwise genetic distance metrics were estimated. The choice of metrics included both biological and geometric (without underlying biological model) distances from the literature. Measures derived from levels of heterozygosity included Weir and Cockerham’s \({F}_{ST}\) (1984), linearised \({F}_{ST}\) (Rousset 1997), and Jost’s \(D\) (2008), estimated in the R packages HIERFSTAT and STRATAG (Archer et al. 2017), respectively. Metrics that do not make biological assumptions included Cavalli-Sforza & Edwards Chord distance (1967), estimated in HIERFSTAT, and Euclidean distances derived from two eigenvector-based multivariate analyses, the principal component analysis (PCA) and factorial correspondence analysis (FCA) for discrete data. The PCA was performed using the dudi.pca function in the ADE4 R package (Dray & Dufour 2007) and pairwise Euclidean distances were calculated between centroids from the first axis, axes 1–2, axes 1–3, axes 1–6, and axes 1–45. PCA axes 1–6 were chosen based on the ellbow technique. Fourty-five axes was the number axes with eigenvalues above average. Similarly, four distances were derived from a factorial correspondance analysis for axis 1, axes 1–2, axes 1–3, and axes 1–10 using dudi.coa (Kimmig et al. 2020).

In contrast to the population-based method, we used data from all 85 sampling sites in the individual-based approach. However, the inclusion of all samples leads to many individuals sampled at the same location, thus an excess of pairwise geographic distances of zero that may skew landscape genetic results (Ruiz-Lopez et al. 2016; Burgess & Garrick 2020). To reduce the number of close-to-zero pairwise geographic distances, we arbitrarly chose four individuals at random from sampling sites with five or more samples. Random point displacement of 1-4 m was applied to individuals with matching sampling locations to generate unique coordinates. To test whether the choice of individuals affected results, we generated three individual-based datasets, each with a different random subset of samples. Shirk et al. (2017) reported that individual-based genetic distances based on multiple-axes PCA maximised model selection accuracy. For each dataset, individual pairwise genetic distances were thus estimated as the Euclidean distance of individual principal component coordinates on one, the first two (1–2), and first three (1–3) axes.

Optimisation of resistance surfaces

Model performance was assessed with the Akaike Information Criterion corrected for small sample sizes (AICc, Akaike 1973; Burnham & Anderson 2002). Because the genetic algorithm is a stochastic process, two independent optimisations were carried out for each candidate surface. The run with the lowest AICc was retained for further model evaluations. To assess the relative support of each optimised resistance surface, we employed a resampling approach implemented as Resist.boot, which sub-sampled 75% of sample locations and resistance distance matrices without replacement and refit the MLPE model and recalculated AICc scores over 1000 iterations with AICc as ranking method. Henceforth, we refer to this modified bootstrapping approach as pseudo-bootstrapping. The candidate surface that had the highest bootstrap support in terms of percentage ranking as top model was considered the best single surface model.

For each population- and individual-based genetic distance response variable, we followed a step-wise model fitting approach (Kimmig et al. 2020) by starting with single surface optimisation SS_optim() for each of the 54 candidate landscape surface layers. A null and distance model were included for comparison. The commuteDistance function implemented in the GDISTANCE R package (v. 1.3–6; van Etten 2017) was used to calculate pairwise cost-distance matrices for the predictor variables. This measure is functionally equivalent to resistance distances calculated with CIRCUITSCAPE (McRae 2006). We employed monomolecular data transformation for continuous variables, except for climate related surfaces, elevation and TWI, for which we also considered Ricker transformations to avoid overfitting (Winiarski et al. 2020a, b). Using the GA.prep() function, we kept default parameter settings, except for increasing the maximum resistance values to 5000, pop.mult to 20, probability of mutation to 0.2, and GA was stopped when no improvement in the objective function was observed over 30 runs. These parameter values were chosen based on preliminary runs that resulted in too few optimisation iterations (< 40) with default settings.

Following the single surface optimisation, we tested multiple surface optimisations using the MS_optim() R function, which combines single surfaces into a composite surface before surface optimisation. All single candidate surfaces which performed significantly better than the ‘Distance’ model, i.e. with AICc lower than the Distance model, were considered for the multi-surface optimisations. However, to reduce the amount of multi-surface optimisations, and thus computational time, we only tested multi-surfaces that contained the top-ranking single surface model after bootstrapping. Candidate covariate surfaces (untransformed) that showed high collinearity (r > 0.6) with an already included model covariate were excluded. As with the single surface optimisation, we ran all multi-surface optimisation in duplicate and performed pseudo-bootstrapping. We continued increasing the number of surfaces included in the model until the more complex model no longer outperformed models with fewer surfaces. When models included two or more categorical resistance surfaces, categorical surfaces were combined into a composite surface by reclassifying values in the order of estimated resistance values from the single surface optimisations. For instance, if the single surface optimisation indicated that presence of ponds was conductive to gene flow but presence of large rivers impeded gene flow, the composite surface grid was coded as 0 for presence of ponds, 1 for the matrix, and 2 for the presence of major rivers (Bowman et al. 2020; Kimmig et al. 2020).

Convergence among empirical surface optimisations was assessed by calculating pairwise Pearson’s correlation coefficients (Pearson’s r) between optimised resistance surfaces using layerStats() from the R package RASTER (v. 3.6–13; Hijmans 2023). To assess whether high model convergence also translated into high correlation between derived conductivity maps, current maps were generated in CIRCUITSCAPE (V.4.0) for the best-performing genetic distance metrics (see below). One hundred focal nodes were randomly placed along the edge of the study area, which was shown to create less bias than the placement of nodes within the study area (Koen et al. 2014). Resulting conductivity maps were compared using Pearson’s r.

Simulations of resistance surface optimisations

Simulations were conducted to evaluate whether the machine learning optimisation approach described above was able to infer the truthful effect of landscape features on gene flow in this specific ecological context and to guide the choice of the most appropriate genetic distance metric. Spatially-explicit demo-genetic simulations were generated in CDPOP (Landguth & Cushman 2010), based on parameters derived from the empirical dataset. Four empirical environmental rasters (i.e. precipitation, roughness, motorways, and major rivers) were transformed to four separate resistance surfaces using the transformation functions (inverse Ricker, inverse Monomolecular, Monomolecular, inverse Monomolecular, respectively), shape parameters (i.e. 4, 0.15, 5, 1), and maximum resistance values (20, 2500, 50, 1000), as observed in the empirical dataset. These generated input resistance surfaces were then employed to create cost distance matrices for each simulated feature constraining individual dispersal during the gene flow simulations (Landguth & Cushman 2010). There were thus four separate simulated scenarios (i.e. precipitation, roughness, motorways, and major rivers), each time with a single feature simulated to significantly impact gene flow.

Simulated sampling sites were limited to ponds with T. cristatus samples in the empirical dataset. As the true abundance of newts at the sampling locations was unknown, it was assumed that sample sizes represented 10% of the total number of newts per pond, which translated into simulating 10 times the number of empirical samples per pond. The assumption of a 10% capture rate was based on similar capture probabilities derived from mark-recapture studies (e.g. p = 0.06–0.13; Unglaub et al. 2021). The simulated genetic data consisted of 15 loci with eight alleles each to mimic the original dataset (15 loci and an average of 7.53 alleles per locus). Simulations were conducted for 100 nonoverlapping generations assuming a random mutation rate of 0.0005. All movement across the landscape followed an inverse square probability with a movement threshold of 0.1. To further respect the empirical ecological and demographic context, simulations were parameterised to reflect the slope of the isolation-by-distance pattern of the empirical dataset (within 0.004), estimated as correlation between Loiselle’s kinship (Loiselle et al. 1995) and the logarithm of the geographic distances between simulated individuals (Rousset 2000). Additional parameter settings for CDPOP are detailed in Supplementary Information Table S1.

Sampling from the simulated data followed the same approach as the empirical analysis, with four individuals per pond for the individual-based models and the same number that were empirically sampled in ponds with 14 or more newts for population-based models. To compare the performance of different genetic distance metrics, surface optimisations in ResistanceGA were carried out with the same three individual-based and 13 population-based genetic distances as for the empirical analysis. Candidate landscape surfaces were limited to the four surfaces used to create the simulated data (i.e. precipitation, roughness, motorways, and major rivers). Single- and multi-feature models with all possible combinations were fitted and compared using pseudo-bootstrapping, as described for the empirical analysis. For each simulated dataset, two independent resistance surface optimisations were run. To assess robustness of results, three distinct sets of simulated individuals were derived from each simulated resistance surfaces for both individual- and population-based simulations, yielding a total of 384 simulated optimisations.

Evaluation of simulation results

To assess whether surface optimisation of the simulated data succeeded in recovering the true resistance surface, Pearson’s r was calculated between the optimised resistance surface and the ‘true’ resistance surface that had been used to generate the given simulated data. We refer to this as ‘resistance recovery’ herein (Beninde et al. 2023). The influence of using AICc or percentage top to order bootstrapping results was evaluated by comparing resistance recoveries between both approaches. Convergence between repeat runs was assessed by calculating Pearson’s r between optimised resistance surfaces, where a value of one would indicate that both runs had converged on the same resistance surface. A two-sample Wilcoxon test was used to assess whether the run repetition with lower AICc yielded higher resistance recovery. Convergence among resistance recoveries of the three independent sets was tested using a Kruskal–Wallis rank sum test in R. Results of the individual- and population-based approaches were compared in terms of the number of features retained in the final model, resistance recovery, and type I error rates. Type I error rate was here defined as the percentage of total iterations in which the top model did not correspond to the true data generating surface. The performance of different genetic distance metrics was evaluated using two criteria, namely the high resistance recovery and high true model identification (low type I error rates). The performance of marginal \({R}^{2}\) in terms of model fit metric was tested by calculating the correlation between marginal \({R}^{2}\) and resistance recovery.

Results

Genetic diversity

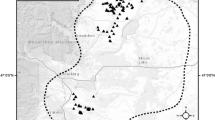
A total of 897 northern crested newt non-lethal tail clip samples were collected from 85 locations in the study area in 2019 and 2020 (Fig. 2A) and genotyped at an average of 14.8 loci (minimum 13 loci). The laboratory inconsistency rate was estimated at 1.04%. Sample sizes per pond ranged from one to 31 samples, with an average of 10.6 samples per pond. Population-based analyses were based on 37 ponds with N ≥ 14 samples (Fig. 2C). Five duplicated and 11 highly-related samples, collected from the same pond, were removed from the dataset prior to data analysis. Among the 555 Hardy–Weinberg proportion tests (37 ponds × 15 loci), 11 tests yielded p < 0.05 prior to multiple-testing correction, with no locus showing significant deviations in more than three tests. The observed number of unadjusted test results fell below the 95% binomial confidence interval (95% CI: 18 – 37) of expected significant tests, indicating that the nominal level of α = 0.05 was too conservative and that results were consistent with an assumption of Hardy–Weinberg proportions. Similarly, following false discovery rate correction, there were no significant deviations from Hardy–Weinberg proportions. No significant deviations from linkage equilibrium were observed (total \({\overline{r}}_{d}\) = 0.0015, p = 0.213). All loci were therefore retained for analysis. Summary population statistics were estimated for thirty-seven ponds where N ≥ 14 (Table 2). The average \({H}_{E}\) and \({H}_{O}\) were estimated at 0.48 (standard deviation (SD) 0.03) and 0.51 (SD 0.04), respectively. Population-specific \({F}_{ST}\) was highest for samples from ponds 4 (Bissen, pop \({F}_{ST}\) = 0.222), 3 (Bissen, pop \({F}_{ST}\) = 0.195), and 19 (Mamer, pop \({F}_{ST}\) = 0.186), with an overall average of 0.098 (SD 0.044, Table 2, Fig. 2C). Pairwise genetic distances ranged between \({F}_{ST}\) = 0 – 0.218, with an average \({F}_{ST}\) estimated at 0.081. The highest levels of genetic divergence were observed in pairs including ponds 3, 4, 19 and 28 (Suppl. Information Figure S4).

Fig. 2
figure 2

A Pond locations with respective sample sizes of crested newts (Triturus cristatus) are shown in relation to major rivers, primary roads and motorways, and urban areas. Sample sizes exclude duplicate and closely related samples. The bounding polygon represents the study area used in the ResistanceGA analysis with its location in respect to neighbouring countries shown in B. C Spatial distribution of population-specific \({F}_{ST}\) estimates coded by colour. Darker colours indicate populations with more divergence from the ancestral population and thus reflect reduced gene flow. Municipal borders are shown. Numbers correspond to location names in Table 2

Full size image
Table 2 Summary statistics for ponds with ≥ 14 samples
Full size table

Genetic clustering

The clustering solution at \(K=\) 13 scored the highest posterior probability \(LnP(D|K)\), with the highest rate of change in the log probability (\(\Delta K\); Evanno et al. 2005) recorded at \(K =\) 2. A levelling-off of the log probability curve, and corresponding local maximum in \(LnP{\prime}{\prime}(K)\), also occurred at \(K =\) 5 (Suppl. Information Figure S5). At \(K =\) 2, samples were partitioned into a southern and a northern cluster, with a latitudinal boundary roughly at 49°39’N, between the communes of Mamer and Kopstal (Fig. 3A, Suppl. Information Figure S6A). Further spatial genetic differentiation was evident at \(K =\) 5 for the samples in Sanem, Mamer, and two locations in Bissen (Fig. 3B). The clustering solution at \(K =\) 13 suggested additional fine-scale genetic structuring (Fig. 3A, Suppl. Information Figure S6B).

Fig. 3
figure 3

A Clustering solution at K = 2, 5, and 13 as estimated in STRUCTURE. Samples are ordered by municipality locations from south (left) to north (right). B Spatial distribution of population admixture averages for K = 5 with colours corresponding to cluster assignments in A

Full size image

Pairwise genetic divergence was significantly correlated to geographic distance with Mantel’s \(r\) estimated at 0.29 (\(p\) < 0.001, Suppl. Information Figure S7).

Varied convergence among optimised resistance surfaces

The input for the population-based resistance optimisations consisted of 666 pairwise genetic distances from the 37 locations (Suppl. Information Figure S8). All genetic distance metrics were highly correlated (Pearson’s r > 0.6, Suppl. Information Figure S9). Among the 56 tested landscape features, models with the topographic descriptor ‘roughness’ consistently yielded the highest pseudo-bootstrap support for all population-based genetic distances, except for Chord’s distance and PCA axes 1–6, for which the geographic distance model outperformed landscape resistance models (Table 3). Roughness was the only covariate retained for models using FCA axis 1 and FCA axes 1–2, Jost’s D, PCA axis 1, and PCA axes 1–45. When employing \({F}_{ST}\), linearised \({F}_{ST}\), and FCA axes 1–3 as genetic distance measure, the final optimised models included the predictors roughness and the soil category Cmeu (soil9), an eutric cambisol. The percentage coverage by motorways and primary roads was retained alongside roughness in the final models for PCA axes 1–2 and axes 1–3.

Table 3 Results of ResistanceGA model optimisations for both population- and individual-based genetic distance metrics
Full size table

When limiting the maximum number of samples per pond to four, 298 individuals were retained for the individual-based analysis, equivalent to 44,253 pairwise genetic distances. While genetic distance metrics correlated strongly within datasets (Pearson’s r > 0.6), correlation was weak between datasets (Suppl. Information Figure S10). In contrast to the population-based genetic distance models, the complexity and composition of individual-based models varied greatly among genetic distances measures (i.e. PCA axis 1, axes 1–2, and axes 1–3) and among datasets (three datasets, each with four randomly chosen samples from ponds with > 4 samples; Table 3). Spring precipitation and percentage coverage by motorways and primary roads were significant predictors of gene flow in six out of the nine fitted models. Variables relating to the presence of major rivers or ponds and soil categories were included in five models. Percentage coverage of various forest types featured in three models, while the topographic characteristics ‘roughness’ and ‘terrain ruggedness index’ were each retained in one out of the nine models. When summarising the percentage contribution estimated across all individual-based models with the highest bootstrap support, climate-related predictors accounted for 33.3%, followed by water-related predictors at 25.3% and terrain cover related to pastures and forests at 12.3%. Road and rail variables contributed 11.2%, soil categories 10.1%, and terrain topography 7.1%. Urban-related variables merely accounted for 0.7% contribution.

Resistance surfaces showed high convergence in terms of pairwise Pearson’s r for population-based models (Pearson’s r = 0.84–1, mean = 0.95, Fig. 4). Conversely, individual-based models yielded low correlation coefficients, even among sets with the same genetic distance metric (Pearson’s r = -0.64–0.53, mean = 0.07). Only a single individual-based model (Set 2, PCA axes 1–2) showed high correlation with the results of the population-based models. Incidentally, this was the only individual-based model that had retained roughness as feature in the final model.

Fig. 4
figure 4

Pearson’s r between optimised resistance surfaces for top-ranking models of empirical dataset derived using individual- and population-based genetic distance metrics and different sets of individuals (S) for the individual-based analysis

Full size image

Only the final model that achieved the highest bootstrap support based on percentage top (%top) is shown for each distance metric.

Differing levels of resistance recovery in simulations

Ordering bootstrap results by ‘percentage top’ and lowest AICc yielded top-ranking models with similar resistance recovery (% top: r = 0.60, AICc: r = 0.59) and number of true model identifications (% top: n = 195, AICc: n = 181 out of 384 models), without statistically significant differences. Hereafter, ranking of bootstrap results was done by percentage top. When comparing between repeat runs, top-ranking models from run 1 and run 2 showed high correlation (Pearson’s r = 0.86, 95% confidence interval (CI) 0.82 -0.90), where the repeat with the lowest AICc resulted in significantly higher resistance recovery (paired Wilcoxon signed rank test, V = 7026, p < 0.005). In subsequent tests, we only retained the top-ranking model from the repeat with the lowest AICc. There were no significant differences in resistance recovery among the three independent sets of simulations (Kruskal–Wallis \({\chi }^{2}\) = 4.04, df = 2, p = 0.13).

While resistance recovery was similar between the individual- (median r = 0.79) and population-based (median r = 0.84) approaches (Wilcoxon signed rank test, W = 2295, p = 0.09, Fig. 5), top-ranking models in the individual-based simulations retained significantly more features (mean n = 1.6) in the final model compared to the population-based ones (mean n = 1.2, Wilcoxon signed rank test, W = 3575, p-value < 0.001). The true simulated surface was identified slightly more frequently in the population-based approach (35.9%) compared to the individual-based approach (30.6%), equivalent to a type I error rate of 64.1% and 69.4%, respectively, but the difference was not statistically significant.

Fig. 5
figure 5

Median Pearson’s r between the true data generating surface and the optimised resistance surface from the simulated datasets for both the individual- (shaded grey) and population-based approaches. Point coloration denotes the nature of the simulated resistance surfaces

Full size image

For the individual-based models, resistance recovery did not differ significantly among the three tested genetic distance metrics (Kruskal–Wallis \({\chi }^{2}\) = 2.80, df = 2, p = 0.25). Conversely, the 13 tested population-wise genetic distances showed clear differences in resistance recovery (Kruskal–Wallis \({\chi }^{2}\) = 25.73, df = 12, p = 0.012, Fig. 5). Across simulated features, Jost’s D was the genetic distance metric with the highest resistance recovery (mean r = 0.96) and identifications of the true resistance surface (58.3%). PCA axes 1–45 yielded the second highest resistance recovery (mean r = 0.87) and true model identifications (41.7%). \({F}_{ST}\) also identified the correct model in 41.7% of scenarios, with an average resistance recovery of 0.70. These three genetic distance metrics were thus retained as the most appropriate measures for the empirical dataset.

There was a significant effect of the underlying simulated landscape features (Kruskal–Wallis \({\chi }^{2}\) = 35.58, df = 3, p < 0.001, Fig. 5). Simulations based on the precipitation resistance surface showed the highest convergence and resistance recovery (median r = 0.97), while results were more variable for simulations with roughness and motorways in the population-based approach (Fig. 5). Simulations with the river resistance surface resulted in very poor resistance recovery scores for both individual- and population-based models (median r = 0.071). In the simulated datasets, marginal \({R}^{2}\) was negatively correlated to resistance recovery for both individual-based (Pearson’s r = -0.18, t = -2.23, df = 154, p = 0.027) and population-based (Pearson’s r = -0.27, t = -1.64, df = 34, p = 0.11) approaches.

Effect of model uncertainty on conductivity maps

The current maps generated in CIRCUITSCAPE using the three best-performing population-based genetic distances in the simulations (Jost’s D, \({F}_{ST}\), PCA axes 1–45) showed areas of high conductivity in the north and south-east of the study area (Fig. 6). High topographical roughness corresponded to areas with high conductivity. In all three maps, the central area was characterised by low conductivity, particularly the map derived from the \({F}_{ST}\) model where the inclusion of eutric cambisols reduced gene flow. Despite strongly correlated resistance surfaces between Jost’s D and \({F}_{ST}\) (Pearson’s r = 0.89), the derived current maps bore significant differences with the surface correlation reduced to 0.64. Current maps built from the resistance surfaces from the Jost’s D and PCA axes 1–45 models showed high convergence (Pearson’s r = 0.996).

Fig. 6
figure 6

Current maps generated in CIRCUITSCAPE for three best population-based genetic distances (according to the simulations). Yellow colour indicates areas with low resistance. The location of ponds with (pink triangles) and without (white dots) northern crested newt samples are shown

Full size image

Discussion

This study assessed the robustness of landscape genetic inferences using the northern crested newt as a case study. Considering the low rate of successful colonisations of newly created and restored breeding ponds by T. cristatus in Luxembourg over the past two decades (ca. 14%, Glesener et al. 2022), there was an urgent need to identify the key landscape features that facilitate or impede the dispersal of the target species. Landscape genetics is a powerful tool to provide evidenced-based understanding on species movement ecology (Segelbacher et al. 2010; Manel & Holderegger 2013). However, concrete applications of landscape genetic inferences to conservation planning may be hindered by a lack of established best practices for new methods in this rapidly evolving field (Richardson et al. 2016).

The population genetic structuring of T. cristatus was characterised by strong spatial clustering, most likely as a result of the species’ limited dispersal ability and high site fidelity (Kupfer & Kneitz 2000). The observed differences in genetic diversity indices (e.g. population-specific \({F}_{ST}\)) among proximate ponds suggested that site specific factors may also play a role in driving differentiation. Broadly partitioned into northern and southern communities in our study area, the 13 distinct clusters followed a stepping stone model of gene flow, implying recurrent gene flow among neighbouring patches and isolation with greater geographic distance. Overall, population genetic differentiation (i.e. pairwise \({F}_{ST}\) estimates) was within the range of previously reported levels for this species (e.g. Haugen et al. 2020). Based on Bayesian clustering and population-specific \({F}_{ST}\), three areas were characterised by higher genetic differentiation from the whole metapopulation. Crested newt clusters in the municipalities of Bissen, Mamer, and Sanem may host populations with reduced genetic connectivity to other breeding populations. The effect of isolation-by-resistance on genetic connectivity was therefore explored using landscape genetics.

Recent studies have highlighted effects of sample sizes, sampling schemes, or spatial scales (Oyler-McCance et al. 2013; Winiarski et al. 2020a, b; Bauder et al. 2021). The choice of the best study design and analytical approaches may therefore not be evident a priori and preliminary analyses or simulations may be required to offer guidance. Given that larger sample sizes were previously linked to higher model accuracy (Landguth et al. 2012; Winiarski et al. 2020a, b), we had anticipated that the individual-based approach with data from 298 individuals at 85 locations would perform better than the population-based approach with a more moderate sample size of 37. However, the simulation results suggested that individual-based models tended to overestimate the complexity of the underlying landscape resistance. This tendency was also reflected in the empirical models, where the individual-based approach yielded significantly more complex multi-surface models compared to the population-based approach. Furthermore, repeated runs with differing sets of individuals led to widely different multi-surface models in the empirical analysis, severely questioning the validity of individual-based inferences. These results corroborate findings by Winiarski et al. (2020a, b), who reported a type I error rate of 78% for their simulated individual-based multivariate models in ResistanceGA. Given the negative correlation between marginal \({R}^{2}\) and resistance recovery, marginal \({R}^{2}\) is not a suitable metric to compare among models derived using different genetic distance measures. This result is accordance with recommendations by Beninde et al. (2023) who also advised against using marginal \({R}^{2}\) as metric to identify the most suitable genetic distance metric.

The source of the poor performance of individual-based optimisations may be overfitting to noise that is inherent to genetic data (Winiarski et al. 2020a, b). In our case, the close spatial proximity of clustered samples might have exacerbated the problem by introducing an excess of close-range distances. We aimed to mediate against this effect by limiting samples to a maximum of four per breeding pond. Other studies have taken more drastic measures and only retained a single sample per raster cell (Ruiz-Lopez et al. 2016; Burgess & Garrick 2020), but such data purging is not a viable option for pond breeding amphibians where clustered sampling is often the norm. Furthermore, such recommendations are currently not based on a systematic evaluation on the effect of clustered sampling in ResistanceGA. Given the clustered occurrence of pond-breeding amphibians, the population-based approach is the most appropriate choice. While the individual-based approach may perform better with more continuously-distributed samples, Beninde et al. (2023) highlighted that resistance recovery tends to be poor when gene flow is impacted by multiple landscape features. The performance of individual-based models might also have been affected by our choice of genetic distance metrics. Comparing different classes of individual-based genetic distances was beyond the scope of the present study and has been addressed elsewhere (Shirk et al. 2017; Beninde et al. 2023). The lack of convergence among individual-based models fitted using different sets of individuals has highlighted the importance of performing true bootstrapping or cross-validation with independent surface optimisations to overcome high type I errors and overfitting (Winiarski et al. 2020a, b). In fact, the pseudo-bootstrap approach of ResistanceGA may provide false confidence in model inferences and should be interpreted with great caution (Winiarski et al. 2020a, b). The extent to which the parameterisation of the genetic algorithm in ResistanceGA may influence results has not been thoroughly tested and could provide an avenue to improve resistance optimisations. While individual-based analyses performed well in other types of landscape genetic analyses (Prunier et al. 2013; Seaborn et al. 2019), challenges persist in their application in ResistanceGA.

Population-based simulations revealed significant differences in convergence and resistance recovery among tested genetic distance metrics. Overall, type I error rates amounted to 64.1%, significantly higher than the 24% reported in a simulation study using larger sample sizes and a synthetic distance metric (Winiarski et al. 2020a, b). Notably, we found significant differences in model performance depending on the nature of the underlying resistance surface, with type I error rates for linear features (i.e. roads and rivers, 83.3%) being nearly double that of continuous features (i.e. precipitation and roughness, 44.9%). Since landscape genetic studies are increasingly being used to inform wildlife corridor designs or to quantify effects of habitat fragmentation, there is an urgent need to conduct more in-depth simulations to validate our results on linear feature surface optimisations as our conclusions are based on a limited number of simulations. The bias towards continuous resistance surfaces in evaluation studies (Peterman et al. 2014; Shirk et al. 2017; Winiarski et al. 2020a, b) raises the question of how many studies might have underestimated the effects of fragmentation by roads due to high type I error rates for linear features. Previous studies found largely congruent model selection using different genetic distance metrics (e.g. \({F}_{ST}\), Jost’s D, Chord, \({G{\prime}{\prime}}_{ST}\), Gutiérrez-Rodríguez et al. 2017; Peterman et al. 2014), but they only compared single feature models. Haugen et al. (2020) reported consistent results for multi-surface model rankings with \({F}_{ST}\) and Chord distance. In our simulations, the commonly used \({F}_{ST}\) was outperformed by Jost’s D in terms of lower type I error rates (16.6% lower) and higher resistance recovery. Since the simulations were tailored to the specific study design of our empirical analysis, we cannot conclude that Jost’s D is the best performing genetic distance metric in other case studies. However, our findings do highlight that the common practice of choosing a single genetic distance metric, often \({F}_{ST}\), may not yield the most robust results and alternative metrics should be explored to assess convergence.

Across the empirical population-based models, the topographic characteristic roughness was repeatedly retained as most significant explanatory variable. The variation in dispersal costs across different topographical terrains have previously been reported as important factor in structuring amphibian populations (Marsh et al. 2005; Giordano et al. 2007; Richards-Zawacki 2009). Here, the association of low resistance with high roughness, such as valleys or hillcrests, may indicate that dispersing T. cristatus follow along valleys or the foot of hills to find new breeding ponds. However, despite highly correlated optimised resistance surfaces of the three best-performing genetic distance metrics (Jost’s D, \({F}_{ST}\), PCA axes 1–45), the resulting conductivity maps revealed large discrepancies. Since the resistance surface derived from \({F}_{ST}\) also included the categorical soil 9 variable (eutric cambisol), the central part of the study area was inferred to have very low conductivity. This example showed that despite largely congruent results of resistance surfaces (e.g. 89% correlation between \({F}_{ST}\) and Jost’s D), any uncertainty in model specifications may be amplified in the derived conductivity maps. In a conservation context, this means that even seemingly subtle differences among optimised resistance surfaces could lead to substantially different inferences and recommendations.

Before recommending roughness as the most important landscape feature driving population genetic structuring in T. cristatus in Luxembourg, further limitations need considering. The impact of linear features such as roads may have been underestimated due to high type I error rates in the resistance model selection. The presence of roads was previously linked to reduced landscape connectivity (Matos et al. 2019; Haugen et al. 2020) and increased mortality (Hels & Buchwald 2001) in T. cristatus. Even if genetic connectivity can be maintained across roads with a few successful dispersers per generation, a depletion effect caused by high road mortality could reduce genetic diversity (Jackson & Fahrig 2011). Additional relationships between the intervening landscape and genetic differentiation may also have been missed if the true defining landscape features were not included among the tested variables. While we considered a variety of landscape and environmental features known to affect amphibian dispersal, the top-performing model may not fully capture the underlying landscape effects of T. cristatus in Luxembourg. The inferences drawn from this study are also limited by our choice of a single spatial scale. Multiple studies have shown the effect of different spatial grains, highlighting scale-specific relationships between gene flow and landscape features (Cushman & Landguth 2010a; Galpern et al. 2012; Bauder et al. 2021; Cox et al. 2021). The present results represent a coarse-scale analysis, which was linked to higher correlations between true and optimised surfaces in ResistanceGA (Winiarski et al. 2020a, b). The spatial extent of the study area and the distance among sampling ponds exceed the average home ranges and dispersal distances of northern crested newts. Results are therefore best described as the effect of landscape on genetic differentiation, rather than gene flow per se. A finer-scale analysis may have revealed more direct effects of landscape features on the dispersal of individuals and may have been more appropriate for the individual-based analysis. The present landscape genetic analysis did not consider potential demographic effects, such as the contribution of spatial heterogeneity in effective population sizes to the variance in genetic distance metrics (Prunier et al. 2017).

The intervening landscape is likely not the only factor driving dispersal and colonisation success by T. cristatus. Sinsch (2014) postulated that landscape resistance might have a smaller effect on the connectivity of local populations in heterogeneous landscapes than previously expected because amphibian dispersal abilities are often grossly underestimated by recapture studies. During the initial dispersal phase, individuals may show low responsiveness to habitat quality, followed by increased path sinuosity and selection of more suitable microhabitats (Pittman et al. 2014; Jarvis 2016). Temporal variation in habitat quality was found to be critical to initiating long distance dispersal (Lowe 2009; Unglaub et al. 2021). Crested newt occurrence was previously linked to patch characteristics, such as macrophyte cover or predatory fish (Baker & Halliday 1999; Denoël et al. 2013). The absence of crested newts may therefore not only reflect dispersal failures due to high landscape resistance, but also habitat suitability (Hartel et al. 2010). The next step would be to conduct a combined analysis of the effects of habitat suitability, demography, and landscape resistance to gain a better understanding on the contribution of each of these factors (e.g. Cianfrani et al. 2013; McCluskey et al. 2022).

Conclusions

Considering the high type I error rates and lack of convergence among derived conductivity maps, the inferences from our landscape genetics analysis bear substantial uncertainty which decision-makers need to factor into subsequent conservation applications. While uncertainty is ubiquitous in conservation biology, failure to acknowledge and treat the sources of uncertainty can lead to poor management decisions (Regan et al. 2005). The challenge in landscape genetics is to identify best practices for new methods, such as ResistanceGA, to increase robustness of results. Based on the findings of the present study and in line with previous studies (notably Shirk et al. 2017; Peterman 2018; Winiarski et al. 2020a, b; Beninde et al. 2023), we reiterate the following ten recommendations and challenges for optimising resistance surfaces in ResistanceGA in view of informing conservation planning:

  • It is important to conduct repeat runs due to the stochastic nature of the optimisation procedure.

  • True bootstrapping should be attempted as the pseudo-bootstrap fails to incorporate uncertainty from optimisations.

  • The effect of the genetic algorithm parameterisation on surface optimisations should be assessed.

  • The choice of the genetic distance metric matters.

  • Marginal R2 should not drive the choice of the most appropriate genetic distance measure.

  • Individual-based surface optimisations may suffer from overfitting to noise, potentially leading to the inclusion of non-influential landscape features.

  • Simulations should be employed to identify the most appropriate study design and genetic distance metric for a given empirical dataset.

  • The type I error rates linked to linear and continuous features should be assessed in in-depth simulation studies.

  • High convergence of optimised resistance surfaces may not translate to high correlation of derived conductivity maps.

  • Possible sources of uncertainty should be critically assessed before making conservation recommendations.

This study underscored the challenges that remain in the optimisation of landscape resistance surface optimisations. While the applications of ResistanceGA are increasing given its flexibility in optimising multiple surfaces and the lack of a priori assumptions on optimisations, it is important to recognise that the performance of ResistanceGA depends on a variety of factors related to the specific study case and should be assessed critically. By doing so, we can enhance the effectiveness by which landscape genetic inferences can inform species conservation and spatial planning.