Pulsating flow in a channel filled with a porous medium under local thermal non-equilibrium condition: an exact solution

Abstract

The present work investigates analytically the problem of forced convection heat transfer of a pulsating flow, in a channel filled with a porous medium under local thermal non-equilibrium condition. Internal heat generation is considered in the porous medium, and the channel walls are subjected to constant heat flux boundary condition. Exact solutions are obtained for velocity, Nusselt number and temperature distributions of the fluid and solid phases in the porous medium. The influence of pertinent parameters, including Biot number, Darcy number, fluid-to-solid effective thermal conductivity ratio and Prandtl number are discussed. The applied pressure gradient is considered in a sinusoidal waveform. The effect of dimensionless frequency and coefficient of the pressure amplitude on the system’s velocity and temperature fields are discussed. The general shape of the unsteady velocity for different times is found to be very similar to the steady data. Results show that the amplitudes of the unsteady temperatures for the fluid and solid phases decrease with the increase in Biot number or thermal conductivity ratio. For large Biot numbers, dimensionless temperatures of the solid and fluid phases are similar and are close to their steady counterparts. Results for the Nusselt number indicate that increasing Biot number or thermal conductivity ratio decreases the amplitude of Nusselt number. Increase in the internal heat generation in the solid phase does not have a significant influence on the ratio of amplitude-to-mean value of the Nusselt number, while internal heat generation in the fluid phase enhances this ratio.

Introduction

Convective heat transfer in porous media has been a subject of intense studies due to its wide range of application in the industries such as oil recovery, geothermal engineering, thermal insulation, carbon storage, heat transfer augmentation, solid matrix or micro-porous heat exchangers and porous radiant burners [1, 2]. Studies regarding the thermal characteristics of non-pulsating flow in porous media are more concentrated on heat transfer enhancement in domains filled with porous materials subjected to a heat source at the wall boundaries or internal heat generation. There were abundance of experimental (e.g., [3,4,5,6,7]), numerical (e.g., [8,9,10,11,12]) and theoretical (e.g., [13,14,15,16,17,18,19,20,21,22]) studies, which demonstrated the use of porous material as a promising passive technique in enhancing forced convection heat transfer in different industrial applications in micro- and large scales. Investigations regarding heat transfer of pulsating flow have mostly been conducted in empty (non-porous) channels and pipes (e.g., [23,24,25]). Understanding the fluid flow and heat transfer of pulsating flow in porous media has a pivotal role to play in biological applications such as blood flow in vessels due to heart beating and also industrial applications such as mesh-type regenerators used in the stirling cycle devices [26,27,28] and electronic cooling by utilizing oscillating flow [29, 30].

In theoretical modeling of heat transfer in porous media, two primary models are generally used. The local thermal equilibrium (LTE) and local thermal non-equilibrium (LTNE) models. The LTE model holds when the heat exchange between the solid and fluid phases is high, and the temperature difference between the two phases is negligibly small [11]. This model requires solving only one energy equation to predict temperature field within the porous medium, which simplifies the analysis of heat transfer in porous media (e.g., [10, 31,32,33,34,35]). LTNE model however requires solving separate energy equations for the two phases in the porous regions, which are coupled through an internal heat exchange term. Hence, the LTNE model leads to more accurate prediction of the temperature fields in porous media (e.g., [8, 20, 36,37,38]). Guo et al. [39] studied numerically heat transfer of pulsating flow based on LTE model in a tube partially filled with a porous medium attached to the pipe walls. They presented and discussed the relationship between the effective thermal diffusivity and thickness of the porous layer. Byun et al. [40] conducted an analytical characterization of heat transfer of oscillatory velocity flow in a large slab of a porous medium with a hot and a cold side using the LTNE model. They defined a criterion for validity of LTE model and reduced the solutions into four regimes of asymptotic solutions. Kuznetsov and Nield [41] provided analytical expressions for pulsating flow and forced convection heat transfer, produced by an applied oscillating pressure in a channel/pipe utilizing LTE model. They [41] found that the fluctuating part of the Nusselt number increases to a maximum value and then decreases with the increase in frequency. This observation was not in agreement with other studies that investigated pulsating flow in an empty channel or tube [24, 25, 42]. Forooghi et al. [42] performed a numerical investigation using the LTNE model for both steady and pulsating flow in a parallel-plate channel partially filled with porous layers attached to the channel walls. They found that an increase in the thermal conductivity ratio between the two phases, or amplitude of the pressure gradient, results in an enhancement in the dimensionless average Nusselt number. Yang and Vafai [36] discussed that the LTE model is not suitable to use for transient heat transfer in porous media. They [36] discussed that the temperature difference between the two phases is relatively small when the process reaches its steady condition. However, during the transient process the temperature difference between the two phases is considerable. Their [36] results revealed that utilizing LTE model for time-dependent problems of heat transfer in porous media induces certain inaccuracies in predicting temperature field [36]. From the previous studies, it could be noted that the problem of pulsating flow in a channel/pipe filled with a porous medium under local thermal non-equilibrium condition has not yet been fully understood. The current work presents an analytical solution to investigate the effects of pulsating flow on the velocity, temperature distributions and Nusselt number in a channel filled with a porous medium under LTNE condition and considering internal heat generation in the fluid and solid phases. There are several practical examples involving internal heat generation in porous media such as electronic cooling, agricultural product storage [13, 43] and metabolic reactions in biological media [21]. The problem of pulsating flow in a medium leads to certain time-dependent governing equations which need to be addressed theoretically or numerically. As discussed above, some attempts have been made to cope with such a problem but in different geometries. Some works addressed unsteady governing equations for stretching permeable sheets using HAM (Homotopy Analysis Method) [44,45,46,47]. Some other interesting analytical solution for different applicable mathematical problems could be found in [48,49,50,51,52,53,54,55,56].

This problem is worth investigating analytically, since the unsteady pulsating fluid flow and the heat transfer between particles and fluid in an unsteady pulsating flow is complex and clearly is expensive to study experimentally. Furthermore, for realistic porous systems, pore-scale modeling of porous systems is computationally prohibitive and hence deploying the volume-averaged method is recommended. In the volume-averaged method, the local thermal non-equilibrium (LTNE) model is deployed to calculate temperatures of the fluid and solid phases in the porous media (as considered in this study) by solving different energy equations for each phase in the media [57]. However, for the volume-averaged solution based on the LTNE model, the internal heat transfer coefficient between the particles and fluid has to be known a priori. This coefficient is required for the term, which couples the two energy equations of the particle and fluid in the porous media. Therefore, the present work aims to shed some light on the problem. The subject is also of interest as a basic research of unsteady forced convection problem.

The Darcy–Brinkman flow model is used to represent the fluid flow in the porous medium [16] and the LTNE model is employed to find exact solutions for the temperature distributions and Nusselt number in the system. The effect of parameters such as thermal conductivity ratio, Biot number, Darcy number, dimensionless frequency, coefficient of pressure amplitude and Prandtl number on the flow and heat transfer characteristics are presented and discussed.

Problem description and governing equations

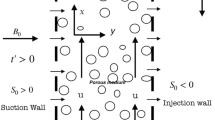
The schematic diagram of the problem is shown in Fig. 1. Fluid flows through a parallel-plate channel filled with a porous medium subjected to a constant heat flux boundary condition. Heat generation in the solid phase, $S_{\text{s}}$ and the fluid phase, $S_{\text{f}}$ are considered uniform but different [13]. The distance between the plates is $2H$ and the heat flux $q_{\text{w}}$ is applied to the channel walls. The incoming flow has pressure gradient, which oscillates in time about a non-zero mean value. Following assumptions are considered to simplify the governing equations [13, 16]:

Fig. 1

Schematic diagram of the problem

• 1. The flow in the porous medium is incompressible and laminar.

• 2. The porous medium is isotropic and homogeneous.

• 3. Thermophysical properties of fluid and solid phases in the porous medium are assumed to be constant.

• 4. Channel walls are impermeable and flow is considered two-dimensional.

• 5. The flow is thermally and hydrodynamically fully developed.

Based on these assumptions, the governing equations are represented as [13, 16]:

Momentum [57]

$$\rho_{\text{f}} \frac{\partial u}{\partial t} = - \frac{\partial p}{\partial x} + \mu_{\text{eff}} \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{\mu }{K}u.$$

(1)

Momentum equation is the sum of unsteady Darcy equation $\rho_{\text{f}} \frac{\partial u}{\partial t} = - \frac{\partial p}{\partial x} - \frac{\mu }{K}u$ and Brinkman term $\mu_{\text{eff}} \frac{{\partial^{2} u}}{{\partial y^{2} }}$, which is unsteady Brinkman-extended Darcy model.

The pressure gradient is considered to vary with time in a sinusoidal waveform about a constant steady value:

$$\frac{\partial P}{\partial x} = \left( {\frac{\partial P}{\partial x}} \right)_{\text{st}} \left( {1 + \gamma \sin \left( {\omega t} \right)} \right),$$

(2)

where $(\frac{\partial P}{\partial x})_{\text{st}}$ is the steady component of pressure gradient [23], $\gamma$ is coefficient of pressure amplitude and $\omega$ is oscillation frequency. This is a known form for the pressure gradient to represent pulsating flow, which was also used in previous works (e.g., [25, 58]).

Using Eq. (2), the momentum Eq. (1) is rewritten as:

$$\rho_{\text{f}} \frac{\partial u}{\partial t} = - \left( {\frac{\partial P}{\partial x}} \right)_{\text{st}} \left( {1 + \gamma \sin \left( {\omega t} \right)} \right) + \mu_{\text{eff}} \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{\mu }{K}u.$$

(3)

Energy equation for the fluid phase is expressed as:

$$\rho_{\text{f}} c_{\text{pf}} \left( {\frac{{\partial T_{\text{f}} }}{\partial t} + u\frac{{\partial T_{\text{f}} }}{\partial x}} \right) = k_{\text{f,eff}} \frac{{\partial^{2} T_{\text{f}} }}{{\partial y^{2} }} + a_{\text{sf}} h_{\text{sf}} \left( {T_{\text{s}} - T_{\text{f}} } \right) + S_{\text{f}} .$$

(4)

Energy equation for the solid phase is written as:

$$\rho_{\text{s}} c_{\text{ps}} \left( {\frac{{\partial T_{\text{s}} }}{\partial t}} \right) = k_{\text{s,eff}} \frac{{\partial^{2} T_{\text{s}} }}{{\partial y^{2} }} - a_{\text{sf}} h_{\text{sf}} \left( {T_{\text{s}} - T_{\text{f}} } \right) + S_{\text{s}} ,$$

(5)

where subscripts f and s represent the fluid and solid phases, respectively. Subscript st refers to steady flow. $\mu$ is the dynamic viscosity of the fluid and $\mu_{\text{eff}} = \mu /\varepsilon$ [59] is the effective viscosity of the porous medium. $K$ is the permeability of the porous medium, ρ is density and $c_{\text{p}}$ is the specific heat. $k_{\text{f,eff}}$ and $k_{\text{s,eff}}$ are the effective thermal conductivity of the fluid and solid phases, respectively. $a_{\text{sf}}$ is the interfacial area per unit volume of the porous medium and $h_{\text{sf}}$ is the fluid-to-solid heat transfer coefficient [16].

Boundary conditions

The following boundary conditions are employed to solve the systems of the governing Eqs. (1)–(5) [13, 16]:

No-slip condition at the channel wall:

$$\left. u \right|_{y = \pm H} = 0.$$

(6)

Symmetry boundary condition is applied at the channel centerline:

$$\left. {\frac{\partial u}{\partial y}} \right|_{y = 0} = 0,$$

(7)

$$\left. {\frac{{\partial T_{\text{f}} }}{\partial y}} \right|_{y = 0} = \left. {\frac{{\partial T_{\text{s}} }}{\partial y}} \right|_{y = 0} = 0.$$

(8)

When the channel wall has a high thermal conductivity with a finite thickness attached to a porous medium, the temperature of the solid and the fluid phases are almost equal at the wall [60, 61]. Using this assumption at the channel wall, Model A boundary condition is adopted at the interface between the porous medium and the channel wall [13, 16]. This model assumes that the prescribed heat flux at the wall is split between two phases relative to the physical values of their effective thermal conductivities and temperature gradients. This model further assumes that the steady component of the temperature of the fluid and solid phases at the wall are equal to the wall temperature [13, 16]:

$$\left. {k_{\text{f,eff}} \frac{{\partial T_{\text{f}} }}{\partial y}} \right|_{y = H} + k_{\text{s,eff}} \left. {\frac{{\partial T_{\text{s}} }}{\partial y}} \right|_{y = H} = q_{\text{w}} ,$$

(9)

$$\left. {T_{\text{f,st}} } \right|_{y = H} = \left. {T_{\text{s,st}} } \right|_{y = H} = T_{\text{w,st}} ,$$

(10)

where $T_{\text{f,st }}$ and $T_{\text{s,st}}$ are the steady components of the temperature of the fluid and the solid phase, respectively, and $T_{\text{w,st}}$ is the steady component of the wall temperature.

Normalization

The following dimensionless variables are introduced to normalize the governing equations and boundary conditions [16, 25, 62]:

$$\begin{aligned} & Y = \frac{y}{H}, \quad X = \frac{4x}{{H {\text{Re Pr}}}}, \quad T^{*} = \frac{{k_{\text{s,eff}} T}}{{q_{w} H}}, \quad M = \frac{{\mu_{\text{eff}} }}{\mu } = \frac{1}{\varepsilon }, \quad {\text{Da}} = \frac{K}{{H^{2} }}, \\ & U = \frac{u}{{u_{\text{m}} }}, \quad \beta = w_{*}^{2} = H^{2} \left( {\frac{\omega }{\vartheta }} \right),\quad t^{*} = \frac{\vartheta t}{{H^{2} }}, \quad {\text{Re}} = \frac{{u_{\text{m}} D_{\text{H}} }}{\vartheta }. \\ \end{aligned}$$

(11)

$u_{\text{m}} = - (\frac{\partial P}{\partial x})_{\text{st}} \frac{{H^{2} }}{\mu }$ is a characteristic velocity. $\vartheta = \frac{\mu }{{\rho_{\text{f}} }}$ is the kinematic viscosity of the fluid and ${\text{Re}}$ is Reynolds number. $w_{*}$ is Womersly number and $\varepsilon$ is the porosity of the porous medium. Using the dimensionless variables, the dimensionless form of momentum Eq. (3) and the associated boundary conditions Eqs. (6) and (7) are written as:

$$\frac{\partial U}{{\partial t^{*} }} = \left( {1 + \gamma \sin \left( {\beta t^{*} } \right)} \right) + M\frac{{\partial^{2} U}}{{\partial Y^{2} }} - \frac{U}{\text{Da}},$$

(12)

$$\left. U \right|_{Y = \pm 1} = 0,$$

(13)

$$\left. {\frac{\partial U}{\partial Y}} \right|_{Y = 0} = 0.$$

(14)

Energy Eqs. (4) and (5) and their associated boundary conditions Eqs. (8) and (10) are also rewritten as:

$${ \Pr } \cdot k\frac{{\partial T_{\text{f}}^{*} }}{{\partial t^{*} }} + U^{*} k\frac{{\partial T_{\text{f}}^{*} }}{\partial X} = k\frac{{\partial^{2} T_{\text{f}}^{*} }}{{\partial Y^{2} }} + {\text{Bi}}\left( {T_{\text{s}}^{*} - T_{\text{f}}^{*} } \right) + S_{\text{f}}^{*} ,$$

(15)

$${\text{Ps}}\frac{{\partial T_{\text{s}}^{*} }}{{\partial t^{*} }} = \frac{{\partial^{2} T_{\text{s}}^{*} }}{{\partial Y^{2} }} - {\text{Bi}}\left( {T_{\text{s}}^{*} - T_{\text{f}}^{*} } \right) + S_{\text{s}}^{*} ,$$

(16)

$$\left. {\frac{{\partial T^{*}_{\text{f}} }}{\partial Y}} \right|_{Y = 0} = \left. {\frac{{\partial T^{*}_{\text{s}} }}{\partial Y}} \right|_{Y = 0} = 0,$$

(17)

$$\left. {\frac{{\partial T^{*}_{\text{s}} }}{\partial Y}} \right|_{Y = 1} + k\left. {\frac{{\partial T^{*}_{\text{f}} }}{\partial Y}} \right|_{Y = 1} = 1,$$

(18)

where $T_{\text{f}}^{*}$ and $T_{\text{s}}^{*}$ are defined as:

$$T_{\text{f}}^{*} = \frac{{k_{\text{s,eff}} T_{\text{f}} }}{{q_{\text{w}} H}}, \quad T_{\text{s}}^{*} = \frac{{k_{\text{s,eff}} T_{\text{s}} }}{{q_{\text{w}} H}}.$$

(19)

The dimensionless variables used in Eqs. (15) and (16) are as:

$$\begin{aligned} & { \Pr } = \frac{{\rho_{\text{f}} c_{\text{pf}} \vartheta }}{{k_{\text{f,eff}} }} = \frac{{c_{\text{pf}} \mu }}{{k_{\text{f,eff}} }}, \quad {\text{Ps}} = \frac{{\rho_{\text{s}} c_{\text{ps}} \vartheta }}{{k_{\text{s,eff}} }}, \quad {\text{Bi}} = \frac{{a_{\text{sf}} h_{\text{sf}} H^{2} }}{{k_{\text{s,eff}} }}, \\ & k = \frac{{k_{\text{f,eff}} }}{{k_{\text{s,eff}} }}, \quad S_{\text{f}}^{*} = \frac{H}{{q_{\text{w}} }}S_{\text{f}} , \quad S_{\text{s}}^{*} = \frac{H}{{q_{\text{w}} }}S_{\text{s}} , \\ \end{aligned}$$

(20)

where Pr is Prandtl number and Ps is a dimensionless variable similar to Prandtl number appeared in the normalization process of solid-phase energy equation, Eq. (5). ${\text{Bi}}$ is Biot number. $k_{\text{f,eff}} = \varepsilon k_{\text{f}}$ and $k_{\text{s,eff}} = \left( {1 - \varepsilon } \right)k_{\text{s}}$ are the effective thermal conductivity of the fluid and solid phases, respectively [16, 59] and $k$ is the thermal conductivity ratio.

Analytical solution for the momentum equation

To solve the momentum Eq. (12), it is divided into steady and unsteady components [25]:

$$U\left( {t^{*} ,Y} \right) = U_{\text{st}} \left( Y \right) + U_{\text{un}} \left( {t^{*} ,Y} \right),$$

(21)

where subscripts st and un refer to steady and unsteady terms, respectively. Using Eq. (21) and considering $\frac{{\partial U_{\text{st}} }}{{\partial t^{*} }} = 0,$ the governing Eq. (12) and the boundary conditions (13) and (14) are written as:

$$M\frac{{{\text{d}}^{2} U_{\text{st}} }}{{{\text{d}}Y^{2} }} - \frac{{U_{\text{st}} }}{\text{Da}} + 1 = 0,$$

(22)

$$\left. {\frac{{{\text{d}}U_{\text{st}} }}{{{\text{d}}Y}}} \right|_{Y = 0} = 0,\quad \left. {U_{\text{st}} } \right|_{Y = 1} = 0,$$

(23)

and

$$\frac{{\partial U_{\text{un}} }}{{\partial t^{*} }} = \gamma \sin \left( {\beta t^{*} } \right) + M\frac{{\partial^{2} U_{\text{un}} }}{{\partial Y^{2} }} - \frac{{U_{\text{un}} }}{\text{Da}} ,$$

(24)

$$\left. {\frac{{\partial U_{\text{un}} }}{\partial Y}} \right|_{Y = 0} = 0,\quad \left. {U_{\text{un}} } \right|_{Y = 1} = 0.$$

(25)

The initial condition for the velocity is considered zero for convenience. However, the correct initial value is obtained by applying the fully developed assumption. The effect of initial condition on solution is discussed later in the paper. Therefore, the initial condition for the momentum equation is written as:

$$\left. {U_{\text{un}} } \right|_{{t^{*} = 0}} = 0.$$

(26)

The steady velocity Eq. (22) has been solved in the previous studies (e.g., [63]) and here only the final solution is presented, which is as:

$$U_{\text{st}} = {\text{Da}}\left( {1 - \frac{{\cosh \left( {ZY} \right)}}{\cosh \left( Z \right)}} \right),$$

(27)

where

$$Z = \frac{1}{{\sqrt {M \times {\text{Da}}} }}.$$

(28)

The unsteady momentum Eq. (24) is a non-homogeneous equation with homogeneous boundary conditions (Eq. 25). Hence, it is solved using the method of eigenfunction expansion [64]. Therefore, the unsteady component of the velocity is given by Eq. (29). The procedure of solving the unsteady velocity using this method is explained in “Appendix” (Sect. 5.1).

$$U_{\text{un}} \left( {t^{*} ,Y} \right) = \mathop \sum \limits_{n = 1}^{\infty } a_{\text{n}} \left( {t^{*} } \right)\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right),$$

(29)

where

$$a_{\text{n}} \left( {t^{*} } \right) = \left( {\frac{{ - 4\gamma \left( { - 1} \right)^{n} }}{{\left( {2n - 1} \right)\pi }}} \right)*\frac{{\left( { - 16{\text{Da}}^{2} \beta \cos \left( {\beta t^{*} } \right) + \left[ {4\left( {2n - 1} \right)^{2} \pi^{2} M{\text{Da}}^{2} + 16{\text{Da}}} \right]\sin \left( {\beta t^{*} } \right) + 16{\text{Da}}^{2} \beta e^{{ - \left( {\frac{{\left( {2n - 1} \right)^{2} \pi^{2} M}}{4} + \frac{1}{\text{Da}}} \right)t^{*} }} } \right)}}{{16\left( {{\text{Da}}\beta } \right)^{2} + \left( {\left( {2n - 1} \right)^{2} \pi^{2} M \cdot {\text{Da}} + 4} \right)^{2} }}.$$

(30)

Analytical solution for the energy equations

The analytical solution of the energy equations is explained in “Appendix”. The distribution of the temperatures in this section is presented in a form of $\theta = T^{*} - T_{\text{w}}^{*}$, which is used to calculate the Nusselt number. See “Appendix” (Sect. 5.2) for more details.

Steady components of the energy equations

The procedure of solving the steady energy equations and finding key parameters are demonstrated in “Appendix” (Sect. 5.2.1). The steady equations of the problem have already been studied and discussed in the previous studies. Kun and Vafai [13] solved the equivalent steady problem using the Darcian flow model. The focus of the present study is on the unsteady solutions and to prevent repetitions, solutions presented by Ref. [13] are provided here.

$$\theta_{\text{f,st}} = \frac{1}{1 + k}\left\{ {\frac{1}{2}\left( {Y^{2} - 1} \right) + \left( {\frac{1}{1 + k} + S_{\text{s}}^{*} } \right)\frac{1}{\text{Bi}} \left[ {\frac{{{ \cosh }\left( {\lambda Y} \right)}}{{{ \cosh }\left( \lambda \right)}} - 1} \right]} \right\},$$

(31)

$$\theta_{\text{s,st}} = \frac{1}{1 + k}\left\{ {\frac{1}{2}\left( {Y^{2} - 1} \right) + \left( {\frac{1}{1 + k} + S_{\text{s}}^{*} } \right)\frac{k}{\text{Bi}} \left[ {1 - \frac{{{ \cosh }\left( {\lambda Y} \right)}}{{{ \cosh }\left( \lambda \right)}}} \right]} \right\}.$$

(32)

where

$$\theta_{\text{f,st}} = \frac{{k_{\text{s,eff}} \left( {T_{\text{f,st}} - T_{\text{w,st}} } \right)}}{{q_{\text{w}} H}},\quad \theta_{\text{s,st}} = \frac{{k_{\text{s,eff}} \left( {T_{\text{s,st}} - T_{\text{w,st}} } \right)}}{{q_{\text{w}} H}}.$$

(33)

$\theta_{\text{f,st}}$ and $\theta_{\text{s,st}}$ are the dimensionless steady temperatures of the fluid phase and solid phase, respectively, and $T_{\text{w,st}}$ is the steady component of the wall temperature.

Unsteady components of energy equations

The unsteady components of the temperature are normalized using the unsteady wall temperature (in the form of $\theta$) to be comparable with the steady components:

$$\begin{aligned} \theta_{\text{f,un}} = \frac{{k_{\text{s,eff}} \left( {T_{\text{f,un}} - T_{\text{w,un}} } \right)}}{{q_{\text{w}} H}} & = \mathop \sum \limits_{{\text{m}} = 1}^{\infty } \frac{{2C\left( {\cos \left( {m\pi Y} \right)\left( {1 + \frac{{m^{2} \pi^{2} }}{\text{Bi}}} \right) - \left( { - 1} \right)^{{\text{m}}} \left( {1 + \frac{{k\left( {1 + \frac{{m^{2} \pi^{2} }}{\text{Bi}}} \right)}}{1 + k}} \right)} \right)}}{{\pi \left( {r_{1 } - r_{2 } } \right)}} \mathop \sum \limits_{{\text{n}} = 1}^{\infty } F_{\text{m,n}} \left( {t^{*} } \right) \\ & \quad + \mathop \sum \limits_{{\text{m}} = 1}^{\infty } \frac{{2C{\text{Ps}}\left( {\cos \left( {m\pi Y} \right) - \left( { - 1} \right)^{{\text{m}}} \left( {\frac{k}{1 + k}} \right)} \right)}}{{\pi \left( {r_{1 } - r_{2 } } \right){\text{Bi}}}} \mathop \sum \limits_{{\text{n}} = 1}^{\infty } R_{\text{m,n}} \left( {t^{*} } \right), \\ \end{aligned}$$

(34)

and

$$\begin{aligned} \theta_{\text{s,un}} = \frac{{k_{\text{s,eff}} \left( {T_{\text{s,un}} - T_{\text{w,un}} } \right)}}{{q_{\text{w}} H}} & = \mathop \sum \limits_{{\text{m}} = 1}^{\infty } \frac{{2C\left( {\cos \left( {m\pi Y} \right) - \left( { - 1} \right)^{{\text{m}}} \left( {1 + \frac{{k\left( {1 + \frac{{m^{2} \pi^{2} }}{\text{Bi}}} \right)}}{1 + k}} \right)} \right)}}{{\pi \left( {r_{1 } - r_{2 } } \right)}} \mathop \sum \limits_{{\text{n}} = 1}^{\infty } F_{\text{m,n}} \left( {t^{*} } \right) \\ & \quad - \mathop \sum \limits_{{\text{m}} = 1}^{\infty } \frac{{2C\left( { - 1} \right)^{\text{m}} k \cdot {\text{Ps}}}}{{\pi \left( {r_{1 } - r_{2 } } \right)\left( {1 + k} \right){\text{Bi}}}} \mathop \sum \limits_{{\text{n}} = 1}^{\infty } R_{\text{m,n}} \left( {t^{*} } \right), \\ \end{aligned}$$

(35)

where $\theta_{\text{f,un}}$ and $\theta_{\text{s,un}}$ are the dimensionless unsteady temperatures of the fluid phase and solid phase, respectively, and $T_{\text{w,un}}$ is the unsteady component of the wall temperature. $F_{\text{m,n}} \left( {t^{*} } \right)$ and $R_{\text{m,n}} \left( {t^{*} } \right)$ are time-dependent coefficients (Eqs. 95, 97 in “Appendix”) and $r_{1 }$ and $r_{2 }$ are roots of a characteristics equation presented by Eq. (89) in “Appendix”.

Parameter $C = \frac{{\partial T_{\text{f,st}}^{*} }}{\partial X}$ in Eqs. (34) and (35) is a constant parameter obtained when solving the steady energy equations (see Sect. 5.2.1 of “Appendix” for more details):

$$C = \frac{{\left( {1 + S^{*} } \right)}}{{k \cdot {\text{Da}}\left( {1 + Z\tanh \left( Z \right)\left( {\frac{{\left( {{\text{Bi}} - Z^{2} } \right)\left( {k - \frac{{Z^{2} k}}{\text{Bi}} + 1} \right)}}{{kZ^{4} - {\text{Bi}}\left( {1 + k} \right)Z^{2} }} - \frac{1}{\text{Bi}}} \right)} \right)}} ,$$

(36)

where $S^{*} = S_{\text{f}}^{*} + S_{\text{s}}^{*}$.

Calculation of Nusselt number (Nu)

The wall heat transfer coefficient is defined as [13]:

$$h_{\text{w}} = \frac{{q_{\text{w}} }}{{T_{\text{w}} - T_{\text{f,b}} }},$$

(37)

with the Nusselt number obtained as [13]:

$${\text{Nu}} = \frac{{h_{\text{w}} \left( {4H} \right)}}{{k_{\text{f,eff}} }} = - \frac{4}{{k\theta_{\text{f,b}} }},$$

(38)

where $4H$ is the hydraulic diameter of the channel and $\theta_{\text{f,b}}$ is the dimensionless bulk mean temperature of the fluid. Considering $\theta_{\text{f,b}} = \theta_{\text{f,st,b}} + \theta_{\text{f,un,b}}$, Eq. (38) is rewritten as:

$${\text{Nu}} = - \frac{4}{{k\left( {\theta_{\text{f,st,b}} + \theta_{\text{f,un,b}} } \right)}},$$

(39)

where $\theta_{\text{f,st,b}}$ and $\theta_{\text{f,un,b}}$ are the dimensionless steady and unsteady bulk mean temperature of the fluid, respectively. For steady flow, Eq. (39) turns into the following form [13]:

$${\text{Nu}}_{\text{st}} = - \frac{4}{{k\theta_{\text{f,st,b}} }}.$$

(40)

$\theta_{\text{f,st,b}}$ is obtained using the following relation [16].

$$\theta_{\text{f,st,b}} = \frac{{\mathop \smallint \nolimits_{0}^{1} \theta_{\text{f,st}} U_{\text{st}} {\text{d}}Y}}{{\mathop \smallint \nolimits_{0}^{1} U_{\text{st}} {\text{d}}Y}}.$$

(41)

Mahmoudi [16] obtained an analytical solution for the equivalent steady equations considering the velocity slip and temperature jump at the channel walls. The solution for $\theta_{\text{f,st,b}}$ and consequently, ${\text{Nu}}_{\text{st}}$, for the present work can be obtained from the analytical solutions presented in [16] by setting the velocity slip coefficient and the temperature jump coefficient to zero.

Using Eqs. (29), (30) and (34), $\theta_{\text{f,un,b}}$ is obtained as:

$$\theta_{\text{f,un,b}} = \frac{{\mathop \smallint \nolimits_{0}^{1} \theta_{\text{f,un}} U_{\text{un}} {\text{d}}Y}}{{\mathop \smallint \nolimits_{0}^{1} U_{\text{un}} {\text{d}}Y}} = \frac{{A\left( {t^{*} } \right)}}{{B\left( {t^{*} } \right)}},$$

(42)

where

$$\begin{aligned} A\left( {t^{*} } \right) & = \mathop \sum \limits_{j = 1}^{\infty } \frac{{2Ca_{\text{j}} \left( {t^{*} } \right)}}{{\pi^{2} \left( {r_{1 } - r_{2 } } \right)}}\left\{ {\mathop \sum \limits_{m = 1}^{\infty } \left[ { - \left( {1 + \frac{{m^{2} \pi^{2} }}{\text{Bi}}} \right)\left( {\frac{{\left( { - 1} \right)^{{\text{j}} + {\text{m}}} }}{{2\left( {j + m} \right) - 1}} + \frac{{\left( { - 1} \right)^{{\text{j}} - {\text{m}}} }}{{2\left( {j - m} \right) - 1}}} \right)} \right.} \right. \\ & \quad \left. { + \frac{{2\left( { - 1} \right)^{j + m} }}{2j - 1}\left( {1 + \frac{{k\left( {1 + \frac{{m^{2} \pi^{2} }}{\text{Bi}}} \right)}}{1 + k}} \right)} \right]\mathop \sum \limits_{{\text{n}} = 1}^{\infty } F_{\text{m,n}} \left( {t^{*} } \right) + \mathop \sum \limits_{{\text{m}} = 1}^{\infty } \frac{\text{Ps}}{\hbox{Bi}}\left[ { - \left( {\frac{{\left( { - 1} \right)^{{\text{j}} + {\text{m}}} }}{{2\left( {j + m} \right) - 1}} + \frac{{\left( { - 1} \right)^{{\text{j}} - {\text{m}}} }}{{2\left( {j - m} \right) - 1}}} \right)} \right. \\ & \quad \left. { + \left. {\frac{{2\left( { - 1} \right)^{{\text{j}} + {\text{m}}} }}{2j - 1}\left( {\frac{k}{1 + k}} \right)} \right]\mathop \sum \limits_{{\text{n}} = 1}^{\infty } R_{\text{m,n}} \left( {t^{*} } \right)} \right\}. \\ \end{aligned}$$

(43)

and

$$B\left( {t^{*} } \right) = \mathop \sum \limits_{{\text{j}} = 1}^{\infty } \frac{{ - 2\left( { - 1} \right)^{\text{j}} a_{\text{j}} \left( {t^{*} } \right)}}{{\left( {2j - 1} \right)\pi }},$$

(44)

where $a_{\text{j}} \left( {t^{*} } \right)$ is obtained by replacing subscript $j$ instead of $n$ in Eq. (30).

Results and discussion

Validation

In this section, we present the validation of the unsteady velocity field in comparison with the analytical solutions of Siegel and Perlmutter [23] presented for pulsating flow in a channel without porous medium. According to Eq. (12) when the Darcy number is high enough the resulted momentum equation will be similar to that in a channel without a porous medium. The applied pressure gradient for the results obtained by Siegel and Perlmutter [23] was in the Cosine waveform [23]. By substituting $\beta t^{*} + \frac{\pi }{2}$ instead of $\beta t^{*}$ in Eq. (30), the unsteady velocity at the channel centerline (Y = 0) for $\beta = 0.1$, $\gamma = 1$ and $M = 1$ obtained from the present solutions is compared against those presented in [23] and shown in Fig. 2. An excellent agreement is observed between the two solutions. To the best of our knowledge, there is no closely relevant work in the literature on unsteady temperature field in a pulsating flow to be considered for validation of the temperature solution presented in this work.

Fig. 2

Unsteady velocity versus time for $\beta = 0.1$, $\gamma = 1$, $M = 1$ at $Y = 0$

Unsteady velocity profile

Figure 3 shows the unsteady velocity profile for $\gamma = 0.5$, $\beta = 20$, $M = 1.1$ at $Y = 0$. The velocity profile for the fully developed solution, i.e., the exponential term $\exp \left[ { - \left( {\left( {2n - 1} \right)^{2} \pi^{2} M/4 + 1/{\text{Da}}} \right)t^{*} } \right]$ in Eq. (30) is not considered. It is seen that the initial transient part decays after a short period of time [23] (here after $t^{*}$ > 0.2). The initial condition was considered zero for convenience. Considering a different initial condition leads to a different exponential term, which decays in a short time. Since only the fully developed oscillatory part of the solution is of interest, for the rest of the results presented here, the initial transient part is not considered [23].

Fig. 3

Unsteady velocity versus time, with and without the initial transient for $\gamma = 0.5$, $\beta = 20$, $M = 1.1$ at $Y = 0$

The effect of Darcy number (Da) on the dimensionless unsteady part of the velocity is shown in Fig. 4 for $\gamma = 0.5$, $\beta = 5$, $M = 1.1$ at $Y = 0$. It is seen that the velocity amplitude has a direct relationship with Da number. Increasing the Da number by a factor ten increases the amplitude of the velocity field by almost the same factor. Increasing Da number is equivalent to increasing the permeability of the porous medium for a fixed channel height. This enhancement results in decrease in the resistance against flow (the term $- \frac{{U_{\text{un}} }}{\text{Da}}$ in Eq. 24), which leads to a higher velocity magnitude. It can be seen from Eq. (27) that the dimensionless steady component of the velocity has also a direct relationship with Da number.

Fig. 4

Unsteady velocity versus time for different ${\text{Da}}$ numbers for $\gamma = 0.5$, $\beta = 5$, $M = 1.1$ at $Y = 0$

Figure 5 shows the unsteady velocity versus dimensionless time for three values of dimensionless frequency ($\beta$), for two Darcy numbers of $10^{ - 3}$ and $10^{ - 1}$, with flow conditions of $\gamma = 0.5$, $M = 1$ at $Y = 0$. It is seen in Fig. 5a that for high ${\text{Da}}$ numbers, the velocity amplitude decreases by increasing the frequency. While for low ${\text{Da}}$ values, the effect of frequency on the velocity amplitude is negligible. If (${\text{Da}} \to 0$) in Eqs. (29) and (30), the simplified equation of the dimensionless unsteady velocity for low Darcy numbers can be written as:

$$U_{\text{un}} \left( {t^{*} ,Y} \right) = \left( {\mathop \sum \limits_{n = 1}^{\infty } \left( {\frac{{ - 4\gamma \left( { - 1} \right)^{n} }}{{\left( {2n - 1} \right)\pi }}} \right)\frac{{16{\text{Da}}\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right)}}{{\left( {\left( {2n - 1} \right)^{2} \pi^{2} M \cdot {\text{Da}} + 4} \right)^{2} }}} \right)\sin \left( {\beta t^{*} } \right).$$

(45)

Fig. 5

Unsteady velocity versus time for $\gamma = 0.5$, $M = 1$ at $Y = 0$ for a ${\text{Da}} = 10^{ - 1}$ and b ${\text{Da}} = 10^{ - 3}$

From Eq. (45), it can be seen that for low Darcy numbers a change in the value of $\beta$ only changes the period of oscillation (as $\sin \left( {\beta t^{*} } \right)$) and does not change the amplitude of unsteady velocity.

Figure 6 shows variation of unsteady velocity component with $Y$ for different dimensionless times during a dimensionless period of oscillation ($\tau^{*} = \frac{2\pi }{\beta }$) for $\gamma = 0.5$, $\beta = 5$, $M = 1.1$ and ${\text{Da}} = 10^{ - 3}$ along with the corresponding steady velocity. As expected, the velocity at the wall ($Y = \pm 1$) is zero and the symmetry condition at the channel centerline is satisfied for all the profiles. The shapes of the unsteady velocity profiles are very similar to that of the steady component.

Fig. 6

Steady and unsteady velocity versus $Y$ during a period for $\gamma = 0.5$, $\beta = 5$, $M = 1.1$ and ${\text{Da}} = 10^{ - 3}$

Unsteady temperature

The results presented in this section are obtained using the mean properties of water as the fluid phase and steel as the solid phase in the porous medium. The thermal properties used are $M = 1.1$, $k = 0.3$, ${ \Pr } = 7.7$, ${\text{Ps}} = 2.5$ and the porosity of the porous medium is $\varepsilon = 0.9,$ for all the results except for the cases mentioned in the text. In addition, similar to the unsteady velocity, here only the fully developed oscillating part of the temperature solution is of interest. Thus, the initial transient part of the temperature profile will not enter the solution. To achieve this, the exponential terms (of the coefficients $F_{\text{m,n}} \left( {t^{*} } \right)$ and $R_{\text{m,n}} \left( {t^{*} } \right)$) in Eqs. (34) and (35) are neglected to obtain the fully developed solutions. As an example, Fig. 7 compares $\theta_{\text{s,un}}$ calculated with and without the initial transient (the exponential terms) for $\gamma = 0.1$, ${\text{Da}} = 10^{ - 5}$, $\beta = 10$, $M = 1.1$, $k = 0.01$,${\text{Bi}} = 0.1$, ${ \Pr } = 6.9$, ${\text{Ps}} = 0.25$ at the centerline of the channel ($Y = 0$). The difference is just up to $t^{*} = 0.5$ and the initial transient decays after $t^{*}$ > 0.5.

Fig. 7

Unsteady temperature of the solid phase versus time for $S^{*} = 0$, $\gamma = 0.1$,${\text{Da}} = 10^{ - 5}$, $k = 0.01$,${\text{Bi}} = 0.1$, $\beta = 10$, $M = 1.1$,${ \Pr } = 6.9$ and ${\text{Ps}} = 0.25$ at $Y = 0$

Figure 8 shows the dimensionless steady and unsteady temperature $\theta$ for the fluid and solid phases as a function of Y at different times without internal heat generations. For both phases, the steady parts are negative meaning that $\theta_{\text{f}}$ and $\theta_{\text{s}}$ are lower than the wall temperature. The steady components of $\theta_{\text{f}}$ and $\theta_{\text{s}}$ are equal to the wall temperature at the channel wall. Away from the wall, the difference between the fluid and solid temperature with the wall temperature increases and reaches to its maximum at the channel centerline. Figure 8 further shows that the unsteady components of $\theta_{\text{f}}$ and $\theta_{\text{s}}$ oscillate around zero near the channel wall, while the unsteady solid temperature $\theta_{\text{s}}$ has a more uniform distribution.

Fig. 8

Steady and unsteady temperature versus $Y$ during a period for $S^{*} = 0$, $\gamma = 0.5$,${\text{Da}} = 10^{ - 5}$, $k = 0.3$,${\text{Bi}} = 0.1$, $\beta = 5$, $M = 1.1$,${ \Pr } = 7.7$ and ${\text{Ps}} = 2.5$ and for a solid phase and b fluid phase

For the unsteady components of the dimensionless temperature distributions, the internal heat generation appears in constant C in Eq. (36). For steady-state Darcian flow (i.e.,${\text{Da}} \to 0$) as Eqs. (31) and (32) show, only the internal heat generation in the solid phase ($S_{\text{s}}^{*}$) influences the dimensionless temperature distributions $\theta_{\text{s,st}}$ and $\theta_{\text{f,st}} ,$ and $S_{\text{f}}^{*}$ has no effect on them. While, for unsteady temperature components as shown in Eq. (36), the sum of the uniform internal heat generation in the solid and fluid phases ($S^{*}$) influences the variation of $\theta_{\text{s,un}}$ and $\theta_{\text{f,un}}$. Figure 9 shows the variation of $\theta_{\text{s,un}}$ and $\theta_{\text{f,un}}$ for $S^{*} = 5$ and for $\gamma = 0.1$, ${\text{Da}} = 10^{ - 5}$, $\beta = 10$, $M = 1.1$,${ \Pr } = 7.7$ and ${\text{Ps}} = 2.5$ at the centerline of the channel ($Y = 0$) for different thermal conductivity ratio $k$ and ${\text{Bi}}$ number.

Fig. 9

Unsteady temperature versus time for fluid and solid phases for $S^{*} = 5$ and for $\gamma = 0.1$,${\text{Da}} = 10^{ - 5}$, $\beta = 10$, $M = 1.1$,${ \Pr } = 7.7$ and ${\text{Ps}} = 2.5$ at $Y = 0$ for a ${\text{Bi}} = 0.5$ and b ${\text{Bi}} = 50$

It is seen that the amplitude of the unsteady dimensionless temperatures for the fluid phase is relatively bigger than the solid phase. Additionally, the dimensionless temperatures of the two phases of all cases decrease with increasing ${\text{Bi}}$ number. Furthermore, the graphs show that for large value of ${\text{Bi}}$, which translates to a strong internal heat transfer between the fluid and solid phases, the difference between $\theta_{\text{s,un}}$ and $\theta_{\text{f,un}}$ is relatively small, which is in agreement with the results already presented for the steady flow [13]. It seems that the LTE model is valid for large Biot numbers in unsteady flows. For large Biot numbers, the amplitudes of unsteady temperatures are very small (close to zero). Therefore, the total value of the dimensionless temperature for the two phases is close to the steady flow. In fact, for large Biot numbers, the effect of unsteadiness on heat transfer decays largely. The figures also illustrate that by increasing the thermal conductivity ratio $k$, the amplitude of $\theta_{\text{s,un}}$ and $\theta_{\text{f,un}}$ decreases and also become similar.

Figure 10 demonstrates the effect of Darcy number on the unsteady dimensionless temperatures $\theta_{\text{s,un}}$ and $\theta_{\text{f,un}}$ for $S^{*} = 0$, $\gamma = 0.1$, $k = 0.3$,${\text{Bi}} = 0.1$, $\beta = 10$, $M = 1.1$, ${ \Pr } = 7.7$ and ${\text{Ps}} = 2.5$ at ($Y = 0$). It is seen that the amplitude of the unsteady temperature for the two phases increases with increase in Da number. As shown in Fig. 4, the amplitude of the unsteady velocity increases with the increase of Da number. This enhancement leads to rising the magnitude of the term $CkU_{\text{un}}$ in the energy Eq. (73), which is in fact the source term of the energy equation, and hence increases the magnitude of the temperature distributions.

Fig. 10

Unsteady temperature versus time for different Darcy (Da) numbers and $S^{*} = 0$, $\gamma = 0.1$,$k = 0.3$,${\text{Bi}} = 0.1$, $\beta = 10$, $M = 1.1$,${ \Pr } = 7.7$ and ${\text{Ps}} = 2.5$ at $Y = 0,$ for a solid phase and b fluid phase

The effect of Prandtl (Pr) number on the unsteady dimensionless temperatures $\theta_{\text{s,un}}$ and $\theta_{\text{f,un}}$ is shown in Fig. 11 for $S^{*} = 0$, $\gamma = 0.1$,${\text{Da}} = 10^{ - 5}$, $k = 0.3$,${\text{Bi}} = 0.1$, $\beta = 10$, $M = 1.1$ and ${\text{Ps}} = 2.5$ at ($Y = 0$). The general trend for the two phases is similar. It is seen that the amplitudes of $\theta_{\text{s,un}}$ and $\theta_{\text{f,un}}$ increase with the increase of Pr number. Prandtl number is defined as the ratio of the momentum diffusivity to thermal diffusivity of the fluid [65]. Hence, increase in the fluid Pr number enhances the influence of heat convection relative to heat conduction in the fluid flow. On the other hand, the main factor of the heat transfer in this flow is the convective heat transfer between the walls and the fluid flow. Thus, it is expected that an increase in Pr number increases the magnitude of the temperature distributions.

Fig. 11

Unsteady temperature versus time for different Prandtl (Pr) numbers and $S^{*} = 0$, $\gamma = 0.1$,${\text{Da}} = 10^{ - 5}$, $k = 0.3$,${\text{Bi}} = 0.1$, $\beta = 10$, $M = 1.1$ and ${\text{Ps}} = 2.5$ at $Y = 0,$ for a solid phase and b fluid phase

Nusselt number (Nu)

Nusselt number obtained using Eq. (39) for different conditions are presented in this section. Similar to the discussion presented for the temperature and velocity fields, since the initial transient part of the Nu number decays shortly, here we only present the results of the fully developed flow. Figure 12 is depicted to investigate the effect of internal heat generation in the solid and the fluid phase on Nu number for $k = 0.3$,${\text{Bi}} = 0.1$,$\gamma = 0.1$, ${\text{Da}} = 10^{ - 5}$, $\beta = 5$, $M = 1.1$,${ \Pr } = 7.7$ and ${\text{Ps}} = 2.5$. The results for each case are compared with Nu numbers for the steady flow with the same conditions. It is seen that for all cases Nu number oscillates around the value of Nu number of the corresponding steady flow that is in agreement with the result presented in previous works [25, 58]. From Eqs. (41) and (42), it is concluded that the amplitude of oscillation of $\theta_{\text{f,un,b}}$ has a direct relationship with the coefficient $C$, and this coefficient increases with the increase in the value of $S^{*}$ based on Eq. (36). Hence, increase in $S^{*}$ results in increasing the amplitude of $\theta_{\text{f,un,b}}$ and consequently Nusselt number, based on Eq. (39). Comparison of Fig. 12a–c shows that an increase in $S_{\text{s}}^{*}$ for a fixed value of $S_{\text{f}}^{*}$ decreases the mean (steady) value of Nu number, while the ratio of the amplitude-to-mean value of Nu number remains almost constant about a value of 0.01. The mean value of Nu number decreases with the increase of $S_{\text{s}}^{*}$ (it means that $\theta_{\text{f,st,b}}$ increases based on Eq. 40) [16] which also results in reduction in amplitude of Nu number based on Eq. (39). On the other hand, an increase in $S_{\text{s}}^{*}$ results in increase of $S^{*}$ that can increase the amplitude of Nu number, which moderates the reduction effect of increase in $S_{\text{s}}^{*}$ on amplitude. These two opposite effects seem to cause the ratio of the amplitude-to-mean value of Nu number be constant with the increase of $S_{\text{s}}^{*}$. Exploring Fig. 12d–f reveals that for a fixed value of $S_{\text{s}}^{*}$, an increase in the value of $S_{\text{f}}^{*}$ does not have a considerable effect on the mean value of Nu number. Because for the steady-state Darcian flow (i.e.,${\text{Da}} \to 0$) only $S_{\text{s}}^{*}$ has effect on the Nusselt number and $S_{\text{f}}^{*}$ does not affect it [16]. Furthermore, it can be seen that the amplitude of the Nu number increases with the increase of $S_{\text{f}}^{*}$, since the value of $S^{*}$ increases.

Fig. 12

Nusselt number versus time for different values of internal heat generation for $k = 0.3$, ${\text{Bi}} = 0.1,\; \gamma = 0.1$, ${\text{Da}} = 10^{ - 5}$, $\beta = 5$, $M = 1.1$, ${ \Pr } = 7.7$ and ${\text{Ps}} = 2.5$

Figure 13 shows the effect of Darcy number (${\text{Da}}$) on Nu number for $S_{\text{s}}^{*} = 0$ and $S_{\text{f}}^{*} = 0$. It is seen that increasing the ${\text{Da}}$ number decreases the mean value of ${\text{Nu}}$ number [16], while increases significantly the amplitude of the oscillation. For example, as Da number increases from $10^{ - 5}$ to $10^{ - 2}$, the mean value of Nu number decreases by about 10%, while the amplitude of oscillation increases by more than 15 times. An increase in Da number increases the amplitude of the unsteady velocity according to Fig. 4 and the amplitude of the $\theta_{\text{f,un}}$ according to Fig. 10. Hence, from Eq. (42) this will increase the amplitude of oscillation of $\theta_{\text{f,un,b}}$, which results in amplifying the amplitude of oscillation of Nu number according to Eq. (39). For the case of ${\text{Da}} = 10^{ - 5}$, the amplitude of $U_{\text{un}}$ and the amplitude of $\theta_{\text{f,un}}$ are so small that hence the oscillation of Nu number is very small.

Fig. 13

Nusselt number versus time for different values of ${\text{Da}}$ numbers with $S_{\text{s}}^{*} = 0$, $S_{\text{f}}^{*} = 0$, $k = 0.3$, ${\text{Bi}} = 0.1, \gamma = 0.1$, $\beta = 5$, $M = 1.1$, ${ \Pr } = 7.7\; {\text{and}}$ ${\text{Ps}} = 2.5$

The effects of thermal conductivity ratio $k$ and Biot number, on the Nu number, are shown in Figs. 14 and 15 for ${\text{Da}} = 10^{ - 5}$ and ${\text{Da}} = 10^{ - 2}$, respectively. Results for each case are compared with Nu numbers for the steady flow with the same conditions. Similar to Fig. 13, it is seen that for low Da number of 10⁻⁵, the ratio of amplitude-to-mean value of the Nusselt number for all cases in Fig. 14 is less than 1%, and the pulsations are almost negligible. This figure indicates that variations in the values of $k$ or ${\text{Bi}}$ do not affect significantly the pulsation of Nu number. From Fig. 15, it is seen that for a high Da number, the amplitude of Nu number reduces with the increase in $k$ or ${\text{Bi}}$.

Fig. 14

Nusselt number versus time for ${\text{Da}} = 10^{ - 5}$ with $S_{\text{s}}^{*} = 0$,$S_{\text{f}}^{*} = 0, \;\gamma = 0.1$, ${\text{Da}} = 10^{ - 5}$, $\beta = 5$, $M = 1.1$,${ \Pr } = 7.7,$ ${\text{Ps}} = 2.5$ for a ${\text{Bi}} = 0.5$ and $k = 0.1$, b ${\text{Bi}} = 50$ and $k = 0.1$, c ${\text{Bi}} = 0.5$ and $k = 10$, and d ${\text{Bi}} = 50$ and $k = 10$

Fig. 15

Nusselt number versus time for ${\text{Da}} = 10^{ - 2}$ with $S_{\text{s}}^{*} = 0$,$S_{\text{f}}^{*} = 0, \;\gamma = 0.1$, ${\text{Da}} = 10^{ - 5}$, $\beta = 5$, $M = 1.1$,${ \Pr } = 7.7,$ ${\text{Ps}} = 2.5$ for a ${\text{Bi}} = 0.5$ and $k = 0.1$, b ${\text{Bi}} = 50$ and $k = 0.1$, c ${\text{Bi}} = 0.5$ and $k = 10$, and d ${\text{Bi}} = 50$ and $k = 10$

The effect of the coefficient of pressure amplitude ($\gamma$ in Eq. 2) is shown in Fig. 16. It is seen that an increase in $\gamma$, increases significantly the amplitude of Nu number, which was also presented in previous works containing pulsatile flow in an empty channel or pipe [24, 25, 62]. This demonstrates that waveform amplitude has a deterministic role in controlling the rate of convective heat transfer between the walls and the fluid flowing in the channel. Figure 17 shows the impact of the dimensionless frequency ($\beta$) on Nu number for $\gamma = 0.1$ and for other conditions similar to Fig. 16. It is seen that as the value of $\beta$ increases, the amplitude of pulsation of Nu number decreases. This is in agreement with the findings of previous works (e.g., [24, 25, 58]). The main influence of $\beta$ is on the period of oscillation, as expected.

Fig. 16

Nusselt number versus time for different values of $\gamma$ with $S_{\text{s}}^{*} = 0$,$S_{\text{f}}^{*} = 0$,$k = 0.3$,${\text{Bi}} = 0.1$, ${\text{Da}} = 10^{ - 5}$, $\beta = 5$, $M = 1.1$,${ \Pr } = 7.7$ and ${\text{Ps}} = 2.5$

Fig. 17

Nusselt number versus time for different values of $\beta$ with $S_{\text{s}}^{*} = 0$,$S_{\text{f}}^{*} = 0$,$k = 0.3$,${\text{Bi}} = 0.1$, $\gamma = 0.1,\; {\text{Da}} = 10^{ - 5}$, $M = 1.1$,${ \Pr } = 7.7$ and ${\text{Ps}} = 2.5$

For the steady-state fully developed flow in a channel filled with a porous material, Nu number is independent of the Prandtl (Pr) number [13, 16]. While for the pulsating flow, Pr number has significant influence on Nu number [25, 41]. Figure 18 shows the effect of Pr number on the Nu number under LTNE condition for ${\text{Da}} = 10^{ - 5}$ (Fig. 18a) and ${\text{Da}} = 10^{ - 2}$ (Fig. 18b). It is seen that for small Da number, the amplitude of Nu number increases slightly with the increase in Pr number. For large Da numbers, as Da increases the amplitude of Nu oscillation increases. Further increase in Da number decreases the amplitude of Nu number. Additionally, it is seen that the effect of Pr number on the Nu number is profound for high Da numbers. Comparing Fig. 18a and b indicates that the effect of Pr number for low Da number is almost negligible. These findings are consistent with the results of Kuznetsov and Nield [41] obtained incorporating the LTE model. Kuznetsov and Nield [41] investigated the effect of the Pr number in a channel filled with a saturated porous medium under LTE model. They found that for large Da numbers, increasing Pr number decreases the amplitude of Nu number. While for small Da numbers, the effect of Pr number on Nu number is found to be negligible.

Fig. 18

Nusselt number versus time for different values of Prandtl (Pr) number with $S_{\text{f}}^{*} = 0$,$S_{\text{s}}^{*} = 0$, $\gamma = 0.1$, $k = 0.3$,${\text{Bi}} = 0.1$, $\beta = 5$, $M = 1.1$ and Ps = 2.5 for a Da = 10⁻⁵ and b Da = 10⁻²

Conclusions

This paper studied analytically the problem of forced convection heat transfer of pulsating flow due to oscillatory applied pressure gradient in a channel filled with a porous medium subjected to a constant wall heat flux. By considering internal heat generations in the solid and the fluid phases in the porous region, energy equations were solved using a local thermal non-equilibrium (LTNE) model. Considering specific conditions at the wall interface, the approach known as Model A for the thermal boundary conditions was used to solve the governing equations. Exact solutions for the unsteady velocity ($U_{\text{un}}$), temperature of the solid phase ($\theta_{\text{s,un}}$) and temperature of the fluid phase ($\theta_{\text{f,un}}$) and Nusselt number (Nu) were obtained. The effect of different parameters is analyzed. These parameters are Darcy number (Da), Prandtl number (Pr), Biot number (Bi), fluid-to-solid thermal conductivity ratio ($k$), heat generation in the solid phase ($S_{\text{s}}^{*}$) and fluid phase ($S_{\text{f}}^{*}$), dimensionless frequency ($\beta$) and the coefficient of pressure amplitude ($\gamma$). Important results of this study are summarized as follows:

• The amplitude of the unsteady velocity increases with the increase of $\gamma$ or ${\text{Da}}$, while decreases with the increase in dimensionless frequency $\beta$.

• The amplitude of the unsteady dimensionless temperatures for the fluid phase is relatively higher than that of the solid phase.

• Increasing the value of $k$ or ${\text{Bi}},$ decreases the amplitude of the unsteady dimensionless temperature for the two phases, while results in reducing the difference between the values of $\theta_{\text{s,un}}$ and $\theta_{\text{f,un}}$.

• For large Bi numbers, the total dimensionless temperature (sum of steady and unsteady components) for each phase was observed to be close to the steady flow. Moreover, for large Bi number the difference between the temperatures of the two phases is small and hence the LTE model is valid.

• Results indicate that Nu number oscillates harmonically around the steady counterpart, which is equal to the mean value of the oscillating Nu number.

• The ratio of amplitude-to-mean value of Nu number remains almost constant with the increase in internal heat generation in the solid phase ($S_{\text{s}}^{*}$), while enhances with the increase in internal heat generation in the fluid phase ($S_{\text{f}}^{*}$).

• Increasing the thermal conductivity ratio $k$ or Bi number reduces the amplitude of Nu number.

• Amplitude of the Nu number increases with the increase in $\gamma$ and ${\text{Da}}$, while decreases with the increase in $\beta$.

• The variation of the Nusselt number due to change in the Prandtl number was found to depend on the value of Da number. For small Da numbers, the amplitude of Nu number increases slightly with the increase in Prandtl number. While, for high Darcy numbers, the amplitude of Nu number increases up to a maximum value. Further increase in Prandtl number decreases the amplitude of Nu number.

Appendix

This section includes solution procedures for the momentum and energy equations in a porous medium with pulsating flow.

Momentum equation

Solutions are obtained using the method of eigenfunction expansion. According to this method, solution for unsteady momentum Eq. (24) is written in the general form as following:

$$U_{\text{un}} \left( {t^{*} ,Y} \right) = \mathop \sum \limits_{n = 1}^{\infty } a_{\text{n}} \left( {t^{*} } \right)\emptyset_{\text{n}} \left( Y \right).$$

(46)

The eigenfunction $\emptyset_{\text{n}} \left( Y \right)$ is found using the related homogeneous problem obtaining from Eq. (24) [64] as:

$$\frac{{\partial U_{\text{un}} }}{{\partial t^{*} }} = M\frac{{\partial^{2} U_{\text{un}} }}{{\partial Y^{2} }} - \frac{{U_{\text{un}} }}{\text{Da}}.$$

(47)

The eigenfunctions of this related homogeneous problem Eq. (47), using boundary conditions Eq. (25), satisfy the following equation:

$$\begin{aligned} & \frac{{{\text{d}}^{2} \emptyset }}{{{\text{d}}Y^{2} }} + \delta^{2} \emptyset = 0, \\ & \left. {\frac{{{\text{d}}\emptyset }}{{{\text{d}}Y}}} \right|_{Y = 0} = 0,\quad \emptyset \left( 1 \right) = 0. \\ \end{aligned}$$

(48)

Equation (48) is a Sturm–Liouville eigenvalue problem [64] and the corresponding eigenfunctions are:

$$\emptyset_{\text{n}} \left( Y \right) = \cos \left( {\delta_{\text{n}} Y} \right);\quad \delta_{n} = \left( {2n - 1} \right)\frac{\pi }{2},\quad n = 1,2,3, \ldots$$

(49)

Using Eq. (49), Eq. (46) is written as:

$$U_{\text{un}} \left( {t^{*} ,Y} \right) = \mathop \sum \limits_{n = 1}^{\infty } a_{\text{n}} \left( {t^{*} } \right)\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right).$$

(50)

Using Eq. (50), the initial condition given in Eq. (26) is written as:

$$0 = \mathop \sum \limits_{n = 1}^{\infty } a_{\text{n}} \left( 0 \right)\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right).$$

(51)

So, the initial value in Eq. (51) is zero;

$$a_{\text{n}} \left( 0 \right) = 0.$$

(52)

All that remains is to determine $a_{\text{n}} \left( {t^{*} } \right)$ in Eq. (50) which solves the non-homogeneous partial differential equations of momentum Eq. (24). To find $a_{\text{n}} \left( {t^{*} } \right),$ the term-by-term differentiations are calculated as:

$$\frac{{\partial U_{\text{un}} }}{{\partial t^{*} }} = \mathop \sum \limits_{n = 1}^{\infty } \frac{{{\text{d}}a_{\text{n}} \left( {t^{*} } \right)}}{{{\text{d}}t^{*} }}\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right),$$

(53)

$$\frac{{\partial^{2} U_{\text{un}} }}{{\partial Y^{2} }} = \mathop \sum \limits_{n = 1}^{\infty } \left( { - \frac{{\left( {2n - 1} \right)^{2} \pi^{2} }}{4}} \right)a_{\text{n}} \left( {t^{*} } \right)\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right).$$

(54)

Equations (53) and (54) are now substituted into Eq. (24), and the resultant equation can be written as:

$$\mathop \sum \limits_{n = 1}^{\infty } \left\{ {\left[ {\frac{{{\text{d}}a_{\text{n}} \left( {t^{*} } \right)}}{{{\text{d}}t^{*} }} + \left( {M\frac{{\left( {2n - 1} \right)^{2} \pi^{2} }}{4} + \frac{1}{\text{Da}}} \right) \cdot a_{\text{n}} \left( {t^{*} } \right)} \right] \cdot \cos \left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right)} \right\} = \gamma \sin \left( {\beta t^{*} } \right).$$

(55)

Due to orthogonality of the eigenfunctions ($\emptyset_{\text{n}} \left( Y \right)$) obtaining from the Sturm–Liouville eigenvalue problem of Eq. (34), the following equation for the time-dependent coefficient of the term $\left[ {{ \cos }\left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right)} \right]$ in Eq. (55) is obtained [64]:

$$\left[ {\frac{{{\text{d}}a_{n} \left( {t^{*} } \right)}}{{{\text{d}}t^{*} }} + \left( {M\frac{{\left( {2n - 1} \right)^{2} \pi^{2} }}{4} + \frac{1}{\text{Da}}} \right) \cdot a_{\text{n}} \left( {t^{*} } \right)} \right] = \frac{{\mathop \smallint \nolimits_{0}^{1} \gamma \sin \left( {\beta t^{*} } \right) \cdot { \cos }\left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right){\text{d}}Y}}{{\mathop \smallint \nolimits_{0}^{1} { \cos }^{2} \left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right){\text{d}}Y}} = \frac{{ - 4 \cdot \left( { - 1} \right)^{n} \cdot \gamma \sin \left( {\beta t^{*} } \right)}}{{\left( {2n - 1} \right)\pi }}.$$

(56)

Equation (56) is a first-order ODE problem with respect to $t^{*}$ which can easily be solved to find $a_{\text{n}} \left( {t^{*} } \right)$. Using initial condition presented in Eq. (52), $a_{\text{n}} \left( {t^{*} } \right)$ is obtained (Eq. 30).

Energy equations

Similar to the procedure deployed to solve for the velocity, the solutions for the temperatures of the two phases are divided into steady and unsteady components [25] as:

$$T_{\text{f}}^{*} = T_{\text{f,st}}^{*} \left( {X,Y} \right) + T_{\text{f,un}}^{*} \left( {t^{*} ,Y} \right),$$

(57)

$$T_{\text{s}}^{*} = T_{\text{s,st}}^{*} \left( {X,Y} \right) + T_{\text{s,un}}^{*} \left( {t^{*} ,Y} \right).$$

(58)

Substituting Eqs. (57) and (58) into Eqs. (15) and (16), the resultant equations are as:

$$\begin{aligned} & { \Pr } \cdot k\left( {\frac{{\partial T_{\text{f,st}}^{*} }}{{\partial t^{*} }} + \frac{{\partial T_{\text{f,un}}^{*} }}{{\partial t^{*} }}} \right) + k\left( {U_{\text{st}} + U_{\text{un}} } \right)\left( {\frac{{\partial T_{\text{f,st}}^{*} }}{\partial X} + \frac{{\partial T_{\text{f,un}}^{*} }}{\partial X}} \right) \\ & \quad = k\left( {\frac{{\partial^{2} T_{\text{f,st}}^{*} }}{{\partial Y^{2} }} + \frac{{\partial^{2} T_{\text{f,un}}^{*} }}{{\partial Y^{2} }}} \right) + {\text{Bi}}\left( {(T_{\text{s,st}}^{*} + T_{\text{s,un}}^{*} ) - (T_{\text{f,st}}^{*} + T_{\text{f,un}}^{*} )} \right) + S_{\text{f}}^{*} , \\ \end{aligned}$$

(59)

$${\text{Ps}}\left( {\frac{{\partial T_{\text{s,st}}^{*} }}{{\partial t^{*} }} + \frac{{\partial T_{\text{s,un}}^{*} }}{{\partial t^{*} }}} \right) = \left( {\frac{{\partial^{2} T_{\text{s,st}}^{*} }}{{\partial Y^{2} }} + \frac{{\partial^{2} T_{\text{s,un}}^{*} }}{{\partial Y^{2} }}} \right) - {\text{Bi}}\left( {(T_{\text{s,st}}^{*} + T_{\text{s,un}}^{*} ) - (T_{\text{f,st}}^{*} + T_{\text{f,un}}^{*} )} \right) + S_{\text{s}}^{*} .$$

(60)

Since $\frac{{\partial T_{\text{f,st}}^{*} }}{{\partial t^{*} }} = 0$ and according to Eq. (57) $T_{\text{f,un}}^{*}$ is not a function of $X$ [25], each of the energy Eqs. (59) and (60) can be divided into two separate steady and unsteady equations and solved separately as explained in the following.

Steady energy equations

Using Eqs. (59) and (60), a new set of steady equations are derived as:

$$kU_{\text{st}} \frac{{\partial T_{\text{f,st}}^{*} }}{\partial X} = k\frac{{\partial^{2} T_{\text{f,st}}^{*} }}{{\partial Y^{2} }} + {\text{Bi}}\left( {T_{\text{s,st}}^{*} - T_{\text{f,st}}^{*} } \right) + S_{\text{f}}^{*} ,$$

(61)

$$0 = \frac{{\partial^{2} T_{\text{s,st}}^{*} }}{{\partial Y^{2} }} - {\text{Bi}}\left( {T_{\text{s,st}}^{*} - T_{\text{f,st}}^{*} } \right) + S_{\text{s}}^{*} .$$

(62)

The flow is considered to be fully developed, implying that $\frac{{\partial T_{\text{f,st}}^{*} }}{\partial X} = C$ is constant [66]. Using a dimensionless variable $\theta_{\text{st}} = \frac{{k_{\text{s,eff}} \left( {T - T_{\text{w,st}} } \right)}}{{q_{\text{w}} H}} = (T^{*} - T_{\text{w,st}}^{*} )$, Eqs. (61) and (62) are rewritten as:

$$kU_{\text{st}} C = k\frac{{\partial^{2} \theta_{\text{f,st}} }}{{\partial Y^{2} }} + {\text{Bi}}\left( {\theta_{\text{s,st}} - \theta_{\text{f,st}} } \right) + S_{\text{f}}^{*} ,$$

(63)

$$0 = \frac{{\partial^{2} \theta_{\text{s,st}} }}{{\partial Y^{2} }} - {\text{Bi}}\left( {\theta_{\text{s,st}} - \theta_{\text{f,st}} } \right) + S_{\text{s}}^{*} ,$$

(64)

where $\theta_{\text{f,st}} = \frac{{k_{\text{s,eff}} \left( {T_{\text{f,st}} - T_{\text{w,st}} } \right)}}{{q_{\text{w}} H}}$ and $\theta_{\text{s,st}} = \frac{{k_{\text{s,eff}} \left( {T_{\text{s,st}} - T_{\text{w,st}} } \right)}}{{q_{\text{w}} H}}$ are the steady dimensionless temperature of the fluid phase and solid phase, respectively.

Some of the previous studies obtained an average value for $\frac{{\partial T_{\text{f,st}} }}{\partial X}$ based on the flow characteristics [13, 16, 67]. Parameter $C = \frac{{\partial T_{\text{f,st}}^{*} }}{\partial X}$ is used to solve the unsteady equations, and its exact solution is found in the present work. To solve steady equations and find C, $\theta_{\text{s,st}}$ is obtained from Eq. (63) and then is substituted into Eq. (64). From Eq. (63), $\theta_{\text{s,st}}$ is derived as:

$$\theta_{\text{s,st}} = \frac{Ck}{\text{Bi}}U_{\text{st}} - \frac{k}{\text{Bi}}\frac{{\partial^{2} \theta_{\text{s,st}} }}{{\partial Y^{2} }} + \theta_{\text{f,st}} - \frac{{S_{\text{f}}^{*} }}{\text{Bi}}.$$

(65)

Substituting Eq. (65) into Eq. (64) and applying velocity solution from Eq. (27) yields:

$$k\frac{{\partial^{4} \theta_{\text{f,st}} }}{{\partial Y^{4} }} - {\text{Bi}}\left( {1 + k} \right)\frac{{\partial^{2} \theta_{\text{f,st}} }}{{\partial Y^{2} }} = Ck\left( {\frac{{\left( {{\text{Bi}} \cdot {\text{Da}} - \frac{1}{M}} \right)\cosh \left( {\frac{Y}{{\sqrt {M{\text{Da}}} }}} \right)}}{{\cosh \left( {\frac{1}{{\sqrt {M{\text{Da}}} }}} \right)}} - {\text{Bi}} \cdot {\text{Da}}} \right) + {\text{Bi}}S^{*} .$$

(66)

The boundary conditions for the steady equations are also derived utilizing a same procedure as for momentum equation by separating steady and unsteady components from Eqs. (17) and (18). The heat flux, $q_{\text{w}}$, is a constant value, and therefore, it is applied to boundary condition of the steady components [24]; so employing the dimensionless variable $\theta$, boundary conditions can be rewritten as:

$$\left. {\frac{{\partial \theta_{\text{s,st}} }}{\partial Y}} \right|_{Y = 0} = \left. {\frac{{\partial \theta_{\text{f,st}} }}{\partial Y}} \right|_{Y = 0} = 0,$$

(67)

$$\left. {\frac{{\partial \theta_{\text{s,st}} }}{\partial Y}} \right|_{Y = 1} + k\left. {\frac{{\partial \theta_{\text{f,st}} }}{\partial Y}} \right|_{Y = 1} = 1.$$

(68)

Furthermore, one more boundary condition is needed to solve steady set of energy equations that is derived from Eq. (10).

$$\left. {\theta_{\text{s,st}} } \right|_{Y = 1} = \left. {\theta_{\text{f,st}} } \right|_{Y = 1} = 0.$$

(69)

Equation (66) is a fourth-order ODE problem and the solution of $\theta_{\text{f,st}}$ is as:

$$\begin{aligned} \theta_{\text{f,st}} & = C_{1} + C_{2} Y + C_{3} \sinh \left( {\lambda Y} \right) + C_{4} \cosh \left( {\lambda Y} \right) \\ & \quad + \left( {\frac{{k \cdot C \cdot {\text{Da}} - S^{*} }}{{2\left( {1 + k} \right)}}} \right)Y^{2} + \left( {\frac{{k \cdot C \cdot {\text{Da}}\left( {{\text{Bi}} - Z^{2} } \right)}}{{kZ^{4} - {\text{Bi}}\left( {1 + k} \right)Z^{2} }}} \right)\frac{{\cosh \left( {ZY} \right)}}{\cosh \left( Z \right)}, \\ \end{aligned}$$

(70)

where

$$\lambda = \sqrt {{\text{Bi}}\left( {1 + k} \right)/k} .$$

(71)

Applying the boundary condition Eqs. (67)–(70) results in:

$$C_{2} = C_{3} = 0.$$

(72)

By applying the boundary condition Eq. (68), the solution for C is finally obtained (Eq. 36).

Unsteady energy equations

Using Eqs. (59) and (60), a new set of unsteady equations are derived as:

$${ \Pr }k\frac{{\partial T_{\text{f,un}}^{*} }}{{\partial t^{*} }} + CkU_{\text{un}} = k\frac{{\partial^{2} T_{\text{f,un}}^{*} }}{{\partial Y^{2} }} + {\text{Bi}}\left( {T_{\text{s,un}}^{*} - T_{\text{f,un}}^{*} } \right),$$

(73)

$${\text{Ps}}\frac{{\partial T_{\text{s,un}}^{*} }}{{\partial t^{*} }} = \frac{{\partial^{2} T_{\text{s,un}}^{*} }}{{\partial Y^{2} }} - {\text{Bi}}\left( {T_{\text{s,un}}^{*} - T_{\text{f,un}}^{*} } \right).$$

(74)

Obtaining $T_{\text{f,uu}}^{*}$ from Eq. (74) yields:

$$T_{\text{f,un}}^{*} = \frac{\text{Ps}}{\hbox{Bi}} \frac{{\partial T_{\text{s,un}}^{*} }}{{\partial t^{*} }} - \frac{1}{\text{Bi}}\frac{{\partial^{2} T_{\text{s,un}}^{*} }}{{\partial Y^{2} }} + T_{\text{s,un}}^{*} .$$

(75)

Substituting Eq. (75) into Eq. (73) and using Eq. (29), the resultant equation is as:

$$\begin{aligned} & \frac{{{ \Pr } \cdot {\text{Ps}}}}{\text{Bi}} \left\{ {\frac{{\partial^{2} T_{\text{s,un}}^{*} }}{{\partial t^{*2} }}} \right\} - \frac{{\left( {{ \Pr } + {\text{Ps}}} \right)}}{\text{Bi}} \left\{ {\frac{{\partial^{3} T_{\text{s,un}}^{*} }}{{\partial^{2} Y\partial t^{*} }}} \right\} + \left( {{ \Pr } + \frac{\text{Ps}}{k}} \right)\left\{ {\frac{{\partial T_{\text{s,un}}^{*} }}{{\partial t^{*} }}} \right\} \\ & \quad + \frac{1}{\text{Bi}}\left\{ {\frac{{\partial^{4} T_{\text{s,un}}^{*} }}{{\partial Y^{4} }}} \right\} - \left( {\frac{1 + k}{k}} \right)\left\{ {\frac{{\partial^{2} T_{\text{s,un}}^{*} }}{{\partial Y^{2} }}} \right\} = - C\mathop \sum \limits_{n = 1}^{\infty } a_{\text{n}} \left( {t^{*} } \right)\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right). \\ \end{aligned}$$

(76)

Equation (76) is a non-homogeneous PDE that can be solved using a similar procedure as momentum equation. Separating components of Eq. (17), this boundary condition for unsteady energy equations is derived as:

$$\left. {\frac{{\partial T^{*}_{\text{f,un}} }}{\partial Y}} \right|_{Y = 0} = \left. {\frac{{\partial T^{*}_{\text{s,un}} }}{\partial Y}} \right|_{Y = 0} = 0.$$

(77)

As it was explained previously, the applied heat flux is applied to steady components of the temperature [24]; consequently, the unsteady components will not have conduction heat transfer at the wall interface;

$$\left. {\frac{{\partial T^{*}_{\text{f,un}} }}{\partial Y}} \right|_{Y = 1} = \left. {\frac{{\partial T^{*}_{\text{s,un}} }}{\partial Y}} \right|_{Y = 1} = 0.$$

(78)

The final form of the temperature is considered to be as:

$$T_{\text{s,un}}^{*} \left( {t^{*} ,Y} \right) = \mathop \sum \limits_{m = 1}^{\infty } b_{\text{m,n}} \left( {t^{*} } \right)\Gamma _{\text{m}} \left( Y \right).$$

(79)

As there are second-order differentiations of $t^{*}$ in Eq. (76), two initial conditions are required. Based on the same idea explained for the momentum unsteady equation, the initial conditions for the unsteady energy equation (Eq. 76) are considered zero for simplicity. However, the correct values are obtained by omitting the developing terms finally, as discussed in the paper.

$$\left. {T_{\text{s,un}}^{*} } \right|_{{t^{*} = 0}} = \left. {\frac{{\partial T^{*}_{\text{s,un}} }}{{\partial t^{*} }}} \right|_{{t^{*} = 0}} = 0.$$

(80)

To calculate the related eigenfunctions ($\Gamma _{\text{m}} \left( Y \right)$), the eigenfunctions were considered in the sinusoidal form as follows:

$$\Gamma _{\text{m}} \left( Y \right) = A_{1} \cos \left( {\delta_{\text{m}} Y} \right) + A_{2} \sin \left( {\delta_{\text{m}} Y} \right),$$

(81)

where $A_{1}$ and $A_{2}$ are constant values. Applying the boundary conditions Eqs. (77) and (78) to Eq. (81), the general form of the eigenfunctions will be as:

$$\Gamma _{\text{m}} \left( Y \right) = \cos \left( {\delta_{\text{m}} Y} \right); \quad \delta_{\text{m}} = m\pi ,\quad m = 1,2,3, \ldots$$

(82)

Substituting Eq. (82) into Eq. (79) yields:

$$T_{\text{s,un}}^{*} \left( {t^{*} ,Y} \right) = \mathop \sum \limits_{m = 1}^{\infty } b_{\text{m,n}} \left( {t^{*} } \right)\cos \left( {m\pi Y} \right).$$

(83)

Applying the initial conditions (Eq. 80) into Eq. (83), the following results are obtained:

$$\left. {b_{\text{m,n}} \left( {t^{*} } \right)} \right|_{{t^{*} = 0}} = \left. {\frac{{{\text{d}}b_{\text{m,n}} \left( {t^{*} } \right)}}{{{\text{d}}t^{*} }}} \right|_{{t^{*} = 0}} = 0.$$

(84)

Substituting Eq. (83) into Eq. (76) yields:

$$\mathop \sum \limits_{m = 1}^{\infty } g_{\text{m,n}} \left( {t^{*} } \right)\cos \left( {m\pi Y} \right) = - C\mathop \sum \limits_{n = 1}^{\infty } a_{\text{n}} \left( {t^{*} } \right)\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right),$$

(85)

where

$$\begin{aligned} g_{\text{m,n}} \left( {t^{*} } \right) & = \frac{{{ \Pr } \cdot {\text{Ps}}}}{\text{Bi}} \left\{ {\frac{{{\text{d}}^{2} b_{\text{m,n}} }}{{{\text{d}}t^{2} }}} \right\} + \left( {\left( {\frac{{m^{2} \pi^{2} }}{\text{Bi}} + 1} \right){ \Pr } + \left( {\frac{{m^{2} \pi^{2} k}}{\text{Bi}} + 1} \right)\frac{\text{Ps}}{k}} \right) \\ & \quad \left\{ {\frac{{{\text{d}}b_{\text{m,n}} }}{{{\text{d}}t}}} \right\} + \left( {m^{2} \pi^{2} \left( {\frac{1 + k}{k} + \frac{{m^{2} \pi^{2} }}{\text{Bi}}} \right)} \right)\left\{ {b_{\text{m,n}} } \right\}. \\ \end{aligned}$$

(86)

The right-hand side of Eq. (85) is specified with respect to variables Y and $t^{*}$; and the left-hand side of the equation is a Fourier Cosine series on the interval $0 \le Y \le L$ (where, L = 1 in this study) [64]; so the Fourier coefficient ($g_{\text{m,n}} \left( {t^{*} } \right)$) can be found using the Fourier series properties as:

$$\begin{aligned} g_{\text{m,n}} \left( {t^{*} } \right) & = \frac{2}{1} \left( { - C\mathop \sum \limits_{n = 1}^{\infty } a_{\text{n}} \left( {t^{*} } \right)\mathop \smallint \limits_{0}^{1} \left( {\cos \left( {\left( {2n - 1} \right)\frac{\pi }{2}Y} \right)\cos \left( {m\pi Y} \right){\text{d}}Y} \right)} \right) \\ & = \frac{2C}{\pi }\mathop \sum \limits_{n = 1}^{\infty } a_{\text{n}} \left( {t^{*} } \right)\left( { - 1} \right)^{m + n} \left( {\frac{1}{{2\left( {m + n} \right) - 1}} - \frac{1}{{2\left( {m - n} \right) + 1}}} \right). \\ \end{aligned}$$

(87)

Using Eq. (87), the following important ODE is obtained from Eq. (86):

$$\begin{aligned} & \frac{{{ \Pr } \cdot {\text{Ps}}}}{\text{Bi}} \left\{ {\frac{{{\text{d}}^{2} b_{\text{m,n}} }}{{{\text{d}}t^{*2} }}} \right\} + \left( {\left( {\frac{{m^{2} \pi^{2} }}{\text{Bi}} + 1} \right){ \Pr } + \left( {\frac{{m^{2} \pi^{2} k}}{\text{Bi}} + 1} \right)\frac{\text{Ps}}{k}} \right) \\ & \quad \quad \left\{ {\frac{{{\text{d}}b_{\text{m,n}} }}{{{\text{d}}t^{*} }}} \right\} + \left( {m^{2} \pi^{2} \left( {\frac{1 + k}{k} + \frac{{m^{2} \pi^{2} }}{\text{Bi}}} \right)} \right)\left\{ {b_{\text{m,n}} } \right\} \\ & \quad = \frac{2C}{\pi }\mathop \sum \limits_{n = 1}^{\infty } a_{\text{n}} \left( {t^{*} } \right)\left( { - 1} \right)^{m + n} \left( {\frac{1}{{2\left( {m + n} \right) - 1}} - \frac{1}{{2\left( {m - n} \right) + 1}}} \right). \\ \end{aligned}$$

(88)

The ODE Eq. (70) is a second-order linear inhomogeneous ODE with respect to $t^{*}$; as the associated homogeneous problem is a constant-coefficient one and consequently its solutions can be obtained easily, method of variation of constants (Lagrange’s Method) can be used to find the general solution of the ODE [68]. To find the solutions, the roots of the characteristic equation for the corresponding homogeneous ODE (Eq. 88) are needed to be obtained in advance.

$$r_{1 } , r_{2} = \frac{{ - \left( {\left( {\frac{{m^{2} \pi^{2} }}{\text{Bi}} + 1} \right){ \Pr } + \left( {\frac{{m^{2} \pi^{2} k}}{\text{Bi}} + 1} \right)\frac{\text{Ps}}{k}} \right) \pm \sqrt {d_{\text{m}} } }}{{2\left( {\frac{{{ \Pr } \cdot {\text{Ps}}}}{\text{Bi}}} \right)}} ,$$

(89)

where $r_{1 } , r_{2}$ are the roots of the characteristic equation of the homogeneous ODE, and $d_{\text{m}}$ is defined as:

$$d_{\text{m}} = \frac{{m^{4} \pi^{4} }}{{{\text{Bi}}^{2} }}\left( {{ \Pr } - {\text{Ps}}} \right)^{2} + \frac{{2m^{2} \pi^{2} }}{\text{Bi}}\left( {{ \Pr } - {\text{Ps}}} \right)\left( {{ \Pr } - \frac{\text{Ps}}{k}} \right) + \left( {{ \Pr } + \frac{\text{Ps}}{k}} \right)^{2} .$$

(90)

The solution of the ODE Eq. (88) can be found now based on the solutions of the associated homogeneous problem employing the method of variation of constants as follows [68]:

$$b_{\text{m,n}} \left( {t^{*} } \right) = B_{1} e^{{r_{1 } t^{*} }} + B_{2} e^{{r_{2 } t^{*} }} + V_{1} \left( {t^{*} } \right) \cdot e^{{r_{1 } t^{*} }} + V_{2} \left( {t^{*} } \right) \cdot e^{{r_{2 } t^{*} }} ,$$

(91)

where $B_{1}$ and $B_{2}$ are constant values; $V_{1} \left( {t^{*} } \right)$ and $V_{2} \left( {t^{*} } \right)$ are functions that are obtained using the method of variation of constants, resulting in the following relations after some brief computations [68]:

$$V_{1} \left( {t^{*} } \right) = \mathop \int \limits_{0}^{{t^{*} }} \frac{{g_{\text{m,n}} \left( {t^{*} } \right) \cdot e^{{ - {\text{r}}_{1 } {\text{t}}^{*} }} }}{{\left( {r_{1 } - r_{2 } } \right)}}{\text{d}}t^{*} ,\quad V_{2} \left( {t^{*} } \right) = \mathop \int \limits_{0}^{{t^{*} }} \frac{{g_{\text{m,n}} \left( {t^{*} } \right) \cdot e^{{ - {\text{r}}_{2 } {\text{t}}^{*} }} }}{{\left( {r_{2 } - r_{1 } } \right)}}{\text{d}}t^{*} ,$$

(92)

with this reminder that the term $g_{\text{m,n}} \left( {t^{*} } \right)$ is the inhomogeneity of the ODE (Eq. 87).

Substituting $V_{1} \left( {t^{*} } \right)$ and $V_{2} \left( {t^{*} } \right)$ from Eq. (92) (or after integrating and obtaining their values) into Eq. (91) and applying Eq. (84) yields:

$$B_{1} = B_{2} = 0.$$

(93)

Calculating $V_{1} \left( {t^{*} } \right)$ and $V_{2} \left( {t^{*} } \right)$ from Eq. (92) and applying their values along with Eq. (93) into Eq. (83), the distribution of $T_{s,un}^{*}$ is obtained as:

$$T_{\text{s,un}}^{*} \left( {t^{*} ,Y} \right) = \mathop \sum \limits_{m = 1}^{\infty } \frac{{2C \cdot { \cos }\left( {m\pi Y} \right)}}{{\pi \left( {r_{1 } - r_{2 } } \right)}} \mathop \sum \limits_{n = 1}^{\infty } F_{\text{m,n}} \left( {t^{*} } \right),$$

(94)

where

$$\begin{aligned} & F_{\text{m,n}} \left( {t^{*} } \right) = \frac{{ - 4\left( { - 1} \right)^{m} \gamma \left( {\frac{1}{{2\left( {m + n} \right) - 1}} - \frac{1}{{2\left( {m - n} \right) + 1}}} \right)}}{{\left( {2n - 1} \right)\pi \left( {16\left( {{\text{Da}}\beta } \right)^{2} + \left( {\left( {2n - 1} \right)^{2} \pi^{2} M \cdot {\text{Da}} + 4} \right)^{2} } \right)}} \\ & \quad *\left\{ { - 16{\text{Da}}^{2} \beta \left( {\frac{{ - r_{1 } { \cos }\left( {\beta t^{*} } \right) + \beta \sin \left( {\beta t^{*} } \right) + r_{1 } e^{{r_{1 } t^{*} }} }}{{\beta^{2} + r_{1 }^{2} }} - \frac{{ - r_{2 } { \cos }\left( {\beta t^{*} } \right) + \beta \sin \left( {\beta t^{*} } \right) + r_{2 } e^{{r_{2 } t^{*} }} }}{{\beta^{2} + r_{2 }^{2} }}} \right)} \right. \\ & \quad + \left( {4\left( {2n - 1} \right)^{2} \pi^{2} M \cdot {\text{Da}}^{2} + 16{\text{Da}}} \right)\left( {\frac{{ - \beta { \cos }\left( {\beta t^{*} } \right) - r_{1} \sin \left( {\beta t^{*} } \right) + \beta e^{{r_{1 } t^{*} }} }}{{\beta^{2} + r_{1 }^{2} }} - \frac{{ - \beta { \cos }\left( {\beta t^{*} } \right) - r_{2} \sin \left( {\beta t^{*} } \right) + \beta e^{{r_{2 } t^{*} }} }}{{\beta^{2} + r_{2 }^{2} }}} \right) \\ & \quad \left. { +\, 64{\text{Da}}^{3} \beta \left( {\frac{{e^{{r_{1 } t^{*} }} - e^{{ - \left( {\frac{{\left( {2n - 1} \right)^{2} \pi^{2} M}}{4} + \frac{1}{\text{Da}}} \right)t^{*} }} }}{{\left( {2n - 1} \right)^{2} \pi^{2} M \cdot {\text{Da}} + 4\left( {1 + {\text{Da}}r_{1} } \right)}} - \frac{{e^{{r_{2 } t^{*} }} - e^{{ - \left( {\frac{{\left( {2n - 1} \right)^{2} \pi^{2} M}}{4} + \frac{1}{\text{Da}}} \right)t^{*} }} }}{{\left( {2n - 1} \right)^{2} \pi^{2} M \cdot {\text{Da}} + 4\left( {1 + {\text{Da}}r_{2} } \right)}}} \right)} \right\} \\ \end{aligned}$$

(95)

Substituting $T_{\text{s,un}}^{*}$ from Eq. (94) into Eq. (75), the distribution of $T_{\text{f,un}}^{*}$ is also obtained as:

$$T_{\text{f,un}}^{*} \left( {t^{*} ,Y} \right) = \mathop \sum \limits_{m = 1}^{\infty } \frac{{2C \cdot \cos \left( {m\pi Y} \right)\left( {1 + \frac{{m^{2} \pi^{2} }}{\text{Bi}}} \right)}}{{\pi \left( {r_{1 } - r_{2 } } \right)}} \mathop \sum \limits_{n = 1}^{\infty } F_{\text{m,n}} \left( {t^{*} } \right) + \mathop \sum \limits_{m = 1}^{\infty } \frac{{2C \cdot \cos \left( {m\pi Y} \right)\left( {\frac{\text{Ps}}{\hbox{Bi}}} \right)}}{{\pi \left( {r_{1 } - r_{2 } } \right)}} \mathop \sum \limits_{n = 1}^{\infty } R_{\text{m,n}} \left( {t^{*} } \right),$$

(96)

where

$$\begin{aligned} & R_{\text{m,n}} \left( {t^{*} } \right) = \frac{{ - 4\left( { - 1} \right)^{m} \gamma \left( {\frac{1}{{2\left( {m + n} \right) - 1}} - \frac{1}{{2\left( {m - n} \right) + 1}}} \right)}}{{\left( {2n - 1} \right)\pi \left( {16\left( {{\text{Da}}\beta } \right)^{2} + \left( {\left( {2n - 1} \right)^{2} \pi^{2} M \cdot {\text{Da}} + 4} \right)^{2} } \right)}} \\ & \quad *\left\{ { - 16{\text{Da}}^{2} \beta \left( {\frac{{r_{1 } \beta {\text{sin}}\left( {\beta t^{*} } \right) + \beta^{2} \cos \left( {\beta t^{*} } \right) + r_{1 }^{2} e^{{r_{1 } t^{*} }} }}{{\beta^{2} + r_{1 }^{2} }} - \frac{{r_{2 } \beta {\text{sin}}\left( {\beta t^{*} } \right) + \beta^{2} \cos \left( {\beta t^{*} } \right) + r_{2 }^{2} e^{{r_{2 } t^{*} }} }}{{\beta^{2} + r_{2 }^{2} }}} \right)} \right. \\ & \quad + \left( {4\left( {2n - 1} \right)^{2} \pi^{2} M \cdot {\text{Da}}^{2} + 16{\text{Da}}} \right)\left( {\frac{{\beta^{2} {\text{sin}}\left( {\beta t^{*} } \right) - r_{1} \beta \cos \left( {\beta t^{*} } \right) + \beta r_{1} e^{{r_{1 } t^{*} }} }}{{\beta^{2} + r_{1 }^{2} }} - \frac{{\beta^{2} {\text{sin}}\left( {\beta t^{*} } \right) - r_{2} \beta \cos \left( {\beta t^{*} } \right) + \beta r_{2} e^{{r_{2 } t^{*} }} }}{{\beta^{2} + r_{2 }^{2} }}} \right) \\ & \quad \left. { +\, 64{\text{Da}}^{3} \beta \left( {\frac{{r_{1} e^{{r_{1 } t^{*} }} + \left( {\frac{{\left( {2n - 1} \right)^{2} \pi^{2} M}}{4} + \frac{1}{\text{Da}}} \right)e^{{ - \left( {\frac{{\left( {2n - 1} \right)^{2} \pi^{2} M}}{4} + \frac{1}{\text{Da}}} \right)t^{*} }} }}{{\left( {2n - 1} \right)^{2} \pi^{2} M \cdot {\text{Da}} + 4\left( {1 + {\text{Da}}r_{1} } \right)}} - \frac{{r_{2} e^{{r_{2 } t^{*} }} + \left( {\frac{{\left( {2n - 1} \right)^{2} \pi^{2} M}}{4} + \frac{1}{\text{Da}}} \right)e^{{ - \left( {\frac{{\left( {2n - 1} \right)^{2} \pi^{2} M}}{4} + \frac{1}{\text{Da}}} \right)t^{*} }} }}{{\left( {2n - 1} \right)^{2} \pi^{2} M \cdot {\text{Da}} + 4\left( {1 + {\text{Da}}r_{2} } \right)}}} \right)} \right\}. \\ \end{aligned}$$

(97)

One condition of Eq. (77) was satisfied (i.e., $\left. {\frac{{\partial T_{\text{s,un}}^{*} }}{\partial Y}} \right|_{Y = 1} = 0$) in the solving process. Checking the resultant equation for $T_{\text{f,un}}^{*}$ (Eq. 96) specifies that the second condition (i.e., $\left. {\frac{{\partial T_{\text{f,un}}^{*} }}{\partial Y}} \right|_{Y = 1} = 0$) is automatically satisfied.

The unsteady component of the wall temperature is required to calculate Nusselt number. Since the heat flux $q_{\text{w}}$ at the wall interface is a constant value which is applied to the steady components boundary condition [24], the following approximate relation based on the energy balance at the wall (Eq. 18) was derived to find the dimensionless unsteady temperature, $T_{\text{w,un}}^{*}$.

$$\left. {\left( {\frac{{\Delta T_{\text{s,un}}^{*} }}{\Delta Y} + k\frac{{\Delta T_{\text{f,un}}^{*} }}{\Delta Y}} \right)} \right|_{Y \approx 1} = 0,$$

(98)

where $\Delta Y$ is a small distance close to the wall, and $\Delta T_{\text{s,un}}^{*}$ and $\Delta T_{\text{f,un}}^{*}$ are defined as:

$$\Delta T_{\text{s,un}}^{*} = \left. {T_{\text{s,un}}^{*} } \right|_{Y = 1} - T_{\text{w,un}}^{*} ,\quad \Delta T_{\text{f,un}}^{*} = \left. {T_{\text{f,un}}^{*} } \right|_{Y = 1} - T_{\text{w,un}}^{*} ,$$

(99)

where $T_{\text{w,un}}^{*} = (k_{\text{s,eff}} T_{\text{w,un}} )/(q_{\text{w}} H)$ is the dimensionless unsteady wall temperature. Substituting Eq. (A. 2.43) into Eq. (98) yields:

$$\begin{aligned} T_{\text{w,un}}^{*} \cong \frac{{\left. {\left( {T_{\text{s,un}}^{*} + kT_{\text{f,un}}^{*} } \right)} \right|_{Y = 1} }}{1 + k} & = \mathop \sum \limits_{m = 1}^{\infty } \frac{{2C \cdot \left( { - 1} \right)^{m} \left( {1 + \frac{{k\left( {1 + \frac{{m^{2} \pi^{2} }}{\text{Bi}}} \right)}}{1 + k}} \right)}}{{\pi \left( {r_{1 } - r_{2 } } \right)}} \mathop \sum \limits_{n = 1}^{\infty } F_{\text{m,n}} \left( {t^{*} } \right) \\ & \quad + \mathop \sum \limits_{m = 1}^{\infty } \frac{{2C \cdot \left( { - 1} \right)^{m} k \cdot {\text{Ps}}}}{{\pi \left( {r_{1 } - r_{2 } } \right)\left( {1 + k} \right){\text{Bi}}}} \mathop \sum \limits_{n = 1}^{\infty } R_{\text{m,n}} \left( {t^{*} } \right). \\ \end{aligned}$$

(100)

Finally, the unsteady temperatures of the two phases can be also normalized in the $\theta$ form ($\theta_{\text{un}} = T_{\text{un}}^{*} - T_{\text{w,un}}^{*}$) using the unsteady wall temperature (see Eqs. 34, 35).