Introduction

One of the most important properties of a thermal insulation material is its thermal conductivity, and this is often the sole selection criterion for furnace constructions. Depending on the application, the insulation material could function for up to 15 years in an industrial furnace. Therefore, only a 5–10 % advantage in insulating properties (lower thermal conductivity) could contribute greatly to energy savings over the service lifetime [1, 2]. Thermal conductivity values are used regularly in furnace design and to calculate the required thickness of insulation in a furnace to achieve a reasonable and safe temperature on the outer shell [3, 4]. Therefore, accurate thermal conductivity measurement of these materials is crucial.

Commercial materials

The insulating materials under investigation in this study are designed for long-term applications at temperatures ranging from 1173 to 1773 K and produced in various different forms such as monolithic, insulating fire bricks and glass fibres [5]. These products have a wide range of applications in many industries as furnace insulation, fire protection or functional products [6]. Fibres are normally the preferred technology in applications for which a high resistance to thermal shock is required. Glass fibres are usually manufactured and supplied in different forms such as bulk, needled blanket or blocks, encapsulated fibres and vacuum-formed panels. Fibre insulation can have a number of advantages over other forms of insulation including low cost, flexibility, ease of installation, low thermal mass and very high resistance to thermal shock which allows rapid firing rates to save energy [7]. However, fibres are not suitable for application in environments with very high gas velocities or in contact with certain molten metals or glasses. A known disadvantage of some types of glass fibres is the health hazards associated with them [8–10]. Conventional fibre insulation materials are commonly known as refractory ceramic fibres (RCF), and these fibres are classified as category 1A or 1B (definite and possible human carcinogen, respectively) [11, 12]. In recent years, major efforts from academic and industrial researchers have led to the development of new generations of refractory glass fibres which are biosoluble and minimise the health risks which were formerly associated with these types of materials. An example of these new fibre insulation materials is the Superwool product range developed by Morgan advanced materials [13, 14]. These products are normally alkaline-earth silicate (AES) glass fibre products which have low biopersistence proven through intra-tracheal (IT) animal testing [15, 16].

Production

Glass fibre insulation products are normally manufactured using noncontinuous methods such as melt spinning, melt blowing or extrusion/spun sol–gel, with melt spinning being the most common method due to its very high throughput and low cost [17–19]. The spinning method incorporates an open electric furnace which forces flow of electricity through the molten glass using high electric current and low voltage. A continuous melt stream is generated by flow of the melt through a nozzle at the bottom of the furnace; the melt stream then hits rapidly rotating spinners which results in fibre formation, and these are blown off the edge of the spinners onto a continuous belt for further downstream processing. The generated fibres are then formed into various shapes and products such as nonwoven blankets, paper or vacuum-formed shapes [6].

Due to the industrial nature of this method, the produced materials are not homogeneous. Glass fibre materials which are produced by melt spinning methods always contain some un-fiberised material which normally occurs in the form of spherical glass particles of various sizes. These are commonly known as ‘shot’ particles. This inhomogeneity impacts on thermal conductivity of the fibrous product and therefore on measured thermal conductivities, limiting the comparability of different measurement techniques.

Thermal properties, heat transfer mechanisms and modelling

Glass fibre insulation is manufactured with various bulk densities, usually in range 60–350 kg m−3 [1, 4, 20]. Bulk densities can significantly affect measured thermal conductivities [21, 22].

The total thermal conductivity of a material can be explained as in (1), from [23]:

$$ k_{\text{total}} = k_{\text{radiation}} + k_{\text{convection}} + k_{\text{conduction}} $$
(1)

A few studies suggest that convection effects in porous materials with bulk densities of >20 kg m−3 or with small pores are usually negligible [24]. However, whereas this may be accurate for natural convection, low-density fibrous insulation materials are usually gas permeable; therefore, heat transfer due to forced convention [25] is not improbable. Miller [26] developed one of the earliest models to explain the heat transfer mechanism in fibrous insulation. In this model, apparent thermal conductivity was predicted as a function of fibre diameter, bulk density and mean temperature.

Numerous studies in recent years [22, 27–31] have led to improved understanding of heat transfer mechanisms through fibrous insulation materials. Several models have been developed [32–36] to predict the thermal conductivity through different mechanisms. In these models, radiation is believed to have a minimal effect at temperatures below 773 K, but it becomes the dominant heat transfer mechanism at high temperatures (>1073 K) [34]. Conduction through the solid structure of the material, which can be considered constant if the material has no transformation, must also be considered [36, 37]. Gas conduction may also occur through the free gas in open porosity which is dependent on pressure, or through isolated gases in the structure of the fibres [38].

The present study aims to identify the most reproducible and accurate method of thermal conductivity measurements for fibre-type insulation materials and to investigate the source of variability in the measurements.

Materials and methods

Test methods

There are several well-established methods for measuring thermal conductivity of insulation materials [39, 40], but only a few of these methods are capable of conducting measurements at temperatures greater than 1273 K [21, 41, 42]. Generally, test methods are based on either transient or steady-state measurements. Transient methods generally have a simple set-up and can be performed rapidly; however, these methods are known to have difficulty measuring nonisotropic and low-density samples [43]. Conventional laser flash methods also have issues with scattering effects in low-density fibre materials which could lead into underestimation of the thermal conductivity [44]. On the other hand, steady-state methods require much more effort in experimental set-up and are consequently expensive and time-consuming to carry out. However, these methods are well known for their unidirectional heat flow which allows for high-accuracy measurements, even for nonisotropic materials, and panel calorimeter methods offer the highest precision in measurement amongst these methods [21]. The guarded hot plate method [45] has the capability to measure thermal conductivities at temperatures below 273 K. It is normally limited to upper measurement temperatures of 773 K, but a few instruments equipped with alumina heaters can conduct measurements at temperatures of up to 1273 K [45]. In this study, thermal conductivity measurements have been taken using laser flash and hot wire transient methods and a panel calorimeter steady-state method.

Hot wire cross-array method

In this method, a furnace is used to heat the specimen to a specified temperature. An additional local heating source (hot wire) which is embedded in the specimen is used to introduce a local temperature rise at the centre of the specimen, and the increase in temperature as a function of time is recorded. The thermal conductivity (k) value can be calculated using the known electrical power input to the hot wire per unit length (P i), elapsed times (t 1, t 2) and temperature change at t 1 and t 1 (\( \Delta \theta_{1} ,\Delta \theta_{2} \)) as shown in (2).

$$ k = \frac{{P_{\rm i} }}{4\pi } \cdot \frac{{\ln \left( {\frac{{t_{2} }}{{t_{1} }}} \right)}}{{\Delta \theta_{2} -\Delta \theta_{1} }} $$
(2)

The hot wire standard method used for measurements in this study was ISO 8894 [46].

Laser flash method

In this method, one face of a thin specimen is subjected to a pulse from a high-intensity laser. This short-duration radiant energy is absorbed by the specimen and results in a temperature rise on the other face of the specimen, the temperature curve as a function of time is recorded and used to calculate the thermal diffusivity (\( \alpha \)). The thermal conductivity (k) can then be calculated using the specimen’s specific heat capacity (C p) and density (ρ) as shown in (3).

$$ k = \alpha C_{\text{p}} \rho $$
(3)

The measurement should be repeated at each temperature of interest in order to produce a thermal conductivity profile as a function of temperature. The standard method used for the laser flash measurement in this study was ASTM E1461 [47].

Panel calorimeter method

Panel calorimeter instruments normally consist of a furnace that uniformly heats one face of the sample, and a calorimeter and guards assembly on the other side of the sample. Temperature sensors are placed on either side of the test specimen (in some instruments, additional sensors are also placed through the thickness of the specimen). During the test, one side of the sample is heated to a set temperature and the control guards on the other side of the sample ensure that heat flow is unidirectional from the hot face to the cold face. This is achieved by monitoring the water temperature rise in each zone and varying the water flow rate through individual guards. Measurements are taken once the system has reached thermal equilibrium for a set continuous period of time.

The calorimeter measures the differential water temperature. These measurements are used in a simple Eq. (4) [48, 49] to calculate the heat flow rate (\( \dot{Q} \)) from the measured temperature difference (\( \Delta T_{\rm w} \)), specific heat capacity of water (C) and mass (m) from water flow rate per unit time (\( \dot{v} \)) and density (ρ). Then, the thermal conductivity (k) between each thermocouple pair with known separation (x) and known mean temperature (\( \Delta T_{\rm tc} \)) can be calculated for the sample placed above the central calorimeter area (A).

$$ k = \frac{{\dot{Q} \cdot x}}{{A \cdot\Delta T_{\rm tc} }} ,\begin{array}{*{20}c} { \dot{Q} = \dot{m} \cdot C \cdot\Delta T_{\rm w} } \\ {\dot{m} = \dot{v} \cdot \rho } \\ \end{array} \to k = \frac{{\left( {\frac{{\dot{v} \cdot \rho }}{t} \cdot C \cdot\Delta T_{\rm w} } \right) \cdot x}}{{A \cdot\Delta T_{\rm tc} }} $$
(4)

BS 1902-5.5 [50] and ASTM C201 [48] standard methods were used in this study for the panel calorimeter thermal conductivity measurements. The main differences between these standards are specimen size and number of specimen temperature sensors; these are considered further in the discussion section.

International standards

Many international standards are associated with high-temperature thermal conductivity testing. These include hot wire (parallel and cross-array) [46, 51, 52] and laser flash [47] among transient methods and guarded hot plate [53] and panel calorimeter [48, 50] among the steady-state methods. These standard methods call for specimens in a variety of different shapes and sizes, and high-temperature capability differs greatly between methods and instruments. A selection of these specifications is presented in Table 1.

Table 1 International standards for thermal conductivity testing
Full size table

Standard reference materials

To the best of the authors’ knowledge, there are currently no standard reference materials or samples for fibre-type insulation that are available for calibration, benchmarking purposes or comparative studies on high-temperature thermal conductivity. Consequently, there have been few comparative studies published on the thermal conductivity of high-temperature insulation materials.

An account of early comparative thermal conductivity studies on fibrous thermal insulation is given in [21]. Transient methods have been reported to measure consistently ~15–20 % higher thermal conductivity values compared to steady-state panel methods. The source of these differences has been attributed to the anisotropy of the material [54, 55].

Thermal conductivities of calcium silicate refractory boards were measured by plate, cylinder and hot wire methods in different directions, and the results were reported to be within ±10 % of one another for the different methods [21]. Thermal conductivity of alumina fibre mats measured through the thermal diffusivity method has been reported to be significantly lower than panel calorimeter method [56]. However, in almost all of the previous studies, difficulties have been reported in terms of reproducibility of results. This has largely been due to anisotropy of the samples, for example, variations in density and structure of samples obtained even from the same batch of product from the same manufacturer. In addition to sample-to-sample variability, there is also the issue of transformations within the sample during measurement at high temperature, which will result in changes in the nature and structure of the material. Due to the nature and production methods of these types of materials, the structure and properties exhibit small variabilities, not only from sample to sample but even within different parts of the same sample. Additionally, these materials have different thermal properties in three dimensions due to orientation of the fibres during manufacture. Therefore, development of a standard sample is crucial to conducting thermal conductivity studies of such materials.

Results

Development of standard reference material

The standard reference material considered in this study was selected to satisfy certain requirements including refractoriness to 1673 K and no more than 4 % permanent linear change in dimensions after heat treatment [57–59]. The standard reference material had to be representative of fibre-type insulation, so similar density and total porosity as well as similar structure were essential to ensure that the thermal properties and heat transfer mechanisms involved at various different temperatures closely matched those of typical fibre insulation materials. More importantly, the material was required to have a good after-service mechanical strength in order to allow for easy handling. This was a particular challenge as strength of fibrous insulation materials normally decreases significantly after they have been exposed to high temperatures. Moreover, the material was required to exhibit minimal transformations during short-term exposure to high temperatures, to ensure that the key physical and chemical properties of the materials would remain unchanged during thermal conductivity measurement at different temperatures and also from one test to another. Finally, a material with minimal health hazard was preferable. The issue with anisotropy of the material can be negligible if the sample is tested in the same direction in all measurements.

The first candidate material which was investigated for development of the standard reference material was 97 mass% Al2O3–3 mass% SiO2 fibres manufactured using the sol–gel method [60]. Alumina-rich fibres are known for their excellent refractoriness, high strength and high temperature stability [61]. To improve the mechanical strength, vacuum-formed panels had been made from these fibres. This material demonstrated very good high-temperature thermal performance as well as stability in terms of transformations. However, the mechanical strength, modulus of rupture (MOR), of the sample after heat treatment was not desirable (MOR < 250 kPa). Several trials were conducted to improve the mechanical strength by increasing the amount of inorganic binders in the vacuum-formed panel. The strength of the board was increased using various treatments, and the maximum measured MOR was 400 kPa for the fired sample. Although this exceeded the industry standards [59], it was considered unlikely to meet the strength requirements for the standard material, and hence, it was not investigated further.

The next candidate material investigated was a new generation of biosoluble high-temperature insulation fibre manufactured by Morgan Advanced Materials using the melt spinning process. It has been exonerated based on European regulations (REACH) [62]. The fibres were made of an alkali aluminosilicate glass. Long-term stability of this material has been confirmed during the development process. To achieve maximum strength, the as-made glass fibres were formed into a rigid vacuum-formed panel using colloidal silica as an inorganic binder. The material was heat-treated for 24 h at 1473 K to ensure that the inorganic binder was fully activated, crystallisation was completed and change in dimensions was minimised. Mechanical testing was carried out on the heat-treated sample, and the material demonstrated an average MOR exceeding 3 MPa tested by standard method [63]. A small sample of the final material was gold-coated by a sputter coater and mounted on conductive carbon sticker for electron microscopy. Figure 1 presents backscattered scanning electron microscopy (SEM) images showing the microstructure of the final sample. On the basis of the above test results which demonstrated the stability of this material, it was decided to select this material as the standard reference material.

Fig. 1
figure 1

Backscattered SEM images showing microstructure of the final standard reference material sample

Full size image

Final materials were produced and heat-treated as described above and subsequently ground and machined to achieve flat surfaces and the required dimensions (as described in Table 1) for testing. As mentioned previously, different test methods require completely different specimen dimensions. In order to cover at least the most common test methods, two sets of samples (named A and B) were produced in the largest specimen dimensions (ASTM C201 [48]) and one was cut into several smaller pieces as shown in Fig. 2 so that it would be compatible with a number of different instruments and methods.

Fig. 2
figure 2

Schematic of the introduced standard reference material, consisting of three layers of 25 mm thick modular specimen

Full size image

Test reproducibility

Testing was carried out using two custom-built panel calorimeter thermal conductivity instruments based on the ASTM C201 standard for castable refractories [48] (no standard method currently exists for fibre insulation materials). These instruments are capable of carrying out thermal conductivity measurements at temperatures of up to 1673 K. The 76 × 76 mm centre calorimeter and guards are constructed of copper with a very thin layer of black paint on the surface for optimised radiation absorption. A thick SiC plate is placed between the heating source and sample to ensure uniform heating. A total of four thermocouples are placed on either side and through the thickness of the sample which will produce three adjacent and three nonadjacent thermocouple pairs per measurement that can all be used to calculate the thermal conductivity as described in panel calorimeter method.

Intra-laboratory single method reproducibility

Both sets of developed samples were tested using both of these instruments separately. Additionally, the samples were tested on the same instrument three times to ensure reproducibility of the results. Measurement results are presented in Fig. 3. Thermal conductivity measurements of the same set of samples measured with the same instrument were reproducible to within ±0.6 %; test results of the same set of samples measured on different instruments were reproducible to within ±5.3 %; test results of different sets of samples measured on the same instrument were reproducible to within ±5.4 %; and test results of different sets of samples measured on the two different instruments were reproducible to within ±10 % as summarised in Table 2.

Fig. 3
figure 3

Initial testing and reproducibility of measurements. The thermal conductivity in all tests was calculated for linear mean temperature of only adjacent sample thermocouple pairs

Full size image
Table 2 Intra-laboratory and inter-laboratory comparison of results reproducibility
Full size table

Inter-laboratory comparison of different methods

In the next stage of this work, standard samples were sent to a selection of established analytical laboratories for thermal conductivity testing using different methods. Results from both transient and steady-state methods were obtained and are presented in Table 2 and Fig. 4.

Fig. 4
figure 4

Inter-laboratory comparison of thermal conductivity measurement methods. Thermal conductivity in the methods using more than two sample thermocouples (TCs) has been calculated for linear mean temperature of only adjacent sample thermocouple pairs

Full size image

No results are presented here for thermal conductivity measurements obtained using the laser flash diffusivity method. Two attempts were made to measure the introduced standard reference sample using an ANTER FlashLine™ 3000 Thermal Diffusivity System at an external laboratory. The instrument required very small sample dimensions (10 × 10 × 3 mm) compared to other methods. The faces of the sample were gold-coated using a sputter coater and were subsequently spray-coated with carbon in order to achieve a uniform emissivity on the sample face which will be the laser’s target. The instrument failed to measure the thermal diffusivity after repeated attempts. This was probably due to the very high level of porosity (89 %) in this material causing scattering of the laser.

Comparison of different insulation materials

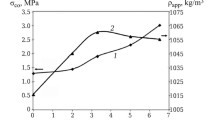
Thermal conductivities of several different fibre insulation materials were measured using the internal panel calorimeter rigs, and results are presented in Fig. 5. Total porosity of these products varied between 87 and 97 %. Maximum use (also commonly known as classification temperature) range of these materials is 1373–1873 K [57]. Thermal conductivity in the classification temperature range has been measured in between 0.02 and 0.70 W m−1 K−1. The effect of bulk density on thermal conductivity of fibre mats and blankets is evident and in good agreement with the literature [21, 42]. For example, the thermal conductivity at 1380 K for a fibre blanket with bulk density of 81 kg m−3 is approximately 29 % greater than that of a blanket made of same type of fibre but with a bulk density of 139 kg m−3. Fibre products normally have low thermal conductivities at temperatures below 773 K, and in most cases, the thermal conductivity is a function of temperature; therefore, testing at high temperatures is necessary to differentiate between the high-temperature performances of these materials.

Fig. 5
figure 5

Thermal conductivities of various different thermal insulation materials as a function of temperature, measured by an adapted ASTM C201 panel calorimeter method calculated for linear mean temperature of only adjacent sample thermocouple pairs

Full size image

Discussion

In agreement with several previous studies, the most reproducible and accurate measurements were obtained using the adapted ASTM C201 steady-state panel calorimeter method. The variability in the intra-laboratory and inter-laboratory results generated in this study using the ASTM C201 method was in good agreement with previous round-robin testing experiments which were published in the standard method [48]; however, this variability has been achieved using a more representative anisotropic fibrous material rather than a dense castable isotropic refractory material with a different thermal conductivity profile, as was used in the previous round robin in [48].

There are several instrumental errors that could explain the observed variability in results. As explained in the panel calorimeter experimental method, the thermal conductivity could be calculated for a mean temperature from any adjacent or nonadjacent thermocouple pair. One concern here is that the temperature profile through the thickness of the sample is usually nonlinear for this type of material. According to all standard methods, it is common practice that the mean temperature between a thermocouple pair is calculated on a linear basis. However, in reality this could deviate from the actual mean temperature. The temperature profile through the thickness of the introduced standard reference sample in this study, measured by four thermocouples during the panel calorimeter test, is presented in Fig. 6. In Fig. 6, the nonlinear regressions for the temperature readings from four sample thermocouples have been calculated using a combination of thermal modelling software [64] and a curve-fitting program [61]. The best fit to the data points was achieved using an inverted hyperbola function (5):

Fig. 6
figure 6

Temperature profile through the sample thickness during the panel calorimeter test. Solid lines represent the linear regression, and broken lines represent nonlinear regression (inverted hyperbola) between the data points

Full size image
$$ y = \frac{x}{A + B\left( x \right)} + C $$
(5)

The calculated integral mean temperatures deviated by up to 8.4 % from linear mean temperatures in the regions of sample thickness which were farthest from the heating source, especially measurements at higher temperatures. However, this variation was considerably lower (0.3–0.7 %) at lower temperatures and closer to the heating source. Subsequently, the fitted function was used to recalculate the thermal conductivity values based on integral mean temperature between each adjacent thermocouple pair, as shown in Fig. 7. Nonlinear regression [65] was used to compare the data. Variations in calculated thermal conductivity values were in range 2.5–4 % at different temperatures.

Fig. 7
figure 7

Variation in thermal conductivity values calculated for linear or integral mean temperature between adjacent thermocouple pairs. Broken line is guide for the eye only

Full size image

The above issue with the nonlinear temperature profile could explain the variabilities in the results obtained from the BS 1902:5.5 panel method; this method uses only two temperature sensors on each side of a thick (75 mm) sample and uses linear mean temperature to report thermal conductivity values.

Other instrumental uncertainties involved in calculations include change in water properties due to temperature such as change in specific heat capacity of water from 4181 J kg−1 K−1 at 298 K to 4179 J kg−1 K−1 at 303 K and change in water density from 997.1 kg m−3 at 298 K to 995.7 kg m−3 at 303 K. Additionally, measurement of water temperature rise with the most precise and reasonably priced platinum resistance temperature sensors is accurate to within ±0.03 K. Moreover, the water flow through the calorimeter is not always perfectly constant, and the flow rate measurement normally includes ±1 % error, even using precise digital flow metres.

Furthermore, uncertainty of the thermocouple pair distance (separation) can introduce substantial errors into the measurements. This could be caused by thermocouple movements during the test or by operator error. Finally, sample thermocouples are only accurate to ±3 K. All of the above instrumental errors above would accumulate (in sum of quadrature) to a ±3 % uncertainty for the ASTM C201 panel calorimeter method.

Conclusions

This study has established good inter-laboratory reproducibility of high-temperature thermal conductivity measurement of a standard high-temperature fibre insulation material using an adapted panel calorimeter method based on the ASTM C201 standard. Some variability has been established in measured thermal conductivities between different test methods including ASTM and BS panel calorimeters, hot wire, and thermal diffusivity by laser flash. Results support the use of adapted methods based on the ASTM C201 standard being the most precise, and this method is suggested for wider use in fibrous insulation thermal conductivity measurement.

The new biosoluble alkali aluminosilicate fibre insulation panel has been introduced as a standard reference material for calibration and benchmarking purposes, and for comparative studies of high-temperature thermal conductivity.