Conductivity of Weakly Disordered Metals Close to a “Ferromagnetic” Quantum Critical Point

Abstract

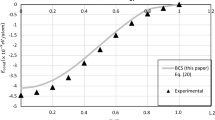
We calculate analytically the conductivity of weakly disordered metals close to a “ferromagnetic” quantum critical point in the low-temperature regime. Ferromagnetic in the sense that the effective carrier potential $V(q,\omega )$, due to critical fluctuations, is peaked at zero momentum $q=0$. Vertex corrections, due to both critical fluctuations and impurity scattering, are explicitly considered. We find that only the vertex corrections due to impurity scattering, combined with the self-energy, generate appreciable effects as a function of the temperature T and the control parameter a, which measures the proximity to the critical point. Our results are consistent with resistivity experiments in several materials displaying typical Fermi liquid behaviour, but with a diverging prefactor of the $T^2$ term for small a.

Appendices

Appendix A: On the Calculation of the Scattering Rate

The derivation below follows that of [12], i.e. (I), and equation numbers refer to (I) as well. In the limit $T \rightarrow 0$ the thermal function $X= \coth (\omega /2T) \; + \; \tanh ((\epsilon -\omega )/2T)$ in Eq. (I-4) becomes $X=2$ for $2T< \omega <\epsilon$, and $X=0$ for $\omega <-2T$ and $\omega >\epsilon$. Then the integration over $\omega$—compare with Eq. (I-7)—amounts to

$$\begin{aligned} 2 \int _{2T}^{\epsilon } {\text {d}}\omega \; \text {Im} \; V(q,\omega ) \; R(q,\omega ) \simeq g \ R_0 \; \ln \left( \frac{(h_q \; a_q)^2+\epsilon ^2}{(h_q \; a_q)^2+ 4T^2} \right) \simeq g \; R_0 \; \frac{\epsilon ^2}{(h_q \; a_q)^2},\nonumber \\ \end{aligned}$$

(48)

for $h_q \; a_q > \epsilon$. The rest of the algebra proceeds as in Eq. (I-8) and onwards. Thus, the scattering rate scales like $\epsilon ^2$ as well, as expected for the FL regime.

Appendix B: The Terms $R_V,R_1,R_2,L$ in Eq. (15)

The terms $R_1,R_2$ each contain a single propagator G. Hence, upon the final integration over momentum k they both yield a small contribution. This is the case because this integration is similar to an integration over $\epsilon _k$ from $-\infty$ to $+\infty$, which can be taken as part of a contour integral closing at infinity. That contour can be taken such that the pole of the G in the integrand lies outside of it and hence yields a zero contribution. C.f. also Ref. [18].

The term $R_V$ is due to the residue from the pole $z=z_0=-i \; a_q \; h_q$ of V(q, z). Here both G’s enter the formula for the residue. However, their poles are on the same semi-plane (i.e. in a combination $G^A G^A$), and the argument for $R_1,R_2$ applies as well.

The term L is the residue from the 2 poles $z=z_k,z_k^*$ of $\Lambda (k,z)$—c.f. Eqs. (36), (37)—with

$$\begin{aligned} z_k = \xi _k + i \; W_k, \;\; W_k^2=S^2-R_k. \end{aligned}$$

(49)

Considering the function

$$\begin{aligned} H(z)=n(z) \; V(q,z) \; G(k+q,i \epsilon _n+ z +i \omega _l)\; G(k+q,i \epsilon _n+z ) \; R_{k+q} \;\; \end{aligned}$$

(50)

we have

$$\begin{aligned} L = \frac{H(z_{k+q})}{z_{k+q}-z_{k+q}^*} + \frac{H(z_{k+q}^*)}{z_{k+q}^*-z_{k+q}}. \end{aligned}$$

(51)

This term is much smaller than $I_V$ because $|\text {Im} \; H(z)| \ll |\text {Re} \; H(z)|$.