1 Introduction

Equations of state (EoSs) are mathematical tools for describing the state of matters. Generalized EOSs are widely used to represent and predict thermodynamic properties and phase equilibria of pure fluids and mixtures. The two-parameter van der Waals (vdW) model (1873) was the first equation to predict vapor–liquid coexistence [1]. Later, numerous modifications to the vdW model have been presented (see for instance, [2,3,4,5,6,7,8,9,10,11,12,13,14]). The most commonly used equations of state are cubic equations, which have been extensively used over the last three decades. Cubic EoSs are a class of equations of state that may be represented by a polynomial when referencing the volume or compressibility factor, in such a way that the highest power in the polynomial is to the third degree [15, 16].

Here, we present a new generalization of the two-parameter vdW EoS and solve analytically the corresponding cubic EoS. Also, we reconsider the generalized vdW EoS in the grand canonical ensemble (GCE) formulation to calculate some measures of the particle number fluctuations such as the scaled variance, skewness, and kurtosis and investigate the critical behavior of their behavior in a vicinity of the critical point.

The paper is organized as follows: In Sect. 2, a new generalization of the vdW model and its corresponding cubic equation are presented. In Sect. 3, the cubic EoS is solved analytically and the critical properties are calculated in the general form. In Sect. 4, the GCE formulation of one family of the generalized vdW equation is derived. In Sect. 5, the particle number fluctuations for different models are studied. Three quantities measuring the particle number fluctuations are calculated and their behavior close to the critical point (CP) is then analyzed. The paper closes with a short discussion given in Sect. 6.

2 Generalized vdW EoS

Here, we consider a new generalization of the two-parameter vdW model [1] in the canonical ensemble (CE) formulation

$$\begin{aligned} P(T,V,N)=\frac{Nk_BT}{V-Nb}-\frac{N^2 a}{V^2\big (1+N\frac{r_1}{V}\big )^k+N^2r_2}. \end{aligned},$$
(1)

where the first term represents the repulsive term and the the second represents the attractive term. The parameters \(r_1,r_2\) are two specific constants that vary depending on the EoS and the parameter k has the physical valid range of \(0\le k \le 2\). The characteristic parameters a and b describe, respectively, the attractive and repulsive interactions between N particles. With different values of k, \(r_1,\) and \(r_2\), most of the well-known EoS can be obtained. Table 1 presents the attractive term of some models, like vdW model [1], SRK model [3], PR model [6], PT model [9], and Nasrifar-Bolland (NB model) [17]. The repulsive term (not shown) is similar in all of these models as defined in Eq. 1.

Table 1 Some of the well-known models are obtained from Eq. 1
Full size table

Using the critical point conditions

$$\begin{aligned} P(T=T_\mathrm{{c}},V=V_\mathrm{{c}})= & {} P_\mathrm{{c}} \end{aligned}$$
(2)
$$\begin{aligned} \Big (\frac{\partial P}{\partial V}\Big )_{T=T_\mathrm{{c}},V=V_\mathrm{{c}}}= & {} 0, \end{aligned}$$
(3)
$$\begin{aligned} \Big (\frac{\partial ^2 P}{\partial V^2}\Big )_{T=T_\mathrm{{c}},V=V_\mathrm{{c}}}= & {} 0. \end{aligned}$$
(4)

EoS (1) can be transformed into the corresponding generalized cubic polynomial in the form

$$\begin{aligned}&V_\mathrm{{c}}^3-\Big [3b+2(k-1)r_1\Big ]NV_\mathrm{{c}}^2+(k-2)r_1\Big [3b+\frac{1}{2}(k-1)r_1\Big ]N^2V_\mathrm{{c}}\nonumber \\&\quad - \frac{1}{2}(k-2)(k-3)N^3br_1^2\nonumber \\&\quad -N^2r_2\big (1+N\frac{r_1}{V_\mathrm{{c}}}\big )^{1-k}\Big \{2V_\mathrm{{c}}+(2-k)Nr_1+(V_\mathrm{{c}}-Nb)\big (1+N\frac{r_1}{V_\mathrm{{c}}}\big )^{-1}\nonumber \\&\qquad \Big [1-(k-2)N\frac{r_1}{V_\mathrm{{c}}}\nonumber \\&\quad +\frac{1}{2}(k-1)(k-2)N^2\frac{r_1^2}{V_\mathrm{{c}}^2}\Big ]\Big \}=0; \quad \quad 0\le k\le 2. \end{aligned}$$
(5)

3 Analytical Solution of the Cubic EoS

The solution of the cubic EoS (5) depends on the value of k as follows:

I- When \(k=0\) and \(r_1=r_2=0\), one obtains the cubic equation of the original vdW model

$$\begin{aligned} V_\mathrm{{c}}^3-3NbV_\mathrm{{c}}^2=0 \end{aligned}$$
(6)

In this case, we obtain the well-known critical point \(V_\mathrm{{c}}=3Nb\), \(k_BT_\mathrm{{c}}=\frac{8a}{27b},\) and \(P_\mathrm{{c}}=\frac{a}{27b^2}\).

II- When \(k=1\), the generalized cubic Eq. 5 reduces to the form

$$\begin{aligned} V_\mathrm{{c}}^3+AV_\mathrm{{c}}^2+BV_\mathrm{{c}}+C=0, \end{aligned}$$
(7)

where

$$\begin{aligned} A=-3Nb, \quad B=-3(r_1b+r_2)N^2\quad \mathrm{and}\quad C=-\big (r_1^2b-r_2b+r_1r_2\big )N^3. \end{aligned}$$
(8)

There are different analytical methods for solving the cubic EoS. Here, we consider Cardano method (see [18, 19]) which can be used to calculate all real and complex roots of cubic polynomials that have only real coefficients. In this method, the cubic polynomial (7) is reduced via the substitution

$$\begin{aligned} V_\mathrm{{c}}=X-\frac{A}{3}, \end{aligned}$$
(9)

which leads to

$$\begin{aligned} X^3-3pX-2q=0, \end{aligned}$$
(10)

with the coefficients

$$\begin{aligned} p=\frac{A^2}{9}-\frac{B}{3} \quad \mathrm{and}\quad q=-\frac{A^3}{27}+\frac{AB}{6}-\frac{C}{2} \end{aligned}$$
(11)

The numbers and types of roots of Eq. 10 depend on the sign of the the polynomial discriminant, \(\Delta \), defined as

$$\begin{aligned} \Delta =q^2-p^3, \end{aligned}$$
(12)

There are three possibilities:

1. If \(\Delta >0,\) there is only one real root and two conjugate-complex solutions

$$\begin{aligned} V_\mathrm{{c}}^{(1)}=r+s-\frac{A}{3} \quad \mathrm{and} \quad V_\mathrm{{c}}^{(2,3)}=\frac{-(r+s)\pm i\sqrt{3}(r-s)}{2}-\frac{A}{3}, \end{aligned}$$
(13)

where

$$\begin{aligned} r=\root 3 \of {q+\sqrt{\Delta }}\quad \mathrm{and} \quad s=\root 3 \of {q-\sqrt{\Delta }} \end{aligned}$$
(14)

The conjugate-complex solutions also may be ignored in the context of cubic EoS, because they do not describe any physical solution.

2. If \(\Delta < 0\), there are three real roots come from the expression

$$\begin{aligned} V_\mathrm{{c}}^{(j)}=2\sqrt{p}\cos \Big (\frac{\theta +2\pi j}{3}\Big )-\frac{A}{3};\quad j=0,1,2. \end{aligned}$$
(15)

The angle \(\theta \) (in radius) is calculated as

$$\begin{aligned} \theta =\mathrm{arccos}\Big (\frac{q}{\sqrt{p^3}}\Big ). \end{aligned}$$
(16)

Equation 15 can be rewritten in a way to provide the roots in ascending order, as follows

$$\begin{aligned} V_\mathrm{{c}}^{(1)}= & {} -\sqrt{p}\Big [\cos \Big (\frac{\theta }{3}\Big )-\sin \Big (\frac{\theta }{3}\Big )\Big ]-\frac{A}{3}; \quad \mathrm{for}\quad j=2,\nonumber \\ V_\mathrm{{c}}^{(2)}= & {} -\sqrt{p}\Big [\cos \Big (\frac{\theta }{3}\Big )+\sin \Big (\frac{\theta }{3}\Big )\Big ]-\frac{A}{3}; \quad \mathrm{for}\quad j=1,\nonumber \\ V_\mathrm{{c}}^{(3)}= & {} 2\sqrt{p}\cos \Big (\frac{\theta }{3}\Big )-\frac{A}{3}; \quad \mathrm{for}\quad j=0. \end{aligned}$$
(17)

3. When \(\Delta =0\), we have \(q=\pm \sqrt{p^3}\), that is, \(\theta =\mathrm{arccos}(\pm 1)\), i.e., \(\theta \) ranges from 0 to \(\pi \). In this case, Eq. 17 can be simplified to obtain the special case of three real roots, where two of them are identical

$$\begin{aligned} V_\mathrm{{c}}^{(1)}=2\sqrt{p}-\frac{A}{3}\quad \mathrm{and} \quad V_\mathrm{{c}}^{(2)}=V_\mathrm{{c}}^{(3)}=-\sqrt{p}-\frac{A}{3}. \end{aligned}$$
(18)

Using the second critical condition (3), one can obtains the critical temperature

$$\begin{aligned} k_BT_c=\frac{a(T_\mathrm{{c}})(2V_\mathrm{{c}}+Nr_1)(V_\mathrm{{c-Nb}})^2 }{\big (V_\mathrm{{c}}^2+Nr_1V_\mathrm{{c}}+N^2r_2\big )^2} \end{aligned}$$
(19)

In this case, the critical compressibility factor \(Z_\mathrm{{c}}\) takes the form

$$\begin{aligned} Z_\mathrm{{c}}=\frac{P_\mathrm{{c}}V_\mathrm{{c}}}{Nk_BT_\mathrm{{c}}}=\frac{V_\mathrm{{c}}(V_\mathrm{{c}}^2-2NbV_\mathrm{{c}}-N^2r_1b-N^2r_2)}{(2V_\mathrm{{c}}+Nr_1)(V_\mathrm{{c}}-Nb)^2}. \end{aligned}$$
(20)

III- When \(k=2\), we obtain the same cubic equation of \(k=1\) (7) and its solution but with \(r_1=2r_1\) and \(r_2=r_1^2+r_2\).

4 The GCE Formulation of the Generalized vdW Model

We consider one family of the generalized vdW model, by taking \(k=1, r_1=2\beta b,\) and \(r_2=\beta ^2 b^2\) in Eq. 1, we obtain

$$\begin{aligned} P(T,V,N)\equiv P(T,n)=k_BT\frac{n}{1-bn}-\frac{an^2}{(1+\beta bn)^2}, \end{aligned}$$
(21)

where \(n=N/V\) is the particle number density. Note that, for \(\beta =0\), the standard vdW model is obtained and for \(\beta =1/\sqrt{3}\), NB model is obtained.

The GCE formulation of (21) can be obtained as follows:

First, we find the free energy F(T, V, N) in the CE formulation, which can be obtained by integrating the thermodynamic identity

$$\begin{aligned} \Big (\frac{\partial F(T,V,N)}{\partial V}\Big )_{T,N}=-P(T,V,N) \end{aligned}$$
(22)

which for the model (21) yields

$$\begin{aligned} F(T,V,N)=F_{id}(T,V-Nb,N)-\frac{Nan}{1+\beta bn}, \end{aligned}$$
(23)

where \(F_{id}(T,V-Nb,N)\) is the free energy of the ideal gas,

$$\begin{aligned} F_{id}(T,V-Nb,N)= -Nk_BT\left\{ \mathrm{ln}\Big [n_Q\big (\frac{1-bn}{n}\big )\Big ]+1\right\} , \end{aligned}$$
(24)

and the quantum concentration \(n_Q\) is given by

$$\begin{aligned} n_Q=\Big (\frac{mk_BT}{2\pi \hbar ^2}\Big )^{3/2} , \end{aligned}$$
(25)

where m is the mass of a particle and \(\hbar \) is Planck\(^{'}\)s constant. Using Eq. 23 for the free energy, we can find all the thermodynamic quantities, such as the chemical potential \(\mu \), the particle number density n, the entropy density s, and the energy density \(\varepsilon \). Differentiating the relation (23) with respect to T and N, one gets S and \(\mu \), respectively

$$\begin{aligned} S(T,V,N)= & {} S_{id}(T,V-Nb,N), \end{aligned}$$
(26)
$$\begin{aligned} \mu (T,V,N)= & {} \mu _{id}(T,V-Nb,N)+bP_{id}(T,V-Nb,N)\nonumber \\&-\frac{an}{1+\beta bn}\Big (1+\frac{1}{1+\beta bn}\Big ), \end{aligned}$$
(27)

where

$$\begin{aligned} S_{id}(T,V-Nb,N)= & {} Nk_\mathrm{{B}}\Big [n_Q\big (\frac{1-bn}{n}\big )+\frac{5}{2}\Big ],\nonumber \\ \mu _{id}(T,V-Nb,N)= & {} k_BT\mathrm{ln}\Big [\frac{n}{n_Q(1-bn)}\Big ]\quad \mathrm{and} \nonumber \\ P_{id}(T,V-Nb,N)= & {} k_BT\big (\frac{n}{1-bn}\big ) \end{aligned}$$
(28)

are the entropy, the chemical potential, and the pressure of the ideal gas, respectively.

Second, we invert the relation (27) to get the particle number density \(n(T,\mu )\) which lies in the heart of the GCE formulation [20]

$$\begin{aligned} n\equiv n(T,\mu )=\frac{n_{id}(T,\mu _{id})}{1+bn_{id}(T,\mu _{id})}, \end{aligned}$$
(29)

where \(n_{id}\) is the density of the ideal gas and \(\mu _{id}=\mu -bP_{id}+\frac{an}{1+\beta bn}\Big (1+\frac{1}{1+\beta bn}\Big )\).

Third, we put \(n(T,\mu )\) back into the CE pressure (21) to obtain the pressure in the GCE

$$\begin{aligned} P(T,\mu )=k_BT\frac{n(T,\mu )}{1-bn(T,\mu )}-\frac{an^2(T,\mu )}{[1+\beta bn(T,\mu )]^2}, \end{aligned}$$
(30)

5 Critical Behavior of the Particle Number Fluctuations

Our concentration in this section will be in the fluctuations of number of particles, which are absent in the CE. The particle number fluctuations in the GCE can be characterized by the following dimensionless cumulants (susceptibilities),

$$\begin{aligned} \chi _n=\frac{\partial ^n\big (P/T^4\big )}{\partial \big (\mu /T\big )^n}, \end{aligned}$$
(31)

which are related to the moments of the particle number distribution by

$$\begin{aligned}&\chi _1=\frac{<N>}{VT^3}, \chi _2=\frac{<(\Delta N)^2>}{VT^3}, \chi _3=\frac{<(\Delta N)^3>}{VT^3}, \nonumber \\&\chi _4=\frac{<(\Delta N)^4>-3<(\Delta N)^2>^2}{VT^3} \end{aligned}$$
(32)

In the GCE, the particle number N fluctuates around its average value \(<N>\) with the normalized probability distribution P(N). Let us introduce the k moment \(<N^k>\)

$$\begin{aligned} <N^k>=\sum _{N}N^kP(N), \end{aligned}$$
(33)

where symbol \(<\dots>\) denotes the GCE averaging, \(\Delta N\equiv N-<N>,\) and the variance \(\sigma ^2=<(\Delta N)^2>\).

Now, we consider three well-known measures of the particle number fluctuations: the scaled variance \(\omega (N)\), the skewness \(S\sigma, \) and the kurtosis \(k\sigma ^2\). The scaled variance \(\omega (N)\) is an intensive measure of N-fluctuations and is given by (Taking \(k_B=1\))

$$\begin{aligned} \omega (N)\equiv \frac{\sigma ^2}{<N>}=\frac{\chi _2}{\chi _1}= & {} \frac{T}{n}\Big (\frac{\partial n}{\partial \mu }\Big )_{T}\nonumber \\= & {} \Big [\frac{1}{(1-bn)^2}-\frac{2an}{T(1+\beta bn)^3}\Big ]^{-1} \end{aligned}$$
(34)

The skewness \(S\sigma \) measures the degree of asymmetry of the distribution P(N) around its mean value \(<N>\) and is defined as

$$\begin{aligned} S\sigma \equiv \frac{<(\Delta N)^3>}{\sigma ^2}=\frac{\chi _3}{\chi _2}= & {} \omega (N)+\frac{T}{\omega }\Big (\frac{\partial \omega }{\partial \mu }\Big )_{T}\nonumber \\= & {} \omega ^2\Big [\frac{1-3bn}{(1-bn)^3}-\frac{6\beta abn^2}{T(1+\beta bn)^4}\Big ] \end{aligned}$$
(35)

The kurtosis \(\sigma ^2\) is the measure of “peakedness” of the probability distribution P(N),

$$\begin{aligned} k\sigma ^2\equiv \frac{<(\Delta N)^4>-3<(\Delta N)^2>^2}{\sigma ^2}= & {} \frac{\chi _4}{\chi _2}\nonumber \\= & {} (S\sigma )^2+T\big (\frac{\partial S\sigma }{\partial \mu }\Big )_{T}\nonumber \\= & {} 3(S\sigma )^2-2\omega (N) S\sigma -6(\omega (N))^3\Big [\frac{b^2n^2}{(1-bn)^4}\nonumber \\&+2\beta ab\frac{n^2(1-\beta bn)}{T(1+\beta bn)^5}\Big ] \end{aligned}$$
(36)

Note that for \(\beta =0,\) the values of \(\omega (N)\), \(S\sigma, \) and \(k\sigma ^2\) of the model (21) coincide with the corresponding results obtained in [21].

To study the critical behavior of the particle number fluctuations close to the CP, we rewrite Eqs. (34), (35), and (36) in terms of the reduced parameters \(P_r=P/P_\mathrm{{c}}\), \(n_r=n/n_\mathrm{{c}},\) and \(T_r=T/T_\mathrm{{c}}\). By solving the cubic quation of Eq. 21 (using the method of Sect. 3), one obtains the critical point

$$\begin{aligned} n_\mathrm{{c}}=\frac{N}{V_\mathrm{{c}}}=\frac{1}{(3+2\beta )b}, \quad k_BT_\mathrm{{c}}= \frac{8a}{27(1+\beta )b}, \quad P_\mathrm{{c}}= \frac{a}{27(1+\beta )^2b^2}. \end{aligned}$$
(37)

The results obtained from Eq. 37 coincide with the critical properties of vdW EoS (\(\beta =0\)) [1], NB EoS (\(\beta =1/\sqrt{3}\)) [17], and \(\beta =1\) [22].

Using Eq. 37, we can rewrite Eqs. 34, 35, and 36 in the reduced form

$$\begin{aligned} \omega (N)= & {} \frac{1}{(3+2\beta )^2}\Big [\frac{1}{\big (3+2\beta -n_r\big )^2}-\frac{27(1+\beta )n_r}{4T_r\big (3+2\beta +\beta n_r\big )^3}\Big ]^{-1}, \end{aligned}$$
(38)
$$\begin{aligned} S\sigma= & {} \frac{1}{(3+2\beta )^2}\Big [\frac{1}{\big (3+2\beta -n_r\big )^2}-\frac{27(1+\beta )n_r}{4T_r\big (3+2\beta +\beta n_r\big )^3}\Big ]^{-2} \nonumber \\&\times \Big [\frac{3+2\beta -3n_r}{\big (3+2\beta -n_r\big )^3}-\frac{81\beta (1+\beta )n^2_r}{4T_r\big (3+2\beta +\beta n_r\big )^4}\Big ], \end{aligned}$$
(39)

and

$$\begin{aligned} k\sigma ^2=3(S\sigma )^2-2\omega (N) S\sigma -6(3+2\beta )^2(\omega (N))^3n^2_r\Big [\frac{1}{(3+2\beta -n_r)^4}\nonumber \\ +27\beta (1+\beta )\frac{(3+2\beta -\beta n_r)}{4T_r(3+2\beta +\beta n_r)^5}\Big ] \end{aligned}$$
(40)

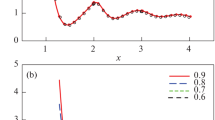
The scaled variance (38) as a function of \(n_r\) and different values of \(\beta \) (0, 0.5, and 1) is plotted in Fig. 1. We notice that \(\omega (N)\rightarrow 1\) as \(n_r\rightarrow 0\) (this corresponds to the ideal gas), \(\omega (N)\rightarrow 0\) as \(n_r\rightarrow 3+2\beta \) (this corresponds to the liquid with the highest possible density), and \(\omega (N)\rightarrow \infty \) at CP (\(T_r=n_r=1\)).

Fig. 1
figure 1

The scaled variance \(\omega (N)\) (38) as a function of \(n_r\) for \(\beta \)=0, 0.5, and 1 at (a) \(T_r=1.7\) and (b) \(T_r=1\)

Full size image

For the skewness, it is clear from (39) that \(S\sigma >0\) at \(n_r<\frac{3+2\beta }{3}\) (the gas phase), \(S\sigma <0\) at \(n_r>\frac{3+2\beta }{3}\) (the liquid phase), and \(S\sigma =0\) at \(n_r=\frac{3+2\beta }{3}\) . We notice also, that \(S\sigma \rightarrow 1\) as \(n_r\rightarrow 0\) and \(S\sigma \rightarrow 0\) as \(n_r\rightarrow 3+2\beta \) (see Fig. 2).

Fig. 2
figure 2

The skewness \(S\sigma \) (39) as a function of \(n_r\) for \(\beta \)=0, 0.5, and 1 at (a) \(T_r=0.7\) and (b) \(T_r=1.7\)

Full size image

Equation 40 shows that at \(T_r<1,\) the kurtosis has a large positive value (leptokurtic) for both \(n_r<\frac{3+2\beta }{3}\) (the gas phase) and \(n_r>\frac{3+2\beta }{3}\) (the liquid phases) (Fig. 3a). We notice also, that the kurtosis has a negative value (platykurtic) at \(T_r>1\) and \(n_r=\frac{3+2\beta }{3}\) (Fig. 3b).

Fig. 3
figure 3

The kurtosis \(k\sigma ^2\) (40) as a function of \(n_r\) for \(\beta \)=0, 0.5, and 1 at (a) \(T_r=0.7\) and (b) \(T_r=1.7\)

Full size image

6 Conclusions

Here, a generalization of the two-parameter vdW model is presented by setting three parameters \(r_1,r_2,\) and k to the attractive term. The cubic equation is calculated exactly (see (5)) and solved analytically for \(0\le k\le 2\), through which the critical properties of the generalized vdW model are determined .

The Grand canonical ensemble formulation of one family of the generalized vdW equation is derived (see (30)). The particle fluctuations are characterized by three quantities scaled variance \(\omega (N)\), skewness \(S\sigma, \) and kurtosis \(k\sigma ^2\). An analytical expressions for these quantities are derived in terms of the reduced variables (\(n_r, T_r)\) for general value \(\beta \) (see (38)–(40)) and analyzed in a vicinity of the critical point . The results for \(\beta =0\) in the present work are consistent with the results obtained in [21].

As seen from Fig. 1, the scaled variance is a positive quantity, approaches the ideal gas in the limit of small densities, i.e., \(\omega (N)\cong 1\), as \(n\rightarrow 0\) and corresponds to the highest possible density (\(\omega (N)\rightarrow 0\)) as \(n_r\rightarrow 3+2\beta \). From Fig. 2, it is seen that the skewness is positive at \(n_r<\frac{3+2\beta }{3}\) (gas phase) and negative (liquid phase) at \(n_r>\frac{3+2\beta }{3}\) for all values of \(T_r\). Also, the skewness \(S\sigma \rightarrow 0\) as \(n_r\rightarrow \frac{3+2\beta }{3}\)(\(n=n_\mathrm{{c}}\) line), and this line is the transition line from gas to liquid phase. From Fig. 3a, it is noticed that the kurtosis is positive at \(T>T_\mathrm{{c}}\) for both \(n_r<\frac{3+2\beta }{3}\) and \(n_r>\frac{3+2\beta }{3}\) and close to the CP, the kurtosis changes rapidly from positive to negative values at \(T>T_\mathrm{{c}}\) (see Fig. 3b).

Finally, it is noticed from the calculations and the figures that the three quantities \(\omega (N)=S\sigma =k\sigma ^2=1\) when the reduced critical density \(n_r\rightarrow 0\), i.e., the vdW EoS corresponds to the ideal gas and the distribution approaches the Poisson distribution. Also, it is found that the fluctuations have a singular behavior close to the critical point where the three quantities (\(\omega (N)\), \(S\sigma, \) and \(k\sigma ^2\)) diverge at the critical point.