Abstract
In Europe, most of the alpine timberline ecotone has been altered by human activities and climate change. Hence, mountain forests are of the highest conservation interest. Here, we screened 25 populations of Swiss stone pine (Pinus cembra L.) from the Carpathians and the Alps, using a set of ten microsatellite primers to assess the relative conservation value of populations sampled in Polish and Slovak Tatra National Parks, where potential extinction risk is the highest within the Carpathian range. Although endangered, with small and fragmented populations, P. cembra in the Tatra Mts. shows high levels of allelic richness (AR = 5.0) and observed heterozygosity (H o = 0.554). Our results suggest that anthropogenic habitat fragmentation has had little impact on DNA variation of Swiss stone pine in the Tatra Mts. However, the effects of changing conditions on the genetic structure may occur with a substantial time delay due to the long life span of P. cembra. Moreover, inbreeding depression may occur in the next generations, since we found inbreeding (F IS = 0.063) and elevated coancestry coefficient (θ = 0.062) in all populations. Also a shallow pattern of genetic differentiation between populations was found, indicating recent fragmentation of a common gene pool that formerly occupied a larger range. Therefore, the Tatra Mts. can be considered as a single conservation unit. Based on our results, we suggest possible conservation activities for Swiss stone pine both in Poland and Slovakia.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In the last two centuries, human impact on the world’s ecosystems has increased and many natural habitats have been changed, degraded, or even destroyed. Among them, ecosystems at the distribution limit of a species are of special conservation interest. The timberline designates the limit of forest growth and typically forms a transition zone between the upper limit of the continuous closed forest and the treeless alpine zone (Tranquillini 1979; Wieser et al. 2009). Unfortunately, over the past millennia, the treeline has been lowered because of timber production (Farrell et al. 2000), livestock grazing (Cairns and Moen 2004), and fire (Carcaillet 1998). The main effect of human influence has been the disappearance of a part of the subalpine forests and the modification of its composition, structure, and spatial patterns (Motta and Lingua 2005). Timberline changes have both demographic and genetic consequences. Several genetic processes are affected when populations are drastically reduced and the landscape is fragmented. Fragmentation may inhibit gene flow among populations and generate genetic differentiation. Small populations are generally prone to elevated inbreeding, genetic drift, and erosion (Hartl and Clark 1988; Pierson et al. 2007). Moreover, geographically peripheral (marginal) populations are expected to have lower genetic diversity and higher genetic differentiation than geographically core populations. However, they may acquire an evolutionary potential for adaptation as well as speciation and may be of high conservation value.
Protection of populations in their natural habitat (in situ) maintains ecological and evolutionary processes, as well as adaptation (Chybicki et al. 2012). However, the conservation of endangered and threatened tree species often requires pro-active ex situ practices, such as the establishment of seed orchards, gene banks, or clone archives. It is therefore very important to choose source populations carefully, using scientific criteria. Poor choice of material for restoration can lead to several problems, such as lower fitness, loss of genetic identity, or outbreeding depression (Hufford and Mazer 2003; Montalvo et al. 1997). Thus, the generally acknowledged strategy for ex situ conservation is to minimize the global coancestry (Caballero and Toro 2000; Montgomery et al. 1997; Saura et al. 2008). Hence, examination of genetic polymorphism is required before initiating any conservation activities (Kato et al. 2013). Better knowledge of the level and distribution of genetic diversity helps choosing conservation units (CUs), which can be defined as a population or group of populations that warrant separate management or priority for conservation because of high genetic and ecological distinctiveness (Funk et al. 2012).
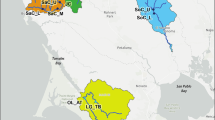
The Swiss stone pine (Pinus cembra) is a monoecious five-needled pine, growing at the timberline in the European mountains. Swiss stone pine is a predominantly outcrossed species, with wind-dispersed pollen, and its wingless seeds are almost exclusively dispersed by the European nutcracker (Nucifraga caryocatactes) (Ulber et al. 2004). It is considered as a glacial relict, whose natural distribution extends from southeastern France over the whole Alpine range of Italy, Switzerland, and Austria, all the way to isolated groups in (a) the Western Carpathians in Poland and Slovakia (Tatra Mountains); (b) the Eastern Carpathians in the Ukraine and Romania; and (c) the Southern Carpathians in Romania (Fig. 1). Palynological records and genetic data suggest that the species colonized the Alps from glacial refugia in or near the eastern or southeastern periphery of the Alps (Gugerli et al. 2009). P. cembra survived the last glaciation also in the Carpathians (Höhn et al. 2009).
Locations of the study populations of Pinus cembra (population names as coded in Table 1): the species natural range in Europe is indicated by the shaded areas (distribution map courtesy by EUFORGEN)
The Tatra Mountains are situated at the Slovak–Polish border and constitute the highest mountain massif within the Carpathian Range of Central Europe (Švajda et al. 2011). Here, Swiss stone pine is growing at the northern margin and fairly isolated from its main distribution range (Fig. 1). Current populations in the entire Tatra region, an area of 300 ha, comprise about 12,000 individuals of P. cembra, of which about 4,000 residuals are in Poland (Chmiel 1996). The need for artificial restoration of this species in Poland has been emphasized (Chmiel 1996; Myczkowski 1955). Early indications of progressive destruction of P. cembra in the Tatra Mts. date back to the 17th century. By the end of the 19th century, restoration efforts were initiated in Poland by sowing and planting individuals from different sources. Unfortunately, in many cases seeds from Alpine or even Siberian origin were used (Paryski 1971), potentially leading to reduced fitness. Today, conservation policy is focused on the prevention of genetic erosion by in situ protection of natural stands. Thus, the entire Polish population of Swiss stone pine within the Tatra National Park is protected by Polish law. Unfortunately, despite 50 years of strict protection, this pine is still believed to be a threatened species in the Polish Tatras (Zwijacz-Kozica and Żywiec 2007).
The main aim of our paper was to illustrate the relevance of range-wide genetic surveys to define best CUs, and to develop efficient management and conservation strategies for active protection of species growing in the timberline ecotone. We used Pinus cembra in the Tatra Mts., as a case study, since it is one of the most seriously affected species by human activities and climate change. Our aim was to compare the genetic parameters obtained with those from other parts of the Carpathians. However, to provide a more comprehensive picture of genetic structure in P. cembra, we also used plant material sampled in the Alps. In order to assess the relative conservation value of stone pine stands in the Tatra Mts., we investigated the levels of genetic polymorphism, inbreeding, coancestry, and effective population size, and tested if a bottleneck had occurred in the recent population history.
Materials and methods
Population sampling
Our analysis included 25 stands from the entire natural distribution range (Fig. 1), 6 of which from the Alps (n = 191) and 19 (n = 627) from the Carpathians. We sampled eleven populations in the Polish and Slovak Tatra National Parks (Table 1). In most stands, fresh needles were collected from adult trees, trying to keep maximum spatial distance between trees. For Austrian populations, we used material from commercial seed harvests from five registered seed collection stands of putative autochthonous origin. Seeds had been collected in 2003 from 20 to 30 mother trees at each site and were derived from different cones for each tree. Seed samples were kept separately until laboratory analyses. Each mother tree was represented in the population seed sample by a maximum of two seeds (Table 2). For DNA analyses, seeds were germinated in petri dishes, and when radicles emerged, megagametophytes and young seedlings were dissected, separated, and extracted.
Molecular methods
Total genomic DNA was extracted from needles and young seedlings using the protocol of Doyle and Doyle (1990). All eight nSSR markers published for P. cembra were tested (Salzer et al. 2009). However, after preliminary tests, locus Pc 25 was excluded from study, because of lack of clearly interpretable mono-locus patterns. Therefore, to increase the genetic power, we tested thirteen nSSR markers designed for P. strobus (Echt et al. 1996). Three of them were polymorphic and were used in this study. These ten nuclear SSR loci were analyzed in two multiplex PCR reactions (Table S1). Seven loci (Salzer et al. 2009) were amplified using the Multiplex Master Mix (Qiagen) according to the manufacturer’s instruction. Another protocol was used to amplify RPS1b, RPS50, and RPS127 (Echt et al. 1996). The PCR products were sized using an ABI PRISM 3130XL capillary sequencer, then the genotypes were scored using GENESCAN 3.7 and GENOTYPER 3.7 (Applied Biosystems).
Statistical methods
Genetic structure
Standard measures of genetic diversity were calculated: observed and effective number of alleles, expected and observed heterozygosity, using INest2 (Chybicki and Burczyk 2009). To compare indices of genetic diversity between populations despite different sample sizes, a rarefaction procedure with HP-Rare 1.0 (Kalinowski 2005) was performed to assess the allelic richness (AR) and private allelic richness (pAR). Significance of differences in mean values of different genetic diversity parameters among mountain ranges (Alps, Tatra Mts., and SE Carpathians) was tested using the non-parametric Kruskal–Wallis test implemented in Past 3 (Hammer et al. 2001), or the permutation test implemented in FSTAT 2.9.3 (Goudet 2001). Genetic structure was also described by multilocus average inbreeding coefficient, calculated using the method implemented in BayeF (Chybicki et al. 2012). Positively and negatively outlying populations in terms of polymorphism levels were identified by bootstrapping lower and upper limits for 95 % confidence intervals (CI) for single-locus AR and comparing with the mean value. The relative contribution of a given population to a global within-(A s ) and between-population allelic diversity (D b ) was estimated by the rarefaction-based method introduced recently by Caballero and Rodriguez-Ramilo (2010). Each population was also characterized by the coancestry coefficient (θ) using a model introduced by Balding and Nichols (1995) implemented in BayeF (Chybicki et al. 2012).
Conservation units
The level of differentiation among and within groups of individuals was estimated by hierarchical analysis of molecular variance (AMOVA; Excoffier et al. 1992) based on a genetic distance matrix of pairwise F ST values using ARLEQUIN 3.5.1.3 (Excoffier and Lischer 2010). AMOVA was employed to estimate and partition the total molecular variances among regions (Tatra Mts., SE Carpathians, and Alps), among populations within region, and within populations. Significance of partitioned variance components was estimated using a 10,000-permutation procedure. A simulated annealing procedure implemented in the spatial analysis of molecular variance (SAMOVA) algorithm (Dupanloup et al. 2002) was used to define groups of populations that are geographically homogeneous and maximally differentiated from each other. To identify the number of clusters best representing the data, we also used AMOVA-based clustering of population using k-Means (Meirmans 2012). In order to better understand the genetic structure of P. cembra populations, a Principal Coordinate Analysis (PCoA) was carried out using GenAlEx v6.5 (Peakall and Smouse 2006). Further, to test for a pattern of isolation by distance (Rousset 1997) in the whole dataset, as well as in the Alps, Tatra Mts., and SE Carpathians, separately, Mantel tests were carried out. The correlation between genetic and geographical distances was tested by 9,999 random permutations with the matrix of pairwise genetic differentiation between populations, using F ST /(1 − F ST ), and a matrix of geographic distance using GenAlEx v.6.5 (Peakall and Smouse 2006). In order to test any association between genetic structure and geographic variables, we performed a multiple regression analysis using MuMIn 1.10.0 under R (CRAN), details are given in Appendix 1 in Supplementary material.
Effective population size
BOTTLENECK was used to compare gene diversity (H e ) of populations to the heterozygosity expected at mutation–drift equilibrium (H eq ), given a specific number of alleles (Cornuet and Luikart 1996). Deviation from mutation–drift equilibrium is expected if populations have experienced a recent demographic decline (bottleneck). To test statistical significance, we used the Wilcoxon signed-rank test under the assumption of the stepwise mutation model (SMM) and the two-phase mutation model (TPM), which assumes 30 % multiple-steps mutations and 70 % single-step mutations. For each mutational model, 1,000 replicates were performed. Effective population size (N e ) was estimated using the single-generation estimators. First, we used LDNE (Waples and Do 2008) to assess N e(LD), the estimator based on linkage disequilibrium measure. Because N e(LD) can be biased due to low frequency alleles (Waples and Do 2010), we omitted alleles with a sample frequency lower than three copies. Second, N e was also assessed in Colony 2 (Jones and Wang 2009), according to the method proposed by Wang (2009), based on the reconstructed proportion of full-, half-sib and unrelated pairs among a cohort of genotyped individuals (hereafter referred to as N e(SA)) (for details see Appendix 2 in Supplementary material).
Results
Genetic structure
In total, 158 alleles were found at ten SSR loci in 818 individuals, with an average of 5.8 per population. The number of detected alleles per locus ranged from 2 (Pc 35) to 34 (Pc 23), with an average of 15.8 per locus. However, due to generally uneven distribution of allele frequencies, the effective number of alleles was only 2.2, on average. Allelic richness based on 32 genes was estimated at AR = 4.9, with values ranging from 3.1 to 5.4 in the Alps and from 3.0 to 5.7 in the Carpathians (Table 2). The single-locus AR values were not homogeneously distributed across populations, as revealed by the Friedman test (χ 2 = 40.51, df = 24, p value = 0.010). However, no significant difference between mountain ranges was detected. Two populations with the lowest AR (F and UA5) can be considered as negatively outlying populations in terms of polymorphism levels, because the approximate 95 % confidence bounds did not include the average AR value. Similarly, no population could be identified as a positive outlier. The pAR ranged from <0.01 (A4) to 0.24 (A5) in the Alps and from <0.01 (PL1, UA5) to 0.27 (UA2) in the Carpathians. There was no significant difference in pAR between mountain chains. The permutation test revealed significantly higher level of expected heterozygosity (H e ) and observed heterozygosity (H o ) in the Tatra Mts. (Table 2) than in the Alps (p = 0.005 and p = 0.013, respectively). However, the differences between these parameters were not significant when comparing Tatra Mts. and SE Carpathians (p = 0.364 and p = 0.186, respectively). In the Alps, only two populations contributed positively both to A s and D b (A3 and A5), whereas three out of five populations had a negative contribution to the total allelic diversity (Fig. 2). This was mostly because of the negative contribution both to the within-population (A s ) and between-population (D b ) components (A1, A2, A4). Among negative outliers, only population F had a positive contribution to between-population allelic diversity (D b ). In contrast to the Alps, most Carpathian populations contributed positively to the total allelic diversity (A t ). However, four of them had also negative contributions to D b (PL3, PL5, PL6, RO3). Three populations had a negative contribution to the total allelic diversity, because of the negative contribution both to within-population (A s ) and between-population (D b ) components (PL1, RO1, UA5). Although the relative contribution of the study populations to allelic richness components is low (<2.5 %), the partitioning method allowed to estimate the global allelic diversity to be at the level A ST = 0.254. Hence, about 25 % of the total allelic diversity is between populations.
Multilocus inbreeding coefficients obtained with INEst (F IS ) revealed a deficiency of heterozygotes in all populations. However, null alleles and inbreeding contributed unevenly to the excessive homozogosity. The average null allele frequency was about 3.7 % (data not shown). Pc 35 appeared the least affected by null alleles (0.2 % on average), while for the others, the average null allele frequency ranged between 1.8 and 8.3 % (above the mean for RPS50, Pc 3, Pc 1b, Pc 7). “Null-free” estimates of F IS were within 0.014–0.187, with the grand average being 6.3 %. Among the study populations, eleven were characterized by higher than average F IS , of which only two were from the Alps, five from the Tatra Mts., and four from the SE Carpathians (Table 2). However, the differences between F IS were not significant when comparing Alps, Tatra Mts., and SE Carpathians (Kruskal–Wallis test, p > 0.05). Multilocus F IS estimates obtained with INEst (0.063) appeared much lower than the classically derived values (i.e., on average 1 − H o /H e = 0.106). Hence, inbreeding explained about 59 % of the large heterozygote deficiency observed in the study populations, and thereby the minor frequency of null alleles (~3.7 %) had a relatively strong effect on the homozygote excess (~41 %).
For the most representative prior (μ = 0.05), θ spanned between 0.018 and 0.301, with the average equal 0.062 (Table 3). Two populations were clearly distinguishable from the rest, namely F and UA5, both having θ above 0.2. There was no significant difference in coancestry coefficients between mountain ranges (Kruskal–Wallis test, p > 0.05).
Conservation units
AMOVA revealed that variation among regions accounted for only 1.39 % of the total variance, 5.25 % among populations within region, and 93.36 % within populations (Table 4). SAMOVA analysis showed that the highest F CT value (0.134) was obtained when the 25 populations were divided into K = 2 groups: the F population, and the other 24 populations. Similarly, the kMeans results indicated two different genetic groups: two western-most populations (A1 and F) and the other populations (Φ CT = 0.129). In the PCoA, the first two axes explained 55.21 % of the variation and indicated separation of three western-most populations in the Alps (F, A1, and A2), and the population from Southern Carpathians (RO1). Thus, most of the populations are clustered in a single group (Fig. 3). The Mantel test revealed the existence of significant correlations between genetic and geographical distances both in the whole dataset (R 2 = 0.465, p = 0.0001), as well as in the Alps (R2 = 0.882, P = 0.004) and Carpathians (R 2 = 0.231, p = 0.0001), but not in the Tatra Mts. and SE Carpathians, analyzed separately (Fig. 4). Regression analyses revealed associations between genetic parameters and geographic variables (Table 5). The significant geographic pattern was revealed for both AR and H e , while no geographic effect was noted for the inbreeding coefficient (F IS ). When the whole data set was analyzed, AR and H e were positively associated with longitude and latitude, respectively. Thus, the level of polymorphism and diversity tended to increase from west to east and from south to north, respectively. At the regional level, the most apparent associations were observed in the Alps, where both AR and H e were positively associated with both longitude and latitude. Conversely, in the SE Carpathians, H e showed a significant decrease with latitude. Apparently, elevation has no effect on the studied genetic parameters. Also, no geographic trends were revealed for the Tatra Mts.
Effective population size
Analyses in BOTTLENECK revealed one case of significant heterozygote excess (Table 3). In population UA5, nine and seven microsatellite loci surveyed in this study, evolved under a strict TPM and SMM model, respectively, indicating that the population remained relatively unstable in recent evolutionary history (the Wilcoxon test; p value <0.05). The LD-based estimates of effective population sizes N e(LD) ranged from 12.5 (UA5) to ∞ (SK2). As compared with N e(LD), the values estimated from reconstructed pedigrees N e(SA) were lower, ranging between 24 (UA5) and 63 (A5). In general, the lowest effective population sizes N e were estimated in UA5, which exhibited pronounced bottleneck signatures (Table 3).
Discussion
Patterns of genetic diversity
Pine species usually exhibit high levels of genetic diversity mainly due to their outcrossing mating system (Loveless and Hamrick 1984). Although P. cembra matches this pattern, the study populations differed in parameters of genetic structure. For example, allelic richness ranged from 3.0 to 5.7, while inbreeding coefficient and average coancestry reached values from 0.014 to 0.187 and from 0.018 to 0.301, respectively. Although we found no significant differences in these parameters when comparing Tatra Mts., Alps, and SE Carpathians, these results should be interpreted with caution, due to seed sampling in Austrian populations. In general, an excess of homozygosity is expected in progeny, whereas an excess of heterozygosity observed in adults may be attributed to selection against homozygotes during lifetime. Thus, genetic diversity estimated on seed samples may bias results against those of adult trees. However, Salzer and Gugerli (2012) inferred that in P. cembra, inbreeding depression is expressed mainly at the prezygotic and/or early embryonic phase by high embryo abortion and low germination success. Thus, the estimates we performed at the stage of young seedlings would be less biased than those at the embryo level. Still, the comparison of genetic diversity between different life stages (young seedlings vs. adult trees) and between populations of different mountain ranges, makes the interpretation of results difficult.
Our results clearly indicate that inbreeding is present in Swiss stone pine. Both sources of inbreeding (selfing and mating among relatives) were noted earlier in P. cembra populations (Lewandowski and Burczyk 2000; Politov et al. 2008; Salzer and Gugerli 2012). In fragmented and isolated populations, where selfing and mating among relatives allow escape from pollen limitation, their benefits come at the cost of inbreeding depression. So far in P. cembra, inbreeding was found at the embryonic stage but not in adult populations (Politov et al. 2008). Selection against inbred progeny is considered the main factor responsible for differences in inbreeding levels between adults and early stages in the life cycle. Our results with an average of F IS = 0.063 were close to those reported for isolated populations of English yew (Chybicki et al. 2012) but much lower than for Pinus rzedowskii and P. pinceana, endangered pine species in Mexico (Delgado et al. 1999, Ledig et al. 2001). We found elevated coancestry coefficients in all populations of P. cembra, which can result from limited gene immigration (Reynolds et al. 1983). Two populations had especially high estimates (above 0.2): F, which is the western-most population in our study, and UA5, where we found indications of a recent bottleneck. Both populations also have the lowest estimates of effective population size.
Nonetheless, the main result of the study is the high genetic diversity found in Swiss stone pine, despite high fragmentation and small population size. This is especially evident in the Tatra Mts., where most of the stands have been decimated and as a consequence, the stone pine occurs mainly in remote areas (Myczkowski and Bednarz 1974; Zwijacz-Kozica and Żywiec 2007). No reduction in genetic diversity is a rather surprising result, although it also has been observed earlier in chloroplast DNA of Swiss stone pine from the Tatra Mts. (Höhn et al. 2009). But since P. cembra is a long-lived species (trees between 500 and 1,000 years of age are reported), with long reproductive life spans (Ulber et al. 2004), the effects of changing conditions on the genetic structure may occur only with a substantial delay (Von Holle et al. 2003; Watt 1947). Moreover, high gene flow in P. cembra in the Tatra Mts. (Chybicki and Dzialuk 2014) and the lack of power to detect may be the alternative explanations of the absence of evidence of genetic diversity reduction in Tatra Mts. However, the latter is less likely because of the extensive sampling in Carpathians and to a lesser degree in Alps, the high number of hypervariable DNA markers and the advanced statistical tests are used to find differences in mean values of genetic diversity parameters.
Up to date, substantially higher differentiation and genetic diversity of Swiss stone pine have been observed in the Carpathians than in the Alps (Belokon et al. 2005; Höhn et al. 2009). Such structure may be a result of spatial isolation hampering gene flow among fragmented populations. In the Alps, Gugerli et al. (2009) found a gradual decline of chloroplast DNA diversity from East to West, along the colonization route from a single glacial refugium located at the (south-) eastern periphery of the Alps. This pattern is in accordance with the ‘‘abundant center model’’ and reflects the process of genetic drift through founder events and/or bottlenecks, coupled with reduced gene flow related to postglacial colonization dynamics. Despite the rather small sample size in the Alps, our results corroborate the separation of western-most populations (Fig. 3). Overall, the pattern of genetic differentiation of Swiss stone pine is rather shallow (Belokon et al. 2005; Gugerli et al. 2001, 2009; Höhn et al. 2009), indicating recent fragmentation of a common gene pool that formerly occupied a larger range.
Perspectives for conservation in Tatra Mts
The high levels of genetic diversity maintained within small and fragmented populations of P. cembra in the Tatra Mts. are encouraging. It seems that these populations were never reduced to a low enough size for extensive genetic drift to occur, and the species is currently not at risk of extinction. Moreover, our results clearly indicate that habitat fragmentation has not yet affected Swiss stone pine, and the species can be considered as a single CU for further breeding and long-term conservation. Thus, for in situ conservation action, we recommend establishment of seed stands for harvesting purposes to obtain sufficient representation of inherent genetic diversity. Since each population represents a large proportion of the genetic diversity within the species, seeds may be collected even in small number of populations. This information is of special value for conservation program because seed production in Swiss stone pine occurs every 2–3 years but only a single year of 4–10 is an abundant mast year (Ulber et al. 2004). Moreover, it would be advisable not to collect seeds in the northernmost population—Dolina Białego (PL1), whose contributions into allelic diversity is negative, and whose coancestry coefficient is almost twice the average for the Tatra Mts. Under random mating, the total coancestry of a population would become inbreeding of the progeny. However, additional studies on adaptive traits in P. cembra are strongly needed to provide more information about morphological, phenological, and physiological adaptations and to support the restoration actions proposed in this study. Further research is needed also to clarify the phenomenon of high genetic diversity maintained in P. cembra in Tatra Mts., because drastic reduction of genetic diversity and loss of rare alleles as a consequence of harvesting have been reported in other five-needle pines, e.g., in P. strobus (Rajora et al. 2000). Moreover, further studies on mating system are required in each source population to minimize the global coancestry (Chybicki and Dzialuk 2014) and to monitor the genetic condition of the next generations. As a consequence, there is urgent need for tightening the cooperation between Poland and Slovakia to protect the gene pool of Swiss stone pine in the Tatra Mts. It is especially important for the protection of Polish populations, where bark beetles have caused serious devastations of stone pines in recent years.
References
Balding DJ, Nichols RA (1995) A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity. Genetica 96:3–12
Belokon MM, Belokon YuS, Politov DV, Altukhov YuP (2005) Allozyme polymorphism of Swiss stone pine Pinus cembra L. in mountain populations of the Alps and the Eastern Carpathians. Rus J Genet 41:1268–1280
Caballero A, Rodriguez-Ramilo ST (2010) A new method for the partition of allelic diversity within and between subpopulations. Conserv Genet 11:2219–2229
Caballero A, Toro MA (2000) Interrelations between effective population size and other pedigree tools for the management of conserved populations. Genet Res 75:331–343
Cairns DM, Moen J (2004) Herbivory influences tree lines. J Ecol 92:1019–1024
Carcaillet C (1998) A spatially precise study of Holocene fire history climate and human impact within Maurienne valley. N French Alps J Ecol 86:384–396
Chmiel J (1996) Naturalny zasięg a rozsiedlenie limby Pinus cembra L. w Tatrach Polskich. In: A Kownacki (ed) Przyroda Tatrzańskiego Parku Narodowego a człowiek. Biologia. vol 2, pp 63–66
Chybicki IJ, Burczyk J (2009) Simultaneous estimation of null alleles and inbreeding coefficients. J Hered 100:106–113
Chybicki IJ, Dzialuk A (2014) Bayesian approach reveals confounding effects of population size and seasonality on outcrossing rates in a fragmented subalpine conifer. Tree Genet Genomes (submitted)
Chybicki IJ, Oleksa A, Kowalkowska K (2012) Variable rates of random genetic drift in protected populations of English yew: implications for gene pool conservation. Conserv Genet 13:899–911
Cornuet JM, Luikart G (1996) Description and power analysis of two tests for detecting recent population bottlenecks from allele frequency data. Genetics 144:2001–2014
Delgado PD, Pilero A, Chaos N, Pirez-Nasser E, Alvarez-Buylla ER (1999) High population differentiation and genetic variation in the endangered Mexican pine Pinus rzedowskii (Pinaceae). Am J Bot 86:669–676
Doyle J, Doyle J (1990) Isolation of plant DNA from fresh tissue. Focus 12:13–15
Dupanloup I, Schneider S, Excoffier L (2002) A simulated annealing approach to define genetic structure of populations. Mol Ecol 11:2571–2581
Echt CS, May-Marquardt P, Hseih M, Zahorchak R (1996) Characterization of microsatellite markers in eastern white pine. Genome 39:1102–1108
Excoffier L, Lischer HEL (2010) Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under Linux and Windows. Mol Ecol Resour 10:564–567
Excoffier L, Smouse PE, Quattro JM (1992) Analysis of molecular variance inferred from metric distances among DNA haplotypes: applications to human mitochondrial DNA restriction data. Genetics 131:479–491
Farrell EP, Führer E, Ryan D, Andersson F, Hüttl R, Piussi P (2000) European forest ecosystems: building the future on the legacy of the past. For Ecol Manag 132:5–20
Funk WC, McKay JC, Hohenlohe PA, Allendorf FW (2012) Harnessing genomics for delineating conservation units. Trends Ecol Evol 9:489–496
Goudet J (2001) FSTAT: a program to estimate and test gene diversities and fixation indices (version 2.93). http://www2.unil.ch/popgen/softwares/fstat.htm. Accessed 29 June 2014
Gugerli F, Senn J, Anzidei M, Madaghiele A, Büchler U, Sperisen C, Vendramin GG (2001) Chloroplast microsatellites and mitochondrial nad 1 intron 2 sequences indicate congruent phylogenetic relationships among Swiss stone pine (Pinus cembra) Siberian stone pine (Pinus sibirica) and Siberian dwarf pine (Pinus pumila). Mol Ecol 10:1489–1497
Gugerli F, Rüegg M, Vendramin GG (2009) Gradual decline in genetic diversity in Swiss stone pine populations (Pinus cembra) across Switzerland suggests postglacial re-colonization into the Alps from a common eastern glacial refugium. Bot Helv 119:13–22
Hammer Ø, Harper DAT, Ryan PD (2001) PAST: paleontological statistics software package for education and data analysis. Palaeontol Electronica 4:9
Hartl D, Clark A (1988) Principles of population genetics, 2nd edn. Sinauer Associates Inc Publishers, USA
Höhn M, Gugerli F, Abran P, Bisztray G, Buonamici A, Cseke K, Hufnagel L, Sebastiani F, Quintela-Sabarís S, Vendramin GG (2009) Variation in the chloroplast DNA of Swiss stone pine (Pinus cembra L) reflects contrasting postglacial history of populations from the Carpathians and the Alps. J Biogeogr 36:1798–1806
Hufford KM, Mazer SJ (2003) Plant ecotypes: genetic differentiation in the age of ecological restoration. Trends Ecol Evol 18:147–155
Jones O, Wang J (2009) COLONY: a program for parentage and sibship inference from multilocus genotype data. Mol Ecol Res 10:551–555
Kalinowski ST (2005) HP-RARE 1.0: a computer program for performing rarefaction on measures of allelic richness. Mol Ecol Notes 5:187–189
Kato S, Imai A, Rie N, Mukai Y (2013) Population genetic structure in a threatened tree Pyrus calleryana vardimorphophylla revealed by chloroplast DNA and nuclear SSR locus polymorphisms. Conserv Genet 14:983–996
Ledig FT, Capó-Arteaga MA, Hodgskiss PD, Sbay H, Flores-López C, Conkle MT, Zquez BB-V (2001) Genetic diversity and the mating system of a rare Mexican piñon Pinus pinceana and a comparison with Pinus maximartinezii (Pinaceae). Am J Bot 88:1977–1987
Lewandowski A, Burczyk J (2000) Mating system and genetic diversity in natural populations of European larch (Larix decidua) and stone pine (Pinus cembra) located at higher elevations. Silvae Genet 49:158–161
Loveless MD, Hamrick JL (1984) Ecological determinants of genetic structure in plant populations. Ann Rev Ecol Syst 15:65–95
Meirmans PG (2012) AMOVA-based clustering of population genetic data. J Hered 103:744–750
Montalvo AM, Williams SL, Rice KJ, Buchmann SL, Cory C, Handel SN, Nabhan GP, Primack R, Robichaux RH (1997) Restoration biology: a population biology perspective. Restor Ecol 5:277–290
Montgomery ME, Ballou JD, Nurthen RK, England PR, Briscoe DA, Frankham R (1997) Minimizing kinship in captive breeding programs. Zoo Biol 16:377–389
Motta R, Lingua E (2005) Human impact on size age and spatial structure in a mixed European larch and Swiss stone pine forest in the Western Italian Alps. Can J For Res 35:1809–1820
Myczkowski S (1955) Naturalne szpalery świerkowe nad górną granicą lasu na stokach Małej Kosistej w Tatrach. Chrońmy Przyr Ojcz 11(2):22–27
Myczkowski S, Bednarz Z (1974) The stone pine Pinus cembra L. In: Myczkowski S (ed) Rodzime drzewa Tatr I. Studia Ośrodka Dokumentacji Fizjologicznej. vol 3, pp 111–139
Paryski W (1971) Sadzenie i przesadzanie limby. In: Białobok S (ed) Limba Pinus cembra L. Nasze drzewa leśne. vol 2, pp 50–56
Peakall R, Smouse PE (2006) GENALEX 6: genetic analysis in Excel Population genetic software for teaching and research. Mol Ecol Notes 6:288–295
Pierson SAM, Keiffer CH, McCarthy BC, Rogstad SH (2007) Limited reintroduction does not always lead to rapid loss of genetic diversity: an example from the American chestnut (Castanea dentata; Fagaceae). Restor Ecol 15:420–429
Politov DV, Pirko YV, Pirko NN, Mudrik EA, Korshikov II (2008) Analysis of mating system in two Pinus cembra L. populations of the Ukrainian Carpathians. Ann For Res 51:11–18
Rajora OP, Rahman MH, Buchert GP, Dancik BP (2000) Microsatellite DNA analysis of genetic effects of harvesting in old-growth eastern white pine (Pinus strobus) in Ontario Canada. Mol Ecol 9:339–348
Reynolds J, Weir BS, Cockerham CC (1983) Estimation of the coancestry coefficient: basis for a short-term genetic distance. Genetics 105:767–779
Rousset F (1997) Genetic differentiation and estimation of gene flow from F-statistics under isolation by distance. Genetics 145:1219–1228
Salzer K, Gugerli F (2012) Reduced fitness at early life stages in peripheral versus core populations of Swiss stone pine (Pinus cembra) is not reflected by levels of inbreeding in seed families. Alpine Bot 122:75–85
Salzer K, Sebastiani F, Gugerli F, Buonamici A, Vendramin GG (2009) Isolation and characterization of polymorphic nuclear microsatellite loci in Pinus cembra L. Mol Ecol Res 9:858–861
Saura M, Perez-Figueroa A, Fernandez J, Toro M, Caballero A (2008) Preserving population allele frequencies in ex situ conservation programs. Conserv Biol 22:1277–1287
Švajda J, Solár J, Janiga M, Buliák M (2011) Dwarf pine (Pinus mugo) and selected abiotic habitat conditions in the Western Tatra Mountains. MRD 31:220–228
Tranquillini W (1979) Physiological ecology of the alpine timberline. Springer, Berlin
Ulber M, Gugerli F, Bozi G (2004) Technical guidelines for genetic conservation and use of swiss stone pine (Pinus cembra L). Technical Report. International Plant Genetic Resources Institute
Von Holle B, Delcourt HR, Simberloff D (2003) The importance of biological inertia in plant community resistance to invasion. J Veget Sci 14:425–432
Wang J (2009) A new method for estimating effective population sizes from a single sample of multilocus genotypes. Mol Ecol 18:2148–2164
Waples RS, Do C (2008) LDNE: a program for estimating effective population size from data on linkage disequilibrium. Mol Ecol Res 8:753–756
Waples RS, Do C (2010) Linkage disequilibrium estimates of contemporary Ne using highly variable genetic markers: a largely untapped resource for applied conservation and evolution. Evol Appl 3:244–262
Watt AS (1947) Pattern and process in the plant community. J Ecol 35:1–22
Wieser G, Matyssek R, Luzian R, Zwerger P, Pindur P, Oberhuber W, Gruber A (2009) Effects of atmospheric and climate change at the timberline of the Central European Alps. Ann For Sci 66:402
Zwijacz-Kozica T, Żywiec M (2007) Fifty-year changes in a strictly protected stone pine population in the Tatra National Park. Nat Conserv 64:73–82
Acknowledgments
This study was supported by a research grant from the Polish National Science Centre (NN304 129336) to AD. We would like to thank Katarzyna Kowalkowska, Ewa Sztupecka for assistance in laboratory work and Jean Ayme Esmiol for needle sampling in France. We are grateful to the personnel in the following National Parks: Tatra, Carpathian, Retezat, Calimani, and Muntii Rodnei, for their practical help in the sample collection. Special thanks to Prof. Reinhard F. Stettler for the careful English revision. We also thank three anonymous reviewers for insightful and constructive comments on a previous version of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Dzialuk, A., Chybicki, I., Gout, R. et al. No reduction in genetic diversity of Swiss stone pine (Pinus cembra L.) in Tatra Mountains despite high fragmentation and small population size. Conserv Genet 15, 1433–1445 (2014). https://doi.org/10.1007/s10592-014-0628-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10592-014-0628-6