Evolution of the characteristic curves in the restricted three-body problem in terms of the mass parameter

Abstract

In this work, we study the evolution of the families of simple symmetric periodic orbits in the restricted three-body problem whatever the value of the mass parameter $\mu$. To classify these characteristic curves, we introduce a topological characterization of both orbits and families. Starting from the work of Strömgren for the Copenhagen case, we analyze the evolution of these families, when the mass parameter $\mu$ varies in (0, 1/2], focusing on their topological characterization, the existence of asymptotic points and the appearance of certain types of orbits such as horseshoe orbits. Lastly, we consider two samples, the Earth–Moon and Sun–Jupiter systems and classify the different types of orbits for these systems.

1 Introduction

The restricted three-body problem (RTBP) is without doubt the most studied problem in Celestial Mechanics. Names like Euler, Lagrange, Laplace, Jacobi, Poincaré, Birkhoff, and many other giants of Celestial Mechanics have their names associated with this problem. In the RTBP, much effort has been dedicated to find and classify periodic orbits because as Poincaré (1892) wrote: “ce que nous rend ces solutions périodiques si précieuses, c’est q’elles sont, pour ainsi dire, la seule brèche par où nous puissions essayer de pénétrer dans une place jusqu’ici réputée inabordable.” Again, we find golden names working on this topic, like Stromgren, Brown, Rabe, Moulton, Hill, Whittaker, Lyapunov, Arenstorf, Brouwer, Hénon, Bruno, Szebehely, Deprit, Broucke, Henrard, or Hadjidemetriou, among many others [see Szebehely (1967) or Hénon (2003) for a complete list]. In autonomous Hamiltonian systems, periodic orbits appear in families. A family of periodic orbits is represented by a smooth one-parameter continuous curve (characteristic curve) in the space of initial conditions of parameters. In Deprit’s words: “natural families actually constitute the skeleton of the stable domains of a dynamic system” (Deprit and Henrard 1968). Although the RTBP is well known for readers of this article, we present a short description of it in order to fix notation and equations we will use in next sections. A clear exposition of this problem can be found in Chapter 8 of Danby’s classical textbook (Danby 1988).

As said before, many efforts have been dedicated to this problem and, in particular, to the determination of periodic orbits. A detailed study of periodic orbits of different types, their classification and evolution can be found in the excellent book written by Hénon (2003). Before this publication, it is worth to mention the huge work developed by Strömgren (1933) and his coworkers at the Copenhagen observatory, considering the case in which both primaries have the same mass ($\mu =0.5$). As a matter of fact, the case $\mu =0.5$ is usually known as Copenhagen problem. In this impressive Mémoir, Strömgren does not only obtain a very high number of symmetric periodic orbits (with no computer!), but he makes a complete classification of families in classes depending on the points the orbit encircles (primaries and equilibria); besides, he describes asymptotic orbits approaching the triangular points, and also, he describes the method used for numerically computing the orbits, which later on has been named grid search and that will be briefly described in the next section.

There are many works dedicated to the finding and classification of periodic orbits in the RTBP besides the authors appearing in the list two paragraphs above, considering specific values of the mass parameter $\mu$, like Bruno and Varin (2006), Hadjidemetriou and Ichtiaroglou (1984), Goudas and Papadakis (2006) or Restrepo and Russell (2018), just to mention a few but interesting works.

To our knowledge, there is no an analogous and systematic study for unequal masses similar to the one carried out by Strömgren (1933). We try to fill this gap in the present article. In order not to miss any orbit, we follow, as Strömgren, the grid search method for $\mu \in (0,0.5]$. Next, we make a new topological classification based on what points the orbit encircles together with its character, direct or retrograde. Special emphasis is dedicated to asymptotic orbits. In so doing, we make a classification of the symmetric periodic orbits and determine subintervals of $\mu$ where some types of families exist and others do not.

The paper is organized as follows. In Sect. 2, we present some basic definitions and results on symmetric periodic orbits and heteroclinic orbits, with some indications on how to compute them. Due to the great variety of periodic orbits, we give a topological classification of these orbits; the classification is based on what points the orbit encircles, its direct or retrograde character, and when necessary, the evolution of asymptotic orbits. In Sect. 3, as a test for our procedure, we compute and classify periodic and heteroclinic orbits in the Copenhagen problem, reproduce those obtained by Strömgren (1933) and name them with our terminology. Once checked that our method of classification is consistent with known results, we move in Sect. 4 to the case of arbitrary mass parameter $\mu \in (0, 0.5)$. In this case, we observe that there are subintervals for $\mu$ in which some types of periodic or heteroclinic orbits exist, but those orbits do not exist for other subintervals. We make a complete classification of the types of periodic orbits we find for all values on each subinterval. At this point, it is worth to mention the work of Goudas and Papadakis (2006) for some specific values of the mass parameter ($\mu =0.0, 0.1,0.2,0.3,0.4,0.5$) where they find families of symmetric periodic orbits with multiple periods (called multiple oscillations in their paper). Because they also present the plots (x, C) for only one oscillation, we may compare our and their results and we can see that there is a good agreement with the ones obtained by these authors for their chosen particular cases of $\mu$. Lastly, in Sect. 4 we compute the periodic orbits for two particular cases, perhaps the most outstanding from a practical point of view, the cases Sun–Jupiter and Earth–Moon, for which the mass parameter is actually small.

2 Formulation and basic aspects of the problem

2.1 The RTBP basics

Let us consider two primary bodies $P_1, P_2$, with masses $m_1, m_2\,(m_1 \ge m_2)$, such that $P_2$ describes a Keplerian circular orbit around $P_1$. The RTBP considers the motion of a third body P, of infinitesimal mass, under the gravitational attraction of the primaries $P_1, P_2$ in such a way that the motion of P does not affect the circular motion of the primaries. We consider only the planar case, that is, the motion of P is always on the plane of the primaries.

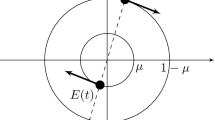
Let us define a synodic reference frame as a frame with the origin at the center of mass of the primaries, the Ox-axis rotating with the direction of the primaries and the Oy-axis the orthogonal to have a direct orthogonal frame. By choosing $m_1+m_2$ as the unit of mass, the radius of the orbit of $P_2$ around $P_1$ as the unit of length and the unit of time such that the gravitational parameter becomes equal to one, the positions of the primaries on the synodic frame are $P_1 (-\mu , 0), \, P_2 (1-\mu , 0)$, where $\mu = m_2 \in (0, 0.5]$ is the so-called mass parameter, and the position of the body P(x, y) will be given by the equations

$$\begin{aligned} \displaystyle \ddot{x} - 2 {\dot{y}} = \frac{\partial \Omega }{\partial x}, \quad \ddot{y} + 2 {\dot{x}} = \frac{\partial \Omega }{ \partial y}, \end{aligned}$$

(1)

where the effective potential is

$$\begin{aligned} \displaystyle \Omega = \frac{1}{2} (x^2+y^2) + \frac{1-\mu }{r_1} + \frac{\mu }{r_2}, \end{aligned}$$

(2)

and

$$\begin{aligned} r_1^2 = (x+\mu )^2 +y^2, r_2^2 = (x-1+\mu )^2 +y^2, \end{aligned}$$

are the distances from P to the primaries $P_1, P_2$, respectively (Fig. 1).

When working with rotating frames, there exists a first integral, the Jacobi’s constant, given by the expression

$$\begin{aligned} C = 2 \ \Omega (x, y) - ({\dot{x}}^2 + {\dot{y}}^2) \end{aligned}$$

(3)

and that can be easily obtained from Eq. (3).

As it is well known, the problem has five equilibrium points called Lagrange points. Three of them $L_1, L_2, L_3$, the collinear points, are on the Ox-axis, and the other two, the triangular ones, $L_4, L_5,$ have the coordinates $(1/2-\mu , \, \pm \sqrt{3}/2)$, forming an equilateral triangle with the primaries (see Fig. 1).

Triangular equilibria, $L_4, L_5$, are unstable for $\mu > \mu _{_R}$ where $\mu _{_R} = 0.0385...$ is the Routh’s mass, see, e.g., (Danby 1988; Deprit and Deprit-Bartholomé 1967)

Fig. 1

Planar restricted three-body problem

2.2 Symmetric periodic orbits

Equations (1) are invariants under the symmetry $(t, x, y, {\dot{x}}, {\dot{y}}) \longrightarrow (-t, x, -y, -{\dot{x}}, {\dot{y}})$, so orbits with two orthogonal crossing to the Ox-axis, separated by a time T/2, are symmetric periodic orbits of period T.

If we take the condition $\varvec{x}(t=0) =\varvec{x}_0 = (x_0, 0, 0, {\dot{y}}_0)$ as the initial condition of an orbit, then, the orbit will be symmetric of period T if, when propagating the orbit, there is a value $t=T/2$ such that $\varvec{x}(t=T/2) = \varvec{x}_{T/2} = (x_{T/2}, 0, 0, {\dot{y}}_{T/2} )$, i.e., the following conditions hold (Strömgren 1933)

$$\begin{aligned} y(T/2; \; x_0, 0, 0, {\dot{y}}_0 ) = 0, \quad {\dot{x}}(T/2; \; x_0, 0, 0, {\dot{y}}_0) = 0. \end{aligned}$$

(4)

Substituting the conditions $(x_0, 0, 0, {\dot{y}}_0)$ in Eq. (3), we find the relation

$$\begin{aligned} {\dot{y}}_0^2 = 2 \ \Omega (x_0, 0)- C_0, \end{aligned}$$

(5)

where $C_0$ is the value of the Jacobian constant for this orbit, which means that the pair $(x_0, C_0)$ characterizes a periodic orbit. For this reason, the families of symmetric periodic orbits are usually graphically presented on the plane (x, C). Taking into account the position of the primaries, the plane (x, C) is divided into three regions $R_l = \{ (x, C) \mid x \in (-\infty , -\mu )\}$, $R_c = \{ (x, C) \mid x \in (-\mu , 1-\mu )\}$, and $R_r = \{ (x, C) \mid x \in (1-\mu , +\infty )\}$.

We will only consider simple periodic orbits with only two orthogonal crossings with the Ox-axis. From a graphic point of view, a symmetric orbit $(x_0, C_0)$ begins at a point $(x_0, 0, 0, {\dot{y}}_0)$, with ${\dot{y}}_0 > 0$ [positive root of equation (5)] and the middle of the orbit corresponds to the point $(x_{T/2}, 0, 0, {\dot{y}}_{T/2})$, with ${\dot{y}}_{T/2} < 0$.

To find families of symmetric periodic orbits, we use the grid search method already used by Strömgren (1933). A more detailed exposition on how to implement this method is described, for instance, in Markellos et al. (1974) and Palacios et al. (2019). The method starts from a regular grid $(x_i, C_j),\, 1 \le i, j \le N,\; N\in {\mathbb {N}}$ on the plane (x, C). Taking two consecutive points $(x_i, C_k), (x_{i+1}, C_k)$, as a pair of initial conditions, we integrate equation (1) until the solutions cross the Ox-axis, then, if ${\dot{x}}_i \cdot {\dot{x}}_{i+1} < 0$ due to continuity there exists a pair $(x_i^*, C_k)$, with $x_i<x_i^*<x_{i+1}$ that represents the initial condition of an orbit that verifies (4). Brent’s method (Brent 1971) is used to find $x_i^*$ because it is very reliable and guarantees convergence. Note also that for the grid search method there is no need to have a small parameter as it happens with the analytical continuation of periodic orbits.

In order to classify these orbits, following the ideas developed in Strömgren (1933), we will introduce a notation that takes into account the following considerations:

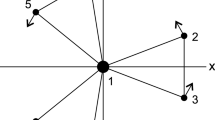
• The direction of rotation of the orbit: direct or retrograde orbits. We name ${\mathcal {D}}($) to the direct orbits and ${\mathcal {R}}($) to the retrograde ones. The orbit will be direct if $x_0 > x_{T/2}$ and retrograde if $x_0 < x_{T/2}$.

• What points, among $P_1, P_2, L_1, L_2, L_3, L_4, L_5$, are surrounded by the orbit. For instance, we shall call ${\mathcal {R}}(P_1 L_1 P_2)$ to a retrograde orbit around the points $P_1, L_1, P_2$. Due to the symmetry, if the orbit surrounds $L_4$ then it also surrounds $L_5$; thus, ${\mathcal {R}}(P_1, L_1, P_2, T)$ stands for an orbit around $P_1, L_1, P_2, L_4, L_5$ where the letter T represents both points $L_4$ and $L_5$.

As an illustration of our notation, we present in Fig. 2 six different orbits: ${\mathcal {R}}(L_1 P_2 L_2 T)$, ${\mathcal {R}}(L_2)$, ${\mathcal {R}}(L_1 T)$, ${\mathcal {D}}(P_1 L_1 P_2 T)$, ${\mathcal {D}}(P_2)$, ${\mathcal {R}}(L_1 P_2 L_2 T)$.

Fig. 2

Six different kinds of symmetric periodic orbits. From left to right and up to down: ${\mathcal {R}}(L_1 P_2 L_2 T)$, ${\mathcal {R}}(L_2)$, ${\mathcal {R}}(L_1 T)$,${\mathcal {D}}(P_1 L_1 P_2 T)$, ${\mathcal {D}}(P_2)$, ${\mathcal {R}}(L_1 P_2 L_2 T)$. Axes (x, y)

Among the various types of orbits, we highlight the following:

• P-orbits: orbits that surround the two primaries (${\mathcal {R}}(P_1 L_1 P_2), {\mathcal {D}}(P_1 L_1 P_2)$). Dvorak (1984) introduces this name to consider the orbits of a planet around a double star. P-orbits encircle the three points $P_1, L_1, P_2$, but they can surround more than these points, for instance ${\mathcal {R}}(L_3 P_1 L_1 P_2 L_2 T)$.

• S-orbit: orbits that surround only one of the primaries (${\mathcal {R}}(P_i), {\mathcal {D}}(P_i), \;i = 1,2$). This notation was also introduced by Dvorak (1984) and represents orbits of a planet around one of the components of a binary systems, or a satellite of a planet.

• Lyapunov orbits: orbits surrounding only one of the collinear points $(L_1, L_2, L_3)$ and close to that point (${\mathcal {R}}(L_i), {\mathcal {D}}(L_i), \;i = 1,2,3$).

• Horseshoe orbits (Brown 1911): orbits surrounding only the triangular points $L_4, L_5$ and the collinear $L_3$, i.e., (${\mathcal {R}}(L_3 T), {\mathcal {D}}(L_3 T)$). Sometimes, the condition that both crossings with the x-axis, one very near $L_3$ (and the other far away from $P_1$), is added (Barrabés and Mikkola 2005). Incidentally, let us mention that Henrard (2002) and Henrard and Navarro (2004) made a study on the evolution of homoclinic orbits and obtained also horseshoe orbits; however, their orbits are not symmetric and, hence, are out of the scope of our present work.

2.3 Heteroclinic orbits

The stable and unstable manifolds of the triangular equilibrium points L$_i$ are defined by

$$\begin{aligned} \left. \begin{array}{l} W^s(L_i) =\left\{ x \in M, \; \lim _{t\rightarrow \infty } \phi (t,x) \rightarrow L_i \right\} , \\ W^u(L_i) = \left\{ x \in M, \; \lim _{t\rightarrow -\infty } \phi (t,x)\rightarrow L_i \right\} , \end{array} \right\} \quad (i=4,5), \end{aligned}$$

respectively, where $M \in {\mathbb {R}}^4$ is the phase space of the restricted three-body problem and $\phi$ represents the flow of the field.

By the symmetry of the problem, each element of the intersection $W^u(L_4) \cap W^s(L_5)$ corresponds to a heteroclinic orbit, labeled ${\mathcal {U}}$, that goes from $L_4$ to $L_5$. In the same way, each element of the intersection $W^s(L_4) \cap W^u(L_5)$ corresponds to another heteroclinic orbit, dubbed ${\mathcal {S}}$, that goes from $L_5$ to $L_4$. Both orbits orthogonally cut the Ox-axis ($y = 0, {\dot{x}} = 0$).

Note: To avoid possible confusion, we emphasize that symbols ${\mathcal {S}}$ and ${\mathcal {U}}$ have no relation with the stable or unstable character.

As said above, triangular equilibria, $L_4, L_5$, are unstable for $\mu > \mu _{_R}$; then, by solving the variational equations of (1), the solution around the unstable triangular equilibria is given by

$$\begin{aligned} \begin{array}{lccl} x(t) &{}=&{} x_{_T} + &{}e^{\lambda _r t} (A_1 \cos \lambda _i t + A_2 \sin \lambda _i t ) + e^{-\lambda _r t} (A_3 \cos \lambda _i t + A_4 \sin \lambda _i t ),\\ y(t) &{}=&{} y_{_T} +&{} e^{\lambda _r t} (B_1 \cos \lambda _i t + B_2 \sin \lambda _i t ) + e^{-\lambda _r t} (B_3 \cos \lambda _i t + B_4 \sin \lambda _i t ), \end{array} \end{aligned}$$

(6)

where $(x_{_T}, y_{_T})$ represents the position of the corresponding triangular point and $\lambda _r, \lambda _i$ are the real and imaginary parts of the eigenvalues of the variational matrix. An adequate election of the constants $A_i, B_i$ allows to have an orbit belonging to either the stable or the unstable manifold (Szebehely 1967).

To find the heteroclinic orbits ${\mathcal {S}}$ (orbits that go from $L_5$ to $L_4$) and ${\mathcal {U}}$ (orbits going from $L_4$ to $L_5$), Gómez et al. (1988) develop a method based on the computation of the manifold by propagating from Eq. (6) the solution starting from a set of initial conditions (x(0), y(0)) that describe a circle with very small radius around the Lagrangian point. From the values of the solutions, when $y = 0$ we plot the curves $(x, {\dot{x}})$ for both the stable and the unstable manifold; the intersections of these curves with the Ox-axis give the cut of the heteroclinic orbit with the Ox-axis. Let us mention that all the obtained numerical values are approximate numbers, and we present them with six significant digits.

Fig. 3

Left: stable manifold, $W^s(L_4)$, for $\mu = 0.45$. Right: unstable manifold, $W^u(L_4)$, for $\mu = 0.45$. Axes $(x,{\dot{x}})$

Figure 3 (left and right) represents both manifolds for $\mu = 0.45$. The intersection of the stable manifold with the Ox-axis gives four points: ($x_1 = -\,1.91259,\, x_2 = -\,0.40554,\, x_3 = -\,0.27021, \, x_4 = 0.56291$), whereas the unstable manifold cuts the Ox-axis at only three points: ($x_1 = 0.37915,\, x_2 = 0.54127,\, x_3 = 1.89059$).

Henceforth, we will use the subscripts l, c, r to represent, respectively, the intervals $(-\infty , -\mu ), (-\mu , 1-\mu )$ and $(1-\mu , \infty )$ where the orbit cuts the Ox-axis, and the number in the superscript (if any) represents the order of appearance of the orbit (from left to right) when more than one heteroclinic orbit cuts the Ox-axis in the same interval. For instance, Fig. 4 shows the seven heteroclinic orbits: ${\mathcal {S}}_l, {\mathcal {S}}_c^1, {\mathcal {S}}_c^2, {\mathcal {S}}_r, {\mathcal {U}}_c^1, {\mathcal {U}}_c^2, {\mathcal {U}}_r$ the case $\mu = 0.5$.

Fig. 4

Left: Heteroclinic orbits ${\mathcal {S}}$, from $L_5$ to $L_4$, for $\mu = 0.45$. Right: heteroclinic orbits ${\mathcal {U}}$, from $L_4$ to $L_5$, for $\mu = 0.45$. Axes (x, y)

Gómez et al. (1988) only studied five cases: $\mu = 0.5,\,0.4,\, 0.3,\,0.2, \,0.1$. In the present paper, we present a more complete study by including in Table 1 six disjoint intervals of $\mu$, in the range (0.107992, 0.5], where the number of heteroclinic orbits changes from one interval to the next one.

Table 1 Evolution of heteroclinic orbits in terms of the parameter $\mu$

Let us describe what happens in those intervals of Table 1. For $\mu = 0.5$, the eight heteroclinic orbits coincide with those discovered by Strömgren (1933) and Hénon (1965) with names: I $({\mathcal {U}}_l)$, III $({\mathcal {U}}_c^1)$, IV $({\mathcal {U}}_c^2)$, V $({\mathcal {U}}_r)$, I’ $({\mathcal {S}}_r)$, III’ $({\mathcal {S}}_c^2)$, IV’ $({\mathcal {S}}_c^1)$, V’ $({\mathcal {S}}_l)$. When $\mu = 0.470111$, the orbit ${\mathcal {U}}_l$ disappears and we have four ${\mathcal {S}}$ orbits and three ${\mathcal {U}}$ orbits until $\mu = 0.380258$ in which (${\mathcal {S}}_c^1, {\mathcal {S}}_c^2$) becomes one and later on disappears. There are two ${\mathcal {S}}$ orbits in $0.380258> \mu > 0.107992$, and three ${\mathcal {U}}$ orbits in $0.470111> \mu > 0.345801$. For $0.345801> \mu > 0.107992$, the number of unstable heteroclinic orbits varies, successively, from three to two [see case $\mu =0.18$, Fig. 5, left], three (see case $\mu =0.15$, Fig. 5, middle) and four (see case $\mu =0.12$, Fig. 5, right) orbits.

Fig. 5

Unstable manifold, $W^u(L_4)$, for $\mu = 0.18$ (left), $\mu = 0.15$ (middle), and $\mu = 0.12$ (right). Axes $(x,{\dot{x}})$

Besides, we introduce other two intervals $I_7= (\mu _{_R}, 0.107992]$ and $I_8=[0.0, \mu _{_R} ]$. The intersection of the curves with the Ox-axis that represents the heteroclinic orbits shows inside the interval $I_7$ a diffusion phenomenon described by Gómez et al. (1988). This phenomenon corresponds to the existence of infinite 0-homoclinic non-degenerate and infinite 1-heteroclinic orbits (see Gómez et al. (1988) for a detailed explanation).

Finally, in $\mu \in I_8$ there is no heteroclinic orbit because the triangular Lagrange equilibria are stable.

2.4 Characteristic curves: topological characterization

Periodic orbits of autonomous Hamiltonian systems appear in families represented by a smooth one-parameter continuous curve, sometimes named characteristic curve, in the space of initial conditions of the parameters.

Each point of a characteristic curve represents an orbit that can be represented by the notation introduced in Sect. 2.2 based on the direction of rotation and the points surrounded by the orbit. The direction of rotation does not change throughout the orbits of a family; however, the surrounded points may vary. We can characterize a family of periodic orbits by indicating the common characterization of all the orbits of the family (as shown in Sect. 2) and the changes that take place at the end points of the characteristic curve. To indicate these changes at the ends of the curve, we write, after the characterization of the common part of the family, brackets with the following information:

• $[\;\;]$: all the orbits of the family have the same characterization.

• $[\; \rightarrow \ldots ]$: the orbits of the one end of the curve are the same as the common characterization, but those of the other end are different.

• $[\ldots \;\rightarrow \; \ldots ]$: Both the ends of the curve are different from the common characterization.

Fig. 6

Several orbits of three families (case $\mu =0.5$). Left: family h. Middle: family g. Right: family x. Axes (x, y)

For example, let us see the left plot of Fig. 6 that contains four orbits ${\mathcal {O}}_1, {\mathcal {O}}_2,{\mathcal {O}}_3, {\mathcal {O}}_4$ of the family h for the case $\mu = 0.5$ (see Fig. 7). We observe that all curves are retrograde and surround the point $P_1$, but if we go over the curve h, from right (${\mathcal {O}}_4$) to left (${\mathcal {O}}_1$) the orbits also surround, successively, the points $L_3, L_1, T$. According to the previous rules, the topological characterization of this family is

$$\begin{aligned} \varvec{{\mathcal {R}}(P_1)}[\,\rightarrow \,\{L_3L_1 T\}\,] \end{aligned}$$

where, in boldface, there is the common part, ${\mathcal {R}}(P_1)$, of all the curves. Inside the brackets, the arrow and the symbols $\{L_3L_1 T\}$ mean that the family begins with a ${\mathcal {R}}(P_1)$ orbit and ends with a ${\mathcal {R}}(L_3 P_1 L_1 T)$ orbit.

In the center plot of Fig. 6, four orbits ${\mathcal {O}}_1, {\mathcal {O}}_2,{\mathcal {O}}_3, {\mathcal {O}}_4$ of the family g for the case $\mu = 0.5$ are represented (see Fig. 7). All the curves of the family are direct and surround only the point $P_1$, then the family is represented by

$$\begin{aligned} \varvec{{\mathcal {D}}(P_1)}[\;\;] \end{aligned}$$

where the empty brackets represent a family in which all the curves surround the same points; in this case, only $P_1$.

2.5 Asymptotic points

According to Theorem 2 of Hénon (1965), for each pair of heteroclinic orbits, one of type ${\mathcal {S}}$ and the other of type ${\mathcal {U}}$, there exists a family of periodic orbits tending asymptotically to this pair of orbits. The end point of this family is named asymptotic point (some times it is also named spiral point). An asymptotic point is characterized by two coordinates $(x_a, C_a)$ where

• $x_a$ represents the value of the coordinate x where the heteroclinic orbit ${\mathcal {S}}$ cuts the Ox-axis.

• $C_a$ is the value of the Jacobi’s constant evaluated at the triangular point with zero velocity: $C_a(\mu ) = 2\, \Omega (1/2-\mu , \sqrt{3}/2) = 3 - \mu +\mu ^2$.

The family x of the case $\mu = 0.5$ (see Fig. 7) is an example of this kind of families. The right plot of Fig. 6 represents three orbits of this family. ${\mathcal {O}}_2$ represents an orbit in the middle of the curve x. Family x ends on the right with the orbit ${\mathcal {O}}_1$ formed by a pair ${\mathcal {S}}_c^1 {\mathcal {U}}_r$ and on the left with the orbit ${\mathcal {O}}_3$ formed by a pair ${\mathcal {S}}_c^2 {\mathcal {U}}_r$. The topological characterization of this family can be written as

$$\begin{aligned} \varvec{{\mathcal {R}}(L_1 P_2 L_2 T)}[\,{\mathcal {S}}_c^1\, {\mathcal {U}}_r\,\longleftrightarrow \,{\mathcal {S}}_c^2\, {\mathcal {U}}_r\,] \end{aligned}$$

where the common part of all the curves, ${\mathcal {R}}(L_1 P_2 L_2 T)$, is represented in boldface. Inside the brackets, the two different ends of the characteristic curve are represented. Figure 8 of the paper of Elipe et al. (2021) shows two more examples of this phenomenon for a different dynamical problem, namely the dipole segment.

Families that tend to an asymptotic point always surround the triangular equilibria T in its vicinity, regardless of whether the common orbits of the family surround T or not.

3 The Copenhagen problem, case $\mu = 1/2$

The case in which the masses of the primaries are equal, known as the Copenhagen case ($\mu = 0.5$), has been studied in detail in Strömgren (1933), Hénon (1965) and Papadakis (1996) and many others. In order to follow the evolution of the families of symmetric periodic orbits for any value of $\mu$, we shall start from this known case; hence, we show here a short review of the main results for $\mu =0.5$. There are 22 characteristic curves in Copenhagen problem (see Fig. 7). Using the notation of Strömgren and Hénon, the 22 families are named, respectively, as a, b, c, f, g, h, i, j, k, l, m, n, o, r, s, t, u, v, w, x, y and z.

Fig. 7

Families of symmetric periodic orbits in Copenhagen problem and zoom of the three encircled areas $Z_l, Z_c$ and $Z_r$. Each point on the plane (x, C) corresponds to a periodic orbit. Axes (x, C)

The characteristic curves are grouped into three classes (Palacios et al. 2019) because of the symmetry originated by the equality of masses:

• 1. first class families, in which all the orbits are symmetric with respect to both axes,

• 2. second class families, in which the orbit and its symmetric one belong to the same family and

• 3. third class families, for which the symmetric orbit of each orbit of the family does not belong to the family.

In particular, the transition from orbits to their symmetric ones in the second class families requires the existence of a double symmetric orbit in the family; then, each second class family intersects with a curve of the first class, and this produces the three intersections $j-k$, $n-c$ and $o-r$.

Table 2 Topological characterization of families of symmetric periodic orbits for $\mu = 0.5$

Table 2 presents all the characteristic curves of the Copenhagen problem with the region in which they appear and with their characterization. In what follows, we enumerate some of the main features of these families.

• Families i and g are formed by two disjoint curves. Then, we use the symbols (i, g) to represent the curve above and with superscript ($i', g'$) to represent the one below.

• Three of these families, a, b, c, begin at each collinear point $L_2, L_3$ and $L_1$, respectively, with retrograde Lyapunov orbits (${\mathcal {R}}(L_2), {\mathcal {R}}(L_3), {\mathcal {R}}(L_1)$) around these points.

• Families $h, f, i, i', g, g'$ begin with S-orbits, $h, i, i'$ surrounding $P_1$ and $f, g, g'$ surrounding $P_2$.

• Figure 7 presents four asymptotic points (${\mathcal {A}}_1, {\mathcal {A}}_2, {\mathcal {A}}_3, {\mathcal {A}}_4$) with a coordinate x equal to the value of the coordinate $x_a$ of the four orbits ${\mathcal {S}}_l, {\mathcal {S}}_c^1, {\mathcal {S}}_c^2, {\mathcal {S}}_r$. Each of these points is the end of four curves corresponding to the four orbits $\,{\mathcal {U}}_l, {\mathcal {U}}_c^1, {\mathcal {U}}_c^2, {\mathcal {U}}_r$. As it has been said in Sect. 2.5, each pair of heteroclinic orbits ${\mathcal {S}} \, {\mathcal {U}}$ corresponds to the end of a characteristic curve. In this case, we have four ${\mathcal {S}}$ orbits and four ${\mathcal {U}}$ orbits; hence, we have 16 curves, l, u, w, x, r, o, s, y, k, t, z, v, that end at an asymptotic point. The rows and columns of Table 3 show the two heteroclinic orbits toward which each of these curves tends (Hénon 1965).

Table 3 Curves ending to the asymptotic points for $\mu = 0.5$

4 Arbitrary mass parameter $\mu < 1/2$

Before starting describing the families evolution, and in order to better understand the meaning of the different subintervals of the mass parameter $\mu$, let us mention that the numbers we present are not exact numbers, but approximate ones with only two significant digits, at difference of Sect. 3, where the changes on the evolution of asymptotic points are given with six significant digits.

4.1 Family m

The family m persists, with the same topological characterization, for all values of $\mu \le 0.50$ (see Figs. 8, 12, 17, 18).

4.2 Symmetry breaking and cases with a value of $\mu$ close to 0.50

When $\mu \ne 0.50$, the symmetry due to the equality of masses of the primaries disappears and the classification of the families as of the first, second and third classes has no longer sense.

In the left part of Fig. 8, we show the characteristic curves for the case $\mu = 0.49$. These are similar to the case $\mu = 0.50$ except for the curves within the enclosed areas $Z_c$ and $Z_r$. This behavior holds for all values $\mu$ close to 0.50.

Fig. 8

Left: characteristic curves for $\mu = 0.49$. Right: zoom of the two encircled areas $Z_c, Z_r$. Axes (x, C)

For $\mu = 0.50$, the three intersections of families, $n-c$, $o-r$ and $j-k$, are a direct consequence of the symmetry of masses; hence, when $\mu \ne 0.50$, these curves do not cross each other. A zoom of the areas $Z_c$ and $Z_r$ is presented in the right part of Fig. 8. The new families ${\tilde{n}}, {\tilde{c}}, {\tilde{j}}, {\tilde{k}}$ have the same topological characterization as the old ones; however, ${\tilde{o}}, {\tilde{r}}$ change slightly with respect to the old ones: One of the two ends of each curve is interchanged with that of the other. The new topological characterization of these uncrossed families is

$$\begin{aligned} \begin{array}{ l l l l } \,{\tilde{r}}: &{} \varvec{{\mathcal {R}}(L_1 T)}[\,{\mathcal {S}}_c^1\, {\mathcal {U}}_c^2\,\longleftrightarrow \,{\mathcal {S}}_c^2\, {\mathcal {U}}_c^2\,], &{} \quad \,{\tilde{o}}: &{} \varvec{{\mathcal {R}}(L_1 T)}[\,{\mathcal {S}}_c^1\, {\mathcal {U}}_c^1\,\longleftrightarrow \,{\mathcal {S}}_c^2\, {\mathcal {U}}_c^1\,].\\ \end{array} \end{aligned}$$

4.3 Behavior near the disappearance of the heteroclinic orbit ${\mathcal {U}}_l$

When $\mu = 0.470111$ (see Table 1), the heteroclinic orbit ${\mathcal {U}}_l$ has disappeared and consequently the four families (u, y, s, k) cannot end at the asymptotic point. In particular, families u, y, s,  disappear and the ${\tilde{k}}$ family ends before reaching the asymptotic point and becomes: $\varvec{{\mathcal {D}}(P_1 L_1 P_2)}[\,\rightarrow \,\{T\}\,]$ (see Fig. 9).

Fig. 9

Families near the asymptotic point ${\mathcal {A}}_4$. Left: $\mu = 0.50$. Middle: $\mu = 0.48$. Left: $\mu = 0.46$. Axes (x, C)

Associated with the changes due to the disappearance of the heteroclinic orbit, we find modifications in the behavior of families close to the asymptotic point ${\mathcal {A}}_4$ that can be observed in Fig. 9.

Before $\mu = 0.470111$ orbit k tends to the asymptotic point ${\mathcal {A}}_4$ and $g', t$ are two disjoint families (Fig. 9, left).

Near $\mu = 0.470111$ (middle plot of Fig. 9), k splits into two separated families: ${\tilde{k}}$ and ${\tilde{k}}'$, that tend to ${\mathcal {A}}_4$. Simultaneously, family $g'$ merges with family t. This new family, that we name ${\tilde{g}}_t$, replaces t as the family ending at the asymptotic point. Its topological characterization is $\varvec{{\mathcal {D}}(P_2)}[\,\rightarrow \,{\mathcal {S}}_r\, {\mathcal {U}}_c^1\,]$.

Finally, ${\tilde{k}}'$ disappears and only ${\tilde{g}}_t$ and ${\tilde{k}}$ persist. Table 4 shows the curves ending to the asymptotic points and the pair of heteroclinic orbits in which their ends for the cases $\mu \in I_1$ (Table 4a) and $\mu \in I_2$ (Table 4b)

Table 4 Curves ending to the asymptotic points for $\mu \in I_1$ and $\mu \in I_2$

4.4 Disappearance of families ${\tilde{n}}$ and ${\tilde{\jmath }}$

Families ${\tilde{n}}$ and ${\tilde{\jmath }}$ keep getting shorter until they finally disappear for the values close to $\mu = 0.44$ and $\mu = 0.42$, respectively.

4.5 Evolution of the family i

For a value between $\mu = 0.42$ and $\mu = 0.41$, the curves i and $i'$ that were joined split into other two ${\tilde{\imath }}$ on the left and ${\tilde{\imath }}'$ on the right. Later, near $\mu = 0.30$, ${\tilde{\imath }}'$ becomes a closed curve, and eventually, for $\mu = 0.26$, ${\tilde{\imath }}'$ has disappeared while ${\tilde{\imath }}$ remains. Figure 10 shows the evolution of i.

Fig. 10

Evolution of the family i. Left: $\mu = 0.42$. Middle: $\mu = 0.41$. Left: $\mu = 0.30$. Axes (x, C)

One of the two ends of i is interchanged with another one of $i'$ to form the new families ${\tilde{\imath }}$ and ${\tilde{\imath }}'$. Their topological characterization is given by

$$\begin{aligned} \begin{array}{ l l l l } {\tilde{\imath }}:&{} \varvec{{\mathcal {D}}(P_1)}[\;\;],&{} \quad {\tilde{\imath }}':&{} \varvec{{\mathcal {D}}(P_1)}[\,\rightarrow \,\{T\}\,]. \\ \end{array} \end{aligned}$$

4.6 Disappearance of the family ${\tilde{k}}$

The family ${\tilde{k}}$ becomes a closed curve for $\mu \approx 0.37$, and it has disappeared when $\mu = 0.35$.

4.7 Evolution of the family w

When $\mu = 0.40$, the closed family w splits into two disjoint curves ${\tilde{w}}$ (above ) and ${\tilde{w}}'$ (below) that have only one end, each one, at the asymptotic point ${\mathcal {A}}_1$. Their topological characterization is

$$\begin{aligned} \begin{array}{ l l l l } {\tilde{w}}: &{} \varvec{{\mathcal {R}}(L_3 P_1 L_1 T)}[\,\rightarrow \, {\mathcal {S}}_l\, {\mathcal {U}}_c^1 \,], &{}\quad \quad {\tilde{w}}': &{} \varvec{{\mathcal {R}}(L_3 P_1 L_1 T)}[\,\rightarrow \, {\mathcal {S}}_l\, {\mathcal {U}}_c^2 \,]. \\ \end{array} \end{aligned}$$

4.8 Behavior near the disappearance of the heteroclinic orbits ${\mathcal {S}}_c^1, {\mathcal {S}}_c^2$

When $\mu = 0.380258$ (see Table 1), the heteroclinic orbits ${\mathcal {S}}_c^1, {\mathcal {S}}_c^2$ and, consequently, the two asymptotic points ${\mathcal {A}}_2$ and ${\mathcal {A}}_3$ of the central region $R_c$ disappear. Figure 11 shows the evolution of the curves ${\tilde{o}}, {\tilde{r}}, x$ near this value of $\mu$.

Fig. 11

Evolution of characteristic curves when the asymptotic points ${\mathcal {A}}_2, {\mathcal {A}}_3$ disappear. Axes (x, C)

In Fig. 11 (up-left), we see the three families ${\tilde{o}}, {\tilde{r}}, x$ for the value $\mu = 0.39$. As $\mu$ approaches the value $\mu = 0.380258$, the x curve closes and splits into two curves ${\tilde{x}}_c$ and ${\tilde{x}}'$ (up-middle of Fig. 11). ${\tilde{x}} _c$ is a closed curve while ${\tilde{x}}'$ becomes the family that tends to the two asymptotic points. After that, the same occurs with ${\tilde{r}}$ that joins and splits into ${\tilde{r}}_c$, closed curve, and ${\tilde{r}}'$ that tends to the points ${\mathcal {A}}_2, {\mathcal {A}}_3$. When $\mu = 0.380258$ ${\mathcal {A}}_2, {\mathcal {A}}_3$ disappear, then ${\tilde{o}}$ becomes ${\tilde{o}}_c$ (closed curve) and families ${\tilde{x}}'$, ${\tilde{r}}'$ no longer tend to asymptotic points (see up-right part of Fig. 11, and down-right of Fig. 11 that shows a zoom of families ${\tilde{o}}$ and ${\tilde{o}}_c$). Down-left and down-middle plots of Fig. 11 represent, respectively, the values $\mu = 0.37, \,0.36$ for which the curves ${\tilde{r}}', {\tilde{x}}', {\tilde{o}}_c, {\tilde{r}}_c, {\tilde{x}}_c$ successively have disappeared. For $\mu = 0.35$, these curves no longer exist. Table 5 (a) shows the families that end at asymptotic points for $\mu \in I_3$.

4.9 Cases $\mu \le 0.345801$

When $\mu = 0.345801$, the heteroclinic orbits ${\mathcal {U}}_c^1, {\mathcal {U}}_c^2$, of the central region, merge into only one orbit ${\mathcal {U}}_c$ and the curves ${\tilde{w}}', z$ disappear. From $0.345801> \mu > 0.170355$, only four curves end at the asymptotic points: two ${\tilde{w}}$ and l in the left region $R_l$ and two more ${\tilde{g}}_t$ and v in the right region (see the right part of Fig. 12; Table 5b).

4.10 Cases $0.34> \mu > 0.18$

From $\mu = 0.34$ until $\mu = 0.18$, there are no more changes. Only the families a, b, ${\tilde{c}}$, f, g, ${\tilde{g}}_t$, h, ${\tilde{\imath }}$, l, m, v, ${\tilde{w}}$ remain with small changes, previously mentioned, in the topological characterization of families with tilde. Figure 12 shows the characteristic curves for the case $\mu = 0.25$ and a zoom over the areas $Z_l, Z_r$.

Fig. 12

Families of symmetric periodic orbits in the $\mu = 0.25$ case and zoom of the two encircled areas. Axes (x, C)

For values of $\mu < 0.18$, many new families appear in three zones: The zone $Z_l$ that surrounds the asymptotic point on the left, the zone $Z_r$ that surrounds the asymptotic point on the right and the zone around the collinear equilibrium point $L_3$.

In general, due to the large number of new families that also appear very close one another, we only name some of them, although we will describe their evolution and topological characterization. To refer to them, we will use Greek alphabet that will be repeated for different families.

4.11 Families around the two asymptotic points ${\mathcal {A}}_1, {\mathcal {A}}_4$ for $\mu \in I_5 \cup I_6$

To understand the evolution of curves in those intervals, we choose three values of $\mu$: two values $\mu = 0.17, \, 0.13 \in I_5$ and another value $\mu = 0.12 \in I_6$.

Figures 13 and 14 represent, respectively, the zones $Z_l$ and $Z_r$ for the values $\mu = 0.17$ (left), $\mu = 0.13$ (center) and $\mu = 0.12$ (right) where the number of unstable manifolds is, respectively, 3 (cases $\mu = 0.17, \, 0.13$) and 4 (case $\mu = 0.12$). To observe the evolution on each of these areas, we will compare Figs. 13 and 14 with the right part of Fig. 12.

Fig. 13

Families around $Z_l$ for cases $\mu = 0.17$ (left), $\mu = 0.13$ (middle) and $\mu = 0.12$ (right). Axes (x, C)

Let us have a look at the $Z_l$ zone (Fig. 13). For $\mu = 0.17$, we find the families $l, {\tilde{w}}$ that end at the asymptotic point ${\mathcal {A}} _1$ as they already did for values greater than this value of $\mu$. In addition, a new family $\alpha$ appears, of type $\varvec{{\mathcal {R}}(L_3 P_1 L_1 P_2 L_2 T)}[\,\rightarrow \,{\mathcal {S}}_l \, {\mathcal {U}}_r ^ 2\,]$ that also ends at $\mathcal {A} _1$. Above these families, there is the family $\alpha '$, of type $\varvec{{\mathcal {R}}(L_3 P_1 L_1 P_2 L_2 T)}[\;\;]$.

In the case $\mu = 0.13$, we find that $\alpha$ joins $\alpha '$ and also there appears another new family $\beta$, of type $\varvec{{\mathcal {R}}(L_3 P_1 L_1 T) }[\;\;]$.

Finally, in the case $\mu = 0.12$, a new unstable manifold has appeared in the central zone, in such a way that the asymptotic point receives four families. For this value of $\mu$, the families l and $\alpha$ evolved forming two new families ${\tilde{l}}$ and ${\tilde{\alpha }}$, such that ${\tilde{l}}$ does not tend to the asymptotic point and becomes of type $\varvec{{\mathcal {R}}(L_3 P_1 L_1 P_2 L_2 T)}[\;\;]$, while the family ${\tilde{\alpha }}$ closes and tends to the asymptotic point at both ends, becoming of the type $\varvec{{\mathcal {R}}(L_3 P_1 L_1 P_2 L_2 T)}[\,{\mathcal {S}}_l \, {\mathcal {U}}_r ^ 1\,\longleftrightarrow \,{\mathcal {S}}_l \, {\mathcal {U}}_r^2\,]$. On the other hand, ${\tilde{w}}$ remains the same, while $\beta$, of type $\varvec{{\mathcal {R}}(L_3 P_1 L_1 T)}[\,\rightarrow \,{{\mathcal {S}}_l \, {\mathcal {U}}_c ^ 2}\,]$, now tends to the asymptotic point.

Fig. 14

Families around $Z_r$ for cases $\mu = 0.17$ (left), $\mu = 0.13$ (middle) and $\mu = 0.12$ (right). Axes (x, C)

The zone $Z_r$ can be seen in Fig. 14. For $\mu = 0.17$, we observe three families v and ${\tilde{g}}_t$ and $v'$ that tend to the asymptotic point ${\mathcal {A}} _4$. Curves v and ${\tilde{g}}_t$ already existed for values greater than $\mu$, while $v'$, of type $\varvec{{\mathcal {R}}(L_2 T)}[\,\rightarrow \,{{\mathcal {S}}_r \, {\mathcal {U}}_r^2}\,]$, appears in the interval $I_5$. In addition, the family $\beta$ of the type $\varvec{{\mathcal {R}}(L_2 T)}[\;\;]$, that appeared for a value $\mu >0.17$, is broken into two ones $\beta _1$ and $\beta '$ belonging to the same type $\varvec{{\mathcal {R}}(L_2 T)}[\;\;]$.

When $\mu$ decreases, families $v, \beta '$ and $v'$ (Fig. 14, left) evolve in such a way that on the one hand, families v and $\beta '$ regroup and, on the other hand, also do families $v'$ and $\beta '$, and all together form a new closed family ${\tilde{v}}$ of type $\varvec{ {\mathcal {R}}(L_2 T)}[\,{\mathcal {S}}_r \, {\mathcal {U}}_r ^ 1\,\longleftrightarrow \,{\mathcal {S}}_r \, {\mathcal {U}}_r^2\,]$ that we can see in the center plot of Fig. 14 for the case $\mu = 0.13$. For this value, $\mu =0.13$, the ${\tilde{g}}_t$ family remains, and there appear three new families: $\beta _2$ of the same type of $\beta _1$; $\delta$ of the type $\varvec{{\mathcal {D}}(P_1 L_1 P_2)}[\;\;]$; and $\gamma$ of type $\varvec{{\mathcal {D}}(P_2 T)}[\;\;]$.

Finally, for $\mu = 0.12$, besides all the families of the case $\mu = 0.13$, there is a new family ${\tilde{\gamma }}$, of the type $\varvec{{\mathcal {D}}(P_2 T)}[\,{\mathcal {S}}_r \, {\mathcal {U}}_c ^ 2\,\longleftrightarrow \,$ ] which for smaller values than $\mu$ will be joined with $\gamma '$.

Table 5 Curves ending at the asymptotic points for $\mu \in I_3$, $\mu \in I_4$, $\mu \in I_5$ and $\mu \in I_6$

Table 5 shows the curves ending at the asymptotic points and the pair of heteroclinic orbits ending at them for the cases $\mu \in I_5$ (Table 5c) and $\mu \in I_6$ (Table 5d).

4.12 Region $R_l$ for cases $\mu < 0.1$

Let us now study the behavior of the characteristic curves in the region $R_l$ for values of $\mu <0.1$. To do that, let us look at the top part of Fig. 15 where this region $R_l$ is shown for the values of $\mu = 0.08$ (left), $\mu = 0.05$ (center) and $\mu = 0.03$ (right). We will pay special attention to the family ${\tilde{l}}$ and to the zones near the asymptotic point and the Lagrange point $L_3$.

Fig. 15

Top: region $R_l$ for $\mu = 0.08,\ 0.05$ and 0.03. Bottom: zoom of the two encircled areas $Z_l^1$ and $Z_l^2$. Axes (x, C)

Recall that family ${\tilde{l}}$ is of the type $\varvec{{\mathcal {R}}(L_3 P_1 L_1 P_2 L_2 T)}[\;\;]$. Observing Fig. 15, we see that for $\mu = 0.08$ and $\mu = 0.05$ a family ${\tilde{l}}_2$ has appeared, close to $L_3$, and which is also of the type $\varvec{{\mathcal {R}}(L_3 P_1 L_1 P_2 L_2 T)}[\;\;]$. As $\mu$ decreases, both families get closer together until finally they join and split again into other two new families ${\tilde{l}}$ and ${\tilde{l}}'$ of the type

$$\begin{aligned} \begin{array}{ l l | l l } {\tilde{l}}: &{} \varvec{{\mathcal {R}}(L_3 P_1 L_1 P_2 L_2 T)}[\;\;] \quad &{} \quad {\tilde{l}}': &{} \varvec{{\mathcal {R}}(L_3 P_1 L_1 P_2 L_2 T)}[\;\;] \\ \end{array} \end{aligned}$$

On the other hand, the areas around the asymptotic point and the Lagrange point are filled with several families very close to each other of type $\varvec{{\mathcal {R}}(L_3 P_1 L_1T)}[\;\;]$, until horseshoe orbits families, $\varvec{{\mathcal {R}}(L_3 T)}[\;\;]$, finally appear.

4.13 Horseshoe orbits

Horseshoe orbits have previously been defined as those that surround only the triangular points $L_4 L_5$ and the collinear one $L_3$, i.e., ${\mathcal {R}}(L_3 T), {\mathcal {D}}(L_3 T)$. The first horseshoe orbits were discovered in the Copenhagen problem (Brown 1911). All orbits in the family u are horseshoe orbits; however, this family only exists for values $0.50 \ge \mu > 0.47$. Furthermore, a few orbits of the family b, the farthest from point $L_3$, are also horseshoe orbits. These horseshoe orbits of b persist for any value of the parameter $\mu$. The main characteristic of these horseshoe orbits is that they cross the Ox-axis far away from the point $L_3$ and very close to the primary $P_1$. The left plot of Fig. 16 shows an example of this kind of orbits.

Fig. 16

Three horseshoe orbits for $\mu = 0.50$ (left), $\mu = 0.08$ (center) and $\mu = 0.03$ (right). Axes (x, y)

We do not find more horseshoe orbits until the small value $\mu = 0.08$. For this value, inside the interval $I_7$, a first family of horseshoe orbits has appeared near the asymptotic point where the diffusion phenomena described previously occur. On the left part of Fig. 15, the zone near the asymptotic point where the first family of horseshoe orbits appears for $\mu = 0.08$ is shown. Above is the general area and below a zoom of the area $Z_l^1$ where the family appears in red. In the center graphic of Fig. 16, we plot one of the orbits of this family. For $\mu < 0.08$, more and more families of this kind appear in this zone.

Let us now look at the right part of Fig. 16 obtained for $\mu = 0.03$. From this value of $\mu$, a new family of horseshoe orbits has appeared very close to the $L_3$ point. This family can be seen in red at the bottom right of Fig. 15. On the right of Fig. 16, we plot one of the orbits of this family.

The main characteristic of these horseshoe orbits for small values of $\mu$ is that their cuts with the Ox-axis are much closer to the point $L_3$ and away from the primary $P_1$. This is precisely one of the conditions indicated in Barrabés and Mikkola (2005) to define a horseshoe orbit.

5 The Earth–Moon and Sun–Jupiter systems

In the previous section, we have analyzed the evolution of the characteristic curves up to the value $\mu \approx 0.02$. However, the most interesting cases from the point of view of celestial mechanics correspond to smaller values. In this context, let us mention the recent work of Restrepo and Russell (2018) that provides a broad database of planar symmetric periodic orbits for many samples of the solar system and the work of Kotoulas and Voyatzis (2020) for families or retrograde periodic orbits of asteroids at some resonances in the Sun–Jupiter system.

In particular, we will present here (Figs. 17, 18) the characteristic curves for the Earth–Moon system ($\mu =0.01215$) and for the Sun–Jupiter system ($\mu = 0.00095359$).

Fig. 17

Characteristic curves for the Earth–Moon system ($\mu =0.01215$). Top: the complete phase space. Bottom: zoom of three zones $Z_l^1, \ Z_l^2$ and $Z_r$. Axes (x, C)

Fig. 18

Characteristic curves for the Sun–Jupiter system ($\mu = 0.00095359$). Top-left: the complete phase space. Top-right and bottom: zoom of different zones. Axes (x, C)

Observing these and other cases with $\mu < 0.02$, we can conclude that the following families persist:

• Families $b, h, m, {\tilde{l}}$ and ${\tilde{l}}'$ in $R_l$

• Families c, f and ${\tilde{\imath }}$ in $R_c$

• Families a, g and ${\tilde{g}}_t$ in $R_r$

In Table 6, we present the topological characterization of these families. All families present the same topological characterization as for values greater of $\mu$ except ${\tilde{g}}_t$ that no longer tends to the asymptotic point because this point does not exist. The family a no longer surrounds the triangular points in their last orbits (the ones closest to the primary $P_2$).

Apart from the previous families, as the value of $\mu$ decreases an increasing number of families of four different types appear. These families appear in small areas of the phase space where it has been necessary to zoom in to better observe them.

In the Earth–Moon case, we observe (Fig. 17) three areas where these new families accumulate: first, the zone $Z_l^1$ around where the asymptotic point previously appeared; second, the zone $Z_l^2$ near the point $L_3$; and finally, the zone $Z_r$ near the point $L_2$.

In the Sun–Jupiter case, we observe (Fig. 18) four areas where these new families accumulate: the zone $Z_l^3$, inside $Z_l^1$, around where the asymptotic point previously appeared; the zone $Z_l^2$ near the point $L_3$; the zone $Z_c$ near the point $L_1$; and finally the zone $Z_r$ near the point $L_2$.

We represent with four different colors the kind of orbits of the different families. The characteristics of these families are summarized as follows:

• Red curves, in $Z_l^1$ and $Z_l^2$ in the Lunar case and in $Z_l^2$ and $Z_l^3$ in the Jupiter case, are families of horseshoe orbits ($\varvec{{\mathcal {R}}(L_3 T)}[\;\;]$). It can be seen that as $\mu$ decreases, there appear horseshoe orbits whose points of intersection with the Ox-axis get closer and closer to the $L_3$ point.

• Blue families, in $Z_l^1$ and $Z_l^2$ in the Lunar case and in $Z_l^2$ and $Z_l^3$ in the Jupiter case, are of the type $\varvec{{\mathcal {R}}(L_3 P_1 L_1 T)}[\;\;]$ and always appear between families in red (type horseshoe $\varvec{{\mathcal {R}}(L_3 T)}[\;\;]$) and families in black (of type $\varvec{{\mathcal {R}}(L_3 P_1 L_1 P_2 L_2 T)}[\;\;]$).

• Green families, in zone $Z_r$ in both cases, are families of the type $\varvec{{\mathcal {D}}(P_1 L_1 P_2)}[\;\;]$.

• Brown families, in zone $Z_c$ in the Jupiter case, are of the type $\varvec{{\mathcal {D}}(P_1)}[\;\;]$. There is also a family of this type in the region $Z_c$ of the Lunar case, between families ${\tilde{\imath }}$ and c.

An example of each type of orbits, for both Lunar and Jupiter cases, is presented in Fig. 19.

Table 6 Topological characterization of the old families $a, b, c, f, g, {\tilde{g}}_t, h, {\tilde{\imath }}, {\tilde{l}}$ and ${\tilde{l}}'$

Fig. 19

Four different kinds of orbits for the Lunar case (up) and Jupiter case (down). Each orbit has the same color as the family of Figs. 17 and  18 to which they belong. Axes (x, y)

6 Conclusions

We present a complete classification of families of symmetric periodic orbits in the restricted circular three-body problem in an analogous way to the one made by Strömgren for equal masses of the primaries (the so-called Copenhagen problem). It has been necessary to introduce a topological classification of the families taking into account the direct or retrograde character, their stability, the number or primaries they encircle. Special emphasis is made on asymptotic orbits.

This topological classification reveals to be very useful, because it allows to have a complete characterization of the families and the determination of some intervals in the domain $\mu \in (0,1/2]$ with the type of families existing on each of these intervals. In our opinion, we extend and complete the seminal work of Strömgren.