A frequency portrait of Low Earth Orbits

Abstract

In this work, we deepen and complement the analysis on the dynamics of Low Earth Orbits (LEO), carried out by the authors within the H2020 ReDSHIFT project, by characterising the evolution of the eccentricity of a large set of orbits in terms of the main frequency components. Decomposing the quasi-periodic time series of eccentricity of a given orbit by means of a numerical computation of Fourier transform, we link each frequency signature to the dynamical perturbation which originated it in order to build a frequency chart of the LEO region. We analyse and compare the effects on the eccentricity due to Solar radiation pressure, lunisolar perturbations and high-degree zonal harmonics of the geopotential both in the time and frequency domains. In particular, we identify the frequency signatures due to the dynamical resonances found in LEO, and we discuss the opportunity to exploit the corresponding growth of eccentricity in order to outline decommissioning strategies.

1 Introduction

It is known that the proliferation of space debris in the Low Earth Orbit (LEO) region has already become a critical issue to handle. In this context, as part of the H2020 ReDSHIFT (Revolutionary Design of Spacecraft through Holistic Integration of Future Technologies) project (Rossi 2017, 2018), a deep analysis to search for passive deorbiting solutions in LEO was carried out, by performing an accurate mapping of the phase space in order to identify stable and unstable regions. A detailed description of the results of the LEO cartography was presented by the authors in Alessi et al. (2018a), while in Alessi et al. (2018b), a general analysis on the role that resonances induced by Solar radiation pressure (SRP) can play in assisting the deorbiting was provided.

In general, the key idea investigated in those works was to identify the orbits and the associated mechanisms, where dynamical perturbations can induce a significant growth of the orbital eccentricity, in order to facilitate passive disposal. Indeed, our numerical study showed that specific perturbations can induce periodical variations in eccentricity and inclination, which can potentially be exploited. Accordingly with our findings, we concluded that in the case of a typical intact object in LEO, with an area-to-mass ratio of the order of $A/m=10^{-2}\,\hbox {m}^{2}/\hbox {kg}$, perturbations such as SRP, lunisolar effects and high-degree zonal harmonics cannot ensure the re-entry on their own but only in combination with the atmospheric drag. If the spacecraft is, instead, equipped with an area augmentation device, which increases the effective A / m by, e.g. two orders of magnitude, then we concluded that SRP alone can drive the dynamics, if the initial inclination of the orbit is close enough to a resonant inclination, given semi-major axis and eccentricity. In particular, in Alessi et al. (2018b), we presented a simplified analysis of the role of the SRP resonances on the eccentricity evolution in LEO. In that work, we derived an analytical upper limit to the maximum eccentricity variation achievable for a given orbit under the SRP perturbation. This limit can be compared with the numerical findings of the propagations described in Alessi et al. (2018a).

In the present work, we make a deeper analysis of the role of the resonances which act in the LEO dynamics, by characterising the eccentricity of a set of orbits in terms of periodic components. Starting from the quasi-periodic time series of eccentricity, computed for a dense grid of initial conditions, we decompose the series in the main spectral components by means of a numerical computation of the Fourier transform. Then, we link each frequency component with the dynamical perturbation responsible for that signature. In this way, we have an additional tool to explore the relative importance of each given gravitational or non-gravitational perturbation in LEO as a function of the initial orbital elements. Indeed, the amplitude of the spectral signature induced by a perturbation on a given orbit gives an estimate of the associated eccentricity variation; this quantity can be compared with the numerical results, in the case that the dynamics is driven by SRP, with the analytical expression found in Alessi et al. (2018b), in order to give a comprehensive and more robust picture of the eccentricity evolution. The final goal of such analysis is to support the cartography in identifying the orbits where a significant growth of eccentricity, led by one or more perturbations, can assist the passive disposal of objects at their end of life. The same analysis can also serve to identify the periodic drifts that operational orbits could experience.

In the past, the study of the chaotic dynamics within the Solar system led (Laskar 1990) to devise a method for a numerical estimation of the size of the chaotic zones, based on the variation in time of the main frequencies of the system. Since then, the algorithm for the frequency analysis was developed to study the stability of the orbits in many multi-dimensional conservative systems, in order to provide a global representation of the dynamics (Laskar et al. 1992; Dumas and Laskar 1993). The frequency map analysis algorithm (numerical analysis of fundamental frequencies–NAFF) is based on a refined and iterative numerical search for a quasi-periodic Fourier approximation of the solution of the system over a finite time span (Laskar 1993). Considering, in particular, the issue of optimal design of artificial satellite survey missions around a non-axisymmetric body, (Noullez et al. 2015) proposed an alternative method with respect to the standard Fourier transform approach to characterise satellite orbits by computing the periodic components in order to identify regular orbits, meant as orbits whose inclination and eccentricity do not vary significantly over a given time scale. Concerning in particular the LEO region, (Celletti and Galeş 2018) studied the dynamics of resonances in LEO with the aim of identifying the location of equilibrium position and their stability. Within the common scope of defining suitable post-mission disposal orbits, they studied analytically, by means of a toy model, whether an object is located in a stable or chaotic region. In such a way, the identification of stable orbits in LEO suggests the detection of possible graveyard orbits. In this paper, we focus on the possibility of exploiting the eccentricity growth induced by one or more dynamical perturbations at given orbits to facilitate the end-of-life re-entry, and we deepen this analysis by characterising the eccentricity evolution in terms of its main frequency components. A comprehensive characterisation of the dynamical evolution of the eccentricity is a key ingredient in order to identify, among other things, possible disposal strategies for operational and future spacecraft.

The paper is organised as follows: in Sect. 2, we briefly describe the dynamical model adopted for the numerical propagation, and we introduce the method to identify the frequency signatures which characterise the eccentricity evolution of a set of LEO orbits. In Sect. 3, we outline the results of our analysis, comparing the results of numerical propagation in the time domain with the findings of the frequency characterisation. Finally, in Sect. 4, we draw some conclusions.

2 Dynamical model and methods

As mentioned before, within the scope of ReDSHIFT, we performed an extensive mapping of the LEO phase space by propagating more than 3 million orbits, as described in Alessi et al. (2017a, b, 2018a),¹ spanning from 500 to 3000 km of altitude over the Earth surface, considering a wide range of eccentricities, $e\in [0:0.28]$, and inclinations, from $0^{\circ }$ to $120^{\circ }$, 16 different $(\varOmega , \omega )$ configurations and two initial epochs. Two possible values of the area-to-mass ratio were considered: $A/m=0.012\,\hbox {m}^{2}/\hbox {kg}$, selected as a reference value for typical intact objects in LEO, and $A/m=1\,\hbox {m}^2/\hbox {kg}$, a representative value for a small satellite equipped with an area augmentation device, as a Solar sail (Colombo et al. 2017). The results of the cartography can be displayed in contour maps showing the lifetime or the maximum eccentricity over the propagation interval as a function of the initial inclination and eccentricity, for each initial semi-major axis. A large set of maps can be found on the ReDSHIFT website.² In the following sections, some examples will be provided. Throughout the text, we will limit our analysis to the case of right ascension of the ascending node, $\varOmega$, and argument of perigee, $\omega$, both equal to $0^{\circ }$, with the initial epoch set to 21 June 2020.

The orbital propagation to obtain the dynamical mapping was carried out over a time span of 120 years by means of the semi-analytical orbital propagator FOP (Fast Orbit Propagator, see Anselmo et al. 1996; Rossi et al. 2009 for details). In a nutshell, FOP applies a singly averaged formulation, by numerically integrating the Lagrange or the Gauss planetary equations applied to the gravitational and non-gravitational perturbations, which act on a body orbiting the Earth. The formulation is non-singular for circular orbits and singular for equatorial orbits. The disturbing potential or the equations of motion are averaged over the mean anomaly of the satellite and propagated using a multi-step, variable step-size and order integrator (Shampine and Gordon 1975).

The perturbations included in FOP are: geopotential harmonics up to degree and order 5; SRP, assuming the cannonball model and accounting for shadows; lunisolar perturbations; atmospheric drag below 1500 km of altitude, adapting the Jacchia–Roberts density model assuming an exospheric temperature of 1000 K and a variable Solar flux at 2800 MHz (obtained by means of a Fourier analysis of data corresponding to the interval 1961–1992). In particular, for the SRP and lunisolar perturbations, object of the analysis of this paper, the disturbing potentials considered in FOP are the following.

For SRP, we have

$$\begin{aligned} \mathcal {R}_{\mathrm{SRP}}=-c_\mathrm{S} \frac{A}{m}r\,\cos {S}, \end{aligned}$$

where $c_\mathrm{S}$ is a coefficient accounting for the Solar radiation pressure at the Earth distance and the reflectivity properties of the satellite, A and m represent the area and the mass of the satellite, respectively, r is the Earth–spacecraft distance and S is the planet-centred angle between the Sun and the spacecraft.

For Solar and Lunar gravitational perturbations, instead, the averaged potential is given by

$$\begin{aligned} \mathcal {R}_B= & {} \frac{\mu _B}{a_B}\sum _{n=2}^{n_{\mathrm{max}}} {\left( \frac{a}{a_B}\right) ^n} \sum _{m=0}^n K_{nm} \sum _{p=0}^n \mathcal {F}_{nmp}(i) \mathcal {H}_{npq}(e) \sum _{h=0}^n \mathcal {F}_{nmh}(i_B)\\&\times \sum _{j=-{j_{\mathrm{max}}}}^{j_{\mathrm{max}}} \mathcal {G}_{nhj}(e_B) \mathcal {S}_{nmqhj}, \end{aligned}$$

where the index B refers to the Sun or the Moon; $K_{nm}$ is a number depending on n and m; $q=2p-n$, because it is a singly averaged formulation; $\mathcal {F}_{nmp}$ and $\mathcal {F}_{nmh}$ are the Kaula inclination functions; $\mathcal {H}_{npq}$ and $\mathcal {G}_{nhj}$ are related to the Hansen coefficients; $\mathcal {S}_{nmqhj}$ depends on the argument of pericentre, right ascension of the ascending node and mean anomaly of the third body, and on the eccentricity, argument of pericentre and right ascension of the ascending node of the satellite. Note that $\mathcal {S}_{nmqhj}$ only depends on five indexes because it is written in a non-singular formulation; all the details can be found in Kwok (1986). For the computation in Alessi et al. (2018a), we assumed $n_{\mathrm{max}}=3$ and $j_{\mathrm{max}}=3$.

2.1 Dynamics in the time domain

We are particularly interested in studying the time evolution of the eccentricity. Indeed, within the search for passive disposal solutions in LEO, the identification of orbits which can experience a significant growth of eccentricity becomes crucial, since in this case the lowering of the orbital perigee helps drag in being effective. Moreover, a variation in eccentricity causes an altitude variation which could become an issue also at the operational stage, for instance in the case of a large constellation.

Lagrange planetary equations (e.g. Roy 1982) show that SRP, lunisolar perturbations and high-degree zonal harmonics³ cause long-term periodic variations in the evolution of eccentricity, when coupled with the oblateness effect, which become quasi-secular in the vicinity of a resonance involving the rate of the right ascension of the ascending node, $\varOmega$, and the argument of perigee, $\omega$. In particular, assuming that the instantaneous variation of the eccentricity for a given orbit is driven by a single perturbative effect, we can write the rate of e in the general form:

$$\begin{aligned} \frac{\mathrm{d}e}{\mathrm{d}t}=T(a,e,i)\,\sin \psi (\varOmega ,\omega ,\lambda _\mathrm{S})\,, \end{aligned}$$

(1)

where T is a coefficient which depends on (a, e, i) and on specific constants according to the given perturbation. The argument $\psi$ can be written in general terms as:

$$\begin{aligned} \psi =\alpha \varOmega +\beta \omega +\gamma \lambda _\mathrm{S}\,, \end{aligned}$$

(2)

where $\alpha ,\,\beta ,\,\gamma =0, \pm 1, \pm 2$ depending on the perturbation and $\lambda _\mathrm{S}$ is the longitude of the Sun with respect to the ecliptic plane, set as $\lambda _S=90.086^{\circ }$ at the starting epoch. A resonance occurs when the condition $\dot{\psi }\simeq 0$ is satisfied.

Table 1 List of the main resonances expected to be found in LEO: argument $\psi _j$, values of the coefficients $\alpha ,\,\beta ,\,\gamma$ and corresponding index j. Resonances from $j=1$ to $j=6$ are due to SRP; resonances 7 and 8 are singly averaged Solar gravitational resonances; resonances from 9 to 11 are doubly averaged lunisolar resonances

The list of the resonances expected from the examination of the disturbing function and found by means of the LEO cartography (Alessi et al. 2018a) are shown in Table 1, where the corresponding expression for $\psi$ and the value of $\alpha ,\,\beta ,\,\gamma$ are highlighted, together with an index ($j=1, \ldots ,11$) associated with each resonance. Resonances indexed from 1 to 6 correspond to the condition

$$\begin{aligned} \dot{\psi }=\bar{\alpha }\dot{\varOmega }\pm \dot{\omega }\pm \dot{\lambda }_S\simeq 0\,, \end{aligned}$$

(3)

with $\bar{\alpha }=0,1$, and are associated with the zero-order expansion of the SRP disturbing function (e.g. Hughes 1977; Krivov et al. 1996). Resonances 7 and 8 are singly averaged Solar gravitational resonances (e.g. Hughes 1980; Breiter 1999), i.e. they occur when the dynamics is averaged with respect to the mean anomaly of the satellite, while resonances from 9 to 11 are associated with doubly averaged lunisolar gravitational perturbations (e.g. Hughes 1980), i.e. they occur when the dynamics is averaged also with respect to the mean anomaly of the Sun or Moon (see, e.g. Roy 1982). The rate of $\varOmega$ and $\omega$ can be found by applying the Lagrange planetary equations and accounting in principle for both the effects of $J_2$ and SRP, while the effect of lunisolar perturbations can be neglected for the range of altitudes considered here (e.g. Milani et al. 1987). The explicit expressions have been given, for instance, in Alessi et al. (2018b). In practice, in Alessi et al. (2018b)-Eq. (5), we have shown that, for an initial orbit with $\varOmega =\omega =0^{\circ }$, at the assumed initial epoch (which corresponds to $\lambda _S\approx 90^{ \circ }$), the rate of $\varOmega$ and $\omega$ due to SRP vanishes, since they are both proportional to $\cos \psi _j$.

Fig. 1

Behaviour of $|\dot{\psi }|$ for each perturbing term $j=1, \ldots ,11$ as a function of the inclination, for $e=0.001$ and $a=7978,\hbox {km}$, in the case $A/m=1\,\hbox {m}^{2}/\hbox {kg}$

In Fig. 1, we display the behaviour of $|\dot{\psi }_j|$ for each perturbing term highlighted in Table 1 ($j=1, \ldots ,11$) as a function of the inclination $i\in [0^{\circ }:120^{\circ }]$ for the case of a quasi-circular orbit ($e=0.001$) with a semi-major axis $a=7978$ km. The location of the resonances on the $x-$axis is identified by the resonant condition $\dot{\psi }_j\,{\simeq }\,0$. The curves have been computed numerically with a tolerance of $10^{-8}$. The figure shows that curves associated with different perturbations may intersect and overlap within our sampling of the phase space, creating a dense network of resonances in the phase space. The location of different resonances may not exactly occur at the same inclination value, but they can be very close in some cases (e.g. in the vicinity of $i=40^{\circ }, 56^{\circ },110^{\circ }$). Thus, depending on the given inclination, it may be hard to distinguish between the concurrent effect of different perturbations and to link the dynamical effect to the perturbation which produces it. To overcome this problem, we can take advantage of the fact that the adopted orbital propagator is set up in such a way that each dynamical perturbation in the model can be individually turned on or off. Since we aim at identifying the specific effect of a given perturbation on the eccentricity evolution and at characterising it in the frequency domain, we consider two simplified models, which fit our purposes:

• model I: SRP on; lunisolar perturbations and drag off; geopotential: only $J_2$;

• model II: SRP off; lunisolar perturbations and drag on; geopotential: $5\times 5$.

Model I is particularly suitable to study the SRP effects on the eccentricity in the case of high A / m objects, when only SRP and drag play a primary role in the evolution. In the case of $A/m=1\,\hbox {m}^{2}/\hbox {kg}$, atmospheric drag is effective in driving a re-entry within 25 years for pericentre altitudes up to $1050\,$km (see Alessi et al. 2018a; Schettino et al. 2019). Since this is a relatively high value, in order to focus on the effect due to SRP, we have decided to switch off the perturbation due to the atmospheric drag.

Model II, instead, is appropriate to study the effects led by lunisolar perturbations and high-degree zonal harmonics: removing from the model the presence of SRP, we avoid the chance of mismodelling, since the resonant inclinations corresponding to lunisolar perturbations and geopotential can be close to those associated with SRP, as appears from Fig. 1. In this case, adopting the low or the high value of A / m does not affect the eccentricity evolution.

2.2 Frequency characterisation of the eccentricity

The starting point for the frequency characterisation is to process the discrete eccentricity time series of a given initial orbit to obtain the discrete Fourier transform through a standard fast Fourier transform (FFT) algorithm (e.g. Oppenheim and Schafer 2010). Given the eccentricity time series, $e(t_k)$, for a set of times $t_k$ from $t_1=1$ to $t_N=2^K$ with K integer,⁴ computed at time steps of $\Delta t=1$ day, the frequency interval $f_j$ is defined from $f_1=1$ up to $f_r=(\frac{t_N}{2}-1)\,\frac{f_S}{t_N}$, where $f_S=1/\Delta t$ is the sampling frequency. We define the discrete Fourier transform of $e(t_i)$, Fe, as

$$\begin{aligned} \mathrm{Fe}(f_j)=\frac{1}{2\pi t_N f_S}\,\sum _{k=1}^{t_N} e(t_k)\exp \left[ -i\frac{2\pi }{t_N}(j-1)(k-1)\right] \,. \end{aligned}$$

The computation is made by an FFT algorithm based on the standard Cooley–Tukey algorithm (Cooley and Tukey 1965). Our aim is, then, to identify the frequency and the amplitude of the main spectral features in the frequency series. The criterion we adopt is to account for any signature in the spectrum whose FFT value is, at least, 10 times stronger than the mean value over the whole spectrum: for each of these signatures, we record the corresponding spectral amplitude and frequency.

A first issue to be considered concerns the time sampling $\Delta t$ of the input series to be transformed. Indeed, from Nyquist theorem, it follows that $f_s/2$ is the highest frequency we can capture from our analysis. Since the perturbations we are interested in have periodicity of the order of months to years,⁵ the sampling $\Delta t=1\,$day, adopted in  Alessi et al. (2017a, b, 2018a), is fully reasonable. On the other side, a more critical issue involves the lowest detectable frequency by our analysis, which is limited by $2/t_N$. This means that with the adopted time span of 120 years, signatures with periodicity up to 60 years would be, in principle, identified. In practice, signatures due to perturbations with periodicity of more than some years are poorly sampled by definition. Thus, we propagate the set of orbits of interest for a longer time span, 600 years, in order to catch unambiguously signatures with periodicity of some tens of years, as expected in the vicinity of a resonance.

3 Analysis of the numerical results

The general results of the LEO dynamical mapping was already extensively described in Alessi et al. (2018a). In the following, we present the results obtained by assuming the two simplified dynamical models, described in Sect. 2.1. First, we consider the case of model I, i.e. we focus on the effect of SRP in the case of the augmented A / m ratio: we briefly recall the main findings in terms of time evolution of the eccentricity, and then we discuss the results of the characterisation in terms of frequency components. Next, we present the same analysis in the case of model II, focusing on the effects of lunisolar perturbations and high-degree zonal harmonics.

3.1 Model I

3.1.1 Analysis in the time domain

We recall that the model accounts, in this case, only for the effect of SRP and $J_2$, while drag and lunisolar perturbations are turned off. We propagate the orbits assuming $A/m=1\,\hbox {m}^2/\hbox {kg}$ and we look for the inclinations where a growth of eccentricity due to SRP occurs. Some illustrative results are shown in Fig. 2: on the left we show the maximum eccentricity achieved over 600 years of propagation as a function of the initial inclination and eccentricity, for initial $a=7978\,\hbox {km}$ (top) and $a=8578\,\hbox {km}$ (bottom), respectively. On the right panels, we display the corresponding lifetime, in years. We recall that the atmospheric drag is effective up to 1050 km of altitude for the adopted A / m ratio. Thus, we selected on purpose two reference values for the initial semi-major axis which are significantly above the region where drag plays a role. If the effect of SRP is able to lower the perigee below 1050 km, then the removal of the drag from the model allows to check if the chance to re-enter or not can be ascribed solely to SRP. In our analysis, we are interested in the extended LEO region, up to 3000 km of altitude, in order to include graveyard orbits. This fact motivates the choice of the semi-major axis $a=8578$ km as a representative one. Moreover, the detailed cartography carried out within the scope of ReDSHIFT helped us in the choice of the two representative values of semi-major axis for the following analysis: we do not expect to find further significant resonances to drive the dynamics in LEO other than the ones identified at these two altitudes.

Fig. 2

Maximum eccentricity (left column) and lifetime over 600 years (right column; in the color bar: in years) as a function of the initial inclination at steps of $\Delta i=0.5^{\circ }$ and e at steps of $\Delta e=0.001$, assuming model I and $A/m=1$ m$^2/$kg, for the initial orbits at $a=7978\,$km (top) and $a=8578\,$km (bottom), with $\varOmega =\omega =0^{\circ }$ and initial epoch 21 June 2020

The lifetime panels show that, in the case an area augmentation device is available on-board, even for high-altitude quasi-circular orbits, a re-entry driven by SRP alone is feasible for inclinations in the vicinity of $40^{\circ }$, which corresponds to the resonant condition:

$$\begin{aligned} \dot{\psi }_1=\dot{\varOmega }+\dot{\omega }-\dot{\lambda }_S\simeq 0\,. \end{aligned}$$

In the case of initial $a=7978\,\hbox {km}$, re-entry can be achieved in about 7 years for initial e ranging from 0.0001 to 0.009 thanks to SRP alone, for an initial orbit at $i=39.5^{\circ }$. In the case of initial $a=8578\,\hbox {km}$, SRP allows to re-enter within 10 years at initial $i=37.5^{\circ }$ and in about 16 years for $i=38^{\circ }$. The other resonances due to SRP, although not able to drive a re-entry, cause, anyway, a remarkable growth in eccentricity, as can be seen from the left panels of Fig. 2, which can be exploited to lower the perigee of the orbit. Referring also to Figure 1 in Alessi et al. (2018b), which shows the location of the 6 main SRP resonances as a function of i and a, we can identify the following resonances corresponding to the bright inclination “corridors”:

• $\dot{\psi }_1\simeq 0$ around $i=40^{\circ }$ (and $i=113^{\circ }$);

• $\dot{\psi }_2\simeq 0$ around $i=80^{\circ }$;

• $\dot{\psi }_3\simeq 0$ and $\dot{\psi }_5\simeq 0$ around $i=58^{\circ }$ and $i=54^{\circ }$, respectively, in the top panel ($a=7978$ km), while they intersect around $i=56^{\circ }$ at $a=8578$ km;

• $\dot{\psi }_4\simeq 0$ and $\dot{\psi }_6\simeq 0$, both occurring in the vicinity $i=70^{\circ }$.

Moreover, we can recognise other features at specific inclinations, appearing as fainter, but still visible, signatures. They can be associated with higher-order terms in the expansion of the SRP disturbing function (e.g. Hughes 1977): in Sect. 3.1.2, their identification will be assisted by the analysis in terms of frequencies.

For completeness, turning on the contribution due to the atmospheric drag in the model, we find that the synergic effect of SRP and drag can support re-entry also at different values of inclinations (resonances) but, typically, only over long time scales. This is shown in Fig. 3, in the case of an initial orbit at $a=7978$ km and $e=0.001$, assuming now model I with the further contribution of the drag. For the same initial orbit, Table 2 shows the lifetime associated with the initial inclination corresponding to the six SRP resonances. The table points out that the addition of the drag in the model can assist the re-entry at inclinations close to the resonant ones, but only in the case of resonance 2 (in addition to resonance 1) the re-entry can take place in less than 25 years.

Fig. 3

Lifetime (in the color bar: in years) as a function of the initial inclination at steps of $\Delta i=0.5^{\circ }$ and e at steps of $\Delta e=0.001$, assuming model I with atmospheric drag and $A/m=1\,\hbox {m}^{2}/\hbox {kg}$, for the initial orbit at $a=7978\,\hbox {km}$, with $\varOmega =\omega =0^{\circ }$ and initial epoch 21 June 2020

Table 2 Resonant inclination $i_{\mathrm{res}}$ and lifetime (in years) for each of the six main SRP resonances, in the case of initial $a=7978\,\hbox {km}$ and $e=0.001$, assuming model I with the addition of atmospheric drag

3.1.2 Analysis in the frequency domain

The analysis of the maximum eccentricity maps (Fig. 2-left panels) shows that, in addition to the six resonances due to the zero-order expansion of the SRP disturbing function, other fainter signatures can be observed at given inclinations. Thus, to build a complete picture of the eccentricity evolution in the LEO phase space, we need to include the first-order terms in the expansion of the SRP disturbing function (e.g. Hughes 1977), which are listed in Table 3.

Table 3 List of the first-order terms, expanding the SRP disturbing function up to first-order (e.g. Hughes 1977): argument $\psi _j$, values of the coefficients $\alpha ,\,\beta ,\,\gamma$ and corresponding index j

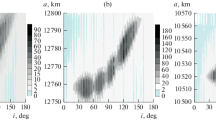
Following the procedure depicted in Sect. 2.2, we identified the main frequency signatures associated with the eccentricity, at each initial condition available. The frequency components detected at each inclination for the two illustrative cases of an initial orbit at $a=7978\,\hbox {km}$ and $a=8578\,\hbox {km}$ in the case of initial $e=0.001$, with $A/m=1\,\hbox {m}^2/\hbox {kg}$, are shown in Fig. 4. Each square in the plot represents a detected frequency component; the color bar refers to the relative amplitude of the frequency signature,⁶ intended as the corresponding intensity peak in the computed Fourier spectrum. Each coloured curve represents the behaviour of the argument $|\dot{\psi }_j |$ as a function of the inclination, with a cusp at the resonant inclination. As it can be seen, the detected signatures match almost exactly the theoretical curves. We also point out that the amplitude of the signatures gradually grows approaching a resonant inclination. In particular, the effects of SRP first-order terms at given inclinations, which could be only partially inferred from the maximum eccentricity maps, can be clearly identified in the frequency chart.

Fig. 4

Frequency signatures (filled squares) detected at each inclination for the initial orbit at $a=7978\,\hbox {km}$ (top) and $a=8578\,\hbox {km}$ (bottom), for initial $e=0.001$, with $A/m=1\,\hbox {m}^2/\hbox {kg}$. The $|\dot{\psi }_j|$ curves are those associated with SRP resonances, shown in Tables 1 and 3. The color bar refers to the relative amplitude of the frequency signature normalised to the maximum detected amplitude

The signatures detected by means of the frequency analysis match the bright corridors detected in the maximum eccentricity maps in the left of Fig. 2. In particular, resonances 3 and 5 (see Table 1), which intersect for $a=8578\,\hbox {km}$, can be individually identified for $a=7978\,\hbox {km}$ both in the contour map and in the frequency chart. Moreover, the frequency chart for $a=8578$ km shows a signature around $i=86^{\circ }$ corresponding to the first-order $\dot{\psi }_{17}$ term, which does not appear for $a=7978\,\hbox {km}$ neither in the contour map nor in the frequency chart. Finally, the $a=7978\,\hbox {km}$ chart shows a signature with singularity at $i=90^{\circ }$ which can be associated with the rate of $\varOmega$, appearing in the second-order expansion of the SRP disturbing function (see, e.g. Hughes 1977).

From the lifetime maps in the right panels of Fig. 2, we know that only in the case of resonance 1 SRP alone can drive a re-entry. Nevertheless, the maximum eccentricity maps show that in the vicinity of a resonance a certain growth of eccentricity occurs anyway. Thus, in the perspective of designing passive disposals and when dealing with operational issues, it is crucial to consider the timescale over which the eccentricity variation takes place. With this in mind, assessing the change in eccentricity led by a perturbation without performing the numerical propagation, i.e. by characterising the LEO phase space in terms of frequencies, represents a very powerful tool.

In Alessi et al. (2018b), we presented a simplified model including only the zero-order SRP resonances, namely ranked from $j=1$ to $j=6$. Assuming that the dynamics is driven by a single resonance, say j, the eccentricity variation was written as [all details can be found in Alessi et al. (2018b)]

$$\begin{aligned} \frac{\mathrm{d}e}{\mathrm{d}t} = -\frac{3}{2}\mathrm{PC}_R\frac{A}{m}\frac{\sqrt{1-e^2}}{na}\mathcal {T}_j\frac{\partial \cos \psi _j}{\partial \omega }\,, \end{aligned}$$

(4)

where $\mathcal {T}_j$ depends on the inclination of the orbit with respect to the equatorial plane. From the above expression, it turns out that the rate of e is proportional to $\sin \psi _j$; thus, by integrating Eq. (4) over time, we showed that the upper limit to the eccentricity variation over the propagation time interval is given by

$$\begin{aligned} \Delta e_j=\left| \frac{3}{2}\mathrm{PC}_R\frac{A}{m}\frac{\sqrt{1-e^2}}{na}\frac{\mathcal {T}_j}{\dot{\psi }_j} \right| = \left| \frac{T_j(a,e,i)}{\dot{\psi }_j}\right| \,. \end{aligned}$$

(5)

The validity of Eq. (5) has been discussed in Alessi et al. (2018b). We recall that in the present paper we are considering the special case where $\varOmega =\omega =0^{\circ }$ and $\lambda _S=90^{\circ }$. On the other side, the amplitude associated with each detected frequency signature in the Fourier transform gives an estimate of the eccentricity increment, as well. Both these values can be compared with the numerically computed maximum eccentricity over 600 years: the three estimates are expected to comply with each other.

A general comparison for the initial orbit at $a=7978\,\hbox {km}$ and $e=0.001$ is shown in Fig. 5: as a function of i, we show the theoretical amplitude $|T_j/\dot{\psi }_j|$ with $j=1, \ldots ,6$ for the six zero-order SRP resonances, the maximum variation in eccentricity, $\Delta e_{\mathrm{max}}$, achieved over the numerical propagation (red circles) and the amplitude of frequency signatures detected by our analysis (filled squares; the color bar refers to the corresponding periodicity, i.e. the inverse of the detected frequency). A similar example for an orbit at $a=8578\,\hbox {km}$ is shown in Schettino et al. (2017).

Fig. 5

Theoretical amplitude $|T_j/\dot{\psi }_j|$ with $j=1, \ldots ,6$ for the six zero-order SRP resonances (solid lines), maximum variation in eccentricity over propagation computed with FOP (red circles) and the frequency signatures detected by our analysis (filled squares; the color bar refers to the corresponding periodicity) as a function of the inclination, for the initial orbit at $a=7978\,\hbox {km}$ and $e=0.001$

The match is very good; moreover, we can observe that, as expected, the brighter squares, associated with signatures with longer periodicity, are found only in the vicinity of resonances.

Looking at the maximum variation in eccentricity achieved during propagation with FOP (red circles), some fainter features can be noticed at inclinations different from those corresponding to the six main resonances. Comparing the inclination of these signatures with the resonant inclinations corresponding to the arguments shown in Table 3, these fainter features can be associated with the first-order terms in the expansion of the SRP disturbing function.

Fig. 6

Comparison between theoretical amplitude $|T_j/\dot{\psi }_j|$ ($j=1$ on the top, $j=2$ on the bottom), maximum variation in eccentricity over propagation computed with FOP (left panels) and the frequency amplitudes detected by our analysis (right panels) as a function of the inclination, for the initial orbit at $a=7978$ km and $e=0.001$ in the case of model I

In Fig. 6, we show a detailed (i, e) zoom around the two main resonances found at this altitude: $\dot{\psi }_1$ corresponding to $i\sim 40^{\circ }$ and $\dot{\psi }_2$ in the vicinity of $i\sim 80^{\circ }$. The maximum eccentricity displayed on the y-axis corresponds to the eccentricity needed to lower the perigee down to 120 km, $e_{120{\text {km}}}=0.185$. Both the squares corresponding to the numerical maximum eccentricity (left panels) and the amplitude of the frequency signatures (right panels) lie on the theoretical curves for $|T_1/\dot{\psi }_1|$ and $|T_2/\dot{\psi }_2|$. This further confirms that the three quantities (theoretical amplitude, numerical maximum eccentricity and amplitude of the frequency signature) provide the same information, and thus one can be adopted in place of the other.

We can notice, however, in the bottom panel on the left of Fig. 6, a disagreement between the theory and the numerical propagation: according to the theory, the maximum eccentricity variation for initial $i=79^{\circ }$ should be sufficient to lead to re-enter, while the $\Delta e_{\mathrm{max}}$ computed with FOP turns out to be lower than $e_{120{\text {km}}}$. The explanation for such a behaviour is that during the propagation also the inclination experiences a variation which moves the object away from the resonance, making the SRP perturbation less effective. In Fig. 7, we show the evolution of e and i over 100 years for the initial condition $a=7978\,\hbox {km}$, $e=0.001$, $i=79^{\circ }$. Both eccentricity and inclination show a periodicity of about 28 years but they are out of phase: the eccentricity starts to grow led by the SRP perturbation; at the same time, the inclination starts to decrease so that when the eccentricity reaches the maximum value $e_{\mathrm{max}}=0.14$, the inclination is at its minimum, $i_{\mathrm{min}}=78.3^{\circ }$, where, as can be inferred from Fig. 6, the perturbation due to the resonant term $\psi _2$ is no longer effective in driving the re-entry.

Fig. 7

Eccentricity (top) and inclination (bottom) evolution over 100 years for initial condition $a=7978\,\hbox {km}$, $e=0.001$, $i=79^{\circ }$ in the case of model I. The inclination computed by propagation (blue line) is compared with the theoretical inclination (red circles) derived from Eq. (7)

This fact shows that the rate of i should be taken into account to provide a full description of this case based on the dynamics. It is beyond the scope of this work to provide a full description on this scenario based on the dynamical systems theory, but we can provide a basic tool to obtain an a priori indication on whether the orbit will exit from the resonance domain before achieving a re-entry.

In Fig. 7, in the panel showing the evolution of the inclination, it is also displayed the behaviour predicted by the theory developed in Daquin et al. (2016) for lunisolar gravitational resonances, which can be applied also in the case of SRP, as shown in Alessi et al. (2018b). In particular, it is demonstrated that there exists an integral of motion, corresponding to

$$\begin{aligned} (\beta \cos {i}-\alpha )\sqrt{\mu a(1-e^2)}=\text {constant}, \end{aligned}$$

(6)

where $\alpha , \beta$ are as defined in Eq. (2). In other words, assuming that the motion of the spacecraft is governed only by the Earth’s monopole, the Earth’s oblateness and the Solar radiation pressure, at any instant we can recover the inclination value from

$$\begin{aligned} i=\pm \arccos {\left( \frac{{\text {constant}}}{\beta \sqrt{\mu a(1-e^2)}}+\frac{\alpha }{\beta }\right) }, \end{aligned}$$

(7)

where the constant can be obtained by evaluating Eq. (6) at the initial epoch. For completeness, in Fig. 8, we show a comparison over 30 years of the eccentricity and inclination evolution computed by propagation assuming model I (blue curve) with the behaviour obtained by assuming the complete dynamical model (red curve), which includes all the perturbations provided by FOP. The initial orbit is the same as in Fig. 7. We can observe that the two models predict the same behaviour, except that, in the second case, the re-entry is ensured (in 13.6 years) by the atmospheric drag.

Fig. 8

Comparison of the eccentricity (left) and inclination (right) evolution over 30 years, computed by propagation assuming model I (blue curve) and including all the perturbations provided by FOP (red curve). The initial orbit is for both cases: $a=7978\,\hbox {km}$, $e=0.001$, $i=79^{\circ }$

In Fig. 9, we show the behaviour predicted for the inclination by Eq. (7), by assuming a maximum variation in eccentricity as in Eq. (5), for resonances 1 and 2. We can notice that in the first case, when we consider an initial inclination in the resonance domain, the variation is not relevant if compared with the curves in the top panel of Fig. 6). In the second case, the variation is instead important, of about $1^{\circ }$ and moves the dynamics towards the edges of the interval where the resonance is effective (compare with the curves in the bottom panel of Fig. 6).

Fig. 9

Predicted inclination variation as a function of the initial inclination, assuming model I, $a=7978\,\hbox {km}$, $e=0.001$. Left: resonance 1. Right: resonance 2

The above discussion showed that the assumption that $T_j$ is a function of the initial values of eccentricity and inclination may provide a misleading information. Figure 10 shows the evolution of $\Delta e_2=T_2(a,e,i)/|\dot{\psi }_2|$, according to Eq. (5), assuming the values of eccentricity and inclination computed at each given time by propagation with FOP, in case of model I, for initial $a=7978\,\hbox {km}$, $e=0.001$, $i=79^{\circ }$. The y-axis upper limit corresponds to a perigee altitude of 120 km. As it can be seen, for the initial value of e and i, the growth of eccentricity $\Delta e_2$ is such that the re-entry driven by resonance 2 is feasible (the curve is not visible in the figure because it is higher than the eccentricity required to re-entry). On the contrary, after only 5 years, the inclination has moved from its initial value (compare with Fig. 7) enough that the corresponding growth in eccentricity due to resonance 2 alone is no more capable to assure the re-entry.

Fig. 10

Evolution of $\Delta e_2=T_2/|\dot{\psi }_2|$ over 60 years, computed by means of Eq. (5) on the e and i values obtained by propagation with FOP in case of model I, for an initial $a=7978\,\hbox {km}$

Finally, similarly to Fig. 6, the comparison between theoretical amplitude, maximum variation in eccentricity computed with FOP and amplitude of the frequency signatures for $a=7978\,\hbox {km}$ and $e=0.001$ in the cases of resonances $3,\,4,\,5,\,6$ due to SRP is shown in Fig. 11. Also in these cases, the agreement is noticeable.

Fig. 11

Comparison between theoretical amplitude $|T_j/\dot{\psi }_j|$ ($j=3,4,5,6$), maximum variation in eccentricity over propagation computed with FOP (left panels) and the frequency amplitudes detected by our analysis (right panels) as a function of the inclination, for the initial orbit at $a=7978\,\hbox {km}$ and $e=0.001$ in case of model I

3.2 Model II

3.2.1 Analysis in the time domain

Model II is particularly suitable to study the perturbation on eccentricity due to lunisolar effects and high-degree terms in geopotential, since SRP has been removed in this case. The effective area-to-mass ratio of the object does not play a role in driving the dynamics, contrary to the case of the previous model, and thus we assume $A/m=0.012\,\hbox {m}^2/\hbox {kg}$ for simulations.

Fig. 12

Maximum eccentricity as a function of the initial inclination at steps of $\Delta i=0.5^{\circ }$ and e at steps of $\Delta e=0.001$, assuming model II and $A/m=0.012\,\hbox {m}^2/\hbox {kg}$, for the initial orbits at $a=7978\,\hbox {km}$ (left) and $a=8578\,\hbox {km}$ (right), with $\varOmega =\omega =0^{\circ }$ and initial epoch 21 June 2020

In analogy to the left panels of Fig. 2, Fig. 12 shows the maximum eccentricity as a function of the initial inclination and eccentricity for an orbit at $a=7978$km (left) and $a=8578\,\hbox {km}$ (right), respectively. In this case, we do not show the corresponding lifetime maps: at these altitudes and for quasi-circular orbits the maps would result blank since neither lunisolar perturbations nor high-degree terms of geopotential are capable to induce a growth of eccentricity such that the perigee is lowered down to altitudes where drag becomes effective. The synergic effect of drag and other perturbations can be possibly exploited at these altitudes only for initial eccentricities higher than 0.1.⁷ The most evident signatures in the maximum eccentricity maps are those at $i=63.4^{\circ },116.6^{\circ }$, also known as critical inclinations (e.g. Beutler 2005), which corresponds to the condition $\dot{\omega }=0$ (resonance 9 in Table 1).

Figure 13 depicts the time evolution of different orbits with initial $a=7978$ km, considering two different initial inclinations: $i=63.4^{\circ }$ (top), which corresponds exactly to the resonant inclination for the condition $\dot{\omega }=0$, and $i=63.5^{\circ }$ (bottom), i.e. only $0.1^{\circ }$ degrees next to the resonant value. The initial eccentricity varies from 0.001 to 0.15: on the left, we show the evolution of eccentricity over 200 years, in the middle, the pericentre altitude and on the right, the apocentre altitude. As it can be seen, the behaviour is different if the initial inclination corresponds exactly to the resonant value or not. Up to initial $e=0.1$, for both inclinations, the eccentricity does not experience a sufficient growth to lower the perigee in order to re-enter. Indeed, for the case of an initial quasi-circular orbit ($e=0.001$), at resonance the perigee lowers only by 70 km after 10 years and 177 km after 25 years, while for $i=63.5^{\circ }$ the decrease in the perigee is 58 km after 10 years and 115 km after 25 years.

At resonance, we can observe that the characteristic period of the eccentricity evolution is clearly longer than in the neighbourhood of the resonance. For example, for $i=63.4^{\circ }$ and $e=0.001$, the eccentricity shows a period of 137 years, while for $i=63.5^{\circ }$, it reduces to 76 years. For higher eccentricities, such as $e=0.13$ and $e=0.14$, at $i=63.4^{\circ }$ the initial growth of eccentricity induced by the perturbation lowers the perigee down to an altitude where atmospheric drag becomes effective. Conversely, for $i=63.5^{\circ }$ the apogee starts to lower, while the perigee is not low enough for drag to be effective in less than 200 years. Finally, for $e=0.15$ the perigee is low enough that re-entry is feasible at both initial inclinations thanks to the atmospheric drag.

Fig. 13

Time evolution of eccentricity (left), perigee altitude (middle) and apogee altitude (right) over 200 years of propagation with FOP, for initial $a=7978\,\hbox {km}$ and $i=63.4^{\circ }$ (top), $i=63.5^{\circ }$ (bottom), for 7 different initial eccentricities: $e=0.001,0.01,0.05,0.10,0.13,0.14,0.15$ in the case of model II, assuming as initial epoch 21 June 2020

Looking at Fig. 12, other fainter signatures at given inclinations can be recognised:

• at $i\simeq 40^{\circ }, 113^{\circ }$, in the $a=7978$ km panel, corresponding to the well-known evection resonance (e.g. Brouwer and Clemens 1961) $\dot{\psi }_8=2(\dot{\varOmega }+\dot{\omega }-\dot{\lambda }_S)\simeq 0$;

• at $i\simeq 56^{\circ }$, visible in the $a=8578$ km panel, corresponding to the condition $\dot{\psi }_{10}=\dot{\varOmega }+2\dot{\omega }\simeq 0$;

• at $i\simeq 70^{\circ }$, clearly recognisable at $a=8578$ km while distinguishable only for very low eccentricities at $a=7978$ km, which corresponds to the resonant condition $\dot{\varOmega }-2\dot{\omega }\simeq 0$, as will be discussed in Sect. 3.2.2.

3.2.2 Analysis in the frequency domain

The frequency components detected at each inclination for the initial orbits at $a=7978\,\hbox {km}$ and $a=8578\,\hbox {km}$, assuming initial $e=0.001$, with $A/m=0.012\,\hbox {m}^2/\hbox {kg}$ are shown in Fig. 14, where each frequency signature corresponds to a filled square and the color bar refers to the relative amplitude found in the Fourier spectrum.

Fig. 14

Frequency signatures (filled squares) detected at each inclination for the initial orbits at $a=7978$ km (top) and $a=8578\,\hbox {km}$ (bottom), assuming initial $e=0.001$, with $A/m=0.012\,\hbox {m}^2/\hbox {kg}$. The $|\dot{\psi }_j|$ curves are those associated with lunisolar resonances, shown in Tables 1 and 4. The color bar refers to the relative amplitude of the frequency signature normalised to the maximum detected amplitude

The solid curves in the figure represent the resonant arguments $\psi _j$, with $j=7, \ldots ,11$, associated with Solar gravitational and lunisolar perturbations, shown in Table 1; the dashed curves refer, instead, to fainter, but still detectable, signatures listed in Table 4. They correspond to the arguments $\psi _j$ with $j=18, \ldots ,20$ associated with singly averaged Solar gravitational resonances, and to the argument $\psi _{21}$ associated with doubly averaged lunisolar perturbations (Hughes 1980).

The main signature in both frequency charts is the one at $i=63.5^{\circ }$ associated with resonance 9, which corresponds also to the brightest corridor in the eccentricity contour maps of Fig. 12. Concerning resonance 8, around $i=40^{\circ }$, the contour maps showed that it is not expected to be relevant for $e=0.001$, while it becomes more important for more eccentric orbits. Indeed, it is only partially detectable in the $e=0.001$ frequency charts of Fig. 14, while its role becomes more evident in the frequency charts of Fig. 15, which correspond to the same initial orbits of Fig. 14 but with $e=0.01$. Comparing the frequency charts corresponding to the two values of eccentricity, we can notice also that resonances $7\,,8\,,11$ and the higher order resonances shown in Table 4 are only partially detectable in the $e=0.001$ frequency charts, while they are clearly recognisable for the $e=0.01$ ones. In particular, the signature due to the $\dot{\psi }_{21}$ term is clearly visible in the $a=8578$ km maximum eccentricity map of Fig. 12 as the bright corridor at $i=69^{\circ }$, and it appears also in the corresponding frequency chart.

Fig. 15

Frequency signatures (filled squares) detected at each inclination for the initial orbits at $a=7978\,\hbox {km}$ (top) and $a=8578\,\hbox {km}$ (bottom), assuming initial $e=0.01$ and $A/m=0.012\,\hbox {m}^2/\hbox {kg}$. The $|\dot{\psi }_j|$ curves are those associated with lunisolar resonances, shown in Tables 1 and 4. The color bar refers to the relative amplitude of the frequency signature normalised to the maximum detected amplitude

Table 4 List of the other detected resonances due to lunisolar perturbations (Hughes 1980): argument $\psi _j$, values of the coefficients $\alpha ,\,\beta ,\,\gamma$ and corresponding index j

Figure 12 showed that the growth of eccentricity that can be reached thanks to high-degree zonal harmonics and/or lunisolar perturbations, for the initial eccentricities considered, is, at most, one order of magnitude less than exploiting SRP in the case of an area augmentation device.

The most favourable case is found in proximity of resonance 9 ($\dot{\omega }\simeq 0$), where $\Delta e_{\mathrm{max}}\simeq 0.02$ can be achieved. As already noticed, the frequency analysis shown in Fig. 14 confirms this finding for both altitudes: the main signature appears at $i=63.5^{\circ }$, corresponding to the cusp of the $|\dot{\psi }_9|$ curve. Figure 16 compares the behaviour of the numerical maximum eccentricity over propagation (cyan squares) and the amplitude found through the frequency analysis (blue squares) around $i=63.5^{\circ }$ for an initial orbit with $a=7978$ km and $e=0.001$. As for the case of model I, there is a very good agreement between the two quantities. We can notice that the growth of eccentricity at $i=63.5^{\circ }$ is mainly due to the perturbing effect of $J_5$. Indeed, if we consider only a $3\times 3$ geopotential instead of $5\times 5$, the increment of eccentricity decreases from $\Delta e_{5\times 5}=0.017$ to $\Delta e_{3\times 3}=0.002$, while if only lunisolar perturbations and $2\times 2$ geopotential are included in the dynamical model, the eccentricity does not experience any variation at this inclination. These results are shown in Fig. 17, which displays the evolution of eccentricity for initial $a=7978$ km and $i=63.5^{\circ }$ for three different models, all including drag and lunisolar perturbations: (i) $5\times 5$ geopotential, (ii) $3\times 3$ geopotential, (iii) $2\times 2$ geopotential.

Fig. 16

Comparison between the maximum variation in eccentricity over propagation computed with FOP (cyan squares) and amplitude of the frequency signatures detected by our analysis (blue squares) in the case of resonance 9, for the initial orbit at $a=7978\,\hbox {km}$ and $e=0.001$

Although at high altitudes in LEO the growth of eccentricity induced by geopotential or lunisolar perturbations is not capable to drive the re-entry, the variation in e can be, anyway, not negligible. Indeed, the perigee and apogee of the orbit can experience an oscillation which should be taken into account if we are dealing with issues as the stability of an operational orbit. This happens, for example, in the considered case of initial $a=7978\,\hbox {km}$ and $e=0.001$ and assuming a $5\times 5$ geopotential as in model II-(i): the perigee undergoes a 76 years periodic evolution with a maximum oscillation of 130 km; after 10 years it experiences a variation of 55 km, while as much as 115 km after 25 years.

Fig. 17

Evolution of e for initial $a=7978$ km and $i=63.5^{\circ }$ for three different models, all including drag and lunisolar perturbations: (I) $5\times 5$ geopotential, (II) $3\times 3$ geopotential, (III) $2\times 2$ geopotential

4 Conclusions

In this paper we studied the evolution of the eccentricity of a large set of orbits both in the time and frequency domains, deepening the work already presented by the authors in Alessi et al. (2018a), Alessi et al. (2018b).

First, we considered the role of SRP in driving the dynamics for an object equipped with an area augmentation device. We found that, for quasi-circular orbits, SRP can be exploited, possibly in concurrence with the atmospheric drag, to lead the disposal within 25 years, but only if the initial orbital inclination is close enough to the resonant inclinations associated with the condition $\dot{\psi }=\dot{\varOmega }\pm \dot{\omega }-\dot{\lambda }_S\simeq 0$ (resonances 1 and 2). In the vicinity of the other zero-order resonances (indexed from 3 to 6), but also in correspondence of the first-order SRP resonances (indexed from 12 to 17), a growth of eccentricity due to SRP takes place in any case but over longer time scales, of the order of tens to hundreds of years. Although this variation of eccentricity cannot be exploited for disposal, it needs to be taken into account for operational purposes in the perspective of identifying long-term stable orbits within LEO. We also point out that, although we adopted a singly averaged dynamics for our analysis, it has been demonstrated that the same results hold in the case of non-averaged dynamics (Schaus et al. 2019).

Moreover, in Alessi et al. (2018b), we presented a simplified theory to analytically evaluate the growth of eccentricity induced by the six main SRP resonances. Here, we showed that the assumption to consider the variation of eccentricity only as a function of the initial (e, i) state could be coarse and that, for given initial orbits, also the role of the variation of inclination over time should be considered, to give a coherent picture of the dynamics.

Then, we focused on the role of lunisolar perturbations and high-degree zonal harmonics. In this case, the growth of eccentricity induced by the perturbations does not cause a lowering of the perigee leading to a re-entry, in the case of quasi-circular orbits. In particular, we analysed the case of the well-known critical inclination, corresponding to the resonant condition $\dot{\omega }\simeq 0$, for an initial quasi-circular orbit at $a=7978$ km. We verified that the computed growth of eccentricity of about two orders of magnitude after 40 years is mainly due to the $J_5$ perturbation, confirming the results found in Alessi et al. (2018a).

Lastly, we point out that a detailed analysis of the libration regions is beyond the scope of this paper. Rather, the analysis performed here is the basis to develop the analytical model on equilibrium points and corresponding stability, associated with the detected frequencies (see, e.g. Alessi et al. 2019).