Abstract
We investigate the evolution of the early-morning boundary layer in a low-mountain valley in south-western Germany during COPS (convective and orographically induced precipitation study) in summer 2007. The term low-mountain refers to a mountainous region with a relief of gentle slopes and with an absolute altitude that remains under a specified height (usually 1,500 m a.s.l.). A subset of 23 fair weather days from the campaign was selected to study the transition of the boundary-layer flow in the early morning. The typical valley atmosphere in the morning hours was characterized by a stable temperature stratification and a pronounced valley wind system. During the reversal period—called the low wind period—of the valley wind system (duration of 1–2 h), the horizontal flow was very weak and the conditions for free convection were fulfilled close to the ground. Ground-based sodar observations of the vertical wind show enhanced values of upward motion, and the corresponding statistical properties differ from those observed under windless convective conditions over flat terrain. Large-eddy simulations of the boundary-layer transition in the valley were conducted, and statistical properties of the simulated flow agree with the observed quantities. Spatially coherent turbulence structures are present in the temporal as well as in the ensemble mean analysis. Thus, the complex orography induces coherent convective structures at predictable, specific locations during the early-morning low wind situations. These coherent updrafts, found in both the sodar observations and the simulation, lead to a flux counter to the gradient of the stably stratified valley atmosphere and reach up to the heights of the surrounding ridges. Furthermore, the energy balance in the surface layer during the low wind periods is closed. However, it becomes unclosed after the onset of the valley wind. The partition into the sensible and the latent heat fluxes indicates that missing flux components of sensible heat are the main reason for the unclosed energy balance in the considered situations. This result supports previously published investigations on the energy balance closure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Turbulent fluxes of heat, moisture, and momentum in the atmospheric boundary layer are of key importance both for the evolution of the boundary layer itself and for the overlying free atmosphere. The accurate knowledge of the magnitude and the vertical profiles of these fluxes and their reliable parametrization are essential for both numerical weather prediction and climate simulations. Sophisticated micrometeorological instrumentation and analysis techniques have successfully been applied in order to determine fluxes over flat and homogeneous terrain.
However, the determination of these fluxes above complex terrain, i.e. mountainous and/or with heterogeneity in land use, remains a challenging task (Foken 2008; Mahrt 2010). The boundary layer in complex terrain is characterized by orographically (Defant 1949; Whiteman 1990, 2000; Zardi and Whiteman 2013) or thermally induced (Segal and Arritt 1992) wind systems. In a convective boundary layer over flat surfaces quasi-stationary turbulence structures evolve (Schmidt and Schumann 1989). Over heterogeneous surfaces (Walko et al. 1992; Dörnbrack and Schumann 1993) coherent structures with surface-scale dependent length scales develop, especially in the lower part of the boundary layer. These flow structures can potentially modify the turbulent fluxes from valleys, thus potentially modifying the evolution of the mountainous boundary layer as a whole. Weigel et al. (2007) and Rotach et al. (2008) investigated the exchange processes in an alpine valley and found strong dependencies of the turbulent fluxes on orography and stratification in the mountainous boundary layer. Mayer et al. (2008) investigated an observed anomaly in the chemical composition of air at a mountain station. This anomaly was traced back to fluxes through the stably stratified valley atmosphere during the reversal of the thermally driven wind system in the morning.
Over homogeneous terrain a strong influence of coherent turbulent structures, i.e. persistent quasi-stationary patterns of turbulent motion, on the turbulent fluxes was shown in several studies (Raasch and Harbusch 2001; Kanda et al. 2004; Inagaki et al. 2006). In particular, the interpretation of micrometeorological measurements in complex terrain requires the comprehensive knowledge of how turbulence is organized at the observational site and its surroundings. This leads to the guiding questions for this study: (i) How does the convective boundary layer in a typical low-mountain valley become organized in the early morning hours after sunrise? (ii) How does an along-valley flow in the morning change the convective structures? (iii) To what extent is the vertical transport in the valley affected? (iv) How are micrometeorological flux measurements at a specific location affected by complex terrain? To address these questions, large-eddy simulations (LES) were conducted, and compared to observations.
A micrometeorological dataset obtained during the field phase of the convective and orographically induced precipitation study (COPS) constitutes the basis of this study (see Eigenmann et al. 2009). The field campaign of summer 2007 in the low-mountain region of south-western Germany and eastern France, i.e. Black Forest and Vosges mountains, is well described in the literature (e.g. Wulfmeyer et al. 2011). The valley in which the observational site is located has a width of approximately 1,300 m and a depth of approximately 300 m, which are typical values for a low-mountain terrain. The objective of the campaign is to understand the influence of the orography of a low-mountain range on precipitation. Several surface flux measurement stations were installed throughout the respective region during the campaign (Eigenmann et al. 2011; Kalthoff et al. 2011). In addition, ground-based sodarFootnote 1/RASSFootnote 2 instruments were installed at several of these stations. Our study uses data from one of these sites where a full energy balance station and a sodar/RASS operated simultaneously. The site Fußbach is located in the Kinzig valley, which is a typical low-mountain valley of the region with a pronounced valley wind system developing on fair weather days in summer.
In micrometeorological field experiments the energy balance is often not closed (e.g. Oncley et al. 2007; Foken et al. 2010). Although many uncertainties are connected with the determination of the components of the energy balance (Mahrt 2010), strong indications exist that the residual occurs due to transport by large-scale eddies or secondary circulations that are not captured by the eddy-covariance method (e.g. Mauder and Foken 2006; Foken 2008; Foken et al. 2010, 2011, Stoy et al. 2013). As these secondary circulations are mainly associated with the sensible heat flux (Foken et al. 2012b), the common approach of distributing the residual according to the Bowen ratio Twine et al. (2000) seems not to be appropriate. However, because the density effect of moisture cannot be excluded, a distribution of the residual according to the buoyancy flux ratio appears to be appropriate. The relative contributions of the sensible and latent heat fluxes to the buoyancy flux are described in Kaimal and Gaynor (1991). Also the COPS energy balance site Fußbach used herein shows an average residual of 21 % during the entire field campaign (see Eigenmann et al. 2011).
The remainder of this article is organized as follows. Sect. 2 describes the data and the methods applied, in particular the numerical model and its set-up. Sect. 3 presents the results and the discussion of them, while conclusions are given in Sect. 4.
2 Methods and Data
2.1 Observational Data
The observations used herein were obtained during the COPS experiment in the low-mountain terrain of the Kinzig valley. Turbulence data were measured at a height of 2 m above the valley surface and friction velocity \(u_{*}\), sensible heat \(Q_{H}\) and latent heat \(Q_{E}\) were calculated with the eddy-covariance method (EC) (Foken et al. 2012), using an averaging time of 30 min. Contributions to the fluxes with a time scale exceeding these 30 min cannot be captured. The geographical location of the site Fußbach is 48\(^\circ \)22\('\)7.8\(''\)N, 8\(^\circ \)1\('\)21.2\(''\)E, 178 m a.s.l. (the position is marked in Fig. 3) and local time is UTC+1 h. Details about the site and the measurement set-up can be found in Metzger et al. (2007) and Eigenmann et al. (2009, 2011). Close to the turbulence station, a sodar/RASS system measured vertical profiles of wind components and virtual temperature. Moreover, the remaining components of the energy balance, net radiation \(Q_{S}^{*}\), and soil heat flux \(Q_{G}\), were measured at the EC site. An overview of the data processing, quality control, and flux characteristics of the turbulent data as well as the calculation of the energy balance is given in Eigenmann et al. (2011). In this article the sign convention for the fluxes is used according to Stull (1988) modified by an opposite sign for the ground heat flux according to Garratt (1992), consequently with the opposite sign in the energy balance equation. See also Foken (2008).
The study of Eigenmann et al. (2009) identified 23 days during the three-month COPS campaign with free convective conditions (mean duration: 85 min, standard deviation: approximately 1 h) based on EC measurements in the early morning hours. Free convective conditions were identified by the stability parameter \(\zeta = z/L\) for \(\zeta <-1\), where \(z\) is the height above the ground and \(L\) is the Obukhov length. These periods were characterized by low horizontal wind speeds due to the reversal of the valley wind system from downvalley flow to upvalley flow. The mean time for the occurrence of free convection on these 23 days is 0815 UTC with a standard deviation of 1 h, corresponding to 3.5 h after sunrise. No moist convection or significant clouds had been observed during the times selected.
The vertical wind speed \(w\) derived from the sodar observations was analyzed for the identified low wind periods. Hereafter this period of low winds is referred to as \(p_{1}\) and the subsequent 2 h of upvalley flow is referred to as \(p_{2}\). Both periods have comparable durations that leave the resulting datasets with comparable cardinalities. In order to make the individual days comparable, each sodar sample of \(w\) was normalized with the Deardorff convective velocity \(w_{*}\) (Deardorff 1970), and \(z\) was normalized with the height of the boundary layer \(z_{i}\). Surface buoyancy fluxes for the calculation of \(w_{*}\) were derived from the EC measurements and values of \(z_{i}\) were determined by a secondary maximum in the reflectivity profiles of the sodar measurements as described in Eigenmann et al. (2009) and suggested by Beyrich (1997). After that, histograms of \(w/w_{*}\) were calculated for three characteristic heights of \(z/z_{i} = 0.25, 0.50 \) and \(0.75\).
2.2 Simulations
2.2.1 Numerical Model
The numerical simulations were conducted using the multiscale geophysical flow solver EULAG (Eulerian/semi-Lagrangian fluid solver) (Smolarkiewicz et al. 1997; Prusa et al. 2008). EULAG solves the non-hydrostatic, anelastic equations of motion, here written in an extended perturbational form (Smolarkiewicz and Margolin 1997),
The set of anelastic equations (1–4) describes the anelastic mass continuity equation (Eq. 1), the three components of the momentum equation (Eq. 2), and the thermodynamic equation (Eq. 3), respectively. Equation 4 solves for the subgrid-scale (SGS) turbulent kinetic energy (TKE) \(e\). In (1–4), the operators \(\mathbf {\nabla }\) and \(\nabla \cdot \) symbolize gradient and divergence, while \(D/Dt\) \(=\) \(\partial /\partial t +\mathbf {v}\cdot \nabla \) is the material derivative, and \(\mathbf {v}\) is the physical velocity vector. The vector representing the gravitational acceleration \(\mathbf {g}\) \(=\) \((0,0,- g)^T\) occurs in the buoyancy term of Eq. 2. The quantities \(\rho _b(z)\) and \(\Theta _b(z)\) refer to the basic states, prescribed hydrostatic reference profiles usually employed in the anelastic approximated equations (Clark and Farley 1984).
In addition to the horizontally homogeneous basic state, a more general ambient (environmental) state is denoted by the subscript \(_e\). The corresponding variables may vary in the horizontal directions and they have to satisfy Eqs. 1–3; see Prusa et al. (2008) for a discussion of ambient state and its benefits. The primed variables \(\mathbf {v}^\prime \) and \(\Theta ^\prime \) appearing in Eqs. 2–3 correspond to deviations from the environmental variables \(\mathbf {v}_e\) and \(\Theta _e\); (\(\mathbf {v}^\prime =\mathbf {v}-\mathbf {v}_e\) and \(\mathbf {\Theta }^\prime =\mathbf {\Theta }-\mathbf {\Theta }_e\)). The quantity \(\pi ^\prime \) in the linearized pressure gradient term in Eq. 2 denotes a density normalized pressure deviation.
The terms proportional to \(\alpha \) and \(\beta \) denote wave-absorbing devices used at the upper boundary of the computational domain, see Smolarkiewicz and Margolin (1997). The coefficients \(\alpha \) and \(\beta \) are functions of the coordinates and are used to define the region and the intensity of the applied damping. The source terms \(\mathbf {D}\) and \(\mathcal {H}\) not explicitly stated in Eqs. 2 and 3 symbolize the viscous dissipation of momentum and the diffusion of heat, respectively. Via both of these terms, the subgrid-scale model enters the equations of motion. \(\mathbf {F}\) symbolizes an additional forcing for specified simulations, see below. The formulation of the TKE production and dissipation term hidden in \(\mathcal {S}\) and the applied parameters follow the description of Sorbjan (1996).
The quantity \(\mathbf {M}\) denotes metric forces due to the curvilinearity of the underlying physical system. In the present work, a non-orthogonal terrain-following system of coordinates \((\overline{x},\overline{y},\overline{z})\) \(=\) \((x,y,H(z-h)/(H-h))\) is used that assumes a model depth \(H\) and an irregular lower boundary \(h(x,y)\) (Gal-Chen and Somerville 1975; Smolarkiewicz and Margolin 1993; Wedi and Smolarkiewicz 2004). The explicit formulation of the transformed system of equations can be found in Prusa and Smolarkiewicz (2003) or, more recently, in Kühnlein et al. (2012). In symbolic form, the resulting system of motion for the prognostic variables \(\Psi \) \(\in \) \(\{u, v, w, \Theta , e\}\) can be written as a flux-form Eulerian conservation law
where \(\rho ^*\) \(=\) \(\rho _b\,G\), with \(G\) as the Jacobian of the transformation. A finite difference approximation of Eq. 5 is
where MPDATA Footnote 3 stands for the non-oscillatory forward-in-time (NFT) advection transport scheme described in Smolarkiewicz and Margolin (1998). The elliptic equation for pressure is solved iteratively with a Krylov-sub space solver, see Thomas et al. (2003). Both elements are integral parts of the EULAG and are fundamental to the stability of the code and the reliability of the results.
2.2.2 Simulation Strategy
Among the broad range of applications documented in the literature, EULAG has been successfully applied to atmospheric boundary-layer flows (see Smolarkiewicz et al. 2007; Piotrowski et al. 2009). For the present study, the set-up was chosen as follows.
The numerical simulations are conducted in a domain of (\(L_x\), \(L_y\), \(H\)) \(=\) (7680, 7680, 2430 m) with a regular grid size of \(\Delta x\) \(=\) \(\Delta y\) \(=\) \(\Delta z\) \(=\) 30 m. For a simulation of 2.5 h physical time, 30,000 timesteps with \(\Delta t\) \(=\) 0.3 s are necessary. The height \(h(x,y)\) of the lower boundary is taken from the advanced spaceborne thermal emission and reflection radiometer (ASTER) digital topographic dataset (NASA LP DAAC 2001) in a 30 m \(\times \) 30 m regular resolution. In all simulations shown here the computational domain is periodic in the horizontal directions. To enable this periodicity the topography was smoothly relaxed within a frame around the actual region of interest. Due to the complex orography and the low inversion layer height the width of the frame could be chosen to be 300 m.
For all simulations an anelastic basic state with a background stratification \(N\) \(=\) 0.01 s\(^{-1}\) is used according to Clark and Farley (1984), resulting in exponentially decreasing \(\rho _b\) and increasing \(\Theta _b\) profiles.
Two different simulation set-ups were designed: first, idealized simulations of an evolving convective boundary layer (CBL) over flat terrain \(h(x,y)\) \(=\) 0 were conducted and they are denoted by \(S\), and, secondly, the CBL was simulated over realistic topography \(h(x,y)\) and these simulations are denoted by \(R\), see Table 1.
All simulations were initialized with a resting fluid, and two different ambient potential temperature profiles \(\Theta _e(z)\) were applied to distinguish between a mixed layer with a capping inversion layer at \(z_{i}\) \(=\) 800 m (Simulations \(S1\) and \(R1\)) and a stably stratified ambient state covering the whole depth of the computational domain (simulations \(S2\) and \(R2\)). Thus, simulations S1 and R1 comprised,
and simulations S2 and R2,
White noise with an amplitude of 0.001 m s\(^{-1}\) was added to the initial vertical wind field in order to initiate convective motions. For the ensemble runs analyzed in Sect. 3.2, eight independent realizations were simulated using the set-up \(R1\). For this purpose, the random generator was seeded differently at the initial time for each realization. Because the three wind components are zero before adding the noise, the random disturbance is 100 % of the absolute value of the wind vector. This ensures that the eight realizations are statistically independent. The numerical simulations were conducted for a dry atmosphere, and the surface kinematic sensible heat flux \(Q_H\) = 0.05 K m s\(^{-1}\) was specified in all runs. The homogeneous heating can be justified because flux differences between different types of land surfaces turned out to be negligible in the observed early-morning situations (see Eigenmann et al. 2011). The effect of orographic shading is not taken into account. Orographically-induced flows (valley winds, upslope flows, etc.) are expected to mainly dominate the properties of the CBL in the valley at this time of the day.
The along-valley winds are part of a mountain plain circulation between a mountain massif and an adjacent plane, in our case the Black Forest and the Upper Rhine Valley, respectively. Due to the small computational domain, the effect of this mesoscale circulation on the flow in the valley is modelled by an additional dynamical forcing \(\mathbf {F}\) \(=\) \((0,-v_{0}(z)\tau ^{-1},0)\) for the meridional wind component \(v\), where \(\tau \) \(=\) \(t_\mathrm{end}\) \(-\) \(t_\mathrm{beg}\) is the period when the forcing is applied. The reference profile for the horizontal wind speed \(v_0(z)\) was derived from the sodar observations, and in simulation \(R2\) the additional forcing \(\mathbf {F}\) is applied. The period from \(t\) \(=\) 0 to \(t_\mathrm{beg}\) represents the observed low wind period \(p_{1}\), and the period from \(t_\mathrm{beg}\) to the end of the simulation represents the up-valley wind period \(p_{2}\). In the remainder of the article two exemplary simulation times referred to as \(t_{1}\) for a specified time in \(p_{1}\) and \(t_{2}\) for a specified time in \(p_{2}\) are chosen in order to compare differences in the simulated periods \(p_{1}\) and \(p_{2}\).
3 Results and Discussion
3.1 Modification of the Energy Balance by the Valley Flow
To analyze the effect of the valley flow on the energy balance derived from the EC flux measurements, the selected periods \(p_{1}\) and \(p_{2}\) are analyzed separately. Figure 1 shows the mean of the fluxes \(Q_{H}\) and \(Q_{E}\) and the sum of both normalized with the available energy \(-Q_{S}^{*}-Q_{G}\) during periods \(p_{1}\) and \(p_{2}\). A closed energy balance requires that the ratio of the sum of the turbulent fluxes \(Q_{H}+Q_{E}\) and the available energy \(-Q_{S}^{*}-Q_{G}\) \(=1\). Altogether, the energy balance is closed in period \(p_{1}\), while in period \(p_{2}\) a residual of 16 % occurs on average (see Fig. 1c). The latter value is close to the average residual of 21 % found during the entire COPS campaign at this site (see Eigenmann et al. 2011).
Bar plots of the mean of the fluxes of \(Q_{H}\) (a), \(Q_{E}\) (b) and the sum of both (c) normalized with the available energy \(-Q_{S}^{*}-Q_{G}\) during the low wind-speed period \(p_{1}\) and the upvalley wind period \(p_{2}\). All symbolic notations used in this caption are defined in Sect. 2.1. Average values for the 23 selected days at the Fußbach site are given for both periods. Also shown are the 95 % confidence intervals that indicate significant differences in the mean values for (a, c)
Regarding Fig. 1a, b, the relative flux contributions missing in period \(p_{2}\) compared to period \(p_{1}\) have exactly the proportions of the buoyancy flux ratio. The buoyancy flux ratio distributes about 85 % of the residual to \(Q_{H}\) and 15 % to \(Q_{E}\) for a typical Bowen ratio of about 0.45 in the observed early-morning situations. As such, Fig. 1 supports the assumption that the residual can be mainly associated with the missing flux components of \(Q_H\) (Foken et al. 2012b). The missing flux components in period \(p_{2}\) are assumed to exist within buoyancy-driven secondary circulations not captured by the EC measurements (e.g. Foken 2008). The transfer of the missing energy into the secondary circulation mainly occurs at significant surface heterogeneities that can be found over complex terrain. Advection-dominated processes (also not captured by EC) probably lead to the transport of the missing energy to these heterogeneities. As the horizontal wind speed becomes low in period \(p_{1}\), all fluxes are observed by the EC station and the energy balance is closed. However, the along-valley wind in period \(p_{2}\) leads to missing advective flux components and thus to the observed residual in this period.
The finding discussed above also supports the choice of a constant heat-flux forcing for the transient simulation \(R2\) (see Sect. 2.2). The same relative forcing by \(Q_{H}\) is achieved for both periods \(p_{1}\) and \(p_{2}\) by adding (for simplification) 100 % of the residual to \(Q_{H}\). In this way, the forcing of period \(p_{1}\) can also be used for period \(p_{2}\). Moreover, no significant relative flux differences of \(Q_{E}\) exist in both periods (see Fig. 1b). Thus, for the questions addressed herein, it appears to be appropriate to concentrate on dry model runs.
3.2 Coherent Structures in the Valley Imposed by Surrounding Orography
In order to investigate the early-morning CBL evolution inside the valley, sodar data from the morning period \(p_{1}\) of the selected days were chosen to create the histograms of the normalized vertical wind \(w/w_{*}\) (see Fig. 2). The observed distributions deviate strongly from probability density functions (pdfs) observed over flat, homogeneous environments as reported in many studies (e.g. Deardorff and Willis 1985; Stull 1988) where pdfs are right-skewed and show a negative maximum. In the lower part of the boundary layer (\(z/z_{i} = 0.25\)) the maximum of the observed distribution at the Fußbach site is shifted towards weak positive values instead of the weak negative values found over flat terrain. Also the observed histogram is far less skewed at this height. To find the cause of this behaviour, idealized simulations of a CBL were performed (simulation \(S1\) and \(S2\), described in Sect. 2.2).
Probability densities of the normalized vertical wind speed \(w/w_{*}\) for three heights (\(z/z_{i} = 0.25, 0.5, 0.75\)). Histograms are derived from sodar observations at the Fußbach site during the low wind-speed periods \(p_{1}\) on the 23 selected days, while curves are derived from the simulation \(S2\). The dotted curve shows the probability density function (pdf) for all points in the horizontal plane, the dashed curve shows the pdf for the conditionally sampled updraft areas only. For the definition of \(w\), \(w_{*}\), \(z\), \(z_{i}\) see Sect. 2.1. For the definition of \(S2\) see Sect. 2.2.2
To gain confidence in the simulations the well known pdfs of the vertical wind in a CBL are calculated for the simulated data of set-up \(S1\). Very good agreement with the published values is found (not shown). Moreover, the simulation results show the well-known spoke patterns of coherent convective motions known from numerous numerical studies (e.g. Schmidt and Schumann 1989). The data from the simulation of set-up \(S2\) are then used to create the pdfs for a CBL with a growing mixed layer, see Fig. 2 (situation closer to the observation period \(p_{1}\)). In this set-up, spoke patterns evolve in the simulated boundary layer that grow slightly in size as the inversion layer height grows in time. A conditional sampling is applied to obtain the pdfs of the coherent updraft areas. The updraft areas are defined as follows: the vertical wind component at a height of 200 m is temporally averaged after a spin-up time of 45 min to the end of the simulation (150 min). All locations on that layer where the average exceeds a value of 0.05 m s\(^{-1}\) define the updraft areas for the entire boundary layer.
The resulting pdfs resemble the properties of the histograms from the sodar data (see Fig. 2). The maximum and the skewness of the pdfs of the conditionally sampled updraft areas match well with those of the histograms of the observational data for all heights. Only the absolute numbers of the probability density do not fully match. A possible explanation for this is that the sodar instrument averages over a specific volume, so that the spread of the resulting pdfs is reduced. This effect becomes larger with height.
We interpret these findings as follows: it is well known that coherent convective motions evolve in a CBL, and which remain quasi-stationary in space and time (see e.g. Stull 1988). This means that the location where a possible sodar instrument is located will remain under an updraft or a downdraft area for a long time. As a consequence, it is very likely that a sodar measurement captures only the statistical properties of a part of the velocity spectrum. The fact that the result from Fig. 2 stems from a composite over 23 periods with similar overall conditions suggests the hypothesis that the sodar instrument was preferentially located at an updraft region.
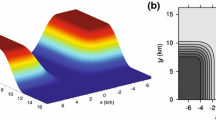
To verify this hypothesis, an ensemble of eight large-eddy simulations (LES) was carried out with realistic topography at the lower boundary (simulation \(R1\)) and different initial noise seeding for \(w\) (see Sect. 2.2.2). Figure 3 shows the ensemble and temporal means of the vertical wind speed at 300 m a.s.l. (approximately 130 m above the valley floor). Although we applied both a temporal mean and an ensemble mean to the simulated data, coherent patterns of the CBL flow field inside the valley remain. These patterns were found to be robust against variations in averaging times and ensemble sizes. This mean flow field has a larger amplitude than its analogue from simulations over flat terrain. We interpret this finding as follows: the surrounding ridges impose coherent convective motions to the valley flow at specific locations during the early morning \(p_{1}\) periods. Their positions relative to the ridges persist, in contrast to the changing locations of the coherent structures in the flat terrain CBL simulation. The position of the observational site is marked by a black circle in Fig. 3 and shows that the site is located in an updraft region.
Ensemble and temporal mean of the vertical wind speed in m s\(^{-1}\) at 300 m a.s.l. for simulation \(R1\) (colour coded). Black solid lines mark the orography in steps of 50 m. Grey contours mark intersection with the orography. The red frame represents the section of the valley shown in Fig. 5. The position of the sodar is indicated by the black circle. For the definition of \(R1\) see Sect. 2.2.2
For the sake of completeness the histograms and the simulated pdfs for \(z/z_{i} = 0.5\) and \(z/z_{i} = 0.75\) are shown in Fig. 2. They show a less clear deviation from the “LES all points” pdfs of the simulation. But the difference between the “LES updraft area” pdfs and the “LES all points” pdfs themselves become also very small at these heights. This restricts the application of the method described in this section to the lower part of the CBL.
3.3 Vertical Transport in the Early-Morning Valley Atmosphere
Based on the same micrometeorological dataset as in this study, Eigenmann et al. (2009) discussed spectral analysis of the EC measurements. These analyses showed an increase of spectral power within turbulent scales of a few minutes during the low wind-speed period \(p_{1}\) in the morning (see Eigenmann et al. 2009). These time scales could be related to the presence of large coherent vertical structures (e.g. plumes or updrafts) with a spatial extent in the order of the boundary-layer height, which are known to be responsible for the majority of the transport within the CBL (see e.g. Stull 1988; Chandra et al. 2010). The occurrence of these turbulent scales in the ground-based EC data indicates that during the period \(p_{1}\), air very close to the ground is able to be transported upwards very efficiently by non-local large-eddy transport processes. The free convective conditions detected simultaneously by the EC measurements also support these findings. By the onset of the up-valley wind the spectral analysis of Eigenmann et al. (2009) does not show these turbulent scales any longer, indicating that the turbulent transport of near-ground air became less effective. The effective vertical transport in period \(p_{1}\) is important because air masses close to the valley bottom are humid, have a characteristic chemical composition, and may possibly be polluted. The effect of the free convective release of surface-layer air masses from the valley bottom on ozone measurements at a mountain-top station was reported by Mayer et al. (2008).
During these free convective situations in period \(p_{1}\), the sodar/RASS observed strong vertical updrafts into the stably stratified valley atmosphere. For illustration, Fig. 4 shows for COPS IOP15b, i.e. 13 August 2007, the morning evolution of vertical wind and virtual potential temperature. In the lower panel of Fig. 4 the observed vertical wind is shown from 0500 to 1300 UTC; the period of low horizontal wind speed in the morning is marked by vertical dashed lines. The times of the profiles plotted in Fig. 4a–d are indicated in the lower panel; at time (a) the profile is shown shortly after sunrise. The overall stable stratification is accompanied by neutral layers up to 80 m and between heights of 140 and 230 m. In (b) the profile is representative of a period of strong coherent vertical updrafts. Near-neutral stratification below 160 m above the valley floor was observed in this period. A weak stable stratification above 160 m can be seen while the corresponding vertical wind speeds remain positive. The strong updraft period is interrupted by a period of weaker vertical winds. The profile in (c) shows that during this short interruption the original stable stratification recovers. After this interruption the vertical wind is again positive and the profile in (d) shows a neutral to unstable profile. In the light of the previous analysis, this individual scene is interpreted as follows: the convection, influenced by the orography, organizes in a way that the updraft and downdraft areas remain quasi-stationary at their spatial location (see Fig. 3). The immobile sodar/RASS instrument observed this quasi-stationary updraft area for a period of approximately 2.5 h (0800 until 1030 UTC). This period is interrupted by a short period of weaker winds at around 0920 UTC, when the quasi-stationary updraft area slightly moves out of view of the sodar/RASS instrument, so that the properties of an attached downdraft area are also observed. In this short period, it can be seen that the stratification of the valley atmosphere above the surface layer is still stable outside the updrafts (Fig. 4c).
Observations from the sodar/RASS system. Upper panel (a–d): profiles of the virtual potential temperature observed by the sodar/RASS in the morning hours of COPS IOP15b (13 August 2007). The times of the profiles are marked in the lower panel. Lower panel (from Eigenmann et al. 2009, modified): vertical wind speeds in colour measured by the sodar/RASS from 0500-1300 UTC. The black dashed vertical lines indicate the period of vanishing horizontal wind speeds (period \(p_1\), see Sect. 2.1)
To better understand the state of the boundary layer in which these observations were made, the transient simulation \(R2\) (see Sect. 2.2) was carried out and analyzed. In Fig. 5, snapshots of the field of the vertical wind speed are shown for two heights and for the time \(t_{1}\) in the low wind-speed period \(p_{1}\) and the time \(t_{2}\) in the up-valley wind period \(p_{2}\). Figure 5a and b show, especially at the lower height, cellular convection at time \(t_{1}\) (e.g. Schmidt and Schumann 1989). In contrast, at time \(t_{2}\) (Fig. 5c, d) hardly any of these regular patterns remain and instead there are now irregular streak-like patterns. The axis of the streak-like structures is aligned roughly in the main wind direction. Roll or streak-like structures in a shear-buoyancy-driven boundary layer are well-described phenomena (e.g. Moeng and Sullivan 1994; Weckwerth et al. 1997; Drobinski et al. 1998; Drobinski and Foster 2003). The locations of updrafts and downdrafts in the instantaneous snapshots at time \(t_{1}\) in Fig. 5a and b agree well with those found in the ensemble and temporal mean in Fig. 3. Figure 6 shows the vertical wind and the temperature stratification for instantaneous vertical slices through the model domain at time \(t_{1}\) (Fig. 6a) and at time \(t_{2}\) (Fig. 6b). Similar to the observations shown in Fig. 4, strong convective updraft structures can be seen in period \(p_{1}\) within the valley that penetrate into the stably stratified free atmosphere up to a height of about 600 m a.s.l. Within a coherent updraft structure a more neutral stratification is found, and in period \(p_{2}\) more neutral stratification can be seen within the entire valley. The vertical extent of the updraft structures is confined to the neutrally stratified valley atmosphere and does not reach into the stably stratified atmosphere above.
Instantaneous situations at a sample timestep in the simulated low wind-speed period \(p_{1}\) (a, b) and for an exemplary timestep in the simulated upvalley wind period \(p_{2}\) (c, d) of the simulation \(R2\) (\(t_{1}\) and \(t_{2}\) respectively). Vertical wind component \(w\) in m s\(^{-1}\) is colour coded. The cross-sections are placed at 210 m (a, c) and 300 m a.s.l. (b, d), respectively. The area shown here is marked by the red frame in Fig. 3. All symbols used in this caption are defined in Sect. 2
Vertical cross-sections perpendicular to the axis of the valley. Instantaneous situations of the simulation \(R2\) are shown for an exemplary timestep in \(p_{1}\) (a) and in \(p_{2}\) (b) (\(t_{1}\) and \(t_{2}\) respectively). Vertical wind \(w\) in m s\(^{-1}\) is colour coded. Black lines are isentropes in steps of 0.2 K. Intersection with the orography is shaded in grey. All symbols used in this caption are defined in Sect. 2
The change of the flow in the periods \(p_1\) and \(p_2\) leads to a modified vertical turbulent transport of TKE. Figure 7 shows the profiles of the transport term of the TKE budget for both times \(t_{1}\) and \(t_{2}\). At time \(t_1\), the profile of the turbulent transport of TKE shows negative values in the lower half of the boundary layer and positive values in the upper half (Fig. 7a). Due to the vertical orientation of the flow in period \(p_1\), the TKE is redistributed vertically by turbulent eddies (Stull 1988). At time \(t_2\) (Fig. 7b), the profile of the turbulent transport of TKE deviates strongly from the situation at \(t_1\); its values are close to zero up to a height of 0.7\(z_{i}\). Above this height positive values prevail, implying that the vertical turbulent transport of TKE has ceased in the period \(p_2\). The positive values above 0.7\(z_{i}\) originate from the production of TKE from outside the valley, i.e. the averaging area (red frame in Fig. 3).
Vertical profiles of the TKE budget terms of buoyancy, shear and transport for the time \(t_{1}\) in \(p_{1}\) (a) and for the time \(t_{2}\) in \(p_{2}\) (b) of the simulation \(R2\). Only points in the valley are considered (see red frame in Fig. 3). All symbols used in this caption are defined in Sect. 2
The profiles for the buoyancy term and the shear term of the TKE budget are plotted in Fig. 7 in the same manner as the profiles described above. During the transition from \(t_1\) to \(t_2\), the profile for buoyancy production of TKE remains positive below 0.7\(z_{i}\) and negative above. The major change here is that the maximum of the buoyant production of TKE is shifted upwards to 0.15\(z_{i}\). This shift is accompanied by an increased shear production of TKE below 0.2\(z_{i}\). The maximum in shear production of TKE at 0.7\(z_{i}\) and at time \(t_2\) derives from the imposed along-valley wind described in Sect. 2.2.2.
The heat-flux profiles and the corresponding vertical gradients of the potential temperature in period \(p_{1}\) are shown in Fig. 8a, b, respectively. The profiles are calculated as a horizontal mean for the area marked with the red frame in Fig. 3. Besides the mean profiles within the valley for all points, profiles for updraft and downdraft areas are analyzed separately. In the centre of the valley boundary layer between heights of about \(0.4z_i\) and \(0.8z_i\) the flux of sensible heat, averaged horizontally over all points in the valley, is counter to the temperature gradient. Regarding the updraft area, the heat flux follows the temperature gradient up to a height of \(0.65z_i\) due to the unstable to neutral stratification. A counter-gradient flux remains above this height up to approximately \(0.9z_i\). Counter-gradient fluxes are a common feature in turbulent flows and are well studied (e.g. Deardorff 1966; Schumann 1987), and counter-gradient turbulent transfer within forest canopies is discussed, e.g., in Denmead and Bradley (1985). The total heat flux is mainly determined by the flux within the coherent upward motions. Together with the findings in Sect. 3.2 (the orography forces the updraft areas to evolve at specific locations), this result leads to the statement that the majority of the transfer takes place at these specific locations.
a Vertical profiles of the gradient of the potential temperature and b normalized vertical profiles of the heat flux \(Q_{H}\) at time \(t_{1}\) of the simulation \(R2\). Only points in the valley are considered (see red frame in Fig. 3). The solid line shows the values for all points in the valley. The dotted lines shows the profile for places with \(w\) \(>\) 0 (up) and the dashed line for places with \(w\) \(<\) 0 (down). The contribution to the heat flux from the subgrid model is shown in (b) as the dash-dotted line. All symbols used in this caption are defined in Sect. 2
4 Conclusions
During the three months of the COPS campaign the surface energy balance at one site in the Kinzig valley was rarely closed, as is common for many energy balance measurements. However, the presented analysis gave the surprising result that the energy balance was closed on average for the low wind period in the morning hours on fair weather days. A closed energy balance indicates that all energy containing motions were captured by the instrumentation and that the assumptions for data processing, i.e. stationarity and homogeneity of the flow, were satisfied. It has to be assumed that due to the vanishing horizontal wind speed all flux components were captured by the EC system at the observational site. After the onset of the valley wind, advective flux components were missing and the desired closure was no longer met. The residual of the energy balance increased to values typical for the full dataset of this site. Our analysis indicates that the residual is mainly associated with the missing flux components of the sensible heat flux.
Large-eddy simulations of the atmosphere in the Kinzig valley were carried out. It was found that the convection in the valley becomes organized due to the surrounding ridges during the low-wind period, resulting in quasi-stationary patterns at preferred locations. This result leads to the conclusion that the sodar/RASS observed only a part of the vertical velocity spectrum. This has implications for future observational set-ups in complex terrain and interpretation of their data.
The simulations indicate that the turbulent transport of TKE within the valley becomes less effective during the morning transition of the valley wind system. Furthermore, heat fluxes counter to the temperature gradient occur together with updrafts in the low wind period in the morning, as shown schematically in Fig. 9. When strong updrafts penetrate into the stably stratified layer (remnant of the nocturnal cooling, Whiteman 2000) counter-gradient heat fluxes occur. We conclude that this finding is similar to effects studied in forest environments (Thomas and Foken 2007; Finnigan et al. 2009).
Schematic view of the turbulent transport during the early-morning low wind-speed periods in the Kinzig valley. Strong updrafts exist at specific, preferential locations in the valley that penetrate into the stably stratified valley atmosphere and extend up to about the height of the surrounding ridges. For simplicity downdraft areas and slope winds are not shown
Notes
Sodar stands for sonic detection and ranging.
RASS stands for radio acoustic sounding system.
MPDATA stands for Multidimensional Positive-Definite Advection Transport Algorithm.
References
Beyrich F (1997) Mixing height estimation from sodar data—a critical discussion. Atmos Environ 31(23):3941–3953
Chandra AS, Kollias P, Giangrande SE, Klein SA (2010) Long-term observations of the convective boundary layer using insect radar returns at the SGP ARM climate research facility. J Clim 23(21):5699–5714
Clark T, Farley R (1984) Severe downslope windstorm calculations in 2 and 3 spatial dimensions using anelastic interactive grid nesting—a possible mechanism for gustiness. J Atmos Sci 41(3):329–350
Deardorff JW (1966) The counter-gradient heat flux in the lower atmosphere and in the laboratory. J Atmos Sci 23(5):503–506
Deardorff JW (1970) Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection. J Atmos Sci 27:1211–1213
Deardorff JW, Willis GE (1985) Further results from a laboratory model of the convective planetary boundary layer. Boundary-Layer Meteorol 32:205–236
Defant F (1949) Zur Theorie der Hangwinde, nebst Bemerkungen zur Theorie der Berg- und Talwinde. Arch Meteorol Geophys Bioklim A1:421–450
Denmead DT, Bradley EF (1985) Flux-gradient relationships in a forest canopy. In: Hutchison BA, Hicks BB (eds) The forest-atmosphere interaction. D. Reidel Publ. Comp, Dordrecht, pp 421–442
Dörnbrack A, Schumann U (1993) Numerical simulation of turbulent convective flow over wavy terrain. Boundary-Layer Meteorol 65:323–355
Drobinski P, Brown RA, Flamant PH, Pelon J (1998) Evidence of organized large Eddies by ground-based doppler lidar, sonic anemometer and sodar. Boundary-Layer Meteorol 88:343–361
Drobinski P, Foster RC (2003) On the origin of near-surface streaks in the neutrally-stratified planetary boundary layer. Boundary-Layer Meteorol 108:247–256
Eigenmann R, Kalthoff N, Foken T, Dorninger M, Kohler M, Legain D, Pigeon G, Piguet B, Schüttemeyer D, Traulle O (2011) Surface energy balance and turbulence network during the convective and orographically-induced precipitation study (COPS). Q J R Meteorol Soc 137(S1):57–69
Eigenmann R, Metzger S, Foken T (2009) Generation of free convection due to changes of the local circulation system. Atmos Chem Phys 9:8587–8600
Finnigan JJ, Shaw RH, Patton EG (2009) Turbulence structure above a vegetation canopy. J Fluid Mech 637:387–424
Foken T (2008) Micrometeorology. Springer, Berlin
Foken T (2008) The energy balance closure problem: an overview. Ecol Appl 18:1351–1367
Foken T, Aubinet M, Finnigan JJ, Leclerc MY, Mauder M, Paw UKT (2011) Results of a panel discussion about the energy balance closure correction for trace gases. Bull Am Meteorol Soc 92:ES13–ES18
Foken T, Aubinet M, Leuning R (2012a) The Eddy Covariance Method. In: Aubinet M, Vesala T, Papale D (eds) Eddy covariance: a practical guide to measurement and data analysis. Springer, Springer Atmospheric Sciences, Berlin, pp 1–19
Foken T, Leuning R, Oncley S, Mauder M, Aubinet M (2012b) Corrections and data quality. In: Aubinet M, Vesala T, Papale D (eds) Eddy covariance: a practical guide to measurement and data analysis. Springer, Berlin, pp 85–131
Foken T, Mauder M, Liebethal C, Wimmer F, Beyrich F, Leps J-P, Raasch S, DeBruin HAR, Meijninger WML, Bange J (2010) Energy balance closure for the LITFASS-2003 experiment. Theor Appl Climatol 101:149–160
Gal-Chen T, Somerville RC (1975) On the use of a coordinate transformation for the solution of the Navier-Stokes equations. J Comput Phys 17:209–228
Garratt JR (1992) The atmospheric boundary layer. Cambridge University Press, UK 316 pp
Inagaki A, Letzel MO, Raasch S, Kanda M (2006) Impact of surface heterogeneity on energy imbalance: a study using LES. J Meteorol Soc Jpn 84:187–198
Kaimal J, Gaynor J (1991) Another look to sonic thermometry. Boundary-Layer Meteorol 56:401–410
Kalthoff N, Kohler M, Barthlott C, Adler B, Mobbs S, Corsmeier U, Träumner K, Foken T, Eigenmann R, Krauss L, Khodayar S, Di Girolamo P (2011) The dependence of convection-related parameters on surface and boundary-layer conditions over complex terrain. Q J R Meteorol Soc 137(S1):70–80
Kanda M, Moriwaki R, Kasamatsu F (2004) Large-eddy simulation of turbulent organized structures within and above explicitly resolved cube arrays. Boundary-Layer Meteorol 112(2):343–368
Kühnlein C, Smolarkiewicz PK, Dörnbrack A (2012) Modelling atmospheric flows with adaptive moving meshes. J Comput Phys 231(7):2741–2763
Mahrt L (2010) Computing turbulent fluxes near the surface: needed improvements. Agric For Meteorol 150(4):501–509
Mauder M, Foken T (2006) Impact of post-field data processing on eddy covariance flux estimates and energy balance closure. Meteorol Z 15(6):597–609
Mayer JC, Staudt K, Gilge S, Meixner FX, Foken T (2008) The impact of free convection on late morning ozone decreases on an Alpine foreland mountain summit. Atmos Chem Phys 8:5941–5956
Metzger S, Foken T, Eigenmann R, Kurtz W, Serafimovich A, Siebicke L, Olesch J, Staudt K, and Lüers J (2007) COPS experiment, Convective and orographically induced precipitation study, 01 June 2007–31 August 2007, Documentation. Work Report University of Bayreuth, Department of Micrometeorology, 34, Print: ISSN 1614–8916, 72 pp
Moeng C-H, Sullivan PP (1994) A comparison of shear- and buoyancy-driven planetary boundary layer flows. J Atmos Sci 51:999–1022
NASA LP DAAC (2001) ‘ASTGTM ASTER Global Digital Elevation Model’. LP DAAC. NASA Land Processes Distributed Active Archive Center, USGS/Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota
Oncley SP, Foken T, Vogt R, Kohsiek W, DeBruin HAR, Bernhofer C, Christen A, van Gorsel E, Grantz D, Feigenwinter C, Lehner I, Liebethal C, Liu H, Mauder M, Pitacco A, Ribeiro L, Weidinger T (2007) The energy balance experiment EBEX-2000. Part I: overview and energy balance. Boundary-Layer Meteorol 123:1–28
Piotrowski Z, Smolarkiewicz P, Malinowski S, Wyszogrodzki A (2009) On numerical realizability of thermal convection. J Comput Phys 228:6268–6290
Prusa JM, Smolarkiewicz PK (2003) An all-scale anelastic model for geophysical flows: dynamic grid deformation. J Comput Phys 190:601–622
Prusa JM, Smolarkiewicz PK, Wyszogrodzki AA (2008) Eulag, a computational model for multiscale flows. Comp Fluids 37(9):1193–1207
Raasch S, Harbusch G (2001) An analysis of secondary circulations and their effects caused by small-scale surface inhomogeneities using large-eddy simulation. Boundary-Layer Meteorol 101:31–59
Rotach MW, Andretta M, Calanca P, Weigel AP, Weiss A (2008) Boundary layer characteristics and turbulent exchange mechanisms in highly complex terrain. Acta Geophys 56(1):194–219
Schmidt H, Schumann U (1989) Coherent structure of the convective boundary layer derived from large-eddy simulations. J Fluid Mech 200:511–562
Schumann U (1987) The countergradient heat flux in turbulent stratified flows. Nucl Eng Des 100(3):255–262
Segal M, Arritt RW (1992) Nonclassical mesoscale circulations caused by surface sensible heat-flux gradients. Bull Am Meteorol Soc 73(10):1593–1604
Smolarkiewicz PK, Grubisic V, Margolin LG (1997) On forward-in-time differencing for fluids: stopping criteria for iterative solutions of anelastic pressure equations. Mon Weather Rev 125(4):647–654
Smolarkiewicz PK, Margolin LG (1993) On forward-in-time differencing for fluids: extension to a curvilinear framework. Mon Weather Rev 121(6):1847–1859
Smolarkiewicz PK, Margolin LG (1997) On forward-in-time differencing for fluids: an Eulerian/semi-Lagrangian non-hydrostatic model for stratified flows. Atmos Ocean 35:127–152
Smolarkiewicz PK, Margolin LG (1998) MPDATA: a finite-difference solver for geophysical flows. J Comput Phys 140(2):459–480
Smolarkiewicz PK, Sharman R, Weil J, Perry SG, Heist D, Bowker G (2007) Building resolving large-eddy simulations and comparison with wind tunnel experiments. J Comput Phys 227:633–653
Sorbjan Z (1996) Numerical study of penetrative and “solid lid” nonpenetrative convective boundary layers. J Atmos Sci 53:101–112
Stoy PC, Mauder M, Foken T, Marcolla B, Boegh E, Ibrom A, Arain MA, Arneth A, Aurela M, Bernhofer C, Cescatti A, Dellwik E, Duce P, Gianelle D, van Gorsel E, Kiely G, Knohl A, Margolis H, McCaughey H, Merbold L, Montagnani L, Papale D, Reichstein M, Saunders M, Serrano-Ortiz P, Sottocornola M, Spano D, Vaccari F, Varlagin A (2013) A data-driven analysis of energy balance closure across FLUXNET research sites: the role of landscape scale heterogeneity. Agric For Meteorol 171:137–152
Stull RB (1988) An introduction to boundary layer meteorology. Kluwer Academic Publishers, Dordrecht, 666 pp
Thomas C, Foken T (2007) Flux contribution of coherent structures and its implications for the exchange of energy and matter in a tall spruce canopy. Boundary-Layer Meteorol 123(2):317–337
Thomas SJ, Hacker JP, Smolarkiewicz PK, Stull RB (2003) Spectral preconditioners for nonhydrostatic atmospheric models. Mon Weather Rev 131(10):2464–2478
Twine TE, Kustas WP, Norman JM, Cook DR, Houser PR, Meyers TP, Prueger JH, Starks PJ, Wesely ML (2000) Correcting eddy-covariance flux underestimates over a grassland. Agric For Meteorol 103:279–300
Walko R, Cotton W, Pielke R (1992) Large-eddy simulations of the effects of hilly Terrain on the convective boundary-layer. Boundary-Layer Meteorol 58(1–2):133–150
Weckwerth TM, Wilson JW, Wakimoto RM, Crook NA (1997) Horizontal convective rolls: determining the environmental conditions supporting their existence and characteristics. Mon Weather Rev 125:505–526
Wedi NP, Smolarkiewicz PK (2004) Extending Gal-Chen and Somerville terrain-following coordinate transformation on time-dependent curvilinear boundaries. J Comput Phys 193:1–20
Weigel A, Chow F, Rotach M (2007) The effect of mountainous topography on moisture exchange between the “surface” and the free atmosphere. Boundary-Layer Meteorol 125:227–244
Whiteman CD (1990) Observations of thermally developed wind systems in mountainous terrain. In: Blumen W (ed) Atmospheric processes over complex terrain of meteorological monographs. American Meteorological Society, Boston, pp 5–42
Whiteman CD (2000) Mountain meteorology: fundamentals and applications. Oxford University Press, Oxford 376 pp
Wulfmeyer V, Behrendt A, Kottmeier C, Corsmeier U, Barthlott C, Craig GC, Hagen M, Althausen D, Aoshima F, Arpagaus M, Bauer H-S, Bennett L, Blyth A, Brandau C, Champollion C, Crewell S, Dick G, Di Girolamo P, Dorninger M, Dufournet Y, Eigenmann R, Engelmann R, Flamant C, Foken T, Gorgas T, Grzeschik M, Handwerker J, Hauck C, Höller H, Junkermann W, Kalthoff N, Kiemle C, Klink S, König M, Krauss L, Long CN, Madonna F, Mobbs S, Neininger B, Pal S, Peters G, Pigeon G, Richard E, Rotach MW, Russchenberg H, Schwitalla T, Smith V, Steinacker R, Trentmann J, Turner DD, van Baelen J, Vogt S, Volkert H, Weckwerth T, Wernli H, Wieser A, Wirth M (2011) The convective and orographically-induced precipitation study (COPS): the scientific strategy, the field phase, and research highlights. Q J R Meteorol Soc 137(S1):3–30
Zardi D, Whiteman CD (2013) Diurnal mountain wind systems’. In: Chow SF, De Wekker FK, Snyder BJ (eds) Mountain weather research and forecasting. Springer, Dordrecht, pp 35–119
Acknowledgments
This study was funded by the Deutsche Forschungsgesellschaft (DFG) within the special priority program SPP1167 (WI 1685/9-1, WI 1685/10-1, FO 226/19-1, FO 226/23-1). The numerical simulations made for this study were carried out at the high performance computing centre of the Deutsches Klima Rechenzentrum (DKRZ) in Hamburg, Germany. We thank Prof. Dr. Werner Eugster and two other anonymous reviewers for their helpful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Brötz, B., Eigenmann, R., Dörnbrack, A. et al. Early-Morning Flow Transition in a Valley in Low-Mountain Terrain Under Clear-Sky Conditions. Boundary-Layer Meteorol 152, 45–63 (2014). https://doi.org/10.1007/s10546-014-9921-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-014-9921-7