1 Introduction

The long-time numerical integration of reversible Hamiltonian systems has been a subject of interest for many years. For the special case of a second-order separable Hamiltonian system, the class of symmetric second-order multistep methods have been identified as excellent candidates for integration, as they are explicit, high-order, and preserve invariants of the system over long-times [14, Ch. XV], [18]. However, for non-separable Hamiltonian systems, these methods are generally not applicable. Thus, one would usually consider a symmetric (or possibly symplectic) Runge–Kutta method (RKM) as an alternative. It is well-known that structure-preserving RKMs are necessarily implicit, which inevitably limits their long-time efficiency. The impact of implicitness can be mitigated to some extent by considering the class of symmetric diagonally-implicit RKMs (DIRKs). Here, since the methods are essentially compositions of the implicit midpoint rule (IMR) [19], the computational cost amounts to the number of its stages multiplied by the cost of IMR.

Alternatively, one could consider selecting a method from the class of symmetric general linear methods (GLMs). In recent work, it has been shown that these methods can preserve quadratic and Hamiltonian invariants over long-times without suffering from the parasitic instability associated with multistep methods [5,6,7]. Furthermore, these methods can be designed such that they consist of a mixture of implicit and explicit stage equations, suggesting they have the potential to outperform symmetric DIRKs, in terms of cost for a given order.

The choice of method will also depend on its order and computational efficiency. At present, symmetric GLMs are mostly limited to 4th-order [6, 17], with the exception of the method presented in [7] that is of 6th-order. Beyond this, the construction of higher-order methods is difficult. In this paper, we present a construction process that is based on the theory of composition for one-step methods (OSMs), such as RKMs, which in the past has been applied to generate composite symmetric (COSY) methods of arbitrarily high order [10, 12, 16, 20, 21]. In particular, we generalise the following OSM-composition formula (see e.g. [14, Ch. II.4]) to GLMs:

$$\begin{aligned} \psi _h(y_0) =\phi ^*_{\beta _kh}\circ \phi _{\alpha _kh}\circ \cdots \circ \phi ^*_{\beta _2h}\circ \phi _{\alpha _2h}\circ \phi ^*_{\beta _1h}\circ \phi _{\alpha _1h}(y_0), \end{aligned}$$
(1.1)

where \(\phi _h\) denotes the OSM and \(\phi _h^*:=\phi _{-h}^{-1}\) denotes its adjoint. In addition, we also consider the GLM generalisation of the following composition

$$\begin{aligned} \psi _h(y_0) = \phi _{\alpha _kh}\circ \cdots \circ \phi _{\alpha _2h}\circ \phi _{\alpha _1h}(y_0), \end{aligned}$$
(1.2)

which is frequently used with symmetric methods of even order \(p\in \mathbb {N}\). Notable examples include the triple jump composition:

$$\begin{aligned} \psi _h(y_0):= \phi _{\alpha _1h}\circ \phi _{\alpha _2h}\circ \phi _{\alpha _1h}(y_0),\quad \alpha _1 = \frac{1}{2-2^{1/(p+1)}}, \quad \alpha _2 = 1-2\alpha _1, \end{aligned}$$
(1.3)

and the Suzuki 5-jump [20]:

$$\begin{aligned} \psi _h(y_0)&:=\phi _{\alpha _1h}\circ \phi _{\alpha _1h}\circ \phi _{\alpha _2h}\circ \phi _{\alpha _1h}\circ \phi _{\alpha _1h}(y_0),\quad \alpha _1= \frac{1}{4-4^{1/(p+1)}}, \nonumber \\ \alpha _2&= 1-4\alpha _1. \end{aligned}$$
(1.4)

The main challenge with constructing a COSY-GLM is understanding how its inputs change between each method evaluation. For OSMs, this is not an issue as there is only one input which approximates the exact solution. However, GLMs possess multiple inputs, each of which takes the form of a B-series. For the special case where these are in Nordsieck form, an appropriate re-scaling of each input is sufficient to guarantee an order increase [17, Ch. 5]. In this paper, we address the issue of general inputs by introducing a nonlinear transformation that puts the GLM into a canonical form. Here, canonical is taken to mean that the resulting method has trivial starting and finishing methods given by its preconsistency vectors u and \(w^{{\mathbf {\mathsf{{H}}}}}\). As a result, its inputs are essentially a Kronecker product of the preconsistency vector u and an approximation to the exact solution. Thus, the method behaves in this respect as if it were a OSM and the theory of composition can be straightforwardly applied to generate high-order COSY-GLMs.

This paper is organised as follows: In Sect. 2 we give an introduction to GLMs. In Sect. 3 we introduce a transformation that puts a GLM into a canonical form. In Sect. 4 we use the canonical transformation to develop composition formulae for GLMs. In Sect. 5, we test our GLM-composition formula by constructing 6th-order COSY-GLMs. Efficiency comparisons are then made between these methods and symmetric DIRKs of the same order. Finally, several long-time Hamiltonian experiments are performed to demonstrate the preservation properties of the methods.

2 General linear methods

Throughout the paper, we assume numerical methods are applied to the following autonomous, initial value problem (IVP)

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}y(t) = f(y(t)), \quad y(0) = y_0, \quad t \in [0,T], \quad T >0, \end{aligned}$$

where \(f:X\rightarrow X\), and the solution \(y:\mathbb {R} \rightarrow X\) is expressed in terms of the flow map \(\varphi _t:X \rightarrow X\) and initial data \(y_0\) such that

$$\begin{aligned} y(t) = \varphi _t(y_0). \end{aligned}$$

Of particular interest will be Hamiltonian IVPs (see e.g. [14, Ch. I.1]):

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t} \begin{bmatrix} p(t) \\ q(t) \end{bmatrix} = \begin{bmatrix} -H_q(p(t),q(t)) \\ H_p(p(t),q(t)) \end{bmatrix}, \quad \begin{bmatrix} p(0) \\ q(0) \end{bmatrix} = \begin{bmatrix} p_0 \\ q_0 \end{bmatrix},\quad t \in [0,T], \quad T >0, \end{aligned}$$

where \(H:X \rightarrow \mathbb {R}\), is the Hamiltonian and \(X = \mathbb {R}^{2d}\), \(d\in \mathbb {N}\).

2.1 Method definition

An \(r \in \mathbb {N}\)-input GLM, for fixed time-step \(h \in \mathbb {R}\), is written as the map \(\mathcal {M}_{ h}:X^r\rightarrow X^r\) acting on inputs \(y^{[n]} \in X^r\) at step \(n\in \mathbb {N}_0\) such that

$$\begin{aligned} Y&= h(A \otimes I_X) F(Y) + (U \otimes I_X)y^{[n]}, \nonumber \\ \mathcal {M}_{ h}(y^{[n]})&= h(B \otimes I_X)F(Y) + (V \otimes I_X)y^{[n]}, \end{aligned}$$
(2.1)

where \(\otimes \) denotes a Kronecker product, \(I_X\) is the identity matrix defined on X,

$$\begin{aligned} y^{[n]} = \begin{bmatrix} y^{[n]}_1 \\ y^{[n]}_2 \\ \vdots \\ y^{[n]}_r \end{bmatrix} \in X^r, \quad Y = \begin{bmatrix} Y_1 \\ Y_2 \\ \vdots \\ Y_s \end{bmatrix} \in X^s, \quad F(Y) = \begin{bmatrix} f(Y_1) \\ f(Y_2) \\ \vdots \\ f(Y_s) \end{bmatrix} \in X^s, \end{aligned}$$

\(s \in \mathbb {N}\) denotes the number of stages and its coefficient matrices are denoted by

$$\begin{aligned} A = [a_{ij}] \in \mathbb {R}^{s \times s}, \quad B = [b_{ij}] \in \mathbb {R}^{r \times s}, \quad U = [u_{ij}] \in \mathbb {R}^{s \times r}, \quad V = [v_{ij}] \in \mathbb {R}^{r \times r}. \end{aligned}$$

For compactness, we will refer to a GLM using its tableau: \(\left[ \begin{array}{c|c} A &{} U \\ \hline B &{} V \end{array} \right] .\)

2.2 Convergence, consistency and stability

Definition 2.1

[3, 4] A GLM with coefficient matrices (A, U, B, V) is said to be

  1. (a)

    Preconsistent, if (1, u, w) is an eigentriple of V, such that \(Vu=u\), \(w^{{\mathbf {\mathsf{{H}}}}} V = w^{{\mathbf {\mathsf{{H}}}}}\) and \(w^{{\mathbf {\mathsf{{H}}}}}u = 1\).

  2. (b)

    Consistent, if it is preconsistent, \(Uu = {\mathbb {1}}\) for \({\mathbb {1}} = [1,1,\ldots ,1]^{{{\mathbf {\mathsf{{T}}}}}} \in {\mathbb {R}}^{s}\) and \(\exists \) \(v \in \mathbb {C}^{r}\backslash \lbrace 0 \rbrace \) such that \(B\mathbb {1}+ Vv = u+v\)

  3. (c)

    Stable, if it is zero-stable, i.e. \(\sup _{n\ge 0}||V^n|| < \infty .\)

The convergence of a GLM is guaranteed if the method is both consistent and stable.

2.3 Starting and finishing methods

Inputs to a GLM generally take the form of B-series. Consequently, a starting method is required to generate the starting vector \(y^{[0]}\) and a finishing method is required to obtain approximations to the solution y(nh).

Definition 2.2

[3, 4] A starting method is defined as the map \(\mathcal {S}_h:X\rightarrow X^r\), where

$$\begin{aligned} \mathcal {S}_h(y_0) = y^{[0]}, \quad \forall \ y_0 \in {X}. \end{aligned}$$

A finishing method is defined as the map \(\mathcal {F}_h:X^r\rightarrow X\) such that

$$\begin{aligned} \mathcal {F}_h\circ \mathcal {S}_h(y_0) = y_0, \quad \forall \ y_0 \in {X}. \end{aligned}$$

Both \(\mathcal {S}_{ h}\) and \(\mathcal {F}_{ h}\) can be viewed as GLMs with tableaux respectively given by

$$\begin{aligned} \left[ \begin{array}{c|c} A_S &{} \mathbb {1}_S \\ \hline B_S &{} u \end{array} \right] , \quad \left[ \begin{array}{c|c} A_S-U_FB_S &{} U_F \\ \hline -w^{{\mathbf {\mathsf{{H}}}}} B_S &{} w^{{\mathbf {\mathsf{{H}}}}} \end{array} \right] , \end{aligned}$$
(2.2)

where u, w are as in the definition for preconsistency,

$$\begin{aligned} A_S \in \mathbb {R}^{\widetilde{s}\times \widetilde{s}}, \quad B_S \in \mathbb {C}^{r \times \widetilde{s}}, \quad U_F \in \mathbb {C}^{\widetilde{s}\times r}, \quad \mathbb {1}_S = [1,\ldots ,1]^{{{\mathbf {\mathsf{{T}}}}}} \in \mathbb {R}^{\widetilde{s}}, \quad \widetilde{s} \in \mathbb {N}, \end{aligned}$$

and it is assumed that

$$\begin{aligned} U_Fu = \mathbb {1}_S. \end{aligned}$$
(2.3)

Remark 2.1

If \(w^{{\mathbf {\mathsf{{H}}}}}\) and \(B_S\) satisfy \(w^{{\mathbf {\mathsf{{H}}}}} B_S = 0^{{{\mathbf {\mathsf{{T}}}}}}\), then the finishing method is trivial, i.e. it reduces to \(\mathcal {F}_{ h}(y^{[n]}) = (w^{{\mathbf {\mathsf{{H}}}}} \otimes I_X)y^{[n]}\). This is desirable as the finishing method need not perform any additional function evaluations to approximate y(nh).

The numerical method in its entirety may now be expressed as the composition

$$\begin{aligned} \mathcal {F}_h\circ \mathcal {M}^n_h\circ \mathcal {S}_h(y_0) \approx \varphi _{nh}(y_0). \end{aligned}$$

Definition 2.3

(GLM Order [3, 4]) The pair \((\mathcal {M}_{ h},\mathcal {S}_{ h})\) is of order \(p\in \mathbb {N}\) if

$$\begin{aligned} \mathcal {M}_h{\circ }\mathcal {S}_h(y_0) = \mathcal {S}_h{\circ }\varphi _h(y_0) + C(y_0)h^{p+1} + O(h^{p+2}), \end{aligned}$$
(2.4)

where \(C(y_0) \ne 0\) is a constant vector depending on the method and various derivatives of f evaluated at \(y_0\).

It is worth mentioning that starting and finishing methods have found application in a variety of areas outside of GLMs. For example, Butcher [2] uses them to achieve an effective order increase in RKMs. Chan and Gorgey [8] apply passive symmetrizers to the Gauss methods, where the symmetrizers are essentially finishing methods. Also, the Gragg smoother used in extrapolation codes (see e.g. [15, Ch. II.9]) is a finishing method that eliminates the leading order parasitic term in the Leapfrog method.

2.4 Composition

The composition of two GLMs, \( \mathcal {M}_{ h}^2\circ \mathcal {M}_{ h}^1\), can be computed using the following tableau:

$$\begin{aligned} \left[ \begin{array}{cc|c} A_1 &{} 0 &{} U_1\\ U_2B_1 &{} A_2 &{} U_2V_1 \\ \hline V_2B_1 &{} B_2 &{} V_2V_1 \end{array}\right] . \end{aligned}$$
(2.5)

where \((A_1,U_1,B_1,V_1)\), \((A_2,U_2,B_2,V_2)\) respectively denote the coefficient matrices of \(\mathcal {M}_{ h}^1\) and \(\mathcal {M}_{ h}^2\) (see e.g. [17, Ch. 2]).

2.5 Equivalence

Definition 2.4

[6] Consider a pair of GLMs with coefficient matrices \((A_1,U_1,B_1,V_1)\) and \((A_2,U_2,B_2,V_2)\). Then, the two are said to be (T, P)-equivalent if there exists an invertible matrix \(T \in \mathbb {C}^{r\times r}\) and an \(s \times s\) permutation matrix P such that their coefficient matrices satisfy

$$\begin{aligned} \left[ \begin{array}{c|c} A_2 &{} U_2 \\ \hline B_2 &{} V_2 \end{array} \right] = \left[ \begin{array}{c|c} P^{-1}A_1P &{} P^{-1}U_1T \\ \hline T^{-1}B_1P &{} T^{-1}V_1T \end{array} \right] . \end{aligned}$$

Permutation-based equivalence arises from the fact that \(F(Y) = PP^{-1}F(Y) = PF(P^{-1}Y)\). Transformation-based equivalence arises from studying the numerical method as a whole:

$$\begin{aligned} \mathcal {F}_{ h}\circ \mathcal {M}_{ h}^n\circ \mathcal {S}_{ h}(y_0)= & {} \mathcal {F}_{ h}\circ (TT^{-1})\mathcal {M}_{ h}^n\circ (TT^{-1})\mathcal {S}_{ h}(y_0) \\= & {} (\mathcal {F}_{ h}\circ T)(T^{-1}\mathcal {M}_{ h}\circ T)^n(T^{-1}\mathcal {S}_{ h})(y_0). \end{aligned}$$

Notice that under the transformation T, both starting and finishing methods also undergo a transformation, with their tableaux now reading as

$$\begin{aligned} \left[ \begin{array}{c|c} A_S &{} {\mathbb {1}}_S \\ \hline T^{-1}B_S &{} T^{-1}u \end{array} \right] , \quad \left[ \begin{array}{c|c} A_S-U_FB_S &{} U_FT \\ \hline -w^{{\mathbf {\mathsf{{H}}}}}B_S &{} w^{{\mathbf {\mathsf{{H}}}}} T \end{array} \right] . \end{aligned}$$

2.6 Symmetry

Definition 2.5

(OSM symmetry [14, Ch. II.4]) Consider the OSM \(\varPhi _h:X \rightarrow X\) and its adjoint method \(\varPhi _h^*:=\varPhi _{-h}^{-1}:X \rightarrow X\). Then, \(\varPhi _h\) is symmetric if \(\varPhi _h(y_0) = \varPhi ^*_h(y_0)\), \(\forall \ y_0 \in X\).

For a GLM, the direct analogue of this definition is quite restrictive. To see this, consider the tableau of the GLM-adjoint method \(\mathcal {M}_{ h}^*:=\mathcal {M}_{- h}^{-1}\):

$$\begin{aligned} \left[ \begin{array}{c|c} UV^{-1}B-A &{} UV^{-1} \\ \hline V^{-1}B &{} V^{-1} \end{array} \right] , \end{aligned}$$
(2.6)

which can be derived as follows: Let \(y^{[n]}\mapsto \mathcal {M}_{ h}^{-1}(y^{[n]})\) in the stage and update Eq. (2.1) and solve for \(\mathcal {M}_{ h}^{-1}(y^{[n]})\) to obtain the inverse method. Then, reverse the sign of h to obtain the adjoint method.

Here, we note that the inverse and adjoint methods exist if and only if \(V^{-1}\) exists. Furthermore, unless V is an involution, then a GLM cannot be symmetric according to the OSM definition. However, it is possible that a GLM is equivalent to its adjoint.

Definition 2.6

(GLM symmetry [6]) A GLM is said to be (L, P)-symmetric if there exists an \(r\times r\) involution matrix L, and an \(s\times s\) symmetric permutation matrix P such that it is (L, P)-equivalent to its adjoint, i.e. if its tableau satisfies

$$\begin{aligned} \left[ \begin{array}{c|c} A &{} U \\ \hline B &{} V \end{array} \right] = \left[ \begin{array}{c|c} P(UV^{-1}B-A)P &{} PUV^{-1}L \\ \hline LV^{-1}BP &{} LV^{-1}L \end{array} \right] . \end{aligned}$$
(2.7)

In terms of maps, the symmetry condition may be equivalently expressed as

$$\begin{aligned} \mathcal {M}_{ h}(y) = L\mathcal {M}_{ h}^*(Ly),\quad \forall \ y \in X^r. \end{aligned}$$

An important observation that should be noted is that the adjoint method requires a different set of starting and finishing methods, namely, \(\mathcal {S}_{-h}(y_0)\) and \(\mathcal {F}_{- h}(y^{[n]})\). This choice ensures that the order of the method is preserved, as is summarised by the following lemma.

Lemma 2.1

[6] If the pair \((\mathcal {M}_{ h},\mathcal {S}_{ h})\) is of order p then the pair \((\mathcal {M}_{ h}^*,\mathcal {S}_{- h})\) satisfies

$$\begin{aligned} \mathcal {M}_{ h}^*\circ \mathcal {S}_{-h}(y_0) = \mathcal {S}_{-h}\circ \varphi _h(y_0) + (-1)^pV^{-1}C(y_0)h^{p+1} + O(h^{p+2}). \end{aligned}$$

2.6.1 Symmetric starting and finishing methods

Since symmetry is defined in terms of equivalence to the adjoint method, it follows that there must exist an alternative set of starting and finishing methods that will not affect the order of the method [6].

Definition 2.7

[6] Consider an (L, P)-symmetric GLM with starting and finishing methods, \(\mathcal {S}_{ h}\) and \(\mathcal {F}_{ h}\), described by the tableaux (2.2). Then, \(\mathcal {S}_{ h}\) and \(\mathcal {F}_{ h}\) are said to be \((L,P_S)\)-symmetric if there exists a symmetric permutation matrix \(P_S\) such that

$$\begin{aligned} \left[ \begin{array}{c|c} A_S &{} {\mathbb {1}}_S \\ \hline B_S &{} u \end{array} \right]= & {} \left[ \begin{array}{c|c} -P_SA_SP_S &{} {\mathbb {1}}_S \\ \hline -LB_SP_S &{} Lu \end{array} \right] , \nonumber \\ \left[ \begin{array}{c|c} A_S-U_FB_S &{} U_F \\ \hline -w^{{\mathbf {\mathsf{{H}}}}}B_S &{} w^{{\mathbf {\mathsf{{H}}}}} \end{array} \right]= & {} \left[ \begin{array}{c|c} -P_S(A_S-U_FB_S)P_S &{} P_SU_FL \\ \hline w^{{\mathbf {\mathsf{{H}}}}}B_SP_S &{} w^{{\mathbf {\mathsf{{H}}}}}L \end{array} \right] . \end{aligned}$$
(2.8)

In terms of maps, condition (2.8) can be written as

$$\begin{aligned} \mathcal {S}_{ h}(y_0) = L\mathcal {S}_{- h}(y_0), \quad \forall ~y_0 \in X, \quad \hbox {and}\quad \mathcal {F}_{ h}(y) = \mathcal {F}_{- h}(Ly), \quad \forall ~y \in X^r. \end{aligned}$$

3 A canonical form for GLMs

In this section we consider equivalent methods that arise from a nonlinear change of coordinates. As we have seen in Sect. 2.5, any change of coordinates will also transform the corresponding starting and finishing methods. It is shown below that there exists a nonlinear transformation that can convert the starting and finishing methods to a trivial form, i.e. they are given by the preconsistency vectors u and \(w^{{\mathbf {\mathsf{{H}}}}}\).

Definition 3.1

A pth-order GLM is said to be canonical if its starting and finishing methods are given by its preconsistency vectors u and \(w^{{\mathbf {\mathsf{{H}}}}}\).

Canonical methods have the important property that their inputs are independent of h. Thus, we can compose multiple canonical methods of different time-steps provided only the preconsistency vectors agree.

Theorem 3.1

Every pth-order GLM \(\mathcal {M}_{ h}\), with starting and finishing methods, \(\mathcal {S}_{ h}\) and \(\mathcal {F}_{ h}\), determined by the tableaux (2.2), is equivalent to a pth-order canonical GLM defined by the composition

$$\begin{aligned} \mathcal {C}_{ h}= T_h^{-1}\circ \mathcal {M}_{ h}\circ T_h, \end{aligned}$$

where \(T_h,T_h^{-1}:X^r\rightarrow X^r\) are respectively determined by the GLM tableaux

$$\begin{aligned} \left[ \begin{array}{c|c} A_S &{} U_F \\ \hline B_S &{} I \end{array} \right] , \quad \mathrm{and} \quad \left[ \begin{array}{c|c} A_S-U_FB_S &{} U_F \\ \hline -B_S &{} I \end{array} \right] , \end{aligned}$$
(3.1)

where \(A_S, U_F, B_S\) are the coefficient matrices of \(\mathcal {S}_{ h}\) and \(\mathcal {F}_{ h}\), and I is the \(r \times r\) identity matrix.

Proof

Let the maps \(T_h,T_h^{-1}:X^r\rightarrow X^r\) be determined by the GLM tableaux (3.1). It can be verified using the GLM-adjoint tableau (2.6), with \(h \mapsto -h\), that the tableau for \(T_h^{-1}\) corresponds to the inverse method of \(T_h\). In other words,

$$\begin{aligned} T_h \circ T_h^{-1}(y) = T_h^{-1} \circ T_h(y) = y, \quad \hbox {for any}\quad y \in X^r. \end{aligned}$$

Now, consider a nonlinear transformation of the numerical method as a whole, i.e.

$$\begin{aligned} \mathcal {F}_{ h}\circ \mathcal {M}_{ h}^n\circ \mathcal {S}_{ h}(y_0)= & {} (\mathcal {F}_{ h}\circ T_h)\circ \left( T_h^{-1} \circ \mathcal {M}_{ h}\circ T_h\right) ^n\circ \left( T_h^{-1} \circ \mathcal {S}_{ h}\right) (y_0) \\= & {} \mathcal {F}_{ h}^{\mathcal {C}}\circ {\mathcal {C}^n_h}\circ \mathcal {S}_{ h}^{\mathcal {C}}(y_0). \end{aligned}$$

Note that the corresponding starting and finishing methods of \(\mathcal {C}_{ h}\) are given by

$$\begin{aligned} \mathcal {S}_{ h}^{\mathcal {C}}:=T_h^{-1} \circ \mathcal {S}_{ h}\quad \hbox {and}\quad \mathcal {F}_{ h}^{\mathcal {C}}:=\mathcal {F}_{ h}\circ T_h, \end{aligned}$$

where the tableaux for \(\mathcal {S}_{ h}\) and \(\mathcal {F}_{ h}\) are given by (2.2). Observe that the composition \(T_h\circ u\) yields a tableau of the form

$$\begin{aligned} \left[ \begin{array}{c|c} A_S &{} U_Fu \\ \hline B_S &{} u \end{array}\right] =\left[ \begin{array}{c|c} A_S &{} {\mathbb {1}}_S \\ \hline B_S &{} u \end{array} \right] , \end{aligned}$$

where we have used \(U_Fu = {\mathbb {1}}_S\) from (2.3). This agrees with the tableau for \(\mathcal {S}_{ h}\) and thus it follows that \(\mathcal {S}_{ h}^{\mathcal {C}}(y_0) = u\otimes y_0\). Also observe that \(w^{{\mathbf {\mathsf{{H}}}}}T_h^{-1}\) yields a tableau of the form

$$\begin{aligned} \left[ \begin{array}{c|c} A_S-U_FB_S &{} U_F \\ \hline -w^{{\mathbf {\mathsf{{H}}}}}B_S &{} w^{{\mathbf {\mathsf{{H}}}}} \end{array} \right] , \end{aligned}$$

which agrees with the tableau for \(\mathcal {F}_{ h}\), thus \(\mathcal {F}_{ h}^{\mathcal {C}}(y) = w^{{\mathbf {\mathsf{{H}}}}}y\).

Now, from the definition of GLM order (2.4) we know \(\mathcal {M}_{ h}\circ \mathcal {S}_{ h}(y_0) = \mathcal {S}_{ h}\circ \varphi _h(y_0) + O(h^{p+1})\). After pre-multiplying by \(T_h^{-1}\) we find

$$\begin{aligned}&T^{-1}_h\circ \mathcal {M}_{ h}\circ (T_h\circ T^{-1}_{h})\circ \mathcal {S}_{ h}(y_0) = T^{-1}_h\circ \mathcal {S}_{ h}(\varphi _h(y_0)) + O(h^{p+1}), \\&\quad \Longrightarrow \mathcal {C}_{ h}(uy_0) = u\varphi _h(y_0) + O(h^{p+1}). \end{aligned}$$

Thus, \((\mathcal {C}_{ h},u)\) is of order p, and by Definition 3.1 it follows that \(\mathcal {C}_{ h}\) is a canonical method. \(\square \)

Remark 3.1

In the above theorem, a different notion of equivalence is used than that was introduced in Definition 2.4, i.e. w.r.t. a nonlinear transformation \(T_h\). However, note that if \(T_h = T_0 = T\) for some \(T \in X^{r\times r}\) then equivalence is defined in the usual sense.

The tableau for the corresponding canonical method of a GLM may be obtained using the tableau composition formula (2.5):

$$\begin{aligned} \left[ \begin{array}{ccc|c} A_S &{} 0 &{} 0 &{} U_F \\ UB_S &{} A &{} 0 &{} U \\ U_FVB_S &{} U_FB &{} A_S - U_FB_S &{} U_FV \\ \hline VB_S &{} B &{} -B_S &{} V \end{array}\right] . \end{aligned}$$
(3.2)

Preservation of symmetry In general, performing a nonlinear change of coordinates runs the risk of destroying certain properties of the underlying GLM. In particular, symmetry is not preserved unless the starting and finishing methods are also symmetric.

Corollary 3.1

Suppose that \(\mathcal {M}_{ h}\) is (L, P)-symmetric. If \(\mathcal {S}_{ h}\) and \(\mathcal {F}_{ h}\) are \((L,P_S)\)-symmetric, then \(\mathcal {C}_{ h}\) is symmetric.

Proof

Since \(\mathcal {S}_{ h}\) and \(\mathcal {F}_{ h}\) are symmetric, this implies that their coefficient matrices satisfy condition (2.8), i.e.

$$\begin{aligned} A_S= & {} -P_SA_SP_S, \quad B_S = -LB_SP_S, \quad Lu = u, \\ U_F= & {} P_SU_FL, \quad w^{{\mathbf {\mathsf{{H}}}}} L = w^{{\mathbf {\mathsf{{H}}}}}. \end{aligned}$$

Upon substitution into the tableaux for \(T_h\) and \(T_h^{-1}\) we deduce that \(T_h = LT_{-h}L\) and \(T_h^{-1} = LT_{-h}^{-1}L\). Now, by the symmetry of \(\mathcal {M}_{ h}\), we observe that

$$\begin{aligned} \mathcal {C}_{ h}= T_h^{-1}\circ \mathcal {M}_{ h}\circ T_h = T_h^{-1}\circ L\mathcal {M}_{ h}^*\circ LT_h = (T_h^{-1}\circ L T_h^{-*})\circ \mathcal {C}_{ h}^*\circ \left( T_h^*\circ LT_h\right) . \end{aligned}$$

However,

$$\begin{aligned} T_h^* \circ LT_h = T_{-h}^{-1} \circ LT_h = T_{-h}^{-1} \circ T_{-h} \circ L = L. \end{aligned}$$

Thus, the canonical method \(\mathcal {C}_{ h}= L\mathcal {C}_{ h}^* \circ L\) is symmetric, as required. \(\square \)

Preservation of parasitism-free behaviour: In recent work [5, 6], it has been shown that structure-preserving GLMs can be designed such that they are free from the influence of parasitism over intervals of length \(O(h^{-2})\) [11]. In particular, if their coefficient matrices and preconsistency vectors satisfy the following condition [6]:

$$\begin{aligned} w^{{{\mathbf {\mathsf{{T}}}}}} BUu = 0. \end{aligned}$$
(3.3)

Corollary 3.2

Suppose that \(\mathcal {M}_{ h}\) satisfies the parasitism-free condition (3.3). Then, \(\mathcal {C}_{ h}\) is also parasitism-free.

Proof

From (3.2), we take the expressions for the B, U matrices of \(\mathcal {C}_{ h}\) and insert into the LHS of (3.3) to find

$$\begin{aligned} w^{{{\mathbf {\mathsf{{T}}}}}} VB_SU_Fu + w^{{{\mathbf {\mathsf{{T}}}}}} BUu - w^{{{\mathbf {\mathsf{{T}}}}}} B_SU_FVu = w^{{{\mathbf {\mathsf{{T}}}}}} B_SU_Fu - w^{{{\mathbf {\mathsf{{T}}}}}} B_SU_Fu = 0, \end{aligned}$$

where we have used \(Vu = u\), \(w^{{{\mathbf {\mathsf{{T}}}}}} V = w^{{{\mathbf {\mathsf{{T}}}}}}\) from the definition of the preconsistency vectors, and \(w^{{{\mathbf {\mathsf{{T}}}}}} BU u = 0\) since \(\mathcal {M}_{ h}\) satisfies (3.3). Thus, \(\mathcal {C}_{ h}\) is also parasitism-free. \(\square \)

Example 3.1

It has been shown by Gragg [13] that the Leapfrog method,

$$\begin{aligned} U_{n+1} = U_{n-1} + 2hf(U_n), \quad \text {or equivalently as a GLM}, \quad \left[ \begin{array}{c@{\quad }|c@{\quad }c} 0 &{} 0 &{} 1 \\ \hline 0 &{} 0 &{} 1 \\ 2 &{} 1 &{} 0 \end{array} \right] , \end{aligned}$$

when initialised with the Euler starter,

$$\begin{aligned} y^{[0]} = \begin{bmatrix} y_0 \\ y_0 + hf(y_0) \end{bmatrix}, \quad \hbox {or equivalently},\quad \left[ \begin{array}{c@{\quad }|@{\quad }c} 0 &{} 1 \\ \hline 0 &{} 1 \\ 1 &{} 1 \end{array} \right] , \end{aligned}$$

yields a global error expansion in even powers of h. In the context of symmetric GLMs, we cannot directly explain this result as the Euler starter is not symmetric with respect to the L-involution of the Leapfrog method: \( L = \begin{bmatrix} 0&1 \\ 1&0 \end{bmatrix}\). However, we can explain Gragg’s result using the canonical form given by (3.2):

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c|c@{\quad }c} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 &{} 1 \\ 1 &{} 0 &{} 0 &{} 0 &{} 1 \\ \hline 1 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 2 &{} -1 &{} 1 &{} 0 \end{array} \right] , \end{aligned}$$

Here, we observe that the second and third stage equations are equivalent, which implies there is a redundancy in the representation of the method. By removing one of these redundant stages (i.e. combining the second and third columns together, then removing the third row), we obtain the irreducible representation given by the tableau

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }|c@{\quad }c} 0 &{} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 &{} 1 \\ \hline 1 &{} 0 &{} 0 &{} 1 \\ 0 &{} 1 &{} 1 &{} 0 \end{array} \right] . \end{aligned}$$

It can now be verified using the symmetry conditions (2.7), that the canonical method is \((L_\mathcal {C},P_\mathcal {C})\)-symmetric where

$$\begin{aligned} L_\mathcal {C} = \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix}, \quad P_\mathcal {C} = \begin{bmatrix} 0&1 \\ 1&0 \end{bmatrix}. \end{aligned}$$

In addition, we observe that the starting and finishing methods, u and \(w^{{\mathbf {\mathsf{{H}}}}}\), are trivially symmetric, i.e. \(L_\mathcal {C}u = u\) and \(w^{{\mathbf {\mathsf{{H}}}}} L_\mathcal {C} =w^{{\mathbf {\mathsf{{H}}}}}\). Thus, the Leapfrog method written out in full is given by

$$\begin{aligned} \mathcal {F}_{ h}\circ \mathcal {M}_{ h}^n\circ \mathcal {S}_{ h}(y_0) = w^{{\mathbf {\mathsf{{H}}}}} \mathcal {C}_{ h}^n \circ uy_0, \end{aligned}$$

where \(w^{{\mathbf {\mathsf{{H}}}}}\), \(\mathcal {C}_{ h}\) and u are all symmetric with respect to \(L_\mathcal {C}\). Finally, we may now apply Theorem 14 of [6], which states that a symmetric GLM of even order p, with symmetric starting and finishing methods, yields a global error expansion in even powers of h.

4 Composition of GLMs

4.1 Composition of canonical methods

Consider a canonical GLM \(\mathcal {C}_{ h}\) with an invertible matrix V. Since inputs to canonical methods are given by their preconsistency vector u we can consider a straightforward generalisation of composition (1.1) to GLMs:

$$\begin{aligned} \mathcal {C}_{ h}^A:=\mathcal {C}_{\beta _k h}^*\circ \mathcal {C}_{\alpha _k h}\circ \cdots \circ \mathcal {C}_{\beta _2 h}^*\circ \mathcal {C}_{\alpha _2 h}\circ \mathcal {C}_{\beta _1 h}^*\circ \mathcal {C}_{\alpha _1 h}. \end{aligned}$$
(4.1)

It can be shown that the conditions on \(\alpha _1,\ldots ,\alpha _k,\beta _1,\ldots ,\beta _k\) required for an order increase agree with those used for the composition of OSMs.

Theorem 4.1

Suppose the pair \((\mathcal {C}_{ h},u)\) is of order \(p\in \mathbb {N}\) and its V-matrix is invertible. Then, the pair \((\mathcal {C}_{ h}^A,u)\) is at least of order \(p+1\) provided

$$\begin{aligned}&\alpha _1+\beta _1 + \alpha _2 + \beta _2 + \cdots + \alpha _k + \beta _k = 1, \end{aligned}$$
(4.2)
$$\begin{aligned}&\alpha _1^{p+1}+(-1)^p\beta _1^{p+1} + \alpha _2^{p+1} + (-1)^p\beta _2^{p+1} + \cdots + \alpha _k^{p+1} + (-1)^p\beta _k^{p+1} = 0. \end{aligned}$$
(4.3)

Proof

Recall that if V is invertible then \(\mathcal {C}_{ h}^{-1}\), and consequently \(\mathcal {C}_{ h}^*\), exist. Thus, the method arising from a composition of the form (4.1) also exists. Now, from Lemma 2.1, if the pair \((\mathcal {M}_{ h},\mathcal {S}_{ h})\) is of order p, i.e.

$$\begin{aligned} \mathcal {M}_{ h}\circ \mathcal {S}_{ h}(y_0) = \mathcal {S}_{ h}\circ \varphi _h(y_0) + h^{p+1}C(y_0) + O(h^{p+2}), \end{aligned}$$

then the pair \((\mathcal {M}_{ h}^*,\mathcal {S}_{- h})\) satisfies

$$\begin{aligned} \mathcal {M}_{ h}^*\circ \mathcal {S}_{- h}(y_0) = \mathcal {S}_{- h}\circ \varphi _{h}(y_0) + (-1)^p h^{p+1} V^{-1}C(y_0) + O(h^{p+2}). \end{aligned}$$

For canonical methods, \(\mathcal {S}_{ h}=\mathcal {S}_{- h}=u\). Thus, for each \(j \in \lbrace 1,\ldots ,k \rbrace \), we have

$$\begin{aligned} \mathcal {C}_{\alpha _j h}(uy_0)&= u\varphi _{\alpha _jh} + \alpha _j^{p+1}h^{p+1}C(y_0) + O(h^{p+2}), \\ \mathcal {C}_{\beta _j h}^*(uy_0)&= u\varphi _{\beta _jh} + (-1)^p\beta _j^{p+1}h^{p+1}V^{-1}C(y_0) + O(h^{p+2}). \end{aligned}$$

Composing these expressions, we find that

$$\begin{aligned} \mathcal {C}^*_{\beta _jh}\circ \mathcal {C}_{\alpha _jh}(uy_0)&= \mathcal {C}^*_{\beta _jh}(u\varphi _{\alpha _jh}(y_0)+C(y_0)h^{p+1}\alpha _j^{p+1} + O(h^{p+2})), \\&= \mathcal {C}^*_{\beta _jh}(u\varphi _{\alpha _jh}(y_0))+V^{-1}C(y_0)h^{p+1}\alpha _j^{p+1} + O(h^{p+2}), \\&= u\varphi _{(\alpha _j+\beta _j)h}(y_0)+V^{-1}C(y_0)h^{p+1}\left( \alpha _j^{p+1}+ (-1)^p\beta _j^{p+1} \right) \\&\quad + O(h^{p+2}), \end{aligned}$$

where we have applied \(\mathcal {C}_{a h}^*(y+z) = \mathcal {C}_{a h}^*(y) + V^{-1}z + O(ah||z||)\), and \(C(\varphi _{ah}(y_0)) = C(y_0) + O(ah)\).

Recursively applying the above result to each \(\mathcal {C}^*_{\beta _jh}\circ \mathcal {C}_{\alpha _jh}\) in the order of \(j=1,\ldots ,k\) we find

$$\begin{aligned} \mathcal {C}_{ h}^A(uy_0)= & {} u\varphi _{\sum _{j=1}^k(\alpha _j+\beta _j)h}(y_0) + V^{-1}C(y_0)h^{p+1}\sum _{j=1}^k\left( \alpha ^{p+1}_j+(-1)^p\beta ^{p+1}_j\right) \\&+ O(h^{p+2}). \end{aligned}$$

Thus, if (4.2) and (4.3) are satisfied, it follows that the pair \((\mathcal {C}_h^A,u)\) is at least of order \(p+1\). \(\square \)

To obtain an adjoint-free composition, i.e. a GLM-generalisation of (1.2), we set \(\beta _j = 0\) for \(j=1,\ldots ,k\) in (4.1). This choice replaces each \(\mathcal {C}_{\beta _j h}^*\) by \(V^{-1}\) to give

$$\begin{aligned} \mathcal {C}_h^{A} = V^{-1}\mathcal {C}_{\alpha _k h}\circ \cdots \circ V^{-1}\mathcal {C}_{\alpha _2 h}\circ V^{-1}\mathcal {C}_{\alpha _1 h}. \end{aligned}$$

Notice here that the final left-hand multiplication by \(V^{-1}\) will not affect the order of the method as \(Vu=u\). In other words, if \((\mathcal {C}_h^{A},u)\) is of order p, then \((V\mathcal {C}_h^{A},u)\) is also of order p, since

$$\begin{aligned} V\mathcal {C}_h^{A}(uy_0) = V\left( u\varphi _h(y_0) + O(h^{p+1})\right) = u\varphi _h(y_0)+ O(h^{p+1}). \end{aligned}$$

Thus, we define the adjoint-free composition of canonical GLMs as

$$\begin{aligned} \mathcal {C}_{ h}^{B}:= \mathcal {C}_{\alpha _k h}\circ \cdots \circ V^{-1}\mathcal {C}_{\alpha _2 h}\circ V^{-1}\mathcal {C}_{\alpha _1 h}. \end{aligned}$$
(4.4)

Corollary 4.1

Let the assumptions of Theorem 4.1 hold. Then, the pair \((\mathcal {C}_{ h}^{B},u)\) is at least of order \(p+1\) provided

$$\begin{aligned}&\alpha _1 + \alpha _2 + \cdots + \alpha _k = 1, \end{aligned}$$
(4.5)
$$\begin{aligned}&\alpha _1^{p+1} + \alpha _2^{p+1} + \cdots + \alpha _k^{p+1} = 0 . \end{aligned}$$
(4.6)

Proof

This follows from Theorem 4.1 with \(\beta _1 = \cdots = \beta _s = 0\), noting that \(Vu = u\). \(\square \)

Remark 4.1

The route we have taken in deriving (4.4) is important, as a direct application of (1.2) to canonical GLMs would fail to include the intermediate multiplications by \(V^{-1}\). So while the composition would be valid, an order increase under conditions (4.5)–(4.6) would not necessarily be achieved since (4.6) would read \(\sum _{j=1}^k\alpha _{k-j+1}^{p+1}V^{j-1} = 0\).

Preservation of symmetry Suppose now that the canonical method is (L, P)-symmetric. Without loss of generality, we restrict our attention to compositions of the form (4.4) as, by definition, a symmetric method is similar to its adjoint.

Corollary 4.2

Let \(\mathcal {C}_{ h}\) be an (L, P)-symmetric, canonical GLM. Then, composition (4.4) is symmetric if \(\alpha _j = \alpha _{k-j+1}\), for \(j=1,\ldots ,k\).

Proof

Taking the adjoint of \(\mathcal {C}_{ h}^{B}\), we find

$$\begin{aligned} \left( \mathcal {C}_{ h}^{B}\right) ^* = \left( \mathcal {C}_{\alpha _k h}\circ \cdots \circ V^{-1}\mathcal {C}_{\alpha _2 h}\circ V^{-1}\mathcal {C}_{\alpha _1 h}\right) ^* = \mathcal {C}_{\alpha _1 h}^*\circ \cdots \circ V\mathcal {C}_{\alpha _{k-1} h}^*\circ V\mathcal {C}_{\alpha _k h}^*. \end{aligned}$$

By assumption, \(\alpha _j = \alpha _{k-j+1}\), for \(j=1,\ldots ,k\). Thus, this becomes

$$\begin{aligned} \left( \mathcal {C}_{ h}^{B}\right) ^* = \mathcal {C}_{\alpha _k h}^*\circ \cdots \circ V\mathcal {C}_{\alpha _{2} h}^*\circ V\mathcal {C}_{\alpha _1 h}^*. \end{aligned}$$

Since \(\mathcal {C}_{ h}\) is symmetric, we have that \(\mathcal {C}_{ h}= L\mathcal {C}_{ h}^*\circ L\) and \(LVL = V^{-1}\). Therefore,

$$\begin{aligned} \left( \mathcal {C}_{ h}^{B}\right) ^*&= (L\mathcal {C}_{\alpha _k h}\circ L)\circ \cdots \circ VL\mathcal {C}_{\alpha _{2} h}\circ LVL\mathcal {C}_{\alpha _1 h} \circ L, \\&= L\mathcal {C}_{\alpha _k h} \circ \cdots \circ V^{-1}\mathcal {C}_{\alpha _{2} h}\circ V^{-1}\mathcal {C}_{\alpha _1 h} \circ L = L\mathcal {C}_{ h}^{B} \circ L, \end{aligned}$$

and the method is symmetric as required. \(\square \)

The above result coupled with the necessity of even order for symmetric methods (cf. Theorem 14 of [6]) implies that the composite method will achieve an increase of two orders, i.e. \(p \mapsto p+2\). Furthermore, this composition can be repeatedly applied to generate canonical COSY-GLMs of arbitrarily high order.

Preservation of parasitism-free behaviour Consider now the case that the canonical method is also parasitism-free.

Corollary 4.3

Let \(\mathcal {C}_{ h}\) satisfy the parasitism-free condition (3.3). Then, composition (4.4) is also parasitism-free.

Proof

Repeatedly applying the tableau composition formula of (2.5), we find that the corresponding B, U matrices of (4.4) are respectively given by

$$\begin{aligned} {[}B\alpha _1 \quad B\alpha _2 \quad \cdots \quad B\alpha _k] \quad \hbox {and}\quad [U^{{{\mathbf {\mathsf{{T}}}}}} \quad U^{{{\mathbf {\mathsf{{T}}}}}} \quad \cdots \quad U^{{{\mathbf {\mathsf{{T}}}}}}]^{{{\mathbf {\mathsf{{T}}}}}}. \end{aligned}$$

Inserting these into the LHS of (3.3), we find

$$\begin{aligned} (w^{{{\mathbf {\mathsf{{T}}}}}} BU u)\sum _{j=1}^{k}\alpha _j = 0, \end{aligned}$$

where we have applied \(w^{{{\mathbf {\mathsf{{T}}}}}} BUu = 0\) since \(\mathcal {C}_{ h}\) is parasitism-free. Thus, composition (4.4) is also parasitism-free. \(\square \)

4.2 Composition of non-canonical methods

Consider now a composition method based on an invertible GLM with arbitrary inputs. The corresponding composition formulae and results all extend straightforwardly from those given in the previous section after making the substitution \(\mathcal {C}_{ h}= T_h^{-1} \circ \mathcal {M}_{ h}\circ T_h\). In particular, the general form of (4.1) is written as

$$\begin{aligned} \mathcal {M}^A_h:= & {} R_A(\alpha _1,\beta _k)\circ \mathcal {M}_{\beta _kh}^* R_A^{-1}(\alpha _k,\beta _k)\circ \mathcal {M}_{\alpha _kh}\circ R_A(\alpha _k,\beta _{k-1})\circ \cdots \circ \\&R_A^{-1}(\alpha _2,\beta _2)\circ \mathcal {M}_{\alpha _2h}\circ R_A(\alpha _2,\beta _1)\circ \mathcal {M}_{\beta _1h}^*\circ R_A^{-1}(\alpha _1,\beta _1)\circ \mathcal {M}_{\alpha _1h}, \end{aligned}$$

where \(R_A(a,b):= T_{ah}\circ T^*_{bh}\), and for (4.4) this is

$$\begin{aligned} \mathcal {M}_{ h}^{B}:=\left( T_{\alpha _1h}\circ T_{\alpha _kh}^{-1}\right) \circ \mathcal {M}_{\alpha _kh}\circ R_B(\alpha _k,\alpha _{k-1})\circ \cdots \circ \mathcal {M}_{\alpha _2h}\circ R_B(\alpha _2,\alpha _1)\circ \mathcal {M}_{\alpha _1h}, \end{aligned}$$
(4.7)

where \(R_B(a,b):=T_{ah}\circ V^{-1}T^{-1}_{bh}\). In addition, the starting and finishing methods are given by

$$\begin{aligned} \mathcal {S}_{ h}^A = \mathcal {S}_{ h}^{B} = \mathcal {S}_{\alpha _1 h} \quad \hbox {and} \quad \mathcal {F}_{ h}^A = \mathcal {F}_{ h}^{B} = \mathcal {F}_{\alpha _1 h}, \end{aligned}$$

where \(\mathcal {S}_{ h}\) and \(\mathcal {F}_{ h}\) are the starting and finishing methods of the base GLM \(\mathcal {M}_{ h}\).

Example 4.1

From composition (4.7), we can obtain the GLM version of the triple jump:

$$\begin{aligned} \mathcal {M}_{ h}^T:= \mathcal {M}_{\alpha _1h}\circ R_B(\alpha _1,\alpha _2)\circ \mathcal {M}_{\alpha _2h}\circ R_B(\alpha _2,\alpha _1)\circ \mathcal {M}_{\alpha _1h}, \end{aligned}$$
(4.8)

where, for \(\mathcal {M}_{ h}\) of even order p, \(\alpha _1\) and \(\alpha _2\) are given in (1.3). Similarly, we can obtain the GLM version of the Suzuki 5-jump:

$$\begin{aligned} \mathcal {M}_{ h}^S:= & {} \mathcal {M}_{\alpha _1h}\circ R_B(\alpha _1,\alpha _1)\circ \mathcal {M}_{\alpha _1h}\circ R_B(\alpha _1,\alpha _2) \nonumber \\&\circ \cdots \mathcal {M}_{\alpha _2h}\circ R_B(\alpha _2,\alpha _1) \circ \mathcal {M}_{\alpha _1h}\circ R_B(\alpha _1,\alpha _1)\circ \mathcal {M}_{\alpha _1h}, \end{aligned}$$
(4.9)

where \(\alpha _1\) and \(\alpha _2\) are given in (1.4).

Stage reductions: Consider the straightforward implementation of a COSY-GLM (e.g. in its canonical form), possibly using multiple iterations, such that the resulting method attains order \(p_D \in \mathbb {N}\). Then, the total number of stages that require evaluation are given by

$$\begin{aligned}&3^\frac{{p_D-p}}{2}\cdot (s+2\tilde{s}) \quad \hbox {when only using }(4.8), \\&5^\frac{{p_D-p}}{2}\cdot (s+2\tilde{s}) \quad \hbox {when only using }(4.9), \end{aligned}$$

where \(\tilde{s}\) denotes the number of stages in the starting method.

Improvements to the implementation can be made by identifying and removing any redundant stages prior to integration. For example, the nonlinear map \(R_B(a,b)\) which is performed between method evaluations has the GLM tableau:

$$\begin{aligned} \left[ \begin{array}{cc|c} (A_S-U_FB_S)b &{} 0 &{} U_F \\ -U_FV^{-1}B_Sb &{} A_Sa &{} U_FV^{-1} \\ \hline -V^{-1}B_Sb &{} B_Sa &{} V^{-1} \end{array}\right] . \end{aligned}$$

Suppose \(A_S\) is an  \(\widetilde{s}\, \times \, \widetilde{s}\) matrix, then this tableau suggests that a total of \(2\widetilde{s}\) stage equations must be solved for each \(R_B(a,b)\)-evaluation. However, if we choose \(U_{F}= {\mathbb {1}}_Sw_1^{{\mathbf {\mathsf{{H}}}}}\), where \(w_1\) is the left eigenvector of V corresponding to eigenvalue \(\zeta =1\), then in the case \(a=b\) (see Suzuki composition (4.9)) we find a reduction to \(\widetilde{s}\)-many stages occurs, i.e. the tableau for \(R_B(a,a)\) actually reads

$$\begin{aligned} \left[ \begin{array}{c|c} A_Sa &{} U_F \\ \hline (I-V^{-1})B_Sa &{} V^{-1} \end{array}\right] . \end{aligned}$$

As reductions of this type are both method and composition dependent, we suggest that each (distinct) nonlinear map \(R_B(a,b)\) is implemented as an individual GLM, with redundant stages removed. Then, compositions such as the Suzuki 5-jump (4.9) would be performed in the fashion

$$\begin{aligned} \mathcal {M}_{ h}^S:= \mathcal {M}_{\alpha _1h}\circ R_1\circ \mathcal {M}_{\alpha _1h}\circ R_3\circ \mathcal {M}_{\alpha _2h}\circ R_2\circ \mathcal {M}_{\alpha _1h}\circ R_1\circ \mathcal {M}_{\alpha _1h}, \end{aligned}$$

where \(R_1 = R_B(\alpha _1,\alpha _1)\), \(R_2 = R_B(\alpha _2,\alpha _1)\) and \(R_3 = R_B(\alpha _1,\alpha _2)\) are each distinct, and irreducible GLMs.

5 Numerical experiments

In following set of experiments, we consider compositions of methods under the triple jump (4.8) and the Suzuki 5-jump (4.9). To indicate which specific composition is used we adopt the naming convention T.method for the triple jump and S.method for Suzuki 5-jump. For example, a triple jump of a method named GLM4A would be referred to as T.GLM4A.

The numerical experiments we consider are as follows: Firstly, we computationally verify that the proposed COSY-formulae yield an appropriate order increase. Here, we consider compositions of 4th to 6th-order methods (see also [17, Ch. 7] for higher order). Secondly, we perform efficiency comparisons in terms of accuracy versus function evaluations. Here, accuracy is measured by either the trajectory error or the maximum absolute deviation in the Hamiltonian. Finally, we investigate long-time Hamiltonian preservation of the composition methods on several reversible Hamiltonian systems. In particular, we consider

(P1) :

Modified pendulum (see [14, Ch. XV.5]): For \(y = [p,q]^{{{\mathbf {\mathsf{{T}}}}}}\),

$$\begin{aligned} H(p,q)&= \frac{1}{2}p^2 - \cos (q)\left( 1-\frac{p}{6}\right) , \\ (p_0,q_0)&= (2,1). \end{aligned}$$
(P2) :

Bead on a wire (see [1]): For \(y = [p,q]^{{{\mathbf {\mathsf{{T}}}}}}\),

$$\begin{aligned} H(p,q)&= \frac{p^2}{2(1+U^{\prime }(q)^2)} + U(q), \quad U(q) = 0.1(q(q-2))^2+0.008q^3, \\ (p_0,q_0)&= (0.49,0). \end{aligned}$$
(P3) :

Kepler (see [14, Ch. I.2]): For \(y = [p_1,p_2,q_1,q_2]^{{{\mathbf {\mathsf{{T}}}}}}\),

$$\begin{aligned} H(p_1,p_2,q_1,q_2)&= \frac{1}{2}(p_1^2+p_2^2) - (q_1^2+q_2^2)^{-\frac{1}{2}}, \\ (p_{10},p_{20},q_{10},q_{20})&= \left( 0,\sqrt{\frac{1+e}{1-e}},1-e,0\right) , \quad e = 0.6. \end{aligned}$$

5.1 Methods

5.1.1 Symmetric GLMs

The following GLMs are both 4th-order, (L, P)-symmetric and satsify the parasitism-free condition (3.3):

$$\begin{aligned} \begin{array}{c@{\quad }c@{\quad }c} \left[ \begin{array}{r@{\quad }r@{\quad }r|r@{\quad }r} 0 &{} 0 &{} 0 &{} 1 &{} 1 \\ -\frac{1}{8} &{} \frac{1}{4} &{} 0 &{} 1 &{} \frac{1}{4}\\ -\frac{1}{8} &{} \frac{1}{2} &{} \frac{1}{4} &{} 1 &{} \frac{1}{4} \\ \hline -\frac{1}{3} &{} \frac{2}{3} &{} \frac{2}{3} &{} 1 &{} 0 \\ -\frac{1}{3} &{} \frac{2}{3} &{} \frac{2}{3} &{} 0 &{} -1\\ \end{array} \right] &{} \qquad &{} \left[ \begin{array}{r@{\quad }r@{\quad }r|r@{\quad }r} 0 &{} 0 &{} 0 &{} 1 &{} 1 \\ \frac{1}{2} &{} \frac{1}{2} &{} 0 &{} 1 &{} -2 \\ \frac{3}{2} &{} \frac{1}{2} &{} 0 &{} 1 &{} -2 \\ \hline \frac{2}{3} &{} \frac{1}{6} &{} \frac{1}{6} &{} 1 &{} 0 \\ \frac{2}{3} &{} \frac{1}{6} &{} \frac{1}{6} &{} 0 &{} -1\\ \end{array} \right] \\ &{} \qquad &{} \\ \hbox {GLM4A} &{} \qquad &{} \hbox {GLM4B} \end{array} \quad \hbox {where} \quad L = \begin{bmatrix} 1&0 \\ 0&-1 \end{bmatrix}, \quad P = \begin{bmatrix} 1&0&0 \\ 0&0&1 \\ 0&1&0 \end{bmatrix}. \end{aligned}$$

In order to attain 4th-order, both GLMs must approximate the starting vector

$$\begin{aligned} y^{[0]} = \begin{bmatrix} y_0 \\ \frac{h}{2}\frac{\mathrm {d}y}{\mathrm {d}t}(0) - \frac{h^3}{24}\frac{\mathrm {d}^3y}{\mathrm {d}t^3}(0) \end{bmatrix}, \end{aligned}$$

which can be achieved using the following \((L,P_S)\)-symmetric starting method:

The corresponding finishing method is given by the first component, i.e. \(\mathcal {F}_{ h}(y) = y_1\).

Note that since both GLMs share the same starting and finishing methods, they also share the same canonical transformation \(T_h\). The tableaux for both \(T_h\) and \(T_h^{-1}\) are given respectively below

where the choice \(U_F = {\mathbb {1}}_Se_1^{{{\mathbf {\mathsf{{T}}}}}}\) has been made such that \(T_h^{-1}\) is also explicit.

Fig. 1
figure 1

Order diagrams. Reference lines of gradient 6 are given by diagonally dotted lines. a Triple jump methods, b Suzuki methods

Full size image
Fig. 2
figure 2

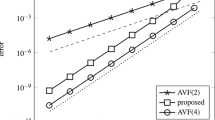
\(\varepsilon _h\)-error versus function evaluation diagrams for the Hamiltonian IVP from Sect. 5.2. a Triple jump, b Suzuki

Full size image

5.1.2 Symmetric RKMs

For comparison, we have chosen methods from the class of symmetric DIRKs which are closest, in the sense of structure, to GLM4A and GLM4B, i.e. their stage equations can be solved sequentially.

Remark 5.1

Higher-order Gauss and Lobatto methods are not considered as their stage equations are typically solved ‘all-at-once’, i.e. in the product space \(X^s\), in conjunction with a sophisticated iteration scheme (see e.g. [9]).

The Butcher tableaux for two 4th-order symmetric DIRKs are given as follows:

$$\begin{aligned} \begin{array}{ccc} \begin{array}{c|ccc} \frac{\alpha _1}{2} &{} \frac{\alpha _1}{2} &{} 0 &{} 0 \\ \frac{1}{2} &{} \alpha _1 &{} \frac{\alpha _2}{2} &{} 0 \\ 1-\frac{\alpha _1}{2} &{} \alpha _1 &{} \alpha _2 &{} \frac{\alpha _1}{2} \\ \hline &{} \alpha _1 &{} \alpha _2 &{} \alpha _1 \end{array} &{} \qquad &{} \begin{array}{c|ccccc} \frac{\alpha _1}{2} &{} \frac{\alpha _1}{2} &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{3\alpha _1}{2} &{} \alpha _1 &{} \frac{\alpha _1}{2} &{} 0 &{} 0 &{} 0 \\ \frac{1}{2} &{} \alpha _1 &{} \alpha _1 &{} \frac{\alpha _2}{2} &{} 0 &{} 0 \\ 1-\frac{3\alpha _1}{2} &{} \alpha _1 &{} \alpha _1 &{} \alpha _2 &{} \frac{\alpha _1}{2} &{} 0 \\ 1-\frac{\alpha _1}{2} &{} \alpha _1 &{} \alpha _1 &{} \alpha _2 &{} \alpha _1 &{} \frac{\alpha _1}{2} \\ \hline &{} \alpha _1 &{} \alpha _1 &{} \alpha _2 &{} \alpha _1 &{} \alpha _1 \end{array} \\ &{} \qquad &{} \\ \hbox {DIRK43} &{} \qquad &{} \hbox {DIRK45} \end{array} \end{aligned}$$

Note that both DIRKs are formed by compositions of the implicit midpoint rule. DIRK43 is based on the triple jump with \(\alpha _1\), \(\alpha _2\) given by (1.3) and DIRK45 is a Suzuki 5-jump with \(\alpha _1\), \(\alpha _2\) given by (1.4).

Fig. 3
figure 3

\(\max _n |H_n - H_0|\) versus function evaluation diagrams for the Hamiltonian IVP from Sect. 5.2. a Triple jump, b Suzuki

Full size image

5.1.3 Implementation

We have ensured the update procedure is consistent across all methods. Specifically, the stage equations are solved sequentially using fixed point iteration. The termination criteria are given by

$$\begin{aligned} ||\varDelta _k||_\infty < 10^{-12} \quad \hbox {and} \quad ||\varDelta _{k+1}||_\infty > ||\varDelta _k||_\infty , \quad k \in \mathbb {N}, \end{aligned}$$

where \(\varDelta _k\) denotes the difference between iterates k and \(k+1\). Also, redundant stages in the COSY-GLMs have been identified and removed prior to each integration.

5.2 Order confirmation

Consider problem (P3) which is known to be \(2\pi \)-periodic (see e.g. [14, Ch. I.2.3]): Let \(T = 10\pi \) and define h such that \(N_h:=T/h\) is an integer. Then, for various values of h, we measure the \(\varepsilon _h\)-error:

$$\begin{aligned} \varepsilon _h:= \left\| \mathcal {F}_{h}\circ \mathcal {M}^{N_h}_{h}\circ \mathcal {S}_{h}(y_0) - y_0\right\| _2. \end{aligned}$$

The order of a method is then approximately given by the gradient of the corresponding plot of \(\log (\varepsilon _h)-\log (h)\). In Fig. 1, we demonstrate that compositions of GLM4A and GLM4B by both the triple jump and Suzuki 5-jump can be applied to yield methods of order \(p=6\).

5.3 Efficiency comparisons

Next, we investigate the computational efficiency of the COSY-GLMs. In particular, we repeat the experiment of Sect. 5.2 and record the total number of function evaluations made during the integration. Comparing this quantity to the \(\varepsilon _h\) error provides us with an estimate on computational cost versus accuracy.

Fig. 4
figure 4

Modified pendulum: \(t \in [0,10^6]\), \(h = 0.5\). a T.GLM4B: Hamiltonian preservation, b S.GLM4B: Hamiltonian preservation

Full size image
Fig. 5
figure 5

Bead on a wire: \(t \in [0,10^6]\), \(h = 0.25\). a T.GLM4B: Hamiltonian preservation, b S.GLM4B: Hamiltonian preservation

Full size image
Fig. 6
figure 6

Kepler: \(t \in [0,10^4\cdot \pi ]\). a T.GLM4B: Hamiltonian preservation with \(h = \frac{\pi }{250}\), b T.GLM4B: angular momentum preservation with \(h = \frac{\pi }{250}\), c S.GLM4B: Hamiltonian preservation with \(h = \frac{\pi }{100}\), d S.GLM4B: angular momentum preservation with \(h = \frac{\pi }{100}\)

Full size image

The results from this experiment are shown in Fig. 2. For a fixed accuracy, it can be seen on average that COSY-GLMs require between 1.66 and 2.5 times fewer function evaluations than the DIRK methods.

In addition to \(\varepsilon _h\) error versus function evaluations, we also consider the maximum deviation of the absolute Hamiltonian error, i.e.

$$\begin{aligned} \max _n |H(y_n)-H(y_0)|, \quad n \in \left\{ 1,\ldots ,\frac{T}{h} \right\} , \end{aligned}$$

versus function evaluations. These results are given in Fig. 3. Similar to before, for a fixed accuracy it can been seen that COSY-GLMs require approximately half the number of function evaluations when compared against the DIRK methods.

5.4 Long-time hamiltonian preservation

Lastly, we investigate the long-time preservation of the Hamiltonian for problems (P1)–(P3) using a COSY-GLM. As the results on computational efficiency indicate that compositions of GLM4A and GLM4B perform similarly, we restrict our attention to compositions of only GLM4B as this requires fewer function evaluations for a fixed time-step.

The results given in Figs. 4, 5 and  6 show that COSY-GLMs approximately preserve the Hamiltonian over long-times. Also, Fig. 6 shows that quadratic invariants such as angular momentum, i.e. \(L:\mathbb {R}^4\rightarrow \mathbb {R}\),

$$\begin{aligned} L(p_1,p_2,q_1,q_2):= q_1p_2 - q_2p_1, \end{aligned}$$

are also approximately preserved. Furthermore, we observe that parasitic instability has yet to manifest itself despite the use of coarse time-steps.

6 Conclusion

A composition technique for generating composite symmetric general linear methods (COSY-GLMs) of arbitrarily high order has been developed and then applied to create new methods of order 6. The process involves using a canonical transformation that alters the starting and finishing methods of a GLM to be in terms of only the preconsistency vectors u and w. The new methods have been shown to be suitable for the long-time integration of reversible Hamiltonian systems that are either separable or non-separable. In particular, numerical experiments have been performed which show that the methods approximately preserve the Hamiltonian and other invariants for the duration of the computation. Furthermore, these methods have been found to be computationally more efficient than symmetric diagonally-implicit Runge–Kutta methods (DIRKs) of the same order, typically requiring half the number of total function evaluations for a fixed accuracy.