1 Introduction

Orbital dynamics around asteroids has become more and more interesting for mission purposes. It also sheds light on our understanding of the evolution of the solar system. This paper focuses on one specific type of asteroid, i.e. the contact binary asteroid, which consists of two lobes that are in physical contact and which represents the mostly bifurcated body. Together with comets, the contact binary body is estimated to constitute 10–20 % of all small solar system bodies (Harmon et al. 2011). Rosetta’s target comet 67P/Churyumov-Gerasimenko was found to be probably a contact binary very recently (August 2014).

The irregular gravitational field induced by an asteroid can be modeled with several different methods (Scheeres 2012). For the study outside of the circumscribing sphere, the method of a spherical harmonic expansion truncated at arbitrary degree and order can be used. When the distance becomes smaller, the polyhedron method of approximation of the shape of a body with triangular faces is more valid (Werner and Scheeres 1996). Another option is to approximate the gravitational field by elementary geometrical shapes (e.g. ellipsoid), in which case closed-form potentials can be obtained.

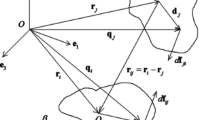
Following the typical mass distribution of a contact binary, the model of a combination of an ellipsoid and a sphere is used in this study, as shown in Fig. 1. This model breaks one axial symmetry, which is different from the geometrical shapes (a straight segment, two orthogonal segments, an ellipsoid, a cube, a thin bar) studied in (Bartczak and Breiter 2003; Bartczak et al. 2006; Elipe and Lara 2003; Halamek and Broucke 1988; Liu et al. 2011b). For this specific configuration, possible formation mechanisms and the relationship between the relative configuration and the rotational angular momentum have been studied in detail in (Scheeres 2007). In addition, this simplified model already captures the main characteristics of the full gravitational field.

Fig. 1
figure 1

The ellipsoid-sphere configuration and the body-fixed frame xyz

Full size image

To gain some insight into the gravitational field of this configuration and the orbital dynamics around such a system, the spherical harmonics expansion is applied. As already mentioned, it is a good representation of a non-spherical gravitational field outside the circumscribing sphere. It has been applied extensively for studying orbital dynamics around planets and moons, for which the zonal and C22 terms are usually dominant and several magnitudes larger than the other tesseral terms. However, for orbital motion close to a contact binary asteroid, it is typically not sufficient to only include the zonal and C22 terms. Due to the highly non-spherical shape of the body, the other tesseral harmonics are much larger and more comparable with the zonal terms than in the case of planets and moons. For instance, the C30, C31 and C33 terms can easily be only one order of magnitude smaller than the C22 and C40 terms or even of the same magnitude, e.g. in the case of Eros and Itokawa (Barnouin-Jha et al. 2006; Scheeres et al. 2000; Yu and Baoyin 2012). Therefore, they should not be ignored during the analysis.

For studying the corresponding orbital dynamics with a spherical harmonics model, numerical (Hu and Scheeres 2004; Lara and Russell 2007; Russell and Lara 2007, 2009), analytical (Ceccaroni and Biggs 2013; Coffey et al. 1994; Liu et al. 2011a; San-Juan et al. 2004) and semi-analytical (Métris and Exertier 1995; Scheeres et al. 2000) methods have been developed. Among them, the traditional averaging method has extensive applications, since it simplifies the system by averaging out the short-term effects while capturing the secular and long-term evolutions. Together with the Lagrange Planetary Equations (LPE), the effect of the harmonics C20, C22, C30 and C40 on orbital elements has been studied by (Scheeres et al. 2000), and they are found to enlarge the orbital eccentricity. By applying the Lie transformations, high-altitude frozen orbits have been obtained analytically by (Ceccaroni and Biggs 2013) for the fast-rotating asteroid Eros, with the harmonics truncated at degree 15.

Actually, the averaging process reduces the three degrees of freedom (3-DoF) to 2-DoF and even 1-DoF. The reduced system then can either be numerically integrated or be solved in closed form. The method of Poincaré sections is a good tool for solving the reduced 2-DoF by numerical integration, as it transforms the 2-DoF system to a two-dimensional map. Common applications can be found in (Broucke 1994; Lara 1996) for finding POs. Generally, frozen orbits can be obtained from the 1-DoF system (Coffey et al. 1994; Liu et al. 2011a). POs however can be generated from the 1-DoF system (Palacián 2007), 2-DoF (Tzirti et al. 2010) and also 3-DoF systems (Lara 1999; Lara and Russell 2007). The eccentricity and pericenter of the frozen orbits always remain constant on average, while those of the POs have small deviations from the ‘mean’ value but will return to the same value after one period. POs, i.e. repeat ground track orbits in the rotating frame, were also found to be a subset of frozen orbits in inertial space (Lara 1999). In addition, the POs can also be explored for determining the stability bounds (Lara and Scheeres 2002). Since the propellant consumption for following these kinds of orbits is usually small, both of them are interesting for mission purposes.

Little research however has been done on finding POs with a 4×4 spherical harmonics model for the highly irregular gravitational field of a contact binary asteroid with this configuration and also with different rotation rates. This will be the focus of this study. In addition, instead of following a global search method, the POs of the original system will be obtained from the Poincaré sections with a numerical search and correction method.

This paper is arranged as follows. In Sect. 2, the gravitational field potential of the ellipsoid-sphere configuration is expanded into a spherical harmonics model. In fact, this kind of expansion has been performed for some specifically shaped bodies, e.g. an ellipsoid or two spheres connected with each other (Balmino 1994), both of which are three-axis symmetric. Therefore, the current work is the first attempt for expanding the gravitational field into spherical harmonics for a geometrical body of which one axis-symmetry has been broken. The general method for obtaining the spherical harmonics for a given body is introduced. In Sect. 3, the contact binary system 1996 HW1 (Magri et al. 2011) (one of the most bifurcated bodies ever found) serves as the study case for testing the accuracy of the truncation at degree and order 4, and further at degree and order 8. The expansion is also checked against the cases when varying the sizes of this configuration. In Sect. 4, the Hamiltonian including the 4×4 harmonics and the rotation of the asteroid is obtained for the analysis of the dynamics. It is reduced to a 1-DoF system by double-averaging, and frozen orbits are identified. The effects of the tesseral harmonics on these frozen orbits are examined. In Sect. 5, by applying Poincaré sections, the phase space structure of the 2-DoF system is obtained at various energy levels and at different rotation rates of the asteroid. In Sect. 6, with a numerical correction method and the initial conditions from the Poincaré maps, a number of POs can be obtained in the single-averaged model and successively in the full non-averaged model.

2 Shape model and geometrical potential

In this study, the contact binary asteroid is modeled as a combination of an ellipsoid and a sphere, as shown in Fig. 1.

The parameters that describe the configuration in Fig. 1 are the three semi-axes of the ellipsoid α,β,γ and the radius of the sphere R. The system is assumed to be homogeneous, with a constant density ρ. It is also assumed that the system rotates uniformly about the z-axis with a velocity \(\vec{\omega}\). The vector from the center of mass of the ellipsoid to that of the sphere is denoted as \(\vec{d}\), where \(| \vec{d} | = \alpha + R\). The mass ratio μ 0 is defined as m s /(m s +m e )=1/(1+αβγ/R 3) (m s and m e are the mass of the sphere and the ellipsoid, respectively). Here the body-fixed frame is defined as the x-axis along the line connecting the mass centers of the two components with positive direction from ellipsoid to sphere, the z-axis along the rotation axis of the body with positive direction pointing along the angular velocity, and the y-axis obtained according to the right-hand rule. With this definition, the asteroid still has xy- and xz-plane symmetry, while the yz-plane symmetry is broken. This makes the problem more complicated, compared to the individual sphere and ellipsoid geometries which have three planes of symmetry. The gravitational potential of this two-component asteroid can be written as

$$\begin{aligned} U_\mathit{se} =& U_\mathit{sphere} + U_\mathit{ellipsoid} \\ =& G(m_{s} + m_{e}) \biggl[ \frac{\mu_{0}}{\vert \vec{r} - (1 - \mu_{0})\vec{d} \vert } \\ &{} + (1 - \mu )U_{e}(\vec{r} + \mu_{0}\vec{d}) \biggr] \end{aligned}$$
(1)

where \(\vec{r} = (x,y,z)\) is the position of a given point P, and U sphere and U ellipsoid are the potentials of the sphere and ellipsoid parts, respectively. The former one can be viewed as a point mass potential, while the later one is expressed as (MacMillan 1958)

$$\begin{aligned} & {U_{e}(\boldsymbol{r}) = \frac{3}{4}\smallint_{\sigma}^{\infty} \phi (\boldsymbol{r},v)\frac{dv}{\Delta (v)} } \\ & {\phi ( \boldsymbol{r},v ) = 1 - \frac{r_{x}^{2}}{\alpha^{2} + v} - \frac{r_{y}^{2}}{\beta^{2} + v} - \frac{r_{z}^{2}}{\gamma^{2} + v} } \\ & {\Delta ( v ) = \sqrt{\bigl(\alpha^{2} + v\bigr) \bigl( \beta^{2} + v\bigr) \bigl(\gamma^{2} + v\bigr)}, \phi ( \boldsymbol{r},\sigma ) = 0 } \end{aligned}$$

where v is an internal variable for the calculation of U e and r=(r x ,r y ,r z ) is the independent variable of function U e . The potential expressed here will serve as the baseline to verify the accuracy of the spherical harmonics expansion studied in the following section.

3 Spherical harmonics expansion

3.1 Method

The gravitational potential in spherical harmonics is usually expressed as follows (Kaula 1966)

$$\begin{aligned} V =& \frac{\mathit{GM}}{r} \Biggl\{ 1 + \sum_{n \ge 2}^{\infty} \sum_{m = 0}^{n} \biggl( \frac{\mathit{Re}}{r} \biggr)^{n}P_{nm}(\sin\theta ) \bigl[ C_{{nm}}\cos ( m \lambda ) \\ &{} + S_{nm}\sin (m\lambda ) \bigr] \Biggr\} \end{aligned}$$
(2)

where GM is the gravitational constant of the asteroid; r,θ and λ are spherical coordinates (the radial distance \(\vert \vec{r} \vert \) from the center of mass to a given point P, latitude and longitude, respectively) in the body-fixed frame; R e is a characteristic physical dimension and is usually defined as half of the largest dimension of the whole body, equal to \(\vert \vec{d} \vert \) as defined in Sect. 2; P nm is the associated Legendre polynomial. C nm and S nm are the coefficients of the spherical harmonics expansion which are determined by the mass distribution within the body. They can be expressed in terms of inertia integrals which are dependent on the geometric representation of the body. Assuming a homogeneous density of the body, the inertia integral I i,j,k is defined as (MacMillan 1958)

$$ I_{i,j,k} = \rho \iiint x^{i}y^{j}z^{k}dxdydz $$
(3)

The triple integration is performed over the entire volume of the body. For bodies symmetric through the xy-, yz- and xz-planes, the inertia integrals are zero if there is an odd number among i,j,k. Therefore, the un-normalized C nm and S nm in inertia integrals are expressed as follows (MacMillan 1958)

$$\begin{aligned} C_{nm} =& ( 2 - \delta_{0m} )\frac{ ( n - m )!}{ ( n + m )!} \cdot \frac{m!}{\mathit{MRe}^{n}} \\ &{} {\fontsize{8.6}{8.8}\selectfont \mbox{$\times \displaystyle\sum_{s = 0}^{t}\sum _{j = 0}^{l}\sum_{p,q,r} \frac{ ( - 1 )^{s + j} [ 2n - 2j - 1 ]j!}{ ( 2s )! ( m - 2s )! ( n - m - 2j )! [ 2j ]p!q!r!} $}} \\ &{} \times I_{m + 2p - 2s,2s + 2q,n - m - 2j + 2r} \\ S_{nm} =& ( 2 - \delta_{0m} ) \frac{ ( n - m )!}{ ( n + m )!} \cdot \frac{m!}{\mathit{MRe}^{n}} \\ &{} {\fontsize{7.8}{8}\selectfont \mbox{$\times \displaystyle\sum_{s = 0}^{t}\sum _{j = 0}^{l}\sum_{p,q,r} \frac{ ( - 1 )^{s + j} [ 2n - 2j - 1 ]j!}{ ( 2s + 1 )! ( m - 2s - 1 )! ( n - m - 2j )! [ 2j ]p!q!r!} $}} \\ &{} \times I_{m + 2p - 2s - 1,2s + 2q + 1,n - m - 2j + 2r} \end{aligned}$$
(4)

Where

$$\begin{aligned} & {\delta_{0m} = \left \{ \begin{array}{l@{\quad}l} 1, & m = 0; \\ 0, & m \ne 0; \end{array} \right . \qquad t = \left \{ \begin{array}{l@{\quad}l} m/2, & m\ \mbox{even}; \\ (m - 1)/2, & m\ \mbox{odd}; \end{array} \right . } \\ & { l = \left \{ \begin{array}{l@{\quad}l} (n - m)/2, &m\ \mbox{even}; \\ (n - m - 1)/2, &m\ \mbox{odd}; \end{array} \right . } \end{aligned}$$
$$\begin{aligned} & {\left \{ \begin{array}{l} {[} 2n ] = 2n \cdot ( 2n - 2 ) \cdot \ldots \cdot 2;\quad [0] = 1; \\ {[} 2n - 1 ] = (2n - 1) \cdot ( 2n - 3 ) \cdot \ldots \cdot 1; \end{array} \right . } \\ & { \left \{ \begin{array}{l} p \ge 0,\ q \ge 0,\ r \ge 0,\quad \mbox{integers}; \\ p + q + r = j. \end{array} \right . } \end{aligned}$$

For simplification, dimensionless units are used in the following study, where the length unit is R e , the gravitational parameter GM=1 and the resultant time unit \(T = \sqrt{\mathit{Re}^{3}/\mathit{GM}}\). From now on, the variables are in dimensionless units however with the same notation. The mathematical expressions for the configuration of this contact binary, which also define the limits of the inertia integral, can be written as

$$\begin{aligned} \left \{ \begin{array}{l} \frac{ ( x + \mu_{0} )^{2}}{\alpha^{2}} + \frac{y^{2}}{\beta^{2}} + \frac{z^{2}}{\gamma^{2}} = 1, \quad - \alpha - \mu_{0} \le x \le \alpha - \mu_{0} \\ ( x - 1 + \mu_{0} )^{2} + y^{2} + z^{2} = R^{2}, \\ \quad - R + 1 - \mu_{0} \le x \le R + 1 - \mu_{0} \end{array} \right . \end{aligned}$$
(5)

With this method, the outcome of the associated spherical harmonics model has been tested against the analytical values available from literature, and in this way verified. For the study case of system 1996 HW1 (Appendix A), the coefficients up to degree and order 8 are obtained and given in Appendix B. It is found that higher-order zonal terms and some tesseral terms, e.g. C31, C40, C60, have the same magnitude as C22.

3.2 Verification

For an ellipsoid, it is found that the external gravitational harmonics converge uniformly down to the surface when \(\alpha < \gamma \sqrt{2}\) (Balmino 1994). For a general body the divergence is severe once the point of interest comes into the circumscribing sphere of the body (MacMillan 1958). Therefore, the analysis of the dynamics based on the above spherical expansion will be restricted to the area outside the circumscribing sphere, which has a dimensionless radius of 1.0725 for system 1996 HW1. The accuracy of this expansion (up to degree and order 4 and 8) is verified by comparing it with the analytical potential formulation Eq. (1). The relative errors of the potential value and the radial acceleration on the circumscribing sphere and also on the sphere with a dimensionless radius equal to 2 are illustrated in Fig. 2. The relative error here is defined as the absolute difference between the potential values or the acceleration from the spherical harmonics expansion and the analytical formulation, divided by the value of the latter one.

Fig. 2
figure 2

(a) The relative error of potential (top) and radial acceleration (bottom) of the 4×4 spherical harmonics expansion for a radius equal to the one of the circumscribing sphere (left) and 2 (right). (b) The relative error of potential (top) and radial acceleration (bottom) of the 8×8 spherical harmonics expansion for a radius equal to the one of the circumscribing sphere (left) and 2 (right). Note the different color scales

Full size image

For the truncation up to degree and order 4, Fig. 2a (top) shows that the maximum error of the potential is about 8×10−2 on the circumscribing sphere and 2×10−3 at a radius of 2. In addition, for the 8×8 expansion (Fig. 2b, top), the potential error reduces to around 2×10−2 and 4×10−5, respectively. As for the radial acceleration, the relative errors are all about one order of magnitude larger than those of the potential due to differentiation. This confirms the expectation that the higher the order of the truncation, the more accurate the expansion. For this irregularly shaped body, the largest errors appear at the outer edge of the smaller component along the most bifurcated direction (λ=0∘ or 360∘ and θ=0∘) i.e. the positive x-axis; we call this point with the largest error ‘critical point’ from now on. For the radius larger than 2, the error reduces rapidly. In addition, it is concluded that the relative error of the expanded 4×4 potential and the radial acceleration is much smaller than 0.3 % and 1.5 %, respectively, when the distance to the center of mass of the system is larger than 2. Of course, the 8×8 model performs better.

In addition, the influence of the configuration on the accuracy of the expansion is also checked. To that end, the radius of the sphere R is varied from zero to the value of the smallest semi-major axis of the ellipsoid component (0.745 km, cf. Appendix A). The maximum relative errors of the expansions for the 4×4 potential at five chosen radius are illustrated in Fig. 3. When R is zero, the model reduces to that of the ellipsoid potential. Its largest relative error is at the magnitudes of 10−2 (circumscribing sphere) and 10−4 (r=2), respectively. For all study cases, the smallest relative error is at R=0, while the largest one comes out for R=0.46 km. This implies that when Revolves from 0 to 0.745 km, at some radius near 0.46 km the most irregular (bifurcated) shape is generated, in which case the 4×4 spherical harmonics approximation does not work so well at the singular point, and a higher-order truncation, e.g. 8×8, is required.

Fig. 3
figure 3

The maximum relative error of the 4×4 spherical harmonics expansion of the potential field at the circumscribing sphere and r=2 for the radius of the sphere at 0, 0.26, 0.46, 0.66, 0.745 km

Full size image

In summary, the spherical harmonics expansion up to degree and order 4 is a good approximation of the gravitational field of the contact binary asteroid especially for a dimensionless radius larger than 2. Therefore, in the following sections, the spherical harmonics truncated at this order are taken into account in the analysis of the dynamics of orbits. The initial conditions are chosen at a distance of no less than 2.

4 Hamiltonian of the truncated system

Taking into account the spherical harmonics up to degree and order 4, and the rotation of the asteroid at rate n a , the Hamiltonian of the truncated system can be written as

$$ \mathcal{H} = \mathcal{H}_{0} + \mathcal{H}_{n_{a}} + \mathcal{H}_{C_{nm}} $$
(6)

where \(\mathcal{H}_{0}\) is the unperturbed Keplerian part, \(\mathcal{H}_{n_{a}}\) comes from the rotation of the asteroid, and \(\mathcal{H}_{C_{nm}}\) represents the spherical harmonics perturbation. All terms of Eq. (6) in spherical coordinates are listed in Appendix C. For simplifying this dynamical system and also capturing its mean characteristics, an averaging method is applied. To this aim, \(\mathcal{H}\) is translated into a function of orbital elements (a,e,i,g,f,h). Here a,e,i,f are the semi-major axis, eccentricity, inclination and true anomaly, respectively. In addition g=ω is the argument of pericenter. The longitude of the ascending node Ω in the frame co-rotating with the asteroid at rate n a is expressed as h=Ω−n a t. The relations between orbital elements and spherical coordinates (r,θ,λ) are given in Appendix D.

For studying the dynamics of a Hamiltonian system, it is convenient to use a canonical set of variables. One common set is the Delaunay variables, which are defined as follows (Chicone 1999)

$$\begin{aligned} & {l = M,\qquad g = \omega,\qquad h = \varOmega - n_{a}t, \qquad L = \sqrt{\mu a}, } \\ & {G = \sqrt{ \mu a \bigl( 1 - e^{2} \bigr)}, \qquad H = \sqrt{\mu a \bigl( 1 - e^{2} \bigr)} \cos i } \end{aligned}$$

where G is the modulus of the angular momentum and H its projection on the z-axis. The equations of motion for a Hamiltonian system are expressed as

$$ \left \{ \begin{array}{l} \frac{dl}{dt} = \frac{\partial \mathcal{H}}{\partial L},\qquad \frac{dL}{dt} = - \frac{\partial \mathcal{H}}{\partial l} \\ \frac{dg}{dt} = \frac{\partial \mathcal{H}}{\partial G},\qquad \frac{dG}{dt} = - \frac{\partial \mathcal{H}}{\partial g} \\ \frac{dh}{dt} = \frac{\partial \mathcal{H}}{\partial H},\qquad \frac{dH}{dt} = - \frac{\partial \mathcal{H}}{\partial h} \end{array} \right . $$
(7)

Since Eq. (7) forms a system with six independent variables l,g,h,L,G,H, the Hamiltonian is a 3-DoF system. In the following study, the orbital elements are used in the averaging analysis, while the Delaunay variables will be employed in the numerical integration part.

4.1 Single-averaged model

By applying the change of variables

$$dM = \frac{r^{2}}{a^{2} ( 1 - e^{2} )^{1/2}}df $$

\(\mathcal{H}\) can be averaged over the mean anomaly M (or l), and the averaged Hamiltonian \(\bar{\mathcal{H}}_{C_{nm}}\) up to degree and order 3 can be given as function of orbital elements (Tzirti et al. 2010)

$$\begin{aligned} & {\bar{\mathcal{H}}_{0} = - \frac{\mu}{2a} } \\ & {\bar{\mathcal{H}}_{n_{a}} = - n_{a}\sqrt{\mu a \bigl( 1 - e^{2} \bigr)} c } \\ & {\bar{\mathcal{H}}_{C_{20}} = - \frac{\mu C_{20}R_{e}^{2}(1 - 3c^{2})}{4a^{3} ( 1 - e^{2} )^{3/2}} } \\ & {\bar{\mathcal{H}}_{C_{22}} = - \frac{3\mu C_{22}R_{e}^{2}(1 - c^{2})}{2a^{3} ( 1 - e^{2} )^{3/2}}\cos (2h) } \end{aligned}$$
$$\begin{aligned} \bar{\mathcal{H}}_{C_{3j}} =& - \frac{3\mu eC_{3i}R_{e}^{3}}{16a^{4} ( 1 - e^{2} )^{\frac{5}{2}}} \bigl[ K_{3j}^{ +} \cos ( g + jh ) \\ &{}+ K_{3i}^{ -} \cos ( g - jh ) \bigr], \quad j = 1,3 \end{aligned}$$

where

$$\begin{aligned} & {c = \cos (i),\qquad K_{31}^{ \pm} = 1 \pm 11c - 5c^{2} \mp 15c^{3}, } \\ & { K_{33}^{ \pm} = 30 \bigl(1 \pm c - c^{2} \mp c^{3} \bigr) } \end{aligned}$$

Extending the averaging \(\mathcal{H}_{C_{nm}}\)of to degree 4, the resultant Hamiltonian is obtained using MAPLE16 and given as

$$\begin{aligned} \bar{\mathcal{H}}_{C_{40}} =& - \frac{3\mu C_{40}R_{e}^{4}}{128a^{5} ( 1 - e^{2} )^{\frac{7}{2}}}\bigl[ - \bigl( 70s^{4} - 60s^{2} \bigr)e^{2}\cos ( 2g ) \\ &{}+ \bigl( 35s^{4} - 40s^{2} + 8 \bigr) \bigl( 2 + 3e^{2} \bigr)\bigr] \end{aligned}$$
$$\begin{aligned} \bar{\mathcal{H}}_{C_{4j}} =& - \frac{45\mu eC_{4j}R_{e}^{4}}{32a^{5} ( 1 - e^{2} )^{\frac{7}{2}}} \bigl[ K_{4j}^{ +} \cos ( 2g + jh )e^{2} \\ &{} + K_{4j}^{ -} \cos ( 2g - jh )e^{2} \\ &{} + K_{4j}\cos ( jh ) \bigl( 2 + 3e^{2} \bigr) \bigr], \quad j = 2,4 \end{aligned}$$

where

$$\begin{aligned} & {s = \sin (i), \qquad K_{42}^{ \pm} = 1 \mp 5c - 6c^{2} \pm 7c^{3} + 7c^{4}, } \\ & { K_{42} = 1 - 8c^{2} + 7c^{4} } \\ & {K_{44}^{ \pm} = 14\bigl( - 1 \mp 2c \pm 2c^{3} + c^{4}\bigr), } \\ & { K_{44} = 14\bigl(1 - 2c^{2} + c^{4}\bigr) } \end{aligned}$$

Since M is averaged out, \(\mathcal{H}\) is reduced to a 2-DoF system with variables g and h

$$ \bar{\mathcal{H}} = \bar{\mathcal{H}}_{0} + \bar{ \mathcal{H}}_{C_{nm}} + \bar{\mathcal{H}}_{n_{a}} $$
(8)

However, the system can be reduced further by a second averaging which is carried out in the next section.

4.2 Double-averaged model

It can be seen that in the single-averaged system the tesseral harmonics still include h=Ω−n a t, which is time related. Therefore, the Hamiltonian can be averaged a second time over h, denoted as \(\tilde{\mathcal{H}}\). It can be shown that the corresponding tesseral terms are all eliminated, thus \(\tilde{\mathcal{H}}_{C_{nm}}\) only consists of contributions from zonal terms, which is actually the zonal approximation of the problem. The Hamiltonian is now reduced to 1-DoF and can be written as

$$ \tilde{\mathcal{H}} = \bar{\mathcal{H}}_{0} + \bar{ \mathcal{H}}_{C_{20}} + \bar{\mathcal{H}}_{C_{40}} + \bar{ \mathcal{H}}_{n_{a}} $$
(9)

The four terms have already been given in Sect. 4.1.

4.2.1 Frozen orbits

Substituting Eq. (9) into the Lagrange Planetary Equations (LPE) (Kaula 1966), the derivatives of the orbital elements e and g can be obtained. With the perturbation from \(\bar{\mathcal{H}}_{C_{20}}\) and \(\bar{\mathcal{H}}_{C_{40}}\), the derivatives of e and g from \(\tilde{\mathcal{H}}\) are given as

$$\begin{aligned} \frac{de}{dt} = - \frac{3R_{e}^{4}\mu}{64a^{7} ( 1 - e^{2} )^{3}n}\bigl[C_{40} \bigl( 70s^{4} - 60s^{2} \bigr)\sin ( 2g )e\bigr] \end{aligned}$$
$$\begin{aligned} \frac{dg}{dt} =& - \frac{3R_{e}^{2}\mu}{128a^{7} ( 1 - e^{2} )^{4}n} \bigl\{ 32C_{20}a^{2} \bigl( 5c^{2} - 1 \bigr) \bigl( 1 - e^{2} \bigr)^{2} \\ & {} + 10C_{40}R_{e}^{2}\cos (2g)\bigl[\bigl(2 - 16c^{2} + 14c^{4}\bigr) \\ &{} + \bigl(63c^{4} - 56c^{2} + 5\bigr)e^{2} \bigr] \\ &{}- 5C_{40}R_{e}^{2}[ \bigl( 12 - 144c^{2} + 196c^{4} \bigr) \\ &{} + \bigl(189c^{4} - 126c^{2} + 9\bigr)e^{2} \bigr\} \end{aligned}$$
(10)

where n is the mean rotation rate of the orbit with semi-major axis a. Frozen orbits can be found by solving \(\dot{e} = \dot{g} = 0\). Only for i 0=67.8∘ or g=0 or ±π/2, \(\dot{e}\) equals zero. However, no solution for \(\dot{g} = 0\) is found at i 0. For the main problem based on C20 only and also the C20+C30 dynamics studied in (Tzirti et al. 2010), frozen orbits exist at i 0=63.4349∘, which is known as the critical inclination. However, the situation is different in the C20+C40 dynamics, which is explained in the following part.

For g=0 and π/2, solutions for \(\dot{g} = 0\) can be obtained in the e–i plane as shown in Fig. 4, in which the frozen eccentricities are all quite large in all cases, except for those close to the bifurcations. Therefore, only parts of them (in the inclination range around 60–63.5∘) are practical as they should not impact on the asteroid. In addition, the frozen eccentricity increases as a becomes larger. Compared with the case of g=π/2, for the case of g=0 the frozen orbit is slightly more eccentric for a given value of i, and the feasible range of i for a practical orbit becomes more narrow. For both situations, no solution exists around i=70∘ or at low inclinations due to this specific C20+C40 dynamics.

Fig. 4
figure 4

Eccentricity-inclination diagrams for the double-averaged system with C20+C40 dynamics at g=0 (left) and π/2 (right). The stars represent the conditions where there is no intersection with the asteroid (1996 HW1). The two black pentagrams represent the two bifurcations for a=2.5

Full size image

Coffey (Coffey et al. 1994) also studied the frozen dynamics including the C20+C40 terms, but with the Lie perturbation method. Using the same values for C20 and C40, Coffey’s results are found to have two similar branches at both g=0 and π/2. There is approximately 1–5 % difference between the results from his method and ours in this double-averaged model, due to the different averaging methods applied. The large difference appears at a large frozen eccentricity. According to his study, for the C20+C40 dynamics, two families (for g=0 and g=π/2) of solutions bifurcate around the critical inclination. As we can see from Fig. 4, there are also two bifurcations (the two black pentagrams) from our results, one at i≈62.5071∘ for g=0 and the other at i≈62.1144∘ for g=π/2, at a=2.5. They are also very close to the critical inclination of the main problem. Further, the bifurcation moves closer to the critical value (63.4349∘) with the increase of a, since the perturbation from spherical harmonics is weakened when orbits are further away from the body. This is consistent with Coffey’s theory and proves that the traditional averaging technique also describes the underlying dynamics quite well.

In general, frozen orbit of planetary problem have a small eccentricity and exists for a large inclination range. However, for asteroids the frozen eccentricity is large and is only present in a limited inclination range. This is probably due to the large C20 and C40 terms, which is always the case for highly irregular asteroids, e.g. 433 Eros and the contact binary in this study.

Similarly, the behavior of the frozen orbits in this system but with different sizes as in Sect. 3.2 is also investigated and shown in Fig. 5. Again the radius of the sphere R is changed from zero to 0.745 km. Several aspects can be noticed. Firstly, the deviations of the frozen eccentricities among different sizes are smaller for a=4 than those for a=2 (note the difference in scale of the y-axis). This means that R has a smaller influence on orbits for larger values of a, which is obvious since the irregular shape of the asteroid has less influence when one is further away. Secondly, at a specific value of a, the frozen eccentricity decreases as R reduces when R>0.46 km, and the opposite occurs when R<0.26 km. It is concluded that there is a transition radius somewhere in between these values, at the right side of which the frozen eccentricity is analogously proportional to the radius R and the opposite happens on the left side; again, due to the manifestation of the irregularity of the contact binary system. In summary, the frozen orbits are highly elliptic and the feasible ones exist at inclinations 60–63.5°.

Fig. 5
figure 5

Eccentricity-inclination diagrams for the double-averaged system with C20 and C40 at g=0 (left) and π/2 (right), when the radius of the sphere varies from 0 to 0.745 km. The straight dashed lines indicate the value of impact eccentricity

Full size image

4.2.2 Effects of Tesseral harmonics

To check the validity of the frozen orbits found in the previous section, a numerical integration is carried out under the influence of different subsets of the 4×4 spherical harmonics in the non-averaged model. One example is given in Fig. 6, where the evolutions of the orbital elements e,i,g are illustrated. The initial frozen condition is

$$\begin{aligned} & {a =2.5,\qquad e = 0.4772,\qquad g = 90^{\circ},\qquad i = 60^{\circ},} \\ & {\varOmega =90^{\circ},\qquad \theta = 60^{\circ} } \end{aligned}$$

With the short-period perturbation of the dominant C20, C40, C22 terms added to the above mean values, the osculating elements are obtained for integration in the non-averaged dynamics. A number of cases from Fig. 4 have been simulated, and they have similar evolutions. It is also found that the more circular (close to the critical inclination) and the larger a of the orbit, the better behavior of its evolution in the non-averaged C20+C40 dynamics.

Fig. 6
figure 6

The effects of different subsets of the 4×4 spherical harmonics model on frozen orbits in the non-averaged 4×4 model (time is dimensionless)

Full size image

For the C20, C40 terms only (Fig. 6A), the short- and long-period oscillations appear as expected. The orbital elements evolve close to the mean value. When the C22 term is added, the inclination i has a large variation and perigee g circulates over the full range from 0 to 360° (Fig. 6B). After inclusion of the 3rd and 4th order tesseral harmonics (Figs. 6C and 6D), the general characteristic are kept except that the oscillations are obvious for the long-period evolution of e. Since the tesseral terms distort the frozen situation, their effect should be considered in the double-averaged model. However, they are all eliminated with the double averaging method applied in this study. The Lie-Deprit perturbation method studied in (Lara 2008) is promising for solving this problem, where the effect of C22 is preserved after double averaging. In the following part, the dynamics of the single-averaged model is studied, where the tesseral terms are kept.

5 Poincaré sections of the single-averaged model

The single-averaged model given by Eq. (8) is studied in this section. Since the time term is implicit, the averaged Hamiltonian \(\bar{\mathcal{H}}\) can be viewed as the integral of motion and is conserved. Since l=M has already been eliminated during the averaging, L and a remain constant as \(\partial \bar{\mathcal{H}}/\partial l = 0\). To explore the global dynamics, the Poincaré map method is employed. In the current study, the Poincaré section on which the flow is cut is defined as the G–g plane with h=π and \(\dot{h} < 0\) (which is always the case as time increases). Given an energy level of the system, i.e. \(\bar{\mathcal{H}}_{\mathit{initial}}\), and an initial condition (L 0,g 0,G 0,h 0), the value of H 0 can be determined numerically. With this initial point, Eq. (7) is integrated over long time intervals, and the events when the solution crosses the G–g plane are recorded throughout the integration. To get a section fully filled with points, we chose a 30×30 grid of initial values (g 0,G 0) for each given \(\bar{\mathcal{H}}_{\mathit{initial}}\) and L 0; therefore the section corresponds to a range of e 0 and i 0. Based on the physical parameters of system 1996 HW1, Figures 7 and 8 present some sections obtained for a=2.5 and 4, respectively, both at n a =0.01. The plots reflect the evolution of phase space of the single-averaged system at different orbital inclinations or energy values.

Fig. 7
figure 7

Poincaré sections for a=2.5 under different energy levels; areas below the dashed line are the impact regions

Full size image
Fig. 8
figure 8

Poincaré sections for a=4 under different energy levels; plots below the dashed line are the impact regions

Full size image

Since the orbital elements of a PO should return to the same values after one period of the orbit (which may cover multiple revolutions), it is actually a fixed point on the map, which can be identified from the center of an island. It is seen from Fig. 7 that the phase space is very different for different energy levels. For 29∘<i<51∘, many islands come forth both in the impact and non-impact regions, implying the existence of POs. One is weakly visible located at the top corner of the map with G=1.58 and g=0 or 2π, while the largest one is at the center of the map with g=π. When the inclination increases (Fig. 7B), the upper part of the map becomes regular without any island apparent, and the region around the largest island is chaotic. For the region around the polar case (Fig. 7C), many islands emerge again but at the very bottom of the map. After that (Fig. 7D), islands surrounded by large chaotic regions appear. Since the impact eccentricity e imp for a=2.5 is 0.56, which corresponds to G=1.31, small-eccentricity POs can be found at low inclinations (Fig. 7A), while high inclinations only give rise to large-eccentricity ones (but still valid from an impact perspective, Fig. 7D). However, the polar PO is not feasible as its eccentricity already exceeds e imp , which is a restriction for practical usage as it might intersect with the asteroid at periapsis (Figs. 7B, 7C).

Now let us go to higher orbits at a=4, with the corresponding e imp =0.725 and G=1.377. As shown in Fig. 8, in general the sections for a=4 are more smooth, compared with those of a=2.5 As expected, the 4×4 spherical harmonics’ influence on orbits is weakened when the orbital altitude increases. Similarly, for 0<i<90∘ (Figs. 8A and 8B), the islands move towards the bottom of the map with the increase of orbital inclination, implying the raise of eccentricity of the POs. No island appears near the polar region (Fig. 8C). When it passes the polar region (Fig. 8D), islands appear again and a new phase structure is generated. Compared with the maps for a=2.5, the ones at higher altitude are already smooth due to the smaller influence of the irregular gravitational field on orbits. However, the same conclusion holds that the phase space is smoother around the polar region than that close to the equatorial plane, implying the larger influence of the irregular gravitational field on the motion in the latter one. As a consequence, the feasible POs tend to appear at low and high inclinations rather than at the polar region.

In addition, a similar analysis has also been performed for different system parameters of this configuration, as done in the study of frozen orbits (Sect. 3.2). It is found that the quantitative characteristics of the maps are similar to those above, for approximately the same a and inclination range if we vary the size of the sphere for this system configuration. Therefore, in the following sections, only the size of system 1996 HW1 is considered for simulations. What’s more, some comparisons can be made with the frozen results obtained from Sect. 4. For the same a,i and g the POs have a close but slightly smaller eccentricity than that of the frozen orbits, and also POs appear in the inclination range where no frozen solution was to be found. This is due to the effects of inclusion of the tesseral harmonics as well as the rotation of the asteroid and also the resultant more abundant dynamics.

6 Periodic orbits

The exact POs can be obtained by numerically modifying the raw initial condition read from the maps. In this section, the POs found in the single-averaged model and then in the non-averaged model are given respectively.

6.1 POs in the single-averaged model

Starting from the initial conditions given from the center of the islands in Figs. 7 and 8, POs are found with the differential correction method (DC) (Lara and Russell 2007; Russell and Lara 2007). The evolution of their eccentricity vectors (defined as [e⋅sin(g),e⋅cos(g)]) is given in Fig. 9 for four different cases, all covering 5 periods of the orbit. It can be observed that all eccentricity vectors repeat their path completely. The paths in Figs. 9A, 9B and 9D are all simple circles, as e has a sin/cos wave oscillation and g varies between 0 and 2π throughout one period. However, the curve in Fig. 9C is more complicated due to the non-trivial variation of e and also the oscillation of g is limited to the range from 1.2π to 1.9π.

Fig. 9
figure 9

Examples of the eccentricity vector evolution for 5 periods of the POs

Full size image

6.2 POs in the non-averaged model

One step further, the POs obtained in the single-averaged model can serve as initial conditions for identifying POs in the full non-averaged model given by Eq. (1). Here, the Levenberg-Marquardt method (Lourakis 2005) is applied, which can be used for searching the zero root of a given system. Several families of POs are obtained, which are illustrated in Fig. 10. In Fig. 10, the blue orbit in each subfigure is modified from the corresponding initial conditions given by Fig. 9. For example, the blue orbit in family A is originally from Fig. 9A. With numerical continuation of energy, many orbits are found for each family. The two orbits at the ends of the continuation are given in red and green, respectively.

Fig. 10
figure 10

Families of POs of the non-averaged system, represented as family A, B, C, D

Full size image

With the Floquet’s Theory, their linear stabilities can be evaluated; a PO is stable if all the eigenvalues of its monodromy matrix have unity magnitude (Chicone 1999). Following (Gómez et al. 2005), the monodromy matrix of a PO usually has the eigenvalues in the form of {1,1,λ 1,1/λ 1,λ 2,1/λ 2}, the stability index is commonly defined as s i =|λ i +1/λ i |,i=1,2. The PO is linearly stable if s i <2, while linearly unstable if s i >2. Bifurcation might occur when s i =2. The linear stability diagrams for these four families of POs are given in Fig. 11.

Fig. 11
figure 11

The linear stability diagram of POs of families A, B, C, D. The two blue dashed lines are the stability index and the red line is the period

Full size image

For family A, the blue orbit and the ‘circular’ green one are both linearly stable, while the eccentric red one is unstable. The eccentric orbits of family B are all unstable. One direction of the continuation leads to an orbit that comes close to the equatorial plane (the green one), while the other (the red one) gradually approaches the polar region. All the orbits of family C are unstable and also highly inclined when they become smaller and closer to the asteroid. For family D in Fig. 10D, the continuation ends at the equatorial plane with a stable yellow orbit. The orbits out of the plane are all unstable.

In all four families, the green orbits have the longest period while the red ones have the shortest period. The period is simply lengthened with the increase of energy. These families also share the same characteristic that the orbits become highly inclined in the close vicinity of the asteroid, resulting from the highly irregular gravitational field. In addition, all families of orbits have multiple revolutions within one period, and the initial conditions of all blue orbits are given in Appendix E. It can be noticed that the radius at some epoch along the orbits is smaller than 2, however this does not play a role since the simulation is already done in the full model (cf. Eq. (1)).

6.3 POs of faster rotating asteroid

In fact, the rotation rate of the asteroid is suspected to have a more important effect on orbital dynamics than that of the size of this system configuration. Therefore, in this section, the work in Sects. 5, 6.1 and 6.2 is repeated but with a rotation rate speeded from up n a =0.01 to n a =0.1. Firstly, the case at a=2.5 is studied. The dynamical phenomena on these sections are found not to be as rich as those at n a =0.01. For low inclinations (Fig. 12A), some ‘thin’ islands are apparent at the very bottom of the map, which are close to the impact eccentricity. The phase space is very regular and islands are absent for higher inclination cases, as shown in Figs. 12B and 12C. Not depicted here, it is found that nearly no island exists at almost all the sections for larger values of a. This means that the faster rotation of the asteroid helps to reduce the effects of the highly irregular gravitational field on orbits and to smooth out the chaotic or irregular regions on the maps. Therefore, the case for a smaller value of a (a=2) is simulated and the results are shown in Figs. 12D–12F. Many islands and chaotic regions now appear again at the low inclination range, as shown in Fig. 12D. Similarly, the islands gradually move towards the bottom with the increase of inclination and even disappear in the polar situation.

Fig. 12
figure 12

Poincaré sections for a=2.5 and 2 at n a =0.1 at different energy levels; areas below the dashed line are the impact regions

Full size image

In addition, it is found that the fast rotation of the asteroid smooths out the phase space. For instance, at a=2.5 but with n a =0.3, there is already no island on the Poincaré maps at different inclinations. The same phenomenon holds for larger a and n a . This means that the rotation rate has a significant influence on the dynamics, rather than the limited effect from the size of the system.

The method for searching POs in the single-averaged model is the same for the case with n a =0.01. The evolution of the eccentricity vector over 5 periods of one sample PO, originally from Fig. 12E, is given in Fig. 13. It can be noticed that it has a similar pattern as those of Figs. 9A, 9B and 9D. Similarly, with the initial conditions from Fig. 13, the PO in the non-averaged model is obtained with the Levenberg-Marquardt method. With the continuation of energy, one family of orbits is obtained and illustrated in Fig. 14. Their general configuration already differ from those in Fig. 10, confirming that fast rotation of the asteroid does affect its surrounding orbit. All three orbits are unstable. The stability diagram of this family is given in Fig. 15. The green one is highly unstable, while the red one is slightly unstable, since one stability line is actually slightly above the line s=2, not exactly on it. For the continuation to the green orbits, the period decreases with the increase of energy probably due to the crossing of the bifurcation line (s=2). It should be mentioned here that it is more difficult in this situation to find the POs in the non-averaged model. This is probably due to the smaller accuracy of the spherical harmonics truncation at degree and order 4 when the orbit is really close to the asteroid and also the fact that more information is lost during the low-order averaging process when the rotation rate of the asteroid is increasing.

Fig. 13
figure 13

The eccentricity vector evolution for 5 periods of the PO in the single-averaged model

Full size image
Fig. 14
figure 14

POs of the original non-averaged system at n a =0.1

Full size image
Fig. 15
figure 15

The linear stability diagram of POs of family E. The two blue dashed lines are the stability index and the red line is the period

Full size image

7 Conclusions

The POs around a contact binary asteroid have been obtained with the spherical harmonics expansion, the averaged Hamiltonian and the numerical modification method. The highly irregular gravitational field is represented by the combination of an ellipsoid and a sphere, and then is expanded into a spherical harmonics model, which is shown to be a good approximation. For system 1996 HW1, the 8th and 4th degree and order expansions have relative errors of the potential of less than 2 % and 8 % at the circumscribing sphere, respectively. The relative errors of the 4×4 truncation are always smaller than 1 % when the orbit radius is larger than 2, under different sizes of the system configuration. The radial acceleration has an error one magnitude larger than that of the potential. It is also found that some high-order terms also have a large magnitude, e.g. C31, C40, C60, in comparison with that of planetary bodies and their moons.

Frozen orbits are obtained from the double-averaged Hamiltonian including the 4th degree and order spherical harmonics. They are examined in the non-averaged model, and the tesseral terms are found to introduce large variations and distort the frozen situation. With Poincaré sections, the phase space structure of the single-averaged model is generated at different energy levels and rotation rates of the asteroid. The dynamics of the 4×4 harmonics is identified and POs are obtained. The disturbing effect of the highly irregular gravitational field on orbit motion is found to be reduced around the polar region as well as in the case of fast rotation of the asteroid. Further with the Levenberg-Marquardt method, some POs of the full non-averaged model are identified, of which the stable ones are interesting for future missions. In addition, this study provides a method for studying orbital dynamics around a highly bifurcated body represented by spherical harmonics.