Abstract
In this paper we provide a stock price model that explicitly incorporates credit risk, under a stochastic optimal control system. The stock price model also incorporates the managerial control of credit risk through a control policy in the stochastic system. We provide explicit conditions on the existence of optimal feedback controls for the stock price model with credit risk. We prove the continuity of the value function, and then prove the dynamic programming principle for our system. Finally, we prove the Viscosity Solution of the Hamilton–Jacobi–Bellman equation. This paper is particularly relevant to industry, as the impact of credit risk upon stock prices has been prominent since the commencement of the Global Financial Crisis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Global Financial Crisis demonstrated the importance of credit risk in stock price models: many firms with high credit risk experienced highly volatile price moves, with some firms declaring bankruptcy (see for instance Haas & Horen, 2012; Ouenniche, 2017; du Jardin, 2019; Affes & Hentati-Kaffel, 2019). Whilst it is recognised in empirical literature that the credit risk of firms can affect stock price behaviour (for example the well-known leverage effect Black, 1976; D’Ecclesia & Clementi, 2019), typically the majority of stock price models do not incorporate an explicit relation between stock prices and the credit risk dynamics. Moreover, key financial Theorems such as the Modigliani–Miller Capital Structure Theorems (Brealey et al., 2017) directly imply that stock prices must be explicitly affected by the credit risk of firms. Yet the standard stock price models of stochastic differential equations have no explicit relation to credit risk. Consequently, stock price models are limited in their modelling in terms of their relation to credit risk.
Given the importance of credit risk in stock price processes, especially since the start of the Global Financial Crisis, we would like to have a stock price model that directly incorporates credit risk dynamics. Additionally, whilst managers have little direct control over the price of stocks (as it is typically dependent on numerous external factors, such as investor psychology Kahneman & Tversky, 1979; Cretarola & Figá-Talamanca, 2019; Kathiravan & Balakrishnan, 2019 and market sentiment Simon & Wiggins, 2001), credit risk is within the direct control of the firm’s management. For example the firm can ”restructure” its debt, it can choose different borrowing instruments (such as secured loans, unsecured loans, bonds etc.) as well as hedge out risks to reduce credit risk e.g. interest rate risk and exchange rate risk.
The fact that management decision making, or equivalently a control policy, impacts credit risk means that the stock price model with credit risk lends itself to a stochastic optimal control model. For example, can we implement a control policy that enables an optimal response to changing credit risk? How would this impact a stock price model, with credit risk dynamics explicitly incorporated within the model? Such an analysis lends itself to formulating the problem in terms of stochastic control systems and is of importance to industrial applications.
Whilst many stochastic differential equation models exist for stock prices, the incorporation of credit risk is limited and so does not provide a comprehensive model for credit risk (such as jump-diffusion models). For example, whilst jump-diffusion models can incorporate credit risk (Zhou et al., 2019) there is no explicit link between credit risk fundamentals and the stock price equation, essentially the jumps follow a random process without any direct reference to credit fundamentals. In fact jump processes are sometimes applied to enhance computational tractability (see for instance Errais, 2019), rather than incorporating credit management fundamentals. Alternative models to stochastic differential equations that incorporate credit risk exist, however such models tend to be regression or heuristic models [such as in Damel et al. (2016)] and so offer limited theoretical development. Consequently, the relation between management or control policy, and the credit risk cannot be reflected in such models.
In this paper we present a stock price model that directly incorporates the credit risk dynamics of the firm. We propose a new stock price model that incorporates credit risk dynamics by formulating a SDE (stochastic differential equation) that has a discrete process \(\Lambda _t\), which is a continuous time, random jump process on a finite state space. Typically, \(\Lambda _t\) is a continuous time Markov chain that models the credit risk dynamics of the firm, and introduces a regime switching component to the SDE modelling our stock price \(X_t\).
Regime switching models have been used to model credit risk (Liang & Wang, 2012) and economic factors (Hamilton & Susmel, 1994; Shi, 2020) hence this model is consistent with current financial modelling of such factors. Additionally, we incorporate within our model the property that the transition rate of \(\Lambda _t\) may also be dependent on the stock price of \(X_t\). This is consistent with financial theory, as current stock price performance also impacts credit risk transitions. Furthermore, stochastic changes in an environment are increasingly being modelled in Mathematics, with such models being applied in ecological systems, biological systems, Physics etc.; see for instance (Bao & Shao, 2016; Mao, 2013; Yin & Zhu, 2010). To the best of our knowledge, our stock price model with credit risk dynamics is the first stock price model of its kind.
In addition to modelling the credit risk dynamics in our stock price model, another distinguishing feature of our model is the incorporation of a decision or control variable which reflects management decisions to manage credit risk. This is represented by \(u_{t}\) and controls the transition rate matrices of \(\Lambda _{t}\) (to be defined in proceeding sections), hence it directly impacts on the transition rate between different credit risk levels and impacts the stock price \(X_t\). This type of control is of particular interest in finance and has not been examined before. In this paper all admissible control policies, in terms of feedback control, are investigated. The compactification method is expanded, so that we can determine full conditions to ensure the existence of optimal feedback controls, with respect to finite-horizon maximisation of the expected stock price. It is also shown that the value function is continuous and the dynamic programming principle is established. We then show that the value function is a viscosity solution of the Hamilton–Jacobi–Bellman equation.
The plan of the paper is as follows: in the next section we introduce our stock price model, and review current stock price models in the financial literature. In the next section we state our main results, that is our key Theorems and a Proposition, in respect of our stock price model. The proceeding section details the proofs of all our Theorems and Proposition, and then finally we end with a conclusion.
2 Preliminaries and stock price model
In this section we introduce our stock price model with credit risk dynamics and the relevant preliminaries. We then review the relevant stock price and credit risk models in the financial literature.
2.1 Stock price model
Let there exist a probability space \((\Omega , \mathcal {F}, \mathbb {P})\) where \(\Omega \) represents the sample space of events, \(\mathcal {F}\) denotes a collection of events in \(\Omega \), with probability measure \(\mathbb {P}\). We have a filtered probability space \(\{\Omega ,\mathcal {F},\{ \mathcal {F}_{t}\}_{t\ge 0},\mathbb {P}\}\), and there also exists the complete filtration \(\{\mathcal {F}\}_{t\ge 0}\). In Finance the model for stock prices is represented by a stochastic differential equation (SDE), that is
where \(X_t\) is the stock price at time t, \(b (\cdot )\) is the drift, \(\sigma (\cdot )\) is the volatility process, and \((B_{t})_{t\ge 0}\) is an \(\mathcal {F}_{t}\) Brownian motion.
For our stock price model under stochastic control, let the stock price \(X_t\) be governed by the following SDE
where we assume \(X_t\ge 0\) for all t, so that negative stock prices do not exist; \(b:\mathbb {R}^{d}\times \mathcal {S} \rightarrow \mathbb {R}^{d}\); \(\sigma :\mathbb {R}^{d}\times \mathcal {S} \rightarrow \mathbb {R}^{d\times d}\). Here \(\mathcal {S}=\{1,2,\ldots ,N\}\), where \(N < \infty \), represents a finite state space. Let \(U=[\lambda _1,\lambda _2]^N\) with \(\lambda _2>\lambda _1>0\). The random process \((\Lambda _t)_{t \ge 0}\) is a continuous time jumping process on \(\mathcal {S}\) whose transition probability satisfies the equation:
for \(\delta >0, \,x \in \mathbb {R}^{d}, u=(u_1,\ldots ,u_N) \in U, \,i,j,\in \mathcal {S}\).
The stochastic control system consists of two major variables \((X_{t}, \Lambda _{t})\): the stock price \(X_{t}\) and is a continuous random variable that satisfies a SDE. Consequently the SDE describes the continuous time evolution of the dynamical system of interest. The second and discrete variable \(\Lambda _{t}\) is a jump process, on a finite state space which represent the credit risk of the firm. The vector \(u=(u_1,\ldots ,u_N)\) is the control term through which one can modify the transition rate of the process \((\Lambda _t)\), and the switching rate may vary according to different state of \((\Lambda _t)\). In order that \(\mathrm {diag}(u_1,\ldots ,u_N) (q_{ij}(x))\) is still a transition rate matrix, we suppose each \(u_k\), \(k=1,\ldots ,N\), is in the closed interval \([\lambda _1,\lambda _2]\) with \(\lambda _1>0\).
Let \(f:[0,\infty )\times \mathbb {R}^d\times \mathcal {S}\times U\rightarrow \mathbb {R}\) and \(g:\mathbb {R}^d\rightarrow \mathbb {R}\) are two bounded continuous functions. As a member of the firm or a stock investor, we would be interested in maximising the following reward function
that is an expectation function of the stock price X at some finite time horizon T. Such T will be fixed throughout this work. This maximisation will be achieved by using the control policy or variable \(u_{t}\), which controls \(\Lambda _{t}\), and this incorporates the management’s decision making control over debt or credit risk. We include \(\mathbb {E}\Big [g(X_T)\Big ]\) in our reward function because an investor (or any member of the firm) typically wants to maximise X at some future point in time T rather than at some indefinite period. Furthermore, the maximisation is typically some function of \(X_T\) rather than just \(X_T\) (such as expected utility) hence we include the function \(g(\cdot )\). In addition to maximising some function of \(X_{T}\) we also include the term \(\mathbb {E}\Big [\int _s^T f(t,X_t,\Lambda _t,u_t)\mathrm{d} t\Big ]\) because investors may also be interested in maximising some generic function over the starting time s and terminal time T.
Our stock price model fundamentally differs from standard models in two important characteristics. Firstly, our stock price model \(dX_{t}\) directly incorporates credit risk: the term \(\Lambda _{t}\) reflects the credit risk of the company which typically impacts the stock price dynamics; this is incorporated by \(\Lambda _{t}\) impacting \(b(\cdot )\) and \(\sigma (\cdot )\). Economically, the state i represents the credit rating of the firm’s debt, hence a state transition means the credit rating also changes. This explicit incorporation of credit risk in stock price models typically does not exist, yet it is well known from empirical evidence that credit risk is a significant factor in stock prices. Hence the incorporation of credit risk in our model is a significant feature.
Secondly, our model incorporates the impact of management decisions upon credit risk. The credit risk in firms is partly determined by management decisions, rather than a function of exogenous factors (such as the economy). For example, management can sell assets to reduce debts and improve credit risk, the firm may change its borrowing specifications (such as borrowing on a fixed interest rate rather than a variable interest rate loan), or hedge out some of it borrowing risks etc.. Consequently, it is essential that the credit risk \(\Lambda _{t}\) is a function of some decision variable. Our model incorporates the management aspect of credit risk by control variable \(u_{t}\), which affects the transition probabilities of \(\Lambda _{t}\). Hence our stock price model provides a more realistic model of credit risk and stock pricing.
The transition \(\Lambda _{t}=i\) to \(\Lambda _{t+\Delta t}=j\) is specified by the transition rate matrix, which is a state dependent and regime switching process. A regime switching representation has been frequently used in finance to represent the dynamics of the credit risk, hence this model is consistent with current financial modelling. The transition matrix for \(\Lambda _{t}\) determines the probability of \(\Lambda _{t}\) moving from one state i to another state j (and this is partly controlled by \(u_{t}\)). This transition rate matrix is also a function of x and i (that is the current stock price and state, respectively). This is because the current stock price x can be taken as a proxy measure of firm performance, which impacts the credit risk of firms. The current state i also impacts credit risk because the dynamics of credit risk is typically modelled as a function of conditional information.
In our stock price model that incorporates credit risk, we would like to examine the impact of policy decisions on \(X_t\). Specifically, we will assume we have a control variable \(u_t\) that can control the transition rate matrix, which directly reflects the management or control of debt in a firm. As the firm typically wants to manage its debt in relation to stock price \(X_{t}\), we would like to determine an optimal control policy of \(u_t\) in response to \(X_{t}\). Precisely, we consider the following kind of control policy:
for some suitable functions \(F:[0,\infty )\times \mathbb {R}^d\times \mathcal {S}\rightarrow U\), which should ensure the equations (1) and (2) admit a solution. This means that the control policy depends on the time t, the stock price \(X_t\), and the current credit risk level \(\Lambda _t\). This control policy reflects the decision of management on credit risk.
We note in passing that whilst other stochastic differential models, such as jump-diffusion models, incorporate credit risk this modelling is limited in scope. For example the jumps are follow a random process without any direct reference to credit fundamentals, nor are jumps controlled by management or control policy decisions. Consequently, the relation between management or control policy, and the credit risk cannot be reflected in such models.
2.2 Current stock price and credit risk models
We now review the asset pricing models for stocks and credit risk modelling. The initial development of asset pricing models did not explicitly incorporate credit risk factors; the standard model for asset pricing assumed constant volatility and drift without any reference to credit risk factors (Black & Scholes, 1973), that is we have geometric Brownian motion
The geometric Brownian motion model has many analytical and computational advantages for stock price modelling. However the simplicity of the model means that it is not able to take into account non-trivial pricing factors that are important to asset pricing (such as credit risk management).
The key development that has arisen in stock price modelling has focused on volatility modelling, rather than other risk factors. For instance the first volatility model development was time dependent volatility (see for example Wilmott, 1998) where
that is volatility is a function of time. In (Merton, 1973) the European call option price associated with this stock price model is derived, using the standard Black–Scholes equation Black and Scholes (1973) with volatility replaced by \(\sigma _{c}\) where
and T is the maturity date of the option.
A logical progression was the incorporation of volatility as a function of stock price; the Constant Elasticity of Variance model is a popular asset pricing model (Cox & Ross, 1976)
A more comprehensive stock price model is incorporating stochastic volatility, that is
where volatility is a function of a stochastic process that is driven by another (possibly correlated) Wiener process \(dB^{2}_{t}\). For example, in Johnson and Shanno (1987) we have
An alternative stochastic volatility model is the Hull-White Model (Hull & White, 1987)
where volatility \(\hat{\sigma }\) defined by
enables one to determine European option prices using the Black–Scholes option pricing equation (Black & Scholes, 1973). The Heston stochastic volatility model (Heston, 1993) takes into account correlation between Wiener processes, that is \(corr(dB^{1}_{t},dB^{2}_{t})=\rho dt\), where the volatility process is given by
As can be observed from the stock price models, they do not generally include credit risk factors.
One additional group of financial stock price models that should also be mentioned is the stock price model governed by Levy processes; these are fundamentally stochastic processes with independent, and stationary increments (see for instance Geman, 2002). Essentially, there are two categories of Levy processes for financial models (Kou, 2014): jump-diffusion and infinite activity Levy processes. In terms of the jump-diffusion models, we have a stochastic differential equation that has some jump component, where the jump component represents some rare event that occurs over a short interval of time (such as a stock market crash). Examples of such jump-diffusion models include Merton’s jump-diffusion model (Merton, 1976), and the double exponential jump-diffusion model in Kou (2002). In infinite activity Levy processes, we can have infinitely many jumps in a short interval of time; a review of such models can be found in Cont and Tankov (2004).
As stock price models did not explicitly take into account credit risk factors, this consequently led to credit risk being modelled separately from stock price models. The first archetypal credit risk model originated from the credit risk model first proposed by Merton (1974). This assumes an option based model for credit risk, using the Black-Scholes option pricing model Black and Scholes (1973). Instead of modelling the stock price the firm’s asset value \(A_t\) is modelled by a SDE:
where \(\sigma _{A}\) is the asset volatility, \(r_{f}\) is the riskless rate and \(\epsilon \in \mathbb {R}\) is the firm’s dividend rate.
Other credit risk models also model asset value (rather than stock prices), for example Zhou (2001) develops a credit risk model that incorporates jumps in the underlying asset
where \(\mu _{1}\) is the expected return on the firm’s assets, \(\mu _{2}, \lambda \) are constants, \(dZ_{t}\) is a Poisson process with intensity \(\lambda \), and \(\xi \) represents the jump process.
Kim et al. (1993) develop a credit risk model by valuing debt in the form of corporate bonds \(G_t\), they also take into account stochastic interest rates (whereas other credit risk models assume constant interest rates). The interest rates in Kim et al. (1993) follow
where \(b_{1}\) and \(b_{2}\) are constants. An additional advantage of the model is that it takes into account the term structure of interest rates and the uncertainty of interest rates over time.
Leland (1994), Leland and Toft (1996), proposes a model that differs from other credit risk models by taking into account strategic default. Therefore debt is modelled as an optimal capital structure problem and this is consistent with Miller–Modigliani capital structure theory (Brealey et al., 2017). The debt is modelled by a bond \(\tilde{D}_{T}\) and is given by
where \(\lambda \) is the coupon payment per year, \(r_{f}\) is the riskless rate, T is the maturity date of the bond, \(\chi \) is the total principal value of the bond, \(\varsigma _{t}\) is the cumulative distribution function of the passage time of bankruptcy, \(\varsigma _{t}^{'}\) is the associated probability density function, \(A^{*}\) is the asset value that triggers default, \(\iota \) specifies the fraction of asset values that is distributed to the bondholders in the event of default. As can be seen, the stock price value is not incorporated within this credit risk model.
Another set of influential credit risk models is the intensity based models, where the time of default \(\tau \) is a random variable, under some risk neutral measure \(\mathbb {Q}\). For example, one could apply the model
where \(\gamma _s\) is some deterministic or stochastic process, representing the intensity of a Poisson process. The time of the first jump in the Poisson process corresponds to \(\tau \).
The first passage time models represent another set of influential credit risk models; such models determine the time at which some value or boundary is first reached (typically at the time some credit related variable triggers some default event). For example, (Longstaff & Schwartz, 1995) develops a model for valuing corporate debt that is exposed to default risk as well as interest rate risk. In Briys and Varenne (1997) a first passage time model is applied in valuing fixed rate debt. Finally, we should also mention credit risk has also been applied to the valuation of vulnerable European options, that is option valuation where some counterparty or option writer is vulnerable to default, see for instance (Klein & Inglis, 2001; Liao & Huang, 2005; Klein, 1996).
Despite the development of credit risk models and stock price models, typically credit risk and stock price models are modelled separately. Consequently, the interaction between credit risk and stock prices is not explicitly incorporated within any models. Additionally, no decision making variable of credit risk management is incorporated within the credit risk, yet this is a fundamental aspect of credit risk. Furthermore, the impact of the Global Financial Crisis has demonstrated the importance of credit risk in stock prices. Consequently, there is a need to explicitly incorporate credit risk in stock price models.
3 Main results
In this section we present our main results, specifically our Theorems, Propositions and Definitions, and in the proceeding sections we derive the proofs. Now we introduce the set of admissible feedback controls studied in this work.
Definition 1
For each \((s,x,i)\in [0,T)\times \mathbb {R}^d\times \mathcal {S}\), an admissible control is a curve \(\alpha =(u_t)_{t\in [s,T]}\) in the action space U satisfying
-
(i)
SDEs (1) and (2) admit strong solution \((X_t,\Lambda _t)\) with initial value \((X_s,\Lambda _s)=(x,i)\).
-
(ii)
There exists a measurable map \(F:[s,T]\times \mathbb {R}^d\times \S \rightarrow U\) such that for almost all \(t\in [s,T]\), \(u_t=F(t,X_t,\Lambda _t)\).
Let us denote by \(\Pi _{s,x,i}\) the collection of all admissible controls \(\alpha \) with initial point \((X_s,\Lambda _s)=(x,i)\). Given two bounded continuous functions \(f:[0,\infty )\times \mathbb {R}^d\times \mathcal {S}\times U\rightarrow \mathbb {R}\) and \(g:\mathbb {R}^d\rightarrow \mathbb {R}\), the reward function with respect to the control \(\alpha \) is given by
The value function is defined by
An admissible control \(\alpha ^*\in \Pi _{s,x,i}\) is called optimal if it holds that \(V(s,x,i)=J(s,x,i,\alpha ^*)\).
We now list below the assumptions used in our work:
-
(H1)
There exists a constant \(C_1>0\) such that
$$\begin{aligned} |b(x,i)-b(y,j)|^2+\Vert \sigma (x,i)-\sigma (y,j)\Vert ^2\le C_1(|x-y|^2+\mathbf {1}_{i\ne j}), \end{aligned}$$for \(x,y\in \mathbb {R}^d\), \(i,j\in \mathcal {S}\), where \(\Vert \sigma \Vert ^2=\mathrm {tr}(\sigma \sigma ')\) and \(\sigma '\) denotes the transpose of the matrix \(\sigma \).
-
(H2)
For every \(x\in \mathbb {R}^d\), \((q_{ij}(x))\) is conservative, i.e. \(q_i(x):=-q_{ii}(x)=\sum _{j\ne i} q_{ij}(x)\), \(i\in \mathcal {S}\). Moreover, \(M:=\sup _{x\in \mathbb {R}^d,i\in \mathcal {S}, u\in U} u_iq_i(x)<\infty \).
-
(H3)
There exists a constant \(C_2>0\) such that for every \(i,j\in \mathcal {S}\), \(x,y\in \mathbb {R}^d\),
$$\begin{aligned} |q_{ij}(x )-q_{ij}(y )|\le C_2 |x-y| . \end{aligned}$$ -
(H4)
For every \(t\in [0,T]\), \(x\in \mathbb {R}^d\), \(i\in \S \), \(u\mapsto f(t,x,i,u)\) is a concave function.
We now state our Theorems.
Theorem 3.1
(Control): Under the conditions (H1)–(H4), for every \((s,x,i)\in [0,T)\times \mathbb {R}^d\times \mathcal {S}\), there exists an optimal admissible control \(\alpha ^*\in \Pi _{s,x,i}\) corresponding to the value function V(s, x, i). Moreover, the value function V(s, x, i) is continuous.
In Shao (2019), Shao has investigated the existence of the optimal feedback control problem for regime-switching diffusion processes. In that paper, besides the control on the transition rate matrix of \((\Lambda _t)\), another control term in the coefficients of the SDE for \((X_t)\) is imposed. But in Shao (2019), only the existence of optimal relaxed control (i.e. probability measure valued control policy) was established, which takes great advantage of the characterization of compact set in the space of probability measures. In this work we further show the existence of an optimal classical control (i.e. real valued control policy).
Let us introduce the \(\sigma \)-algebra associated with an admissible control. For an \(\alpha \in \Pi _{s,x,i}\), denote by \((X_t^\alpha ,\Lambda _t^\alpha )\) the controlled processes satisfying (1) and (2). Let
where \((B_t)\) is the Brownian motion given by (1). Corresponding to the filtration \(\{\mathscr {F}_{s,t}^\alpha \}_{s\le t\le T}\), denote by \(\mathscr {T}_{s,T}^\alpha \) the set of stopping times taking values in [s, T].
Theorem 3.2
(Dynamic programming principle) Assume that (H1)–(H4) hold, then it holds
We now state our next definition, and so first define
for \(u =(u_1 ,\ldots ,u_N )\in U\). 3 consider the following Hamilton–Jacobi–Bellman equation
Definition 2
Let \(v:[0,T]\times \mathbb {R}^d\times \mathcal {S}\rightarrow \mathbb {R}\) be a continuous function.
-
(i)
v is called a viscosity subsolution of (9) if
$$\begin{aligned} -\frac{\partial \varphi }{\partial t}(t_0,x_0,i_0)-\sup _{u\in U}\big \{\mathscr {A}^u \varphi (t_0,x_0,i_0)+f(t_0,x_0,i_0,u)\big \}\le 0, \end{aligned}$$for all \((t_0,x_0,i_0)\in [0,T)\times \mathbb {R}^d\times \mathcal {S}\) and for all \(\varphi \in C^2([0,T)\times \mathbb {R}^d\times \mathcal {S})\) such that \((t_0,x_0,i_0)\) is a maximum point of \(v-\varphi \).
-
(ii)
v is called a viscosity supersolution of (9) if
$$\begin{aligned} -\frac{\partial \varphi }{\partial t}(t_0,x_0,i_0)-\sup _{u\in U}\big \{\mathscr {A}^u \varphi (t_0,x_0,i_0)+f(t_0,x_0,i_0,u)\big \}\ge 0, \end{aligned}$$for all \((t_0,x_0,i_0)\in [0,T)\times \mathbb {R}^d\times \mathcal {S}\) and for all \(\varphi \in C^2([0,T)\times \mathbb {R}^d\times \mathcal {S})\) such that \((t_0,x_0,i_0)\) is a minimum point of \(v-\varphi \).
-
(iii)
We say that v is a viscosity solution of (9) if it is both a viscosity subsolution and a viscosity supersolution of (9).
We now state our next Theorem.
Theorem 3.3
(Viscosity Solution): Assume that (H1)–(H4) hold, then the value function V(s, x, i) is a viscosity solution of the Hamilton-Jacobi-Bellman equation
with the boundary condition \(V(T,x,i)=g(x)\) for \((x,i)\in \mathbb {R}^d\times \S \).
4 Proof of the results
In this section, we shall present the proofs and arguments of the previous Theorems.
4.1 Proof of control theorem
In order to prove Theorem 3.1 (Control) we first generalize the set of control policies to introduce the admissible relaxed controls in order to use the result of Shao (2019, Theorem 2.3), and then show the optimality can be realized by a U-valued admissible control policy.
Let \(\mathscr {P}(U)\) denote the set of all probability measures over U, which is endowed with the weak convergence topology. Since U is a compact set of \(\mathbb {R}^N\), it is known that so is \({\mathscr {P}}(U)\). For any measurable function \(h:U\rightarrow \mathbb {R}\), it can be viewed as a function on \({\mathscr {P}}(U)\) in the following natural way
provided the integral exists. We denote by
the first moment of \(\mu \), which must be finite by virtue of the compactness of U.
Definition 3
For each \((s,x,i)\in [0,T)\times \mathbb {R}^d\times \mathcal {S}\), an admissible relax control is a curve \(\tilde{\alpha }=(u_t)_{t\in [s,T]}\) in the space \({\mathscr {P}}(U)\) satisfying
-
(i)
SDEs (1) and (2) admit strong solution \((X_t,\Lambda _t)\) with initial value \((X_s,\Lambda _s)=(x,i)\).
-
(ii)
There exists a measurable map \(F:[s,T]\times \mathbb {R}^d\times \S \rightarrow {\mathscr {P}}(U)\) such that for almost all \(t\in [s,T]\) \(u_t=F(t,X_t,\Lambda _t)\).
The set of all admissible relaxed control \(\tilde{\alpha }\) with initial value (s, x, i) is denoted by \(\widetilde{\Pi }_{s,x,i}\). Correspondingly, we generalize the reward function J as follows:
Let
\(\tilde{\alpha }\in \widetilde{\Pi }_{s,x,i} \) is call optimal if \(J(s,x,i,\tilde{\alpha })=\widetilde{V}(s,x,i)\). Note that \(\Pi _{s,x,i}\) can be embedded into \(\widetilde{\Pi }_{s,x,i}\) by putting \(\mu _t(\mathrm{d} u)=\delta _{u_t}(\mathrm{d}u)\), where \(\delta _u\) stands for the Dirac measure at the point u. Therefore,
Proof of Theorem 3.1
(Control) According to Shao (2019, Theorem 2.3), there exists an optimal relaxed control \(\tilde{\alpha }^*=(u_t^*)\in \widetilde{\Pi }_{s,x,i}\) such that
where \((X_t^{\tilde{\alpha }^*}, \Lambda _t^{\tilde{\alpha }^*})\) is the associated controlled process. Due to (H4) and Jensen’s inequality, the concavity of f implies that
Therefore, we have
On the other hand, let \(u_t^*=m_1(\mu _t^*)\), \(t\in [s,T]\). It is clear that \(u_t^*\in U\) by the convexity of \(U=[\lambda _1,\lambda _2]^N\). We shall show that \(\alpha =(u_t^*)\) satisfies the conditions of Definition 1, and hence is the desired optimal admissible control. First, note that the control \(\mu _t^*\) acts on the transition rate matrix of \((\Lambda _t)\) through \(m_1(\mu _t)=u_t^*\), so \((X_t^{\tilde{\alpha }^*},\Lambda _t^{\tilde{\alpha }^*})\) is also a controlled process corresponding to \(\alpha \) satisfying SDEs (1) and (2). Second, since \(\tilde{\alpha }^*=(\mu _t^*)\) is an admissible relaxed control, there exists a measurable map \(F:[s,T]\times \mathbb {R}^d\times \S \rightarrow {\mathscr {P}}(U)\) such that for almost all \(t\in [s,T]\)
Define
Then G is a measurable map from \([s,T]\times \mathbb {R}^d\times \S \) to U, and
which implies the condition (ii) of Definition 1 is satisfied. We conclude that \(\alpha =(u_t^*)\) is an admissible control.
At last, noticing (14) and (13), we get
Also, \(J(s,x,i,\alpha )\le V(s,x,i)\) by definition. Therefore,
and \(\alpha =(u_t^*)\) is an optimal admissible control as desired.
The continuity of V(s, x, i) can be proved in the same way as Shao (2019, Theorem 3.1) by noting \(V(s,x,i)=\widetilde{V}(s,x,i)\) in (15), which is omitted to save space. \(\square \)
Note that to obtain the existence of optimal classical control from the existence of optimal relaxed control is not an easy work in general. We refer to Haussmann and Lepeltier (1990) for a general discussion on this topic.
4.2 Proof of proposition: dynamic programming principle
We prove Proposition 3.2 (Dynamic Programming Principle) by adopting the classical method to establish the dynamic programming principle; see, for instance, (Pham, 2009, Section 3.3). On the one hand, according to the definition of the value function and the pathwise uniqueness of SDEs (1) and (2) [cf. (Yin & Zhu, 2010, Theorem 2.1) or (Shao, 2015, Theorem 2.3)], it is easy to see that
On the other hand, for every \(\alpha _\varepsilon =(u_r^\varepsilon )\in \Pi _{s,x,i}\) and each stopping time \(\theta \in \mathscr {T}_{s,T}^{\alpha _\varepsilon }\), due to Theorem 3.1, under the condition that \((\theta ,X_\theta ^{\alpha _\varepsilon },\Lambda _\theta ^{\alpha _\varepsilon })=(t,y,j)\), there exists an optimal admissible control \( \alpha ^*=(u^*_r)\in \Pi _{t,y,j}\) such that
Then, according to the measurable selection theorem [cf. (Bertsekas, 1978, Chapter 7) or (Shao, 2019, Proposition 3.3)],
is well defined such that \(\tilde{\alpha }:=(\tilde{u}_r)_{r\in [s,T]}\) is in \(\Pi _{s,x,i}\). Hence \(J(s,x,i,\tilde{\alpha })\le V(s,x,i)\). Moreover,
Therefore,
By the arbitrariness of \(\alpha _\varepsilon \in \Pi _{s,x,i}\), we have
The desired result follows from (16) to (19). \(\square \)
4.3 Proof of viscosity solution theorem
We prove Theorem 3.3 (Viscosity Solution) by firstly proving the supersolution property of V and then the subsolution property of V.
Proof of Theorem 3.3
(Viscosity Solution): We first prove the viscosity supersolution property of V. Let \((t_0,x_0,i_0)\in [0,T)\times \mathbb {R}^d\times \mathcal {S}\) and \(\varphi \in C^2([0,T)\times \mathbb {R}^d\times \mathcal {S})\) be a test function such that
Take an arbitrary point \(\tilde{u}\in U\) and consider the constant control \(\alpha =(u_t)\) with \(u_t\equiv \tilde{u}\). It is obvious that constant control \(\alpha \) is admissible. Denote by \((X_t^\alpha ,\Lambda _t^\alpha )\) its associated controlled process given by (1) and (2). Applying the dynamic programming principle, Theorem 3.2, we have
where \(u_t^\alpha =\tilde{u}\). It follows from (20) that \(V\ge \varphi \) on \([0,T)\times \mathbb {R}^d\times \mathcal {S}\). Thus,
Applying Itô’s formula (cf. Yin & Zhu, 2010) to \(\varphi \in C^2([0,T)\times \mathbb {R}^d\times \mathcal {S})\), we obtain
Dividing both sides of (22) by \(t-t_0\) and sending t downward to \(t_0\), by the almost surely right continuity of paths of \((X_r^\alpha ,\Lambda _r^\alpha )\) and the mean value theorem, the random variable inside the expectation in (22) converges almost surely to
By the arbitrariness of \(\tilde{u}\) in U, it follows that V is a viscosity supersolution of Eq. (10).
Next, we go to investigate the viscosity subsolution property. Let \((t_0,x_0,i_0)\in [0,T)\times \mathbb {R}^d\times \mathcal {S}\) and \(\varphi \in C^2([0,T)\times \mathbb {R}^d\times \mathcal {S})\) be a test function such that
We will show the result by contradiction.
Assume
Then by the continuity of \(\mathscr {A}^u \varphi \) and the compactness of U, there exist \(\varepsilon >0\) and \(\eta >0\) such that for any \(0\le t-t_0<\eta \), \(|x-x_0|<\eta \), it holds
Take a sequence of \((t_m)_{m\ge 1}\) in \((t_0,T)\) such that \(\lim _{m\rightarrow \infty } t_m=t_0\). For each \(u\in U\) and its associated constant control \(\alpha =(u_t)\) with \(u_t\equiv u\), define a stopping time \(\tau \in \mathscr {T}_{t_0,T}^\alpha \) by
According to the dynamic programming principle Theorem 3.2, for each \(m\ge 1\) there exists an \(\alpha _m=(u_t^{(m)})\in \Pi _{t_0,x_0,i_0}\) such that
where \(\theta _m=t_m\wedge \tau ^{\alpha _m}\), \((X_t^{\alpha _m},\Lambda _t^{\alpha _m})\) denotes the controlled process associated with \(\alpha _m\). Invoking (24), it follows that
By virtue of Itô’s formula,
Invoking (26) and the definition of the stopping time \(\tau ^{\alpha _m}\), we obtain that
On the other hand,
where in the last inequality we have used condition (H2). Therefore,
Since
we obtain
which contradicts (29). Consequently,
and V is a viscosity subsolution of (10).
Consequently, V is a viscosity solution of (10). \(\square \)
5 Numerical experiments
In this section we conduct numerical experiments to demonstrate our main results to the optimal control problem; this section also provides a precise study of the optimal solutions from an operational and financial point of view. We calibrate our model to empirical financial data on the S&P 500 index and describe our calibration process. We present our empirical results and analyse our findings.
5.1 Model and implementation
In this section we explain our model, we then discuss the calibration and implementation.
5.1.1 Model
To demonstrate empirical analyses on our model specified in Eq. (1), we examine the equation:
where \((B_t)\) is a one-dimensional Brownian motion, and let \((X_t,\Lambda _t)\) be the solution to Eq. (32). We note that similar models to Eq. (32) have been widely applied in finance (e.g. for modelling option prices in incomplete markets Guo, 2001) and so provides a viable model for financial purposes.
The variable \((\Lambda _t)\) is a continuous-time Markov chain over \(\S =\{1,2\}\), independent of \((B_t)\), which represents the credit risk of the firm. Economically, a state transition represents that the credit rating of the firm is also changing. This explicit incorporation of credit risk in stock price models typically does not exist, yet it is well known from empirical evidence that credit risk is a significant factor in stock prices. This property distinguishes the model from standard stock price models as \(dX_{t}\) directly incorporates credit risk. We define \(\Lambda _{t}=1\) to represent the good credit rating or state of the firm, whereas \(\Lambda _{t}=2\) defines the bad credit rating or state of the firm.
As mentioned previously the credit risk in firms is partly determined by management decisions, rather than exogenous factors (such as the economy). For example, the management can sell assets to reduce debts and improve credit risk, or hedge out some of its borrowing risks etc.. Consequently, it is essential that the credit risk \(\Lambda _{t}\) is a function of some decision variable. Our model incorporates the management aspect of credit risk by the control variable \(u_{t}\), which affects the transition probabilities of \(\Lambda _{t}\). We therefore specify the transition rate matrix for \(\Lambda _{t}\) as
for \(u_1,u_2\in U=[\kappa _1,\kappa _2]\) with \(\kappa _1,\kappa _2>0\). Hence the probabilities for state transitions are influenced by management decisions (or equivalently the control variables \(u_1,u_2\)).
In order to optimise the problem we require a reward function. We specify
where \(0<p<1\) is a constant, and g(x) is the power utility function of CRRA (constant relative risk aversion) type, and p is a constant that specifies the level of risk aversion of the individual, We chose the CRRA utility function for our model because the CRRA function is frequently used to model the risk averse behaviour of investors. Our reward function is therefore given by
where \((X_t)\) is the solution to Eq. (32) with initial value \((X_s,\Lambda _s)=(x,i)\). We recall that we include \(\mathbb {E}\Big [g(X_T)\Big ]\) in our reward function because an investor typically wants to maximise X at some future point in time T, rather than at some undefined period. Consequently, the value function V(s, x, i) is given by
5.1.2 Calibration and implementation
To calibrate our model in Eq. (32) a range of calibration methods exist (see for example Hamilton, 1994 and in particular regime switching calibration methods). We apply the maximum likelihood estimation method for calibrating Eq. (32), using the method given in Hardy (2001). This calibration method has been previously applied to financial data, modelling financial applications and it is also utilised by the Society of Actuaries. Hence the calibration method in Hardy (2001) is suitable for our financial modelling experiments.
Our model in Eq. (32) is a two state Markov chain, that is our variable \((\Lambda _t)\) is a Markov chain over \(\S =\{1,2\}\). The calibration method in Hardy (2001) is particularly pertinent to two state Markov chains, such as in Eq. (32). In fact in Hardy (2001) it was found that no significant improvement in modelling was found if the Markov states were increased to \(\S =\{1,2,3\}\). Hence the calibration method in Hardy (2001) will provide suitable calibration results for our numerical experiment.
Using the calibration method in Hardy (2001), we obtain the state transition matrix associated with Eq. (33), hence we determine the transition probabilities \(\mathbb {P}(\Lambda _{t+\delta }\!=\!j|\Lambda _{t}\!=\!i)\), \(\forall i,j\). The parameter set \(\{b_{\Lambda _t},\sigma _{\Lambda _t}\}\) for the Eq. (32) is estimated by determining the probability distribution parameters associated with each Markov state in \(\S =\{1,2\}\). The parameter set \(\{b_{\Lambda _t},\sigma _{\Lambda _t}\}\), \(\forall \Lambda _t\), is estimated using the method in Hardy (2001) by maximising the likelihood of the parameters with the respect to the associated data set. As stated in Hardy (2001) the maximisation of the likelihood functions (and therefore the calibration of all parameters) may be achieved with any standard search methods.
The model in Eq. (32) is calibrated using daily closing prices for the S&P 500 index. The S&P 500 index is a standard data set that is chosen for financial modelling and Markov switching calibrations, see for instance (Zheng et al., 2019; Hardy, 2001; Dhesi et al., 2019). The S&P 500 index also provides a representative data set for most stock prices that trade on most stock exchanges, hence our calibration and practical results will be relevant to most stock price models.
The calibration was undertaken using S&P 500 index data over a time period of 20 years, from January 1st 2000 to January 1st 2020; this trading period was chosen for specific reasons in our numerical experiments. Firstly, the 20 year time period provides a substantially large data set that covers multiple business cycles, and multiple phases of the business cycle (such growth and expansion phases). Consequently, our calibration results will not be bias towards any particular business cycle, or a phase of a business cycle. Hence our calibration results will be more reliable.
Secondly, we have chosen our data set’s time period to incorporate asset prices prior to, during, and after the commencement of the Global Financial Crisis. As the purpose of our model is to incorporate the impact of credit states upon asset prices (in particular as a response to the impact that the Global Financial Crisis was observed to have had on asset prices) we must therefore incorporate the Global Financial Crisis time period in our data. Hence we include data before, during and after the commencement of the Global Financial Crisis. This will provide more pertinent practical results in our numerical experiments.
To obtain results on market risk on our model in Eq. (32) we require a simulation method. To simulate our model we apply Monte Carlo simulation so that we can generate the associated stock price sample paths and produce results for market risk measurement. To implement Monte Carlo simulation we apply a discretisation method to Eq. (32): we employ the Euler discretisation method, which is a standard discretising method stochastic processes such as geometric Brownian motion (see Brandimarte, 2006 for more information).
To measure market risk we applied the standard risk measure VaR (Value at Risk), which is applied in industry (Dowd, 2011). The VaR\(_{\zeta }\) risk measure, at the cumulative probability \(\zeta \), is defined as
or, alternatively as
where \(L_t = X_{t-\Delta t}-X_{t}\), with \(\Delta t\) set to 1 trading day. Hence \(VaR_{\zeta }\) specifies the maximum loss (over 1 trading day), at cumulative probability \(\zeta \), with \(\Phi (.)\) as the cumulative function on the loss distribution, and \(\Phi (.)^{-1}\) as the associated inverse cumulative distribution function. To enable comparison of losses at different probabilities, we calculate the loss \(L_t\) in percentage terms, that is \(\tilde{L}_t\) where
In addition to \(VaR_{\zeta }\) calculations, we also provide frequency plots of \(L_{t}\) over 1000 simulated trading days. The frequency plots also provide information on the distribution of losses, and so provide more information on the risk profile.
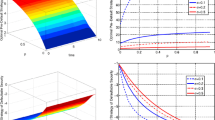
To calculate the value function V(t, x, i) for our model (32), the solution is provided in the Appendix. The p in Eq. (34) is related to the degree of risk aversion of an investor; as investors associated with the stock market tend to be risk takers (rather than saving money in a bank account) we set p to reflect less conservative investment. Consequently, we set p as low as possible within the boundaries \(0<p<1\), hence we set \(p=0.1\). Using our calibrated values for \(b_i,\sigma _i\) we deduce that \(\phi (t)=\phi _1(t)=\phi _2(t)={\mathrm{e}}^{\rho (T-t)}\), \(\forall t\in [0,T]\). We then plot V(t, x, i) at \(t=0\), using the equation \(V(t,x,i)=\phi (t)g(x)\) (see the Appendix for more information) for different x and T values.
To provide an extensive analysis from a financial and operational point of view, we examine the impact of different control policy values \(u_{1},u_{2}\) upon our model (32) through scenario analyses. The control policy values \(u_{1},u_{2}\) relate to different management decisions and also correspond to different transition probabilities \(\mathbb {P}(\Lambda _{t+\delta }\!=\!j|\Lambda _{t}\!=\!i)\). To examine different policy decisions we examine 4 different scenarios, where we vary the transition probabilities as given in Table 4. As can be seen in Table 4, the transition probabilities \(\mathbb {P}(\Lambda _{t+\delta }\!=\!j|\Lambda _{t}\!=\!i)\) are varied to reflect different control policies (or equivalently \(u_{1},u_{2}\) values); scenario 1 represents worst management, with management improving as the scenario number increases.
In Table 4 we provide a wide range of transition probabilities \(\mathbb {P}(\Lambda _{t+\delta }\!=\!j|\Lambda _{t}\!=\!i)\), for each scenario, whilst also specifying \(\mathbb {P}(\Lambda _{t+\delta }\!=\!j|\Lambda _{t}\!=\!i)\) within the bounded probability interval values [0, 1] and comparable to table 1 values. To give an example, \(\mathbb {P}(\Lambda _{t+\delta }\!=\!2|\Lambda _{t}\!=\!1)\) is highest in scenario 1, implying that the probability of falling into a worse credit state is highest. Similarly under scenario 4, where we have the best management, \(\mathbb {P}(\Lambda _{t+\delta }\!=\!2|\Lambda _{t}\!=\!1)\) is lowest and so implies it is least likely to fall into the worse credit state.
To examine the control policy impact in terms of financial and operational points of views, we simulate the credit states \(\Lambda _{t}\) and the stock price sample paths over 1000 time steps in each scenario. Additionally we provide a frequency plot and VaR calculation over 1000 simulated trading days for each scenario. The frequency plots and VaR measurements over different scenarios provide information on market risk changes with control policies.
5.2 Results
In this section we present our results.
5.2.1 Calibrated results
5.3 Scenario results
5.3.1 Scenario 1 results
5.3.2 Scenario 2 results
5.3.3 Scenario 3 results
5.3.4 Scenario 4 results
5.4 Analysis
Tables 1 and 2 provide the results of our calibration for the model in equation (32); we also provide the associated Value function V(.) plot in Fig. 1 over different values of x and T. In Figs. 1, 2 and 3 we provide simulation results over 1000 time steps, using our calibrated parameters in Tables 1 and 2. In Fig. 1 we simulate the credit states \(\Lambda _{t}\), in Fig. 2 we provide 3 simulated stock price sample paths, and in Fig. 3 we provide a frequency plot of daily losses. In Table 3 we also provide VaR risk measurement of daily losses, over different VaR levels (or cumulative probabilities) at 90%, 95% and 99%. We provide VaR losses as percentage losses (\(\tilde{L}_{t}\)) to enable comparison to other VaR calculations.
The results in Tables 1 and 2 are consistent with our expectations. In Table 1 we observe that \(\mathbb {P}(\Lambda _{t+\delta }\!=\!1|\Lambda _{t}\!=\!1)\) and \(\mathbb {P}(\Lambda _{t+\delta }\!=\!2|\Lambda _{t}\!=\!2)\) have high probabilities, implying that the stock price tends to persist in its current state, rather than transitioning between credit states. This is consistent with empirical observations, as credit states cannot change quickly between good and bad states easily (since firms take time to resolve credit issues).
The calibration results for the volatility \(\sigma _{\Lambda }\) and drift values \(b_{\Lambda }\) (in Table 2) are consistent with the credit states. In credit state \(\Lambda =1\), \(b_{1}\) is positive and so implies that the stock is growing with time, which is consistent with a good credit state. In \(\Lambda =2\), \(b_{2}\) is negative and so implies that the stock is decreasing with time, which is consistent with a bad credit state. Additionally, the volatility \(\sigma _{2}\) in the bad credit state \(\Lambda =2\) is higher than volatility in the good credit state \(\sigma _{1}\). This is consistent with empirical and theoretical expectations because volatility is considered a proxy for risk, hence volatility should increase when a firm is in a worse credit state.
In Fig. 1 we simulate the credit states 1 and 2, over 1000 time steps, using our calibration results. As expected, our model spends the majority of its time in state 1, with the current state tending to persist rather than frequently switching between states. Using the calibration results in Tables 1 and 2, we simulate 3 sample paths of stock prices, over 1000 time steps, in Fig. 2. Such sample paths are consistent with our results, where we expect the model to be in state 1 for the majority of the time. Consequently, we expect stock prices to grow over time.
In Table 3 and Fig. 3 we provide risk analysis information on the model. In Fig. 3 the plot displays the daily losses and their frequencies, over a sample of 1000 time steps. We note that negative losses imply positive price gains. The right hand tail of the plot for positive losses implies that there is significant market risk, as tail losses are used as a measure of market risk. In Table 3 the VaR values at different levels also provide a measure of market risk. We note that at the 99% level that the loss is 15.77%, suggesting that significant market risk exists in the model as a stock market crash can be considered a 10% decline in a single trading day.
In Fig. 4 we present a plot of our value function V(.) at \(t=0\). We plot V(.) for different x and T values, using the calibrated parameter values in Tables 1 and 2 for our model. As can be observed in Fig. 4 we notice that for larger values of T that it significantly increases V(.); additionally at \(T=10,000\) we notice that increasing x has an observable impact on V(.). As V(.) gives the maximum expected utility associated with \(X_{T}\), we expect V(.) to increase with x and T, as \(X_t\) tends to increase with both x and T.
In Sect. 5.3 we provide our scenario results for different control policy values \(u_{1},u_{2}\); this enables us to understand the optimal solutions from an operational and financial point of view as we vary management or control policy values. The associated state transition probabilities \(\mathbb {P}(\Lambda _{t+\delta }\!=\!j|\Lambda _{t}\!=\!i)\) for different control policy values \(u_{1},u_{2}\) are provided in Table 4. For each scenario we provide a simulation over 1000 time steps of the credit states \(\Lambda _{t}\) to examine the credit states. We simulate 3 stock price sample paths over 1000 time steps to examine the different sample path behaviour under each scenario. We also provide frequency plot distributions over 1000 samples and VaR risk measurements to analyse the changes in market risk.
As can be seen in the credit state simulation graphs in Figs. 5, 8, 11 and 14, the results provide a consistent trend in their patterns. As the control policies \(u_{1},u_{2}\) (or equivalently the management decisions) affect the transition probabilities \(\mathbb {P}(\Lambda _{t+\delta }\!=\!j|\Lambda _{t}\!=\!i)\), the stock price persists in the worse credit state \(\Lambda _{t}=2\) more frequently. In scenarios 1 and 2, where we have worse management, we can observe in Figs. 5 and 8 that the stock is more frequently in state 2. However, in scenarios 3 and 4, where where have better management, the stock is more frequently in state 1 (see Figs. 11 and 14).
In Figs. 6, 9, 12 and 15 we plot 3 sample paths under each scenario. As we can observe in Figs. 6 and 9, in scenarios 1 and 2 we have poor management (or control policy) and so the stock price does not tend to increase over time. This reflects the property that the tendency to enter the worse credit states reduces the stock price. In the better managed (or control policy) conditions of scenarios 3 and 4 we observe in Figs. 12 and 15 that the stock prices are growing with time, reflecting that the stock tends to be in a better credit state over time. Hence our results are consistent with our expectations, and demonstrate the impact of the control policy values \(u_{1},u_{2}\) on asset prices.
We now analyse the market risk under each scenario by examining the frequency plot and VaR values. As can be seen in Figs. 7, 10, 13 and 16 the choice of policy values \(u_{1},u_{2}\) has a significant impact on market risk. As the management improves (or equivalently the policy values \(u_{1},u_{2}\)) from scenario 1 to 4 we notice that market risk decreases. This is because losses in the right hand tail of the frequency plots decrease; the right hand tail becomes increasingly smaller and so the probability and magnitude of losses also decrease. For example in Fig. 16 the right hand tail is essentially non-existent, implying low risk of losses, however in Fig. 7 the right tail is substantial and so we can expect a higher frequency and magnitude of losses. Such observations are consistent with our expectations because worse management (or policy values \(u_{1},u_{2}\)) lead to worse credit states, and so causes higher losses.
The changes in control policy values are reflected in the VaR risk measurement results in Tables 5, 6, 7, and 8. As can be observed in Tables 5, 7, and 8, the VaR losses \(\tilde{L}_{t}\) at all probability levels \(\zeta \) are higher as the scenario number decreases; that is as the control policy or management becomes worse. In fact in scenario 4, where we have better management, the VaR at 99% is 7.97% whereas in scenario 1 the VaR at 99% is 16.69%. Therefore risk has more than doubled from scenario 4 to 1, at the VaR 99% threshold for market risk measurement.
6 Conclusion
This paper provides the first stock price model that explicitly incorporates credit risk dynamics, under a stochastic optimal control system. The stock price model is also able to incorporate managerial control of credit risk through a control policy in the stochastic system. This paper is particularly relevant given that credit risk was seen as a major cause of the Global Financial Crisis. We provide explicit conditions on the existence of optimal feedback controls for the stock price model with credit risk, we prove the continuity of the value function, and then prove the dynamic programming principle for our system. Finally, we prove the Viscosity solution of the Hamilton–Jacobi–Equation.
We provide numerical experiments to demonstrate our model, using data from the S&P 500 index to calibrate our model. The S&P 500 index data is sampled over a period of 20 years, from January 2000 to January 2020, and therefore provides a comprehensive data set for analysis. Additionally, our data set includes data points before, during and after the Global Financial Crisis, and so incorporates a pertinent credit risk event in our model. Our empirical results are presented and discussed in the paper, and we find the empirical results are consistent with our expectations.
In terms of future work, we would like to extend our model to include portfolios of stocks, rather than individual stocks. This would be particularly relevant to industry as firms typically hold positions in portfolios, rather than single assets. Secondly, we would like to investigate different stochastic processes, such as mean reverting stochastic differential equations, and analyse the impact on control variables. Such mean reverting processes are especially important to many cyclical asset prices such as commodities. Finally, in future work we would like to investigate the pricing of derivatives, such as European options, when applying our model with credit risk.
References
Affes, Z., & Hentati-Kaffel, R. (2019). Forecast bankruptcy using a blend of clustering and MARS model: case of US banks. Annals of Operations Research, 281, 27–64.
Bao, J., & Shao, J. (2016). Permanence and extinction of regime-switching predator-prey models. SIAM Journal on Mathematical Analysis, 48(1), 725–739.
Black, F. (1976). Studies of stock market volatility changes. Proceedings of the American Statistical Association, Business and Economic Statistics Section, 1(1), 177–181.
Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy, 81(3), 637–654.
Brandimarte, P. (2006). Numerical methods in finance and economics: a matlab-based introduction. New York: Wiley.
Brealey, R. A., Myers, S. C., & Allen, F. (2017). Principles of corporate finance. New York: McGraw-Hill.
Briys, E., & Varenne, F. D. (1997). Valuing risky fixed rate debt: An extension. The Journal of Financial and Quantitative Analysis, 32(2), 239.
Cont, R., & Tankov, P. (2004). Financial Modelling with Jump Processes. USA: CRC Press.
Cox, J., & Ross, S. (1976). The valuation of options for alternative stochastic processes. Journal of Financial Economics, 3(1), 145–66.
Cretarola, A., & Figá-Talamanca, G. (2019). Detecting bubbles in bitcoin price dynamics via market exuberance. Annals of Operations Research.
Bertsekas, S. S. D. (1978). Stochastic optimal control: the discrete-time case. USA: Academic Press.
Damel, P., Thi, H. A. L., & Peltre, N. (2016). The challenge in managing new financial risks: adopting an heuristic or theoretical approach. Annals of Operations Research, 247(2), 581–598.
Dhesi, G., Shakeel, B., & Ausloos, M. (2019) Modelling and forecasting the kurtosis and returns distributions of financial markets: irrational fractional Brownian motion model approach. Annals of Operations Research. https://doi.org/10.1007s10479-019-03305-z.
Dowd, K. (2011). An introduction to market risk measurement. New York: Wiley Finance.
du Jardin, P. (2019). Forecasting bankruptcy using biclustering and neural network-based ensembles. Annals of Operations Research. https://doi.org/10.1007/s10479-019-03283-2.
D’Ecclesia, R., & Clementi, D. (2019). Volatility in the stock market: ANN versus parametric models. Annals of Operations Research. https://doi.org/10.1007/s10479-019-03374-0.
Errais, E. (2019). Pricing insurance premia: a top down approach. Annals of Operations Research. https://doi.org/10.1007/s10479-019-03459-w.
Geman, H. (2002). Pure jump lévy processes for asset price modelling. Journal of Banking and Finance, 26(7), 1297–1316.
Guo, X. (2001). Information and option pricings. Quantitative Finance, 1(1), 38–44.
Haas, R. D., & Horen, N. V. (2012). International shock transmission after the lehman brothers collapse: Evidence from syndicated lending. American Economic Review, 102(3), 231–237.
Hamilton, J. (1994). Time series analysis. USA: Princeton University Press.
Hamilton, J., & Susmel, R. (1994). Autoregressive conditional heteroskedasticity and changes in regime. Journal of Econometrics, 64(1–2), 307–33.
Hardy, M. (2001). A regime-switching model of long-term stock returns. North American Actuarial Journal, 5(2), 41–53.
Haussmann, U., & Lepeltier, J. (1990). On the existence of optimal controls. SIAM Journal on Control and Optimization, 28, 851–902.
Heston, S. (1993). A closed-form solution for options with stochastic volatility with applications to bond and currency options. Review of Financial Studies, 6(2), 327–43.
Hull, J., & White, A. (1987). The pricing of options on assets with stochastic volatilities. The Journal of Finance, 42(2), 281–300.
Johnson, H., & Shanno, D. (1987). Option pricing when the variance is changing. The Journal of Financial and Quantitative Analysis, 22(2), 143–151.
Kahneman, D., & Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica, 47(2), 263–91.
V.S., S.M., Kathiravan, C., & Balakrishnan, S. (2019). Investor behavior and weather factors: evidences from Asian region. Annals of Operations Research.
Kim, I. J., Ramaswamy, K., & Sundaresan, S. (1993). Does default risk in coupons affect the valuation of corporate bonds?: A contingent claims model. Financial Management, 22(3), 117.
Klein, P. (1996). Pricing black-scholes options with correlated credit risk. Journal of Banking and Finance, 20(7), 1211–1229.
Klein, P., & Inglis, M. (2001). Pricing vulnerable european options when the option’s payoff can increase the risk of financial distress. Journal of Banking & Finance, 25(5), 993–1012.
Kou, S. (2014). Lévy processes in asset pricing. Wiley StatsRef: Statistics Reference Online.
Kou, S. G. (2002). A jump-diffusion model for option pricing. Management Science, 48(8), 1086–1101.
Leland, H. E. (1994). Corporate debt value, bond covenants, and optimal capital structure. The Journal of Finance, 49(4), 1213.
Leland, H. E., & Toft, K. B. (1996). Optimal capital structure, endogenous bankruptcy, and the term structure of credit spreads. The Journal of Finance, 51(3), 987.
Liang, X., & Wang, G. (2012). On a reduced form credit risk model with common shock and regime switching. Insurance: Mathematics and Economics, 51(3), 567–575.
Liao, S.-L., & Huang, H.-H. (2005). Pricing black-scholes options with correlated interest rate risk and credit risk: an extension. Quantitative Finance, 5(5), 443–457.
Longstaff, F. A., & Schwartz, E. S. (1995). A simple approach to valuing risky fixed and floating rate debt. The Journal of Finance, 50(3), 789–819.
Mao, X. (2013). Stabilization of continuous-time hybrid stochastic differential equations by discrete-time feedback control. Automatica, 49(12), 3677–3681.
Merton, R. (1973). Theory of rational option pricing. Bell Journal of Economics and Management Science, 4(1), 141–183.
Merton, R. (1976). Option pricing when underlying stock returns are discontinuous. Journal of Financial Economics, 3(1–2), 125–144.
Merton, R. C. (1974). On the pricing of corporate debt: The risk structure of interest rates. The Journal of Finance, 29(2), 449–470.
Ouenniche, T. K. J. (2017). An out-of-sample evaluation framework for DEA with application in bankruptcy prediction. Annals of Operations Research, 254, 235–250.
Pham, H. (2009). Continuous-time stochastic control and optimization with financial applications. Berlin Heidelberg: Springer-Verlag.
Shao, J. (2015). Strong solutions and strong feller properties for regime-switching diffusion processes in an infinite state space. SIAM Journal on Control and Optimization, 53, 2462–2479.
Shao, J. (2019). The existence of optimal feedback controls for stochastic dynamical systems with regime-switching. submitted.
Shi, Y. (2020). Long memory and regime switching in the stochastic volatility modelling. Annals of Operations Research.
Simon, D., & Wiggins, R. (2001). S & P futures returns and contrary sentiment indicators. Journal of Futures Markets, 21(5), 447–462.
Wilmott, P., et al. (1998). Derivatives: the theory and practice of financial engineering. New York: Wiley.
Yin, G., & Zhu, C. (2010). Hybrid switching diffusions: properties and applications. In: IEEE Control Systems Magazine (Vol. 30, pp. 74–75). Berlin: Springer.
Zheng, K., Li, Y., & Xu, W. (Jan. 2019). Regime switching model estimation: spectral clustering hidden Markov model. Annals of Operations Research.
Zhou, C. (2001). The term structure of credit spreads with jump risk. Journal of Banking & Finance, 25(11), 2015–2040.
Zhou, Q., Yang, J.-J., & Wu, W.-X. (2019). Pricing vulnerable options with correlated credit risk under jump-diffusion processes when corporate liabilities are random. Acta Mathematicae Applicatae Sinica, English Series, 35(2), 305–318.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of value function solution
According to Theorem 3.3 the value function V is a solution to the Hamilton–Jacobi-Bellman equation
with the boundary condition \(V(T,x,i)=g(x)\). Here
Based on the linear coefficients of \((X_t)\), we are looking for the candidate solution to (36) in the form
By substituting such V(t, x, i) into (36), we derive that \(\phi \) should satisfy the following interaction system of ordinary differential equations (ODEs):
with \(\phi _1(T)=\phi _2(T)=1\), where we denote by \(\phi _i(t)=\phi (t,i)\) for \(i=1,2\),
The closed-form solutions to (38) and (39) are non-trivial, however we can consider first a simple case, and then give an explicit solution inductively. If we consider the ODEs
The solutions are given explicitly by
where
Based on the solution to \(\phi _1(t)\) and \(\phi _2(t)\), we consider the explicit solution to (38) and (39), which further provides us the explicit form of the value function \(V(t,x,i)=\phi _i(t)g(x)\). The construction is divided into the following cases.
-
(i)
If \(\rho _1=\rho _2=\rho \), then \(\phi _1(t)=\phi _2(t)={\mathrm{e}}^{\rho (T-t)}\) for all \(t\in [0,T]\).
-
(ii)
If \(\rho _1\ne \rho _2\), then \(\phi _1(t)\not \equiv \phi _2(t)\). Therefore, there exists \(t_0\in (0,T]\) such that \(\phi _1(t)\ge \phi _2(t)\) for all \(t\in [0,t_0]\) or \(\phi _2(t)\ge \phi _1(t)\), which depends on the specific values of \(\rho _i, q_i, T\). As the method to construct solutions is similar, we assume that \(\phi _1(t)\ge \phi _2(t)\) for \(t\in [0,t_0]\). Then, by virtue of (38) and (39), it holds
$$\begin{aligned} \phi _1(t)= & {} \frac{\tilde{\beta }_2+\rho _1}{\tilde{\beta }_2-\tilde{\beta }_1}{\mathrm{e}}^{\tilde{\beta }_1(t-T)}+ \frac{\tilde{\beta }_1+\rho _1}{\tilde{\beta }_1-\tilde{\beta }_2}{\mathrm{e}}^{\tilde{\beta }_2(t-T)}, \end{aligned}$$(42)$$\begin{aligned} \phi _2(t)= & {} \frac{(\tilde{\beta }_1\!+\!\rho _1)(\tilde{\beta }_1\!+\!\rho _1\!-\!q_1)}{q_1(\tilde{\beta }_1-\tilde{\beta }_2)}{\mathrm{e}}^{\tilde{\beta }_1(t-T)} +\frac{(\tilde{\beta }_1\!+\!\rho _1)(\tilde{\beta }_2 \!+\!\rho _1\!-\!q_1)}{q_1(\tilde{\beta }_2-\tilde{\beta }_1)}{\mathrm{e}}^{\tilde{\beta }_2(t-T)}, \end{aligned}$$(43)where
$$\begin{aligned} \tilde{\beta }_1= & {} \frac{1}{2}\big (\kappa _1q_1+\kappa _2q_2-\rho _1-\rho _2+ \sqrt{(\rho _1-\rho _2+\kappa _2q_2-\kappa _1q_1)^2+4\kappa _1\kappa _2q_1q_2}\big ),\\ \tilde{\beta }_2= & {} \frac{1}{2} \big (\kappa _1q_1+\kappa _2q_2-\rho _1-\rho _2-\sqrt{(\rho _1-\rho _2+\kappa _2q_2-\kappa _1q_1)^2+4\kappa _1\kappa _2q_1q_2}\big ). \end{aligned}$$If \(\phi _1(t)<\phi _2(t)\) in \([0,t_0]\) we only need to modify the definition of \(\tilde{\beta }_1,\tilde{\beta }_2\) to obtain the explicit solution by (42) and (43). Inductively, we can obtain the explicit solutions \(\phi _1(t)\) and \(\phi _2(t)\) on the whole interval [0, T], and further the value function \(V(t,x,i)=\phi _i(t)g(x)\) as desired.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shao, J., Mitra, S. & Karathanasopoulos, A. Optimal feedback control of stock prices under credit risk dynamics. Ann Oper Res 313, 1285–1318 (2022). https://doi.org/10.1007/s10479-021-04002-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-04002-6