Skip to main content
SpringerLink
Log in

Forecast bankruptcy using a blend of clustering and MARS model: case of US banks

  • S.I.: Risk in Financial Economics
  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

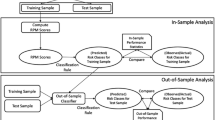
In this paper, we compare the performance of two non-parametric methods of classification and regression trees (CART) and the newly multivariate adaptive regression splines (MARS) models, in forecasting bankruptcy. Models are tested on a large universe of US banks over a complete market cycle and run under a K-fold cross validation. Then, a hybrid model which combines K-means clustering and MARS is tested as well. Our findings highlight that (i) Either in training or testing sample, MARS provides, in average, better correct classification rate than CART model (ii) Hybrid approach significantly increases the classification accuracy rate in the training sample (iii) MARS prediction underperforms when the misclassification of the bankrupt banks rate is adopted as a criteria (iv) Finally, results prove that non-parametric models are more suitable for bank failure prediction than the corresponding Logit model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

  1. The specificity represents the number of the (AB) classified in the group of the (AB).

  2. The sensitivity represents the percentage of the (NAB) correctly classified.

References

  • Affes, Z., & Hentati-Kaffel, R. (2017). Predicting us banks bankruptcy: Logit versus canonical discriminant analysis. Computational Economics, 1–46. https://doi.org/10.1007/s10614-017-9698-0.

    Article  Google Scholar 

  • Altman, E. I. (1968). Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. The Journal of Finance, 23(4), 589–609.

    Article  Google Scholar 

  • Anandarajan, M., Lee, P., & Anandarajan, A. (2001). Bankruptcy prediction of financially stressed firms: An examination of the predictive accuracy of artificial neural networks. Intelligent Systems in Accounting, Finance and Management, 10(2), 69–81.

    Article  Google Scholar 

  • Andalib, A., & Atry, F. (2009). Multi-step ahead forecasts for electricity prices using narx: A new approach, a critical analysis of one-step ahead forecasts. Energy Conversion and Management, 50(3), 739–747.

    Article  Google Scholar 

  • Anderberg, M. R. (2014). Cluster analysis for applications: Probability and mathematical statistics: A series of monographs and textbooks (Vol. 19). New York: Academic press.

    Google Scholar 

  • Barr, R. S., Siems, T. F., et al. (1994). Predicting bank failure using DEA to quantify management quality. Federal Reserve Bank of Dallas: Technical report.

    Google Scholar 

  • Beaver, W. H. (1966). Financial ratios as predictors of failure. Journal of accounting research, 4, 71–111.

    Article  Google Scholar 

  • Boyacioglu, M. A., Kara, Y., & Baykan, Ö. K. (2009). Predicting bank financial failures using neural networks, support vector machines and multivariate statistical methods: A comparative analysis in the sample of savings deposit insurance fund (SDIF) transferred banks in Turkey. Expert Systems with Applications, 36(2), 3355–3366.

    Article  Google Scholar 

  • Breiman, L., Friedman, J., Stone, C. J., & Olshen, R. A. (1984). Classification and regression trees. Boca Raton: CRC Press.

    Google Scholar 

  • Carter, C., & Catlett, J. (1987). Assessing credit card applications using machine learning. IEEE Expert, 2(3), 71–79.

    Article  Google Scholar 

  • Chen, M.-Y. (2011). Predicting corporate financial distress based on integration of decision tree classification and logistic regression. Expert Systems with Applications, 38(9), 11261–11272.

    Article  Google Scholar 

  • Cole, R. A. & Gunther, J. (1995). A camel rating’s shelf life. Available at SSRN 1293504.

  • Collier, C., Forbush, S., Nuxoll, D., & O’Keefe, J. P. (2003). The SCOR system of off-site monitoring: Its objectives, functioning, and performance. FDIC Banking Review Series, 15(3), 17.

    Google Scholar 

  • De Andrés, J., Lorca, P., de Cos Juez, F. J., & Sánchez-Lasheras, F. (2011). Bankruptcy forecasting: A hybrid approach using fuzzy c-means clustering and multivariate adaptive regression splines (MARS). Expert Systems with Applications, 38(3), 1866–1875.

  • Demirgüç-Kunt, A., & Detragiache, E. (1997). The determinants of banking crises-evidence from developing and developed countries (Vol. 106). Washington, D.C.: World Bank Publications.

    Google Scholar 

  • Friedman, J. H. (1991). Multivariate adaptive regression splines. The Annals of Statistics, 19(1), 1–67.

    Article  Google Scholar 

  • Frydman, H., Altman, E. I., & KAO, D.-L. (1985). Introducing recursive partitioning for financial classification: The case of financial distress. The Journal of Finance, 40(1), 269–291.

  • Gepp, A., Kumar, K., & Bhattacharya, S. (2010). Business failure prediction using decision trees. Journal of Forecasting, 29(6), 536–555.

    Article  Google Scholar 

  • Godlewski, C. J., et al. (2003). Modélisation de la prévision de la défaillance bancaire une application aux banques des pays emergents. Document de travail LARGE: Université Robert Schuman Strasbourg.

    Google Scholar 

  • Hanweck, G. A., et al. (1977). Predicting bank failure. Board of Governors of the Federal Reserve System (US): Technical report.

    Google Scholar 

  • Hartigan, J. A. (1975). Clustering algorithms. New york: Wiley.

    Google Scholar 

  • Iturriaga, F. J. L., & Sanz, I. P. (2015). Bankruptcy visualization and prediction using neural networks: A study of US commercial banks. Expert Systems with Applications, 42(6), 2857–2869.

    Article  Google Scholar 

  • Jain, A. K., & Dubes, R. C. (1988). Algorithms for clustering data. Englewood Cliffs: Prentice-Hall Inc.

    Google Scholar 

  • Jones, S., & Hensher, D. A. (2004). Predicting firm financial distress: A mixed logit model. The Accounting Review, 79(4), 1011–1038.

    Article  Google Scholar 

  • Kolari, J., Glennon, D., Shin, H., & Caputo, M. (2002). Predicting large US commercial bank failures. Journal of Economics and Business, 54(4), 361–387.

    Article  Google Scholar 

  • Lanine, G., & Vander Vennet, R. (2006). Failure prediction in the Russian bank sector with logit and trait recognition models. Expert Systems with Applications, 30(3), 463–478.

    Article  Google Scholar 

  • Lenard, M. J., Alam, P., & Madey, G. R. (1995). The application of neural networks and a qualitative response model to the auditor’s going concern uncertainty decision. Decision Sciences, 26(2), 209–227.

    Article  Google Scholar 

  • Martin, D. (1977). Early warning of bank failure: A logit regression approach. Journal of Banking & Finance, 1(3), 249–276.

    Article  Google Scholar 

  • McKee, T. E., & Greenstein, M. (2000). Predicting bankruptcy using recursive partitioning and a realistically proportioned data set. Journal of Forecasting, 19(3), 219–230.

    Article  Google Scholar 

  • Odom, M. D. & Sharda, R. (1990). A neural network model for bankruptcy prediction. In IJCNN International Joint Conference on neural networks, 1990 (pp. 163–168).

  • Ohlson, J. A. (1980). Financial ratios and the probabilistic prediction of bankruptcy. Journal of accounting research, 18(1), 109–131.

    Article  Google Scholar 

  • Pantalone, C. C., & Platt, M. B., et al. (1987). Predicting commercial bank failure since deregulation. New England Economic Review, 37–47.

  • Sánchez-Lasheras, F., de Andrés, J., Lorca, P., & de Cos Juez, F. J. (2012). A hybrid device for the solution of sampling bias problems in the forecasting of firms’ bankruptcy. Expert Systems with Applications, 39(8), 7512–7523.

    Article  Google Scholar 

  • Sinkey, J. F. (1979). Problem and failed institutions in the commercial banking industry. London: Wiley.

    Google Scholar 

  • Thomson, J. B. (1991). Predicting bank failures in the 1980s. Economic Review-Federal Reserve Bank of Cleveland, 27(1), 9.

    Google Scholar 

  • West, M., Harrison, P. J., & Migon, H. S. (1985). Dynamic generalized linear models and bayesian forecasting. Journal of the American Statistical Association, 80(389), 73–83.

    Article  Google Scholar 

  • Zhang, G., Hu, M. Y., Patuwo, B. E., & Indro, D. C. (1999). Artificial neural networks in bankruptcy prediction: General framework and cross-validation analysis. European Journal of Operational Research, 116(1), 16–32.

    Article  Google Scholar 

  • Zmijewski, M. E. (1984). Methodological issues related to the estimation of financial distress prediction models. Journal of Accounting research, 22, 59–82.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Centre d’Economie de la Sorbonne, Université Paris1 Panthéon-Sorbonne, Maison des Sciences Economiques, 106-112 Boulevard de l’Hôpital, 75013, Paris, France

    Zeineb Affes & Rania Hentati-Kaffel

Authors
  1. Zeineb Affes
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rania Hentati-Kaffel
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rania Hentati-Kaffel.

Additional information

This work was achieved through the Laboratory of Excellence on Financial Regulation (Labex ReFi) supported by PRES heSam under the reference ANR-10-LABX-0095.

Appendix A: Basis function

Appendix A: Basis function

Basis functions For 2008

$$\begin{aligned} \begin{array}{l} BF2 = max( 0, 0.0801 - EQTL);\\ BF3 = max( 0, NPLGL - 0.1099) * BF2;\\ BF7 = max( 0, NPLGL - 0.0823) * BF2;\\ BF10 = max( 0, 0.0249 - EQTA);\\ BF12 = max( 0, 0.3165 - NPLGL);\\ BF36 = max( 0, TLTD - 0.7878) * BF10;\\ \end{array} \end{aligned}$$

The final model is expressed as follows:

$$\begin{aligned} Y = 0.1248 - 525.1 * BF3 + 534.753 * BF7 - 0.4066 * BF12 - 209.952 * BF36; \end{aligned}$$
(7)

The basis function BF2 does not appear in the model but it contributes in the construction of others basis function (BF3 and BF7). From BF2, on variable EQTL (capital adequacy proxy), data is grouped into two sets: the first one is assigned 0 for all EQTL values that are more than 0.08 and the second set contains the elevation values that are below a threshold (e.g., c = 0.08) Indeed, the BF3 is defined as a combination between NPLGL and EQTL. This basis function has a negative effect on the target variable only when the value of NPLGL exceeds 0.109 and the value of EQTL is lower than 0.08. The basis function (BF7) which is a combination of (BF1) with NPLGL, have a positive impact on the output. In other word, a value of NPLGL greater than 0.08 multiplied by a value of EQTL lower than 0.08 affects negatively the target ‘Y’. Moreover, a decrease in the value of NPLGL above 0.316 (in BF12) will decrease the variable ‘Y’. The negative effect of (BF36) appears only when the value of TLTD at least 0.787 and BF10 is positive (for EQTA lower than 0.0248).

Basis functions For 2009

$$\begin{aligned} \begin{array}{l} BF15 = max( 0, EQTA - 0.0129);\\ BF17 = max( 0, EQTA - 0.0296);\\ BF44 = max( 0, 0.0540 - EQTA);\\ BF45 = max( 0, ROA + 0.0222) * BF44;\\ \end{array} \end{aligned}$$

The final Model is expressed as below:

$$\begin{aligned} Y = 0.8895 - 48.1527 * BF15 + 47.3615 * BF17 + 2537.87 * BF45; \end{aligned}$$
(8)

We note that BF15 is zero for value of EQTA lower than 0.0129. A negative sign for the estimated beta factor of BF15 indicates a decrease of the output variable. On the other hand a value of EQTA greater than 0.0296 (BF17) effects positively the target variable. We also note the presence of interaction between predictor variables, which means that the effect of a predictor on the target variable may depend on the value of another predictor. We see in the definition of the BF45 that the effect of the variable ROA on the output variable depends on the value of the ratio EQTA. The effect of this interaction can be explained as follow. If the value of EQTA is lower than 0.054 and the value of ROA is above \(-\,0.022\), it has a positive impact on the target variable.

Basis functions For 2010

$$\begin{aligned} \begin{array}{l} BF2 = max( 0, 0.0799 - EQTL);\\ BF10 = max( 0, 0.9418 - TLTD) * BF2;\\ BF13 = max( 0, ROA + 0.0083);\\ BF14 = max( 0, -0.0083 - ROA);\\ BF18 = max( 0, 0.0333 - EQTA) * BF13;\\ BF32 = max( 0, 0.0283 - EQTL);\\ BF34 = max( 0, 0.0143 - EQTA) * BF32;\\ BF49 = max( 0, EQTA - 0.0635);\\ BF50 = max( 0, 0.0635 - EQTA);\\ BF51 = max( 0, EQTL - 0.0315) * BF50;\\ BF53 = max( 0, EQTL - 0.0301) * BF50;\\ BF55 = max( 0, ROA + 0.0135) * BF50;\\ BF59 = max( 0, TLTD - 0.5167) * BF50;\\ BF63 = max( 0, TDTA - 0.9018) * BF49;\\ \end{array} \end{aligned}$$

The final model is expressed as follows:

$$\begin{aligned} Y= & {} 0.0083 + 31.5524 * BF10 - 2.2643 * BF14 - 11481.2 * BF18 \nonumber \\&\quad -\, 130.002 * BF34 + 6537.12 * BF51 \nonumber \\&\quad -\, 6486.5 * BF53 + 2271.61 * BF55 + 38.4564 * BF59 + 192.971 * BF63; \end{aligned}$$
(9)

The BF2 does not appear in the model but it contributes to compute the BF10. Indeed, for values of TLTD and EQTL respectively lower than 0.94 and 0.0798, the BF10 has a positive effect on the output variable. For a value of ROA inferior than \(-\,0.00827\) (BF14) impacts negatively the target value. We also note that the interaction between EQTA and ROA (BF18) has a negative effect on the target variable for a value of EQTA lower than 0.033 and ROA upper than \(-\,0.008\). Moreover the negative impact of the BF34 appears only when EQTA is below 0.0143 and EQTA lower than 0.028. The BF49 and BF50 together define a piecewise linear function of EQTA with a knot of 0.0635. The values of these basis functions are positives when the value of EQTA is respectively superior to 0.0635 and inferior than 0.0635. The basis function BF50 is not involved in the model but it’s used to compute the BF51, BF53, BF55 and BF59. Indeed, when the value of EQTL is above 0.0314 and the EQTA is lower than 0.0635, then the output variable will increase. On the other hand, a value of EQTL greater than 0.03 and EQTA below 0.0635, have a negative effect on the target variable. A positive impact of the BF55 and BF59 on the target variable appear respectively for ROA bigger than \(-\,0.0135\) and TLTD higher than 0.516 multiplied by the BF50. The BF63 has a positive effect on the output variable for a value of TDTA superior to 0.9 and an EQTA higher than 0.0635.

Basis functions For 2011

$$\begin{aligned} \begin{array}{l} BF2 = max( 0, 0.0707 - EQTL);\\ BF4 = max( 0, 0.0773 - NPLGL) * BF2;\\ BF12 = max( 0, -0.02489 - ROA) * BF2;\\ BF25 = max( 0, 0.0367 - EQTA);\\ BF27 = max( 0, -0.0216 - ROA) * BF25;\\ \end{array} \end{aligned}$$

The final model is expressed as follow:

$$\begin{aligned} Y = 0.0026 + 14.7799 * BF2 - 301.097 * BF4 - 413.205 * BF12 + 577.801 * BF27; \end{aligned}$$
(10)

As it can be seen, the positive effect of the BF2 appears only when the value of EQTL is lower than 0.07. The BF2 was used in the construction of other basis functions (BF4 and BF12). In fact, we note that the BF4 and BF12 have a negative impact on the target variable for values of NPLGL inferior than 0.077 and ROA lower than \(-\,0.0248\), multiplied by BF2. The BF27 is a function of the variable of ROA with a knot of \(-\,0.0216\) multiplied by the BF25. It means that when the value of ROA is lower than \(-\,0.0216\) and the value of EQTA is inferior than 0.0367, we note a positive impact on the target variable.

Basis functions For 2012

$$\begin{aligned} \begin{array}{l} BF2 = max( 0, 0.0667 - EQTA);\\ BF12 = max( 0, 0.0049 - EQTA);\\ BF14 = max( 0, 0.0325 - EQTA);\\ BF15 = max( 0, ROE + 1.9250);\\ BF16 = max( 0, -1.9250 - ROE);\\ BF19 = max( 0, NPLGL - 0.0767) * BF14;\\ BF30 = max( 0, 0.1372 - NPLTA) * BF2;\\ BF43 = max( 0, LLRTA - 0.0197) * BF14;\\ BF45 = max( 0, LLRTA - 0) * BF12;\\ BF49 = max( 0, NPLGL - 0.1597) * BF14;\\ BF74 = max( 0, LLRTA - 0) * BF16;\\ \end{array} \end{aligned}$$

The final model is expressed as follow:

$$\begin{aligned} Y= & {} 0.1712 - 0.0873 * BF15 + 411.003 * BF19 + 55.1609 * BF30 + 587.585 * BF43 \nonumber \\&\quad -\, 1132.57 * BF45 - 449.155 * BF49 - 0.0138 * BF74; \end{aligned}$$
(11)

The basis functions BF2, BF12 and BF14 appear in the construction of others basis functions (BF19, BF30, BF43, BF45 and BF49) only when the values of EQTA are respectively inferior to 0.0667, 0.00495 and 0.0325. The BF30 has a positive impact on the target when the value of NPLTA is lower than 0.137 multiplied by BF2. A positive impact on the output appears for values of NPLGL superior to 0.076 and a value of LLRTA above 0.197, multiplied by BF14. But for value of NPLGL upper than 0.159 and an EQTA lower than 0.0325, we note a negative effect on the target variable. Moreover we note the presence of interaction between the LLRTA ratio and two other variables (EQTA and ROE). The positive effect of BF45 appears for a value of LLRTA higher than 0 and EQTA lower than 0.00495. The BF74 have a positive effect on the target value when LLRTA is superior to 0 and ROE is less than \(-\,1.925\). We also note that a value of ROA higher than \(-\,1.925\) (BF15) impacts negatively the target.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Affes, Z., Hentati-Kaffel, R. Forecast bankruptcy using a blend of clustering and MARS model: case of US banks. Ann Oper Res 281, 27–64 (2019). https://doi.org/10.1007/s10479-018-2845-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-018-2845-8

Keywords

JEL Classification

Search

Navigation