A design rule for constant depth microfluidic networks for power-law fluids

Abstract

A biomimetic design rule is proposed for generating bifurcating microfluidic channel networks of rectangular cross section for power-law and Newtonian fluids. The design is based on Murray’s law, which was originally derived using the principle of minimum work for Newtonian fluids to predict the optimum ratio between the diameters of the parent and daughter vessels in networks with circular cross section. The relationship is extended here to consider the flow of power-law fluids in planar geometries (i.e. geometries of rectangular cross section with constant depth) typical of lab-on-a-chip applications. The proposed design offers the ability to precisely control the shear-stress distributions and predict the flow resistance along the bifurcating network. Computational fluid dynamics simulations are performed using an in-house code to assess the validity of the proposed design and the limits of operation in terms of Reynolds number for Newtonian, shear-thinning and shear-thickening fluids under various flow conditions.

1 Introduction

Over millions of years, biological systems have evolved through the numerous trial-and-error procedures of natural selection to perfect design solutions that often surpass those developed by Man. The field of biomimetics has turned into an increasingly active area of research that studies and imitates naturally inspired systems in order to advance modern technology through the use of innovative materials and geometrical optimisation.

An area where biomimetic principles are proving useful is in the design and optimisation of bifurcating fluid distribution networks. Branching networks are numerous in natural systems and can be found in many processes which are often responsible for controlling fluids that present complex rheological behaviour. Examples include the vascular system that drives blood and other vital substances throughout the body, the oxygen transfer system in the human lungs, or the water transport through the xylem in the bifurcating networks of plants and trees (McCulloh et al. 2003).

Microfluidics offers the possibility of mimicking the natural environment at the dimensional scale of many biological processes (Domachuk et al. 2010). Hence, bifurcating microfluidic devices may find applications in many processes, such as blood plasma separation (Li et al. 2012; Tripathi et al. 2013; Yang et al. 2006), which exploits the plasma skimming concept in which red blood cells concentrate in the high flow rate region away from walls (Faivre et al. 2006).

Another example is the use of microfabricated branching networks to design applications that artificially assist the oxygen system in the human body (Potkay et al. 2011; Kniazeva et al. 2012).

The ability of microfluidics to provide adequate and controlled flow conditions may also benefit areas such as stem cell research (Zhang and Austin 2012) and tissue engineering. Microfluidics could assist studies related to the deformability of red blood cells (Pinho et al. 2013) and those investigating blood flow mechanisms, providing important information for diagnosing diseases and treating patients (Lima et al. 2008). As recently pointed out by DesRochers et al. (2014), microfabricated networks can be used as 3D cell culture microenvironments, in order to generate cell interactions that are unlikely to be replicated in 2D techniques, providing suitable conditions to carry out studies related to kidney diseases. In addition, bifurcating structures offer the ability to carry out many experiments in parallel, a characteristic referred to as ‘scaling out’. An example of this is the exposure of shear-sensitive cells to different flow conditions being investigated simultaneously in a single experiment. Microfluidic bifurcating networks have also been used by various authors in biological and chemical applications to generate precise concentration gradients (Dertinger et al. 2001; Jeon et al. 2000; Hu et al. 2011; Weibel and Whitesides 2006) due to their superior performance compared with conventional techniques, or as microstructure evaporators, for which better and more accurate designs are essential in order to achieve the best possible performance (Brandner 2013).

Most of the scientific fields of interest referred to previously require the handling of non-Newtonian fluids that exhibit shear-dependent viscosity (i.e. shear-thinning or shear-thickening behaviour). Hence, it is of great interest to develop intelligent designs that offer the ability to control the flow of these fluids in lab-on-a-chip networks by generating precise shear-stress distributions at the walls and specific flow resistances along the microfluidic networks to suit a particular application.

Here, we propose a biomimetic rule based on the optimum relationship expressed by Murray (1926), for designing manifolds that can produce desired flow characteristics for non-Newtonian, power-law fluids in microfluidic planar devices of rectangular cross section. We have validated the biomimetic rule using numerical simulations which focus on the estimation of the average shear stress at the walls of each generation and the flow resistance along the networks.

In Sect. 2, a theoretical analysis of the problem is presented leading to the basic set of equations that need to be solved for designing an appropriate manifold. Our proposed biomimetic rule is validated numerically in Sect. 3, for various power-law fluids in different customised geometries. We also discuss the limits of the design in terms of the Reynolds number. The main conclusions are summarised in Sect. 4.

2 Theoretical basis

2.1 Circular cross-sectional networks

In bifurcating networks, the optimum relationship between the diameter of the parent and daughter vessels of circular cross section was expressed by Murray (1926) using the principle of minimum work. This relationship is now known as Murray’s law and states that the cube of the diameter of the parent vessel ($\phi _{0}$) is equal to the sum of the cubes of the diameters of the daughter vessels ($\phi _{1},\phi _{2}$):

$$ \phi _{0}^3 = \phi _{1}^3 + \phi _{2}^3 $$

(1)

Murray’s original relationship was derived for fully developed flow of Newtonian fluids in circular ducts to match the basic shape of most biological distribution systems, such as the vascular system, and can be considered as a particular case of constructal theory (Bejan 2005; Bejan and Lorente 2006). Considering a symmetric bifurcating network where $\phi _{1}=\phi _{2}$, it follows that

$$ \phi _{0}^3 = 2\phi _{1}^3 $$

(2)

Murray’s law can be generalised (Emerson et al. 2006; Barber and Emerson 2008) for designing microfluidic manifolds that have specific fluidic conditions, by modifying the relationship (2) with the use of a branching parameter, $X$:

$$ X = \frac{\phi _{0}^3}{2\phi _{1}^3} $$

(3)

It is obvious that for $X=1$, Murray’s law is recovered, but a range of relationships between the parent and the consecutive generations can be achieved for $X\ne 1$. If the value of the parameter $X$ is held constant through the branching network, then it can be shown that the diameter of generation $i$ is given by

$$ \phi _{i} = \frac{\phi _{0}}{\left( 2X\right) ^{i/3} } $$

(4)

where the index $i=0,1,2,\ldots N$ refers to the number of each generation in the network. It should be noticed that in the cases of $X\ne 1$, the minimum work principle is no longer valid and Eq. (4) allows us to customise manifolds for applications that require a particular gradient of shear stress or flow resistance along the branching network.

For a symmetric system, the volumetric flow rate halves at each bifurcation. Therefore, for generation $i$, the volumetric flow rate is given by

$$ Q_{i} = 2^{-i}Q_{0} $$

(5)

Using Eqs. (4) and (5), the mean flow velocity in each generation, $\bar{u}_{i}$, can be shown to be

$$ \bar{u}_{i} = \bar{u}_{0} \left( \frac{1}{2}X^{2}\right) ^{i/3} $$

(6)

The wall shear stress for fully developed laminar flow in a circular pipe can be written (see White 2006) as follows:

$$ \tau = \frac{8\mu \bar{u}}{\phi } $$

(7)

Substituting Eqs. (4) and (6) into (7) shows that the shear stress in each segment will obey

$$ \tau _{i} = \tau _{0}X^{i} $$

(8)

where $\tau _{0}$ is the wall shear stress in the inlet vessel. Equation (8) clearly shows that if Murray’s law is obeyed (${X=1}$), then the magnitude of the wall shear stress remains the same at every point in the branching hierarchy. However, by changing the value of $X$, it is possible to introduce an element of control into the shear-stress distribution. Equation (8) represents a general biomimetic rule that can be applied to any channel, irrespective of the cross-sectional geometry.

2.2 Rectangular cross-sectional networks

Microfluidic manifolds used in lab-on-a-chip applications are typically fabricated using techniques such as soft- or photo-lithography, and wet and dry etching, resulting in networks with non-circular cross sections of constant depth. Emerson et al. (2006) extended Murray’s law for Newtonian fluids to non-circular ducts of rectangular and trapezoidal cross section. The main difference is that for a circular pipe, the stress distribution at the walls is uniform, whereas for non-circular channels it varies along the wetted perimeter. Taking into account the mean wall shear stress, Emerson et al. (2006) proposed the following biomimetic relationship:

$$ \bar{\tau _{i}} = \bar{\tau _{0}}X^{i} $$

(9)

The average wall shear stress $\bar{\tau }$ is related to the Fanning friction factor, $f$ as (White 2006)

$$ \bar{\tau } = \frac{1}{2}\rho \bar{u}^{2} f=\frac{1}{2}\rho \bar{u}^{2} \frac{Po}{Re}= \frac{\mu \bar{u} Po}{2{D_{{\text{h}}}}} $$

(10)

where $f$ is defined as the ratio of Poiseuille number, Po, and Reynolds number, Re, $\rho$ is the density, $\mu$ the Newtonian fluid viscosity, $\bar{u}$ the average velocity of the fluid, and ${D_{{\text{h}}}}$ the hydraulic diameter of the channel defined as ${D_{{\text{h}}}}=4\,\times \,\text {area/wetted perimeter}$.

The proposed biomimetic principle has the advantage of enabling the design of manifolds with specific shear-stress distributions along the microfluidic network (i.e. $X\ne 1$) and the ability to control the flow within the network. Here, we expand this relationship, originally proposed for Newtonian fluids, to consider also non-Newtonian power-law fluids.

2.2.1 Extension to power-law fluids

Flows of power-law fluids differ from Newtonian fluids in many ways, often because the viscosity can no longer be considered constant and independent of the shear rate. In this work, we consider power-law fluids which are described by the Ostwald-de Waele model, in which the viscosity, $\eta$, is a function of shear rate, $\dot{\gamma }$:

$$ \eta (\dot{\gamma }) = k\dot{\gamma }^{n-1} $$

(11)

where $k$ is the consistency index that is related to the magnitude of the viscosity and $n$ is the power-law index. When $n=1$, the Newtonian behaviour is recovered, predicting constant viscosity in steady shear. For $n<1$, the fluid is described as shear-thinning, with the viscosity decreasing for increasing shear rate, while for $n>1$ the fluid is described as shear-thickening with the fluid becoming more viscous as the deformation rate is increased.

By analogy with Newtonian fluids, the mean wall shear stress for a power-law fluid in a circular duct can be expressed as

$$ \bar{\tau } = \frac{1}{2}\rho \bar{u}^{2} f=\frac{1}{2}\rho \bar{u}^{2} \frac{16}{Re^{*}} $$

(12)

where $Po=16$ and $\textit{Re}^{*}$ is the generalised Reynolds number for a power-law fluid, defined as (Metzner and Reed 1955)

$$ Re^{*} = \frac{\rho \bar{u}^{2-n} {D_{{\text{h}}}}^{n} }{8^{n-1}K} $$

(13)

As demonstrated by Kozicki et al. (1966), for a power-law fluid flow in an arbitrary cross-sectional duct, $K$ is given by

$$ K = k\left( b^{*}+\frac{a^{*}}{n}\right) ^n $$

(14)

where the variables $a^{*}$ and $b^{*}$ are parameters that depend on the aspect ratio of the geometry examined. For the case of a circular duct, $a^{*}=1/4$ and $b^{*}=3/4,$ and thus, the correct value of $Po=16$ is recovered for the Newtonian case ($n=1$; Rohsenow et al. 1998). For rectangular channels of constant depth, these parameters can be evaluated by solving the following set of equations:

$$ \begin{aligned}& a^{*} = \frac{1}{2\left( 1+ \frac{1}{\alpha _{i}^{*}} \right) ^{2}} \times \\& \quad \frac{1}{\left[ 1+ 4\sum \limits _{j=0}^{\infty } \frac{\left( -1\right) ^{j+1}}{\left( \frac{2j+1}{2}\pi \right) ^{3}} \frac{1}{\cosh \left( \frac{2j+1}{ 2 }\pi \alpha _{i}^{*} \right) } \right] }\\ \end{aligned}$$

(15)

and

$$ \begin{aligned}& a^{*} + b^{*} = \frac{1}{2\left( 1+ \frac{1}{\alpha _{i}^{*}} \right) ^{2}} \times \\ & \quad \frac{3}{\left[ 1-\frac{192}{\pi ^{5}} \frac{1}{\alpha _{i}^{*}} \sum \limits _{j=1,3,5,\ldots }^{\infty } \frac{1}{j^{5}} \tanh \left( \frac{j \pi \alpha _{i}^{*}}{2} \right) \right] } \\ \end{aligned}$$

(16)

where $\alpha _{i}$ is the ratio of depth $d$ over the width $w_{i}$ of each generation $i$. It should be noted that Eqs. (15) and (16) are only valid when the width of the channel is greater than or equal to the depth of the channel (i.e. $\alpha _{i}\le 1$). To obtain the values of $a^{*}$ and $b^{*}$ when $\alpha _{i}>1$, the fraction should be inverted. Hence

$$\begin{aligned} \alpha _{i}^{*} =\left\{ \begin{array}{ll} d/w_{i} \quad \text {if} \quad d \le w_{i} \\ w_{i}/d \quad \text {if} \quad d > w_{i} \end{array}\right. \end{aligned}$$

(17)

Clearly, the geometrical parameters, $a^{*}$ and $b^{*}$, act as correction factors for the Poiseuille number, with Po depending on the geometry and thus on $a^{*}$ and $b^{*}$. In the specific case of Newtonian fluid flow ($n=1$), these parameters produce the correct value of Po in a rectangular cross section provided that $Po= f Re = 16(a^{*}+b^{*}).$

Considering a circular duct, Po is constant regardless of the diameter, and the wall shear-stress distribution is uniform. This is not the case for non-circular ducts, where the wall stresses vary along the perimeter, with Po depending on the channel’s aspect ratio. Consequently, the Poiseuille number needs to be evaluated for each different cross section considered. Using Eqs. (12) and (13), the fully developed mean shear stress along any branch of the network can be written as

$$ \bar{\tau }_{i} = \frac{8^{n}\bar{u}^{n}_{i}K_{i}}{{{D_{{\text{h}}}}}^{n}_{i}} $$

(18)

Substituting Eq. (18) into (9) yields:

$$ \frac{\bar{u}_{i}^{n}K_{i}}{{D_{{\text{h}}}}^{n}_{i}} = \frac{\bar{u}_{0}^{n}K_{0}}{{D_{{\text{h}}}}^{n}_{0}}X^{i} $$

(19)

Considering a symmetric network where the flow halves at each bifurcation, then

$$ \bar{u}_{i}^{n} = \left( \frac{Q_{i}}{A_{i}}\right) ^{n}=\left( \frac{2^{-i}Q_{0}}{A_{i}}\right) ^{n} $$

(20)

where $A_{i}$ refers to the cross-sectional area of generation $i$.

From the combination of Eqs. (19) and (20) and after some mathematical re-arrangement, we propose the following equation, derived from the biomimetic rule:

$$ \alpha _{i}^{n}\left( 1+\alpha _{i}\right) ^{n}\left( b_{i}^{*}+\frac{a_{i}^{*}}{n}\right) ^n = \alpha _{0}^{n}\left( 1+\alpha _{0}\right) ^{n}\left( b_{0}^{*}+\frac{a_{0}^{*}}{n}\right) ^n \left( 2^{i}\right) ^{n}X^{i} $$

(21)

It can be seen that the biomimetic design rule is a function of the power-law index of the fluid but independent of its density.

By solving the set of Eqs. (15), (16) and (21), we can design bifurcating manifolds of rectangular cross-sectional areas for power-law and Newtonian fluids. The design will allow specific shear-stress distributions along each consecutive generation depending on the value of the branching parameter, $X$. When $X=1$, Murray’s law is obeyed and the manifolds will produce identical average wall stresses in each segment of the network where the flow is fully developed. By varying $X$, we have the ability to design manifolds with different stress distributions along the network depending on the needs of each specific application.

2.2.2 Flow resistance gradient

When designing microfluidic manifolds, the estimation of the total flow resistance and the pressure distribution are often of high importance. Based on Hartnett and Kostic (1989), Son (2007) reported the following relationship between flow rate and pressure drop for power-law fluid flow in a rectangular channel:

$$ \left( \frac{\Delta P}{2L}\right) \left( \frac{wd}{w+d}\right) = \left[ \left( \frac{6Q}{wd^{2}}\right) \left( 1+\frac{d}{w}\right) \left( \frac{2}{3}\right) \right] ^{n} k\left( b^{*}+\frac{a^{*}}{n}\right)^n $$

(22)

After some mathematical manipulations using Eqs. (18) and (22), the tangential stress at each segment can be related to the pressure drop, resulting in the fundamental relationship:

$$ \bar{\tau }_{i} = \frac{\Delta P_{i} {D_{{\text{h}}}}_{i}}{4L_{i}} $$

(23)

In biological systems, the length of an individual segment of a branching hierarchy is often proportional to its diameter, as discussed by West (1990). In order to extend Murray’s law to non-circular microchannels, Emerson et al. (2006) proposed that this biological principle can be generalised for non-circular cross sections by assuming that the length of each vessel is proportional to its hydraulic diameter. We have adopted the same assumption here for consistency with other research on transport networks (Liu et al. 2010; Shan et al. 2011). Using this assumption, and considering that the hydraulic resistance, $R$, of a channel is defined by the ratio of pressure drop, $\Delta P$, to the flow rate, $Q$, the resistance of a single segment of generation $i$ can be related to the resistance in the inlet channel ($i=0$) and the branching parameter by

$$ \frac{R_{i}}{R_{0}} = \left( 2X\right)^{i} $$

(24)

analogous to the Newtonian case reported by Emerson et al. (2006).

Using an electrical circuit analogy for parallel resistances to express the hydraulic flow in the network, the total resistance between the inlet and the end of the segment at generation $i$ can be written as

$$ {R_{{\text{tot}}}}_{i} = R_{0} + \frac{R_{1}}{2} + \cdots + \frac{R_{i}}{2^{i}} $$

(25)

Hence, for a network composed of $N+1$ consecutive generations, the total flow resistance in the design can be written as

$$ {R_{{\text{tot}}}}_{N} = R_{0} + \frac{R_{1}}{2} + \cdots + \frac{R_{i}}{2^{i}} + \cdots + \frac{R_{N}}{2^{N}} = R_{0}\sum \limits _{i=0}^{N} X^{i} $$

(26)

where ${R_{{\text{tot}}}}_{N}$ refers to the total resistance between the inlet (at the start of generation $i=0$) and the outlet (at the end of the channel in generation $i=N$). Expanding the series on the right-hand side of Eq. (26), the total network resistance may be expressed as

$$\begin{aligned} {R_{{\text{tot}}}}_{N} = \left\{ \begin{array}{ll} R_{0} \left( X^{N+1}-1\right) / \left( X-1 \right) \text {,} \quad X\ne 1 \\ R_{0}\left( N+1\right) \text {,} \qquad \qquad X=1 \end{array}\right. \end{aligned}$$

(27)

3 Numerical simulations

3.1 Numerical method and problem set-up

The validation of the proposed biomimetic rule for designing bifurcating microfluidic networks with rectangular cross-sectional areas, described in the previous section, is achieved by performing computational fluid dynamics simulations.

The flow is considered to be laminar, incompressible and isothermal and is solved numerically using the continuity and momentum equations together with the power-law stress-strain constitutive equation:

$$ \nabla \cdot \mathbf {u} = 0 $$

(28)

$$ \rho \left( \frac{\partial {\mathbf {u}}}{\partial {t}} + \mathbf {u}\cdot \nabla \mathbf {u}\right) = -\nabla p - \nabla \cdot \boldsymbol{\uptau }$$

(29)

$$ \boldsymbol{\uptau} =k\dot{\gamma }^{n-1}\dot{\boldsymbol{\upgamma }} $$

(30)

where $p$ is the pressure, $\boldsymbol{\uptau}$ is the extra stress tensor, $\dot{\boldsymbol{\upgamma} }$ is the shear rate tensor and $\dot{\gamma }$ is the magnitude of the shear rate tensor.

The governing equations are solved using an in-house numerical code, based on a fully implicit finite volume method, using collocated meshes (Oliveira et al. 1998). Rhie and Chow (1983) interpolation is employed for coupling the pressure and velocity fields enabling the use of the SIMPLEC algorithm for collocated meshes to solve the continuity and momentum equations. The convective terms are discretised using the CUBISTA high-resolution scheme (Alves et al. 2003), while the diffusive terms employ a central difference scheme. The time-dependent terms in the momentum equation are discretised using a first-order implicit Euler scheme.

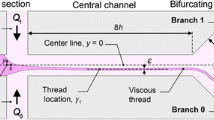
A uniform velocity is applied at the inlet, and creeping flow conditions ($Re \rightarrow 0$) are considered throughout, unless stated otherwise. No-slip boundary conditions are applied at the walls, while zero streamwise gradients are assumed at the outlets of the network. In order to reduce the computational demands, symmetry boundary conditions are considered along the central planes $y=0$ and $z=0$ (cf. Fig. 1).

Fig. 1

Microfluidic bifurcating network of constant depth with four generations ($i=0,1,2,3$) designed for a Newtonian fluid with aspect ratio $\alpha _{0}=0.5$ and $X=1$. The dashed-dotted line illustrates the symmetry conditions about $y=0$

Fig. 2

Normalised wall shear stress (a) and flow resistance (b) for various fluids along the four generations of the bifurcating network designed for a Newtonian fluid for $\alpha _{0}=0.5$ and $X=1$ (Table 1)

In this paper, we consider networks having four consecutive generations of constant depth, as typically found in microfluidics applications, where all channels designed were assumed to have a depth of d = 125 μm. For most cases examined, the inlet channel ($i=0$) rectangular cross section was taken to be 250 μm × 125 μm, resulting in an inlet aspect ratio of $\alpha _{0} = d/w_{0} = 0.5$, but other aspect ratios in the range $0.2\le \alpha _{0} \le 1.0$ have also been considered. The length of each segment is set to be proportional to its hydraulic diameter ($L_{i}=20{D_{{\text{h}}}}_{i}$). Finally, the meshes used to discretise the physical domain consist of approximately 2.2 to 2.4 million grid cells depending on the flow geometry, with the minimum cell size given by $0.013 \le \frac{\delta x_{0}}{{D_{{\text{h}}}}_{0}} = \frac{\delta y_{0}}{{D_{{\text{h}}}}_{0}} = \frac{\delta z_{0}}{{D_{{\text{h}}}}_{0}} \le 0.022$ according to the specific configuration.

Numerical computations are performed for several values of the branching parameter, $X$, for a consistency index of $k=10^{-3}\, \hbox {N\,s}^{\text{n}}\,\hbox {m}^{-2}$ and a range of power-law indices, $n$, varying from shear-thinning to shear-thickening behaviour ($n=[0.2,\ 2.0]$). For all the cases considered, the validity of Eq. (9) and the ability to generate a desired distribution of average wall shear stress throughout the network are evaluated by averaging the shear stresses developed at the perimeter walls of the channel at each branch.

3.2 Networks with uniform shear-stress distribution ($X=1$)

In this section, we report our results for $X=1$, when the principle of minimum work is obeyed, and we solve the biomimetic design set [Eqs. (15), (16) and (21)] for Newtonian and power-law fluids.

The geometrical characteristics for each consecutive generation computed for a Newtonian fluid ($n=1$) are given in Table 1 for $\alpha _{0}=0.5$ and are in agreement with those presented by Barber and Emerson (2008). For this particular case ($X=1$ and $\alpha _{0}=0.5$), comparing the geometrical values for the Newtonian fluid (Table 1) with the parameters computed for various power-law fluids (ranging from highly shear-thinning to shear-thickening) presented in Table 2, it is clear that the differences between the proposed geometries are small and the widths do not exhibit significant variations (maximum deviation of 1.7 % in $w_{1}$). Based on this observation, we use the geometry obtained for a Newtonian fluid ($n=1$) and examine the flow characteristics of different fluids with power-law indices ranging from $n=0.2$ (shear-thinning) to $n=2.0$ (shear-thickening). This universality is very interesting for experimental studies, since the same microfluidic network can be used for a range of fluids.

Table 1 Geometrical parameters and dimensions of a planar bifurcating network with inlet aspect ratio $\alpha _{0}=0.5$ obtained for a Newtonian fluid ($n=1$)

Fig. 3

Comparison of the bifurcating networks of rectangular cross section and inlet aspect ratio $\alpha _{0}=0.5$ created for Newtonian fluids with $L_{i} = 20{D_{{\text{h}}}}_{i}$, using different branching parameters, $X$

Table 2 Geometrical parameters and dimensions of planar bifurcating networks with inlet aspect ratio $\alpha _{0}=0.5$ obtained for power-law fluids with $n= 0.2, 0.6, 1.6$ and 2.0

In Fig. 2a, we present a comparison between theory and computational predictions for the normalised average wall shear-stress distribution along the bifurcating network. For the Newtonian case, good agreement between theoretical (Eq. 9) and numerical predictions is found, as reported by Emerson et al. (2006) and Barber and Emerson (2008). The relative error between the CFD calculations for $n=1$ and theory is less than 0.4 %. Furthermore, it can be seen that although the geometry was designed for Newtonian fluids, it also works well for the power-law fluids. Clearly, the response for both shear-thinning and shear-thickening fluids is similar to the Newtonian fluid, yielding a uniform average wall shear stress ($\bar{\tau }_{i} \simeq \bar{\tau }_{0}$) along the network segments. More specifically, for the shear-thickening fluid with $n=2.0$, a maximum deviation of 1.35 % from the Newtonian behaviour is reported, while for the shear-thinning fluid with $n=0.2$, the maximum deviation is less than 1 %. Figure 2b shows the total flow resistance (computed using Eq. 25) at each consecutive generation. The total flow resistance can be seen to vary linearly for all fluids, thereby corroborating the good agreement between theory and numerical results for both the power-law and Newtonian fluids.

Fig. 4

Normalised wall shear stress (a) and flow resistance (b) along the network with $a_{0}=0.5$, designed for a Newtonian fluid with $X=1.25$ and $X=0.75$

Other values of inlet aspect ratio ($\alpha _{0}$) have also been tested ($\alpha _{0}=0.2,\,0.3$ and $1.0$), in order to investigate the applicability of the channel’s universality for $X=1$. The Newtonian-designed geometry for each case was used in the simulations, similar to the case of $\alpha _{0}=0.5.$ For a square inlet cross section ($\alpha _{0}=1.0),$ the Newtonian geometry is once again suitable for all fluids tested ($n=0.6,1 \text { and } 1.6),$ but for the smaller aspect ratios of $\alpha _{0}=0.2$ and $\alpha _{0}=0.3,$ the power-law fluid response deviates from the Newtonian behaviour, indicating that customised geometries tailored to the specific power-law fluid under consideration should be used. These results are not shown here for conciseness, but additional data regarding the dimensions of the customised geometries for $X=1$ and $\alpha _{0}=0.2,\,0.3$ and $1.0$ are given in Online Resource 1.

3.3 Networks with nonuniform shear-stress distribution ($X\ne 1$)

When the value of the branching parameter differs from unity ($X\ne 1$), the geometries generated by solving the biomimetic set of equations will produce manifolds with well-defined shear-stress gradients. The ability to generate nonuniform, but known, shear-stress gradients is one of the advantages of the proposed biomimetic design. It should be noted though that for $X\ne 1$, the principle of minimum work is no longer satisfied. Here, the cases of ${X=1.25}$ and $X=0.75$ are considered, corresponding to a positive or negative gradient of the shear-stress distribution along the network. We investigate the response of a Newtonian, a shear-thinning (with $n=0.6$) and a shear-thickening (with $n=1.6$) fluid.

The characteristics of the geometries generated for a Newtonian fluid flow with $X=1.25$ and $X=0.75$ are given in Table 3. Comparing these new configurations with that for $X=1$ (Table 1), it is clear that the geometries exhibit large differences in the widths of each generation, which consequently affect the length of each generation and thus the total length of the microfluidic network, as illustrated in Fig. 3. The designed channels used in all three cases have the same proportionality between the lengths and the hydraulic diameters of each segment ($L_{i}=20{D_{{\text{h}}}}_{i}$).

Table 3 Geometrical parameters and dimensions of planar bifurcating networks with initial aspect ratio $\alpha _{0}=0.5$ and branching parameters $X=1.25$ and $X=0.75$, designed for a Newtonian fluid

Using a similar approach to that reported in Sect. 3.2 for $X=1$, first we analyse the flow of power-law fluids using the geometry obtained for a Newtonian fluid. Figure 4a shows the normalised average wall shear stress in each consecutive generation of a network designed for a Newtonian fluid with $X=1.25$. For the case of $n=1$, the CFD results are in very good agreement with the results presented by Emerson et al. (2006) and Barber and Emerson (2008) and with theory (Eq. 9), resulting in a maximum deviation of less than 0.5 %. When $X=1.25$, the average wall shear stress increases at each consecutive generation, resulting in a positive gradient along the network as imposed by setting the branching parameter to a value greater than unity ($X>1$) in the biomimetic rule. However, unlike the equivalent case for $X=1$, the use of the Newtonian geometry produces very different shear-stress distributions along the network for each power-law fluid tested (Fig. 4a). It is clear that for a branching parameter $X=1.25$, the power-law fluids will not display the desired behaviour when flowing in the Newtonian-designed geometry. This is also highlighted from the deviations in the resistances shown in Fig. 4b.

In view of the previous findings, individual geometries for each power-law fluid have been designed based on our biomimetic rule; the dimensions of each network are presented in Table 4.

Table 4 Geometrical parameters and dimensions of planar networks with initial aspect ratio $\alpha _{0}=0.5$ and branching parameter $X=1.25$, for power-law fluids with $n=0.6$ and $n=1.6$

Fig. 5

Normalised average velocities along the bifurcating networks customised for each fluid obtained for $\alpha _{0}=0.5$, and $X=1$ (a) and $X=1.25$ (b)

Fig. 6

Normalised wall shear stress (a) and flow resistance (b) along the customised bifurcating networks ($\alpha _{0}=0.5$), designed using the biomimetic principle [Eq. (21)]. Four customised geometries were considered corresponding to $n=0.6$ and $n=1.6$ with $X=1.25$ and $X=0.75$

Comparing the geometrical characteristics for $n=0.6$ and $n=1.6$ with those for the Newtonian fluid (Table 3; $X=1.25$), there are clear differences in the widths of each generation. Hence, unlike the $X=1$ case, where the average velocity ratios ($\bar{u_{i}}/\bar{u_{0}}$) along the bifurcating networks are similar for both the Newtonian and power-law fluids (Fig. 5a), for $X=1.25$, the average velocities required to give the desired wall shear-stress gradient for each fluid are clearly very different (Fig. 5b).

When the shear-thinning fluid ($n=0.6$) is flowing in the Newtonian geometry for $X=1.25$, it is consistently exposed to lower average velocities in each consecutive generation when compared to its customised geometry. On the other hand, the shear-thickening fluid is exposed to higher-average velocities when the Newtonian geometry is used, leading to high shear-stress ratios as the fluid thickens (as shown in Fig. 4a). Consequently, the total resistance in the same microfluidic network is different for the various fluids (Fig. 4b). Additionally, for $X=1.25$, the velocity variation at the first bifurcation (Fig. 5b) exhibits a non-monotonic behaviour for the shear-thinning ($n=0.6)$ and Newtonian ($n=1$) cases.

Fig. 7

Contour plots of the normalised wall shear stress along the bifurcating networks ($\alpha _{0}=0.5$), for a power-law fluid flow with $n=0.6$ in the Newtonian-designed geometry (Table 3) (a) and in the customised geometry (Table 4) (b) for $X=1.25$

We now consider the case of the geometry designed for a Newtonian fluid with $X=0.75$. The computational results for $n=1$ are shown in Fig. 4a and are also in good agreement with theory with a deviation of less than 0.6 %. For the power-law fluids, we observed a similar, but opposite behaviour to that exhibited for $X=1.25$. Examining the customised geometrical parameters for each power-law index for $X=0.75$ shown in Table 5, it is clear that the flow in the Newtonian geometry will produce higher shear-stress gradients than desired for shear-thinning fluids, while in contrast, lower shear stress will develop for the shear-thickening fluids at the walls of the microfluidic manifold. In a similar fashion to the $X=1.25$ case, the total resistance for $X=0.75$ along the microfluidic network is significantly different for the various fluids (Fig. 4b).

Fig. 8

Contour plots of the normalised wall shear stress along the bifurcating networks ($\alpha _{0}=0.5$), for a power-law fluid flow with $n=1.6$ in the Newtonian-designed geometry (Table 3) (a) and in the customised geometry (Table 4) (b) for $X=1.25$

In summary, when the network is designed for a Newtonian fluid for $X\ne 1$ and $\alpha _{0}=0.5$, the power-law fluid behaviour diverges from the Newtonian response and the geometries designed for Newtonian fluids are not appropriate for applications that require the handling of power-law fluids. Customised geometries should then be generated for each power-law fluid. Numerical simulations have been performed to examine the fluidic conditions in the customised geometries (Tables 4 and 5). Figure 6a shows that when the customised geometries are designed using Eq. (21), both shear-thinning and shear-thickening fluids obey the biomimetic principle, by yielding the predicted tangential shear-stress distributions. At the same time, the differences in the widths are reflected on the lengths of each generation and the flow resistances along the networks shown in Fig. 6b demonstrate that the biomimetic rule is in good agreement with theory. For each fluid considered, a maximum deviation of 2 % for the case of $X=1.25$ and 1 % for the case of $X=0.75$ has been observed; these errors correspond to the case of the shear-thickening fluid in the last (outlet) generation of the networks.

Table 5 Geometrical parameters and dimensions of planar networks with initial aspect ratio $\alpha _{0}=0.5$ and branching parameter $X=0.75$, for power-law fluids with $n=0.6$ and $n=1.6$

A comparison between the normalised wall shear-stress distribution along the microfluidic networks in the Newtonian-designed and the customised geometries for the shear-thinning ($n=0.6$) and shear-thickening ($n=1.6$) fluids is shown in the contour plots of Figs. 7 and 8, respectively, for the case of $X=1.25$. In both cases, the microfluidic networks have the same inlet aspect ratio of $\alpha _{0}=0.5$ and thus the same normalised wall shear-stress distribution in the inlet channel ($i=0$), but only the customised geometries generate the desired gradients of the shear stresses in the subsequent generations.

Fig. 9

Normalised network total resistance as a function of the inlet Reynolds number ($Re^{*}_{0}$) defined in Eq. (13) for Newtonian, shear-thinning ($n=0.6$) and shear-thickening ($n=1.6$) fluids using the Newtonian-designed geometry for $\alpha _{0}=0.5$ and $X=1$ (Table 1)

3.4 Effect of increasing Reynolds number

The theoretical analysis described in Sect. 2 and the biomimetic design we are proposing assume that the flow is fully developed and laminar, hence the assumption of creeping flow in our numerical simulations. Although low Reynolds numbers are easily achieved at the microscale, imposing a truly creeping flow experimentally is not possible. Thus, it is important for practical applications to know the limit of validity of our design rule when increasing the Reynolds number. Figure 9 shows a comparison of the normalised total network resistance for increasing Reynolds number obtained for Newtonian, shear-thinning ($n=0.6$) and shear-thickening ($n=1.6$) fluids in the bifurcating network designed for a Newtonian fluid (Table 1).

For Reynolds numbers up to a value of $Re^{*}_{0}=30$, the CFD results are in good agreement with theory for all fluids with a maximum relative error of approximately 2 %. For $Re^{*}_{0}\ge 100$, the CFD results clearly overpredict the theoretical resistance, with a relative error of 13 % for the Newtonian and 8 % for the power-law fluids when $Re^{*}_{0}=100$. It should be noted that in these cases, the flow is unable to reach a fully developed state in the branches of each generation, with secondary flows reported at the first bifurcation. It is also important to note that we are considering geometries with $90^{\circ }$ bends, and thus by smoothing this configuration, it is likely that higher Re can be achieved while maintaining the desired performance. Furthermore, the value of $L/{D_{{\text{h}}}}$ was set to 20, and by increasing this value, we also expect that the limits of the validity in terms of $Re^{*}_{0}$ will increase. However, increasing the length in practical applications is not always viable as the increase in pressure might endanger the integrity of lab-on-a-chip devices.

4 Conclusions

We have proposed a biomimetic design rule for constructing bifurcating microfluidic networks with rectangular cross-sectional areas based on the biological principle first expressed by Murray. Murray’s law was originally derived for Newtonian fluids in circular ducts under laminar and fully developed flow conditions. In the present paper, this work has been extended for use with power-law fluids in non-circular networks typical of microfluidic applications. Designing manifolds using the new biomimetic rule offers the ability to generate customised flow characteristics for both power-law and Newtonian fluids. For a given application, the proposed design rule is able to provide control over the flow field and, in particular, over the wall shear-stress distribution along the network, by carefully selecting a branching parameter which governs the change in channel dimensions at each bifurcation.

When the value of the branching parameter is equal to unity ($X=1$) and the inlet aspect ratio is $\alpha _{0}=0.5$ or $\alpha _{0}=1.0$, the geometries for power-law fluids generated using our biomimetic design have negligible differences relative to those designed for a Newtonian fluid. In this case, the principle of minimum work underlying Murray’s law is obeyed and the Newtonian and the power-law fluids exhibit similar responses even when the Newtonian geometry is used. This universality in terms of geometry is useful especially for experimental purposes, since the same device can be used effectively for different fluids. However, when for example $\alpha _{0}=0.2$ or $0.3$, the network’s universality is no longer valid and customised geometries should be used for each particular power-law index. In addition, we should note that although the ratios of the average wall shear stresses are the same for Newtonian and power-law fluids, the magnitude of the wall shear stresses depends on the particular fluid flow conditions.

When gradients of wall shear stresses along the bifurcating network are required (i.e. $X\ne 1$), different geometries must be used for each power-law fluid in order to achieve the desired flow characteristics. In this case, the biomimetic rule allows us to create customised geometries to provide the desired flow field.

The proposed designs are valid when fully developed flow is reached in each generation of the network, and therefore, creeping flow conditions have been considered throughout this paper, which is a good approximation for most microfluidic flows. However, the limits of the design were tested in terms of Reynolds numbers to guide experiments, where obtaining truly creeping flow is not possible. Our numerical calculations show that for $Re^{*}_{0}\gtrsim 30$ care should be taken as the results start to deviate from the predictions. In particular, the choice of using channels with $90^{\circ }$ bends imposes a limitation in terms of the Reynolds number that can be used. This could be improved by using smoother corners or with the use of Y-junction-shaped bifurcations where friction losses would be reduced.

We believe that our proposed biomimetic approach for designing microfluidic networks will benefit research areas that require devices capable of controlling the shear-stress field. Examples such as stem cell research, where there is a need for tuning the microenvironment around stem cells in various ways, and applications requiring separation (e.g. blood plasma extraction, which is highly influenced by the properties of the flow field) may benefit from using customised bifurcating geometries.