Flow front mobility of rock avalanches as a function of flow volume, grain size, channel width, basal friction and flow scale

Abstract

The ability to predict the mobility of rock avalanches is necessary when designing strategies to mitigate the risks they pose. A popular mobility indicator of the flow front is the Heim’s apparent friction coefficient ${\mu }_{H}$. In the field, ${\mu }_{H}$ shows a decrease in value as flow volume V increases. But this correlation has been a mystery as to whether it is due to a causal relationship between V and mobility since: (1) field data of ${\mu }_{H}$ do not collapse onto a single curve because typically widely scattered and (2) laboratory experiments have shown an opposite volume effect on the center of mass mobility of miniature flows. My numerical simulations confirm for the first time the existence of a functional relationship of scaling parameters where ${\mu }_{H}$ decreases as V increases in unsteady and nonuniform 3D flows. Data scatter is caused by ${\mu }_{H}$ that is affected by numerous other variables besides V. The interplay of these variables produces different granular regimes with opposite volume effects. In particular, ${\mu }_{H}$ decreases as V increases in the regime characterized by a relatively rough subsurface. The relationship holds for large-scale flows that, like rock avalanches, consist of a very large number of fine clasts traveling in wide channels. In these dense flows, flow front mobility increases as flow volume increases, as channel width increases, as grain size decreases, as basal friction decreases and as flow scale increases. Larger-scale flows are more mobile because they have larger Froude number values.

Introduction

The mobility of dry and dense granular flows of angular rock fragments that are characteristically unsteady and nonuniform such as rock avalanches (Hungr et al. 2014) and pyroclastic flows of the block-and-ash flow type (Cas and Wright 1988) is complex to predict because it is governed by a large number of variables whose interplay modifies their individual effects. These variables include flow volume, grain size, channel width, basal friction and stress level (i.e., flow scale). But flow mobility is affected also by initial conditions and additional phenomena (such as the degree of the initial compaction of the rock fragments, the presence of obstacles etc.) that are characterized by a large number of possibilities. Notwithstanding this complexity, functional relationships providing a multivariate and coherent explanation of the concomitant effects of the abovementioned variables on the mobility of the center of mass of dense granular flows of angular rock fragments can be obtained by means of dimensional analysis (Cagnoli 2021). The center of mass is the only single point whose mobility depends on the energy dissipation of all clasts. Therefore, the apparent coefficient of friction ${\mu }_{A}$ computed as the ratio of the vertical to the horizontal displacements of the center of mass is an informative measure of energy dissipation.

The flow front has more complicated behaviors because it does not have the same unique properties of the center of mass. Its importance is due to the fact that the front is that part of the flow that interacts first with whatever is located on the flow path. In particular, the Heim’s apparent friction coefficient ${\mu }_{H}$ computed as the ratio of the vertical to the horizontal distances between the rear top end of the slope scarp and the front of the deposit has called a great deal of attention because of its significant decrease in the field as the volume of the rock avalanche increases (e.g., Heim 1932; Scheidegger 1973; Corominas 1996; Mitchell et al. 2020). This significant decrease has been explained by means of, for example, mud lubrication (Heim 1932), a cushion of trapped air (Shreve 1968), a friction reduction mechanism due to dispersive pressures called mechanical fluidization (Davies 1982), the closely related vibrational loosening of the so-called acoustic fluidization (Melosh 1979), intergranular water support (Legros 2002) and clast fragmentation (Davies and McSaveney 2009). It has also been suggested that this mobility increase is the result of only the longer lengthwise spread of larger volume deposits (Davies 1982; Staron and Lajeunesse 2009). However, none of these explanations has so far obtained universal acceptance.

Concerning intergranular water support, the fact is that rock avalanches are dry because their extensive fragmentation during motion generates new intergranular spaces that cannot be filled by water during their relatively short travel time (Hungr et al. 2014) and block-and-ash flows (e.g., Saucedo et al. 2004) are dry because of their high volcanic temperatures. Concerning mechanical fluidization, its assumption of a decrease of friction in rapidly-sheared dry granular material as velocity increases, because particles are forced away from each other, was proven to be incorrect by experimental measurements (Hungr and Morgenstern 1984a, b) and by numerical simulations. For example, 2D numerical simulations of unsteady flows (Campbell et al. 1995) indicate that both apparent friction coefficients ${\mu }_{H}$ and ${\mu }_{A}$ are increasing functions of the shear rate. Similarly, friction in steady flows increases as shear rate increases (Jop et al. 2006). Indeed, a functional relationship obtained by means of 3D numerical simulations of large-scale unsteady flows (of the rock avalanche type) predicts on a rough subsurface a decrease of ${\mu }_{A}$ as the volume of the flows increases because particle agitation per unit of flow mass and, consequently, the energy dissipation per unit of travel distance decrease (Cagnoli 2021). Notably, the explanation based on shear rate and that based on particle agitation are equivalent because particle agitation decreases as the shear rate decreases in these open channel flows.

Field measurements of ${\mu }_{H}$ are typically widely scattered when plotted versus flow volume V (e.g., Corominas 1996). The questions therefore arise as to whether (1) the negative correlation observed in the field between ${\mu }_{H}$ and V is due to a cause-and-effect relationship and (2) this increase in mobility needs special friction reduction mechanisms (such as those provided by an air cushion, mud lubrication or gas fluidization) to be explained. In this paper, the same 3D numerical simulations carried out by Cagnoli (2021) to study the mobility of the center of mass of granular flows of angular rock fragments are used to study the mobility of the flow fronts. Numerical simulations are preferred to field data and laboratory experiments for the following reasons. Field data are affected by a combination of measurement uncertainties and unknown initial and boundary conditions that limit their usefulness. Laboratory experiments that are 1 g underestimate the stress level of large-scale rock avalanches (Bowman et al. 2010; Cagnoli 2021) to such an extent that miniature flows display a flow volume effect on the center of mass mobility that is the opposite (Cagnoli and Romano 2012) of that of large-scale flows (Cagnoli 2021).

Here, it is demonstrated that the complexity of granular flows is such that, as the numerous variables affecting ${\mu }_{H}$ change in value, distinctly different flow regimes are generated. In particular, ${\mu }_{H}$ decreases as flow volume V increases in the regime characterized by a relatively rough subsurface. This was shown to be the case also with ${\mu }_{A}$ in large-scale flows (Cagnoli 2021). The typical wide scatter of field data is the result of the fact that ${\mu }_{H}$ is affected by other variables besides V. Here, it is concluded that the increase of the front mobility as V increases is indeed predicted by a cause-and-effect functional relationship. This relationship pertains to the denser part of large-scale flows which travel on a rough subsurface and that consist of a large number of relatively fine clasts that are laterally unconstrained by too narrow channels. In nature, these are all characteristics found in rock avalanches and dense pyroclastic flows.

Method

3D numerical simulations

The numerical simulations are three-dimensional and are based on the discrete element method. They are carried out by means of software EDEM with the same contact model illustrated by Cagnoli and Piersanti (2015). The flows whose front mobility is examined here are those whose mobility of the center of mass was explained by means of functional relationships of scaling parameters in Cagnoli (2021), which is the companion paper where more information about simulations and flows is available.

Slope and particle features

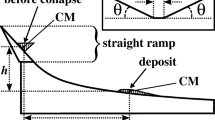
The granular flows travel down a three-dimensional channel with a longitudinal profile (Fig. 1) that consists of an upper straight ramp and a lower curved part whose combined length is ~ 1.6 m. The straight ramp slopes at a 47° angle from the horizontal. The hyperbolic sine equation of the longitudinal profile of the curved part with variables in meters is

Fig. 1

Longitudinal profile of the channels. The inset shows the trapezoidal cross-section in the transverse direction of both the straight ramp and the curved portion of the channels. The Heim’s coefficient is computed for each volume percent ($vol\%$) as the ratio of the vertical to the horizontal distance between the rear top end of the granular mass before release and the front of that $vol\%$ of deposit

$$\begin{array}{c}z=0.3-0.085\;\text{sinh}^{-1}\left(11.765\;x\right)\end{array}.$$

(1)

This equation is that of the slightly modified profile of Mayon volcano in the Philippines (Becker 1905) and the trapezoidal transverse cross-section of both channel parts (inset in Fig. 1) corresponds in nature to a V-shaped topographic incision with sediment infilling in the center (see photos in Zhang and Yin (2013) and in Quan Luna et al. (2012)). The lateral side inclination $\theta$ (Fig. 1) is the same in all simulations (27°) since different $\theta$ values would result in different flow mobility (Cagnoli and Piersanti 2017).

The angular rock fragments of geophysical flows are simulated by means of cubic particles only considering that different proportions of different clast shapes would result in different flow mobility (Cagnoli and Piersanti 2015). Before their collapse under the influence of gravity (no gate is used to avoid frictional forces that have no counterpart in nature), the granular masses (whose clasts touch one another) randomly fill numerical spaces at the top of the ramp. The volumes of these polyhedral spaces are proportional to the granular masses so that the same bulk density of the granular material before collapse is always ensured considering that different degrees of the initial compaction would result in different flow mobility (Cagnoli and Piersanti 2015). After the collapse, the granular masses accelerate downslope and reach a maximum speed before decelerating and forming a final deposit that is more elongated than thick. The final deposits have a distal distribution of (more or less isolated) frontal clasts whose relative overall mass (when compared with the mass of the main part of the deposit) varies greatly.

Flow volume, grain size, channel width, basal friction and flow scale

The thirty-six numerical simulations presented here are those of flows which differ in flow volume, grain size, channel width, basal friction and flow scale (i.e., stress level). These flows do not contain fluids (water, mud or gas) neither intergranular nor at their base. Each simulated flow represents at the same time a model flow in the laboratory and its corresponding prototype in nature (Table 1) because they have identical values of the same scaling parameters.

Table 1 Granular flow characteristics

The scale of each flow in the simulations is set by multiplying its acceleration of gravity by $n$ (Cagnoli 2021), where $n$ is the geometric scaling factor equal to the ratio of a characteristic length ${\lambda }_{P}$ in the natural prototype to the corresponding length ${\lambda }_{M}$ in the model:

$$n=\large \frac{{\lambda }_{P}}{{\lambda }_{M}}.$$

(2)

This results in model flows whose stresses are equal to those of their corresponding large-scale prototypes in nature (Cagnoli 2021). The three $n$ values considered here are 1, 100 and 1000, which result in three accelerations of gravity in the models equal to 9.8, 980 and 9800 m/s² respectively (even if gravity in the corresponding natural prototypes is always 9.8 m/s²). The model flows with $n=1$ have miniature laboratory flows as corresponding prototypes, whereas the model flows with $n=100$ and $n=1000$ have, as corresponding prototypes, flows that are 100 and 1000 times bigger, respectively, than the miniature flows (Cagnoli 2021). Table 1 summarizes the characteristics of the numerical simulations. In all figures, data points and curves are colored red when $n=1000$, orange when $n=100$ and blue when $n=1$.

Flows in a channel whose model width is equal to 0.001 m (simulations R, S and T in Table 1) have been added to those studied in Cagnoli (2021). Therefore, the model channel width w is here equal to 0.001, 0.006 and 0.026 m, so that, when $n$ is equal to 1, 100 and 1000: (a) the prototypal narrower channels are 0.001, 0.1 and 1 m in width respectively, (b) the prototypal intermediate channels are 0.006, 0.6 and 6 m in width respectively, and (c) the prototypal wider channels are 0.026, 2.6 and 26 m in width respectively (Table 1). Here, width w is measured as the smallest distance between the inclined sidewalls (inset in Fig. 1).

The cubic clasts (2700 kg/m³ in density) in the model flows have edges (i.e., grain size $\delta$) equal to 0.0005, 0.001 and 0.002 m, which: (a) when $n=100$ correspond to prototypal grain sizes equal to 0.05, 0.1 and 0.2 m respectively, and (b) when $n=1000$ correspond to prototypal grain sizes equal to 0.5, 1 and 2 m respectively (Table 1). In particular, there are three flows at each scale $n$ that differ only in grain size (Table 1): the finest grain size is in simulations C, H, O, the intermediate grain size is in simulations B, G, N and the coarsest grain size is in simulations A, F, M. There are also two flows at each scale $n$ that differ only in volume (Table 1): the larger volume is in simulations C, H, O and the smaller volume in simulations E, L, Q. These lists of simulation identification letters are in increasing order of $n$ (Table 1). The number of clasts (that ranges from 1231 to 78815) is the same in model and corresponding prototypal flows (Table 1). Here, volume V is always computed as that of the solid mass (Table 1).

The eighteen simulations in Table 1 with different values of flow volume, grain size, channel width and flow scale have been carried out once with large values of the coefficients of static and rolling friction between clasts and subsurface (${\mu }_{Scs}=0.9$ and ${\mu }_{Rcs}=0.07$, respectively) and once with small values of these quantities (${\mu }_{Scs}=0.45$ and ${\mu }_{Rcs}=0.035$, respectively). The large values are twice as much the small values and their simulations are hereafter referred to as those on relatively rough and relatively smooth subsurface, respectively (where the properties of the “subsurface” are those of both the lateral sides and the basal surface). Tables 2 and 3 list the values of Poisson’s ratios, shear moduli, densities and coefficients of restitution. These quantities have the same values in all simulations. The values of the properties in Table 2 and 3 indicate that these simulations are those of flows of rock fragments (Peng 2000).

Table 2 Material properties

Table 3 Properties governing interactions

Dimensionless parameter describing the mobility of the flow front

Since the location of the front of a deposit can be ambiguous because of the presence of a relatively long distal distribution of (more or less isolated) particles, it is introduced here the concept of the front of a portion of deposit (inside the deposit) where this portion is a volume percent ($vol\%$) of the deposit measured from the rear end (Fig. 1). This means that $vol\%$ is 0 at the rear end and 100 where the most distal clast is located. The values of $vol\%$ considered here are 80, 85, 90, 95 and 99 (100 is not taken into consideration in case a few clasts exited the computational domain).

The Heim’s coefficient (e.g., Scheidegger 1973) measures the mobility of the flow front. Here, it is computed for the front of each $vol\%$ of deposit as follows

$${\mu}_{Hvol\%} = \frac{\large{h}_{vol\%}}{\large{l}_{vol\%}},$$

(3)

where ${h}_{vol\%}$ and ${l}_{vol\%}$ are the distance, in the vertical and horizontal direction, respectively, between the rear top end of the granular mass before release (or of the scarp on the slope in nature) and the front of that $vol\%$ of deposit (Fig. 1).

Dimensional analysis

The dimensional analysis carried out by Cagnoli (2021), beside the apparent friction coefficient ${\mu }_{A}$, considers the following variables: flow volume V, channel width w, grains size $\delta$, acceleration of gravity g (which contains flow scale $n$), flow length L, flow speed u and the coefficients of static (${\mu }_{Scs}$) and rolling friction (${\mu }_{Rcs}$) between clasts and subsurface. The results of the dimensional analysis are functional relationships relating ${\mu }_{A}$ to: (1) granular scaling parameters that are products or ratios of characteristic numbers of particles, (2) the Froude number and (3) the two coefficients of basal friction. Here, the validity of these functional relationships is tested when ${\mu }_{A}$ is replaced by ${\mu }_{Hvol\%}$. Since the values of flow length L and flow speed u cannot be set directly by the modelers in laboratory experiments and numerical simulations, those discussed in this paper are the effects on flow front mobility of flow volume V, grains size $\delta$, channel width w, flow scale $n$ and basal friction.

Granular scaling parameters

For flows on a rough subsurface, Cagnoli (2021) introduced the following dimensionless parameter:

$$\psi = \frac{\large{\delta }^{2}}{\large{V}^{1/3}w}.$$

(4)

Parameter $\psi$ is the product of the reciprocal of

$$\Gamma = \frac{\large{V}^{1/3}}{\large \delta}$$

(5)

and the reciprocal of

$$\Omega = \frac{\large w}{\large \delta},$$

(6)

where the dimensionless quantity $\Gamma$ is an increasing function of the total number of clasts in the granular flow since it corresponds to $V/{\delta }^{3}$, whereas $\Omega$ is an increasing function of the number of clasts that fit along the channel width in the channel transverse direction. Therefore, $\Gamma$ and $\Omega$ are characteristic numbers of particles.

For flows on a smooth subsurface, Cagnoli (2021) introduced the following dimensionless parameter:

$$\zeta = \frac{\large V}{\large {w}^{3}}.$$

(7)

Parameter $\zeta$ is the product of $\Gamma$ and the reciprocal of $\Omega$ that are raised to the 3rd power.

Froude number

The ratio of inertial to gravitational forces is called Froude number:

$$Fr = \frac{u}{\sqrt{L\;g\;\cos\!\alpha}}.$$

(8)

Here, as in Cagnoli (2021), L is the length of the flow when with maximum speed (measured as the distance along the slope between the most distal and most proximal clasts), u is the maximum speed (measured as the maximum during the flow descent of the average speed of all particles), α is the slope inclination in the position of the center of mass of the flow when with maximum speed (whose value also cannot be set directly by the modelers in laboratory experiments and numerical simulations) and g (that contains $n$) is the acceleration of gravity.

Results

Flow front mobility on a rough subsurface

In Fig. 2a–c, ${\mu }_{Hvol\%}$ on a rough subsurface is plotted versus $vol\%$. These plots allow the comparison among all flows of the effects of flow volume, grain size, channel width and flow scale on the front mobility as $vol\%$ varies. However, since the curves in Fig. 2a–c do not relate, to one another, scaling parameters containing the abovementioned variables and they are not functional relationships (data points of different flows do not collapse onto the same curve), the effect of each variable in these plots can be identified only by comparing flows that do not differ in the values of the other variables. Needless to say, front mobility increases as $vol\%$ increases for obvious geometric reasons.

Fig. 2

Coefficient ${\mu }_{Hvol\%}$ versus $vol\%$ on the rough subsurface. The unfilled circles represent the two flows that differ only in volume: large and small circles for the large volume (simulations C, H, O, thicker solid best fitting lines) and the small volume (simulations E, L, Q, dotted best fitting lines), respectively. The three flows that differ only in grain size (best fitted by solid lines) are shown, in increasing order of grain size, by the larger unfilled circles (simulations C, H, O, thicker solid best fitting lines), the diamonds (simulations B, G, N, thinner solid best fitting lines) and the squares (simulations A, F, M, thinner solid best fitting lines). The + markers represent the flows in the narrowest channel (simulations R, S, T, dashed best fitting lines) and the × markers those in the widest channel (simulations D, I, P, dashed best fitting lines). The plots with red (a), orange (b) and blue (c) data are those whose $n$ is set equal to 1000, 100 and 1, respectively

Concerning the volume effect as illustrated by Fig. 2a–c, the comparison of the fronts of the two flows that differ only in volume (both have the same finest grain size and are shown in these plots by unfilled circles) indicates that in the range $80\le vol\%\le 95$ the fronts of the larger volume flow (the larger circles best fitted by the thicker solid curves) have a mobility larger than that of the corresponding fronts of the smaller volume flow (the smaller circles best fitted by dotted curves). The best fitting curves of these fronts of these two flows with different volumes appear to be virtually equidistant at small $vol\%$ values. At $vol\%=99$, instead, the front of the larger volume flow (larger circles) is less mobile than that of the smaller volume flow (smaller circles). These two opposite volume effects are the same at the three $n$ values (plots a, b, c in Fig. 2), but, as $n$ decreases, the mobility differential of the corresponding fronts of the two different volume flows decreases in the range $80\le vol\%\le 95$, whereas it increases at $vol\%=99$. At $vol\%=99$, the fronts of these two different volume flows are more mobile than at smaller $vol\%$ values (to such an extent that these most distal fronts do not plot along the best fitting curve of the smaller $vol\%$ values of the same flow), and it is the mobility of the smaller volume flow that significantly increases as $n$ decreases.

Concerning the channel widths in Fig. 2a–c, the flows in channels with different width also differ in grain size and/or flow volume. In any case, as expected in flows that differ only in channel width, the fronts of the flows in the largest channels (the × markers in the plots) are more mobile than those in the narrowest channels (the + markers in the plots) at all $vol\%$ values. In the range $80\le vol\%\le 95$, their best fitting curves (dashed lines) diverge as $vol\%$ increases. At $vol\%=99$, their mobility is larger than at smaller $vol\%$ values (to such an extent that these most distal fronts do not plot along the best fitting curve of the smaller $vol\%$ values of the same flow) and the fronts in the largest channel much more so (with an increase in mobility as $n$ decreases). This is true at all three scales $n$ (plots a, b, c in Fig. 2).

Concerning the grain size effect as illustrated by Fig. 2a–c, the comparison of the fronts of the three flows that differ only in grain size (their markers in descending order of grain size are squares, diamonds and the larger unfilled circles, all of them best fitted by solid lines) indicates that the best fitting curves of the two larger grain sizes (the thinner solid lines) intersect that of the finest grain size (the thicker solid lines) at a $vol\%$ that decreases as $n$ decreases. The $vol\%$ of this intersection is also smaller as the coarser grains increase in size. Therefore, (1) at small $vol\%$ values (where the flows are denser) the fronts of the two coarser grain size flows are less mobile than the corresponding fronts of the finest grain size flow, whereas at large $vol\%$ values they are more mobile (and much more so at $vol\%=99$) and (2) the more mobile distal part of the two coarser grain size deposits is longer as $n$ decreases. Thus, at $vol\%=99$, the fronts of the two coarser grain size flows do not plot along the best fitting curve of the smaller $vol\%$ values of the same flow (the coarser the grain size, the larger the mobility when compared with that of the same grain size at $vol\%=95$). This is true at all three scales $n$ (plots a, b, c in Fig. 2).

Figure 3a–c reveals the existence (in a region of the parameter space of the data on the rough subsurface) of a functional relationship with a positive linear correlation between ${\mu }_{Hvol\%}$ and $\psi$. This relationship is valid in the range $80\le vol\%\le 95$ when, here, $V/{\delta }^{3}>\sim {1.4\cdot 10}^{4}$ and $w/\delta \ge 12$ (Table 4). It is revealed by the fact that the data points (filled circles in the plots) collapse onto a single straight line for each one of these $vol\%$ values. The three flows at each $n$ whose data points are fitted by this relationship are those on the rough subsurface with the larger Froude number values (their averages are $0.5367\pm 0.0078$ at $n=1000$, $0.5315\pm 0.0042$ at n = 100, $0.5166\pm 0.0078$ at $n=1$). According to this relationship, flow front mobility increases as flow volume increases, as channel width increases and as grain size decreases. However, importantly, the coefficient of determination ${R}^{2}$ of the linear relationship is larger at larger $n$ as well as at smaller $vol\%$ (i.e., where the flows are denser). Specifically: ${R}^{2}\gtrsim 0.99$ at $vol\%\le 90$ when n=1000, ${R}^{2}>0.99$ only at $vol\%=80$ when n=100, and ${R}^{2}\lesssim 0.92$ at all $vol\%$ values when $n=1$ (Fig. 3). Therefore, the functional relationship appears only approximately valid for the fronts of large $vol\%$ values as well as for the flows with small $n$ (i.e., where ${R}^{2}<0.99$).

Fig. 3

Coefficient ${\mu }_{Hvol\%}$ versus parameter $\psi$ on the rough subsurface. Each $\psi$ value is that of a different flow. Each flow is represented by five data points: one data point for each one of the five $vol\%$ values (${\mu }_{Hvol\%}$ increases as the value of $vol\%$ decreases). The straight lines (one for each $vol\%$) best fit the data points whose behavior is exactly or approximately explained by Eq. (9). The insets zoom in on the upper left corner of the plots. The + markers represent the flows in the narrowest channel (simulations R, S, T) whereas the diamonds (simulations B, G, N, with the intermediate grain size) and the squares (simulations A, F, M, with the coarsest grain size) those with the two coarser grain sizes but the same volume. Circled markers are those of $vol\%=99$. The ${R}^{2}$ values are shown in the same vertical order of the straight lines they belong to. The plots with red (a), orange (b) and blue (c) data are those whose $n$ is set equal to 1000, 100 and 1, respectively

Table 4 Values of V/${\delta}^{\mathit{3}}$ and w/$\delta$ ratios

Figure 3a–c also shows the three flows at each $n$ on the rough subsurface (diamonds, + markers and squares) whose front behavior is not explained by the functional relationship between ${\mu }_{Hvol\%}$ and $\psi$. These flows have, here, $V/{\delta }^{3}<\; \sim {10}^{4}$ and/or $w/\delta \le 6$ (Table 4). They are those on the rough subsurface with the smaller Froude number values (their averages are $0.5052\pm 0.0051$ at $n=1000$, $0.5018\pm 0.0065$ at $n=100$, $0.4980\pm 0.0071$ at $n=1$). This functional relationship is also not valid, at all scales $n$, for all fronts of $vol\%=99$ whose data points are widely scattered (they are represented by circled markers in Fig. 3a–c).

Figure 4 displays the linear relationship between the mean ${\mu }_{Hvol\%}$ and the mean Froude number of the three flows at each $n$ for which the functional relationship between ${\mu }_{Hvol\%}$ and $\psi$ in Fig. 3 (exactly or approximately) holds. There is one straight line for each $vol\%$ (the larger the $vol\%$, the lower in the plot the straight line). Averages are computed to reduce the scatter that besets Froude number data. In the range $80\le vol\%\le 95$, ${\mu }_{Hvol\%}$ decreases as the Froude number increases (the best fitting straight lines have ${R}^{2} \gtrsim 0.98$). The error bars of the Fr values at $n=1$ do not overlap with those at larger $n$ (i.e., their Fr values are significantly different).

Fig. 4

Mean coefficient ${\mu }_{Hvol\%}$ versus mean Froude number Fr where the averages are over the three flows on the rough subsurface whose front behavior is explained (exactly or approximately) by Eq. (9). Each straight line best fits the data of one $vol\%$. The blue, orange and red data are those whose $n$ is set equal to 1, 100 and 1000, respectively. The larger the scale $n$, the larger the Fr value

Figure 5 illustrates the effect of scale $n$ on the flow front mobility. In this figure, mean ${\mu }_{Hvol\%}$ (averaged over the six simulations with the same $n$) is plotted versus $vol\%$. It is clear that the mobility of the fronts increases as $n$ increases in the range $80\le vol\%\le 95$, whereas the average front of the largest scale flows is the less mobile one at $vol\%=99$ (and each best fitting curve, one for each $n$, of the smaller $vol\%$ values does not fit the data point of $vol\%=99$).

Fig. 5

Mean coefficient ${\mu }_{Hvol\%}$ (the averages are over the six flows with the same $n$) versus $vol\%$ on the rough subsurface. The curves best fit the data. The blue, orange and red data are those whose $n$ is set equal to 1, 100 and 1000, respectively

Flow front mobility on a smooth subsurface

In Fig. 6a–c, ${\mu }_{Hvol\%}$ on a smooth subsurface is plotted versus $vol\%$. These plots allow the comparison among all flows of the effects of flow volume, grain size, channel width and flow scale on the front mobility as $vol\%$ varies. However, since the curves in Fig. 6a–c do not relate, to one another, scaling parameters containing the abovementioned variables and they are not functional relationships (data points of different flows do not collapse onto the same curve), the effect of each variable can be identified in these plots only by comparing flows that do not differ in the values of the other variables. Needless to say, front mobility increases as $vol\%$ increases for obvious geometric reasons.

Fig. 6

Coefficient ${\mu }_{Hvol\%}$ versus $vol\%$ on the smooth subsurface. The unfilled circles represent the two flows that differ only in volume: large and small circles for the large volume (simulations C, H, O, solid best fitting lines) and the small volume (simulations E, L, Q, dotted best fitting lines), respectively. The three flows that differ only in grain size (whose data points here overlap) are shown, in increasing order of grain size, by the larger unfilled circles (simulations C, H, O), the diamonds (simulations B, G, N) and the squares (simulations A, F, M). The + markers represent the flows in the narrowest channel (simulations R, S, T, dashed best fitting lines) and the × markers those in the widest channel (simulations D, I, P, dashed best fitting lines). The plots with red (a), orange (b) and blue (c) data are those whose $n$ is set equal to 1000, 100 and 1, respectively

Concerning the volume effect as illustrated by Fig. 6a–c, the comparison of the fronts of the two flows that differ only in volume (they have the finest grain size and are shown in the plots by unfilled circles) reveals that, in the range $80\le vol\%\le 95$, the fronts of the larger volume flow (the larger circles best fitted by solid curves) have a mobility smaller than that of the corresponding fronts of the smaller volume flow (the smaller circles best fitted by dotted curves). These two sets of data points are best fitted by curves that appear to be roughly equidistant at smaller $vol\%$ values and to converge at larger $vol\%$ values (so that their mobility differential is virtually non-existent at $vol\%=99$). This volume effect is the same at the three scales $n$ (plots a, b and c in Fig. 6).

Concerning the channel widths in Fig. 6a–c, the flows that travel in channels with different width also differ in grain size and/or flow volume. In any case, as expected in flows that differ only in channel width, the fronts of the flows in the largest channel (× markers in the plots) are more mobile than those in the narrowest channel (+ markers in the plots) at all $vol\%$ values. Their best fitting curves (dashed curves) appear to be roughly equidistant when for small $vol\%$ fronts and to converge (without coming together) at larger $vol\%$ values. This is true at the three scales $n$ (plots a, b, c in Fig. 6).

Concerning the grain size effect as illustrated by Fig. 6a–c, the comparison of the fronts of the three flows that differ only in grain size (their markers in descending order of grain size are squares, diamonds and the larger unfilled circles) indicates that grain size on the smooth subsurface has no effect on ${\mu }_{Hvol\%}$ at all $vol\%$ values since the three markers overlap (even if at $vol\%=99$ some scatter of the coarsest grain size fronts, the squares, exists). This is true at the three scales $n$ (plots a, b and c in Fig. 6).

Figure 7 illustrates the linear functional relationship between ${\mu }_{Hvol\%}$ and ${\text{log}}\left(\zeta \right)$. In Fig. 7, the data points of all three scales $n$ together are best fitted by one single straight line for each $vol\%$. The only best fitting straight line with ${R}^{2}>0.99$ (onto which the data points perfectly collapse) is that of $vol\%=95$. Instead, these lines have only ${\sim 0.96\le R}^{2}\le\, \sim 0.98$ in the range $80\le vol\%\le 90$ because of the small misalignment of the two central clusters of data points that are those, at the three scales $n$, of the two flows which differ only in volume plus those with the larger of these two volumes that differ only in grain size (i.e., nine data points along each line have the same third, from the left, value of ${\text{log}}(\zeta )$). The smaller ${R}^{2}$ ($\sim 0.90$) is that of $vol\%=99$, whose ${\mu }_{Hvol\%}$ values, at the three scales $n$, of the flows that differ only in grain size (the nine data points with the same third, from the left, value of ${\text{log}}(\zeta )$) are clearly more scattered. Therefore, the functional relationship appears to be exactly valid at $vol\%=95$ and approximately valid at the smaller $vol\%$ values, whereas it is less so at $vol\%=99$. Figure 7 shows that, on the smooth subsurface with a change in slope, the flow front mobility increases as flow volume decreases and as channel width increases. This figure implies that on the smooth subsurface the flow front mobility is not affected by grain size and it is not affected by flow scale since parameter $\zeta$ does not contain them.

Fig. 7

Coefficient ${\mu }_{Hvol\%}$ versus the logarithm of parameter $\zeta$ on the smooth subsurface. One straight line for each $vol\%$ best fits the fronts (of all scales $n$ together) whose behavior is exactly or approximately explained by Eq. (10)

Figure 8 confirms that scale $n$ on a smooth subsurface has no effect on flow front mobility. In this figure, mean ${\mu }_{Hvol\%}$ (averaged over the six simulations with the same $n$) is plotted versus $vol\%$. The three data sets (each one for a different scale $n$) are best fitted by curves that completely overlap. The mean Froude number of the six flows with $n=1$ is $0.9499\pm 0.0185$, that of the six flows with $n=100$ is $0.9432\pm 0.0189$, and that of the six flows with $n=1000$ is $0.9500\pm 0.0166$. Thus, these Froude number values are not significantly different since their error bars overlap.

Fig. 8

Mean coefficient ${\mu }_{Hvol\%}$ (the averages are over the six flows with the same $n$) versus $vol\%$ on the smooth subsurface. The three best fitting curves (one for each $n$ value) overlap. The blue, orange and red data are those whose $n$ is set equal to 1, 100 and 1000, respectively

Discussion: flow front mobility in numerical simulations

The flows whose front behavior can be modeled by means of functional relationships of scaling parameters can be identified in Figs. 3 and 7 (for the rough and smooth subsurface, respectively) because in these plots there exist regions of the parameter space where data points collapse onto single straight lines. These figures clearly show that the flows on a rough and those on a smooth subsurface belong to different granular regimes. However, the complexity of granular flows is such that there are fronts and flows with significantly different behaviors also on the rough subsurface. Here below, the different regimes and the different behaviors are illustrated and their relevance for rock avalanches is explained. Here, the term rock avalanche is used loosely to include volumes bigger and smaller than the 10⁶ m³ value of Hsü (1975) in a spectrum of flows where differences occur as detailed below.

Front mobility on a rough subsurface of $80\le vol\%\le 95$ of flows consisting of a large number of small clasts in wide channels

On a rough subsurface, Figs. 3 and 4 indicate that the following functional relationship $\mathcal{F}$ of scaling parameters

$$\mu_{Hvol\%}=\mathcal{F}\left(\frac{\delta^2}{V^{1/3}w},\frac u{\sqrt{L\;g\;\cos\!\alpha}},\mu_{Scs},\mu_{Rcs}\right),$$

(9)

exactly or approximately, holds in the range $80\le vol\%\le 95$ of flows with $V/{\delta}^{3}$ > ~1.4 ⋅ 10⁴ (i.e., consisting of a large number of relatively small particles) and $w/\delta \ge 12$ (i.e., in relatively wide channels). In these plots, there are three flows at each scale $n$ that have these characteristics (in boldface in Table 4). In Fig. 3a–c, these flow fronts are shown by filled circles that collapse onto the straight lines of the relationship (one straight line for each $vol\%$). In Eq. (9), the first independent parameter is $\psi$ (Eq. (4)) and the second is the Froude number Fr (Eq. (8)). Equation (9) is the relationship valid also for ${\mu }_{A}$ when on the rough subsurface at high stress level (Cagnoli 2021).

According to the linear relationship between ${\mu }_{Hvol\%}$ and $\psi$ (Fig. 3a–c), flow front mobility increases as flow volume increases, as channel width increases and as grain size decreases. These effects are valid for flows that (like rock avalanches) are dense. In these dense flows, all other features the same, an increase of flow volume V or a decrease of grain size $\delta$ (i.e., an increase of the value of $V/{\delta }^{3}$) increase the number of clasts in the flow so that particle agitation per unit of flow mass (that is due to the interaction with the channel surfaces, Figs. 9 and 10) and, consequently, the energy dissipation per unit of travel distance decrease (Cagnoli 2021). In Fig. 2a–c, this volume effect is clearly confirmed by the relative position of the large and small unfilled circles. An increase of the channel width (all other features the same) increases mobility because it decreases the motion resisting effect per unit of flow mass of the sidewalls (Cagnoli 2021). According to the relationship between ${\mu }_{Hvol\%}$ and Fr that is linear, the mobility of the fronts increases as the Froude number increases (Eq. (9) in Fig. 4). In particular, flow front mobility increases as flow scale $n$ increases (Fig. 5), because the Froude number of larger scale flows is larger (Fig. 4). This means that, as flow scale increases, the increase of the inertial forces is faster than that of the frictional motion resisting forces due to gravity. For example, the flow maximum speed is larger in larger scale flows (Cagnoli 2021). The increase of flow scale $n$ (all other features the same) also decreases particle agitation per unit of flow mass (Cagnoli 2021). The two components of basal friction are included in Eq. (9) because their decrease causes an increase of mobility (compare Figs. 3 and 7).

Fig. 9

Denser portion of flows that differ only in flow volume. Particle agitation per unit of flow mass (due to the interaction with the subsurface) decreases as V increases. The flow at the top has a larger volume. More agitated particles shown as more separated polygons

Fig. 10

Denser portion of flows that differ only in grain size. Particle agitation per unit of flow mass (due to the interaction with the subsurface) increases as $\delta$ increases. The flow at the top has a coarser grain size. More agitated particles shown as more separated polygons

With $n=1000$ (Fig. 3a), the three prototypal flows for which Eq. (9) holds range in volume between ~ 4000 and ~ 14500 m³. Although these volumes are not as large as those of the largest rock avalanches, the increase in mobility as V increases is shown in the field by landslides ranging in volume between $\sim 10$ and ${\sim 10}^{10}$ m³ (Corominas 1996). Therefore, these three prototypal flows are also expected to have a mobility that increases as V increases. In nature, rock avalanches and pyroclastic flows with small volumes are common and they can cause extensive damage (Jiang and Towhata 2013; Salvatici et al. 2016). Moreover, the landslides with volumes between $\sim {10}^{3}$ and ${\sim 10}^{4}$ m³ reported by Corominas (1996) have ${\mu }_{H}$ that decreases from a maximum value of ~ 0.8 (as V increases) and comparable values of ${\mu }_{H}$ are obtained here too for similar volumes V (Fig. 3a). Therefore, Eq. (9) is expected to hold also for the most mobile flows of Heim’s plots (such as those shown by Corominas 1996) whose particularly small ${\mu }_{H}$ values are due to a combination of values of V, w and $n$ that are larger and values of $\delta$ and basal friction that are smaller than those adopted here.

In Fig. 3, the ${R}^{2}$ value of the linear relationship is larger at larger $n$ as well as at smaller $vol\%$ (i.e., when and where the flow is denser). Thus, Eq. (9) holds exactly at $vol\%\le 90$ when n=1000 because ${R}^{2}\gtrsim 0.99$, and at $vol\%=80$ when n=100 because ${R}^{2}>0.99$. On the contrary, the linear relationship is only approximately valid for all $vol\%$ fronts in laboratory miniature flows with $n=1$ (here, their volumes range between ~${4\times 10}^{-6}$ and ~${1.45\times 10}^{-5}$ m³) because ${R}^{2}\lesssim 0.92$ (Fig. 3c). Indeed, the ${R}^{2}$ of a functional relationship is expected to be particularly large in numerical simulations (since they are unaltered by laboratory and field uncertainties), unless small ${R}^{2}$ values are the result of phenomena (such as isolated collisions) whose outcome is intrinsically erratic. For the same reason, Eq. (9) only approximately holds for the larger $vol\%$ fronts of the larger-scale flows. Importantly, however, as far as these larger $vol\%$ fronts are concerned, their ${R}^{2}$ values are expected to increase in flows with a very large $V/{\delta }^{3}$ ratio since this results in a particle agitation per unit of flow mass that is so small (because of a larger mean flow density) that their deposits have a distal distribution of isolated clasts, if any, that can be disregarded because relatively too small in overall mass, that is, ${\mu }_{H99\%}$ and ${\mu }_{H80\%}$ are relatively closer in value (Cagnoli and Romano 2012). More on this issue in the next subsection.

Front mobility of $vol\%=99$ of flows on a rough subsurface

On a rough subsurface, all ${\mu }_{H99\%}$ data points (circled markers in Fig. 3a–c) are so widely scattered at all three scales $n$ that a correlation between ${\mu }_{H99\%}$ and $\psi$ is not plausible and their front behavior is not explained by Eq. (9). Their large mobility in Fig. 3 is due to a phenomenon that dominates on the most distal fringes of the flows. This phenomenon is the consequence of the gradual decrease of the solid volume fraction toward the flow distal end (see also Zhou and Sun 2013) due to the concomitant decrease of the number of particles in the same direction (Fig. 11). This results in the number of clasts on the flow most distal fringes that is so small (Fig. 11) that clast interactions (which dissipate energy) become much less frequent and the fragments are able to travel spectacularly more since they dissipate much less energy per unit of travel distance. These clasts are saltating when they are able to travel in ballistic trajectories. Indeed, each flow front of $vol\%=99$ is so much more mobile that its data point in Fig. 2a–c lies well below the best fitting curve of the smaller $vol\%$ values of the same flow.

Fig. 11

Interpolated histogram of number of clasts every 10 m (the inset shows the most frontal 30 m). This figure indicates that the number of clasts decreases gradually toward the flow frontal end (located at the origin of the plot) where this number is always quite small. In the flows illustrated here, the overall mass on the most distal fringes of the flow is very small in relation to the mass of the entire flow. Two curves are shown: that of prototype of simulation O on the smooth subsurface (green data) and that of prototype of simulation O on the rough subsurface (brown data). Both curves are those of the fully developed flows when with maximum speed. The distances are at the scale of the prototypes whose grain size is 0.5 m. The flow on the rougher subsurface is longer

In Fig. 3a–c, this phenomenon affects a larger percental portion of the flow mass (since the front of $vol\%=95$ is also quite mobile) in the flows with the largest $\psi$ value (represented by squares) that are those consisting of only the smaller number of larger clasts. Figure 2a–c also confirms that this phenomenon has an important effect in flows with only a small number of particles (i.e., the two flows with the larger grain sizes but the same volume and the smaller volume flow) that have already a relatively small solid volume fraction along their entire length due to their characteristic small mean density (Cagnoli and Romano 2012; Cagnoli 2021). In these flows (Fig. 2a–c), the fronts of $vol\%=99$ (that are governed by a distinct clast movement mechanism where clasts are saltating) are so much more mobile that their volume and grains size effects on mobility are the opposite of those experienced by the fronts that in Fig. 3 collapse onto straight lines. Indeed, Fig. 2a–c shows that: (1) the front of $vol\%=99$ of the smaller volume flows (smaller unfilled circles) is more mobile than that of the larger volume flows (larger unfilled circles) and (2) the fronts of $vol\%=99$ of the two coarser grain size flows (diamonds and squares) are more mobile than that of the finest grain size flows (larger unfilled circles) and much more so than at $vol\%=95$. Wider channels (× markers) increase the discharge of the granular material and at $vol\%=99$ this effect is larger than at smaller $vol\%$ values (Fig. 2a–c) because of the larger number of saltating clasts (this is prefigured in the range $80\le vol\%\le 95$ by the downward diverging of the × from the + data points toward $vol\%=95$). Smaller basal friction increases the mobility of the fronts of $vol\%=99$ with the exception of the flow with the fewest clasts (represented by squares) because of the much smaller solid volume fraction that such a flow can develop on a rough subsurface (compare Figs. 2 and 6). It is expected that a very small solid volume fraction means a larger number of saltating clasts with larger travel distances.

Therefore, on a rough subsurface, flow volume has two opposite effects on the front mobility of a $vol\%$: one where the solid volume fraction is very small (such as at $vol\%=99$) and one where the flow is dense (such as at $80\le vol\%\le 95$). In both instances, particle collisions (which always dissipate energy) decrease: in the first case when (since the clasts are saltating) there are too few clasts per unit of travel distance (and this affects a larger percental flow portion spread along a longer distance, the smaller the flow volume, Fig. 12, so that the distal front becomes more mobile) and in the second case when clasts are too little agitated (and this is more so, the larger the flow volume, Fig. 9, so that the inner front becomes more mobile).

Fig. 12

Distal end of flows that differ only in flow volume. The flow at the top has a larger flow volume. Dashed rectangles encircle saltating clasts (that is where the solid volume fraction is significantly small)

The spectacular mobility of the saltating clasts on the flow most distal fringes ($vol\%\gtrsim 99$, Fig. 3a–c) is a phenomenon that affects a percental portion of the mass of the deposit that becomes smaller as the mean density of the flow increases, that is: (1) as flow clasts increase in number (i.e., clasts decrease in size (Fig. 10) or flow volume increases (Fig. 9), all the other features the same) and (2) as flow scale increases. In nature, this is the case when the rock avalanches have very large values of $V/{\delta }^{3}$, and as a consequence, their deposits have a distal distribution of isolated clasts, if any, that can be disregarded because relatively too small in overall mass (Cagnoli and Romano 2012). This means that ${\mu }_{H99\%}$ and ${\mu }_{H80\%}$ are relatively closer in value. This is confirmed in Fig. 3a–c (and insets) by the flows with the second, from the left, $\psi$ value, that are precisely the flows consisting of the largest number of smallest clasts. Considering the three flows with $n=1000$ that differ only in grain size ($V\sim {10}^{4}$ m³), the solid mass volumes of their distal distribution range from 50 to 800 m³ as their grain sizes range from 0.5 to 2 m. Thus, in the limit, as $V/{\delta }^{3}$ goes to infinity, the mass of the distal distribution is expected to go to zero.

The smaller stresses at smaller $n$ allow a further decrease in solid volume fraction so that, in this case, on the distal fringes of the flow, there are more saltating clasts with larger travel distances. For example, Fig. 5 shows that the average mobility of the front of $vol\%=99$ at $n= 1000$ is smaller than that at smaller $n$ values, and this is so because of the smaller stresses at smaller $n$. Moreover, at $vol\%=99$, the mobility in the widest channel (× markers) increases much more than that in the narrowest channels (+ markers) because of an increase in number of saltating clasts that becomes bigger as the channel widens and more so as $n$ decreases (Fig. 2a–c). The influence of scale $n$ on the flow volume effect at $vol\%=99$ can be appreciated in Fig. 2a–c where the differential between the front mobility of the flows that differ only in volume (the smaller and larger unfilled circles for the smaller and larger V, respectively) increases as $n$ decreases since the smaller stresses at smaller $n$ decrease further the solid volume fraction and this is more so in the smaller volume flow that contains fewer clasts. On the contrary, in the range $80\le vol\%\le 95$, the mobility differential of the flows that differ only in V decreases as $n$ decreases since, in this range of $vol\%$ values, it is the smaller V that lies above in the plot and the fronts of the larger V flow are those whose mobility decreases faster as $n$ decreases (Fig. 2a–c). Therefore, the detection of the Heim’s volume effect in laboratory miniature flows with $n=1$ is made difficult by three phenomena: (1) the decrease in the range $80\le vol\%\le 95$, as $n$ decreases, of the mobility differential of the fronts of the flows that differ in V (Fig. 2), (2) the opposite volume effect of the fronts of $vol\%=99$ (Fig. 2) and (3) the larger scatter of the data points fitted by the straight lines of Eq. (9) when $n=1$ (Fig. 3c). These first two phenomena explain, on a rough subsurface, the increase of ${\mu }_{A}$ as V increases in miniature laboratory flows with $n=1$ (Cagnoli 2021).

Front mobility on a rough subsurface of $80\le vol\%\le 95$ of flows consisting of only a small number of large clasts and/or in a too narrow channel

In Fig. 3a–c, the fronts of $80\le vol\%\le 95$ of flows on a rough subsurface with $V/{\delta }^{3}$ < ~10⁴ (i.e., consisting of only a small number of relatively large clasts) and/or $w/\delta \le 6$ (i.e., laterally constrained by a relatively too narrow channel) have behaviors that are also not explained by Eq. (9). Even if these features (in italic in Table 4) are not those of large rock avalanches, they are expected to occur in nature as well.

In Fig. 3, the two flows at each $n$ consisting of only a small number of large clasts (diamonds and squares) are characterized by a significant decrease of the solid volume fraction and their smaller $vol\%$ fronts (besides $vol\%=99$) are mobile enough to lie below the straight lines of Eq. (9). The same phenomenon is experienced by the center of mass of flows consisting of only a small number of large particles whose mobility is measured by ${\mu }_{A}$ (Cagnoli 2021). Indeed, the comparison in Fig. 2a–c of the three flows that differ only in grain size (solid best fitting curves) show that the fronts of the two flows with the coarser grain sizes (diamonds and squares best fitted by the thinner solid curves) have a mobility that increases as $vol\%$ increases to such an extent that their best fitting curves intersect that of the fronts of the finest grain size flow (larger unfilled circles best fitted by the thicker solid curve). This intersection occurs at a $vol\%$ that becomes smaller as $n$ decreases (Fig. 2) because of the concomitant further decrease in solid volume fraction due to the smaller stresses at smaller $n$. The intersection at different $vol\%$ values of the different grain sizes shows that the inward propagation of a sufficiently smaller (to be effective in increasing front mobility) solid volume fraction depends also on grain size. With $vol\%$ values larger than that of the intersection, the fronts of the coarser grain size flows are more mobile than the corresponding fronts of the finest grain size flow (as for $vol\%=99$ where this increase in mobility is so large that the data point does not plot on the best fitting curve of the small $vol\%$ values of the same grain size flow and where the coarsest grain size front is the most distant from this curve). With $vol\%$ values smaller than that of the intersection, the fronts of the coarser grain size flows are less mobile than the corresponding fronts of the finest grain sizes flow. The coarsest grain size fronts (squares) are expected to plot above the intermediate grain size fronts (diamonds) and their best fitting curves to intersect at $vol\%$ values smaller than 80. The fronts of these flows, too, are more mobile when basal friction decreases (compare Figs. 2 and 6).

Therefore, on a rough subsurface, grain size has two opposite effects on the front mobility of a $vol\%$: one where the solid volume fraction is very small and one where the flow is dense (Cagnoli 2021). In both instances, particle collisions (which always dissipate energy) decrease: in the first case when (since the clasts are saltating) there are too few clasts per unit of travel distance (and this affects a larger percental flow portion spread along a longer distance, the coarser the clasts, Fig. 13, so that the distal front becomes more mobile) and in the second case when the clasts are too little agitated (and this is more so, the finer the clasts, Fig. 10, so that the inner front becomes more mobile). The first behavior concerns the more distal fronts (in particular that of $vol\%=99$). The second behavior concerns the inner fronts.

Fig. 13

Distal end of flows that differ only in grain size. The flow at the top has a coarser grain size. Dashed rectangles encircle saltating clasts (that is where the solid volume fraction is significantly small)

In Fig. 3, there is also one flow at each $n$ that is laterally constrained by a particularly too narrow channel (+ markers). These flows have a large number of clasts but they probably experience a disproportionately different interaction with the sidewalls of the channel because its transverse cross-section has virtually changed from trapezoidal into V-shaped. Thus, they do not plot along the straight lines of Fig. 3a–c. The fronts of the flows inside the narrowest channel are the least mobile at all $vol\%$ values as visible in Fig. 2a–c (+ markers). The fronts of these flows, too, are more mobile when basal friction decreases (compare Figs. 2 and 6).

Front mobility of flows on a smooth subsurface

On a smooth subsurface, Fig. 7 indicates that the following functional relationship $\mathcal{G}$ of scaling parameters

$${\mu }_{Hvol\%}= \mathcal{G}\left({\mathrm{log}}\left(\frac{V}{{w}^{3}}\right),{\mu }_{Scs},{\mu }_{Rcs}\right),$$

(10)

exactly or approximately, holds in the range $80\le vol\%\le 99$. In Fig. 7, data points of all scales $n$ together are best fitted by one straight line for each $vol\%$. Importantly, their ${R}^{2}$ values are relatively small in the range $80\le vol\%\le 90$ and much smaller at $vol\%=99$. Thus, for these $vol\%$ values, Eq. (10) is only approximately valid. It is only for $vol\%=95$ that Eq. (10) is exactly valid because the data points collapse onto one single straight line whose ${R}^{2}>0.99$. These straight lines show that flow front mobility increases as flow volume decreases and as channel width increases. This volume effect is clearly confirmed in Fig. 6a–c by the relative positions of the two unfilled circles in the range $80\le vol\%\le 95$. Basal friction is included in Eq. (10) because its decrease causes an increase of mobility (compare Figs. 2 and 6) with the exception of the front of $vol\%=99$ in the fewest clast flow (represented by squares) that is more mobile on the rough subsurface as already explained. The difference on the smooth subsurface between the functional relationship with ${\mu }_{Hvol\%}$ (Eq. (10)) and that with ${\mu }_{A}$ (Cagnoli 2021) is that here the logarithm of $\zeta$ (Eq. (7)) has been introduced to deal with a larger range of values.

The flow volume effect in Eq. (10) is a geometric effect caused by the backward accretion of the deposit when the flow is coming to a stop on a change in slope and an increase of volume (Fig. 14) causes a larger backward shift of the deposit rear end (Cagnoli and Romano 2012) and of the same $vol\%$ front (Fig. 6). However, this volume effect disappears at $vol\%=99$ (Fig. 6a–c) where the particularly large mobility of the individual saltating particles becomes dominant (independently from V) so that the mobility differential due to V vanishes. Indeed, in Fig. 7, the gradient of the straight line of $vol\%=99$ is smaller than the gradients of the straight lines of the other $vol\%$ values.

Fig. 14

On a smooth enough subsurface with a change in slope, because of the backward accretion of the deposit, the larger the flow volume, the bigger the backward shift of the deposit rear end and of the front of the same $vol\%$

In Eq. (10), a wider channel increases the discharge of the particles by reducing the motion resisting effect of the sidewalls per unit of flow mass. The mobility differential between the fronts in the narrowest and widest channels (+ and × markers, respectively, in Fig. 6) decreases toward $vol\%=99$ where the particularly large mobility of the saltating clasts reduces the differential due to w. This too results in a decrease of the gradient of the straight line of $vol\%=99$ in Fig. 7.

Importantly, the flow front mobility in Eq. (10) is independent of grain size and flow scale $n$. Figure 6a–c confirms that flow mobility on a smooth subsurface does not depend on grain size (indeed squares, diamonds and the larger unfilled circles overlap), and Fig. 8 confirms that flow mobility on a smooth subsurface does not depend on flow scale $n$ (indeed the three curves overlap). The independence from grain size and flow scale is due to the fact that particle agitation that these two variables govern (and that affects mobility by means of its energy dissipation) cannot significantly develop on a subsurface that is not rough enough (Cagnoli 2021).

The reason why the value of ${R}^{2}$ increases as $vol\%$ increases in the range $80\le vol\%\le 95$ (Fig. 7) is that, the mobility differential, at the three scales $n$, between the fronts of the two flows that differ only in V (i.e., the two central clusters of data points in Fig. 7) gradually decreases as $vol\%$ increases (as shown by Fig. 6a–c), and it is only at $vol\%=95$ that this differential is such that the data points in Fig. 7 are aligned. The small value of ${R}^{2}$ ($\sim 0.90)$ at $vol\%=99$ (Fig. 7) is instead caused by the larger scatter of the data, at the three scales $n$, of the flows that differ only in grain size (the cluster of data points with the third, from the left, value of ${\text{log}}\left(\zeta \right)$). This is due to the fact that, again, on the most distal fringes of the flows, the solid volume fraction is significantly small and the outcome of the collisions of individual saltating fragments is more erratic and this is more so in flows consisting of only a small number of coarse particles (the squares in Fig. 6a–c). An increase of the value of $V/{\delta }^{3}$ in nature is expected to decrease the data scatter and increase the ${R}^{2}$ value also for the most distal portions (such as the fronts of $vol\%\sim 99$) of deposits on a smooth subsurface.

Discussion: flow front mobility of rock avalanches and explanation of their high mobility

The dense flows that in the numerical simulations travel on a relatively rough subsurface and in wide channels and that consist of a large number of small clasts are those whose front mobility (according to Eq. (9)) increases as flow volume increases as in Heim’s plots of field data. Moreover, the mobility of the most distal fronts of these flows is described more accurately by Eq. (9): (1) the larger the flow scale (since ${R}^{2}$ increases) and (2) the larger the number of relatively small particles in the flow (since ${\mu }_{H99\%}$ is relatively closer in value to the ${\mu }_{Hvol\%}$ of the inner fronts). In nature, these are characteristics of rock avalanches that travel on the rough subsurface of a mountain slope when they have very large $V/{\delta }^{3}$ values. That said, single rock fragments detaching from the flow proper and traveling further than the main deposit are to be expected in particular in relatively small flows (and this also needs to be considered when hazards are assessed in nature). Importantly, there is no need of a special friction reduction mechanism (such as mud lubrication or an air cushion in rock avalanches and gas fluidization in block-and-ash flows) to increase the flow front mobility since these mechanisms are absent in the numerical simulations where mobility increases as V increases. Similarly, in these simulations, clasts do not break when traveling and therefore the observed mobility increase cannot be due to clast fragmentation.

The flows whose fronts do not behave according to Eq. (9) increase the scatter of field data in Heim’s plots because they can occur in nature as well. For example, a rock avalanche is expected to travel on a particularly smooth subsurface when on the ice of a glacier (Sosio et al. 2012). In this case, the volume effect on mobility is the opposite of that of Eq. (9) (compare Figs. 3 and 7). On a subsurface smooth enough, rock fragments move en mass, i.e., clast speed does not change significantly at different distances along the normal to the subsurface (Cagnoli 2021). However, flows do not behave according to Eq. (9) also on a rough subsurface when they consist of only a small number of large clasts or when laterally constrained inside a too narrow channel. The scatter of field data in Heim’s plots is typically wide also because ${\mu }_{H}$ does not depend only on V (as the Heim’s plot assumes), but also on (among other variables) grain size, channel width, basal friction and flow scale.

According to Eq. (9), an increase of flow volume V on a rough subsurface (all other features the same) causes an increase of mobility. This is so because an increase of the number of particles in the flow (i.e., an increase of the value of $V/{\delta }^{3}$) causes a decrease of particle agitation per unit of flow mass (Fig. 9) and consequently a decrease of energy dissipation per unit of travel distance (Cagnoli 2021). Importantly, the presence of a single grain size in the flows (as in these simulations), versus that of a distribution of different grain sizes as in nature (e.g., Dufresne et al. 2016), does not prevent this volume effect from occurring. This is so since once the flows are dense enough because of a relatively large volume, differences in the grain size distribution can be ineffective. But the value of $V/{\delta }^{3}$ increases also when grain size $\delta$ becomes smaller (Fig. 10), so that, for the same reason, mobility increases when (all other features the same) grain size decreases on a rough subsurface (Cagnoli 2021). An increase of flow scale increases flow mobility because it also causes a decrease of particle agitation per unit of flow mass as a result of the internal stresses that increase in value (Cagnoli 2021). Here, I have compared flows in channels with different width where a larger channel width increases flow mobility because it helps the discharge of the granular material by reducing the sidewall effects per unit of flow mass. However, flows in channels can be more mobile than those which spread laterally because without lateral confinement (Strom et al. 2019). In dense flows, a decrease of basal friction increases front mobility.

The increase of mobility as flow volume increases (straight lines in Fig. 3) is consistent with the increase of mobility as flow scale increases (Fig. 5) because in both cases the size of the flow increases. However, the increase of flow volume V and the increase of flow scale $n$ have a different effect on flow shape. This is so since the increase of flow scale produces bigger flows that are geometrically similar in shape, whereas the increase of volume produces flows that are disproportionately longer because, as V increases, the increase of the length of a flow is faster than that of its thickness (see, for example, figure 10 in Lo (2000)) as a result of gravity that acts in the vertical direction. Therefore, larger volume flows are longer and their deposits have a longer downslope spread.

The largest mobility of the most mobile rock avalanches in nature can be explained by Eq. (9) with a combination of values of V, w and $n$ that are larger and values of $\delta$ and basal friction that are smaller than those adopted in the simulations. Importantly, larger-scale rock avalanches are more mobile (and this is true for both the fronts and the center of mass (Cagnoli 2021)) because they have larger Froude number values (Fig. 4). Therefore, as flow scale increases, the increase of the inertial forces is faster than that of the frictional motion resisting forces due to gravity. In short, larger-scale rock avalanches with large volumes are lengthwise highly elongated masses of rock fragments that travel more because of a larger value of the Froude number.

Conclusions

The numerical simulations indicate that, for rock avalanches, there exists a functional relationship of scaling parameters where an increase of flow volume V causes an increase of flow front mobility. This can be said because data points of different flows collapse onto the same curves. Therefore, the correlation between mobility and V is not spurious (i.e., due to, for example, a third variable). Field data instead are affected by so many uncertainties and they are typically so widely scattered that they are unsuitable for establishing whether the correlation (whose existence they have revealed) is due to a causal relationship or not. It has also been shown here that this mobility increase as V increases does not require special friction reduction mechanisms such as those provided by an air cushion, mud lubrication or clast fragmentation in rock avalanches and gas fluidization in pyroclastic flows.

The flow front mobility increase as V increases pertains to large-scale flows consisting of a large number of small fragments that travel on a rough subsurface and in wide channels. In nature, these are characteristics found in dense rock avalanches descending mountain slopes. The functional relationship that predicts an increase of mobility as V increases does not hold on a rough subsurface when the flows consist of only a small number of large clasts or when they are laterally constrained by a too narrow channel. It does not hold also in flows traveling on a smooth subsurface (such as on the ice of a glacier). Indeed, the complexity of granular flows is such that the interplay of the different variables generates significantly different granular regimes that exist in nature as well and that concur to increase the data scatter in Heim’s plots of field data.

Field data of flow front mobility are widely scattered also because they do not depend only on volume (as Heim’s plot assumes) but also on other variables including grain size, channel width, basal friction and flow scale. The data points of the numerical simulations collapse onto single curves precisely because they are values of scaling parameters that consider the concomitant effects on mobility of all these variables together. This is important because the effect on mobility of one variable depends on the values of the other variables. Here, it is thus provided a comprehensive and multivariate explanation of the concomitant effects on flow front mobility of all the abovementioned variables whose individual effects are consistent with one another. A multivariate theory is necessary to explain the multi-regime complexity of granular flow behavior in nature.

In general, a granular flow experiences an accordion effect where some of its inner fronts are more mobile and others are less mobile than the corresponding ones of a different flow. On a rough subsurface, an increase of flow volume increases the inner front mobility in the denser part of the flow whereas it decreases it on the most distal fringes. On a smooth enough subsurface with a change in slope, an increase of flow volume decreases the inner front mobility in the denser part of the flow whereas it does not generate significant differences in mobility on the distal fringes. On a rough subsurface, an increase in grain size decreases the inner front mobility in the denser part of the flow whereas it increases it on the distal fringes. On a smooth enough subsurface, an increase in grain size does not generate differences in the inner front mobility. On a rough subsurface, an increase in flow scale increases the inner front mobility in the denser part of the flow whereas it decreases it on the distal fringes. On a smooth enough subsurface, an increase of flow scale does not generate differences in the inner front mobility. An increase of basal friction decreases the inner front mobility (except on the distal fringes of flows consisting of only a small number of coarse clasts). An increase in channel width always increases the inner front mobility. However, as $V/{\delta }^{3}$ goes to infinity (such as in large rock avalanches), the overall saltating mass on the distal fringes goes to zero, i.e., it is, if any, very small in comparison with the overall mass of the denser part of the flow which is where the fronts behave according to Eqs. (9) and (10).

Therefore, in dense rock avalanches consisting of a large number of small clasts that travel on the rough subsurface of a mountain slope and in wide channels, flow front mobility increases (1) as flow volume increases, (2) as grain size decreases, (3) as channel width increases, (4) as basal friction decreases and (5) as flow scale increases (whereas the particles that detach from the dense part of the flow and outrun it behave differently but they, if any, are relatively small in overall mass). Larger volume flows are more elongated in the downslope direction and both an increase of flow volume and an increase of flow scale reduce particle agitation that dissipates energy. Importantly, larger-scale flows are more mobile because they have larger Froude number values. Therefore, as flow scale increases, the increase of the inertial forces is faster than that of the frictional motion resisting forces due to gravity.