Stress level effect on mobility of dry granular flows of angular rock fragments

Abstract

Granular flows of angular rock fragments such as rock avalanches and dense pyroclastic flows are simulated numerically by means of the discrete element method. Since large-scale flows generate stresses that are larger than those generated by small-scale flows, the purpose of these simulations is to understand the effect that the stress level has on flow mobility. The results show that granular flows that slide en mass have a flow mobility that is not influenced by the stress level. On the contrary, the stress level governs flow mobility when granular flow dynamics is affected by clast agitation and collisions. This second case occurs on a relatively rougher subsurface where an increase of the stress level causes an increase of flow mobility. The results show also that as the stress level increases, the effect that an increase of flow volume has on flow mobility switches sign from causing a decrease of mobility at low stress level to causing an increase of mobility at high stress level. This latter volume effect corresponds to the famous Heim’s mobility increase with the increase of the volume of large rock avalanches detected so far only in the field and for this reason considered inexplicable without resorting to extraordinary mechanisms. Granular flow dynamics is described in terms of dimensionless scaling parameters in three different granular flow regimes. This paper illustrates for each regime the functional relationship of flow mobility with stress level, flow volume, grain size, channel width, and basal friction.

Introduction

The understanding of the energy dissipation mechanisms of dense flows of rock fragments such as rock avalanches (Hungr et al. 2014) and block-and-ash flows (Cas and Wright 1988) is essential in hazard mitigation efforts. This understanding is however frustrated by the intricate interplay of the too many variables governing the mobility of these flows. With this in mind, we have studied in the laboratory (Cagnoli and Romano 2010, 2012a, b) and with numerical simulations (Cagnoli and Piersanti 2015, 2017, 2018) the effects of grain size, flow volume, and channel width on the mobility over a rough subsurface of dry granular flows of angular rock fragments. But these are not the only important variables.

Rock avalanches and the dense underflow of block-and-ash flows are dry granular flows of angular rock fragments. Rock avalanches are dry because their extensive fragmentation during motion generates new intergranular spaces that cannot be filled by water during their relatively short travel times (Hungr et al. 2014). Pyroclastic flows are dry because of their high volcanic temperatures. In nature, these flows descend down open channels with speed varying over time and space so that they are characteristically unsteady, nonuniform, with a free top surface and some lateral confinement. These features (unsteady, nonuniform, dry, able to dilate vertically, and laterally confined) are defining and need to be shared with flow models.

The validation of laboratory modelling by means of field-scale flows is not straightforward because natural flows are too fast and too dangerous to be approached at close range and direct measurements of relevant quantities can be precluded. Moreover, most flows in nature are too large to be replicated with a unity-scale factor in indoor or outdoor experimental facilities and scaling criteria are usually poorly fulfilled. Field data also do not necessarily provide trustworthy validations of numerical simulations since any good match can be due to compensating errors caused by speculative values of too many variables and boundary conditions (Dyson 2004).

Nevertheless, small-scale flows are widely studied in many laboratories to gain insight into the behavior of their larger counterparts in nature. But since solid stresses are much smaller in small-scale granular flows than in their full-scale field counterparts (Hungr and Morgenstern 1984), a fundamental question arises concerning the influence of the stress level on the mobility of granular flows. For example, speed, thickness, and surface inclination of a steady and uniform layer of moving glass beads discharged from a hopper in a laboratory were modeled by means of the μ(I)-rheology (Jop et al. 2006), where the ratio between shear and normal stresses seems to decrease as the normal stress increases, even if it is not clear the impact that this sort of decrease, if any, may possibly have on the mobility of geophysical flows at scales larger than that of the laboratory.

By increasing the acceleration of gravity n times inside a geotechnical centrifuge, an experimenter can replicate field-scale stress levels in a 1/n scale model (Bowman et al. 2010; Ng et al. 2017). A centrifuge can therefore be useful, but granular flows in it are affected by undesired effects such as 1) the flow runouts that are modified by Coriolis acceleration when flow motion has a radial component within the centrifuge, 2) the gravity experienced by the flow that changes as function of its distance from the rotation axis, and 3) the bulk density of the flow that is affected by its orientation (Bowman et al. 2012; Turnbull et al. 2015; Bryant et al. 2015; Cabrera and Wu 2017).

Since previous studies have risen the issue of the stress level without delineating its consequences on flow mobility, here, to avoid the undesired effects of laboratory centrifuges, the important role played by the stress level on granular flow dynamics is detailed by carrying out numerical simulations of scale down granular flows where the acceleration of gravity is made to vary in value without the use of a centrifuge. This enables an assessment of the relevance of small-scale laboratory experiments when modelling geophysical flows. It also provides a quantitative explanation of the stress level effect on flow mobility in a coherent and multivariate framework of the interplay between stress level, grains size, flow volume, channel width and basal friction. This allows the description of granular flow mobility in three different regimes by means of dimensionless scaling parameters that are the result of a dimensional analysis.

Geometry of slope and particles in the 3D numerical simulations

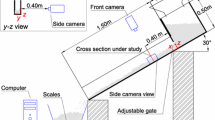
The model slope upon which the scale-down granular flows travel consists of an upper straight ramp and a lower curved portion whose combined length is ~1.6 m (Fig. 1). The hyperbolic sine equation of the longitudinal profile of the curved portion with variables in meters is

Fig. 1

Longitudinal profile of the channels. The inset shows their trapezoidal cross-section. CM stands for center of mass

$$ z=0.3-0.085{\sinh}^{-1}\left(11.765\ x\right). $$

(1)

To comply with geometric and kinematic similarity requirements, this equation is that of the slightly modified profile of Mayon volcano in the Philippines (Becker 1905) and the trapezoidal cross section of both slope parts (Fig. 1) corresponds in nature to a V-shaped topographic incision with sediment infilling in the centre (see photo 14 in Zhang and Yin (2013) and photo 6 in Quan Luna et al. (2012)). The lateral side inclination θ (Fig. 1) is the same in all simulations (27°) since different θ values result in different flow mobility (Cagnoli and Piersanti 2017). The slope of the straight portion is 47° from the horizontal. This same slope geometry was used in the laboratory by Cagnoli and Romano (2010, 2012a, b) and in the numerical simulations by Cagnoli and Piersanti (2015, 2017, 2018). In nature, rock clasts are angular and angular clasts need to be considered in the numerical simulations as well. Here, they are simulated by one angular shape only (cubic) considering that different proportions of different clast shapes result in different flow mobility (Cagnoli and Piersanti 2015).

Scaling of stresses, accelerations, forces, speeds, and time

The geometric scaling factor n is defined as the ratio of a characteristic length λ in the natural prototype (subscript P) to the corresponding length λ in the model (subscript M):

$$ n=\frac{\lambda_P}{\lambda_M}. $$

(2)

Since the densities of the different materials are the same in simulations and natural counterparts, both volumes V and masses m have ratios of model to prototype equal to 1/n³.

For the stresses to be the same in model and natural prototype, the acceleration of gravity in the model has to be n times larger than that in the prototype (otherwise the stresses are underestimated). The consequences of

$$ {a}_M=n\cdotp {a}_P $$

(3)

(where a is an acceleration such as that of gravity g) on the scaling of stresses, forces, speeds, and time are as follows. The stresses σ are equal in model and prototype because

$$ {\sigma}_P=\frac{F_P}{A_P}=\frac{m_P\cdotp {a}_P}{A_P}=\frac{n^3\cdotp {m}_M\cdotp \frac{a_M}{n}}{n^2\cdotp {A}_M}=\frac{F_M}{A_M}={\sigma}_M, $$

(4)

where F is force and A is area. The relationship between the forces is

$$ {F}_P={m}_P\cdotp {a}_P={n}^3\cdotp {m}_M\cdotp \frac{a_M}{n}={n}^2\cdotp {F}_M. $$

(5)

Speeds in model and prototype are identical, whereas time in model is n times smaller than that in prototype because

$$ \frac{\Delta {u}_P}{t_P}={a}_P=\frac{a_M}{n}=\frac{\Delta {u}_M}{n\cdotp {t}_M}, $$

(6)

where u is speed and t time, so that

$$ {u}_P={u}_M $$

(7)

and

$$ {t}_P=n\cdotp {t}_M. $$

(8)

The stress level is represented hereafter by the geometric factor n, because, when Eq. (3) is true: 1) the stress level is equal in model and corresponding prototype and 2) the stress level in model and corresponding prototype is proportional to n (a stress in a large-scale prototype is equal to n multiplied by the stress in its small-scale model computed with n = 1).

Scaling of flow mobility and its functional relationships

The reciprocal of mobility of a flow is measured by using the apparent coefficient of friction

$$ {\mu}_A=\frac{h}{l}, $$

(9)

where h is the vertical drop of the centre of mass of the granular material and l is its horizontal distance of travel. Distances h and l are measured from the position of the centre of mass of the granular masses at rest before collapsing to the position of the centre of mass of the final deposits (Fig. 1). The center of mass is the only point that can be used as proxy for the entire flow since it is the only point that moves as though the total mass of all clasts were concentrated there and all external forces were applied there.

The aim of this paper is to find out the functional relationships of flow mobility (or its reciprocal μ_A) with quantities such as grain size δ, flow volume V, flow length L, channel width w, flow speed u, stress level (represented by geometric factor n that enters model gravity g) and the coefficients of static (μ_Scs) and rolling (μ_Rcs) friction between clasts and subsurface:

$$ {\mu}_A={\mathcal{F}}_1\left(\delta, V,L,w,u,g,{\mu}_{Scs},{\mu}_{Rcs}\right). $$

(10)

Grain size δ is considered the pertinent length scale for the grain-scale mechanics that generates the stresses whereas flow length L is considered the pertinent length scale for the flow as a whole (Iverson et al. 2010). Speed u is needed for gravity g to enter a dimensionless scaling parameter for dynamic similarity. Since the granular masses collapse from rest and their speed gradually increases to reach a maximum value and then it decreases before deposition, quantity u is this maximum speed. Friction coefficients μ_Scs and μ_Rcs are not only those of the basal surface but also those of the lateral surfaces which slope toward the centre of the channels and constrain the granular masses also from below (Fig. 1). In general, granular flow mobility is affected by many more quantities whose values are held deliberately constant in this study as will be shown later. Moreover, there are no intergranular fluids (such as gases or water) that can alter solid interactions.

Equation (10) has nine quantities with two fundamental dimensions (length and time). For this reason, according to the Pi Theorem of dimensional analysis (Barenblatt 1996), it is equivalent to a functional relationship containing seven dimensionless parameters. In this new relationship, grain size δ is used to scale the other variables with only length as their dimension, u and g are combined together, whereas μ_A, μ_Scs and μ_Rcs are already dimensionless parameters and do not need to be combined:

$$ {\mu}_A={\mathcal{F}}_2\left(\frac{V^{1/3}}{\delta },\frac{L}{\delta },\frac{w}{\delta },\frac{u}{\sqrt{gL}},{\mu}_{Scs},{\mu}_{Rcs}\right). $$

(11)

In Eq. (11), grain size δ is used to scale V, L and w because δ affects the energy dissipation of the flows by determining their number of clasts and clast number density and thus their clast agitation (Cagnoli and Romano 2010, 2012b; Cagnoli and Piersanti 2017, 2018). Indeed, the first independent dimensionless ratio is an increasing function of the total number of particles in the flow, whereas the second and third ratios are an increasing function of the number of particles distributed in space along the flow length and width, respectively. The fourth independent dimensionless ratio is a Froude number.

Scaling of inertial and gravitational forces: the Froude number

The main forces affecting the dynamics of dense granular flows (such as rock avalanches or block-and-ash flows) are inertial and gravitational forces (gravity is their driving force). The ratio of inertial to gravitational forces is called Froude number that can be written also as

$$ Fr=\frac{u}{\sqrt{L\ g\cos \alpha }}, $$

(12)

since slope angle α is dimensionless.

It is usually the thickness H of the flow that is adopted in Eq. (12) as characteristic length L (Choi et al. 2017). Here, Fr with H has a value averaged over all the flows of this paper equal to 5.6 ± 0.2 that falls within the range from 0.5 to 7.6 typical of natural debris flows (Cui et al. 2015). However, H varies so much from the front to the rear of the flow (Ng et al. 2019) and in different moments during the flow travel time that Fr with H can acquire, for a single flow, a large range of possible values. Moreover, H in granular flows is an ambiguous concept because of their ever-changing dilated top surface made of agitated and colliding particles. In particular, the erratic positions of agitated particles introduce a larger percentage error in H than in the length of these flows because flow length is much longer than H and H does not increase as significantly as flow length does when flow volume increases (see for example graph 10 in Lo (2000)). Thus, a comparison of Fr values computed with H by different authors can be misleading. Flow speed as well differs significantly during the travel time and in different positions within a flow. In addition, slope inclination α is not constant along a curved chute.

To avoid uncertainties, here Fr is computed for the granular flows when they have reached their maximum speed. Therefore, u is this maximum speed (computed as the maximum during the flow descent of the average speed of all particles), L is the length of the flow with maximum speed (computed as the distance along the slope between the most distal and most proximal clasts) and α is the slope inclination in the position of the center of mass of the flow with maximum speed. These characteristic quantities are straightforward to measure and generate no ambiguities. However, since the Froude number neglects the micro-interactions that occur in granular flows such as grain-grain contacts and collisions (Choi et al. 2015), other scaling parameters are needed to fully characterize the granular flow behavior.

Granular scaling parameter χ for a rough subsurface

The first three independent variables of Eq. (11) are combined to define the following dimensionless parameter:

$$ \upchi =\frac{V^{1/3}\delta }{L\ w}. $$

(13)

Parameter χ is the product of

$$ \Gamma =\frac{V^{1/3}}{\delta } $$

(14)

and the reciprocal of

$$ \upgamma =\frac{L\ w}{\delta^2}. $$

(15)

The dimensionless quantity Γ is an increasing function of the total number of clasts in the granular flow since it corresponds to V/δ³. The dimensionless quantity γ is an increasing function of the number of clasts in contact with the channel basal surface since it is proportional to the number of clasts whose sum of cross-sections covers completely an area L times w (the cross-sectional area of a clast is δ²). Quantities in Eq. (13) are again those of granular flows with maximum speed. L is their length and V is the sum of all clast volumes in each flow (i.e., the volume of its solid mass). Width w is the smallest distance between the inclined sidewalls that is where the flows are laterally constrained the most (Fig. 1). Cagnoli and Romano (2012a) and Cagnoli and Piersanti (2017) showed that μ_A is proportional to χ according to a linear relationship in scaled-down granular flows on a rough subsurface and n = 1.

Granular scaling parameter ψ for a rough subsurface

The first and third independent variables of Eq. (11) are combined to define the following dimensionless parameter

$$ \psi =\frac{\delta^2}{V^{1/3}w}. $$

(16)

Parameter ψ is the product of the reciprocal of Γ (Eq. (14)) and the reciprocal of

$$ \Omega =\frac{w}{\delta }, $$

(17)

which is an increasing function of the number of clasts that fit the channel width along the transversal direction. Quantities in Eq. (16) are those of flows with maximum speed as in Eq. (13). Cagnoli and Romano (2012b) and Cagnoli and Piersanti (2018) introduced ψ for small-scale granular flows on a rough subsurface and n = 1.

Scaled clast agitation

The fluctuation of the total force exerted by the granular flows on the subsurface is used to compare the basal clast agitation of the flows. The magnitudes F_i of this force form a time series of values that are equally spaced in time from the initial collapse of the granular mass to after its final deposition. The following parameter is computed in a selected time window of the time series:

$$ D=\frac{\Delta F}{\overline{F}}, $$

(18)

where $\overline{F}$ is the average force exerted by the entire flow on the subsurface in that time window and

$$ \Delta F=\sqrt{\left\langle {\left({F}_i-{P}_i\right)}^2\right\rangle } $$

(19)

is the average (symbolized by the angle brackets) deviation of magnitudes F_i from the values P_i of a second-order polynomial fitting the data points (or two second-order polynomials when the data points are asymmetrically distributed). For the comparison between the D values to be meaningful, this time window has the same size (here 30 data points) and is located in the same moment of flow history in all simulations.

The larger ΔF, the larger the number of force values that are more different from the fitting curve so that ΔF measures particle agitation (the fitting curve represents the F_i values with zero agitation). Parameter D is thus a scaled particle agitation at the base of the flows. It is worth noting that an average squared deviation occurs in the definition of the so-called granular temperature as well (Ogawa 1978). Cagnoli and Romano (2012b) and Cagnoli and Piersanti (2018) showed that D computed for basal stresses is proportional to parameter ψ according to a linear relationship in scaled-down granular flows on a rough subsurface and n = 1.

3D numerical simulations

The numerical simulations are three-dimensional and are based on the discrete element method (DEM). This method upholds the defining granular nature of the geophysical flows studied here by taking into consideration all clast-clast and clast-boundary interactions. In DEM simulations, there is no need to impose a criterium for deposition since the flows stop by themselves when they dissipate all their kinetic energy. The DEM software employed has been developed by DEM Solutions Ltd. and is called EDEM. Its contact model is illustrated by Cagnoli and Piersanti (2015).

In these DEM simulations the granular flows travel on a 3D channel created by means of a CAD software (Fig. 2) with the geometry of Fig. 1. The software uses in its calculations the mass, volume, and moment of inertia of the cubic clasts, whereas the impact forces during particle collisions are estimated as a function of the overlapping of sets of rigidly connected spheres inscribed within the cubes (Fig. 2). This type of numerical simulations (Cagnoli and Piersanti 2015, 2017, 2018) has been validated by laboratory experiments (Cagnoli and Romano 2010, 2012a, b) which confirm that the simulations account well for the interactions of angular clasts and that the functional relationships obtained by means of the discrete element method are real. At low stress level, this is demonstrated by comparing the results illustrated here with those of the above-mentioned laboratory experiments. At high stress level, DEM simulations predict the same flow volume effect on flow mobility observed in the field as will be shown later.

Fig. 2

3D view of one of the channels used in the numerical simulations. The inset shows the clast cubic shape with the inscribed spheres

Table 1 illustrates the fifteen combinations of the values in both numerical models and corresponding natural prototypes of geometric scaling factor n, gravity g, slope height, channel width w, grain size δ and granular mass m. The number of clasts in a model and the corresponding prototypal flow is identical (Table 1). The three n values considered here are 1, 100, and 1000, which result in three accelerations of gravity in the numerical models equal to 9.8, 980, and 9800 m/s², respectively (even if gravity in their corresponding natural prototypes is always 9.8 m/s²). The three n values result also in prototypal slope heights equal to 0.5, 50, and 500 m, respectively (even if the slope height in the model is always 0.5 m). The model channel width w is 0.006 and 0.026 m, which for n equal to 1, 100, and 1000, in the prototypal narrower channel correspond to 0.006, 0.6, and 6 m, respectively, and in the prototypal wider channel correspond to 0.026, 2.6, and 26 m, respectively. The cubic clasts in the numerical models have edges (i.e., grain size) equal to 0.0005, 0.001, and 0.002 m, which with n = 100 correspond to prototypal grain sizes equal to 0.05, 0.1, and 0.2 m, respectively, and with n = 1000 correspond to prototypal grain sizes equal to 0.5, 1, and 2 m, respectively.

Table 1 Characteristics of numerical simulations

All fifteen simulations illustrated in Table 1 (named with letters from A to Q) have been carried out, once, with large values of the coefficients of static and rolling friction between clasts and subsurface (μ_Scs = 0.9 and μ_Rcs = 0.07, respectively) and, once, with small values of these quantities (μ_Scs = 0.45 and μ_Rcs = 0.035, respectively). The large values are twice as much the small values and their simulations are hereafter referred to as those on rough and smooth subsurface, respectively. Thus, this paper presents the results of thirty numerical simulations. In Table 1, for each n value: 1) the simulations of the first three columns are those of flows which differ in grain size, 2) the simulations of the third and fifth columns are those of flows which differ in volume, and 3) the simulation of the fourth column is that of a flow in a wider channel.

Tables 2 and 3 list the values of Poisson’s ratios, shear moduli, densities, coefficients of restitution, and coefficients of static and rolling friction in clast-clast interactions. These quantities are those mentioned before to have the same values in all simulations. The values of the properties in Tables 2 and 3 indicate that these simulations refer to flows of rock fragments traveling on a mountain slope (Peng 2000).

Table 2 Material properties

Table 3 Properties governing interactions

Initial collapses

No gate has been used to release the granular material from rest at the top of the slope. This is so to free the system of the unnecessary frictional forces between clasts and gate. The granular masses instead collapse under the influence of gravity. Before this collapse, the clasts are in contact with one another and in random positions inside numerical spaces representing rock cliffs or volcanic domes. One of them is shown in red at the top of the channel in Fig. 2. The volumes of these polyhedral spaces are proportional to the granular masses so that the same compaction and bulk density of the granular material before collapse is ensured considering that different degrees of this initial compaction would cause different flow mobility (Cagnoli and Piersanti 2015).

Final deposits

The deposited granular material consists always of two portions: a more proximal heap that is much more elongated than thick (the deposit of the flow proper) and a more distal distribution of isolated clasts. The distal distribution is formed by clasts that are not part of the flow proper because, at least to some extent, they travelled singly with reduced interactions among them. Figure 3 shows some of these clasts travelling separately in front of a flow. In previous publications, μ_A was computed by considering the centre of mass of only the deposit of the flow proper (Cagnoli and Romano 2010, 2012a; Cagnoli and Piersanti 2015, 2017). In this paper instead, μ_A is computed by considering the overall centre of mass of deposit of flow proper plus distal distribution together. There are two reasons to do so: 1) with a small number of large clasts, it can be difficult to locate the dividing line between deposit of flow proper and distal distribution and 2) the clasts of the distal distribution pose a threat that has to be considered when assessing natural hazards.

Fig. 3

Frontal view of a granular flow on a rough subsurface. Geometric factor n is 1, grain size δ is 2 mm, and the channel width w is 6 mm

The position of the overall center of mass is thus the result of different travel mechanisms: that of the flow proper and that of the clasts of the distal distribution. But this second component has a little effect on the position of the overall center of mass when the granular flow consists of a large number of fine clasts because the mass of the distal distribution is, in relative terms, too small. Here, this is the case with all flows that have grain sizes in their models equal to 0.0005 and 0.001 m. Only in the three flows (one for each n value) that have a grain size in their models equal to 0.002 m, the overall center of mass is significantly more mobile than that of only the deposit of the flow proper.

Results: granular flow speeds and basal forces

Under the influence of gravity, the granular masses collapse and accelerate downslope so that they reach a maximum speed before decelerating and forming a final deposit (examples on rough and smooth subsurface are in Figs. 4 and 5, respectively). Table 4 shows these maximum speeds averaged over the five simulations with the same n for both rough and smooth subsurface. Speeds (identical in numerical model and corresponding natural prototype) are larger on the smooth than on the rough subsurface and they increase as the scale of the prototype (i.e., n) increases (Table 4).

Fig. 4

Longitudinal cross-sections of a granular flow on a rough subsurface. Geometric factor n is 1, grain size δ is 0.5 mm, and the channel width w is 6 mm. Time t_M since the initial collapse is shown

Fig. 5

Longitudinal cross-sections of a granular flow on a smooth subsurface. Geometric factor n is 1, grain size δ is 0.5 mm, and the channel width w is 6 mm. Time t_M since the initial collapse is shown

Table 4 Maximum speed (m/s) of granular flows

The granular flows on a rough subsurface and those on a smooth subsurface have radically different vertical profiles of speed. On a rough subsurface, clast speed shows a significant increase in value from the base to the top of the flow (Fig. 6). On a smooth subsurface, the speed of the clasts is virtually the same at different heights within the flow whose clasts move thus en masse (Fig. 7).

Fig. 6

Vertical profile of speed in a longitudinal cross-section of a flow on a rough subsurface. Geometric factor n is 1, grain size δ is 0.5 mm, and the channel width w is 6 mm. Time t_M since the initial collapse is shown

Fig. 7

Vertical profile of speed in a longitudinal cross-section of a flow on a smooth subsurface. Geometric factor n is 1000, grain size δ is 0.5 mm, and the channel width w is 6 mm. Time t_M since the initial collapse is shown

Figure 8 illustrates an example of flow history from initial collapse to after the final deposition (Figs. 4 and 5) in terms of the force exerted by the flow on the subsurface. When force magnitudes F_i (introduced in the paragraph of Eq. (18)) are plotted versus time, they always exhibit two local maxima (shown by arrows in Fig. 8). The first one occurs during the initial deformation of the granular mass that follows its initial collapse. The second one occurs in the time window when the granular flow reaches its maximum speed and has acquired its fully developed shape of travel. In all simulations, agitation D (Eq. (18)) is computed in this second time window whose data points have always a concave down distribution with an inflection point toward the end and are thus fitted by two partially overlapping second order polynomials (Fig. 8).

Fig. 8

Force F_M exerted by a granular flow on the subsurface versus time t_M. Geometric factor n is 1000, grain size δ is 1 mm, channel width w is 26 mm, the subsurface is rough. The two local maxima are shown by arrows. Parameter D is computed in the time window with blue data points (fitted by two partially overlapping second-order polynomials that are shown by different colors)

Results: granular flow mobility on a rough subsurface

Functional relationships

For the rough subsurface, the reciprocal of mobility μ_A of the same fifteen granular flows is plotted once versus parameter χ in Fig. 9a and once versus parameter ψ in Fig. 9b. In both panels, data points are best fitted by least squares straight lines and second-order polynomials. Specifically, the relationship between μ_A and χ (Fig. 9a) and the relationship between μ_A and ψ (Fig. 9b) is linear as long as the mass of the distal distribution of clasts is relatively small. For each geometric factor n, this is the case for the four data points with smaller χ (Fig. 9a) and smaller ψ (Fig. 9b). When, on the other hand, the mass of the distal distribution is relatively important in relation to that of the deposit of the flow proper, the overall center of mass becomes more mobile since the clasts of the distal distributions travel singly (at least in part) and acquire a larger mobility with respect to that of the linear relationship because of their smaller number of solid-solid interactions per unit of time. This larger mobility is not due to the value of either the grain size or χ or ψ, but it occurs when the clasts that form the flow are both small in number and relatively coarse in grain size (granular flows with the same coarse grain size but a sufficiently larger number of clasts are expected to plot along the fitting straight lines). In Fig. 9, the flows with a too small number of coarse clasts are those that, one for each n value, have the largest χ and the largest ψ. It is for this reason that the three sets of five data points with the same n can be fitted by a second-order polynomial and not by a straight line. If the distal distribution of clasts is removed from the calculation of the final position of the centre of mass, the data points with largest χ and largest ψ will move toward their own linear relationship that is the place the deposit of the flow proper belongs to (Cagnoli and Romano 2010, 2012a; Cagnoli and Piersanti 2015, 2017).

Fig. 9

Reciprocal of mobility μ_A of the fifteen flows on a rough subsurface plotted once versus χ (a) and once versus ψ (b). Blue, orange, and red refer to a geometric scaling factor n equal to 1, 100, and 1000, respectively. In both panels and for each n, least squares straight lines best fit the first four data points with smaller abscissa, whereas least squares second-order polynomials best fit all five data points. Data points of flows distinguishable only by different volumes are pierced by arrows (the larger the arrowhead, the larger the volume). The curves of the false functional relationships are in grey. The curves of the true functional relationships are in blue, orange and red

The corresponding linear relationships of the two panels in Fig. 9 are however mutually exclusive because, as flow volume increases, in Fig. 9a flow mobility decreases, whereas in Fig. 9b flow mobility increases. To understand when μ_A is a function of χ and when it is a function of ψ, it is necessary to compare, for each n value, the mobility of the two granular flows distinguishable only by different volumes since all their other features are identical. In Fig. 9, their data points are pierced by arrows (the larger the arrowhead, the larger the volume) and, in Table 1, they are named C and E with n = 1, H and L with n = 100 and O and Q with n = 1000. Their data points in Fig. 9 shows that flow mobility decreases as flow volume increases when n is equal to 1 and 100, whereas flow mobility increases as flow volume increases when n is equal to 1000. These mobility differentials are significant because they are the results of numerical models and are not affected by field or laboratory measurement errors. The distance along the slope between the centres of mass of the two prototypal volumes with n = 1000 is large enough to be clearly measurable in the field where it is ~15 m. The difference between the μ_A values of the two different volumes decreases from n = 1 to n = 100 and it switches sign somewhere between n = 100 and n = 1000 with a change from a low stress regime to a high stress regime whose flow volume effects are the opposite of one another.

This switch is illustrated by the values of the coefficient of determination R² that represents the proportion of the variation of μ_A that can be explained by a fitting curve (Devore 2000). In Fig 9a, R² decreases significantly as n increases across the switch for both the straight lines (where with n equal to 1, 100, and 1000, R² is 0.9812, 0.9955, and 0.952, respectively) and the second-order polynomials (where with n equal to 1, 100, and 1000, R² is 0.9974, 0.9877, and 0.9205, respectively). Conversely in Fig 9b, R² increases significantly as n increases across the switch for both the straight lines (where with n equal to 1, 100, and 1000, R² is 0.8881, 0.9457, and 0.9935, respectively) and the second-order polynomials (where with n equal to 1, 100, and 1000, R² is 0.8889, 0.9485, and 0.9976, respectively). Values of R² > 0.99 indicate perfect fitting because they mean that virtually 100% of the variation of μ_A is explained by the curve. On the contrary, values of R² ≤ 0.952 occurs when the functional relationship is false because it does not predict the correct flow volume effect. Therefore, μ_A is a function of χ for n equal to 1 and 100 (Fig. 9a), whereas μ_A is a function of ψ for n equal to 1000 (Fig. 9b). In Fig. 9, the functional relationships that are false are shown in grey and those that are true are shown in blue, orange and red.

Figure 9 illustrates that the only quantity which (by being missing in χ or ψ) prevents all data points of each regime from collapsing on to one single curve is the stress level (represented by n that enters model g). This is so because: 1) all curves are virtually parallel, 2) the curves are distinguished only by different n values and 3) parallel curves distinguished only by different n are expected also with n > 1000. Thus, a functional relationship of μ_A with χ or ψ needs also (to explain the variation of μ_A in each regime) an independent scaling parameter for the stress level such as the Froude number Fr that contains g. Indeed, the very good fitting (R² = 0.98) of the straight line in Fig. 10 confirms that μ_A is also a function of Fr. Fig. 10 is the plot of mean μ_A versus mean Fr where these mean values are over the simulations with the same n. Figure 10 is able to reveal this good fitting because by averaging the same number of simulations with differences in the same variables, the data scatter that besets Fr is reduced. In Fig. 10, although the differences between the Fr values seem small, they correspond in the field to differences in flow speed (Table 4) and flow length (proportional to n) that are larger than any possible error of measurement. Concerning basal friction, since it has an obvious effect on flow mobility, the dimensionless parameters μ_Scs and μ_Rcs also need to be added to the functional relationships of μ_A.

Fig. 10

Mean reciprocal of mobility μ_A versus mean Froude number Fr for flows on a rough subsurface where each mean is over the values with the same n. The error bars are computed as error of the mean. Blue, orange, and red refer to a geometric scaling factor n equal to 1, 100, and 1000, respectively. A least squares straight line best fits the data points

All things considered, Figs. 9a and 10 demonstrate that on a rough subsurface at low stress level (here for n equal to 1 and 100) the following functional relationship is true:

$$ {\mu}_A={\mathcal{F}}_3\left(\frac{V^{1/3}\ \delta }{L\ w},\frac{u}{\sqrt{L\ g\ \cos \alpha }},{\mu}_{Scs},{\mu}_{Rcs}\right). $$

(20)

Moreover, Figs. 9b and 10 demonstrate that on a rough subsurface at high stress level (here for n equal to 1000) the following functional relationship is true:

$$ {\mu}_A={\mathcal{F}}_4\left(\frac{\delta^2}{V^{1/3}\ w},\frac{u}{\sqrt{L\ g\ \cos \alpha }},{\mu}_{Scs},{\mu}_{Rcs}\right). $$

(21)

Thus, flow mobility on a rough subsurface is affected by the stress level, but it is not governed by the Froude number alone. It is governed also by grain size δ, flow volume V, channel width w and basal friction (i.e., μ_Scs and μ_Rcs combined). These are the five quantities whose effects are examined below because they are those whose values can be directly assigned by the experimenter in the laboratory or the modeller in the numerical simulations as an initial condition, whereas flow length L, flow speed u and slope α cannot.

Grain size

On a rough subsurface at both low and high stress level, according to the linear relationships in Fig. 9, the finer the grain size, the more mobile the center of mass of the granular flow. The increase of mobility as grain size decreases was explained by the fact that the finer the grain size (all other quantities constant), the larger the number of clasts per unit of flow mass so that the agitation due to the interaction with the rough subsurface penetrates relatively less inside the flows and the smaller this agitation, the smaller the energy dissipated by the granular flow per unit of travel distance (Cagnoli and Romano 2010, 2012a, b; Cagnoli and Piersanti 2015, 2017, 2018). Clast agitation affects energy dissipation through frictional and collisional interactions and by diverting energy into directions different from the downslope one. A finer grain size flow is thus like a car whose engine consumes less fuel per unit distance. The difference between the low (Fig. 9a) and the high (Fig. 9b) stress level regimes is that, in the first case μ_A is proportional to the grain size (Eq. (20)), whereas in the second case it is proportional to the grain size squared (Eq. (21)). This contrasts with the linear relationship between agitation D and ψ, where D is directly proportional to the grain size squared at both low and high stress level (Fig. 11). The attenuation at low stress level of the increase of mobility due to a finer grain size is caused by a counteracting action such as that of the flow volume effect explained next.

Fig. 11

Clast agitation D versus parameter ψ for flows on a rough subsurface. Blue, orange, and red refer to a geometric scaling factor n equal to 1, 100, and 1000, respectively. Least squares straight lines best fit the data points with the same n

Flow volume

On a rough subsurface at low stress level (here for n equal to 1 and 100), according to the linear relationships in Fig. 9a that are true, the larger the flow volume (all other quantities constant), the less mobile the center of mass of the granular flows (Eq. (20)). This flow volume effect was explained by the fact that a deposit accretes backward when forming on a slope whose inclination changes since the flow front reaches the less steep part of the curved slope and stop before the rear (Cagnoli and Romano 2012a; Cagnoli and Piersanti 2015, 2017). In this case, the larger the volume, the larger the quantity of granular material that accumulates at the back and the more proximal becomes the final position of the centre of mass. This is a geometric effect that is able to counteract that of the decrease of clast agitation D in Fig. 11 (and related energy dissipation) as flow volume increases (Cagnoli and Romano 2012b; Cagnoli and Piersanti 2018).

On a rough subsurface at high stress level (here for n equal to 1000), according to the linear relationship in Fig. 9b that is true, the larger the flow volume (all other quantities constant), the more mobile the center of mass of the granular flows (Eq. (21)). In this regime, both reciprocal of mobility μ_A (Fig. 9b) and clast agitation D (Fig. 11) are a function of ψ, where flow volume is in the denominator. Thus, in this case, there is no geometric effect that is able to counteract that of the decrease of clast agitation D in Fig. 11 (and related energy dissipation) as flow volume increases.

Channel width

On a rough subsurface at both low and high stress level, according to the linear relationships in Fig. 9, the narrower the channel (all other quantities constant), the less mobile the center of mass of the granular flows (Eqs. (20) and (21)). Two explanations were provided (Cagnoli and Piersanti 2017). First, as a geometric effect at low stress level, since the deposit propagates backward, the narrower the channel, the longer this backward propagation. Second, in a narrower channel at both high and low stress level, the retarding effect of the sidewalls is expected to be larger. Indeed, Fig. 11 shows that D and w are inversely proportional so that the narrower the channel, the larger the clast agitation and the related energy dissipation per unit of flow mass. This is so since particle agitation is generated also in contact with the two sidewalls and the smaller their distance, the larger the proportion of more agitated clasts in the flow (Cagnoli and Piersanti 2018).

Stress level

On a rough subsurface, according to Fig. 9, the larger the stress level (i.e., the larger n), the larger the mobility of the centre of mass (i.e., the smaller μ_A). This phenomenon can again be explained in terms of particle agitation that dissipates energy, because clast agitation D becomes smaller as the stress level (i.e., factor n) becomes larger (Fig. 11). This stress level effect pertains to flow dynamics. Indeed, an increase of the geometric factor n causes an increase of the Froude number (Fig. 10).

Results: granular flow mobility on a smooth subsurface

Functional relationship

On a smooth subsurface, to explain the variation of the reciprocal of mobility μ_A, it is necessary to use a new scaling parameter. This is obtained when the first and the reciprocal of the third independent variables of Eq. (11) are multiplied together and raised to the 3rd power:

$$ \zeta =\frac{V}{w^3}. $$

(22)

In Fig. 12, the variation of μ_A of all fifteen data points is explained so thoroughly by a straight line (whose R² is 0.9984), that grain size and stress level (both missing in ζ) cannot have any effect on flow mobility over a smooth subsurface. Indeed in Fig. 12, μ_A is indistinguishable in flows with only different grain size or only different stress level (all other features the same).

Fig. 12

Reciprocal of flow mobility μ_A versus parameter ζ for flows on a smooth subsurface. All fifteen data points with different n value are plotted. A least squares straight line best fits all of them

The excellent fitting of the straight line in Fig. 12 demonstrates that on a smooth subsurface it is true that

$$ {\mu}_A={\mathcal{F}}_5\left(\frac{V}{w^3},{\mu}_{Scs},{\mu}_{Rcs}\right), $$

(23)

where basal friction (i.e., μ_Scs and μ_Rcs) is added because with an obvious effect on mobility that is larger on a smooth (Fig. 12) than on a rough subsurface (Fig. 9). Thus, μ_A on a smooth subsurface is governed only by flow volume V, channel width w and basal friction.

Flow volume and channel width

The linear relationship in Fig. 12 indicates that the larger the flow volume, the smaller the mobility of the granular flows, whereas this mobility increases as the channel becomes wider. This flow volume effect can again be explained by the backward accretion of the deposit and this channel width effect by the fact that the narrower the channel, the longer the backward propagation. Both effects are geometric in character.

Results: particle agitation

A comparison between Figs. 11 and 13 shows that particle agitation D is significantly smaller on a smooth subsurface than on a rough subsurface. This is so even if, on both rough and smooth subsurface: 1) parameter D is proportional to parameter ψ and 2) parameter D decreases as the stress level (i.e., n) increases.

Fig. 13

Clast agitation D versus parameter ψ for flows on a smooth subsurface. Blue, orange, and red refer to a geometric scaling factor n equal to 1, 100, and 1000, respectively. Least squares straight lines best fit the data points with the same n

Discussion

Natural and artificial granular flows

Small-scale granular flows with n = 1 are relevant for industrial applications (food technology, pharmaceutical production, construction engineering) whereas flows with larger n refers to geophysical flows in nature. Indeed, all flows with n > 1 examined here have maximum speeds (Table 4) as high as those of natural rock avalanches since both are well >5 m/s (Hungr et al. 2001).

When investigating a phenomenon, it is instructive to take into consideration the end members of a spectrum of possibilities even if here this approach generates large values of the apparent coefficient of friction μ_A (Fig. 9). A plethora of involved theories has been suggested to explain the high mobility of rock avalanches (as detailed for example by Hungr (2006)), but with no general agreement on their validity. My dimensional analysis more simply shows that flow mobility can increase in nature with respect to that in Fig. 9 by means of (besides a less dissipative subsurface) a further increase of the stress level due to scale n (plus a further increase of flow volume V at high stress level) and a further decrease of the grain size δ. The mobility of the center of mass also increases in wider channels. In addition, for geometric reasons, the flow front is always more mobile than the center of mass.

In terms of computational effort, a numerical simulation of a 1/n scaled-down granular flow where gravity is increased n times is equivalent to a corresponding simulation whose size and gravity are those in nature, because both have the same number of clasts (Table 1). But without a predetermined discriminating factor such as n, it is difficult to differentiate between the functional relationships existing in Fig. 9, whose data points also belong to parallel curves that are in too close proximity to be easily identified. Similarly, experimental and field measurements because of their unavoidable inaccuracy would be too scattered for the different functions to be clearly discernible.

Different flow regimes

The thirty numerical simulations analyzed here demonstrate that flow dynamics on a rough subsurface (Fig. 9) is so different from that on a smooth subsurface (Fig. 12) that they belong to different flow regimes. Moreover, because of the opposite effects that flow volume can have on flow mobility, flow dynamics on a rough subsurface is better split into two distinct regimes: one at low (Fig. 9a) and one at high (Fig. 9b) stress level. Hence, three granular flow regimes are identified: 1) a mobility regime on a rough subsurface at low stress level, 2) a mobility regime on a rough subsurface at high stress level, and 3) a mobility regime on a smooth subsurface that is unaffected by the stress level. Thus, geophysical flows on a sufficiently smooth subsurface (Fig. 12) do not need to be modeled in a centrifuge with larger g (at least when n ≤ 1000). The geophysical granular flows for which the stress level must be considered when assessing their mobility are those on a relatively rough subsurface, where the switch between low and high stress level regimes occurs somewhere between n = 100 and n = 1000 (Fig. 9). The functional relationships (linear or second-order polynomials) of flow mobility in the three regimes (Figs. 9, 10, and 12) have coefficients that are expected to depend on the physical properties of clasts and terrain. In these relationships (Eqs. (20), (21), and (23)), the effects on flow mobility of basal friction, stress level, grain size, flow volume, and channel width are commented as follows.

Basal friction

Basal friction influences flow mobility in all regimes and the transition between regimes on rough and smooth subsurface is clearly a function of its value. Here this transition occurs somewhere between the two examined endmembers whose basal friction is represented by μ_Scs and μ_Rcs combined (Table 3). As expected, the larger the basal friction, the smaller the mobility (compare Figs. 9 and 12).

Flow dynamics is dominated by clast agitation on a rough subsurface (Fig. 9), whereas it is dominated by the sliding en masse of all clasts together on a smooth subsurface (Fig. 12). Indeed, the main difference between these flow dynamics (that results in different energy dissipations per unit of travel distance) is that clast agitation D is much higher on a rough (Fig. 11) than on a smooth subsurface (Fig. 13). Granular agitation is so small on a smooth subsurface that clast speed does not change significantly along the flow depth (Fig. 7). This friction regime on a smooth subsurface however is not quasi-static (Jan and Shen 1997) because the speed of its flows can reach tens of meters per second (Table 4). Also, the collision regime on a rough subsurface is not Bagnoldian (Jan and Shen 1997) because Bagnold’s flows consist of neutrally buoyant spheres constrained not only laterally but also vertically inside a container (whereas clasts in geophysical flows are affected by gravity and their ensemble can dilate vertically since they travel in open channels) plus Hunt et al. (2002) showed that Bagnold’s results appear to be dictated by the design of his experimental facility.

Stress level and grain size

It is precisely because of the different importance of clast agitation in the two regimes that stress level (i.e., n) and grain size govern granular flow mobility on a rough subsurface (Fig. 9), whereas they do not do so on a smooth subsurface (Fig. 12). Indeed, both stress level and grain size concur to determine the amount of clast agitation where this agitation is generated (i.e., on a rough subsurface, Fig. 11), but they cannot do so when clast agitation is to a large extent suppressed (i.e., on a smooth subsurface, Fig. 13). On a rough subsurface, flow mobility increases as the stress level increases (Fig. 9) because an increase of the stress level causes a decrease of clast agitation and related energy dissipation (Fig. 11).

On a rough subsurface, the decrease of grain size causes an increase of flow mobility. This is an effect confirmed by other studies (Cagnoli and Romano 2010; Mollon et al. 2015; Cagnoli and Piersanti 2017; Lai et al. 2017). There is also field evidence that in rock avalanches grain size decreases as travel distance increases (Davies and McSaveney 2009; Zhang et al. 2016). Importantly, here the new data set shows that two functional relationships exist on a rough subsurface: 1) a relationship true at low stress level where flow mobility is inversely proportional to the grain size (Eq. (20)) and 2) a relationship true at high stress level where flow mobility is inversely proportional to the grain size squared (Eq. (21)). The attenuation of the grain size effect at small stress level is caused by a counteracting effect such as the backward accretion of the deposit that reduces the increase of mobility as grain size decreases. An attenuation mechanism must exist at low stress level since particle agitation that dissipates energy is proportional to grain size squared at both high and low stress level (Fig. 11). Thus, it is only on a rough subsurface at high stress level that both flow mobility (Fig. 9b) and particle agitation (Fig. 11) are a function of parameter ψ, where grain size squared occurs in the numerator. The proportionality between granular temperature (i.e., particle agitation) and the square of grain size descends also from the kinetic theory of granular flows (Jenkins and Savage 1983; Armanini 2013).

Flow volume

Flow volume has a geometric consequence on flow mobility that is analogous on both the rough subsurface at low stress level (Fig. 9a) and the smooth subsurface (Fig. 12). In both cases, since the deposit accretes backward, the larger the flow volume the larger the backward shift of the final location of the center of mass. This geometric effect is able to counteract that due to the influence that flow volume has on clasts agitation (Figs. 11 and 13) and related energy dissipation. A mobility decrease of the center of mass as flow volume increases was observed also in the experiments by Okura et al. (2000). But it remains to be ascertained whether the sign of a mobility change of a geometric effect depends also on the slope shape that here is constant. Importantly, on a rough subsurface at low stress level, the presence of flow length L in the denominator of parameter χ (Eq. (13)), where an increase of L increases flow mobility (Fig. 9a), can be explained considering that the more proximal sections of a flow exert a downward force on the more distal ones. Indeed, on a curved slope that is gradually steeper toward the top, the longer the flow, the larger the difference between the slope-parallel component of g acting on the most proximal and most distal sections of the flow so that the more proximal sections push forward the more distal ones with a greater force.

It is on the rough subsurface at high stress level that flow volume has an effect on flow mobility that accords with its effect on clast agitation and related energy dissipation. In this case, both flow mobility (Fig. 9b) and particle agitation (Fig. 11) are a function of ψ, where flow volume is in the denominator. This flow volume effect (where flow mobility increases as flow volume increases) agrees with the famous relationship observed in the field between the Heim’s coefficient and the volume of particularly large rock avalanches (Heim 1932; Scheidegger 1973; Mitchell et al. 2020). Here too it occurs only with the larger prototypes (n = 1000) and it is expected also with n > 1000. Thus, small-scale laboratory flows with n = 1 do not replicate all features of large-scale flows in nature (Davies and McSaveney 1999). But, in contrast to μ_A, the Heim’s coefficient acquires exceedingly small values since it is the ratio of the vertical fall to the horizontal distance from the crest of the scarp to the deposit most distal reach that can be very distal as result of the long longitudinal spreading of large flows (Davies 1982). Since the planimetric area inundated by a deposit is proportional to a power of its volume (Griswold and Iverson 2008), a very long spreading is expected in relatively narrow valleys filled with very large deposits. For example, the Canadian rock avalanches examined by Mitchell et al. (2020) range in volume from 0.1 to 500 million m³. Although here the prototypes of the flows with n = 1000 range in volume from ~4000 to ~14500 m³, relatively small flows occur in nature as well. For example, dry granular flows with volumes smaller than 10000 m³ destroyed roads in China in 2008 (Jiang and Towhata 2013) and gravity-induced pyroclastic flows with volumes smaller than 45000 m³ are documented in Stromboli, Italy (Salvatici et al. 2016).

It is important to understand that quantities such as flow volume and stress level are not the same in terms of physical meaning as far as flow mobility is concerned. Indeed, by changing the value of volume V in Eqs. (20) and (21), the position of the granular flow in Fig. 9 changes only along one of the curves because V in the granular scaling parameters is there to express the number of clasts in the flow as per Eq. (14). For a granular flow to change curve in Fig. 9, it is the value of the scale n that needs to change and by doing so also the stress level in the granular flow changes. A change of the number of particles alone does not change the curve where the flow is plotted because flows with only different numbers of particles are not geometrically similar since flow thickness and flow length change at different rates when flow volume changes. In particular, since gravity acts downward, flow thickness does not increase as significantly as the flow length does when flow volume increases (see for example graph 10 in Lo (2000)) and a relatively small increase of flow depth is not able to significantly increase the stress level within the flow.

Channel width

Channel width has a geometric effect on flow mobility, but it also influences clast agitation. Mobility decreases as the channel narrows because of a geometric consequence of the deposit backward accretion on both a rough subsurface at low stress level and a smooth subsurface (Figs. 9a and 12). But since clast agitation and channel width are inversely proportional on both rough and smooth subsurface at all examined stress level (Figs. 11 and 13), clasts agitation per unit of flow mass and its related energy dissipation increase as the channel narrows.

Conclusions

Three new granular flow regimes are identified: 1) a mobility regime on a rough subsurface at low stress level, 2) a mobility regime on a rough subsurface at high stress level, and 3) a mobility regime on a smooth subsurface that is unaffected by the stress level. An important novel result of this paper is to reveal for each regime its functional relationship of flow mobility with key quantities such as stress level, flow volume, grain size, channel width, and basal friction (Eqs. (20), (21), and (23)). These relationships are linear when the flow proper comprises most of the travelling granular mass.

The regime on a sufficiently smooth subsurface is characterized by flows that slide en masse and whose mobility is not affected by the stress level (Eq. (23)). Thus, sliding geophysical flows in nature can be modeled in the laboratory with no need to increase the acceleration of gravity in a centrifuge.

The geophysical granular flows whose mobility is affected by the stress level are those on a relatively rough subsurface (Eqs. (20) and (21)) where clast agitation determines their dynamics. Indeed, on a rough subsurface, flow mobility increases as the stress level increases. Another very important novel result is that, on a rough subsurface, as the stress level increases, the effect that an increase of flow volume has on flow mobility switches sign from causing a decrease of mobility at low stress level (Eq. (20)) to causing an increase of mobility at high stress level (Eq. (21)). The latter functional relationship is the first equation that accounts for the famous Heim’s mobility increase with the increase of the volume of large rock avalanches. This increase was detected so far only in the field and for this reason it was considered inexplicable without resorting to extraordinary mechanisms.