Introduction

Heavy rainfall always occurs more often because of global warming and climate changes, causing the triggering of natural phenomena, such as floods and landslides (Willems et al. 2012; IPCC 2021: Climate Change 2021). In some regions, the frequency of rainfall-induced shallow landslides has been predicted to increase up to 300%, based on the Representative Concentration Pathway RCP 8.5 climate change scenario (Jakob and Owen 2021). Shallow landslides can cause extensive damage when interacting with the anthropized environment and the elements at risk (people, infrastructure, buildings); meanwhile, the restoration costs are not always negligible. Landslide risk assessment is therefore essential for the identification of risk areas, and it is a preliminary step to design mitigation measures and solutions for landscape adaptations to climate changes, aimed at reducing any future damage (Fell et al. 2008; Corominas et al. 2014).

Risk assessment is achieved by quantitative risk analysis (QRA), which is a consolidated method suitable to assign priority to mitigation actions (Corominas et al. 2014; Peng et al. 2015; Lentini et al. 2019). QRA requires extensive information on the factors defining the risk itself: hazard, vulnerability, and exposure (Varnes 1984). Hazard defines the probability that a landslide of a given intensity (magnitude) will occur in a certain location (susceptibility) within a specific period (frequency) (Brardinoni and Church 2004; Remondo et al. 2005; van Westen et al. 2006; Guthrie et al. 2008; Fan et al. 2017; Zhang et al. 2020). Vulnerability is defined as the degree of damage/loss, depending on the landslide intensity and the state of the element at risk (Lee and Jones 2004; Hollenstein 2005; Liu 2006; Papathoma-Köhle et al. 2015; Zhou et al. 2022). Exposure is defined as “People, property, systems, or other elements present in hazard zones that are thereby subject to potential losses” by the United Nations Office for Disaster Risk Reduction (UNDRR) (Santangelo et al. 2021) and it measures the importance of the element at risk in terms of costs, sometimes included in the vulnerability evaluation (Abdulwahid and Pradhan 2017).

Examples of QRA are related to small areas (Huang et al. 2013; Abdulwahid and Pradhan 2017) and only a few attempts to extend it to large areas have been done (Peng et al. 2015; Caleca et al. 2022). This is due to the specificity of data on vulnerability and exposure, which are often unavailable even for small municipalities, for instance, the resistance of the elements at risk (Li et al. 2010), presence of alternative roads in the transport network (Sim et al. 2022), and economic values of buildings, forest, or crops that can be damaged by landslides (unit construction costs), in addition, the number of people (Pellicani et al. 2014), economic impact of landslides on the road network, in terms of restoration costs of damaged roads and neighbouring damaged public buildings (Donnini et al. 2017), and costs of any mitigation measures (Galve et al. 2016). In most cases, the accuracy of risk assessment relies on the hazard evaluation and vulnerability and exposure are considered through simplified indices.

Hazard assessment reflects the main phases of landslide phenomena, i.e. failure (susceptibility) and post-failure (propagation), as well as evaluations on frequency occurrence. Due to the complexity of methods for propagation analyses (Brardinoni and Church 2004; Guthrie et al. 2008; Fan et al. 2017; Zhang et al. 2020) and the typical lack of inventories for temporal and frequency predictions (Ghosh et al. 2012; Pellicani et al. 2014; Jaedicke et al. 2014), it is commonly reduced to a susceptibility estimation.

Models for susceptibility assessment can be classified into “black-box” and physically based (PBM), which differ in how they relate the phenomenon triggering to the causative factors (responsible for the phenomenon occurrence): the first through knowledge-driven (Turrini and Visintainer 1998; Guzzetti et al. 1999; Mandaglio et al. 2016) or data-driven procedures, the latter based on empirical-statistical relationships (Lee and Pradhan 2007; Abella and van Westen 2008; Felicisimo et al. 2012; Castelli and Lentini 2013; Li et al. 2017; Reichenbach et al. 2018); the second adopts physics-derived formulations. Recently, there is an increasing spread of machine learning (ML) approaches, which depend on artificial intelligence (AI): thanks to the database of historical landslides, a mathematical model is “learned” to relate maps of causative factors to susceptibility levels (Marjanović et al. 2011; Dou et al. 2020; Chen and Li 2020; Ng et al. 2021; Abbaszadeh Shahri and Maghsoudi Moud 2021; Azarafza et al. 2021a). AI-based methods have some limitations: the derived mathematical formulations are strongly site-specific; moreover, they do not allow to predict the temporal susceptibility in most cases. Another delicate aspect is that reliable models are obtained from overlay procedures and weighting of causative factors which must be carefully selected, to have a sufficient number and be cleaned from possible outliers (Abbaszadeh Shahri et al. 2019). Since risk assessment is already simplified by neglecting very specific evaluations on vulnerability and exposure, as discussed above, analyses based on knowledge- or data-driven methods (also ML) appear to provide further simplifications, making methodologies site-specific and time-independent. All these inconveniences are not encountered when using PBM, whose formulations are derived from observation of the experimental reality.

PBM analyse slope stability, mostly through limit equilibrium methods (LEM) which allow to evaluate a safety factor from the fundamentals of statics. The most important existing LEM are discussed in recent overviews, classified according to the analysis dimension or type of failure surface (Azarafza et al. 2021b; Mafi et al. 2021; Firincioglu and Ercanoglu 2021). For rainfall-induced shallow landslides, the subject of our paper, literature provides examples of PBM based on one-dimensional LEM, relying on the infinite slope scheme, and mainly differing in the hydrological model adopted to consider rainfall infiltration and its effect on soil strength (Montgomery and Dietrich 1994; Pack et al. 1998; Montrasio 2000; Baum et al. 2002; Montrasio and Valentino 2007; Montrasio et al. 2011; Rossi et al. 2013; Medina et al. 2021). The simplest ones introduce only a water head representing the infiltrated rainfall, while the whole infiltration process is studied through the complex ones (Baum et al. 2002). A compromise of the modelling complexity needs to be accepted, in favour of applicability at large territories (from municipality to regional scale), demanding reasonable time and space.

A good choice may be SLIP (shallow landslides instability prediction), i.e. a LEM-based PBM which includes the effect of rainfall on the unsaturated soil strength and allows to analyse even the temporal variation of stability (Montrasio 2000). The model, applied to different territories, showed excellent predictive skills (Montrasio and Valentino 2007, 2008; Montrasio et al. 2009, 2011, 2012, 2014, 2015, 2016; Schilirò et al. 2016; Montrasio and Schilirò 2018). Its simplicity makes it suitable for application even on a large scale and the results can be handled for susceptibility and risk assessment.

This paper presents a methodology for risk assessment based on susceptibility evaluated through SLIP, and so specific for rainfall-induced shallow landslides. A simplified procedure is introduced to weigh SLIP results considering vulnerability and exposure, and more in general the probability of the element at risk to be reached by the landslides. Thanks to the SLIP accuracy in the susceptibility evaluation, the methodology can be referred to as semi-quantitative. The methodology is applied to the municipality of Gioiosa Marea (Sicily, south Italy), an area prone to landslides, often consisting in shallow movements induced by rainfall. Due to an underdeveloped road network in this area, the traffic disruptions related to landslides caused inconveniences for months or even years. Two events, occurred in November 2015 and March 2016 which interfered with infrastructures, are considered as target for the model calibration.

The “SLIP model for risk assessment” section briefly shows the SLIP model and presents the new methodology for risk assessment, based on the SLIP results which are weighed according to distanced from elements at risk. The “The case study of Gioiosa Marea (Sicily)” section provides a description of the study area, the calibration of the SLIP model parameters through the prediction of the past target events, the identification of risk areas in the whole municipality, as well as a specific risk analysis limited to the area of a tunnel located in the state road SS113, whose disruption could cause several social and economic damage. Finally, a discussion of the new methodology is reported in the “Results” section. SLIP is demonstrated to provide accurate susceptibility assessment; moreover, the assessed risk through the proposed methodology represents a relevant starting point to plan mitigation measures.

SLIP model for risk assessment

Brief description of the SLIP model

SLIP (shallow landslide instability prediction) is a simplified PBM, formulated by Montrasio (2000) that predicts the triggering of rainfall-induced shallow landslides. This type of landslides involves the topsoil, i.e. a shallow soil layer which is highly permeable because of the macropores due to the anthropic and/or wildlife activities. They are commonly considered translational sliding movements occurring on planar failure surfaces (Hungr et al. 2014; Zieher et al. 2017a, b). For this reason, in SLIP, the “infinite slope” scheme is applied to a slice of the topsoil of thickness H and the safety factor FS is evaluated as:

$$FS=\frac{tan\varphi'}{tan\beta}+\frac{c'_{tot}}{\gamma H\;cos\;\beta\;\mathit{sin}\;\beta}$$
(1)

The safety factor depends therefore on morphological parameters (slope angle β) and physical and mechanical soil parameters (unit weight \(\upgamma\), cohesion \(c{\mathit'}_{tot}\), and friction angle \(\varphi\mathit'\)). In its original formulation (Montrasio 2000), the term \(c{\mathit'}_{tot}\) included the effective cohesion \(c\mathit'\) (proper of overconsolidated cohesive soils) and the apparent cohesion of the soil \({c}_{\psi }\), due to partial saturation. Recently, Montrasio et al. (2023) have updated the SLIP formulation with the effects of vegetation on slope stability, expressed in mechanical terms with an extra cohesion \({c}_{r}\) (root cohesion), which model the root reinforcement. The relationship of soil total cohesion is:

$$c{\mathit'}_{tot}\mathit=c'+{\text{c}}_\psi\text{+}{\text{c}}_\text{r}$$
(2)

Partially saturated soil is characterised by apparent cohesion \({c}_{\psi }\) depending on the degree of saturation Sr (in a dry or full saturated soil \({c}_{\psi }\) is null). Montrasio (2000) provided an experimentally based relationship for the evaluation of cψ and simplified assumptions to consider the effects of the infiltrating rainfall on the soil strength:

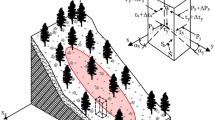
$${\text{c}}_{\psi }\text{=}{\text{A}}{\text{S}}_{\text{r}}{\text{ (1-}{\text{S}}_{\text{r}}\text{) }}^{\lambda }{\text{(1-m)}}^{\alpha }$$
(3)

A, λ, and α are modelling parameters, while m is the term which introduces the rainfall effects based on the following considerations. Rainwater of a single rainfall infiltrates the topsoil through preferential channels (macropores), determining a local full saturation of the shallow soil: this is schematised as randomly located “saturation bubbles” (Fig. 1a). Montrasio (2000) assumed to concentrate the bubbles in a layer of full saturated soil, which is a share of the total height under consideration; each rainfall height hj (occurred at t = tj) causes instantaneously a rate mj (Fig. 1b).

Fig. 1
figure 1

Assumptions and simplifications of the SLIP model. a Saturation bubbles due to rainfall infiltration through the topsoil macropores. b Fully saturated soil layer simplifying the saturation bubbles. c Temporal variation of rainfall effects on soil’s saturation

Full size image

The latter changes then with time according to the soil permeability and other natural phenomena, such as evapotranspiration. By summing the effects of all the rainfall of a specific time window (total number of events ω), the thickness of the saturated layer is m*H, being m expressed as:

$$\textit{m}\text{(t)= }\frac{\text{1}-\beta^\ast}{\textit{nH}\text{(1-}{\textit{S}}_\textit{r}\text{)}}\sum\nolimits_{\mathrm j=1}^{\mathrm\omega}h_j\text{e}^{-{\textit{k}}_\textit{t}\text{(t-}{\text{t}}_\text{j}\text{)}}$$
(4)

n is the soil porosity and kt the slope drainage. \({\beta }^{*}\) is the rainfall interception, due to the vegetation canopy; this coefficient has been introduced by Montrasio et al. (2023) to consider the vegetation effects even from a hydraulic point of view. Figure 1c shows an example with three recorded rainfall data (h1, h3, and h4), the negative exponential temporal variation of the effect of each recording on soil’s saturation (m1(t), m3(t), and m4(t)), and their sum m(t) representing the rainfall total effect; in the figure, the term \(\frac{\text{1}-\beta^\ast}{\textit{nH}\text{(1-}{\text{S}}_\text{r}\text{)}}\) of Eq. (4) is abbreviated with Γ.

Temporal-spatial stability evaluation through MATLAB algorithm X-SLIP

The formulation described in the “Brief description of the SLIP model” section, related to a volume element, may be applied spatially to a territory, if the morphological, soil, and vegetation parameters, as well as the rainfall information, are available. Recently, Gatto and Montrasio (2023) have presented a new open-source algorithm, named X-SLIP, fully implemented in MATLAB environment. X-SLIP allows us to distribute the SLIP model on a large scale and derive maps of safety factor (FS). The algorithm is based on a grid approach: the area is discretised by pixels, making up the grid, and parameters required by SLIP are assigned to each pixel through specific procedures. The reference grid is obtained from the digital terrain model (DTM), which represents one of the most important raw data for X-SLIP. Analyses can be limited to certain territorial limits (municipality, province, or region) of specific shapes, indicated by a proper shapefile, defining the study area. Among the DTM pixels, only the ones belonging to the intersection with the study area are therefore considered. Different approaches are adopted to assign the parameters.

The morphological parameter (slope angle β) is evaluated by applying the gradientm function to the elevation matrix extracted from DTM and the georeferencing vector (in geographic coordinate system). The soil parameters are assigned based on the lithological map, after associating a parameter set for each lithological type. According to the polygon including the query pixel (identified through the inpoly function), parameters are given to the reference grid. The same approach is used for the vegetation parameters, with the use of the vegetation map or the information on vegetation included in the land use map. For the evaluation of the apparent cohesion of the soil, influenced by rainfall, it is important to determine the rainfall spatial distribution. Specifically, a natural neighbour algorithm is used to interpolate rainfall data recorded by rain gauges, treated as irregular grid points.

To cover a certain area, the use of some DTM tiles could be necessary, not always made up by the same number of pixels. Data import and storage are facilitated with variables of type “cell”, which allow to save even matrices of different dimensions. Each column contains information related to a DTM. Cell arrays are used to store morphological, soil, and vegetation parameters. Rain data are stored in matrix cell (data related to a specific rainfall event in the rows, while in the column data are referred to each DTM).

The stability analysis performed spatially on large scale provides maps of FS, one representative of the stability at a given time. These results are used first for susceptibility assessment, then for risk assessment.

Susceptibility and risk assessment

Spatial results of FS may be grouped into FS-classes, each related to a different occurrence “probability”: unstable pixels have FS < 1, pixels with FS between 1 and 2 are likely to become unstable, pixels with FS ranging between 2 and 5 are unlikely to fail, while pixels with FS more than 5 are almost surely stable. These classes may provide a sort of susceptibility measure, quantified through a specific weight WFS, decreasing with steps of 25% (from 100 to 25%) according to the FS value. The values of WFS adopted for each FS group are summarised in Table 1.

Table 1 Groups of FS and assigned weights WFS
Full size table

Such a susceptibility assessment is advantageous because it may disregard the proper choice of number and type of input data, as well as the index-overlay analysis required to derive weights in AI-based procedures (Abbaszadeh Shahri et al. 2019). The limit in adopting a PBM-based method to assess susceptibility is the determination of model parameters to evaluate FS. For soil parameters, this can be achieved through experimental tests or back-analyses procedures, the latter making the method data-driven (i.e. depending on the landslide inventory). According to the extension of the area to be studied, experimental tests may be expensive because of the numerosity of specimens needed or field tests to be performed (Bicocchi et al. 2019). Meanwhile, back-analyses cannot be used to derive all the model parameters due to the indeterminacy of the mathematical problem. A simplified but effective approach introduced by Montrasio et al. (2011) consisted in adopting mean values, different according to the soil type, experimentally derived for similar soils. Some of these values can be adjusted for the spatial prediction, while the slope drainage coefficient kt is the only back-analysed parameter for a reliable temporal prediction. Soil parameters are therefore differentiated according to the geology maps, but further spatial variability within each geology class should be also considered (Zieher et al. 2017a, b).

Risk depends on the likelihood of triggered phenomena to provoke damages. The first condition to be verified is that triggered shallow landslides should reach and interfere with elements at risk: this depends on runout distance and propagation mode. The caused damage thus differs according to the detached volume and the propagation velocity, as well as the element vulnerability. Our methodology considers the possibility to have any damage, disregarding its quantification, with different distance-dependent weights representing the interference probability (they are a sort of exposure measure). After the identification of elements at risk from the map of land uses, the Euclidean distance from the selected elements is evaluated for each DTM pixel through the pdist function. The exposure weight Wexp is assigned according to the distance from the closest element (minimum distance). Data related to past events reported that runout distances of shallow landslides hardly exceed 120 m (Huang and Tang 2014; Fan et al. 2020); weights are therefore differentiated in the range 0–120 m, while for distances greater than 120 m, a precautionary low value is assumed. Even in this case, weights range from 25 to 100% probability (Table 2).

Table 2 Distance ranges and exposure weights Wexp
Full size table

Risk level is finally computed for each pixel as:

$$R=W_{FS}\cdot W_{exp}\;$$
(5)

In a sense, this methodology allows to weigh susceptibility according to interference probability, so that high-susceptible areas very far from any element at risk can be assumed as low-risk areas. Such a simplified approach allows to derive a spatial distribution of risk areas. However, propagation analyses should be performed to demonstrate that the triggered landslides may travel the assumed minimum distances.

The case study of Gioiosa Marea (Sicily)

General description and target events

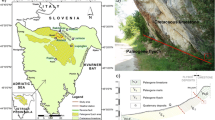
Gioiosa Marea is an Italian municipality in the province of Messina (Sicilian Region, Italy) which extends for 26 km2. Its location is shown in Fig. 2a. In this territory, many landslides occur as documented by the Italian Inventory of landslides provided by ISPRA (Higher Institute for Environmental Protection and Research) (Fig. 2b). Seventy-two of the surveyed landslides are slides. The hydrogeological risk of the area is reported in the regional hydrogeological plan (Fig. 2c). Four risk classes were defined: low-risk R1, medium-risk R2, high-risk R3, and very high-risk R4; the extensions of each class with respect of the total area are respectively 0.11%, 0.04%, 0.20%, and 0.23%. From 2009 to now, many landslides have been triggered by rainfall, and when occurred near infrastructures, they caused inconvenience for years. An in-depth risk assessment is therefore needed.

Fig. 2
figure 2

The study area (Gioiosa Marea municipality) belonging to Messina Province in Sicily (Italy). a Framework of the study area. b Susceptibility distribution according to the Italian Landslide Inventory. c Risk distribution, according to the hydrogeological plan

Full size image

SLIP is calibrated by selecting rainfall-induced shallow landslides recently occurred: one on 1st November 2015, close to the sports field (Fig. 3a), and two on 14th March 2016 at two different locations, the state road SS113 (Fig. 3b) and on a private road which allows to access to a hotel (Fig. 3c). The latter phenomenon isolated some German tourists staying in the hotel for hours. Table 3 summarises the raw data adopted for X-SLIP application, together with sources, data type, and original resolution.

Fig. 3
figure 3

Position and photographic reportage of target events occurred on 1st November 2015 close to the sports field (a) and 14th March 2016, on the state road SS 113 (b), and on a hotel private road (c)

Full size image
Table 3 Raw data adopted for the X-SLIP simulations (Sicilian Region Database is available at https://www.sitr.regione.sicilia.it)
Full size table

Morphology

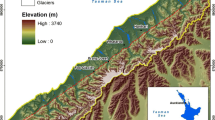
The reference grid where the SLIP model is applied is obtained by intersecting the digital terrain model (DTM) of the area with the shapefile of the geographic municipality limits. DTM from the ATA Lidar flight 2007–2008 is used, and properly chosen dated prior to the analysed events to represent the morphology before the studied landslides. Four DTM tiles are needed to cover the whole municipality; the resolution of each DTM (originally 2 m) is reduced to 20 m to improve the computational efficiency and coherently with the extent of phenomena under examination. With such a resolution, each DTM matrix has dimensions 270 × 366 (almost 100 k pixels). By intersection with the municipality limits, only 58 k pixels are considered. The analysis is confined to areas potentially unstable, excluding pixels belonging to inhabited centres, factories, facilities, or rocks. This information is provided by the regional Land Cover shapefile. Figure 4 shows the distribution of areas excluded by the analysis because assumed “unconditionally stable”.

Fig. 4
figure 4

Areas excluded from the SLIP analysis

Full size image

A map of elevations is illustrated in Fig. 5a, reporting altitudes ranging from 0 to 1013 m above sea level. As described in the “Temporal-spatial stability evaluation through MATLAB algorithm X-SLIP” section, morphology parameters (slope and aspect angle) can be evaluated through the MATLAB built-in gradientm function. Figure 5b illustrates the map of slopes, which are mostly included between 20 and 50 degrees.

Fig. 5
figure 5

Morphology parameters computed from the DTM. a Elevation. b Slope

Full size image

Lithology

Since stability analyses are not limited to a single slope but extended to large areas, non-uniform soil parameters are adopted, being more representative of reality. The lithology-based approach suggested by Montrasio and Valentino (2008) is adopted, considering shallow soil layers deriving from the rock erosion (De Luiz Rosito Listo and Vieira 2012). Figure 6 shows the lithological map of the study area, provided in digital format (shapefile) by the Basin Authority of the Hydrographic District of Sicily (Gagliano et al. 2019). The area is made up mainly of Metamorphic Rocks and Marl and Marly limestone, with several zones covered by debris (Fig. 6a). Soil parameters required by the SLIP model are assigned following the simplified approach proposed by Montrasio and Valentino (2008): lithological units having similar mechanical properties are grouped into soil categories and mean parameters are given to each soil type. In our studies, we group the lithological units into four types (Fig. 6b). Table 4 summarises the association soil category—lithological units, together with the adopted state, mechanical, and drainage parameters for the soil, deriving from previous laboratory characterisation or back analyses (Montrasio et al. 2011, 2014).

Fig. 6
figure 6

Geographic data required to assign the soil parameters. a Lithological map. b Distribution of the adopted soil categories, whose corresponding parameters are reported in Table 4

Full size image
Table 4 Lithology-soil category association
Full size table

Vegetation

Figure 3 shows that the study area was covered by vegetation, at least where phenomena occurred. Vegetation is therefore considered in our stability analyses. Differently from the AI-based models, which include vegetation through normalised difference vegetation index (NDVI) (Abbaszadeh Shahri et al. 2019; Chen and Li 2020), we introduce it by means of specific physical parameters. Many studies have discussed how vegetation contributes to slope stability mainly through roots and foliage; a review of the most relevant studies on this topic has been presented by Montrasio and Gatto (2020). As described in the “Brief description of the SLIP model” section, Montrasio et al. (2023) have recently introduced these contributions into the formulation of the SLIP model, as root cohesion cr and canopy rainfall interception β* (see Eqs. (2) and (4)). Both cr and β* are plant-specific and agronomic literature is often oriented to their determination. Figure 7 shows the distribution of the most widespread vegetation types in the study area (each over 1.5%); this data is included in the map of land use. Note that the area is mainly covered by olive trees and oaks. Parameters coherent to the vegetation types are assigned according to values reported by previous studies (Xiao et al. 2000; Gómez et al. 2001; Mattia et al. 2005; Van Beek et al. 2005; Herbst et al. 2007; Bischetti et al. 2009; García Estringana et al. 2014; Wang et al. 2019; Lin et al. 2020; Dong et al. 2020); Table 5 summarised the vegetation species and the corresponding adopted parameters, according to the literature references and considering mean values in the soil shallow layer involved in the stability analysis (H = 1.2 m). Note that for oaks, literature does not provide the root cohesion related to the specific types of the area (Quercus ilex and Quercus suber); mean value of cr obtained for Quercus pubescens and Quercus cerris by Burylo et al. (2011) and Cazzuffi et al. (2014) has been adopted. In areas not covered by vegetation, null cr is set, while the infiltrating rainfall is reduced according to the slope (the term 1- β* of Eq. (4) is evaluated as the cosine of the slope angle, following the suggestions of Lei et al. 2020).

Fig. 7
figure 7

Distribution of vegetation types, according to the land use map

Full size image
Table 5 Vegetation types and adopted parameters
Full size table

Rainfall

Montrasio et al. (2011) demonstrated that the apparent cohesion of the soil, which depends on saturation, can be suitably represented in the stability analyses by the degree of saturation related to 30 days before the event (Sr0), together with rainfall occurred from 30 days before until the event under analysis. Both information are put together in Eq. (4). To analyse the stability at the target events (1st November 2015 and 14th March 2016), rains recorded from 30th September to 1st November 2015 and from 11th February to 14th March 2016 are considered respectively. Data is provided by the Agro-Meteorological Information Service of Sicily: hourly recordings at the gauging stations of Patti, Militello Rosmarino, Mistretta, San Fratello, Torregrotta, and Antillo are considered. Figure 8 shows the location of the stations, while Fig. 9a, b show the time history of rainfall recorded in Patti (the closest station to the study area) 30 days before the two target events. Since rainfall data is unregularly spaced, the scatteredInterpolant function is employed to distribute each hourly recording to pixels of the reference grid.

Fig. 8
figure 8

Location of rain gauge stations of the Agro-Meteorological Information Service of Sicily

Full size image
Fig. 9
figure 9

Rainfall trends in the 30 days preceding the two target events. a 30th September–1st November 2015 and b 11th February–14th March 2016

Full size image

Montrasio et al. (2011) also discussed the importance of the value of Sr0: the suggested seasonal values reported in Table 6 have been adopted also in this study. Specifically, values of 0.75 and 0.8 are used respectively for the target event of 1st November 2015 and 14th March 2016.

Table 6 Values of the initial degree of saturation, suggested by Montrasio et al. (2011)
Full size table

Results

Spatial–temporal calibration

The calibration of the SLIP model to the study area is performed punctually, by considering the safety factor evaluated in the DTM pixels which are the closest to the detected landslides under examination. The morphology parameters and the lithological and vegetation types (with the corresponding parameters) of these pixels are reported in Table 7. With these values, landslides occurred on 1st November 2015 (Fig. 10a) and 14th March 2016 (Fig. 10b, c) are well-captured by the SLIP model.

Table 7 Summary of morphological, lithological, and vegetation parameters for the target events
Full size table
Fig. 10
figure 10

Trend of the safety factor FS obtained from the application of the SLIP model in the DTM pixel closest to the location of occurred target events

Full size image

For the temporal information of the events, the news reported in the local online newspapers is considered because official data on the survey of these phenomena is missing. While the 2015 event appears to have occurred in the afternoon, the 2016 events happened in the morning. This is perfectly aligned with the analyses performed by SLIP, which detect the instability on 1st November 2015 at 6 pm and on 14th March 2016 at 5 am.

Validation

Maps of FS related to the whole municipality of Gioiosa Marea and evaluated at the trigger time of the two target events (1st November 2015 6 pm and 14th March 2016 5 am) are shown respectively in Fig. 11a, b. Results are grouped into classes, according to the ranges in Table 1. A colour scale is defined as a function of the FS values: red for FS ranging between 0 and 1, orange between 1 and 2, yellow between 2 and 5, light green if FS is major than 5.

Fig. 11
figure 11

Results of SLIP elaboration at time. a 1st November 2015 06 pm. b 14th March 2016 05 am

Full size image

A worse result can be noticed at the first event (Fig. 11a); this reflects the higher rainfall of the period, shown in Fig. 9a. We assume that it is representative for the susceptibility assessment of the area. This result is validated by comparison with susceptible areas detected by the Italian Inventory of Landslides. Polygons of detected phenomena are shown in Fig. 12a, together with pixels coloured according to the analysis results. It is noticed that most of the included pixels have FS less than 2; the percentage of pixels belonging to each of FS classes is reported in Fig. 12b. Specifically, 23.4% are pixels unstable and 63.5% are likely to be unstable, according to our classification. This agrees with our assumption to associate larger susceptibility indices (from 0.75 to 1) with this range (Table 1).

Fig. 12
figure 12

Comparison of susceptible areas in SLIP and the Italian Inventory of landslides. a Representation of analysis pixels and polygons of surveyed landslides. b Percentage of pixels of each FS class inside the inventory polygons

Full size image

For further support of our results, the receiver operating characteristic (ROC) (Metz 1978) curve is computed to evaluate the quality of X-SLIP to predict susceptibility. Generally, a ROC curve defines the prediction quality of a mathematical model through the so-called true positive rate TPR and true negative rate TNR. For deterministic analyses of slope stability, pairs of TNR-TPR are defined by choosing FS thresholds (or cut-off values FScut-off) which allows to distinguish between stable (negative) from unstable (positive) pixels. The positive and negative pixels can be furthermore classified as true (true positive TP and true negative TN) or false (false positive FP and false negative FN), by comparison with known landslide and non-landslide positions. TPR and TNR are then computed as:

$$\textit{TPR=}\frac{\textit{TP}}{\textit{TP+FN}}$$
(6a)
$$\textit{TNR=}\frac{\textit{TN}}{\textit{TN+FP}}$$
(6b)

Values of FScut-off range between 0 and 50. For each FScut-off, positive pixels (FS < FScut-off) are defined as TP if included in polygons of surveyed landslides (Fig. 12); otherwise, they are classified as FP. Meanwhile, negative pixels are classified according to areas external to the IFFI polygons. The area under curve (AUC), i.e. the integral of TPR-TNR curve, quantifies the prediction quality. According to Hosmer and Lemeshow (2000), the prediction is as follows: acceptable for AUC = 0.7–0.8, excellent for AUC = 0.8–0.9, outstanding for AUC > 0.9. We have calculated AUC by applying MATLAB trapz function to the ROC curve.

Figure 13 shows the resulting ROC curve. The red point represents the result for threshold FS = 1; here, TPR is 21.9%, while TNR is 99.3%. The correspondence is evident between this TPR and the value shown in Fig. 12b for FS = 0–1. As regards the AUC, it is 86%, meaning that the prediction quality is excellent.

Fig. 13
figure 13

ROC curve evaluated from the analysis results and the polygons representing slides in the Italian Inventory of Landslides

Full size image

Risk assessment on municipality scale

The simplified methodology described in the “Susceptibility and risk assessment” section is now applied to provide a spatial risk evaluation. First, susceptibility weights WFS are associated with the FS values, according to Table 1. For each DTM pixel, distances from the closest element at risk are then evaluated; the selected elements are mining areas, recreational and sports areas, ruin areas and landfills, villages and rural buildings, cemeteries, industrial settlements, railways lines, roads, and residential areas. The previous are all the locations where the occurrence of a shallow landslide could cause damage on people, properties, and roads. Distances are grouped according to Table 2 (Fig. 14) and exposure weights Wexp are assigned.

Fig. 14
figure 14

Distribution of distances of each reference grid pixel from the closest element at risk

Full size image

Finally, risk is computed through Eq. (5). Figure 15 illustrates how risk is distributed in the study area, with reference to the two events of 1st November 2015 6 pm (Fig. 15a) and 14th March 2016 5 am (Fig. 15b). In both figures, the pie chart shows low (0–0.25), medium (0.25–0.5), and high-risk level (0.5–1) respectively with blue, yellow, and red colour.

Fig. 15
figure 15

Spatial distribution of the weighed risk in the study area during the target events. a 1st November 2015 06 pm. b 14th March 2016 5 am

Full size image

It is noted that the risk is greater in the first event. This is coherent with the susceptibility observed in Fig. 11. Around the selected “elements at risk”, the risk is high in both events. For its validation, this result is compared with risk areas remarked in the regional hydrogeological plan (polygons in Fig. 2c). Due to the small size of such areas, we omit a comparison map (as done in Fig. 12a for susceptibility) but we match the risk level computed from our methodology, grouped in four classes according to the risk value: RL1 = 0–0.25; RL2 = 0.25–0.5; RL3 = 0.5–0.75; RL4 = 0.75–1. As discussed in the “Brief description of the SLIP model” section, the regional plan indicates four risk classes (R), referred to as R1 (low risk), R2 (medium risk), R3 (high risk), and R4 (very high risk). Figure 16 shows what is the risk level of pixels included in each R class.

Fig. 16
figure 16

Percentage of pixels in each risk class provided by the hydrogeological plan (R1 low risk, R2 medium risk, R3 high risk, R4 very high risk), having different risk levels evaluated through the proposed SLIP-based methodology (RL1 = 0–0.25, RL2 = 0.25–0.5, RL3 = 0.5–0.75, RL4 = 0.75–1)

Full size image

R1 polygons contain more than 95% of pixels where the computed risk is very low, ranging from 0 to 0.25 (RL1); the remaining percentage is related to pixels where the risk is 0.25 to 0.5 (RL2). All pixels inside R2 polygons have RL1 risk level (0–0.25). In R3 and R4 polygons, besides RL1 and RL2 pixels, there is also a small percentage of high-risk pixels, with risk ranging from 0.5 to 0.75 (RL3). No pixels with a very high-risk level (0.75 to 1) are counted in any R- polygon. Two aspects must be observed. In the regional plan, the risk is evaluated by associating different weights depending on the type of element at risk: higher risk is given to inhabited centres or important public buildings (e.g. schools, churches) than in scattered houses. This differentiation is neglected in our analyses, which consider only an interference probability. Moreover, since there is no specification on the landslide type, some high-risk areas of the regional plan could be related to phenomena other than shallow landslides, not well-captured by the SLIP model. In general, our results are precautionary because there are a larger number of high-risk areas but more calibrations events are needed to improve the reliability of the proposed methodology.

Risk assessment of a tunnel of the state road SS113 in the municipality of Gioiosa Marea

The simplified methodology has been applied to an area of limited extension, in order to perform a detailed risk analysis and detect the exact position around the element at risk where it should be better to design the mitigation measures. The tunnel located in the state road SS 113 is selected for this analysis: its closure and disruption because of structural damage caused by impacting landslides could bring important economic and social damage, because it is the only state road connecting the neighbouring municipalities. Figure 17 shows an aerial photo of the tunnel under discussion; debris deposits can be noted on the tunnel roof, meaning that past landslides have already interfered with the infrastructure. However, there is no information on when these phenomena occurred.

Fig. 17
figure 17

Aerial photo of the SS113 tunnel in the municipality of Gioiosa Marea

Full size image

The risk analysis is performed by using a new reference grid, derived from a recent digital terrain model; the smaller area extension allows to consider a better resolution (2 × 2 m), keeping the analysis computational efficiency. Slopes and elevations evaluated from the new DTM are more representative of the actual morphology, modified by the landslide events occurred in last decade. Soil and vegetation parameters are the same of the model calibration, discussed in previous sections. Even rainfall is the same as previous analyses because it relates to past events where critical conditions are reached. Results of a parametric analysis are shown, obtained by selecting the limit Sr0 values from Table 6 (Sr0 equal to 0.6 and 0.8), and considering also Sr0 = 0.9, representative of a particularly rainy period.

It is observed that susceptibility is greater with the 2015 rainy events (Fig. 18) because the recorded rainfall is more intense than in March 2016 (Fig. 19). Accordingly, risk results in being greater in Fig. 18. Stability is more precarious for Sr0 tending to 1, because even modest rainfall can bring the soil to full saturation, meaning loss of apparent cohesion. Three high-risk areas (yellow colour) are clearly visible on all the maps, two of which are close to the tunnel under examination. This result is important to orient mitigation measures. With reference to the highest risk (Fig. 18c), the extension of risk areas is computed after grouping the results into four classes: very low risk (0–0.25), low risk (0.25–0.50), medium risk (0.5–0.70), and high risk (0.75–1). Since very low risk is related to areas almost surely stable and/or where triggered shallow landslides are unlikely to cause damage, the very low class is excluded from this evaluation. Percentages of each area are shown in Fig. 20. It can be observed that the risk is medium in about 40% of the vulnerable area, while it is high only in approximately the 5%. This result should encourage public administrations to design measure for the mitigation of risk in such high-risk areas.

Fig. 18
figure 18

Results of susceptibility and risk analyses performed with the rainfall of 30th September–1st November 2015 and (a) Sr0 = 0.6; (b) Sr0 = 0.8; and (c) Sr0 = 0.9

Full size image
Fig. 19
figure 19

Results of susceptibility and risk analyses performed with the rainfall of 13th February–14th March 2016 and (a) Sr0 = 0.6; (b) Sr0 = 0.8; and (c) Sr0 = 0.9

Full size image
Fig. 20
figure 20

Extension of areas with low-, medium-, and high-risk levels

Full size image

Discussion

SLIP is one of the existing PBM for the occurrence prediction of rainfall-induced shallow landslides. After a proper selection of some soil parameters, predictions are performed not only spatially but also temporally. This is a relevant advantage if compared with AI-based methods (Ali et al. 2021; Chen and Chen 2021; Ng et al. 2021). However, compared to other PBM such as TRIGRS or HIRESSS, the SLIP modelling simplifies some aspects, e.g. the infiltration process, or neglects others, e.g. the different soil behaviour between imbibition and drying (Baum et al. 2010; Montrasio et al. 2011; Rossi et al. 2013). Nevertheless, SLIP simplicity, together with its physical parameters which are easily evaluated, makes it suitable for the prediction of shallow landslides over large areas (Montrasio et al. 2014).

Results have shown that it may also assess susceptibility; pixels with FS ranging between 0 and 2 cover almost all the detected areas in susceptibility maps of historical databases. There is quite a large number of pixels related to high susceptibility; this may be related to the spatial assignment of soil parameters which is recognised as responsible with uncertainties (Jiang et al. 2022). Although the authors have differentiated such parameters according to a geology-based procedure, a further differentiation should be introduced for pixels even within the same geology class (Depina et al. 2020; Liao and Ji 2021). This would represent the reality and might improve the accuracy of susceptibility assessment. The accuracy prediction has been quantified through the ROC curve. Threshold values of FS varying from 0 to 50 have been selected. Each positive pixel (FS < FScut-off) is classified as positive or negative based on its belonging to the polygons of historical datasets. Although the adopted approach is simplified, the prediction computed is excellent and comparable with the one computed from site-specific data-driven ML methods (Abbaszadeh Shahri et al. 2019; Azarafza et al. 2021a).

A procedure is introduced to assess risk through indices representing the probability of trigger and interference with element at risk in the anthropized environment; the index-based approach is common for simplified risk assessment (Jaedicke et al. 2014; Peng et al. 2015; Lentini et al. 2019). The methodology, defined as semi-quantitative as it is based on a PBM model, has provided the identification of different risk levels in the study area. Due to its simplifications, the procedure can be considered as a preliminary tool that needs further refinements. It can be improved by validating the adopted indices Wexp representing interferences, through analyses of real distances that triggered landslides can travel, also based on morphology (post-failure analyses). Considerations already included in QRA can also be included, for instance, indices for economic value of properties, damage suffered, and restoration costs (Corominas et al. 2014). The authors are aware that increasing the complexity of the procedure would reduce the scale of applicability, but a compromise could be reached. In addition to the methodology refinement, future application will consider also the implementation of specific engineering measures to increase the stability of risk areas, e.g. through the adoption of ad hoc naturalistic solutions.

To encourage the application of the proposed methodology, its reliability needs to be further supported. Here, a limited validation has been presented because of poor detail of available data in the regional hydro-geological plan. Risk areas shown in the regional hydro-geological plan have a very small extension. Moreover, no specification on the related landslide type is provided. Where risk appears to be overestimated by our procedure, the risk of regional databases could be related to deeper landslide movement, different from the shallow ones considered through SLIP. Further analyses will focus on extended calibration in areas where the available databases including past events are larger and the information more detailed.

Conclusion

This study has shown the risk assessment performed through a physically based model (PBM), whose parameters may be easily derived. By PBM, the triggering of rainfall-induced shallow landslides may be predicted even temporally after a proper calibration. PBM-based susceptibility assessment can be achieved through the cluster of safety factors provided by the model, validated by databases of historical landslides (if available). The weighing of susceptibility results according to distances from elements at risk of the anthropized environment is a simplified but useful approach to identify areas where mitigation measures should be implemented at a very detailed scale. Further analyses must be conducted on propagation analyses, to investigate distances and velocity of travelling triggered landslides and to estimate provoked damage.