A framework for temporal and spatial rockfall early warning using micro-seismic monitoring

Abstract

Rockfall risk is usually characterized by a high frequency of occurrence, difficulty in prediction (given high velocity, lack of noticeable forerunners, abrupt collapse, and complex mechanism), and a relatively high potential vulnerability, especially against people and communication routes. Considering that larger rockfalls and rockslides are generally anticipated by an increased occurrence of events, in this study, a framework based on microseismic monitoring is introduced for a temporal and spatial rockfall early warning. This approach is realized through the detection, classification, and localization of all the rockfalls recorded during a 6-month-long microseismic monitoring performed in a limestone quarry in central Italy. Then, in order to provide a temporal warning, an observable quantity of accumulated energy, associated to the rockfall rolling and bouncing and function of the number and volume of events in a certain time window, has been defined. This concept is based on the material failure method developed by Fukuzono-Voight. As soon as the first predicted time of failure and relative warning time are declared, all the rockfalls occurred in a previous time window can be located in a topographic map to find the rockfall susceptible area and thus to complement the warning with spatial information. This methodology has been successfully validated in an ex post analysis performed in the aforementioned quarry, where a large rockfall was forecasted with a lead time of 3 min. This framework provides a novel way for rockfall spatiotemporal early warning, and it could be helpful for activating traffic lights and closing mountain roads or other transportation lines using the knowledge of the time and location of a failure. Since this approach is not based on the detection of the triggering events (like for early warnings based on rainfall thresholds), it can be used also for earthquake-induced failures.

Introduction

The economic and population development, increasing access and construction in mountainous areas, bring people and infrastructures to a higher exposure to slope hazards (Dammeier et al. 2011). Reliable slope hazard prediction on brittle rock is still a hard task, due to the lack of noticeable forerunners preceding abrupt failures as well as the complex mechanisms not fully understood yet (Carlà et al. 2017). Nowadays, there are several ways to perform landslide early warning. One way is to monitor displacements (Iovine et al. 2006; Blikra 2012; Kristensen et al. 2013; Lombardi et al. 2017; Intrieri et al. 2019), which is a direct indicator of slope instability. Although future developments in the exploitation of interferometric satellites might lead to a bloom of regional scale early warning systems (Raspini et al. 2018), displacements are normally exploited at slope scale. The lack of long-term prefailure deformations compatible with the acquisition frequency of even the most modern displacement monitoring systems makes this kind of measurement not suitable for rockfalls. Furthermore, the typically small dimensions of detaching blocks are often beyond the spatial resolution capabilities of imaging instruments or even single point networks, such as extensometer and inclinometer, which would require to be installed on every single block that is potentially unstable. Another, more common, approach to perform landslide early warning is based on rainfall monitoring, which is mostly used for regional-scale systems. Through defining a duration-intensity threshold of rainfall, and considering the susceptible map and catalogs of landslides, a spatiotemporal forecasting of the failure can be achieved (Rosi et al. 2012; Segoni et al. 2015, 2018; Salvatici et al. 2018). As the relation between rockfall occurrences and rainfall is not very clear, since many other factors are involved, such as rock temperature, rock moisture, wind intensity, and air temperature (Matsuoka 2019), this kind of monitoring is not optimal for a rockfall early warning system.

Considering that rockfalls generate ground vibrations during crack nucleation, crack propagation, and eventually the collapse and the subsequent movement along the slope and to the ground, a geophones network can be used to record them. Important information on the characteristics of the seismic source could be derived from a three-components seismogram (e.g., the event type, energy, duration, location, back-azimuth, and developing process) that not only occurred on the surface but also in the subsurface (Deparis et al. 2008; Vilajosana et al. 2008; Helmstetter and Garambois 2010; Hibert et al. 2011; Coviello et al. 2019). Therefore, an early warning system can be set up by monitoring the seismic signals emitted by surface and subsurface slope dynamics (Amitrano et al. 2005; Lacroix and Helmstetter 2011; Lenti et al. 2012; Walter and Joswig 2012; Van Herwijnen et al. 2016; Schöpa et al. 2018). Seismic monitoring turns out to be a valid means for rockfall study and provides a complementary solution to displacement-based early warning systems since it can also give information about surface processes.

The microseismic monitoring can be applied:

• In a short time inversion analysis for an individual landslide: the seismograms and spectrograms are consistent with the dynamic process (location, trajectory, volume, energy, and mechanism of evolution) of the landslide, e.g., different waveform peaks recorded in the seismogram correspond to the collapsed material impacting and rebounding on the ground; the onset time, duration, and speed of a landslide can also be interpreted from the seismogram and the spectrogram (Berrocal et al. 1978; Kanamori and Given 1982; Ekström and Stark 2013; Yamada et al. 2013; Burtin et al. 2014; Hibert et al. 2014, 2015, 2017a; Del Gaudio et al. 2018; Guinau et al. 2019; Li et al. 2019; Zhang et al. 2019);

• In long-term unmanned monitoring: microseismic monitoring could help to develop an early warning system by observing the parameters’ variation in both waveform and seismic events detected; in addition, by estimating the hypocenters of the seismic sources, it could help to identify the most dangerous zones in the monitored area and analyze the correlation with tectonics, climate, etc., to design effective mitigation measures accordingly (Satriano et al. 2011; Kao et al. 2012; Coviello et al. 2015; Manconi et al. 2016; Hibert et al. 2017b, c; Arosio et al. 2018; Schöpa et al. 2018).

Based on the observation that the number of rockfalls increases before a larger rockslide (Suwa 1991; Suwa et al. 1991; Amitrano et al. 2005; Huggel et al. 2005; Rosser et al. 2007; Szwedzicki 2003; Hibert et al. 2017b) and the fundamental law for failure material proposed by Voight (1988) after Fukuzono (1985), here, we propose a framework for a rockfall spatiotemporal early warning using microseismic monitoring. This framework is complemented with two algorithms (Feng et al. 2020a, b) for rockfall detection and classification and for seismic event localization. In the next sections, the algorithms used will be shortly described, but since they can be replaced in the proposed methodology with any suitable alternative, they are not the focus of this paper.

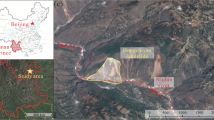
Study area

The test site, Torgiovannetto, is a former quarry located in the northward facing slope of Mount Subasio, 2 km NE from the city of Assisi (Perugia, Umbria Region, Central Italy; Fig. 1). An 182,000-m³ unstable rock mass is located in the top area of the quarry (Lotti et al. 2015, 2018; Antolini et al. 2016; Gracchi et al. 2017). It was first observed on May 2003, and it is suggested that the main predisposing factor of the instability was the quarrying activity (Intrieri et al. 2012). Now the extracting activities are stopped, and the potential collapse is dealt with by using mitigation measurements (Gigli et al. 2014). A risk is also related to rockfall, for which more detailed information can be found in Feng et al. (2019).

Fig. 1

Photographs of the back fracture of the landslide, of the lithology and of the studied slope, with indication of the boundaries of the unstable mass. The red star in the lower right corner marks the study area in Italy. Modified from Intrieri et al. (2012)

A microseismic network equipped with four stations acquiring data in a continuous mode from December 2012 to July 2013 was installed (Lotti et al. 2015). Each station consists of a S45 triaxial seismometer with a natural frequency of 4.5 Hz cable-connected to a 24-bit digitizer from SARA Electronic Instrument Company. The sampling frequency (F_s) was set to 200 Hz. Data were recorded in miniSEED format (“Data-only” volume) and subsequently converted in SAC format for processing operations.

In this study, a 6-month-long (1st January–30th June 2013) microseismic dataset (which includes the recording of earthquakes, tremors, and rockfalls), and a 3D terrestrial laser scan were used to map landslide susceptible areas.

Methodology

The general framework proposed in this study is based on the observation that the occurrence of rockfall and small landslides increases over time prior to a larger failure (Huggel et al. 2005; Rosser et al. 2007; Szwedzicki 2003). Suwa (1991) and Suwa et al. (1991) proposed that the magnitude of the ultimate failure is proportional to the level of precursory behavior, and this suggests a dependence on the scale of the precursory events (Rosser et al. 2007). This phenomenon has been validated also for volcanic eruptions (that obey to the same precollapse behaviors as landslides, as demonstrated by Voight 1988) by the long-period observation of Hibert et al. (2017b). These authors continuously monitored, from 2007 to 2011, the Piton de la Fournaise volcano using seismically triggered video cameras, and analyzed the temporal evolution of the daily number of rockfalls. They found that the most active period, in terms of both the number of rockfalls occurrences and the volumes of material displaced, was the one immediately preceding the collapse of the Dolomieu crater. In this paper, instead of using the occurrence frequency of rockfall as a proxy for predicting a larger failure, the accumulated energy (A_e) recorded by a seismic network when the rock hits the ground (which is a function of the volume) was employed.

The whole framework is illustrated in Fig. 2 and is described in detail in the next section. To perform this framework, the first step is transforming seismic data recorded by the instruments into a data format that can be processed, in order to detect and classify the different seismic events by a rockfall detection and classification model. The second step is extracting all the seismic signals and features of the rockfalls, such as onset time and duration; then, A_e and the accumulated energy increment (ΔA_e) in a time window are calculated, and, if ΔA_e exceeds a fixed threshold, 1/A_e is calculated, a time of failure is automatically extrapolated, and a warning time declared. In parallel, as soon as the time of failure is computed, all the rockfalls detected in a fixed time window before the triggering of the first alarm time are localized in a topographical map to find the susceptible area from where the events probably originated.

Fig. 2

The framework of the proposed spatiotemporal rockfall early warning

Temporal forecasting

Let us assume that a series of rockfalls (R₁, R₂, ⋯, R_M) is detected in a time period (t₀ − t). Instead of the real event source energy, a parameter represented by the sum of the relative seismic energy (E_s), measured in m²/s² and recorded through the seismic network, is adopted in this study, in order to reduce the chance of introducing calculation errors of the environmental influence and the effects caused by the energy loss through propagation attenuation, rock fragmentation, and heat generation (Amitrano et al. 2005; Dammeier et al. 2011). Therefore, the relative seismic energy of the rockfall series is E₁, E₂, ⋯, E_M, and the seismic signal time series of one rockfall recorded in component j and station k, is presented as x_kj1, x_kj2, ⋯, x_kjN.

There are four three-component geophones employed in this case, so the sum of the relative seismic energy (E_s) of one rockfall and the accumulated energy (A_e(t)) of the rockfall series from time t₀ to t, respectively, are:

$$ {E}_s=\overset{k=4}{\sum \limits_{k=1}}\ \overset{j=3}{\sum \limits_{j=1}}\ \overset{i=N}{\sum \limits_{i=1}}{x}_{kji}^2 $$

(1)

$$ {A}_{e(t)}=\overset{s=M(t)}{\sum \limits_{s=M\left({t}_0\right)}}{E}_s\kern0.5em $$

(2)

where i, j, k, and s are the number of seismic samples, components, seismic stations, and rockfalls, respectively. M(t) is the accumulated number of rockfalls at the time t in the rockfall series.

In order to trigger the calculation of the time of failure, a sliding time window is created, and the accumulated energy increment (ΔA_e(t)) in that sliding window at time t is continuously calculated according to Eq. 3. It is important to note that this parameter represents an empirical threshold (δ) below which the forecasting methods are not implemented because they would probably trigger false alarms. In the study area, the length of the sliding window was set equal to 1 h (the yellow area in Fig. 3) and stepped by 1 min, while the empirical threshold (δ) was set equal to 0.5 m²/s². Such value can be calibrated once that more data and experience on the specific site are gathered.

$$ \Delta {A}_{e(t)}=\overset{s=M(t)}{\sum \limits_{s=M\left(t-1h\right)}}{E}_s $$

(3)

Fig. 3

a An example of failure forecasting using experimental data relative to rockfalls occurred on 15th Jan 2013 at Torgiovannetto (“Temporal and spatial estimation” section). The red dashed line is the linear fit line of 1/A_e; b detail of how 1/A_e is approximated with a linear fit

The times when ΔA_e(t) exceeds a certain threshold (δ) (here called “alarm time”, t_a) are shown as red circles in Fig. 3. If ΔA_e is still over the threshold, the warning is maintained, indicating that the energy in the system calculated in the reference time window is still high.

Consistently with Voight (1988), who extended the application of the Fukuzono (1985) method to a set of different variables, including seismic quantities, in this framework a modified version of the classic Fukuzono-Voight method is proposed. The material failure law described by the Fukuzono-Voight method is presented in Eq. 4. As demonstrated by Voight, the seismic quantity (Ω) (such as the square root of cumulative energy released) is an observable quantity suitable for early warning, and A is a constant. Similarly, this method was also applied in the studies of Amitrano et al. (2005). Therefore, in this case, the accumulated energy (A_e) of rockfalls is adopted as $\dot{\Omega}$, and the forecasting is made through the linear fit of the inverse of A_e. The forecasting method used in this study is shown in Eq. 5. Generally, this observable quantity should represent Ω (and not $\dot{\Omega}$ as in our case), and the forecasting method of Fukuzono should use the inverse of $\dot{\Omega}$ against time (for example, if Ω is the displacement, the forecasting is made through the inverse velocity). In this case, since A_e is already characterized by very abrupt accelerations, extrapolating the 1/A_e line until it intercepts the time axis gives approximately the same results as using the inverse of the rate of A_e, but the rate of A_e generates a much noisier time series (Fig. 3).

$$ {\dot{\Omega}}^{-\alpha}\cdotp \ddot{\Omega}-A=0 $$

(4)

$$ {A_{e(t)}}^{-1}-A=0 $$

(5)

In practice, once the first t_a is declared, a linear fitting processing is initialized using A_e(t)⁻¹ (as in Eq. 6) from time t_a − 1 h to t_a in a sliding window to obtain the slope (d) of the linear fit. The function of the linear fit is shown in Eq. 7, and Eq. 8 shows how to calculate the supposed collapse time (t_c). To show the results more clearly, a normalized accumulated energy (N_e) was adopted by adding 0.99 to the denominator, since A_e of rockfalls measured in m²/s² is typically a very small number (in the order of 10⁻²–10⁻⁵). An example of this procedure employing real data gathered at Torgiovannetto is shown in Fig. 3.

$$ (d)=\mathrm{linear}\ \mathrm{fit}\ \left(\frac{1}{A_{e\left(t-1h\right)}},\frac{1}{A_{e\left(t-1h+1\right)}},\cdots, \frac{1}{A_{e(t)}}\kern0.5em \right) $$

(6)

$$ d\left({t}_c-{t}_a\right)+\frac{1}{A_{e\left({t}_a\right)}+0.99}=0 $$

(7)

$$ {t}_c={t}_a-\frac{1}{d\left({A}_{e\left({t}_a\right)}+0.99\right)} $$

(8)

where t_c − t_a is the lead time and the warning period is t_c2 − t_a, where we define t_c2 as the last forecasted time of collapse calculated at the last alarm time t_a2. In our case, the linear fit is performed by the ployfit function in MATLAB.

Spatial estimation

As soon as t_a and t_c are calculated, all the rockfall events occurred before, within a fixed time window, can be localized on a topographic map and the susceptible area can be found consequently.

In this case, the method of seismic polarization (polarization bearing, P-B method) was adopted for rockfall localization. The method uses the polarization from a three-component sensor to calculate the source back azimuth through finding the correct P wave from event signal, which is commonly used in earthquake localization (Flinn 1965; Jurkevics 1988). Vilajosana et al. (2008) and Guinau et al. (2019) extended the technique to rockfall localization.

Starting from this point, the P-B method was optimized by means of an overdetermined matrix based on the geophone network. A confidence weight for each sensor was proposed according to the received signal quality and the reliability of the calculated back azimuths. Moreover, three marker parameters were compared with properly select frequency bands in seismic polarization: energy, rectilinearity, and special permanent frequency band. Finally, 30 of 96 frequency bands with the strongest energy are suggested to perform the P-B localization (P-B-30E). One example of P-B-30E localization from an in situ test consisting in manually released rockfall is shown in Fig. 4. For each rockfall, the coordinates of the starting and ending points were measured, and the trajectory was recorded using two video cameras. In this case, four impacts were picked and automatically localized in a topographic map (Fig. 4b). All the estimated positions are closely distributed along the real rockfall trajectory; the maximum error is impact #4 with 48.2 m, and the minimum error is impact #1 with 10.2 m. The details about this method are described in Feng et al. (2020b).

Fig. 4

a The pink line indicates the real block trajectory observed in situ. The cyan spots represent each block impact localized with the P-B-30E method, and the white triangles are seismic stations; b the original signal of the same artificial rockfall with highlighted in gray the impacts analyzed with the polarization method

Moreover, the early warning framework can also be implemented with alternative or complementary localization methods, such as those based on arrival times (Gracchi et al. 2017), beam-forming (Lacroix and Helmstetter 2011), and amplitude source location (Pérez-Guillén et al. 2019).

Rockfall detection and classification

All the data are examined with an ad hoc program, DEtection and STorage of ROckfall (DESTRO, Feng et al. 2020a), to detect and classify all the seismic events that occurred in the monitoring period. The events have been grouped in the following classes: earthquake (EQ), rockfall (RF), and tectonic tremor (TR); other microevents and ambient noise are also detected and classified but not considered in our analysis. The examples of signals and frequencies of these events are shown in Fig. 5. Moreover, the event spatial scales are also classified as: point event (P), very local event (vL), local event (L), slope scale event (S), and regional event (R), which means that a certain event has been detected and classified correctly by respectively one component, one seismic station (at least two components), two seismic stations, and more than two seismic stations. Given their very local nature, point events are generally considered as noise and therefore not considered in the elaborations.

Fig. 5

Original signal traces and time-frequency wavelet transforms of the four event types: EQ, TR, artificial RF, natural RF. The signals are recorded at component east–west of station TOR 1. Contrarily to artificial RFs (which were all generated by releasing blocks along the slope), natural RFs are events that were only detected through DESTRO but not observed. In this regard, note how a natural RF (g, h) has the same waveform (multispikes), duration, amplitude, and high frequencies as an artificial RF (e, f). The color bars in b, d, f, and h indicate the intensity (m/s) of signals

The validation of DESTRO has been done through a 2-day-long test where 90 rocks taken from the site were manually released along the slopes of Torgiovannetto quarry and recorded with two cameras and the seismic network. A detailed description of the experiment can be found in Feng et al. (2019). To describe the classification capability of DESTRO, we defined three variables, true positive (TP), false positive (FP), and false negative (FN), respectively, equal to the number of rockfall correctly classified as rockfall, the number of events misclassified as rockfall, and the number of rockfalls misclassified as noise. The recall (TP/(TP + FN)) of DESTRO in the experiment is 98% (88 rockfalls (TP) correctly detected out of the 90 released; other two rockfalls (FN) misclassified that being characterized by a particularly low signal). This value represents the confidence against false negative (i.e., the probability of missing an event is only 2%). On the other hand, 21 events (FP) in excess were detected, for a total of 109 signals classified as rockfalls. Even a manual check on these 21 extra signals made it impossible to distinguish them from the verified rockfalls. Probably these represent actual involuntary rockfalls caused by the passage of the experiment operators or even small natural rockfalls that went unnoticed. This means that the precision (TP/(TP + FP)) of DESTRO (i.e., of detecting real rockfalls from raw seismic data) is ≥ 81% (where 81% represents the assumption that the 21 extra events detected were all errors). The details of this program are described by Feng et al. (2020a).

Results

For slope stability evaluation and susceptibility mapping, data from a significant monitoring time period (1st–31st January 2013), when a higher number of rockfalls was detected, are chosen from the entire 6-month-long dataset.

Rockfall occurrence frequency

In this 1-month period, 1322 EQ, 585 TR, and 428 RF were detected. It should be pointed out that, among RF events, also very small-scale failures (i.e., small rolling stones but not microseismic cracks) are included. In detail, considering the scales of the events classified as RF, there are 416 very local events (vL), 8 local events (L), and 4 slope scale events (S). The detection and classification results are plotted in Fig. 6.

Fig. 6

a All the seismic events detection and classification results relative to the 1st–31st January 2013 time period; b distribution of RF in terms of spatial scale

To better understand the slope stability evolution and seismic events occurrence frequency, the distribution of detected seismic events (e.g., EQs and RFs) and their parameter A_e are plotted in Fig. 7 and Fig. 8, respectively. In Fig. 7, each event is represented with a point whose diameter is proportional to its seismic spectral maximum amplitude; a maximum dimension was set corresponding to a fixed threshold (0.025 m/s for RFs and 0.008 m/s for EQs, in this case). The different scales of RF are marked with different colors. In Fig. 8, the precipitation measured every 5 min and the accumulated precipitation in this month are also correlated with A_e.

Fig. 7

The accumulated number of RFs and EQs recorded in the 1st–31st January 2013 time period. The maximum amplitude of RFs and EQs in this period is 0.084 m/s (RF-vL) occurred at 11:38:40 on the 15th of January and 0.025 m/s (2.5 Magnitude, located approximately 25 km southeast from the study area) occurred at 15:53:52 on the 31st of January, respectively

Fig. 8

A_e times series relative to EQ and RF, correlated with precipitation (from 1st to 31st January 2013)

Figures 7 and 8 highlight that the curves of the accumulated number of RFs and A_e of RFs display a step-shaped behavior, with the steps indicating the sudden occurrence of many RFs in a short time. Usually, a series of vL events happened before L and S events. The onset of the maximum increment of rockfalls (hereafter named “rockfall paroxysm”) occurred at 9:20:00 of 15 January 2013 (Fig. 8), followed a heavy rainfall that ended at 19:10:00 of 14 January 2013 and consisting in 42.2 mm recorded in the previous 24 h (the maximum daily precipitation in this month). Moreover, no significant correlation between earthquakes and the occurrence of rockfall events was found in the entire dataset. Therefore, the rockfall paroxysm was probably induced by this rainfall event after a delay of 14 h. This suggests and confirms the observation by Lotti et al. (2018) that, at least at Torgiovannetto quarry, the main triggering factors are probably the environmental conditions, such as rainfall.

Temporal and spatial estimation

To simulate a warning relative to rockfall events, the inverse value of A_e versus time was calculated in the three most active days of rockfall, between 14th and 16th January 2013. In the presented case, the input parameter of the empirical threshold (δ) of ΔA_e in the 1-h sliding window is set equal to 0.5 m²/s², and all the time points (stepped in 1 min) that exceeded the threshold are marked as t_a (the red circles in Fig. 9). The rockfall occurrence frequency of these 3 days is plotted in Fig. 10.

Fig. 9

Rockfall early warning from 14th to 16th January 2013; the red point on x-axis is the predicted time of collapse (t_c)

Fig. 10

a Rockfall and earthquake occurrence frequency in 3 days, from 14th to 16th January 2013. The size of the diamonds and circles are proportional to the amplitude of the data, and a maximum dimension was set corresponding to a fixed threshold. The RF-L event marked in the dashed square is RF-L-IV, the longest and most powerful RF in this period. b Seismic signal of RF-L-IV

In these 3 days, 101 RF events were recorded, including five RF-L events (named from I to V in Table 1). Figure 10 clearly shows the rockfall paroxysm and displays event IV (highlighted in a dashed square) as the longest and most powerful. The signal of RF-L-IV recorded along the east–west component of station TOR 3 is shown in Fig. 10b. The seismic signal of RF-L-IV displays that plenty of minor RFs anticipated RF-L-IV, and many others were later induced and were recorded after the large event.

Table 1 Main seismic features of RF-L events occurred in 14th–16th Jan 2013. Since these events were detected by more than one station, for each event only the value relative to the station that recorded the maximum values are reported

Furthermore, in this case, based on the proposed early warning framework, a time of failure prediction was performed (Fig. 9). The first t_a and t_c are at 11:12:00 and 11:15:00 of the 15th January 2013, respectively; the last t_a and t_c are at 12:52:00 and 14:07:00 of the 15th January 2013, respectively. Therefore, the warning period is from 11:12:00 to 14:07:00 of the 15th January 2013. Within this warning time frame, two relatively large events (IV and V) occurred at 11:54:40 and 12:06:32 respectively that is with a 42-min and 54-min lead time available, respectively, counting from the first t_a.

As soon as the first t_a was declared, all the rockfalls detected in the sliding window (from t_a − 1 h to t_a) before the triggering of the first t_a have been localized with the improved P-B method. Moreover, in the presented case, all the rockfalls occurred in 3 days (5 RF-L and 96 RF-vL events) are localized on a topographic map to clearly show the susceptible area. Particularly, the five RF-Ls in Table 1 are marked as cyan points in Fig. 11a.

Fig. 11

a Localization result of the rockfalls detected in the 14th–16th January 2013 time period; the color bar indicates the altitude of the topographical map in meters; the cyan points indicate the five RF-Ls in Table 1 (RF-L-II and RF-L-III are overlapping). b Digital elevation model (DEM) of Torgiovannetto quarry with a resolution of 0.25 m; the blue triangles and yellow points are representing the seismic stations and video cameras, respectively. The position of station TOR 3 in b is not an absolute position, since the forest located on the upper hill prevented the light from the LiDAR to pass through the tree cover

The localization results in Fig. 11a show that most rockfalls originated from the area near station TOR 2, and some rockfalls came from the upper part of the former quarry. Consistently, as visible from the field surveys and the 3D light detection and ranging (LiDAR) scan (Fig. 12b), there is an area near station TOR 2 marked by the presence of a debris talus that confirms the susceptibility to rockfalls of this portion of the former quarry (where the rockfall paroxysm also occurred), while the upper part of the slope is an unstable rock wedge as introduced in the “Study area” section (Fig. 1). Once the area has been delimited, the early warning system can also by complemented with other countermeasures that would benefit from this spatial information, for example by forbidding access to the area (especially for active open-pit mines), turning on traffic lights, closing endangered streets, automatically activating, or intensifying monitoring in that area.

Fig. 12

Application of the rockfall forecasting methodology to the 1st January–30th June 2013 dataset of Torgiovannetto quarry. Missing data (such as between 1st and 4th of April) are due to battery depletion and replacement

Application to long-term monitoring

This methodology has also been applied to the long-term monitoring data from 1st January to 30th June 2013 (Fig. 12). A total of six warnings have been identified in these 6 months, the largest event being the one occurred in January and previously analyzed. However, there is an issue that should be pointed out when performing a long-term (at least a few months) real-time forecasting; in fact, since A_e is a cumulated value, its value is constantly increasing. When A_e is sufficiently high, variations of 1/A_e become very small and difficult to notice and the linear fit is more difficulty performed. Therefore, it is recommended that the value of A_e is reset to zero periodically depending on the state of activity of the slope (e.g., monthly). In this case the value of A_e is reset to zero on a monthly basis.

Conclusions

In this study, a framework for rockfall spatial and temporal early warning using a microseismic monitoring network was proposed. According to the original application of the classic Fukuzono-Voight failure forecast method, an observable quantity of accumulated energy (A_e) of rockfall is adopted for rockfall early warning. Whenever, over a sliding time window, the threshold ΔA_e is exceeded, an alarm time is declared. As confirmed by several studies in literature, an increased amount of rockfalls occurring in a short time often takes place before a larger detachment. This is represented as an abrupt step in a rockfall occurrence frequency curve against time, which is considered as a significant foretell sign of an imminent event. As soon as the first alarm time and consequent time of failure forecast are declared, all the rockfalls previously occurred within a fixed sliding time window are localized on a topographic map to simultaneously show the rockfall susceptible area.

The monitoring performed by microseismic networks is not only specific for slope surface phenomena but also for subsurface movement or cracking, which can significantly complement the drawbacks of image-based techniques such as satellite or ground-based InSAR. The relatively low cost of geophones potentially makes this rockfall early warning framework available to a larger of end-users.