Abstract
Predicting the time of failure is a topic of major concern in the field of geological risk management. Several approaches, based on the analysis of displacement monitoring data, have been proposed in recent years to deal with the issue. Among these, the inverse velocity method surely demonstrated its effectiveness in anticipating the time of collapse of rock slopes displaying accelerating trends of deformation rate. However, inferring suitable linear trend lines and deducing reliable failure predictions from inverse velocity plots are processes that may be hampered by the noise present in the measurements; data smoothing is therefore a very important phase of inverse velocity analyses. In this study, different filters are tested on velocity time series from four case studies of geomechanical failure in order to improve, in retrospect, the reliability of failure predictions: Specifically, three major landslides and the collapse of an historical city wall in Italy have been examined. The effects of noise on the interpretation of inverse velocity graphs are also assessed. General guidelines to conveniently perform data smoothing, in relation to the specific characteristics of the acceleration phase, are deduced. Finally, with the aim of improving the practical use of the method and supporting the definition of emergency response plans, some standard procedures to automatically setup failure alarm levels are proposed. The thresholds which separate the alarm levels would be established without needing a long period of neither reference historical data nor calibration on past failure events.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction and rationale for the study
Monitoring slopes potentially affected by instability is an activity of fundamental importance in the field of geomechanics. The interpretation of monitoring data is one of the main point of emphasis when trying to predict the time of geomechanical failure (T f ) or to assess the probability of an imminent rock slope collapse. Although a universal law which successfully accomplishes this goal for all the types of failure mechanisms and lithology does not exist, a good number of empirically derived methods and equations have been produced in the last decades. These are usually based on the recurrent observation before failure of certain relationships in the strain or displacement data, eventually linked to some intrinsic properties of the rock mass (Ventura et al. 2009). For example, Mufundirwa et al. (2010) evaluated T f as the slope of the t(du/dt)-du/dt curve, where du/dt is the displacement rate. Newcomen and Dick (2015) recently reported the “boundary conditions” for different failure mechanisms based on the correlation between the Rock Quality Mass (RMR) index and the observed highwall strain percentage. Federico et al. (2012) presented 38 case studies where velocity and acceleration were measured up to the slope collapse and found that in those instances, a common relationship between the logarithms of these two parameters is approximately satisfied just prior to failure. The most diffused approaches for T f prediction are those based on the accelerating creep theory, which has been repeatedly studied by different authors under slightly different perspectives (Saito 1969; Fukuzono 1985; Cruden and Masoumzadeh 1987; Crosta and Agliardi 2003) and from which derives that the time of slope failure can be predicted by extrapolating the trend towards zero of the inverse velocity-time plot. The most notorious description of the topic was made by Voight (1988, 1989), who extended the theory to the behaviour of materials in terminal stages of failure and proposed a relation between displacement rate and acceleration, influenced by two dimensionless parameters (A and α):
where Ω is the observed displacement and the dot refers to differentiation with respect to time (i.e. \( \overset{.}{\varOmega } \) represents velocity and \( \ddot{\varOmega} \) acceleration). He then provided an analytical solution for the forecast of T f that may be utilized especially when the inverse velocity plot approaches zero with a striking non-linear trend (perfect linearity is verified for α = 2), which would make more uncertain the use of the graphical solution. A and α are not necessarily constants and can change if different time increments are considered (Voight 1988; Crosta and Agliardi 2003); Voight (1988), in fact, supposed that the mechanisms of deformation and the conditions of loading are time invariant, an assumption which may very well not agree with reality. The accuracy of the analytical method is thus heavily influenced by the precision and frequency of the monitoring data (Voight 1989). Anyway, experience suggested (Fukuzono 1985; Voight 1988, 1989) that α is frequently nearly equal to 2, which made linear fitting of inverse velocity-time data a simple and much preferred tool to predict T f of slopes displaying strong acceleration phases. Petley et al. (2002) observed that the form of the inverse velocity plot is in fact predominantly linear for landslides where generation of a new shear surface and crack propagation are the dominant processes. Rose and Hungr (2007) also assessed that the inverse velocity plot often approaches linearity, especially during the final stages of failure; they also highlighted the need to seek consistent linear trends in the data and their changes. On this subject, Dick et al. (2014) suggested that the linear fitting procedure should only include data following the identification of Onset Of Acceleration (OOA) points; they also advised that additional fitting should be performed if a TU point (Trend Update, i.e. significant change in the acceleration trend) is detected.
Here, we are not attempting to give a review of the methods briefly described above. Certainly, the inverse velocity method (INV) has become a widely applied tool for failure prediction and the simplicity of use is its most powerful feature. Nevertheless, INV has some important limitations and its application requires experienced users. In particular, INV can be used only for slopes which fail in accordance to the accelerating creep theory, excluding, for example, cases of structural (Mufundirwa et al. 2010) or brittle (Rose and Hungr 2007) failure. Rose and Hungr (2007) provided a list of elements that can cause variation of displacement rates and thus hamper the performances of INV. The theoretical method was actually obtained from constant and controlled laboratory conditions, which are extremely unlikely to be satisfied on natural slopes and field conditions. Such limitations can include measurement errors and random instrumental noise, local slope movements, variation of the displacement rates driven by periodically changing factors (e.g. rainfall, groundwater, snowmelt, human activities, etc.), α significantly diverging from 2, and lack of clear OOA and TU points acceptably earlier than the occurrence of the failure event. Moreover, INV assumes that velocity at failure is infinite; this condition is obviously not verified and in fact velocity at failure varies for different rock types, volumes, mechanisms of failure and slope angles (Newcomen and Dick 2015). All these elements can decisively hamper the interpretation of the inverse velocity plot, thus affecting the accuracy and reliability of T f predictions and eventually discouraging users from using the method during the monitoring program.
For these reasons, it is of crucial importance to correctly process the velocity time series in order to remove as much as possible these disturbing effects, which here are generally termed “noise” for simplicity. Data filtering is indeed essential to help locating OOA and TU and to increase the degree of fitting of the linear regression line (growth of the coefficient of determination R 2 on the inverse velocity plot is usually a good indicator that an acceleration phase is occurring at the slope). In this paper, we make reference to two types of noise:
-
“Instrumental noise” (IN), caused by the accuracy of the monitoring instrument
-
“Natural noise” (NN) that includes all the other afore-mentioned factors causing possible divergence of the slope movements from the theoretical linear behaviour of the inverse velocity plot towards failure, as derived from Fukuzono’s and Voight’s models
To our knowledge, a detailed study devoted to testing different methods of data smoothing on a collection of case histories in order to thoroughly evaluate their performances, determine the effects of noise on the reliability of T f predictions and eventually obtain related guidelines for an optimal utilization of INV does not appear to have been yet produced to date. Dick et al. (2014) carried out a sensitivity analysis for an open pit mine slope failure case history, which showed that variation of T f for rates filtered over a short time period produced larger variations compared to rates filtered over a longer time period; however, the topic was not comprehensively examined as in the terms proposed here, and the main focus was directed towards the correct handling of spatially distributed ground-based radar data in monitoring open pit mine slopes. It should also be noted that different filters may generate different results depending on the shape of the rate acceleration curve and on the level of noise intensity. Therefore, testing should be performed on various types of case studies.
In the following section, we consider and execute data smoothing on velocity data from three landslide case histories and extend the analysis also to the collapse of a man-made structure of significant cultural heritage. Each of these events (all in Italy) displayed a noticeable accelerating trend towards failure. In particular, the episodes considered are:
-
1.
The Mount Beni rockslide (December 2002), characterized in general by low-medium values of slope velocities approaching the event (A ≈ 0.1; see later sections)
-
2.
The catastrophic Vajont landslide (October 1963), which was anticipated by extremely high movement rates (A ≈ 0.04; Voight 1988)
-
3.
A roto-translational slide on a volcanic debris talus (Stromboli Volcano, August 2014)
-
4.
The collapse of a section of medieval walls in the historical town of Volterra (March 2015)
Afterwards, we create two ideal velocity time series in agreement with Voight’s model and we introduce on them a set of randomly generated low- and high-intensity noise; consequently, we evaluate the resulting effects on the performances of INV and apply data smoothing. Finally, based on the experience acquired from both the real and simulated case studies, we propose some procedures for a practical analysis of the inverse velocity plots. These proposed guidelines address both the aspect of data handling and the issue of objectively establishing the alarm setup process for the emergency plan.
Methodology
As previously mentioned, the most powerful feature of INV is probably its simplicity. Under many aspects, it is of great advantage, in scenarios of risk assessment and management, if users can rely on quick and practical methods to evaluate the state of the monitored phenomenon and determine the possibility of an imminent calamitous event, a task which is not always possible to accomplish because of physical reasons and/or technological constraints. Accordingly, we tested two among the most common and easy-to-use smoothing algorithms, i.e. the moving average and the exponential smoothing. Specifically, we considered three forms of filter:
-
1.
A short-term simple moving average (SMA), where the smoothed velocity at time t is:
and n = 3
-
2.
A long-term simple moving average (LMA), where n = 7 in (2)
-
3.
An exponential smoothing function (ESF), where
and the smoothing factor is β = 0.5
If the time interval between adjacent measurements is constant, the type of moving average as in (2) is equivalent to the simple equation utilized by Dick et al. (2014)
where t i is the most recent time and d i is the most recent cumulative value of displacement.
Obviously, there is no formally correct rule or procedure in order to establish the order of the moving averages. In fact, this is highly dependent on data quality and temporal frequency. High acquisition rates, which in the field of slope monitoring are typical of advanced remote sensing techniques (e.g. ground-based radar, GPS and total stations), usually require to perform smoothing over a greater number of measurements. Conversely, low acquisition rates will hide much of the background noise, causing on the other hand the inability to trace short-term movements and delaying the identification of eventual trend changes; in such instance, smoothing should thus be performed over relatively less measurements, compared to data obtained at high acquisition rates. It follows that the number of data points within the time series does not necessarily influence in a significant way the accuracy of failure predictions. It is difficult to determine a priori the minimum number of acquisitions, in addition to those necessary to apply the aforementioned filters (i.e. n), that is required to confidently extrapolate linear trends in the inverse velocity plot. Undoubtedly, a populated data set will help determine more clearly how well the time series is fitted by the linear regression line, thus giving an important indication about the reliability of the prediction. In any case, modern monitoring technologies, which can measure displacements several times per day, ensure that the former is no longer a common issue and typically provide users with a more than acceptable amount of data points in the time series, unless the monitoring activities are initiated extremely close to the failure event.
With reference to the failure events presented in this paper, which were mostly characterized by low acquisition rates of the displacements (about 1 measurement/day or less), using values of n > 7 in (2) seemed to level out excessively the trend changes which were actually due to OOAs. Moreover, the wider the temporal window over which smoothing is performed, the higher the lag that is introduced to the time series; consequently, in scenarios of near-real time monitoring, it is probably not practical or convenient to use windows of smoothing which span over too long time periods. Considering the aforementioned acquisition rates of the reviewed data, a LMA with n = 7 seems a reasonable compromise. Regarding the SMA, Eq. (2) with n = 3 is typically considered the most basic filter for smoothing a hypothetical outlier in a linear time series; this moving average responds quickly to trend changes and is sensitive to slight fluctuations in the data. For this reason, it is selected for comparison to the “slower” and less sensitive LMA. This work is not focused on determining if a certain value of n is the most ideal for treating displacement measurements, since this will certainly vary from case to case depending on several factors such as acquisition rate, landslide velocity and background noise. As described more thoroughly in the following sections, both short- and long-term moving averages provide in fact benefits and downsides in time series analysis; the intent is therefore to evaluate how these properties influence the reliability of failure predictions and if short-term or long-term moving averages should be preferred for the application of the inverse velocity method.
Finally, in (3), a smoothing factor of 0.5 maintains a good balance between smoothing effect and sensitivity to trend changes in the data. An ESF has the form of a geometric progression and therefore, differently from a moving average, takes into account all past data, with recent observations having greater weight than older ones.
Results
Failure case histories
Mt. Beni rockslide
On 28 December 2002, a landslide occurred on the Eastern flank of Mt. Beni (Central Italy), on a slope which had been previously exploited by quarrying activity until the 1980s (Fig. 1a). The failure mechanism, involving jointed massive basalts overlying ophiolitic breccias, was characterized by a volume of about 500,000 m3 and has been classified as a rockslide/rock topple (Gigli et al. 2011). Several distometric bases were put in place along the perimetral crack (Fig. 1b) and recorded cumulative displacements since April 2002. Increasing rates, ranging from few millimetres up to few centimetres per day, were detected by most of the devices starting from September 2002 until the collapse of 28 December. According to eyewitnesses, the event began at about 4:30 a.m. local time. Gigli et al. (2011) made particular reference to distometric base 1-2, since this recorded the longest and most consistent progressive acceleration in the time series of displacements; they ultimately calculated a failure forecast according to the linear extrapolation of the trend in the inverse velocity plot, which could be distinguished since 2 August already (Fig. 2a). Although it provides a good estimate that failure is going to occur, fitting of these data gives a T f which anticipates the actual failure (T af ) by 4 days and a half (ΔT f = T af -T f = 4.5), as is also shown by the related life expectancy plot in Fig. 3a. Life expectancy plots are very useful tools to examine the course with time of the T f predictions, updated on an on-going basis each time a new measurement is available (Mufundirwa et al. 2010; Dick et al. 2014).
Photo of the Mt. Beni rockslide (a) and topographic map displaying the location of distometric bases (b, from Gigli et al. 2011)
Inverse velocity plots for data filtered by means of SMA, LMA and ESF are given in Fig. 2. In this case, short-term moving average smoothing eliminates the small steps in the raw data curve, yielding a significantly improved T f (ΔT f = 1.1); on the other hand, long-term moving average, despite determining a slightly better fitting, generates a considerably negative ΔT f (−4.3) and most importantly delays the identification of the OOA point by 1 month. The latter aspect is verified even more for the exponentially smoothed velocities. Their poor linearity would have also made their use in the emergency scenario quite troublesome, even if, in retrospect, it is found that the last T f value is highly accurate. Respective life expectancy plots (Fig. 3) display additional, valuable information: All datasets, beside velocities filtered by means of ESF, converge parallel to the actual time to failure line. However, raw data consistently give anticipated forecasts of the time of failure, whereas SMA allows forecasts to get decisively closer to the actual failure line since November 21. In Fig. 3c, predictions approach the actual values already on late October but finally diverge towards significantly negative ΔT f , which is something to avoid in risk management of geological hazards (concept of “safe” and “unsafe” predictions, Mufundirwa et al. 2010). Exponential smoothing produces a reliable T f in correspondence of the last measurement, but the predicted time to failure line does not have a regular pattern, if compared to the others.
A slightly different, but really interesting example from the Mt. Beni rockslide, which is not reported in Gigli et al. (2011), is given by displacement rates measured at the distometric base 15-13. Especially in its last phase, the final acceleration (Fig. 4a) is quite irregular (i.e. progressive-regressive wall movement; Newcomen and Dick 2015). Moreover, it seems to have a slightly concave shape with respect to base 1-2, possibly suggesting α lower than 2. We may thus refer these features to one or more of the natural noise factors. The reliability of the linear fitting of the inverse velocity graph results to be strongly affected and produces a time of failure forecast which precedes the last actual measurement acquired on December 20, hence well ahead of T af (approximately 8 days, Figs. 4a and 5a). Here, SMA does not exhibit a noticeable improvement in terms of smoothing, and the consequent T f is equivalent to T f from raw data. Again, exponential smoothing introduces irregularity on the plot and delays the OOA point. In this case, filtering by means of the long-term moving average produces better results under every aspect: OOA is found at the same time than in the raw data, steps in the inverse velocity line are eliminated (thus improving also the degree of fitting) and accuracy of T f is much higher (ΔT f = 2); the related life expectancies converge close to the actual time to failure line already from late November, 1 month before the event. On the contrary, predicted lines from Fig. 5a, b are horizontal in their first section and ultimately do not get near the actual expectancy line.
Summarizing, the Mt. Beni case study, as analysed here, showed that linear fitting of unfiltered inverse velocity data, although surely constituting an indicator of the on-going acceleration of the slope movements, produced T f which anticipate by several days the actual time of collapse. Smoothing data with simple moving average algorithms allowed to benefit from improved qualities of fitting and of T f predictions. In particular, long-term moving average gave optimal results for the noisier, less linear (α < 2) time series from distometric base 15-13, while short-term moving average performed better when applied to the more regular measurements registered by distometric base 1-2. Exponential smoothing did not produce satisfying improvements to these data.
Vajont landslide
The 1963 Vajont disaster in Northeast Italy has been one of the most catastrophic landslides in history, and many authors have studied the event under different perspectives. Without entering into the complex details of the failure mechanism, as these have already been largely described and discussed (and still are), the collapse occurred at about 10:39 p.m. local time on 9 October 1963, when a 270 million m3, mostly calcareous rock mass detached from the slope of Mt. Toc and slid at 30 m/s into the newly created Vajont reservoir (Fig. 6). The consequent tsunami wave overtopped the dam and killed 2500 people in the villages downstream. The pre-failure movements of the unstable material were strongly controlled by the water level in the valley floor and creeping motions began to be observed immediately since the creation of the reservoir (Havaej et al. 2015). The final chain of events started with the April 1963 reservoir filling cycle; the final rupture followed 70 days of downslope accelerating movements (Helmstetter et al. 2004). According to measurements from four benchmarks installed at different positions on the mountain slope, pre-failure velocities were extremely high: Among these, benchmarks 5 and 63 in particular were the ones which showed a clear state of accelerating creep, with displacement rates ranging from ≈5 mm/day up to over 20 cm/day (Fig. 7a , b) and a total cumulative deformation of a few meters (Muller 1964). In Fig. 7, measurements from Mt. Beni are also plotted in order to show the different orders of magnitude in the displacement between the two landslides (Fig. 7a) and the different shape of the curves (Fig. 7b). Distometric base 1-2 of Mt. Beni indeed shows significantly lower rates relatively to both Vajont benchmarks. Data from base 15-13 are instead in the same order of magnitude, but the acceleration is “stepped” rather than exponential. This further indicates the need to perform high-degree smoothing on this time series (Fig. 4).
Velocity measurements for benchmarks 5 (a) and 63 (b) of the Vajont landslide (from Muller 1964) and for distometric bases 1-2 (a) and 15-13 (b) at Mt. Beni, for reference. Both benchmarks display significantly higher rates than 1-2 distometer. 15-13 distometer is characterized by rates of the same order of magnitude as those at Vajont, but the increase of velocity occurs through “steps” rather than exponentially suggesting the need to perform a high-degree data smoothing (Fig. 3). c, d Inverse velocity analysis for benchmark 63 installed on Mt. Toc
In Fig. 7c, the inverse velocity plot for the unfiltered measurements of benchmark 63 is shown. Even though a slight step-like pattern can be noticed, the graph is remarkably linear as a whole and, most importantly, the linear trend line fits particularly well the last points leading up to failure. Therefore, if recorded velocities are regularly high since the initial stages of acceleration, i.e. A ≈ 0.04 (as in Vajont data; Voight 1988) or lower, and if the assumption of α = 2 is consistently satisfied, it is suggested not to apply any strong data filtering, in order to avoid loss of sensitivity with regard to actual downward trends. At most, linear fitting of short-term averaged velocities may also be conducted in parallel to the fitting procedure of the original data. For benchmark 63, SMA yields a slightly better fitting and a slightly more accurate T f (ΔT f = 0.3) with respect to results from the original data (ΔT f = 1.1, Fig. 7d). Conversely, inverse velocity plot from benchmark 5 (Fig. 8a) seems to have a pattern quite similar to that of distometric base 15-13 at Mt. Beni (Fig. 4a): After the fourth point of the dataset, the trend appears to assume a certain concavity (α < 2) and consequently, as opposed to benchmark 63, the last velocity points before failure are not well fitted by the linear regression line. This causes again a premature T f prediction, which anticipates also the time of the last measurement on 8 October (ΔT f = 2.7, Fig. 8a). Excellent linearization is produced by LMA and ESF (Fig. 8), with the first one also determining an extremely accurate T f (ΔT f = 0.1). From the relative life expectancy plot, it can be seen that a correct prediction about the time of failure could have been given about 10 days earlier than the actual event; in further support of their reliability, the forecasts of the time of failure remained consistent after each of the last six displacement measurements. On the other hand, life expectancies from the raw data are always some days off the actual time-to-failure line.
Again, as in the Mt. Beni case study, it is not argued that velocities from benchmarks at Mt. Toc were not indicating a clear accelerating trend towards slope collapse. Nevertheless, it is found out that the accuracy of T f predictions could be improved by appropriately smoothing out data and thus linearize the respective inverse velocity plots. Equivalently to distometric base 15-13 at Mt. Beni, results showed that, for fast-moving slopes, if α < 2, it is suggested to filter data with a long-term moving average; instead, if α ≈ 2, it seems more convenient to proceed with the regular inverse velocity analysis performed on an on-going basis or, at most, to filter data with a short-term moving average.
Stromboli debris talus roto-translational slide
On 7 August 2014, a debris talus located below the Northeastern crater (NEC) of Stromboli Volcano was affected by a roto-translation slide, evolving into a rock avalanche on a 30°–45° steep slope called “Sciara del Fuoco”, and followed by the opening of an eruptive vent localized at ≈650 m a.s.l. (≈100 m below the NEC, Di Traglia et al. 2015; Rizzo et al. 2015; Zakšek et al. 2015). Debris cone material likely reached the sea, but tsunami waves were not recorded. Growth stages of this debris talus at Stromboli are a common phenomenon related to the explosive activity, which produces accumulation of volcaniclastic debris around the active craters (Calvari et al. 2014). Contrariwise, the roto-translational slides occurred at the onset of the 2002–2003, 2007 and 2014 flank eruptions, characterized by magma propagation from the central conduit towards the NEC (Di Traglia et al. 2014, 2015). The debris talus is composed by loose volcaniclastic material, prevalently breccias alternating with tuff, lapillistones and thin (<2–3 m) lava flows (Apuani et al. 2005). The NEC area has been continuously monitored by a Ground-Based Interferometric Synthetic Aperture Radar (GBInSAR) system (Di Traglia et al. 2014, Fig. 9). The latter recorded an increase in the line-of-sight displacement rate of the debris talus starting from 30 May 2014. The curve of deformation rate for this period presents a high degree of noise (Fig. 10a). This is mostly due to the dynamics of the magma within the volcanic edifice: At Stromboli, successive cycles of filling and emptying of the plumbing system can cause phases of inflation and deflation of the entire crater area, thus adding natural noise to the displacements of the debris talus. For this reason, strong negative velocities are displayed at times in Fig. 10a and a definite raise in rates can be observed only from late July. This final acceleration was made up of relatively low-medium rates, from few millimetres per day up to a peak velocity of 40.4 mm/day on 6 August 2014. Since 04:01 GMT on 7 August 2014, the GBInSAR recorded complete loss in coherence in the debris cone sector, consistently with a fast movement of the summit area (i.e. T af ).
Cumulative map of displacements of Stromboli crater area, as measured along the radar line-of-sight between 1 January 2010 and 6 August 2014. Range and cross-range resolution are on average 2 m × 2 m. Map and time series of displacements (Fig. 10a) are obtained by “stacking” the interferograms phase using 8-h averaged SAR images, with a measurement accuracy of ±0.5 mm (Antonello et al. 2004; Intrieri et al. 2013; Di Traglia et al. 2014; Di Traglia et al. 2015). Interferometric phase can be corrupted by noise (decorrelation), caused by the contribution of scatterers summing up differently among SAR acquisitions and estimated by a calculation of the “coherence” between two images (values in the range 0–1). The displacement time series was measured in the area of the debris talus which showed high coherence (>0.9) during the analysed period. In the insert, the location of Stromboli Island is also shown
In Fig. 10a, the OOA is found about only 1 week before the slope collapse. Hence, it was not possible to produce with confidence a failure prediction, as only few measurements could be collected between OOA and T af (Fig. 10b). Data filtering, eliminating short-term fluctuations and highlighting longer-term cycles, is here of invaluable help, as it may allow an earlier detection of the OOA point. With LMA (Fig. 11), the latter is found on 27 July, but the inverse velocity line appears to be excessively smoothed out, causing a late T f prediction (ΔT f = −1.7); ESF generates the OOA on 24 July and provides a slightly better failure forecast (ΔT f = −1.3), despite a worse fitting (R 2 = 0.77). SMA undoubtedly produces, in this case, the best results overall (Fig. 11a, b): A trend towards the x-axis begins already on 23 July, the level of fitting is high (R 2 = 0.88) and T f is extremely reliable (ΔT f = −0.4). In fact, from the life expectancy plot in Fig. 11b, it can be seen that a roughly correct time of failure forecast could have been made consistently since 3 August, approximately 4 days before the actual collapse of the debris talus. Similarly to the time series of distometric base 1-2 at Mt. Beni, it is found that, when accelerations towards failure are characterized by moderate velocity values, it is more reliable to filter data by means of SMA. This is even more important for the Stromboli case study, where failure is usually anticipated by a very brief final acceleration phase and therefore an early identification of the OOA is highly needed. A short-term moving average has higher sensitivity towards trend changes in the data and thus appears to be the most helpful mean of analysis, with regard to this specific issue.
Collapse of the medieval city walls in Volterra
Volterra is one of the most well-known cultural heritage sites in Central Italy. The town, originated as an Etruscan settlement, later became an important medieval centre. During this period, the perimeter walls, which still surround the town, were built. Some of these have their foundation over cemented sand deposits, which sit on top of the stratigraphic column and overlap a formation made up of marine clays. On 31 January 2014, a 35-m long and 9.5-m high portion of the historic walls suddenly collapsed. After this event, a GBInSAR system was installed to monitor the deformation of the entire SW side of the city walls (Pratesi et al. 2015; Fig. 12). Since late February, generally high displacement rates of another portion of the walls were captured; after an initial phase of roughly linear movements (≈2 mm/day), finally velocities increased decisively on 1 March (Fig. 13a) and, shortly thereafter, the area completely collapsed in the early afternoon of 3 March 2014. Pratesi et al. (2015) attributed the source of the instabilities to the accumulation of water above the impermeable clays and to the resulting overpressure exerted on the upper incoherent sands. This was confirmed by the fact that high movement rates were registered only at the bottom of the wall, in agreement with a slightly roto-translational motion caused by loss in base support.
a Overview of the Volterra case study: the location of the GB-InSAR system is indicated by the yellow star, whereas the red stars highlight the two collapse events occurred on the medieval walls. b, c Photos of the first and second Volterra city wall collapses of 31 January 2014 and 3 March 2014, respectively
Displacement rate (a), inverse velocity analysis (b–e) and life expectancy analysis (f) relatively to the second collapse event of the Volterra city walls. The time series in (a) was extracted from the radar pixel which showed the highest coherence as well as the highest displacements during the analysed period (Pratesi et al. 2015). In b–d, plots do not provide clear linear trends; therefore, failure predictions cannot be made with acceptable confidence
The Volterra case study is of particular interest, as it does not strictly imply a failure on a natural slope, but rather on a man-made structure built on unstable terrain. This does not necessarily constitute a limit for INV, as Voight (1989) affirms that the model is thought to be applicable to a variety of fields where mechanical failure is involved, including earth sciences, materials science and engineering. However, the apparent lack of a linear trend toward zero in the inverse velocity plot of the unstable part of the walls discouraged its use during the terminal phase of the emergency (Fig. 13b). Following the recurrence of above-average rate values (from ≈2–3 to 19.4 mm/day), authorities were informed about the high probability of an imminent collapse, but a T f estimation process was not carried out.
It can be argued that accelerations affected by strong deviation from the ideal inverse velocity linearity are those in more need of high-degree smoothing. In fact, SMA and ESF (Fig. 13c, d) do not generate useful improvements from raw data in terms of readability of the inverse velocity plot and again a T f prediction would not be advised. Contrariwise, LMA filter provides a clear OOA and an obvious linear trend line to the x-axis (R 2 = 0.98, Fig. 13e). Results show that final T f is just few hours earlier than T af (ΔT f = 0.5 days). The relative life expectancy plot indicate that roughly accurate forecasts of the time of wall collapse could have been made as soon as 27 February, as all the subsequent points forming the predicted time-to-failure line lie in close proximity to the actual time-to-failure line.
Therefore, if rate values seem to diverge from the expected behaviour of the INV model, it is suggested to try performing time of failure analyses only following the application of strong filters to the data. The usefulness of this process is even greater if relatively low movement rates are involved in the acceleration phase and, consequently, little variations in velocity values can give rise to confusing spikes in the inverse velocity plot.
Effect of noise on the reliability of T f predictions
From the analysis of failure case histories, it resulted that data smoothing can provide several types of advantages, depending on the properties of the velocity curves: When a general trend toward failure is already evident in the raw data (e.g. Mt. Beni, Vajont), it is still possible to obtain more reliable T f predictions; when measurements have a high level of noise and the final phase of acceleration is short-lived (e.g. Stromboli debris talus), an earlier OOA can be identified; when data seem to imply that linear INV is not applicable (e.g. Volterra), it might be possible to deduce the obscured trend toward failure, if present. Particularly in the last two instances, applying filters could be decisive in allowing, in practice, the use of INV. Among the considered examples, it was noticed that measurements at Stromboli and Volterra were affected by high noise intensity and strongly needed to be filtered in order to apply the method, while at Mt. Beni and Vajont, the level of disturbance was smaller and affected just the reliability of T f predictions.
With the aim of performing additional analyses, we now simulate the introduction of random sets of noise on two ideal time series which, initially, are created in accordance to Voight’s model for rates approaching failure. These series are calculated based on the equations that better approximate the actual trends of displacements registered at Mt. Beni (distometric base 1-2) and Vajont, meaning that the parameters A and α must be estimated accordingly. As reckoned by Voight (1988), this can be accomplished by plotting log-velocity against log-(t f –t). Such plot for data from distometric base 1-2 at Mt. Beni is shown in Fig. 14a. Solving for the equation of the best-fit line, one obtains A = 0.102 and α = 1.994, remarkably close to the condition of perfect linearity; approximating for α = 2 yields A = 0.099. Since the general Voight’s equation for rate at any given time prior to failure is equivalent to the general Saito expression for creep rate \( \overset{.}{\varepsilon } \) (Voight 1988; Saito 1969)
where E = [A(α − 1)]1/(1 − α) and n = 1/(α − 1), data are well described by v = 10(t f − t)− 1 as proved in Fig. 14b. For displacements at Mt. Toc (Vajont), Voight (1988) found that rates can be suitably expressed by v = 27(t f − t)− 1 with A = 0.037 and α = 2. By substituting in the two equations values of time-to-failure from 60 to 1, we simulate rates of two slopes with similar behaviour to Mt. Beni and Mt. Toc and in agreement with a condition of perfect linearity in the inverse velocity plot.
As previously mentioned, we then add to these series of velocities several sets of random noise, meaning both IN and NN. We consider IN as additive noise, while NN as multiplicative noise. The first is in fact related to the precision of the monitoring device, which is typically not dependent on the amount of movement occurred (we hypothesize an instrumental accuracy of ±1 mm). Conversely, natural noise, which is determined by the factors disrupting the ideal linearity of slope accelerations (i.e. variations of A and α), is proportional to the stage of failure. This can be easily seen in (5): Equivalent changes of A and α will cause bigger differences between actual and theoretical velocities as the time-to-failure decreases. Also, in INV, velocity at failure is considered infinite, an assumption which obviously is not verified in nature. Values of “disturbed” velocities are thus computed as
where R r is a randomly generated number between [−1, +1] and R f is a fixed constant which indicate the applied intensity of natural noise. Certainly, (6) is a simplification of an otherwise very complex and unpredictable phenomenon; nonetheless, it can stand as a quick and generally effective approximation for the purposes of this analysis.
According to this approach, examples of a strong NN component (R f = 0.2) added to the series of ideal rates for Mt. Beni and Mt. Toc (Vajont) are described, and the effects of data smoothing in improving the reliability and usability of the inverse velocity method are thus further evaluated. Mt. Beni (1-2) and Vajont both represent excellent cases of slope acceleration prior to failure. Mt. Beni was characterized by noticeably lower velocities (i.e. higher value of A) with respect to Mt. Toc. It follows that, when an equal noise intensity is introduced to the respective rate curves, the effects on the analysis of inverse velocity plots will be different. This can be easily observed in Figs. 15 and 16. Graphs have been divided in two sections, before and after an identified OOA/TU point. As previously said, this marks either the point after which a trend toward the x-axis can be clearly defined or a change in the trend slope and usually occurs together with a reduction in data noise (Dick et al. 2014).
Simulation for Mt. Beni (Fig. 15a) shows that, over 60 observations, an OOA can be probably identified at t = 29 and that a reliable T f prediction could be performed by using measurements thereafter. Scatter in the first half of the plot would not allow, in a real-time monitoring scenario, to safely determine a trend. This is also confirmed by the low value of R 2. SMA and ESF both yield no great improvement in terms of scatter in the first part of the dataset and the OOA is found basically at the same time than in the original series. Conversely, LMA generates better smoothing across the entire series and a clear OOA is found already at t = 14, with a final ΔT f = 0.5. LMA thus produces, in this case, notable benefit to the INV analysis.
The Vajont simulation gives different points of interest: The presence of an overall trend toward zero remains generally clear and T f predictions could be initiated quite early in the series (Fig. 16a). Probably, a TU or OOA would be safely found at t = 17 or thereabout. Similarly to what suggested in the real case history of benchmark 63, LMA smooths out excessively the inverse velocity line and, consequently, a sensibly negative ΔT f is found (−2.5). Both LMA and ESF have TU/OOA at t = 14. Instead, SMA produces a reliable T f (ΔT f = 0.6) and the earliest OOA at t = 11.
Several other simulations, with different sets of randomly generated values of noise, were performed. Although the random nature of the process can sometimes yield slightly different results with respect to the ones presented here, the same general behaviour was observed.
Discussion: proposing standard procedures for inverse velocity analyses
INV can be a powerful tool for estimating the time of geomechanical failure. Based on the results displayed in the previous sections, it is also clear that the reliability and the applicability of the method can be decisively improved by appropriately treating data. General guidelines for ideal data filtering of velocity data could be suggested, specifically:
-
If movement rates are consistently high (i.e. A ≈ 0.4 or lower), it is not advised to perform data smoothing, as it would generally yield no real improvements to the INV analysis and cause less sensitivity to actual trend changes. Only SMA could provide some benefits in terms of both OOA/TU identification and reliability of T f . In general, focus should be put mostly on updating T f predictions on an on-going basis and on searching for new TU points in the data.
-
If movement rates are low (i.e. A ≈ 0.1 or higher) and/or noise has significant intensity, data smoothing is of great importance in order to perform INV analyses and, sometimes, could make the difference between being able to make effective T f forecasts or not (e.g. distometric base 15-13 at Mt. Beni, Stromboli debris talus and Volterra). IN mainly influences the initial stage of the acceleration, significantly delaying the identification of OOA/TU points. At the same time, NN may also disturb the linearity of the last stages of acceleration and thus hamper the accuracy of T f predictions. Depending on the properties of the rate curve and on the particular behaviour of the slope, it was observed that different filters could give better results in different case studies. Therefore, T f predictions should be made while applying both short- and long-term filters and simultaneously studying the related trend lines. Exponential smoothing could also be run in parallel for comparison.
It should be noticed that studying trends of displacement rate remains in great part exposed to a high degree of subjectivity. In INV, much of the analysis is not executed following pre-defined procedures but is rather based on the personal interpretation and experience of the user. Dick et al. (2013, 2014) indeed explained that there is no fixed rule for identifying the OOA and TU points, while Rose and Hungr (2007) recommended that best-fits should be constantly re-evaluated in light of possible trend changes and of qualitative observations in the field. As shown in the case histories presented here and as hinted also by Dick et al. (2014), different techniques for data smoothing may be alternatively more suitable, depending on the specific characteristics of the velocity curves, on the properties of the monitoring device and on the requirements of the emergency plan. On top of that, it is obvious that the linear extrapolation of inverse velocity data trending toward the x-axis should not be considered as a precise forecast of the time of failure, but rather as a general estimation only.
We thus propose the introduction of some standard procedures for the analysis of inverse velocity plots; once established, these may be performed automatically and with little input from the user. We think that this would provide benefits especially when dealing simultaneously with multiple series of measurements, as in the case of point cloud data (e.g. ground-based radar), total station prisms, etc. These procedures concern the identification of OOA and TU points and the setup of two different alarm levels, which would support the definition of the emergency plans. Like in mining operations, exceeding the thresholds between adjacent alarm levels could instantly prompt pre-determined actions of evacuation and/or slope remediation (Read and Stacey 2009).
First alarm threshold: onset of acceleration
We consider the occurrence of an OOA as the first alarm threshold. Such event, which indicates the beginning of a progressive stage of failure (Zavodni and Broadbent 1980), would trigger the initiation of inverse velocity analyses, meaning that linear fitting may be applied only to velocity data from OOA onwards. Best-fits should be constantly revised to make sure that they successfully describe the most recent acquisitions. Predictions should also be updated on an on-going basis each time a new measurement is available and until failure occurs or, otherwise, an End Of Acceleration (EOA) point is detected (i.e. regressive stage of failure); an EOA signals the return to the condition of safety. As previously demonstrated, identifying the OOA does not depend only on the user’s interpretation but also on the degree of smoothing with which data are treated. In the case of moving averages, using a long time period in the calculations highlights longer-term trends but can introduce more lag to data; on the other hand, shorter time periods generate higher responsiveness to slight trend changes, which in turn may just represent minor fluctuations.
In time series analysis, a crossover between a shorter-term and a longer-term average is typically one of the most basic signals suggesting the occurrence of a trend change in the raw data (Olson 2004; Shambora and Rossiter 2007). A crossover is defined as the point where a short-term moving average (c-SMA) line crosses through a long-term one (c-LMA). Here, we consider that, if the c-SMA crosses above the c-LMA (“positive crossover”), the beginning of an uptrend and hence the occurrence of an OOA is signalled, while the opposite indicates the beginning of a downtrend (“negative crossover”) and the occurrence of an EOA. The orders of the short-term and long-term moving averages should be previously selected and can vary depending on the intensity of data noise; typically, in the context of moving average crossover analyses, the c-SMA is set so that it already smooths out significantly most of the slighter fluctuations, while the c-LMA is calculated over three or four times the c-SMA time period. The concept of c-SMA/c-LMA for the crossover analysis is therefore not necessarily related to the aforementioned use of SMA/LMA for improving time of failure predictions, since a higher degree of smoothing must usually be used in order to avoid false crossover points between the moving averages. This may cause to establish different types of c-SMA and of c-LMA for different case studies, depending on the properties and the noise of the rate curves.
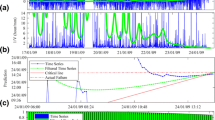
The technique has been applied to the Stromboli debris talus and Mt. Beni movement series; those two only, among the examined case histories, have in fact enough points in the dataset in order to find a c-LMA. As already discussed several times, the GBInSAR series from Stromboli has a high degree of noise; therefore, a moving average calculated over seven measurements (which is equivalent to the LMA in Sections Methodology and Results) was arbitrarily selected as the c-SMA. A moving average calculated over 21 measurements was consequently picked up as the c-LMA. The first positive crossover is found on 8 July (Fig. 16a) but is then followed by a negative crossover, which determines an EOA and the termination of the failure forecasts. A new positive crossover is detected on 18 July and leads up to the debris talus collapse on 7 August. Remarkably, the OOA is established even earlier than what had been done through visual examination of the data (Figs. 10 and 11). The other example is relative to the distometric base 1-2 at Mt. Beni (Fig. 17). The rate curve is in extreme accordance with the linear inverse velocity model (Fig. 14); hence, no substantial smoothing is required for the crossover analysis. A MA(3) and a MA(9) were selected as the c-SMA and c-LMA, respectively. The only positive crossover is found on 12 August and is not revoked until the slope collapse on 28 December, more than 4 months later. The OOA is detected roughly at the same time than through manual identification (Fig. 2).
Some key benefits may thus derive from the application of this type of approach. During the monitoring activity, an indication that a certain target has experienced a positive crossover (i.e. exceeded the first alarm threshold) could be issued automatically. In this way, the necessity to perform a subjective OOA analysis of the different rate curves would be avoided. This would be of great importance especially in radar applications, which can theoretically provide the user with thousands of time series of movement to evaluate at the same time. In terms of risk assessment on a slope, observing the spatial distribution of these alarms could allow to readily estimate the size of the instability and thus determine if the detected onset of an acceleration phase is the expression of a local movement or instead the signal of an incoming partial/total failure event.
Second alarm threshold: failure time window
Extrapolation of the linear best-fit line to infinite velocity surely cannot be considered as an exact prediction of the time of failure. T f is influenced by the assumptions and simplifications implied in the INV model and also by the degree of data smoothing applied. In previous sections, it was shown how the performances of different filters can vary, depending on the properties of the rate curve; however, selecting the most appropriate smoothed time series can usually be done safely only in retrospect, during the post-event evaluation of the displacements which led up to failure. Therefore, the presence of a trend in the inverse velocity plot must be considered just as an indication that failure is presumably going to occur in proximity of its point of intersection with the x-axis.
We propose a quick and reproducible procedure to define the time interval during which the occurrence of a failure event is considered highly probable (“failure window”, T fw ). The failure window is obtained by projecting simultaneously the best-fits of both a SMA and LMA. This will yield two diverse T f , with the difference between T f(LMA) and T f(SMA) being indicated as Δ; here, assuming T f(SMA) < T f(LMA) , T fw was determined between:
The former corresponds to the period of activation of the second alarm level, i.e. the second alarm threshold is exceeded at time \( T={T}_{f(SMA)}-\raisebox{1ex}{$\varDelta $}\!\left/ \!\raisebox{-1ex}{$2$}\right. \). Understandably, there is no exact rule as to how use Δ for establishing the T fw limits. These should be appropriately set based on the preferences of the user, on how well data seem to accommodate the INV in terms of noise and linearity and, most importantly, on the level of acceptable risk for the monitored case study. T fw must be wide enough to account for the uncertainty implied with the failure predictions, while on the other hand, excessive precaution might trigger too early activations of the second alarm threshold; the nature of the elements at risk and the characteristics of the emergency scenario should be carefully evaluated in order to assess the appropriate width of the failure window. Relatively to the case studies presented in this paper, the aforementioned T fw limits were evaluated as the most suitable for successfully including T af and not providing a too conservative alarm threshold (Fig. 18). The Stromboli debris talus and Mt. Beni (distometric base 1-2) slope failures are again used for reference to provide an overview of the methodology: Failure windows have been calculated on the third last measurement of the rate curves (respectively 3 and 26 days before failure), in order to test the procedure to data of both high- and low-temporal resolution. For Stromboli (Fig. 18a), on 4 August, the second alarm threshold is placed in the early morning of 6 August and T fw lasts until 9 August, successfully including T af with a convenient safety margin. The width of the failure window is about 3½ days. For Mt. Beni (Fig. 18b), the prediction performed on 2 December determines a wider failure window, spanning from late 23 December 2002 to early 2 January 2003 (≈10 days). T af lies in the middle between T f(SMA) and T f(LMA) and thus also in the centre of the T fw interval. Similar results, based on the application of the same procedure on both Vajont (benchmark 5) and Volterra monitoring data, are also shown in Fig. 18c, d.
The failure window must be continuously updated each time a new measurement is available, and consequently, new T f(SMA) and T f(LMA) predictions are performed. With this approach, it would be possible to recognize with a certain advance when the second alarm level will approximately be triggered and thus when the related emergency response actions will have to be taken. The eventual consistency over time of the T fw boundaries can be considered as a strong element of support that failure will actually occur within the identified time frame. Lower Δ values suggest that measurements (and thus the forecasts) can be considered reliable, while higher Δ values indicate that the downward trend in the inverse velocity plot is less clear, determining an increased width of the failure window and more uncertainty surrounding T af . The value of Δ and the accuracy of the method in general is also influenced by the number and frequency of measurements available.
It is again intended that this simple and practical approach, once established within the monitoring program, could be extended to all the rate curves available and serve as a standard and automatic procedure to setup in real time the alarm level of each measuring point. Like for the moving average crossover approach, this may result of great advantage especially when simultaneously dealing with multiple targets (e.g. point cloud data). By estimating in advance when and on which points the second alarm threshold will be exceeded, more time would be provided to evaluate the risk in terms of size and probability of failure and promptly implement the pre-determined evacuation and/or remediation strategies.
Conclusions
The inverse velocity method is a powerful tool for predicting the time of geomechanical failure of slopes and materials displaying accelerating trends of movement. Because of the simplicity of use, its linear form (α = 2) is arguably the most common mean of analysis of displacement data for this type of emergency scenarios. The assumed linear trend of inverse velocity toward infinite must be considered as an approximate estimation of the time of failure, and its reliability is heavily dependent on the degree of instrumental and natural data noise. Noise can also decisively delay the identification of the onset of acceleration and trend update points. Smoothing measurements of deformation rate is thus a crucial process of INV analyses and possibly must rely on quick and easily applicable algorithms. In this study, two moving averages and an exponential smoothing function have been tested in order to filter velocities acquired at three large slope failures and one city wall collapse case histories. In general, moving averages seemed to provide better fitting than exponential smoothing. It also resulted that filters have different performances depending on the shape of the inverse velocity curve and on the intensity of deformation rates. Following these findings, some general guidelines to suitably perform data smoothing were thus deduced. Because it may not be possible to safely carry out this interpretation process until the late stages of acceleration or even thereafter, some standard procedures for the setup of failure alarm levels were defined by employing both short- and long-term moving averages. The first alarm threshold identifies the OOA and is established following the implementation of the moving average crossover rule. The second alarm threshold corresponds to the time of activation of the failure window, which is calculated based on the forecasts of both SMA and LMA. The failure window defines the time frame during which the occurrence of the collapse event is considered most probable. The user would be able to anticipate when the thresholds will presumably be exceeded and, therefore, when the pre-determined response actions may have to be taken. Equally importantly, if several measuring targets are included within the dataset (e.g. point cloud data), major benefit would derive from the ability to simultaneously and automatically assess the alarm level of each point. The analysis of the spatial distribution of the alarms would determine a prompt estimation of the size of the instability and of the probability of an imminent failure.
References
Antonello G, Casagli N, Farina P, Leva D, Nico G, Sieber AJ, Tarchi D (2004) Ground-based SAR interferometry for monitoring mass movements. Landslides 1(1):21–28
Apuani T, Corazzato C, Cancelli A, Tibaldi A (2005) Physical and mechanical properties of rock masses at Stromboli: a dataset for volcano instability evaluation. B Eng Geol Environ 64:419–431
Calvari S, Bonaccorso A, Madonia P, Neri M, Liuzzo M, Salerno GG, Behncke B, Caltabiano T, Cristaldi A, Giuffrida G, La Spina A, Marotta E, Ricci T, Spampinato L (2014) Major eruptive style changes induced by structural modifications of a shallow conduit system: the 2007-2012 Stromboli case. B Volcanol 76(7):1–15
Crosta GB, Agliardi F (2003) Failure forecast for large rock slides by surface displacement measurements. Can Geotech J 40:176–191
Cruden DM, Masoumzadeh S (1987) Accelerating creep of the slopes of a coal mine. Rock Mech Rock Eng 20:123–135
Di Traglia F, Nolesini T, Intrieri E, Mugnai F, Leva D, Rosi M, Casagli N (2014) Review of ten years of volcano deformations recorded by the ground-based InSAR monitoring system at Stromboli volcano: a tool to mitigate volcano flank dynamics and intense volcanic activity. Earth-Sci Rev 139:317–335
Di Traglia F, Battaglia M, Nolesini T, Lagomarsino D, Casagli N (2015) Shifts in the eruptive style at Stromboli in 2010-2014 revealed by ground-based InSAR data. Sci Rep 5. doi: 10.1038/srep13569
Dick GJ (2013) Development of an early warning time-of-failure analysis methodology for open pit mine slopes utilizing the spatial distribution of ground-based radar monitoring data. M.A.Sc thesis, The University of British Columbia, Vancouver, BC
Dick GJ, Eberhardt E, Cabrejo-Liévano AG, Stead D, Rose ND (2014) Development of an early-warning time-of-failure analysis methodology for open-pit mine slopes utilizing ground-based slope stability radar monitoring data. Can Geotech J 52:515–529
Federico A, Popescu M, Elia G, Fidelibus C, Interno G, Murianni A (2012) Prediction of time to slope failure: a general framework. Environmental Earth Science 66(1):245–256
Fukuzono T (1985) A new method for predicting the failure time of slopes. Proceedings, 4th International Conference & Field Workshop on Landslides, Tokyo, pp 145–150
Gigli G, Fanti R, Canuti P, Casagli N (2011) Integration of advanced monitoring and numerical modeling techniques for the complete risk scenario analysis of rockslides: the case of Mt. Beni (Florence, Italy). Eng Geol 120:48–59
Havaej M, Wolter A, Stead D (2015) The possible role of brittle rock fracture in the 1963 Vajont Slide, Italy. Int J Rock Mech Min Sci 78:319–330
Helmstetter A, Sornette D, Grasso J-R, Andersen JV, Gluzman S, and Pisarenko V (2004) Slider block friction model for landslides: application to Vaiont and La Clapière landslides. J Geophys Res 109. doi: 10.1029/2002JB002160
Intrieri E, Di Traglia F, Del Ventisette C, Gigli G, Mugnai F, Luzi G, Casagli N (2013) Flank instability of Stromboli volcano (Aeolian Islands, Southern Italy): integration of GB-InSAR and geomorphological observations. Geomorphology 201:60–69
Mufundirwa A, Fujii Y, Kodama J (2010) A new practical method for prediction of geomechanical failure. Int J Rock Mech Min Sci 47:1079–1090
Muller L (1964) The rock slide in the Vaiont valley. Felsmech Ingenoirgeol 2:148–212
Newcomen W, Dick G (2015) An update to strain-based pit wall failure prediction method and a justification for slope monitoring. Proceedings, Slope Stability 2015, Cape Town, pp 139–150
Olson D (2004) Have trading rule profits in the currency markets declined over time? J Bank Financ 28:85–105
Petley DN, Bulmer MH, Murphy W (2002) Patterns of movement in rotational and translational landslides. Geology 30:719–722
Pratesi F, Nolesini T, Bianchini S, Leva D, Lombardi L, Fanti R, Casagli N (2015) Early Warning GBInSAR-Based Method for Monitoring Volterra (Tuscany, Italy) City Walls. IEEE J Sel Top App 8(4):1753–1762
Read J, Stacey P (2009) Guidelines for open pit slope design. CSIRO Publishing, Collingwood, VIC, Australia
Rizzo AL, Federico C, Inguaggiato S, Sollami A, Tantillo M, Vita F, Bellomo S, Longo M, Grassa F, Liuzzo M (2015) The 2014 effusive eruption at Stromboli volcano (Italy): inferences from soil CO2 flux and 3He/4He ratio in thermal waters. Geophys Res Lett 42(7):2235–2243
Rose ND, Hungr O (2007) Forecasting potential rock slope failure in open pit mines using the inverse-velocity method. Int J Rock Mech Min Sci 44:308–320
Saito M (1969) Forecasting time of slope failure by tertiary creep. Proceedings, 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, pp 677–683
Shambora WE, Rossiter R (2007) Are there exploitable inefficiencies in the futures market for oil? Energ Econ 29:18–27
Ventura G, Vinciguerra S, Moretti S, Meredith PH, Heap MJ, Baud P, Shapiro SA, Dinske C, Kummerow J (2009) Understanding slow deformation before dynamic failure. In: Tom Beer (ed) Geophysical Hazards, 1st edn. Springer Netherlands, pp. 229-247
Voight B (1988) A method for prediction of volcanic eruption. Nature 332:125–130
Voight B (1989) A relation to describe rate-dependent material failure. Science 243:200–203
Zakšek K, Hort M, Lorenz E (2015) Satellite and Ground Based Thermal Observation of the 2014 Effusive Eruption at Stromboli Volcano. Remote Sens 7(12):17190–17211
Zavodni ZM, Broadbent CD (1980) Slope failure kinematics. Bulletin, Canadian Institute of Mining 73(816):69–74
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Carlà, T., Intrieri, E., Di Traglia, F. et al. Guidelines on the use of inverse velocity method as a tool for setting alarm thresholds and forecasting landslides and structure collapses. Landslides 14, 517–534 (2017). https://doi.org/10.1007/s10346-016-0731-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10346-016-0731-5