Abstract
The ETS-NOCV analysis was applied to describe the σ-hole in a systematic way in a series of halogen compounds, CF3-X (X = I, Br, Cl, F), CH3I, and C(CH3)nH3-n-I (n = 1,2,3), as well as for the example germanium-based systems. GeXH3, X = F, Cl, H. Further, the ETS-NOCV analysis was used to characterize bonding with ammonia for these systems. The results show that the dominating contribution to the deformation density, Δρ 1 , exhibits the negative-value area with a minimum, corresponding to σ-hole. The “size” (spatial extension of negative value) and “depth” (minium value) of the σ-hole varies for different X in CF3-X, and is influenced by the carbon substituents (fluorine atoms, hydrogen atoms, methyl groups). The size and depth of σ-hole decreases in the order: I, Br, Cl, F in CF3-X. In CH3-I and C(CH3)nH3-n-I, compared to CF3-I, introduction of hydrogen atoms and their subsequent replacements by methyl groups lead to the systematic decrease in the σ-hole size and depth. The ETS-NOCV σ-hole picture is consistent with the existence the positive MEP area at the extension of σ-hole generating bond. Finally, the NOCV deformation density contours as well as by the ETS orbital-interaction energy indicate that the σ-hole-based bond with ammonia contains a degree of covalent contribution. In all analyzed systems, it was found that the electrostatic energy is approximately two times larger than the orbital-interaction term, confirming the indisputable role of the electrostatic stabilization in halogen bonding and σ-hole bonding.

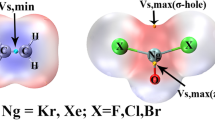
Graphical representation of the σ-hole on the halogen atom, based on the molecular electrostatic potential (upper row) and the NOCV deformation-density channel Δρ 1 (lower row and the right-hand side plot)
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Halogen bonds formed between terminal halogen atoms (X) and Lewis bases (B), R–X…B, play essential role in chemistry and biochemistry [1–8]. In parallel to hydrogen bonding [9, 10], these type of connections attracted recently considerable attention. It has been shown that selective and directional character of these interactions make them very important not only in determination of biological structures but also in rational design of solid materials [1–8].
The first steps toward understanding the geometry and reactivity of halogen bonded systems originate from the works of Hassel et al. [11, 12], Parthasarathy et al. [13], and Mertrangolo et al. [14, 15]. In addition, it is necessary to reference the computational studies of Price et al. [16] and Allen et al. [17]. These works allowed to observe that R–X…B unit adopts linear structure (the angle R–X…B is 180°), whereas the electrophilic species (Lewis acids–A) make the R–X…A angle in the range from 90 up to 120°. In addition the possible role of the electrostatic and the charge transfer components were discussed [16, 17].
The novel concept that explains the origin of halogen bonding was proposed recently by Politzer and coworkers [1, 3, 6, 7, 18–32]. The authors noticed for the first time, based on the molecular electrostatic potential (MEP), anisotropy in distribution of the charge on halogen atom, resulting in the existence of the positive-MEP area on the outer part of halogen atom which is collinear with the R-X bond [1, 6, 7]. Later this phenomenon was connected with an electron deficiency at the outer part of the halogen atom, the so called σ-hole [18]. Hence, the halogen atom of R–X is characterized by strong anisotropy of the electron density distribution. The existence of σ-hole at terminal halogen atom leads to electrostatic attraction with Lewis bases. Accordingly, the halogen bonding is driven mainly by the electrostatic term [1, 3, 6, 7, 18–32]. Very recently, Politzer and coworkers extended the σ-hole concept to analysis of π-holes [33]. It is noteworthy that non-typical halogen bonds of the type RNC…FCl have been studied recently by Del Bene et al. [34] and subsequently by Politzer et al. [35] Authors noted very high binding energies (~20–30 kcal mol−1) and significant stretch of the F–Cl connection due to formation of RNC…FCl bond (by ca. 0.3 Å). Politzer and Murray [34] reported, based on the analysis of molecular electrostatic potential and the averaged ionization energies, that it is due to polarization of RNC unit that can lead to significant dative component of RNC…FCl bond.
We have recently proposed the natural orbitals for chemical valence (NOCV) [36, 37] combined with the extended-transition-state (ETS) energy-decomposition analysis [38]. This scheme allows for separation and quantitative assessment of the contributions to deformation density (Δρi) originating from the electron charge transfer channels (σ, π, δ, etc.) [36, 37]. This picture is further enriched by providing the energetic contributions (ΔE i ) to the bond energy within ETS-NOCV scheme [39]. It has been shown that NOCV’s lead to a compact description of not only metal–ligand or covalent connections [36, 37, 39], but also of hydrogen bonding [40]. We have verified recently the applicability of ETS-NOCV scheme in a description of halogen bonding, showing in particular, that the dominating contribution to the deformation density exhibits the negative-value area that corresponds to σ-hole [41].
The main goal of the present study is to analyze the ETS-NOCV representation of σ-hole in a more detailed, systematic way in a series of halogen compounds, CF3-X (X = I, Br, Cl, F), CH3I, C(CH3)nH3-n-I (n = 1,2,3), as well as for the example germanium-based systems. XGeH3, X = F, Cl, H. The ETS-NOCV scheme will be further used to characterize bonding with ammonia for all analyzed systems.
Computational details
All the DFT calculations presented here are based on the Amsterdam density functional (ADF2009) program in which ETS-NOCV scheme was implemented [42–45]. The Becke-Perdew exchange-correlation functional [46, 47] was applied (BP86) with an inclusion of the dispersion correction (BP86-D) [48]. A triple-zeta STO basis containing two sets of polarization functions, based on the frozen core approximation, was adopted for all of the elements (TZ2P). Auxiliary s, p, d, f and g STO functions, centered on all nuclei, were used to fit electron density and obtain accurate Coulomb potentials in each SCF cycle. Relativistic effects were included using the ZORA formalism.
Bonding analysis presented in this study is based on the ETS-NOCV approach [39] which is a combination of the extended transition state (ETS) [38] method with the natural orbitals for chemical valence (NOCV) scheme [36, 37]. In our analysis, each system is divided up into two individual fragments as shown schematically by green vertical lines in Fig. 1. Then we used the ETS-NOCV method to study the interaction between these subsystems.
In the ETS energy decomposition scheme [38], the interaction energy ΔE int between the fragments (exhibiting geometries as in the combined molecule) is divided into three components:
The first term, ΔE elstat, corresponds to the classical electrostatic interaction between the fragments as they are brought to their positions in the final molecule. The second term, ΔE Pauli, accounts for the repulsive Pauli interaction between occupied orbitals on the fragments in the combined molecule. The third stabilizing term, ΔE orb, represents the interactions between the occupied molecular orbitals of one fragment with the unoccupied molecular orbitals of the other fragments as well as mixing of occupied and virtual orbitals within the same fragment (inner-fragment polarization). This energy term may be linked to the electronic bonding effect coming from the formation of a chemical bond.
The natural orbitals for chemical valence allow for a decomposition of the differential density Δρ into NOCV-contributions (Δρ k ):
based on diagonalization of the deformation-density matrix in the basis set representation [36, 37]. In addition, within the combined ETS-NOCV [39] scheme, the deformation-density based picture is enriched by the energetic estimation, \( \varDelta E_{{orb}}^k \),that arises from a decomposition of the aforementioned ETS orbital-interaction energy into the contributions corresponding to NOCV charge-transfer channels, Δρ k ; \( \varDelta E_{{orb}}^k \):
It is necessary to mention at this point that the total orbital interaction term includes the inter-fragments electron flow as well as the intra-fragment polarization; thus, depending on the terminology used it could be considered as the polarization energy component [3, 49, 50].
The contours and the color-coded plots of the NOCV deformation density contributions and molecular electrostatic potential were plotted based on ADF-GUI interface [51].
As has already been mentioned, we will use the dispersion corrected BP86-D functional [48], hence, the dispersion correction (ΔE disp) will be added to ΔE int values to describe the total bonding energy:
Results and discussion
ETS-NOCV description of σ-hole in F3C-I and the halogen bond in F3C-I…..NH3
Let us start the discussion with two illustrative examples of the ETS-NOCV interpretation of bonding. We will first characterize the bond between the CF3 fragment and the iodine atom in F3C-I, and then we will describe the interaction between the CF3I and ammonia molecule in F3C-I…..NH3. The former example allows us to discuss and visualize the σ-hole in this system, while the latter demonstrates the NOCV picture of halogen bonding [41].
In Fig. 1 (top row, left-hand side plot) we present the contour plot of the dominating NOCV contribution Δρ 1 in the deformation density, \( \varDelta \rho = {\rho^{{\mathrm{CF3I}}}}--({\rho^{{\mathrm{CF3}}}} + {\rho^{\mathrm{I}}}) \). The presented contour shows a formation of covalent C–I σ-bond; the corresponding ETS-NOCV orbital interaction energy is \( \varDelta E_{{orb}}^1 = - 98.4kcal/mol \). It should further be noted that the contour of Δρ 1 shows significant charge anisotropy around the iodine atom, that is important for the reactivity, as the halogen atom can simultaneously act as electron donor and acceptor [18, 19, 52]. However, a feature of the contour of Δρ 1 that is the most important for our further discussion, is an outflow of the electron density from the outer area of iodine atom, at the extension of the C-I bond. Such a negative part of Δρ 1 describes the formation of σ-hole within the ETS-NOCV picture.
In Fig. 2 (top row, left-hand side plot) another graphical representation of the ETS-NOCV σ-hole in CF3I is shown: a color-representation of the Δρ 1 on the molecular surface (ρ = 0.001 a.u.). This plot is compared with the corresponding visualization of molecular electrostatic potential (top row, right-hand side plot). A comparison of the ETS-NOCV and MEP plots demonstrates a clear correspondence of the negative part of Δρ 1 with the positive MEP at the tip of the iodine atom.
Since both, contour plots of Fig. 1 and colored-surface plot of Fig. 2 are quite qualitative, in Fig. 3 we present yet another graphical representation of σ-hole, i.e., the values of Δρ 1 along the bond-line, outside of the halogen atom. Here, we can clearly see that Δρ 1 exhibits a minimum value, corresponding to σ-hole. Again, in the right-hand side column in Fig. 3, the corresponding MEP plot, as a function of the distance from the iodine atom, is shown. The corresponding numerical values that characterize the Δρ 1 minimum, and the MEP value at the point corresponding to the σ-hole minimum are listed in Table 1.
Let us now discuss the ETS-NOCV results for the halogen bond between the CF3I and ammonia molecule in F3C-I…..NH3. In Table 2 we collect results of the energy decomposition analysis. Before discussing the results it should be pointed out that in the present study the ZORA relativistic approach was applied; therefore, the presented F3C-I…NH3 bond-energy and its components are slightly different from those of our previous work (not including relativistic correction) [41].
As shown in Table 1, the total interaction energy between F3C-I and NH3 is −7.0 kcal mol−1. The results show that the total stabilization of the system is mainly due to the electrostatic interaction (-16.7 kcal mol−1), that is almost two times larger than the orbital interaction energy (−9.6 kcal mol−1), in agreement with the previous studies emphasizing the role of electrostatic stabilization [18, 19, 41].
The dispersion energy, −1.3 kcal mol−1, is of minor importance here, as it was shown in the case of other systems with σ-hole bonding [18, 19, 41, 53]. It should, however, be noted that Riley et al. [53] studied similar molecules (CY3X----OCH2, X = Cl, Br, I, Y = H, F) containing formaldehyde donor, based on SAPT-energy decomposition scheme – for these molecules both the electrostatic and the dispersion factors were found to be similarly important (moreover, for X = Cl and Y = H,F, the dispersion was visibly more important than the electrostatic term) [53]. It is also necessary to note that due to inherent methodological differences between SAPT and DFT-D approaches one can obtain different absolute values characterizing the role of dispersion [54]. Role of the dispersion in the aromatic compounds was recently characterized by Riley et al. [55].
The leading NOCV deformation density channel, Δρ 1, that describes the halogen bonding between CF3I molecule and ammonia, is shown in Fig. 1 (top row, right-hand side plot). The contour plot of Δρ 1 shows the covalent bonding contribution that originates from the electron transfer from both the nitrogen and iodine atoms to the bonding region between I and N atoms. Also, the donation from the NH3 fragment to CF3I is clearly visible, with the decrease in the electron density on ammonia and the increase in the region of the CF3 group. Accumulation of electron density at carbon atom of CF3 is in line with an increase in the carbon s–orbital contribution due to halogen bonding, shown recently by Grabowski with NBO method [52].
It should be emphasized that Δρ 1 is the only NOCV contribution localized in the halogen bond area, with the corresponding energy contribution ΔE 1 orb = −8.9 kcal mol−1, that covers over 93 % of the orbital interaction energy; the remaining NOCV channels (not shown) describe the intra-fragment polarization and are characterized by much lower energies (stabilization up to −0.2 kcal mol−1).
Comparison of σ-hole in F3C-X and halogen bonding with NH3, for X = I, Br, Cl, F
Similarly to CF3I molecule, we used ETS-NOCV method to characterize σ-hole and halogen bonding in the analogous systems involving other halogen atoms, X = Br, Cl, F in CF3X. The contours of the main NOCV charge-transfer channel (Δρ 1) for all the systems are collected in the left-hand side column of Fig. 1. The corresponding color-coded representation of Δρ 1 is presented Fig. 2 (left-hand side column), together with the similar MEP plots (right-hand side column). In panel a of Fig. 3, the linear Δρ 1 plots at the extension of the C-X bond (as a function of the distance from atom X) are compared for the systems with different halogens. The corresponding numerical values that characterize the Δρ 1 minimum, and the MEP value at the point corresponding to the σ-hole minimum are listed in Table 1.
The results of Figs. 1, 2, 3a, and Table 1 show consistently a decrease in the σ-hole “depth” (Δρ 1 minimum value) and “size” (spatial extension of the negative Δρ 1 area) in the order: I, Br, Cl. In particular, the decrease of the σ-hole size is clear from the contour plot of Fig. 1 and the color-coded plot of Fig. 2, while the decrease in σ-hole depth is nicely demonstrated by the linear plots of Fig. 3a. The minimum values of Δρ 1 are −0.92*10−3 a.u.; −0.48*10−3 a.u., and −0.30*10−3 a.u., for I, Br, and Cl, respectively (see Table 1). When going from I to Cl, the position of the minimum moves closer to the halogen atom; the position, measured as the distance from the atom X, changes from 1.64 Å for I, through 1.62 Å for Br, to 1.60 Å for Cl. For fluorine, in the case of the contour of Δρ 1 (Fig. 1) and its color-coded representation (Fig. 2), practically no σ-hole (negative Δρ 1) is visible; a very shallow minimum of Δρ 1 (−0.02*10-3 a.u.) appears at a relatively large distance of 1.88 Å.
The picture resulting from ETS-NOCV analysis concerning σ-hole in the CF3X systems are fully consistent with the results of the previous studies based on analysis of MEP [1] and NBO [18]. To compare the NOCV and MEP picture in a more detailed way, based on the calculations within the same methodology, in the right-hand columns of Figs. 2 and 3 the corresponding MEP plots are presented; the numerical values of MEP at the point corresponding to the minimum of Δρ 1 are in addition listed in the last column of Table 1. A comparison of Δρ 1 and MEP plots in Fig. 2 show a nice qualitative correspondence of the negative Δρ 1 and positive MEP areas at the tip of the halogen atom. The plots of Fig. 3 and the values from Table 1 show a decrease of MEP values in the order I > Br > Cl > F; the MEP values at the Δρ 1 mininum changes from 0.125 a.u. for I, through 0.082 a.u. for Br, down to 0.060 a.u. for Cl. For the system with fluorine, the MEP is no longer positive at the tip of the halogen atom, but becomes negative; the MEP value at the minimum of Δρ 1 is −0.002 a.u.
The trends in σ-hole, discussed above, are reflected by the halogen bond energies in the F3C-X interacting with ammonia. The stabilization in the total bond energy decreases in the order: F3C-I (−7.0 kcal mol−1), F3C-Br (−4.3 kcal mol−1), F3C-Cl (−2.6 kcal mol−1). For F3C-F---NH3 there is practically no bonding; no minimum corresponding to the halogen bond was found within the used DFT approach. We will comment on the F3C-F---NH3 interaction in a more detail later.
As for the iodine-system discussed in the previous section, for X = Br and Cl the electrostatic contribution is roughly two times larger (−10.4, −5.0 kcal mol−1 for Br, Cl, respectively) than the orbital interaction term (−5.8, −2.5 kcal mol−1 for Br, Cl, respectively). The most important NOCV charge-transfer channel, Δρ 1, accounts for 93 %, 95 %, and 97 % of the orbital interaction contribution, for I, Br, and Cl (ΔE 1 orb = −8.9, −5.5, and −2.4 kcal mol−1, respectively). The NOCV plots in the left-hand side column of Fig. 1 clearly show that the NOCV picture of halogen bonding is qualitatively the same for I, Br, and Cl: for all those systems the covalent component of halogen bond is seen; only the spatial extension of the corresponding Δρ 1 contours decreases.
Let us now discuss the F3C-F---NH3 system. As we mentioned above, the DFT methodology applied here does not allow to find a minimum corresponding to the halogen bonding. In addition to the standard, unconstrained geometry optimization, we have performed a set of constrained optimizations, with a frozen, increasing F-N distance, starting from the linear C-N-F structure with R F-N = 2.00 Å. Up to the distance of 2.24 Å the systems stays roughly linear, and afterward the C-N-F angle starts strongly deviate from linearity. The interaction between CF4 and ammonia is repulsive within used methodology (e.g., at R F-N = 2.1 and 2.2 Å the total bonding energy ΔE tot is +0.2 and +0.1 kcal mol−1, respectively); the dispersion energy is slightly stabilizing (−0.5 kcal mol−1 and −0.4 kcal mol−1, at 2.1 Å and 2.2 Å, respectively), but not large enough to overcome the repulsive part of the interaction energy. Certainly, these small energy values are not quantitatively meaningful, and they will be strongly influenced by the methodology used, so that we do not discuss all the interaction-energy components here. Our point is just to qualitatively illustrate the lack of pronounced halogen bonding for F3C-F---NH3. Further, in the last column of Fig. 1 (right-hand side plot), for comparison with other systems, we plotted the example of the main NOCV Δρ 1 channel for R F-N = 2.15 Å, that shows only the intra-fragment polarization, without the covalent halogen-bonding features; it should be emphasized that for other points that we analyzed (for R F-N = 2.00 − 2.24 Å) the corresponding Δρ 1 plots are qualitatively indistinguishable.
Therefore, it may be concluded that in CF3-X systems the ETS-NOCV analysis shows, in agreement with previous studies [1, 18], that the size and depth of σ-hole decreases in the order X = I, Br, Cl, F. This trend is reflected by the changes in MEP, as well as the changes in the NOCV Δρ 1 component in F3C-X---NH3, and the strength of the interaction with ammonia.
Influence of carbon-substituents in R1R2R3C-I on σ-hole and halogen bonding
After discussing the σ-hole and halogen bonding in CF3X systems, now we would like to present the ETS-NOCV results for the related CH3I, and C(CH3)nH3-n-I (n = 1,2,3) molecules, in which the fluorine atoms of CF3I are first replaced by hydrogen atoms, and then further by methyl groups. The respective plots describing ETS-NOCV σ-hole are shown and compared with the corresponding MEP plots in Figs. 3b and 4; the respective numerical data are collected in Tables 1 and 2.
A comparison of the results for CF3I (Fig. 2, 3a, Table 1) and CH3I (Fig. 3b, 4, Table 1) show that the exchange of fluorine atoms with hydrogens has a relatively strong effect on the iodine σ-hole: the minimum changes from −0.9*10−3 a.u. in CF3I to -0.5*10−3 a.u. CH3I. This is consistent with MEP picture: the value of MEP at the Δρ 1 minimum decreases from 0.125 a.u. in CF3I to 0.053 CH3I.
Consistently, a similar effect is observed for the halogen bond energies and their components (Table 2). The total stabilization due to halogen bonding decreases by ca. 4.0 kcal mol−1 (from −7.0 kcal mol-1 to −3.0 kcal mol−1 in CH3I). The corresponding decrease in stabilization due to orbital interaction is 5.1 kcal mol-1 (from the value of −9.6 kcal mol−1 in CF3I to −4.5 kcal mol−1 in CH3I). The decrease in the electrostatic stabilization is 8.5 kcal mol−1 (from the value of −16.6 kcal mol−1 in CF3I to −8.1 kcal mol−1 in CH3I). Thus, the ETS-NOCV analysis provides similar conclusions to those previously published by Politzer et al. [1].
Introducing the methyl substituents on carbon leads to the further decrease in the σ-hole depth. For subsequent methyl substitution the minimum value of Δρ 1 changes in the sequence: -0.3*10−3 a.u., −0.2*10−3 a.u., −0.1*10−3 a.u. in C(CH3)H2I, C(CH3)2HI, and C(CH3)3I, respectively. Again, the data of Tables 1 and 2 show that this is reflected by the changes in MEP at the σ-hole minimum (0.042, 0.022, 0.012 a.u.. respectively), as well as by the halogen-bond energies (−2.5, −2.0, -1.9 kcal mol−1, respectively) and their components.
σ-hole in GeH3-X and bonding with NH3
Although the concept of σ-hole was proposed originally to rationalize the halogen bonding, it was shown later by Politzer and coworkers [3, 22, 33, 34] that it is useful as well for explanation of the weak, bonding interactions in other systems. Therefore, we would like here to use ETS-NOCV to describe and visualize σ-hole in the example germanium compounds, GeH3X, X = F, Cl, H, and their interaction (σ-hole bonding) with ammonia molecule. It was shown recently [22] that the molecular electrostatic potential exhibits the positive-value area on the outer part of germanium atom, at the extension of the X-Ge bond (i.e., between three Ge-H bonds); this was rationalized by the σ-hole concept, analogous to those observed at halogen atom in the compounds that can form halogen bonding [18–21].
In order to describe σ-hole formation within the ETS-NOCV scheme, we again apply the two fragment approach, with X and GeH3 considered as the fragments. Similarly to the systems described in the previous sections, we present in the left-hand side column of Fig. 5 the contours of the dominant NOCV deformation-density contribution of σ-symmetry, Δρ 1, for the X-GeH3. The color-coded representation of Δρ 1 is shown in Fig. 6, and compared with the corresponding MEP plots. Finally, in Fig. 7, the linear plots of Δρ 1 as a function of the distance from germanium atom are presented and compared with the corresponding MEP curves. The numerical values characterizing the NOCV σ-hole minimum and MEP are listed in Table 3. The σ-hole bonding with ammonia is described by the contours of Δρ 1 for XH3Ge---NH3 (right-hand column of Fig. 5), and the ETS-NOCV bond-energy components are listed in Table 4.
The results show that, the main Δρ 1 ETS-NOCV channel exhibits for FH3Ge the extended negative-value area that corresponds to σ-hole (Fig. 5). In the color-coded representation on the molecular surface (Fig. 6), this area corresponds to the MEP-positive-value area. For ClH3Ge the σ-hole size (spatial extension) and depth (minimum value) are smaller than for the system with fluorine (Figs. 5, 6, 7); the Δρ 1 minimum value changes from −3.2*10−3 a.u. (at 1.28 A) for FH3Ge to −2.63*10−3 a.u. (at 1.25 A) in ClH3Ge. This corresponds to the decrease in MEP at the minimum from 0.248 a.u. to 0.247, respectively. In the case of H4Ge a very shallow minimum of Δρ 1 (−0.5*10−3 a.u.) is observed at a relatively long distance from germanium (1.76 A); it corresponds to a small positive value of MEP (0.051 a.u.).
The presence of σ-hole in XH3Ge, X = F, Cl, is responsible for stabilizing interaction with ammonia and correlates qualitatively with the σ-hole-bonding energy (−5.8 kcal mol−1 for F and −5.3 kcal mol−1 for Cl). The ETS analysis shows that the electrostatic energy is approximately two times larger that the orbital interaction component, similarly to the systems discussed in the previous sections: for X = F the electrostatic contribution is −20.3 kcal mol−1 and the orbital-interaction energy is −9.3 kcal mol−1; for X = Cl the two components are −16.3 kcal mol-1 and −7.7 kcal mol−1, respectively. The NOCV Δρ 1 contour (right-hand side part of Fig. 5) exhibits features qualitatively similar to the systems described in the previous sections: the covalent Ge-N bond and the charge-transfer H3N➔GeH3X.
In the case of GeH4, the interaction with ammonia is slightly attractive (−1.1 kcal mol−1) due to dispersion (−1.6 kcal mol−1); the sum of the remaining components is repulsive (+0.5 kcal mol−1). A relatively weak electrostatic (−3.8 kcal mol−1) and orbital interaction (−1.6 kcal mol−1) contributions are not large enough to overcome the Pauli repulsion (5.9 kcal mol−1). The Δρ 1 contour exhibit a very small covalent-bonding area, being dominated by the intra-fragment polarization.
As for halogen bonding discussed in the previous sections, the results presented here for the ETS-NOCV description of the σ-hole in germanium compounds and their σ-hole-bonding with ammonia are in a qualitative agreement with the picture emerging from the previous studies [1–4, 18–34], emphasizing the role of σ-hole formation for the electrostatic stabilization of bonding.
Polarization effect on σ-hole and halogen bonding
It has been shown in ref [56] that the electric field can induce the σ-hole. Accordingly, polarization of one fragment by the interacting, partner fragment is an important factor in determining the strength and direction of hydrogen (and by implication halogen) bonds. In a similar manner we will characterize here the influence of polarization on the NOCV-picture of σ-hole in CF3I. Further, the ETS-NOCV description using the mutually-polarized fragments will be presented for CF3I---NH3 bonding, and compared with the non-polarized case.
In order to polarize CF3I molecule we used the point-charge model, with point-charges placed in the position of the atoms of NH3 : q N = −q; q N = +q/3, for q changing between 0.0 and 1.2 . The results are presented in Fig. 8.
Changes in the ETS-NOCV deformation-density contribution Δρ1 (panel A) and the molecular electrostatic potential (panel B) for F3C-I at the extension of C–I bond, due to electrostatic field of ammonia, modeled by point charges q N = −1/3q H ; for q changing between 0 and 1.2. The black line (q = 0) corresponds to non-polarized system (shown in panel A of Fig. 3 – red line)
As it can be seen from panel A of Fig. 8 the polarization by ammonia increases the “depth” of σ-hole on iodine: the ∆ρ1 minimum-value becomes more negative with the increase in the negative charge (on ammonia nitrogen atom). It is fully consistent with the picture emerging from the molecular electrostatic potential presented in panel B of Fig. 8, demonstrating increase of the positive MEP. Thus, the NOCV analysis shows the polarization-induced (or here - enhanced) σ-hole, in a qualitative agreement the data presented in ref [56].
It is interesting at this point to analyze how the ETS-NOCV description of CF3I---NH3 bonding will change upon considering the polarized fragments in ETS-NOCV calculations (as compared to non-polarized species NH3 and CF3I). In order to achieve this goal we have first performed the calculations for the fragments polarized by the point-charges in the positions of the other-fragment atoms: NH3 in the field of point charges placed in the atomic positions of CF3I; and for CF3I fragment in the field of point charges placed in the atomic positions of ammonia. Mulliken and Hirshfeld charges were condidered, as presented in part A of Fig. 9. Subsequently, we applied ETS-NOCV analysis using the polarized-fragments as a reference. The results are presented in Table 5. The fragment density change due to polarization is shown in Fig. 9.
Halogen bonded system, CF3I---NH3, together with Mulliken (blue color) and Hirshfeld (red color) atomic charges (panel A), used to model the mutual polarization of the fragments. In panel B the contour of deformation density, \( \varDelta {\rho_{{pol}}} \), describing the polarization of the CF3I and NH3 fragments is presented; \( \varDelta {\rho_{{pol}}} = ({\rho_{{C{F_3}I - polarized - by - N{H_3}}}} - {\rho_{{C{F_3}I}}}) + ({\rho_{{N{H_3} - polarized - by - C{F_3}I}}} - {\rho_{{N{H_3}}}}) \)
It can clearly be seen from Table 5 that applying polarized fragments leads to a slightly more stabilizing value of the total intreaction energy as compared to the results based on non-polarized fragments, i.e., ΔE tot is lower by 0.16 kcal mol−1 for Hirshfeld charges and by 0.07 kcal mol−1 for Mulliken charges. The increase in the stabilization energy comes from the fact that the reference polarized fragments are higher in energy than non-polarized fragments (optimized KS electron density corresponding to the minimum of energy).
Now, it is interesting to examine the changes in the ETS-bond-energy components due to polarization of the fragments. The results of Table 5 show that the increase in the bond stabilization is almost solely due to an increase in the stabilization originating from the electrostatic contribution (ΔE elstat is lowered by 0.55 – 0.68 kcal mol−1). This result is consistent with the polarization-picture of σ-hole discussed above: the polarization (the partner-electric-field) induced increase in the σ-hole “depth” and the corresponding increase in the positive MEP at the tip of iodine is reflected by the increased electrostatic stabilization of interaction with ammonia (negatively charged nitrogen atom).
Further, the results of Table 5 show that the orbital interaction term (ΔEorb) appears to be less stabilizing when going from non-polarized to polarized fragments (by 0.36 kcal mol−1 for Mulliken charges and by 0.54 kcal mol−1 for Hirshfeld charges). This result may appear surprising and counter-intuitive at the first look: one might expect the increase in orbital-interaction when the σ-hole becomes “deeper”. However, after analyzing this effect in details, it seems to be physical and correct, and in fact could be expected. Namely, when we express the density changes and the bond-energy using the non-polarized fragments as the reference, the mutual fragment polarization is included in the NOCV density-changes, and the fragment-polarization energy is included in the orbital-interaction energy term. When, in the second-case, we express the density changes and the bond-energy using the polarized fragments as the reference, the mutual fragment polarization (or rather, its part due to the partner-electric-field) is excluded from both, NOCV density changes and the orbital-interaction-energy contribution. As a result, since part of the stabilization energy has already been subtracted from the orbital-intaraction energy by considering polarized fragments, its final value becomes less negative in the polarized-fragment reference case than in the non-polarized fragment case.
The above reasoning is further confirmed when we inspect the polarization changes in the fragment-electron densities, see part B of Fig. 9, it is clearly seen that inclusion of the point charges at positions of neighboring fragments leads to the charge outflow from I–N bonding region, hence, the weakening/destabilization of σ-bonding is observed, ΔEpol = +0.07 kcal mol−1 (Mulliken), ΔEpol = +0.16 kcal mol−1 (Hirshfeld).
The remaining bonding components (ΔEdisp and ΔEPauli) are practically the same. It should finally be mentioned that the polarization not involved in the σ-component of CF3I---NH3 bonding, measured by difference ΔE orb – ΔE orb 1, also practically does not change when we consider polarized fragments (0.6–0.7 kcal mol−1 in both cases).
Summarizing, the above results show that mutual polarization of the NH3 and CF3I fragments is one of the factors stabilizing halogen bonding, by increase in the σ-hole “depth” and the electrostatic-interaction-energy component. Here, however, we considered only one example; more studies for other systems are required.
Conclusions
In our previous article [41], we have shown that ETS-NOCV approach can be used to successfully describe halogen bonding, and that the dominating contribution to the deformation density exhibits the negative-value area that corresponds to σ-hole. In the present study we analyzed the ETS-NOCV representation of σ-hole in a more detailed, systematic way in a series of halogen compounds, CF3-X (X = I, Br, Cl, F), CH3I, and C(CH3)nH3-n-I (n = 1,2,3) as well as for the example germanium-based systems. XGeH3, X = F, Cl, H. We also used ETS-NOCV scheme to characterize bonding with ammonia for these systems. In particular, we have used three different graphical representations of the ETS-NOCV results useful for qualitative and quantitative characterization of σ-hole: the contour plots, color-coded molecular surface, and the linear plots of Δρ 1 at the extension of the σ-hole-generating bond.
The results of presented analysis showed that the dominating contribution to the deformation density, Δρ 1 , exhibits the negative-value area (σ-hole area) with a minimum. It was shown that the “size” (spatial extension of negative value) and “depth” (minium value) of the σ-hole varies for different X in CF3-X, and is influenced by the carbon substituents (fluorine atoms, hydrogen atoms, methyl groups). In particular, the size and depth of σ-hole decreases in the order I, Br, Cl, F in CF3-X. In CH3-I and C(CH3)nH3-n-I, compared to CF3-I, introduction of hydrogen atoms and their subsequent replacements by methyl groups lead to the systematic decrease in the σ-hole size and depth.
It was further shown that the size and depth of the ETS-NOCV representation of σ-hole by Δρ 1 corresponds qualitatively to the positive MEP area at the extension of σ-hole generating bond, demonstrating, in agreement with the previous works [1, 18], that existence of σ-hole is responsible for this important feature of MEP. To further strengthen this point in Fig. 10 we show the correlation between the minimum value of Δρ 1 and the MEP value at the Δρ 1 minimum.
Correlation between the σ-hole minimum (minumim value of the ETS-NOCV deformation-density contribution, Δρ 1 ) and the MEP value at the minimum-point for all studied systems (see Table 1).
Finally, our results show that the σ-hole bond with ammonia contains a large degree of covalent contribution. It should be emphasized, that any energy partitioning method includes some arbitrariness due to the fact that the contributions to the total interaction energy are not physical observables. However, the presence of the covalent contribution in σ-hole bonding was demonstrated not only by the ETS orbital-interaction energy, but as well by the NOCV deformation density contours. Concerning the interaction-energy components, in all analyzed systems, it was found that the electrostatic energy is approximately two times larger than the orbital-interaction term. Thus, the results of the present analysis confirm the indisputable role of the electrostatic stabilization in halogen bonding and σ-hole bonding, emphasized in the previous articles by Politzer and coworkers [1–4, 18–34].
References
Politzer P, Lane P, Concha MC, Ma Y, Murray JS (2007) J Mol Model 13:305–311
Legon AC (2008) In: Metrangolo P, Resnati G (eds) Halogen bonding fundamentals and applications. Springer, Berlin, pp 17–64
Politzer P, Murray JS, Clark T (2010) Phys Chem Chem Phys 12:7748–7757
Legon AC (2010) Phys Chem Chem Phys 12:7736–7747
Erdѐlyi M (2012) Chem Soc Rev 41:3547–3557
Brinck T, Murray JS, Politzer P (1992) Int J Quantum Chem. Quantum Biol Symp 19:57–64
Murray JS, Paulsen K (1994) Politzer P. Proc Indian Acad Sci (Chem Sci) 106:267–275
Auffinger P, Hays FA, Westhof E, Shing Ho P (2004) Proc Natl Acad Sci 101:16789–16794
Grabowski SJ (ed) (2006) Hydrogen bonding—new insights. Springer,Berlin
Grabowski S (2011) Chem Rev 111:2597–2625
Hassel O, Stromme KO (1958) Nature 182:1155–1156
Hassel O (1970) Science 170:497–502
Ramasubbu N, Parthasarathy R, Murrayrust P (1986) J Am Chem Soc 108:4308–4314
Metrangolo P, Meyer F, Pilati T, Resnati G, Terraneo G (2008) Angew Chem Int Ed 47:6114–6127
Bertania R, Sgarbossaa P, Venzob A, Lelj F, Amatic M, Resnatid G, Pilati T, Metrangolod P, Terraneod G (2010) Coord Chem Rev 254:677–695
Price SL, Stone AJ, Lucas J, Rowland RS, Thornley AE (1994) 116: 4910–4918
Lommerse JPM, Stone AJ, Taylor R, Allen FH (1996) 118:3108–3116
Clark T, Hennemann M, Murray JS, Politzer P (2007) J Mol Model 13:291–296
Politzer P, Murray JS, Concha MC (2008) J Mol Model 14:659–665
Murray JS, Concha MC, Lane P, Hobza P, Politzer P (2008) J Mol Model 14:699–704
Murray JS, Lane P, Politzer P (2008) Int J Quantum Chem 108:2770–2781
Murray JS, Lane P, Politzer P (2009) J Mol Model 15:723–729
Riley KE, Murray JS, Politzer P, Concha MC, Hobza P (2009) J Chem Theor Comput 5:155–163
Politzer P, Murray JS, Lane P, Concha MC (2009) Int J Quantum Chem 109:3773–3780
Murray JS, Lane P, Nieder A, Klapötke TM, Politzer P (2010) Theor Chem Acc 127:345–354
Politzer P, Murray JS, Macaveiu L (2010) J Mol Struct THEOCHEM 943:53–58
Politzer P, Murray JS, Bulat FA (2010) J Mol Model 16:1731–1742
Shields ZP, Murray JS, Politzer P (2010) Int J Quantum Chem 110:2823–2832
Murray JS, Riley KE, Politzer P, Clark T (2010) Aust J Chem 63:1598–1607
Murray JS, Concha MC, Politzer P (2011) J Mol Model 17:2151–2157
Metrangolo P, Murray JS, Pilati T, Politzer P, Resnati G, Terraneo G (2011) Crys Growth Des 11:4238–4246
Riley KE, Murray JS, Fanfrlík J, Řezáč J, Solá RJ, Concha MC, Ramos FM, Politzer P (2011) J Mol Model 17:3309–3318
Murray JS, Lane P, Clark T, Riley KE, Politzer P (2012) J Mol Model 18:541–548
Politzer P, Murray JS (2012) Theor Chem Acc 131:1–10
Del Bene JE, Alkorta I, Elguero J (2010) J Phys Chem A 114:12958–12962
Mitoraj M, Michalak A (2007) J Mol Model 13:347–355
Michalak A, Mitoraj M, Ziegler T (2008) J Phys Chem A 112(9):1933–1939
Ziegler T, Rauk A (1977) Theor Chim Acta 46:1–10
Mitoraj M, Michalak A, Ziegler T (2009) J Chem Theor Comput 5(4):962–975
Kurczab R, Mitoraj MP, Michalak A, Ziegler T (2010) J Phys Chem A 114:8581–8590
Mitoraj MP, Michalak A (2012) J Mol Model. doi:10.1007/s00894-012-1474-4.
te Velde G, Bickelhaupt FM, Baerends EJ, Fonseca Guerra C, van Gisbergen SJA, Snijders JG, Ziegler T (2001) J Comput Chem 22:931–967, and refs therein
Baerends EJ, Ellis DE, Ros P (1973) Chem Phys 2:41–541. Baerends EJ, Ros P (1973) Chem Phys 2:52–59
te Velde G, Baerends EJ (1992) J Comput Phys 99:84–98
Fonesca Geurra C, Visser O, Snijders JG, te Velde G, Baerends EJ (1995) In: Clementi E, Corongiu G (eds) Methods and techniques in computational chemistry METACC-9. STEF, Cagliari, pp 303–395
Becke A (1988) Phys Rev A 38:3098–3100
Perdew JP (1986) Phys Rev B 34:7406–7406
Grimme S, Anthony J, Ehrlich S, Krieg H (2010) J Chem Phys 132:154104-1–1154104-19. doi:154104-1
Chen J, Martinez TJ (2007) Chem Phys Lett 438:315–320
Sokalski WA, Roszak SM (1991) J Mol Struct THEOCHEM 80:387–400
Visser O, Leyronnas P, van Zeist WJ, Lupki M (2008) ADF-GUI 2009.01, SCM, Amsterdam, The Netherlands, http://www.scm.com
Grabowski S (2011) J Phys Chem A 115:12340–12347
Riley KE, Hobza P (2008) J Chem Theor Comput 4:232–242
Hesselmann A (2011) J Phys Chem A 115(41):11321–11330
Riley KE, Murray JS, Fanfrlík J, Řezáč J, Solá RJ, Concha MC, Ramos FM, Politzer P (2012) J Mol Model. doi:10.1007/s00894-012-1428-x
Hennemann MJ, Murray JS, Politzer P, Riley KE, Clark T (2012) J Mol Model 18:2461–2469
Acknowledgments
The financial support from the National Science Center in Poland (grant N N204 198040) is acknowledged. M.P.M. acknowledge the financial support from Polish Ministry of Science and Higher Education (“Outstanding Young Researchers” scholarship 2011–2014).
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Dyduch, K., Mitoraj, M.P. & Michalak, A. ETS-NOCV description of σ-hole bonding. J Mol Model 19, 2747–2758 (2013). https://doi.org/10.1007/s00894-012-1591-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00894-012-1591-0