Introduction

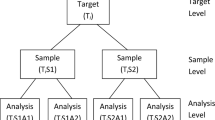
Measurement uncertainty (MU) can be defined as ‘a parameter, associated with the result of a measurement that characterises the dispersion of the values that could reasonably be attributed to the measurand’ [1]. The requirement for reliable estimates of the measurement uncertainty (MU) in chemical measurements is well known, and there is increasing awareness that the sampling process often adds a significant contribution to the value of MU. A well-established method of calculating MU, including the contribution from sampling, is provided by the duplicate method [2]. This is an empirical method of uncertainty estimation, requiring repetition of the sampling protocol at a number of (ideally randomly selected) sampling targets. A formal definition of a sampling target is given as the ‘portion of material, at a particular time, that the sample is intended to represent’, and should be defined prior to designing the sampling plan [2]. Each of the resultant samples is chemically analysed two or more times, typically in a laboratory, although potentially in situ using mobile measuring tools (e.g. portable X-ray fluorescence), or using on-site laboratory methods, which are increasingly being employed [3].

Most commonly, the duplicate method is applied to a number of sampling targets, eight sampling targets being the recommended minimum [4]. Two physical samples are then acquired from each target, either by using a reinterpretation of the sampling protocol, or sometimes in the case of spatial sampling, by separating the location of the two samples around the nominal location by a distance that is assessed to be a reasonable representation of the effect of the heterogeneity of the analyte(s) of interest on that reinterpretation. Each of the two samples so acquired is then analysed twice. So, in the case of I = 8 (where I is the number of targets or duplicate sampling locations, and if the duplicate samples are acquired from I locations on the original sampling plan) there is a total overhead of 3 × 8 = 24 additional measurements. This balanced experimental design (abbreviated to I × 2 × 2 here) is used in most cases.

Subsequent data analysis is carried out using nested analysis of variance (ANOVA), resulting in values representing estimates of the uncertainty due to the sampling process, the uncertainty from the analysis, and also the combined MU which is calculated from the sums of squares of the sampling and analytical components. The ANOVA itself can be carried out in one of two ways, either using a standard formulaic or classical approach, or alternatively with the use of a robust algorithm. The robust method can be useful when the measurement set may contain a small proportion (up to 10 %) of outlying values, as these can have a disproportionate effect on the means and standard deviations calculated by the classical form of ANOVA [2]. When outliers are present, robust ANOVA can provide better estimates of the parameters of the underlying population of measurements.

In uncertainty estimation, it is common practice to multiply the standard deviation of the measurements by a coverage factor (a k-factor). The value k = 2 is often considered to be a suitable approximation for a confidence level of 95 % if the probability distribution is approximately normal and the effective degrees of freedom is suitably large [1]. The value k = 2 is used because for a normal distribution 95 % of the area beneath the normal curve is within 1.96 standard deviations from the mean. However, we are almost always using an estimate of the standard deviation, and k = 2 can only be considered a good approximation when the exact or approximate degrees of freedom of this estimate is large. Typically, n = 30 is considered to be large enough. The ideal case where n is larger than 30 is often not practical, because of the costs of additional sample collection and the additional laboratory analyses needed to produce the uncertainty estimate. In these situations, the expanded uncertainty derived using k = 2 will be an underestimate. An alternative approach is to use percentage points on a Student’s t-distribution to calculate the k-factor. This approach is straightforward for a simple experiment taking n replicates, where the degrees of freedom used in the t calculation is n – 1. However, when the standard deviation is calculated from a linear combination of variances that have been derived from an ANOVA, the resultant distribution does not have a standard form. Then the degrees of freedom to use in the t calculation needs to be approximated in some way.

The objective of this study is to provide more reliable estimates of measurement uncertainty that include the extra contribution that arises from using estimated, rather than true, values of the standard deviations. In the case of classical ANOVA, it is feasible to derive an improved coverage factor (k-factor) for the combined measurement uncertainty using the t-distribution and a value for degrees of freedom based on the Satterthwaite approximation [5]. Calculating an appropriate coverage factor for linear combinations of estimated variances from robust ANOVA is more complex, but can be achieved using a method based on bootstrapping.

Improved estimate of measurement uncertainty from classical ANOVA

For the nested ANOVA described above, where I = the number of targets, J = the number of samples and K = the number of analyses, the ANOVA table can be represented as shown in Table 1. Here the subscripts T, S and A also correspond to target, sampling and analysis, SS is sum of squares, df is degrees of freedom, MS is mean square and EMS is expected mean square. Variances at the target, sampling and analysis levels are shown as \({\sigma }_{{\text{T}}}^{2}\), \({\sigma }_{{\text{S}}}^{2}\) and \({\sigma }_{{\text{A}}}^{2}\) , respectively.

Table 1 ANOVA table for nested design
Full size table

In the case of a single analysis of a single sample, an unbiased estimator of the combined variance representing the square of the measurement uncertainty is [6]:

$$\hat{\sigma }_{M}^{2} = \hat{\sigma }_{A}^{2} + \hat{\sigma }_{S}^{2} = {\text{MS}}_{A} + \frac{{{\text{MS}}_{S} - {\text{MS}}_{A} }}{K} = \frac{K - 1}{K} {\text{MS}}_{A} + \frac{1}{K} {\text{MS}}_{S}$$
(1)

The distribution of the linear combination of two independently distributed mean squares in Eq. 1 does not have a standard form. An established method of tackling this problem is to approximate its distribution by a simple multiple of χ2, with degrees of freedom calculated using the Satterthwaite approximation [5]. The approximate degrees of freedom can then be used to calculate a percentage point from a Student’s t-distribution that can further be used as a multiplication factor on the standard uncertainty to obtain an approximate 95 % coverage.

In general, if V is an estimate of variance derived from a number, n, of independent mean squares MSi with degrees of freedom νi such that \(V= \sum_{i}^{n}{({a}_{i} {\text{MS}}}_{i})\) for constants ai, then Satterthwaite’s approximate degrees of freedom for V is given by:

$$\nu \approx \frac{{\left( {\mathop \sum \nolimits_{i = 1}^{n} a_{i } {\text{MS}}_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \frac{{\left( {a_{i } {\text{MS}}_{i} } \right)^{2} }}{{\upsilon_{i} }}}}$$
(2)

In Eq. 2 there are just two mean square values MSA and MSS, with degrees of freedom IJ(K − 1) and I(J − 1), respectively. The constants in the linear combination are a1 = (K − 1)/K and a2 = 1/K (Table 1). Substituting into Eq. 2 gives:

$$\nu_{M} \approx \frac{{\left( {\frac{K - 1}{K}{\text{MS}}_{A} + \frac{1}{K} {\text{MS}}_{S} } \right)^{2} }}{{\frac{{\left( {\frac{K - 1}{K} {\text{MS}}_{A} } \right)^{2} }}{{IJ\left( {K - 1} \right)}} + \frac{{\left( {\frac{1}{K} {\text{MS}}_{S} } \right)^{2} }}{{I\left( {J - 1} \right)}}}}$$
(3)

In the special case that J = K = 2, Eq. 3 reduces to:

$$\nu_{M} \approx \frac{{I\left( {{\text{MS}}_{A} + {\text{MS}}_{S} } \right)^{2} }}{{\frac{{{\text{MS}}_{A}^{2} }}{2} + {\text{MS}}_{S}^{2} }}$$
(4)

Simulations were run in Matlab R2016b software supplied by MathWorks to investigate the performance of the method in this special case. The aim was to estimate the coverage probability of a 95 % confidence interval \(x \pm {t}_{{\upsilon }_{{\text{M}}}, 0.975 }{\widehat{\sigma }}_{{\text{M}}}\) when a measurement x is sampled from \(N(\mu , {\sigma }_{{\text{M}}}^{2})\), and when the measurement variance is estimated as in the ANOVA above and degrees of freedom νM calculated using Eq. 4.

Simulations were run with J = K = 2 and for values of I equal to 2, 4, 8 and 16. In each case µ, the value of which does not affect the result was set to 0. Since the variances \({\sigma }_{{\text{A}}}^{2}\) and \({\sigma }_{{\text{S}}}^{2}\) will only affect the results by their quotient, \({\sigma }_{{\text{A}}}\) was set to 1, and \({\sigma }_{{\text{S}}}\) was varied on a log2 scale from − 4 to 4. On this scale, a step of one unit corresponds to a doubling of the quotient of standard deviations. For each simulation, a measurement x was sampled from \(N(\mu , {\sigma }_{{\text{M}}}^{2})\). MSA and MSS were sampled from the appropriate χ2 distributions, and used to obtain an estimate of νM using Eq. 4. This enabled a confidence interval to be calculated, and compared with µ. The coverage probability was estimated by the proportion of times µ was found to be within this interval in 107 repetitions. An average value of νM was also calculated. Results for the case I = 8 are shown in Fig. 1.

Fig. 1
figure 1

a Estimated coverage probabilities and b average calculated degrees of freedom (df) for I = 8, J = 2, K = 2

Full size image

The coverage probabilities in Fig. 1 (a) are all very close to 0.95. The degrees of freedom in Fig. 1 (b) tends to I(J − 1) = 8 when \({\sigma }_{{\text{S}}}\) becomes much larger than \({\sigma }_{{\text{A}}}\). This behaviour is to be expected when the sampling variance increasingly dominates.

Simulations were also run for the cases I = 2, 4 and 16. In all cases, the coverage probabilities were close to 0.95. In the worst case (I = 2), these ranged between 0.93 and 0.96. It would be unusual (and not recommended [4]) for an experiment to be performed with such a low number of targets.

Comparisons of the coverage probabilities for the improved k-factors, with those simulated for k = 2, are shown in Figs. 2 and 3. For the case I = 16 (Fig. 3 (b)), coverage values for k = 2 might be considered acceptable; in all other cases, k = 2 gives coverage values that are too small, the difference becoming more pronounced as I gets smaller.

Fig. 2
figure 2

Comparison of coverage probabilities where ▲ represents the improved k-factor derived using degrees of freedom from Eq. 4, and ● represents k = 2, for a I = 2, b I = 4

Full size image
Fig. 3
figure 3

Comparison of coverage probabilities where ▲ represents the improved k-factor derived using degrees of freedom from Eq. 4, and ● represents k = 2, for a I = 8, b I = 16. Note the change in scale (coverage probability) from Fig. 2

Full size image

Improved estimate of measurement uncertainty from robust ANOVA

In the case of robust ANOVA, using the algorithm described in [7], it is not possible to obtain a corrected estimate of the k-factor mathematically. However, we can use a large number of bootstrapped samples (in the statistical sense) generated as described in [7] to make an estimate of the k-factor.

To motivate our approach, consider the case where we have independent variables X and s where:

$$X\sim N(0, \sigma )$$

and:

$$\frac{{\nu s}^{2}}{{\sigma }^{2}} \sim {\chi }_{\nu }^{2}$$

for some degrees of freedom ν. Then it is a standard result that the random variable \(T=X/s\) has a t-distribution with ν degrees of freedom. One way to derive this result would be to integrate W from the joint probability density function (pdf) of T and W, where W = \({\sigma }^{2}/ {s}^{2}\).The integral involved, which is analytically tractable, results in the pdf of the t-distribution. We could obtain the same result numerically by taking a large sample of size N from the distribution of W = \({\sigma }^{2}/ {s}^{2}\) and averaging N different normal pdfs, one for each value of W in the sample. If each of these pdfs is evaluated on a grid of discrete values, then the result will be a pdf of T tabulated on the same grid.

In the case of the robust ANOVA algorithm [7], the \(\sigma\) becomes \({\sigma }_{{\text{M}}}\) and the quotient \({\sigma }_{{\text{M}}}^{2}/{\widehat{\sigma }}_{{\text{M}}}^{2}\) does not have a standard distribution, so that analytical integration is not possible. To carry out the numerical integration, we use a bootstrapping method. A bootstrap sample of size 2000 from the observed data is used to generate a sample from the distribution of \({\widehat{\sigma }}_{{\text{M}}}^{2}\), which is converted into a sample from the distribution of the quotient \({\sigma }_{{\text{M}}}^{2}/{\widehat{\sigma }}_{{\text{M}}}^{2}\), using the mean of the values of \({\widehat{\sigma }}_{{\text{M}}}^{2}\) as the numerator, i.e. replacing the unknown \({\sigma }_{{\text{M}}}^{2}\) by its bootstrap estimate. This sample from the quotient is then used to implement the numerical integration described above. This procedure would provide a sample from the correct t-distribution in the tractable case. The modest sample size of 2000 was chosen to enable implementation in Excel [8]. The distribution of T was tabulated in steps of 0.01, which is sufficient to determine a k-factor that is accurate to two decimal places. Because the distribution of T is symmetrical, the tabulation can begin at 0 (corresponding to a cumulative probability of 0.5) and increase until the cumulative probability is greater than or equal to 0.975, when t will be equivalent to the k-factor for a coverage probability of 0.95.

Method validation/discussion

Further simulations were performed to test the performance of the modified uncertainty calculations by estimating the coverage provided by the modified k-factors.

In the case of normally distributed data, a simulation of 50,000 repetitions was run, smaller than the previous one because the robust ANOVA computations are more demanding. For each repetition, data were simulated from an 8 × 2 × 2 experimental design with mean = 100 and a top-level (sampling target) standard deviation = 10. Both classical and robust ANOVA were applied and the variances estimated, as well as the modified uncertainties and k-factors. Coverage was measured by counting the number of times µ was contained within the confidence limits centred on a single simulated observation from \(N(\mu , {\sigma }_{{\text{M}}}^{2})\) and with width given by the modified k-factors and the estimated variances. The results of these simulations are shown in Table 2. In all cases, the estimate coverage percentages are close to the nominal 95 %, indicating that the modified k-factors are able to provide a good estimate of the uncertainty value.

Table 2 Results of coverage simulations using 50,000 datasets, each randomly generated from normal distributions with no outlying values, showing results for both classical ANOVA using the Satterthwaite method, and robust ANOVA using the numerical integration of bootstrap samples
Full size table

Further simulations were run on data that included outlying values in the ANOVA input. These data were obtained by simulating data from normal distributions as before, and for each simulation selecting one target at random, and adding 6 × the standard deviation either to one sample at the sampling stage (Table 3) or to one analysis to act as the outlier (Table 4).

Table 3 Results of coverage simulations (50,000 datasets) each randomly generated from a normal distribution with the random inclusion of outlying values at the sampling level in the ANOVA. Showing results for both classical ANOVA using the Satterthwaite method, and robust ANOVA using bootstrapping
Full size table
Table 4 Results of coverage simulations (50,000 datasets) each randomly generated from a normal distribution with the random inclusion of outlying values at the analytical level. Showing results for both classical ANOVA using the Satterthwaite method, and robust ANOVA using bootstrapping
Full size table

All of the coverage probabilities in Tables 3 and 4 are greater than the nominal value of 0.95. In each of two cases, the last in Table 3 and the first in Table 4, the outlying value was applied to the smaller variance component, consequently it had little effect overall, and the coverage probability is very close to 0.95. Where the outlier is applied to the sampling or analytical component with larger variance (i.e. standard deviation = 10 in Tables 3 and 4), the variance estimate for the classical analysis has been inflated by the outlying value, as would be expected. It is also known that variance estimates derived by the robust algorithm will tend to be greater than those of the underlying normal distributions, particularly when the outlier is at the sampling level, and there are only eight pairs of duplicates [7]. Tables 3 and 4 show that when an outlier occurs in the larger variance component, the coverage probabilities estimated by both classical and robust ANOVA are very conservative, although the extent is a little disappointing in the robust case.

Conclusion

Empirical methods of uncertainty estimation are typically based on an estimated standard deviation. An improvement to the usual practice of obtaining an expanded uncertainty by multiplying the standard deviation by 1.96 or 2 for 95 % coverage is possible for smaller samples, by using the Student’s t-distribution. When the uncertainty is calculated as a linear combination of variances that have been derived from an ANOVA, the t-distribution does not hold exactly but it is possible to calculate an approximate degrees of freedom to use to find percentage points on a t-distribution. A mathematical solution has been used and validated for classical ANOVA, and performs well in simulated trials with normally distributed data.

An alternative solution, based on numerical integration using bootstrap samples, has also been devised for cases where the ANOVA is performed using a robust algorithm. The robust ANOVA down-weights outlying values when their number is small. Simulations suggest that robust ANOVA also performs well on normally distributed data, and is conservative, though less so than the classical analysis, in the presence of outliers. The approaches that have been described for deriving a modified k-value for both classical and robust ANOVA are an improvement on the method of multiplying by k = 2, where the coverage would be less than 95 % for smaller sample sizes.