Abstract
Strain gradient plasticity has been the subject of extensive research in the past 40 years in order to model size effects in metal plasticity, on the one hand, and provide finite width shear bands in the simulation of localization phenomena, on the other hand. However, the use of the emerging models is still limited to academic applications and has not yet been adopted by industry practitioners. The present paper systematically reviews the pros and the cons of gradient plasticity at finite strains based on the gradient of scalar plastic variables, in particular the gradient of the cumulative plastic strain. It proposes benchmark tests addressing both size effect modeling and plastic strain localization simulation. It includes new analytical solutions for validation of FE implementation. It focuses on the micromorphic approach to gradient plasticity, as a convenient method for implementation in FE codes. New features of the analysis include the comparison of three distinct formulations of rate-independent gradient plasticity at finite deformations, based on the multiplicative decomposition of the deformation gradient and on quadratic potentials with respect to gradient terms. The performance of micromorphic and Lagrange-multiplier-based strain gradient plasticity models is evaluated for various monotonic and cyclic loading conditions including confined plasticity in simple glide and tension, bending and torsion at large deformations. Limitations are pointed out in the case of bending and torsion, which can be overcome for instance by the use of the gradient of equivalent plastic strain model.

























Similar content being viewed by others
Notes
To establish this expression, the following equation was used:
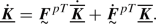
It can be checked that
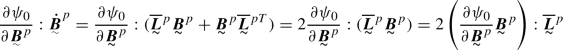
assuming that
 is symmetric.
is symmetric.
References
Venkatraman, R., Bravman, J.C.: Separation of film thickness and grain boundary strengthening effects in Al thin films on Si. J. Mater. Res. 7(8), 2040–2048 (1992). https://doi.org/10.1557/JMR.1992.2040
Stölken, J.S., Evans, A.G.: A microbend test method for measuring the plasticity length scale. Acta Mater. 46(14), 5109–5115 (1998). https://doi.org/10.1016/S1359-6454(98)00153-0
Fleck, N.A., Hutchinson, J.W.: Strain gradient plasticity. Adv. Appl. Mech. 33, 295–361 (1997)
Mu, Y., Zhang, X., Hutchinson, J.W., Meng, W.J.: Dependence of confined plastic flow of polycrystalline Cu thin films on microstructure. MRS Commun. 6, 289–294 (2016). https://doi.org/10.1557/mrc.2016.20
Nye, J.F.: Some geometrical relations in dislocated crystals. Acta Metall. 1, 152–162 (1953)
Ashby, M.F.: The deformation of plastically non-homogeneous materials. Philos. Mag. J. Theor. Exp. Appl. Phys. 21(170), 399–424 (1970). https://doi.org/10.1080/14786437008238426
Fleck, N.A., Hutchinson, J.W.: A phenomenological theory for strain gradient effects in plasticity. J. Mech. Phys. Solids 41(12), 1825–1857 (1993). https://doi.org/10.1016/0022-5096(93)90072-N
de Borst, R., Pamin, J., Sluys, L.J.: Computational issues in gradient plasticity. In: Continuum models for materials with microstructure, pp. 159–200. Wiley (1995)
Mazière, M., Forest, S.: Strain gradient plasticity modeling and finite element simulation of Lüders band formation and propagation. Contin. Mech. Thermodyn. 27(1), 83–104 (2015). https://doi.org/10.1007/s00161-013-0331-8
Botta, A.S., Venturini, W.S., Benallal, A.: BEM applied to damage models emphasizing localization and associated regularization techniques. Eng. Anal. Bound. Elem. 29(8), 814–827 (2005). https://doi.org/10.1016/j.enganabound.2005.04.006
de Borst, R., Pamin, J., Geers, M.G.D.: On coupled gradient-dependent plasticity and damage theories with a view to localization analysis. Eur. J. Mech. A. Solids 18(6), 939–962 (1999). https://doi.org/10.1016/S0997-7538(99)00114-X
Peerlings, R.H.J., de Borst, R., Brekelmans, W.A.M., De Vree, J.H.P.: Gradient enhanced damage for quasi-brittle materials. Int. J. Numer. Methods Eng. 39(19), 3391–3403 (1996). https://doi.org/10.1002/(SICI)1097-0207(19961015)39:19\(<\)3391::AID-NME7\(>\)3.0.CO;2-D
Needleman, A.: Material rate dependence and mesh sensitivity in localization problems. Comput. Methods Appl. Mech. Eng. 67(1), 69–85 (1988). https://doi.org/10.1016/0045-7825(88)90069-2
Saanouni, K., Hamed, M.: Micromorphic approach for finite gradient-elastoplasticity fully coupled with ductile damage: formulation and computational aspects. Int. J. Solids Struct. 50(14), 2289–2309 (2013). https://doi.org/10.1016/j.ijsolstr.2013.03.027
Davaze, V., Vallino, N., Langrand, B., Besson, J., Feld-Payet, S.: A non-local damage approach compatible with dynamic explicit simulations and parallel computing. Int. J. Solids Struct. 228, 110999 (2021). https://doi.org/10.1016/j.ijsolstr.2021.02.010
Russo, R., Phalke, V., Croizet, D., Ziane, M., Forest, S., Girot Mata, F.A., Chang, H.J., Roos, A.: Regularization of shear banding and prediction of size effects in manufacturing operations: a micromorphic plasticity explicit scheme. Int. J. Mater. Form. 15, 21 (2022). https://doi.org/10.1007/s12289-022-01657-9
Eringen, A.C., Suhubi, E.S.: Nonlinear theory of simple micro-elastic solids-I. Int. J. Eng. Sci. 2(2), 189–203 (1964). https://doi.org/10.1016/0020-7225(64)90004-7
Suhubi, E.S., Eringen, A.C.: Nonlinear theory of micro-elastic solids-II. Int. J. Eng. Sci. 2(4), 389–404 (1964). https://doi.org/10.1016/0020-7225(64)90017-5
Germain, P.: The method of virtual power in continuum mechanics. Part 2: microstructure. SIAM J. Appl. Math. 25(3), 556–575 (1973). https://doi.org/10.1137/0125053. (Society for Industrial and Applied Mathematics)
Forest, S.: Micromorphic approach for gradient elasticity, viscoplasticity, and damage. J. Eng. Mech. 135(3), 117–131 (2009). https://doi.org/10.1061/(ASCE)0733-9399(2009)135:3(117)
Kiefer, B., Waffenschmidt, T., Sprave, L., Menzel, A.: A gradient-enhanced damage model coupled to plasticity-multi-surface formulation and algorithmic concepts. Int. J. Damage Mech 27, 253–295 (2018). https://doi.org/10.1177/1056789516676306
Wulfinghoff, S., Böhlke, T.: Equivalent plastic strain gradient enhancement of single crystal plasticity: theory and numerics. Proc. R. Soc. A Math. Phys. Eng. Sci. 468(2145), 2682–2703 (2012). https://doi.org/10.1098/rspa.2012.0073. (Publisher: Royal Society)
Ling, C., Forest, S., Besson, J., Tanguy, B., Latourte, F.: A reduced micromorphic single crystal plasticity model at finite deformations. Appl. Strain Local. Void Growth Ductile Met Int. J. Solids Struct. 134, 43–69 (2018). https://doi.org/10.1016/j.ijsolstr.2017.10.013
Scherer, J.M., Besson, J., Forest, S., Hure, J., Tanguy, B.: Strain gradient crystal plasticity with evolving length scale: application to voided irradiated materials. Eur. J. Mech. A. Solids 77, 103768 (2019). https://doi.org/10.1016/j.euromechsol.2019.04.003
Scherer, J.M., Phalke, V., Besson, J., Forest, S., Hure, J., Tanguy, B.: Lagrange multiplier based vs micromorphic gradient-enhanced rate-(in)dependent crystal plasticity modelling and simulation. Comput. Methods Appl. Mech. Eng. 372, 113426 (2020). https://doi.org/10.1016/j.cma.2020.113426
Ohno, N., Okumura, D.: Higher-order stress and grain size effects due to self-energy of geometrically necessary dislocations. J. Mech. Phys. Solids 55, 1879–1898 (2007)
Forest, S.: Questioning size effects as predicted by strain gradient plasticity. J. Mech. Behav. Mater. 22, 101–110 (2013)
Berdichevsky, V.L.: Continuum theory of dislocations revisited. Contin. Mech. Thermodyn. 18, 195–222 (2006)
Svendsen, B., Bargmann, S.: On the continuum thermodynamic rate variational formulation of models for extended crystal plasticity at large deformation. J. Mech. Phys. Solids 58, 1253–1271 (2010)
Forest, S., Guéninchault, N.: Inspection of free energy functions in gradient crystal plasticity. Acta. Mech. Sin. 29, 763–772 (2013)
Wulfinghoff, S., Forest, S., Böhlke, T.: Strain gradient plasticity modeling of the cyclic behavior of laminate microstructures. J. Mech. Phys. Solids 79, 1–20 (2015). https://doi.org/10.1016/j.jmps.2015.02.008
Nellemann, C., Niordson, C.F., Nielsen, K.L.: Hardening and strengthening behavior in rate-independent strain gradient crystal plasticity. Eur. J. Mech. A. Solids 67, 157–168 (2018). https://doi.org/10.1016/j.euromechsol.2017.09.006
El-Naaman, S.A., Nielsen, K.L., Niordson, C.F.: An investigation of back stress formulations under cyclic loading. Mech. Mater. 130, 76–87 (2019). https://doi.org/10.1016/j.mechmat.2019.01.005
Bardella, L.: Size effects in phenomenological strain gradient plasticity constitutively involving the plastic spin. Int. J. Eng. Sci. 48, 550–568 (2010). https://doi.org/10.1016/j.ijengsci.2010.01.003
Bayerschen, E., Böhlke, T.: Power-law defect energy in a single-crystal gradient plasticity framework: a computational study. Comput. Mech. 58, 13–27 (2016). https://doi.org/10.1007/s00466-016-1279-x
Jebahi, M., Cai, L., Abed-Meraim, F.: Strain gradient crystal plasticity model based on generalized non-quadratic defect energy and uncoupled dissipation. Int. J. Plast 126, 102617 (2020). https://doi.org/10.1016/j.ijplas.2019.10.005
Abatour, M., Ammar, K., Forest, S., Ovalle-Rodas, C., Osipov, N., Quilici, S.: A generic formulation of anisotropic thermo-elastoviscoplasticity at finite deformations for finite element codes. working paper or preprint (2021). https://hal.archives-ouvertes.fr/hal-03462216v2
Green, A.E., Naghdi, P.M.: A general theory of an elastic-plastic continuum. Arch. Ration. Mech. Anal. 18(4), 251–281 (1965). https://doi.org/10.1007/BF00251666
Miehe, C., Apel, N., Lambrecht, M.: Anisotropic additive plasticity in the logarithmic strain space: modular kinematic formulation and implementation based on incremental minimization principles for standard materials. Comput. Methods Appl. Mech. Eng. 191(47), 5383–5425 (2002). https://doi.org/10.1016/S0045-7825(02)00438-3
Kröner, E.: Allgemeine Kontinuumstheorie der Versetzungen und Eigenspannungen. Arch. Ration. Mech. Anal. 4(1), 273–334 (1959). https://doi.org/10.1007/BF00281393
Lee, E.H., Liu, D.T.: Finite strain elastic-plastic theory with application to plane-wave analysis. J. Appl. Phys. 38(1), 19–27 (1967). https://doi.org/10.1063/1.1708953
Mandel, J.: Equations constitutives et directeurs dans les milieux plastiques et viscoplastiques. Int. J. Solids Struct. 9(6), 725–740 (1973). https://doi.org/10.1016/0020-7683(73)90120-0
Forest, S., Sievert, R.: Elastoviscoplastic constitutive frameworks for generalized continua. Acta Mech. 160, 71–111 (2003)
Forest, S.: Nonlinear regularization operators as derived from the micromorphic approach to gradient elasticity, viscoplasticity and damage. Proc. R. Soc. A Math. Phys. Eng. Sci. 472(2188), 20150755 (2016). https://doi.org/10.1098/rspa.2015.0755
Friedlein, J., Mergheim, J., Steinmann, P.: Observations on additive plasticity in the logarithmic strain space at excessive strains. Int. J. Solids Struct. 239–240, 111416 (2022). https://doi.org/10.1016/j.ijsolstr.2021.111416
Steinmann, P.: Formulation and computation of geometrically non-linear gradient damage. Int. J. Numer. Methods Eng. 46(5), 757–779 (1999). https://doi.org/10.1002/(SICI)1097-0207(19991020)46:5\(<\)757::AID-NME731\(>\)3.0.CO;2-N
Geers, M.G.D., Engelen, R.A.B., Ubachs, R.J.M.: On the numerical modelling of ductile damage with an implicit gradient-enhanced formulation. Revue Européenne des éléments Finis 10(2–4), 173–191 (2001). https://doi.org/10.1080/12506559.2001.11869246
Geers, M.G.D., Ubachs, R.L.J.M., Engelen, Roy A.B..: Strongly non-local gradient-enhanced finite strain elastoplasticity. Int. J. Numer. Methods Eng. 56(14), 2039–2068 (2003). https://doi.org/10.1002/nme.654
Geers, M.G.D.: Finite strain logarithmic hyperelasto-plasticity with softening: a strongly non-local implicit gradient framework. Comput. Methods Appl. Mech. Eng. 193(30), 3377–3401 (2004). https://doi.org/10.1016/j.cma.2003.07.014
Martinez-Paneda, E., Niordson, C.F.: On fracture in finite strain gradient plasticity. Int. J. Plast 80, 154–167 (2016). https://doi.org/10.1016/j.ijplas.2015.09.009
Anand, L., Aslan, O., Chester, S.A.: A large-deformation gradient theory for elastic-plastic materials: strain softening and regularization of shear bands. Int. J. Plast. 30–31, 116–143 (2012). https://doi.org/10.1016/j.ijplas.2011.10.002
Zhang, Y., Lorentz, E., Besson, J.: Ductile damage modelling with locking-free regularised GTN model. Int. J. Numer. Meth. Eng. 113(13), 1871–1903 (2018). https://doi.org/10.1002/nme.5722
Poh, L.H., Peerlings, R.H.J., Geers, M.G.D., Swaddiwudhipong, S.: An implicit tensorial gradient plasticity model—formulation and comparison with a scalar gradient model. Int. J. Solids Struct. 48(18), 2595–2604 (2011). https://doi.org/10.1016/j.ijsolstr.2011.05.019
Wulfinghoff, S., Bayerschen, E., Böhlke, T.: Conceptual difficulties in plasticity including the gradient of one scalar plastic field variable. PAMM 14(1), 317–318 (2014). https://doi.org/10.1002/pamm.201410146
Jebahi, M., Forest, S.: Scalar-based strain gradient plasticity theory to model size-dependent kinematic hardening effects. Contin. Mech. Thermodyn. 33(4), 1223–1245 (2021). https://doi.org/10.1007/s00161-020-00967-0
Gurtin, Morton E.: On a framework for small-deformation viscoplasticity: free energy, microforces, strain gradients. Int. J. Plast 19, 47–90 (2003). https://doi.org/10.1016/S0749-6419(01)00018-3
Gudmundson, P.: A unified treatment of strain gradient plasticity. J. Mech. Phys. Solids 52, 1379–1406 (2004). https://doi.org/10.1016/j.jmps.2003.11.002
Fleck, N.A., Willis, J.R.: A mathematical basis for strain-gradient plasticity theory. Part II: tensorial plastic multiplier. J. Mech. Phys. Solids 57(7), 1045–1057 (2009). https://doi.org/10.1016/j.jmps.2009.03.007
Lorentz, E., Benallal, A.: Gradient constitutive relations: numerical aspects and application to gradient damage. Comput. Methods Appl. Mech. Eng. 194(50), 5191–5220 (2005). https://doi.org/10.1016/j.cma.2004.12.016
Chen, Y., Lorentz, E., Besson, J.: Crack initiation and propagation in small-scale yielding using a nonlocal GTN model. Int. J. Plast 130, 102701 (2020). https://doi.org/10.1016/j.ijplas.2020.102701
Chen, Y., Lorentz, E., Dahl, A., Besson, J.: Simulation of ductile tearing during a full size test using a non local Gurson–Tvergaard–Needleman (GTN) model. Eng. Fract. Mech. 261, 108226 (2022). https://doi.org/10.1016/j.engfracmech.2021.108226
Felder, S., Kopic-Osmanovic, N., Holthusen, H., Brepols, T., Reese, S.: Thermo-mechanically coupled gradient-extended damage-plasticity modeling of metallic materials at finite strains. Int. J. Plast 148, 103142 (2022). https://doi.org/10.1016/j.ijplas.2021.103142
Besson, J., Cailletaud, G., Chaboche, J.-L., Forest, S.: Non-linear Mechanics of Materials. Solid Mech. Appl. (2010). https://doi.org/10.1007/978-90-481-3356-7
Boehler, J.P.: Applications of Tensor Functions in Solid Mechanics. CISM Courses and Lectures No. 292, Udine. Springer, Wien (1987). https://doi.org/10.1007/978-3-7091-2810-7
Zheng, Q.S.: Theory of representations for tensor functions-A unified invariant approach to constitutive equations. App. Mech. Rev. 47, 545–587 (1994)
Aifantis, E.C.: On the microstructural origin of certain inelastic models. J. Eng. Mater. Technol. 106(4), 326–330 (1984). https://doi.org/10.1115/1.3225725
Forest, S., Aifantis, E.C.: Some links between recent gradient thermo-elasto-plasticity theories and the thermomechanics of generalized continua. Int. J. Solids Struct. 47(25), 3367–3376 (2010). https://doi.org/10.1016/j.ijsolstr.2010.07.009
Z-set. Non-linear material & structure analysis suite (2022). URL www.zset-software.com
Besson, J., Foerch, R.: Large scale object-oriented finite element code design. Comput. Methods Appl. Mech. Eng. 142, 165–187 (1997)
Foerch, R., Besson, J., Cailletaud, G., Pilvin, P.: Polymorphic constitutive equations in finite element codes. Comput. Methods Appl. Mech. Eng. 141, 355–372 (1997)
Bittencourt, E., Needleman, A., Gurtin, M.E., Van der Giessen, E.: A comparison of nonlocal continuum and discrete dislocation plasticity predictions. J. Mech. Phys. Solids 51, 281–310 (2003)
Fleck, N.A., Hutchinson, J.W., Willis, J.R.: Guidelines for constructing strain gradient plasticity theories. J. Appl. Mech. 82, 071002 (2015)
Mareau, C.: Thermodynamic framework for variance-based non-local constitutive models. Contin. Mech. Thermodyn. 34, 1173–1195 (2022). https://doi.org/10.1007/s00161-022-01113-8
Hütter, Geralf: Homogenization of a Cauchy continuum towards a micromorphic continuum. J. Mech. Phys. Solids 99, 394–408 (2017). https://doi.org/10.1016/j.jmps.2016.09.010
Peerlings, R.H.J.: On the role of moving elastic-plastic boundaries in strain gradient plasticity. Modell. Simul. Mater. Sci. Eng. 15(1), S109–S120 (2007). https://doi.org/10.1088/0965-0393/15/1/S10
Nouailhas, D., Cailletaud, G.: Tension-torsion behavior of single-crystal superalloys: experiment and finite element analysis. Int. J. Plast 11(4), 451–470 (1995). https://doi.org/10.1016/S0749-6419(98)80004-1
Ghiglione, F., Forest, S.: On the torsion of isotropic elastoplastic Cosserat circular cylinders. J. Micromech. Mol. Phys. 6, 1–14 (2022). https://doi.org/10.1142/S2424913021420078
Phalke, V., Kaiser, T., Scherer, J.M., Forest, S.: Modeling size effects in microwire torsion: a comparison between a Lagrange multiplier-based and a \(\text{ Curl } \text{ F}^{\text{ p }}\) gradient crystal plasticity model. Eur. J. Mech. A/Solids 94, 104550 (2021). https://doi.org/10.1016/j.euromechsol.2022.104550
Xu, Y., Poh, L.-H.: Localizing gradient-enhanced rousselier model for ductile fracture. Int. J. Numer. Meth. Eng. 119, 826–851 (2019). https://doi.org/10.1002/nme.6074
Sarkar, S., Singh, I.V., Mishra, B.K.: A localizing gradient plasticity model for ductile fracture. Comput. Methods Appl. Mech. Eng. 388, 114205 (2022). https://doi.org/10.1016/j.cma.2021.114205
Yasayanlar, S., Kaçmaz, B., Özdemir, I.: Localizing implicit gradient damage based treatment of softening in elasto-plasticity. Procedia Struct. Integr. 35, 18–24 (2022). https://doi.org/10.1016/j.prostr.2021.12.043
Diamantopoulou, E., Liu, W., Labergere, C., Badreddine, H., Saanouni, K., Hu, P.: Micromorphic constitutive equations with damage applied to metal forming. Int. J. Damage Mech 26, 314–339 (2017). https://doi.org/10.1177/1056789516684650
Miehe, C.: A multifield incremental variational framework for gradient type standard dissipative solids. J. Mech. Phys. Solids 59, 898–923 (2011)
Kocks, U.F., Mecking, H.: Physics and phenomenology of strain hardening: the FCC case. Prog. Mater Sci. 48(3), 171–273 (2003). https://doi.org/10.1016/S0079-6425(02)00003-8
Ren, S., Mazière, M., Forest, S., Morgeneyer, T.F., Rousselier, G.: A constitutive model accounting for strain ageing effects on work-hardening. Appl. C-Mn Steel. Comptes Rendus MéCanique 345(12), 908–921 (2017). https://doi.org/10.1016/j.crme.2017.09.005
Aslan, O., Cordero, N.M., Gaubert, A., Forest, S.: Micromorphic approach to single crystal plasticity and damage. Int. J. Eng. Sci. 49(12), 1311–1325 (2011). https://doi.org/10.1016/j.ijengsci.2011.03.008
Gurtin, M.E.: A gradient theory of small-deformation isotropic plasticity that accounts for the Burgers vector and for dissipation due to plastic spin. J. Mech. Phys. Solids 52, 2545–2568 (2004). https://doi.org/10.1016/j.jmps.2004.04.010
Bardella, L.: On a mixed energetic-dissipative constitutive law for non-proportional loading, with focus on small-scale plasticity. Proc. R. Soc. A 477, 20200940 (2021). https://doi.org/10.1098/rspa.2020.0940
Fassin, M., Eggersmann, R., Wulfinghoff, S., Reese, S.: Gradient-extended anisotropic brittle damage modeling using a second order damage tensor—theory, implementation and numerical examples. Int. J. Solids Struct. 167, 93–126 (2019). https://doi.org/10.1016/j.ijsolstr.2019.02.009
Langenfeld, K., Mosler, J.: A micromorphic approach for gradient-enhanced anisotropic ductile damage. Comput. Methods Appl. Mech. Eng. 360, 112717 (2020). https://doi.org/10.1016/j.cma.2019.112717
Sprave, L., Menzel, A.: A large strain gradient-enhanced ductile damage model: finite element formulation, experiment and parameter identification. Acta Mech. 231, 5159–5192 (2020). https://doi.org/10.1007/s00707-020-02786-5
Holthusen, H., Brepols, T., Reese, S., Simon, J.-W.: A two-surface gradient-extended anisotropic damage model using a second order damage tensor coupled to additive plasticity in the logarithmic strain space. J. Mech. Phys. Solids 163, 104833 (2022). https://doi.org/10.1016/j.jmps.2022.104833
Rezaee-Hajidehi, M., Sadowski, P., Stupkiewicz, S.: Deformation twinning as a displacive transformation: finite-strain phase-field model of coupled twinning and crystal plasticity. J. Mech. Phys. Solids 163, 104855 (2022). https://doi.org/10.1016/j.jmps.2022.104855
Davaze, V., Vallino, N., Feld-Payet, S., Langrand, B., Besson, J.: Plastic and fracture behavior of a dual phase steel sheet under quasi-static and dynamic loadings. Eng. Fract. Mech. 235, 107165 (2020). https://doi.org/10.1016/j.engfracmech.2020.107165
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Consistent tangent matrices in the numerical implementation
The derivation of the consistent tangent matrix for a time-independent plastic model is detailed in this first Appendix. For the sake of brevity, only the model with a micromorphic variable associated with cumulative plastic strain is detailed in the following.
The global resolution algorithm requires the following partial derivatives:


with



At Gauss point level, constitutive equations are integrated using a \(\theta \)-method [63]. The values of all integrated variables evaluated at an intermediate time designated by \(\theta \in [0,1]\) are
The set of Eq. (57) can be gathered in the following form:
Since Eq. (80) is highly nonlinear, it is usually solved by means of a Newton method which requires the calculation of the Jacobian matrix

where  is the normal to the yield surface. The value \(\theta =1\) (implicit integration) is used in the present work for rate-independent plasticity.
is the normal to the yield surface. The value \(\theta =1\) (implicit integration) is used in the present work for rate-independent plasticity.
Appendix B
Analytical solution for confined plasticity under shear
Consider the boundary value problem of Fig. 1a and introduced in Sect. 3.1. The strip is 2h-wide and infinite in the y-direction (invariant solution in this direction). In the case of a hardening plate (i.e., H \(\ge \) 0), the microplastic variable \(p_\chi \) is set to zero at \(x=\pm h\) (Dirichlet higher-order boundary conditions). In the case of a softening plate (i.e., H < 0), \(p_\chi \) is free at \(x=\pm h\) far from the localization zone (Neumann higher-order conditions). The first balance equation reads

which yields
Therefore, \(\sigma _{12}=\tau \), taken positive without loss of generality, is uniform in the plate. The second balance equation is

where the constitutive equations for generalized stresses are given by

The differential equation governing the microplastic variable \(p_\chi \) reads
The yield function is given by

where \(\sigma _\textrm{eq}=\sqrt{3}~\tau \) is the von Mises stress. By combining Eqs. (86) and (87), the following partial differential equation for \(p_\chi \) is obtained:
Three different cases can be distinguished: perfect plasticity (\(H=0\)), hardening (\(H>0\)), and softening (\(H<0\)) behavior.
1.1 B.1 Case 1: perfect plasticity (\(H = 0\))
In this case, Eq. (88) reduces to
whose solution is
where \(C_1\) and \(C_2\) are integration constants to be determined from boundary conditions:
Finally, the fields of micromorphic deformation and cumulative plastic strain are
Further, the expression of the uniform stress \(\tau \) in the plate is
Using Eq. (93), Eq. (94) reduces to
The parabolic profiles p(x) et \(p_\chi (x)\) are illustrated by Fig. 26 and used for the validation of the FE implementation of the model. It is apparent in Fig. 26a that the value \(H_\chi =10^5\) MPa ensures a very small difference \(|p-p_\chi |\). It follows that the presented solution is almost identical to the solution of the same problem using the Aifantis strain gradient plasticity model. Increasing the parameter A flattens the profiles indicating that plastic deformation is more difficult to develop and higher stresses are reached. The limit \(H_\chi \rightarrow \infty \) in Eq. (95) provides the shear stress level for the Aifantis model:
The limit \(A\rightarrow \infty \) shows that deformation is then purely elastic: \(\tau = \mu {\overline{\gamma }}\). The plastic strain gradient would be too high to develop. In contrast, setting \(A=0\) provides the classical elastic-perfectly plastic solution. The previous formula also reveals the apparent hardening modulus depending on A and the width h.
a Analytic vs. numerical fields of cumulative plastic strain p and micromorphic variable \(p_\chi \) for confined simple glide; b distribution of cumulative plastic strain for different values of the generalized modulus A. The profiles are given for the prescribed overall shear value \({\overline{\gamma }} =0.2\)
1.2 B.2 Case 2: H > 0 (hardening)
For a strictly positive linear hardening modulus, the solution of Eq. (88) reads
where
This formula defines the inverse characteristic length \(\omega \) as a function of the plastic hardening modulus and higher-order parameters. The integration constants \(C_3\) and \(C_4\) are obtained by applying boundary conditions:
It follows that
and
The value of \(\tau \) is given by
where \(Z_h=\dfrac{\sqrt{3}}{H}\left( 1-\sqrt{\dfrac{A H_\chi }{H(H+H_\chi )}}\dfrac{\tanh (\omega h)}{h} \right) \). These results are illustrated by Fig. 27. A clear difference \(|p-p_\chi |\) is visible in Fig. 27a for a low value of the penalty modulus \(H_\chi =10^3\) MPa. This difference almost vanished in Fig. 27b when \(H_\chi \) is sufficiently high. This indicates again that the gradient plasticity model by [66] is a limit case of the micromorphic model as \(H_\chi \) tends to infinity. The hyperbolic profiles can be recognized in Fig. 27c and d. Low values of the higher-order modulus A lead to flat distribution of plastic strain where high curvatures are reached for high values of A.
1.3 B.3 Shear localization solution in micromorphic plasticity (Case 3: \(H < 0\))
The development of a shear localization band in a homogeneous matrix strip is studied. The strip has a thickness of 2h in the x-direction and is infinite in the y-direction of the 2D shear plane. The stress state is homogeneous with

The localization band of finite width \(2x_c<2h\) is entirely contained in the material strip. It is assumed that no plastic flow takes place outside the localization band so that the following zones can be defined:
-
\(-h \le x \le -x_c\): elastic domain, labeled with “−" superscript;
-
\( |x | \le x_c\): plastic domain, without any label;
-
\(x_c \le x \le h\): elastic domain, labeled with “+" superscript.
Periodicity boundary conditions are applied at the boundaries \(x=\pm h\). Solutions are derived for the micromorphic plasticity model in the small deformation framework, using the standard von Mises plasticity yield function and softening modulus \(H<0\). The limit case of the Aifantis strain gradient plasticity model is also obtained. The cumulative plastic strain field p(x) and the plastic microstrain \(p_\chi (x)\) are functions of the sole variable x. The displacement field takes the following form:
where \({{\bar{\gamma }}}\) is the applied mean glide amount and u(x) is the unknown displacement fluctuation. The shear strain component is
where \(u'(x) = \textrm{d}u/\textrm{d}x\).
The material is described by a linear hardening law with initial yield stress \(R_0\) and negative hardening modulus \(H< 0\).
1.3.1 B.3.1 Solution in the elastic domain
In the elastic domain, the micro-plastic strain \(p^\pm _\chi (x)\) is the solution of the following differential equation:
This equation admits solutions of exponential type with wave number \(\omega _\chi \). For symmetry reasons, assuming localization at the center of the plastic zone, the plastic microstrain and higher-order stress \(b_x = A p_\chi '(x)\) are, respectively, even and odd functions. Since \(b_x\) is periodic, it must vanish at the boundary (flat profile of microstrain):
It follows that
where \(\alpha ^\pm \) are integration constants to be determined from boundary conditions.
1.3.2 B.3.2 Solution in the plastic domain
The yield conditions reads
As a consequence of equilibrium, the shear stress \(\tau \) is uniform. Due to the linear softening law \(H<0\), the previous equation admits harmonic solutions with the wave number
assuming \(H+H_\chi > 0\). This defines the inverse intrinsic length \(\omega _{\chi p}\) in the plastic zone. The plastic microstrain profile takes the form
The plastic strain is obtained from the plastic microstrain field by the following equation, valid for \(|x|\le x_c\):
The definition of the location \(x_c\) is given by
Four unknowns remain: \(\alpha ^+, \alpha ^-, C, x_c\) to be determined from left-over continuity requirements.
1.3.3 B.3.3 Continuity conditions
The interface conditions to be enforced are the following:
-
Continuity of microstrain at \(x=x_c\): \(p_\chi (x_c) = p_\chi ^+(x_c)\),
$$\begin{aligned} \alpha ^+ \cosh (\omega _\chi (h-x_c)) = \frac{\sqrt{3}\tau - R_0}{H} + C \cos (\omega _{\chi p} x_c). \end{aligned}$$(113) -
Continuity of microstrain at \(x=-x_c\): \(p_\chi (x_c) = p_\chi ^-(-x_c)\)
$$\begin{aligned} \alpha ^- \cosh (\omega _\chi (h-x_c)) = \frac{\sqrt{3}\tau - R_0}{H} + C \cos (\omega _{\chi p} x_c). \end{aligned}$$(114)It follows from the two previous equations that
$$\begin{aligned} \alpha ^+ = \alpha ^- = \alpha . \end{aligned}$$(115) -
Continuity of the higher-order stress component at \(x_c\): \(b_x(x_c) = b^+_x(x_c) \, \Longrightarrow \, p_\chi '(x_c) = p_\chi ^+\,\!'(x_c)\),
$$\begin{aligned} \alpha ^+\omega _\chi \sinh (\omega _\chi (h-x_c)) = C \omega _{\chi p} \sin (\omega _{\chi p} x_c). \end{aligned}$$(116) -
Continuity of the higher-order stress component at \(-x_c\): \(b_x(-x_c) = b^-_x(-x_c) \, \Longrightarrow \, p_\chi '(-x_c) = p_\chi ^-\,\!'(-x_c)\). This condition turns out to be automatically fulfilled once the result (115) is taken into account.
Only three unknowns remain, namely \(\alpha ,C,x_c\), which are determined from the three Eqs. (112), (113), and (116).
1.3.4 B.3.4 Transcendental equation for the plastic zone boundary
The equation to be solved for \(x_c\) is obtained by computing the ratio of Eq. (116) by (113):
after elimination of \(C \cos (\omega _{\chi p} x_c)\) term by means of (112).
The location \(x_c\) is therefore a zero of the function
which results in the announced transcendental equation.
Once \(x_c\) is determined, the constant C and \(\alpha \) are computed from (112) and (116):
It remains to derive the relation between \({{\bar{\gamma }}}\) and \(\tau \). This is done by means of the elasticity law:
Integration of this equation over the interval \([-h,h]\), after accounting for the periodicity of u, provides the relation between shear stress and applied shear strain:
where the average plastic strain is
Finally,
The problem can therefore be solved for each given value of the shear stress \(\tau \). The corresponding applied shear is computed from Eq. (123). Conversely, for prescribed shear \({{\bar{\gamma }}}\), the unknowns \(\tau \) and \(x_c\) are determined by solving the nonlinear system (118) and (123).
1.3.5 B.3.5 Limit case: strain gradient plasticity
The solution is straightforwardly found in the case of Aifantis strain gradient plasticity, either directly from the strain gradient plasticity equations or as a limit case of the previous micromorphic solution. The plastic field p(x) is the solution of the yield condition
in the whole plastic domain \(|x|\le x_c\). The negative hardening modulus \(H<0\) is responsible for the localization phenomenon. A harmonic solution with wave number
is found. It is the limit of the micromorphic wave number (109) by increasing the penalty on the difference between the cumulative plastic strain p and the plastic microstrain \(p_\chi \). The boundary of the plastic zone is defined by the condition
Finally, the localization band can be described by the following sinus branch:
with maximum plastic strain \(2(\sqrt{3}\tau - R_0)/H\) at \(x=0\). Using the Hooke law (120) and periodicity of displacement, the relation between shear stress and shear strain is obtained:
This relation is also obtained from the micromorphic solution (123) in the limit \(H_\chi \rightarrow \infty \), which leads to \(\tan (\omega _{\chi p}x_c)\rightarrow 0\).
1.3.6 B.3.6 Example and discussion of multiple solutions
The previous solutions are illustrated in a specific case characterized by the parameters given in Table 5. The analytical solutions are compared to finite element simulations based on the micromorphic plasticity model at small deformations. The finite element simulation is illustrated by the deformed states of the strip and plastic microstrain fields of Fig. 28.
Finite element simulation of shear localization in a micromorphic strip. Deformed states \({{\bar{\gamma }}} = 0.; 0.05; 0.1; 0.15; 0.2\), from top to bottom, respectively. The fields of plastic microstrain \(p_\chi \) are also given. The parameters of the simulation are given in Table 5
The limit case of strain gradient plasticity is illustrated by Fig. 29 where the analytical solution is compared to the FE simulations using the micromorphic model with the penalty parameter \(H_\chi = 10^5\) MPa. The same excellent agreement is observed using the Lagrange-multiplier-based model.
Figure 30 shows that the transcendental equation \(f(x)=0\), see Eq. (118), admits three solutions for \(x_c\) in the interval [0, h], namely \(x_c \simeq 1.198, 2.604, 4.012\) mm.
Figure 31 shows perfect agreement between the analytical and FE solutions, for the lowest value of \(x_c\). The regularity of the \(p_\chi (x)\) profile is clearly visible with vanishing tangents around \(x=\pm 2\) mm. In contrast, the p(x) function is not differentiable at \(\pm x_c\) and reaches higher peak value than the smoother microplastic strain \(p_\chi (x)\).
Figures 32 and 33 show the solutions obtained for the other possible values of \(x_c\). They correspond to the existence of two or three coexisting bands. However, these solutions cannot be accepted because it is apparent that the cumulative plastic strain variable takes negative values at some places, which is forbidden. This means that these solutions must be reconsidered by taking possible elastic unloading into account. This explains why these two- or three-branch solutions are not found in the FE analysis. Note also that the number of finite width localization bands is limited by the size 2h of the strip element.
Strain gradient plasticity solution of the shear localization problem with parameters listed in Table 5
Comparison between analytical and FE solutions of the shear localization problem for the micromorphic plasticity model and the smallest positive solution of the transcendental equation, with parameters listed in Table 5
Analytic solution of the shear localization problem using the second smallest positive value of \(x_c\), with parameters listed in Table 5
Analytic solution of the shear localization problem using the third smallest positive value of \(x_c\), with parameters listed in Table 5
1.3.7 B.3.7 Regularity of the Laplacian term
It is instructive to analyze the profiles of the Laplacian of the plastic and microplastic variables since it plays a fundamental role in the modeling approach. In the strain gradient plasticity limit case, the function p(x) and its first derivative are continuous at \(x=x_c\), as discussed in Sect. B.3.3 and illustrated in Fig. 29. In contrast, the second derivative
is expected to experience a discontinuity at \(x=x_c\). The discontinuity takes the value
With the parameters given in Table 5, the jump takes the value 1.47 mm\(^{-2}\). This is clearly demonstrated by Fig. 34.
According to the micromorphic model, \(p_\chi (x)\) and \(p_\chi '(x)\) are continuous functions at \(x=x_c\). The second derivative is computed as
The last result is obtained after consideration of Eqs. (113) and (119). The Laplacian of \(p_\chi \) is therefore also continuous at \(x_c\). This is a consequence of the second balance law (84) of the micromorphic model and constitutive laws for the generalized stresses a and \({{\varvec{\underline{b}}\,}}\). The latter equation results in PDE (86) which implies the continuity of the Laplacian \(\varDelta p_\chi \) under the condition that p is continuous as it is the case in the present example. The Laplacian is therefore continuous as soon as \(p-p_\chi \) is. This does not hold for the Laplacian of p(x). This is illustrated by Fig. 34 where the micromorphic response is compared to the constrained case. Note that \(x_c=1.198\) mm in the micromorphic case, which is smaller than \(x_c = 1.571\) mm found in the limit case of strain gradient plasticity. This ranking is also apparent in Fig. 34.
Note that in the constrained strain gradient plasticity model the Lagrange multiplier \(\lambda \) is directly proportional to the Laplace term. Its FE discretization with continuous shape functions is not compatible with the existence of discontinuities of the Laplacian. This may result in local oscillations around \(x=x_c\) depending on the mesh size, see the discussion in [25].
1.3.8 B.3.8 Convergence of various energies to the strain gradient plasticity case
The free energy potential adopted in the considered example for the micromorphic model is

where \(\underset{^\approx }{\varvec{C}}\) denotes the fourth-order tensor of elasticity. The micromorphic part of the free energy is
In contrast, the Aifantis strain gradient plasticity model can be described by the following free energy potential:

The plastic strain gradient part of the free energy is
It is instructive to study the convergence of the micromorphic energy contribution \(\psi ^\chi \) toward the gradient energy \(\psi _\nabla \) in the limit \(H_\chi \rightarrow \infty \), in the particular case of shear localization.
Profiles of the Laplacian of plastic strain \(p''(x)\) in the limit case of strain gradient plasticity (Aifantis model) and \(p_\chi ''(x)\) in the micromorphic case, with parameters given in Table 5. Analytic and FE results are compared
Various energy profiles in the shear localization zone. The predictions of the micromorphic model for two values of the penalty modulus (\(H_\chi =100\) MPa on the left, \(H_\chi =1000\) MPa on the right) are compared to the strain gradient plasticity solution. The other parameters are taken from Table 5
The profiles of the various contributions to the free energy of the micromorphic model are drawn in Fig. 35 for two values of the penalty modulus: \(H_\chi =100\) MPa and \(H_\chi =1000\) MPa. In the more constrained case (\(H_\chi =1000\) MPa), the gradient energy \(\psi _\nabla \) is found to almost coincide with the micromorphic energy \(\psi ^\chi \), the penalty contribution \(H_\chi (p-p_\chi )^2/2\) being negligible.
For the lower value \(H_\chi =100\) MPa, the energy densities \(\psi _\nabla \) and \(\psi ^\chi \) differ significantly. This is due, on the one hand, to the non–negligible contribution of the \(H_\chi (p-p_\chi )^2/2\) term and, on the other hand, to high values of the gradient micromorphic contribution
compared with \(\psi _\nabla \).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Abatour, M., Forest, S., Ammar, K. et al. Toward robust scalar-based gradient plasticity modeling and simulation at finite deformations. Acta Mech 234, 911–958 (2023). https://doi.org/10.1007/s00707-022-03411-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-022-03411-3




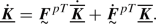
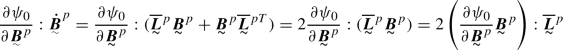
 is symmetric.
is symmetric.








