Abstract
A gradient-enhanced ductile damage model at finite strains is presented, and its parameters are identified so as to match the behaviour of DP800. Within the micromorphic framework, a multi-surface model coupling isotropic Lemaitre-type damage to von Mises plasticity with nonlinear isotropic hardening is developed. In analogy to the effective stress entering the yield criterion, an effective damage driving force—increasing with increasing plastic strains—entering the damage dissipation potential is proposed. After an outline of the basic model properties, the setup of the (micro)tensile experiment is discussed and the importance of including unloading for a parameter identification with a material model including damage is emphasised. Optimal parameters, based on an objective function including measured forces and the displacement field obtained from digital image correlation, are identified. The response of the proposed model is compared to a tensile experiment of a specimen with a different geometry as a first approach to validate the identified parameters.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The design of metal forming processes requires increasingly more accurate models to predict material behaviour in order to use more of the forming capability of the material and to more accurately predict safety margins, ultimately saving costs and energy. To this end, the description of damage, particularly damage preceding failure, needs to be improved together with the development of predictive simulation tools and models, e.g. by means of a regularised continuum damage formulation coupled to finite plasticity.
The field of damage mechanics dates back to the original findings from Kachanov [22] and further development by Rabotnov [50], who proposed a single scalar damage variable to model the effects of creep damage. For many years, only isotropic damage was considered, which, however, is in contrast to the anisotropic nature of damage mechanisms. In order to capture anisotropic damage phenomena, a tensorial damage variable may be introduced [9, 13, 23, 30]. Damage evolves with increased loading, and the form of anisotropy can change during loading. These changes may be captured by an approach which, by means of related mappings, introduces a fictitious undamaged configuration and which defines a tensorial damage variable, see [17, 41,42,43] amongst others. Research on anisotropic damage formulations is a continuously active area of research, see, e.g., [29, 64], to name but a few.
While initially only creep damage was considered, the term damage has since been extended to many different physical mechanisms and phenomenological effects, see, e.g., [44] for an overview. The present contribution focuses on ductile damage in metallic materials, i.e. we consider damage effects under large plastic deformations such as decohesion of the inclusion matrix interface as well as growth and coalescence of microvoids. Ductile damage models can be divided into micromechanically motivated models and phenomenological damage models. The probably most prominent candidate from the first category is the model based on void volume fractions proposed by Gurson [20] and its extensions by Tvergaard and Needleman [60] as well as by Rousselier [52]. Many researchers have worked on and with these models, see, e.g., the recent contributions [12, 66] and references cited therein. Phenomenological models are typically referred back to the \(1-d\) approach established by Lemaitre [31, 32] and Krajcinovic [25] and are continuously further developed, see, e.g., [5, 10, 24, 63]. A detailed literature review on ductile damage and fracture can be found in [8].
A well-known deficiency of damage models is the possible loss of ellipticity of the governing equations, which, in the context of finite elements, may lead to mesh-dependent results. To remedy mesh dependence, non-local damage theories have been proposed. The contributions by Bažant et al. [6, 7] introduce a non-local damage variable which is defined as the integral value of an only pointwise-defined, local damage variable. However, non-local formulations based on gradients are more common to use. Theories incorporating strain gradients were established at an earlier stage, see, e.g., [14, 48, 59], but thereafter theories based on gradients of other variables, such as damage, were proposed [57, 58]. Initially, the gradients of other variables were incorporated directly. However, this results in a cumbersome treatment of the Karush–Kuhn–Tucker conditions on global finite element level, e.g. by an active-set algorithm [34, 35] or by nonlinear complementarity functions [19]. Gradient-enhanced or micromorphic theories [16, 18] allow a more efficient implementation and were adopted in the field, see, e.g. [46, 49, 62, 65]. Effort has been made to explore efficient implementations of gradient enhancement into commercial finite element tools [47, 55]. A different approach to efficiently include gradients was published recently [21]. The gradient-enhanced theory was recently extended to incorporate non-constant regularisation parameters [45, 61, 65]; i.e. the gradient contribution in the free Helmholtz energy is weighted by a term dependent on history variables, e.g. the damage state itself. Another focus lies on the regularisation of anisotropic damage formulations, see, e.g., [1, 29].
A major challenge for the simulation of production processes is the identification of suitable material parameters. A detailed description of the parameter identification process in combination with the finite element method is given in [38]. Parameter identification in combination with gradient damage models is first reported in [37], though without taking full-field measurements into account. Further information regarding parameter identification is summarised in the review contributions [4, 39]. In recent years, [53] has worked on parameter identification for a local Lemaitre model including full-field data, but has tested the framework only with numerically perturbed simulation data. In [2], a GISSMO failure surface identification is performed using full-field measurements obtained via DIC (digital image correlation). Direct determination of the change in the elastic modulus—already identified as a suitable measure to quantify damage in [33]—during loading/unloading of DP800 is reported in [3].
Experimentally, damage mechanisms in DP800 were recently identified in [26] by means of algorithmic detection and categorisation of voids in large panorama images obtained by electron microscopy—a novel methodology validated against established methods in [27]. The authors primarily observed (brittle) martensite cracking at small plastic strains and a shift towards ductile mechanisms as the plastic strains increase. The dominating ductile mechanisms are void nucleation, e.g. in the form of phase boundary decohesion, and void plasticity. These mechanisms acting on the microscale will be considered in the phenomenological material model by means of their effects on the macroscale, i.e. the reduction in elastic stiffness and their influence on the evolution of damage and plasticity.
The modelling approach pursued within this contribution aims at an accurate prediction of damage and plasticity preceding macroscopic failure in order to establish a material model which can be used to simulate forming processes and which is able to quantify a safety margin. To this end, a finite strain formulation of gradient-enhanced ductile damage conceptually following the small-strain contribution [24] is adopted.
Introducing multiple damage functions—each damage function affects a different contribution in the constitutive model—together with the multi-surface formulation results in a very flexible model, capable of capturing rather brittle behaviour as well as very ductile behaviour. The influence of triaxiality and Lode parameter on damage evolution is implicitly taken into account by a split of the elastic energy into volumetric and isochoric parts, each multiplied with a different damage function. By controlling the damage parameters for the volumetric and isochoric contribution independently, damage evolution is driven by (stress) triaxiality. It has been shown that triaxiality is an important factor for driving pore growth, whereas the Lode parameter is connected to microcrack elongation [40, 67]. Triaxiality and Lode parameter have been explicitly taken into account for damage evolution in the modelling of ductile fracture in [67].
The multi-surface approach pursued herein couples damage to plasticity in a typical manner by using an effective stress in the yield function. see, e.g., [28]. Therefore, plasticity can evolve even in highly damaged material states. The recently published model [11], which includes kinematic hardening, follows a conceptually similar multi-surface approach as established as this work proceeds. Analogous to the effective stress, a novel effective damage driving force is proposed. In order to facilitate damage evolution under high plastic strains—especially for low levels of hardening or already saturated hardening—the effective damage driving force increases with increasing plastic strains.
The applicability of the proposed material model to DP800 is shown by means of microtensile experiments on two geometrically different specimens from DP800 steel sheets. In order to be able to capture the degradation effect, the monotonous tensile loading of the specimens is interrupted multiple times for a full unloading. The experiment is observed by a camera, so that the full displacement field can be obtained from DIC. Experiments on one specimen geometry are used for parameter identification. The parameter identification approach incorporating full-field measurements chosen in this work is directly based on [51] and uses an objective function formulated in terms of the force and the displacement field. The experiments on the other specimen geometry are used to validate the identified parameter set.
The paper is organised as follows. Section 2 briefly summarises the balance equations and the finite element implementation. The continuous form of the constitutive material model is described in Sect. 3, and an algorithmic implementation is given thereafter. The basic properties of the material model are discussed in Sect. 4. The next section deals with parameter identification. It is split into the description of experiments, the corresponding set-up of the simulation, the choice of the objective function and the presentation of the identified material parameters. Section 6 deals with the validation, and finally, Sect. 7 summarises the contribution and points out future research directions.
1.1 Notation
Let \(\varvec{a} = a_i\,\varvec{e}_i\) and \(\varvec{b} = b_i\,\varvec{e}_i\) be vectors, \(\varvec{C} = C_{ij}\,\varvec{e}_i\otimes \varvec{e}_j\) and \(\varvec{D} = D_{ij}\,\varvec{e}_i\otimes \varvec{e}_j\) tensors of second order and \({\varvec{\mathsf {E}}} = E_{ijkl}\,\varvec{e}_i\otimes \varvec{e}_j\otimes \varvec{e}_k\otimes \varvec{e}_l\) a tensor of fourth order with \(\{\varvec{e}_{1,2,3}\}\) a fixed orthonormal basis. Then, the single contraction \(\varvec{a} = \varvec{C}\cdot \varvec{b}\) is given as \(a_i\,\varvec{e}_i = C_{ij}\,b_j\,\varvec{e}_i\) and the double contraction \(\varvec{C} = {\varvec{\mathsf {E}}} : \varvec{D}\) is defined as \(C_{ij}\,\varvec{e}_i\otimes \varvec{e}_j = E_{ijkl}\,D_{kl}\,\varvec{e}_i\otimes \varvec{e}_j\). Furthermore, we define the non-standard dyadic products \(\varvec{C}\,\underline{\otimes }\,\varvec{D} = C_{il}\,D_{jk}\,\varvec{e}_i\otimes \varvec{e}_j\otimes \varvec{e}_k\otimes \varvec{e}_l\) and \(\varvec{C}\,\overline{\otimes }\,\varvec{D} = C_{ik}\,D_{jl}\,\varvec{e}_i\otimes \varvec{e}_j\otimes \varvec{e}_k\otimes \varvec{e}_l\).
2 Governing equations
In this section, essential kinematic relations are briefly summarised and the gradient-enhanced continuum damage framework used is introduced. The governing balance equations are derived in line with the approach detailed in [62]. The section closes with a representation of a finite element formulation, the related discretisation and the linearisation for a solution with a Newton–Raphson scheme.
2.1 Kinematics
Let  be a domain in reference configuration with referential placement
be a domain in reference configuration with referential placement  . The motion is described by
. The motion is described by  mapping referential to spatial placements
mapping referential to spatial placements  with t denoting time. Infinitesimal referential line elements
with t denoting time. Infinitesimal referential line elements  are transformed to their spatial counterparts
are transformed to their spatial counterparts  with the help of the deformation gradient, defined as
with the help of the deformation gradient, defined as

Furthermore, referential and spatial infinitesimal volume elements  and
and  are related via the determinant of
are related via the determinant of  , i.e.
, i.e.

whereas referential and spatial infinitesimal surface elements  and
and  , with their area unit normals \(\varvec{N}\) and \(\varvec{n}\), transform according to
, with their area unit normals \(\varvec{N}\) and \(\varvec{n}\), transform according to

2.2 Local and non-local energy contributions
Following the approach of [16, 58, 62], an additional (global) field variable  is introduced. This field variable
is introduced. This field variable  is coupled to the local damage state variable
is coupled to the local damage state variable  in a penalty term and is henceforth denoted as non-local damage variable. The gradient enhancement of the model is achieved by only incorporating the gradient of the non-local damage variable, allowing us to solve the ensuing Karush–Kuhn–Tucker problem on a (local) material point level. Consequently, an additive split of the Helmholtz energy into a local part
in a penalty term and is henceforth denoted as non-local damage variable. The gradient enhancement of the model is achieved by only incorporating the gradient of the non-local damage variable, allowing us to solve the ensuing Karush–Kuhn–Tucker problem on a (local) material point level. Consequently, an additive split of the Helmholtz energy into a local part  and a non-local part
and a non-local part  is assumed, i.e.
is assumed, i.e.

where  is a set of internal state variables connected to the modelling of plasticity. The non-local part of the Helmholtz energy is specified by
is a set of internal state variables connected to the modelling of plasticity. The non-local part of the Helmholtz energy is specified by

where  is denoted as penalty parameter and where
is denoted as penalty parameter and where  is referred to as regularisation parameter in the following. As this work proceeds,
is referred to as regularisation parameter in the following. As this work proceeds,  shall be considered to be constant. The particular choice of the non-local energy contribution is not unique, see Remark 1.
shall be considered to be constant. The particular choice of the non-local energy contribution is not unique, see Remark 1.
Remark 1
In general, one may introduce gradients of the micromorphic variable into the non-local energy contribution. For the damage model considered here, this is either the referential gradient  or its spatial counterpart
or its spatial counterpart  . For a gradient-enhanced crystal plasticity model, the advantages and interpretation of gradients with respect to the reference configuration, the intermediate configuration and the current configuration are discussed in [36]. For the phenomenological damage model considered in the present work, where the damage variable cannot directly be related to any quantity on the microscale, an interpretation of the different gradient choices is not straightforward. Hence, the (constant) parameter
. For a gradient-enhanced crystal plasticity model, the advantages and interpretation of gradients with respect to the reference configuration, the intermediate configuration and the current configuration are discussed in [36]. For the phenomenological damage model considered in the present work, where the damage variable cannot directly be related to any quantity on the microscale, an interpretation of the different gradient choices is not straightforward. Hence, the (constant) parameter  is denoted as regularisation parameter and not as classic characteristic length, even though it correlates with the width of the damage zone. In this contribution, the gradient with respect to the reference configuration is chosen (5), since for tensile loading one typically observes
is denoted as regularisation parameter and not as classic characteristic length, even though it correlates with the width of the damage zone. In this contribution, the gradient with respect to the reference configuration is chosen (5), since for tensile loading one typically observes  and a stronger regularisation can be expected. Furthermore, the regularisation properties may be controlled more precisely by letting the regularisation parameter depend on the current and/or past state of deformation, i.e.
and a stronger regularisation can be expected. Furthermore, the regularisation properties may be controlled more precisely by letting the regularisation parameter depend on the current and/or past state of deformation, i.e.  , as other researches proposed, see, e.g., [61, 65]. Due to the already quite numerous parameters which need to be identified in the subsequent parameter identification, the regularisation parameter shall be constant in this work.
, as other researches proposed, see, e.g., [61, 65]. Due to the already quite numerous parameters which need to be identified in the subsequent parameter identification, the regularisation parameter shall be constant in this work.
2.3 Weak formulation
The total energy of the quasi-static system considered is described by the total potential energy, i.e.

split into internal and external contributions. The internal energy depends on the Helmholtz energy  and is given by
and is given by

Assuming that only deformation-independent (dead) loads act on the body, the external potential energy is defined by

with the (dead) body force  and the (dead) traction forces
and the (dead) traction forces  acting on the surface
acting on the surface  . Following the postulate of minimum potential energy, i.e.
. Following the postulate of minimum potential energy, i.e.


one obtains the governing system of equations in weak form as


whereby homogeneous Neumann boundary conditions are assumed in (12).
2.4 Discretisation
The boundary value problem is discretised in time and space. Since the quasi-static problem shall not explicitly depend on time, the simulated time is only used to incrementally apply external loads. The actual time step is obtained as \(t_{n+1} = t_n + \varDelta t_n\)n, where the time increment \(\varDelta t_n\) is not necessarily constant. In view of the discretisation in space, configuration  is subdivided into
is subdivided into  finite elements so that
finite elements so that

To each element e, there are  nodes attached which are referred to the deformation
nodes attached which are referred to the deformation  and, respectively,
and, respectively,  nodes which are referred to the non-local damage field
nodes which are referred to the non-local damage field  . The referential placements
. The referential placements  are interpolated with shape functions
are interpolated with shape functions  resulting in
resulting in

where  is the referential placement at node A. Following an isoparametric concept (
is the referential placement at node A. Following an isoparametric concept ( ) together with the Bubnov–Galerkin method, one obtains
) together with the Bubnov–Galerkin method, one obtains

Inserting the discretisation (15) into the weak forms (11) and (12) allows us to separate the nodal values from the test functions, and, together with the definitions of the internal and external forces



the discretised weak forms result in

The occurring derivatives can be identified as the Piola stress tensor  and the nonlinear damage driving forces, i.e.
and the nonlinear damage driving forces, i.e.

2.5 Linearisation
The nonlinear equations (19) are solved with an iterative Newton–Raphson scheme. A Taylor series expansion at iteration step \(i+1\), neglecting further higher-order terms, yields


where  and
and  are the increments of the respective field. The total derivatives of the residuals are computed elementwise. Introducing the stiffness contributions
are the increments of the respective field. The total derivatives of the residuals are computed elementwise. Introducing the stiffness contributions




with  being the second-order identity tensor, and aggregating all nodal quantities in the element quantities
being the second-order identity tensor, and aggregating all nodal quantities in the element quantities

allows the assembly of the global residual, stiffness matrix and increments as

Finally, one obtains the global linearised system

3 A multi-surface ductile damage model
This section deals with the formulation of the material model. Adopting an additive split of the elasticity-related parts of the Helmholtz energy into volumetric and isochoric contributions entails, in combination with different damage functions, an implicit influence of stress triaxiality and Lode parameter on damage evolution. A multi-surface formulation shall be established including plastic and damage dissipation potentials which are based on effective driving forces. The damage driving force is thereby influenced by the plasticity-related state and vice versa. Moreover, associated evolution equations are derived and thereafter discretised in time. The algorithmic formulation of the material model is then presented. The Lagrange multiplier associated with plasticity can be obtained from a radial return scheme in principal stress space. Together with the Lagrange multiplier connected to damage, a two-surface problem arises which may be solved with an active-set algorithm.
3.1 Continuous formulation
Assuming a multiplicative split of the deformation gradient  , the elastic Finger tensor and its spectral decomposition are given by
, the elastic Finger tensor and its spectral decomposition are given by

The logarithmic strains  are defined as
are defined as

and the volumetric and isochoric logarithmic strains are obtained as

The local part of the Helmholtz energy is split into a volumetric, an isochoric and a plastic contribution, to be specific

with compression and shear moduli  and
and  . The hardening parameters are
. The hardening parameters are  and
and  , see also Remark 2. The internal state variables
, see also Remark 2. The internal state variables  are assumed to be the plastic part of the deformation gradient
are assumed to be the plastic part of the deformation gradient  and the variable
and the variable  representing effects of proportional hardening. The dependence of the local Helmholtz energy on the total and plastic part of the deformation gradient is implicitly taken into account via the elastic logarithmic strains
representing effects of proportional hardening. The dependence of the local Helmholtz energy on the total and plastic part of the deformation gradient is implicitly taken into account via the elastic logarithmic strains  . The so-called damage functions
. The so-called damage functions  degrade the effective elastic properties of the material for increasing values of the local damage variable
degrade the effective elastic properties of the material for increasing values of the local damage variable  , i.e.
, i.e.

where the parameter  influences the rate of degradation and where
influences the rate of degradation and where  weights the influence on the different termsFootnote 1. The local damage variable
weights the influence on the different termsFootnote 1. The local damage variable  is only constrained to be nonnegative, but not constrained from the above which is in contrast to classic \([1-d]\) approaches and also advantageous for the algorithmic treatment as this work proceeds.
is only constrained to be nonnegative, but not constrained from the above which is in contrast to classic \([1-d]\) approaches and also advantageous for the algorithmic treatment as this work proceeds.
The dissipation inequality in local form is given by

with the material time derivative  and the spatial velocity gradient
and the spatial velocity gradient  . Following the framework of standard dissipative materials, the driving forces
. Following the framework of standard dissipative materials, the driving forces  include the (spatial) Mandel stresses, an isotropic hardening stress and a damage driving force, to be specific
include the (spatial) Mandel stresses, an isotropic hardening stress and a damage driving force, to be specific



Representation (36) requires isotropic elastic properties so that  turns out to be symmetric. By inserting the driving forces into the dissipation inequality (35) and with the split of the spatial velocity gradient into an elastic and plastic part,
turns out to be symmetric. By inserting the driving forces into the dissipation inequality (35) and with the split of the spatial velocity gradient into an elastic and plastic part,  with
with  , one obtains the reduced dissipation inequality
, one obtains the reduced dissipation inequality

A multi-surface formulation is proposed in order to determine the evolution of damage and plasticity. Therefore, damage can evolve independently from plasticity which is important for the regularisation framework, see [24]. Furthermore, it offers excellent flexibility in terms of obtaining a ductile or brittle response. The admissible domain for the driving forces  is the union of the admissible plastic and admissible damage domain, i.e.
is the union of the admissible plastic and admissible damage domain, i.e.

The admissible damage and plasticity domains are each governed by dissipation potentials  and
and  , respectively, such that
, respectively, such that


The dissipation potentials are formulated in terms of effective driving forces  and
and  in the form of
in the form of

The effective Mandel stresses  can be motivated by the postulate of strain equivalence, where the load-bearing cross section is reduced by the factor
can be motivated by the postulate of strain equivalence, where the load-bearing cross section is reduced by the factor  in the damaged state. In analogy to the effective Mandel stresses, the damage driving force
in the damaged state. In analogy to the effective Mandel stresses, the damage driving force  is divided by a function dependent on the proportional hardening variable
is divided by a function dependent on the proportional hardening variable  , see also Remark 2. For the plastic dissipation potential
, see also Remark 2. For the plastic dissipation potential  , a von Mises yield surface with isotropic hardening is assumed, i.e.
, a von Mises yield surface with isotropic hardening is assumed, i.e.

with the initial yield stress  . The damage dissipation potential, given by
. The damage dissipation potential, given by

compares the effective damage driving force  to a threshold value
to a threshold value  multiplied by a term that increases from zero to one with increasing local damage variable
multiplied by a term that increases from zero to one with increasing local damage variable  and that additionally depends on the parameter
and that additionally depends on the parameter  . The effects of this additional term are elaborated in Remark 4. Straightforward calculation of damage driving force
. The effects of this additional term are elaborated in Remark 4. Straightforward calculation of damage driving force  results in an expression dependent on the elastic logarithmic strains. However, it is possible to transform
results in an expression dependent on the elastic logarithmic strains. However, it is possible to transform  into an expression dependent on stress triaxiality and equivalent stress, see Appendix A.1. Stress triaxiality (and Lode parameter) has been identified as an important quantity driving damage evolution, see, e.g., [67] amongst others.
into an expression dependent on stress triaxiality and equivalent stress, see Appendix A.1. Stress triaxiality (and Lode parameter) has been identified as an important quantity driving damage evolution, see, e.g., [67] amongst others.
Associative evolution equations are obtained as



with two Lagrange multipliers  and
and  . The underlying Karush–Kuhn–Tucker (KKT) conditions result in two sets of loading and unloading conditions,
. The underlying Karush–Kuhn–Tucker (KKT) conditions result in two sets of loading and unloading conditions,

Based on (44), the flow direction of plastic deformation in (46) specifies to  .
.
Remark 2
The specific form of the plastic contribution in the Helmholtz energy (33) is a generalisation of linear isotropic hardening through the parameter  , with
, with  together with (44, 47) corresponding to linear hardening. For
together with (44, 47) corresponding to linear hardening. For  , the transition between the elastic and plastic stages (in the load–displacement diagram) becomes smooth, as is observed in dual-phase steels such as DP800 for which a parameter identification is carried out later on in Sect. 5. Other forms of nonlinear hardening, such as saturation-type hardening, can be considered but may have adverse side effects. To give an example,
, the transition between the elastic and plastic stages (in the load–displacement diagram) becomes smooth, as is observed in dual-phase steels such as DP800 for which a parameter identification is carried out later on in Sect. 5. Other forms of nonlinear hardening, such as saturation-type hardening, can be considered but may have adverse side effects. To give an example,  and consideration of saturation-type hardening may lead to a state of quasi-perfect plasticity. At this state, no further damage may evolve, since the elastic strains remain constant. This motivated the introduction of the effective damage driving force, (43).
and consideration of saturation-type hardening may lead to a state of quasi-perfect plasticity. At this state, no further damage may evolve, since the elastic strains remain constant. This motivated the introduction of the effective damage driving force, (43).
Remark 3
An alternative formulation can be obtained by multiplying plastic potential  . Instead of an effective stress measure entering the plastic potential, the current yield surface is shrunk with evolving damage. In a similar way, damage potential
. Instead of an effective stress measure entering the plastic potential, the current yield surface is shrunk with evolving damage. In a similar way, damage potential  can be multiplied with hardening-dependent function
can be multiplied with hardening-dependent function  , such that the current damage threshold is decreased by plastic hardening. For the model chosen here, with associated evolution equations, these modifications lead to the same effective material behaviour, but they may influence the numerical robustness. Formulating a model as described above allows a comparison with the (small-strain) crystal-plasticity model incorporating damage proposed in [54]. To this end, the here-proposed dissipation potentials governing evolution of damage and plasticity might alternatively be formulated as
, such that the current damage threshold is decreased by plastic hardening. For the model chosen here, with associated evolution equations, these modifications lead to the same effective material behaviour, but they may influence the numerical robustness. Formulating a model as described above allows a comparison with the (small-strain) crystal-plasticity model incorporating damage proposed in [54]. To this end, the here-proposed dissipation potentials governing evolution of damage and plasticity might alternatively be formulated as


The potentials proposed in [54] are given by


with constants \(r_0\), \(Y_0\) and \(\beta \). The similar structure of (50, 51) and (52, 53) becomes obvious, with two main differences: firstly, the structure following [54] is additive, while the structure in this contribution is multiplicative—these differences are analogous to the additive and multiplicative decomposition of strains and deformation gradient, respectively. Secondly, the function \(\varLambda (\bullet )\) is monotonically increasing, while  is monotonically decreasing. This difference stems from the different damage formulations in the two models. The damage variable proposed in [54] can be interpreted as an inelastic strain-type contribution, whereas the damage variable in this contribution corresponds to a reduction in stiffness.
is monotonically decreasing. This difference stems from the different damage formulations in the two models. The damage variable proposed in [54] can be interpreted as an inelastic strain-type contribution, whereas the damage variable in this contribution corresponds to a reduction in stiffness.
Remark 4
In the damage dissipation potential (45), the threshold value is weighted by the term  , which results in an initial (
, which results in an initial ( ) threshold value of zero. However, due to the exponential type of the term, the threshold value quickly increases. In the overall response, this results in a smooth transition into the damage region. Therefore, the numerical robustness is improved and a more controlled interplay of damage and plasticity is possible. Consequently, a response with higher ductility can be obtained. Alternatively, one may introduce a constant (initial) threshold value, since an immediate onset of damage is difficult to physically interpret. Other researchers have proposed terms with similar effect; e.g. [10] introduced the so-called damage hardening—comparable to proportional hardening for plasticity—in the context of crystal plasticity [54] suggested an internal Helmholtz energy with mixed contributions containing isotropic damage as well as proportional hardening, see also Remark 3.
) threshold value of zero. However, due to the exponential type of the term, the threshold value quickly increases. In the overall response, this results in a smooth transition into the damage region. Therefore, the numerical robustness is improved and a more controlled interplay of damage and plasticity is possible. Consequently, a response with higher ductility can be obtained. Alternatively, one may introduce a constant (initial) threshold value, since an immediate onset of damage is difficult to physically interpret. Other researchers have proposed terms with similar effect; e.g. [10] introduced the so-called damage hardening—comparable to proportional hardening for plasticity—in the context of crystal plasticity [54] suggested an internal Helmholtz energy with mixed contributions containing isotropic damage as well as proportional hardening, see also Remark 3.
3.2 Algorithmic formulation
The algorithmic treatment of the evolution equations requires a discretisation in time. The evolution equations for isotropic hardening (47) and isotropic damage (48) are discretised with an implicit backward Euler scheme. In order to fulfil the plastic incompressibility condition,  , an implicit exponential integration scheme is applied for the integration related to the evolution of plastic deformation contributions. For the particular model chosen, this results in a radial return scheme. For better readability, the index \(n+1\), referring to the current time step \(t_{n+1} = t_n + \varDelta t\), is omitted as this work proceeds and only quantities from the previous time step are indexed with n. With the incremental Lagrange multipliers
, an implicit exponential integration scheme is applied for the integration related to the evolution of plastic deformation contributions. For the particular model chosen, this results in a radial return scheme. For better readability, the index \(n+1\), referring to the current time step \(t_{n+1} = t_n + \varDelta t\), is omitted as this work proceeds and only quantities from the previous time step are indexed with n. With the incremental Lagrange multipliers  and
and  , the discretised evolution equations result in
, the discretised evolution equations result in



The algorithmic update for the plastic deformation gradient  requires the return direction in the intermediate configuration
requires the return direction in the intermediate configuration  , defined with the Mandel stresses in the intermediate configuration
, defined with the Mandel stresses in the intermediate configuration  . Computing the deviatoric spatial Mandel stresses
. Computing the deviatoric spatial Mandel stresses  in spectral decomposition, i.e.
in spectral decomposition, i.e.

the spatial return direction can be identified as

where the principal directions  of the spatial stresses coincide with the principal directions of the elastic Finger tensor due to isotropic elasticity. The return direction
of the spatial stresses coincide with the principal directions of the elastic Finger tensor due to isotropic elasticity. The return direction  transforms in the same manner as the plastic velocity gradient
transforms in the same manner as the plastic velocity gradient  , i.e.
, i.e.  .
.
Let  denote the trial elastic Finger tensor computed with the current deformation gradient
denote the trial elastic Finger tensor computed with the current deformation gradient  and the plastic deformation gradient of the previous time step
and the plastic deformation gradient of the previous time step  as
as

For the particular model considered, the principal directions  coincide with the principal directions of the trial state
coincide with the principal directions of the trial state  . Consequently, the relation
. Consequently, the relation  holds, such that the computation of the updated Lagrange multipliers can be performed in principal stress space, i.e. only two scalar equations need to be solved. The update of the elastic Finger tensor can be written as
holds, such that the computation of the updated Lagrange multipliers can be performed in principal stress space, i.e. only two scalar equations need to be solved. The update of the elastic Finger tensor can be written as

A modified representation of the functions  and
and  in the form of
in the form of


is employed, where the perturbation parameter \(\epsilon > 0\) is typically in the order of \(10^{-3}\) to \(10^{-5}\). The functions  and
and  relate inversely to each other. The main goal of the perturbation parameter is to stabilise the global Newton–Raphson scheme for the strongly coupled problem; i.e. damage evolution depends on plasticity evolution and vice versa. While in the converged state
relate inversely to each other. The main goal of the perturbation parameter is to stabilise the global Newton–Raphson scheme for the strongly coupled problem; i.e. damage evolution depends on plasticity evolution and vice versa. While in the converged state  with \(a_\epsilon \gg 1\) holds, during the Newton–Raphson iterations
with \(a_\epsilon \gg 1\) holds, during the Newton–Raphson iterations  may occur which may lead to divergence. Consequently, the perturbation parameter \(\epsilon \) has no visible influence on the response of the simulation.
may occur which may lead to divergence. Consequently, the perturbation parameter \(\epsilon \) has no visible influence on the response of the simulation.
3.2.1 Update of Lagrange multipliers in principal stress space
Several solution procedures exist in order to solve this multi-surface problem, cf. [24], the active-set strategy of which will be adopted here. To shorten the notation, \({\bar{\bullet }}\) is introduced as the n-tuple of eigenvalues of the tensor \(\bullet \) and the derivative of the damage functions with respect to the damage variable is abbreviated as

Considering an elastic trial step,  , both dissipation potentials are evaluated; see Table 1, step 4. If the KKT conditions (49) are fulfilled, the current step remains elastic and the update of internal variables and the computation of stresses and driving forces are straightforward. If any KKT condition is violated, the active-set algorithm starts. In fact, a simplistic algorithmic form of the active-set algorithm can be employed here since only two conditions need to be fulfilled. This reduces the maximum number of remaining cases to three: a) only plasticity evolves; b) only damage evolves; and c) damage and plasticity evolve.
, both dissipation potentials are evaluated; see Table 1, step 4. If the KKT conditions (49) are fulfilled, the current step remains elastic and the update of internal variables and the computation of stresses and driving forces are straightforward. If any KKT condition is violated, the active-set algorithm starts. In fact, a simplistic algorithmic form of the active-set algorithm can be employed here since only two conditions need to be fulfilled. This reduces the maximum number of remaining cases to three: a) only plasticity evolves; b) only damage evolves; and c) damage and plasticity evolve.
Let the active set \({\mathcal {A}}\) be a subset of the total set \({\mathcal {T}}\) composed of the plastic and damage part,  . The initial active set in iteration \(k=1\) is determined by the values of the inelastic potentials, i.e.
. The initial active set in iteration \(k=1\) is determined by the values of the inelastic potentials, i.e.  if
if  and
and  otherwise. For the current active set \({\mathcal {A}}_k\), the corresponding Lagrange multipliers are solved subject to
otherwise. For the current active set \({\mathcal {A}}_k\), the corresponding Lagrange multipliers are solved subject to  and/or
and/or  using a Newton–Raphson scheme. Since the Newton–Raphson scheme for the cases where only damage or only plasticity is active requires the same quantities as in the case where both damage and plasticity evolve, only the latter case is detailed here. The Newton–Raphson scheme is set up with the unknowns
using a Newton–Raphson scheme. Since the Newton–Raphson scheme for the cases where only damage or only plasticity is active requires the same quantities as in the case where both damage and plasticity evolve, only the latter case is detailed here. The Newton–Raphson scheme is set up with the unknowns  , the residuum
, the residuum  and the Jacobian
and the Jacobian  given by
given by

In each iteration, the update of variables depending on Lagrange multipliers  is computed and the entries of the new residuum are determined; see Table 2, step 3. The entries of Jacobian
is computed and the entries of the new residuum are determined; see Table 2, step 3. The entries of Jacobian  are described in Appendix A.2. Each iteration is completed by updating the unknown Lagrange multipliers as
are described in Appendix A.2. Each iteration is completed by updating the unknown Lagrange multipliers as

The Newton–Raphson scheme is deemed converged once  is smaller than a chosen tolerance. The active-set algorithm continues in the next iteration by updating the active set \({\mathcal {A}}_{k+1} = {\mathcal {A}}_k\). First, the set with the smallest (negative) incremental Lagrange multiplier is removed and the multiplier reset to zero, i.e.
is smaller than a chosen tolerance. The active-set algorithm continues in the next iteration by updating the active set \({\mathcal {A}}_{k+1} = {\mathcal {A}}_k\). First, the set with the smallest (negative) incremental Lagrange multiplier is removed and the multiplier reset to zero, i.e.

Secondly, the largest inactive constraint is added to the active set, i.e.

If the active set did not change, i.e. \({\mathcal {A}}_{k+1}\) is identical to \({\mathcal {A}}_k\), the active-set algorithm is finished, otherwise an update for the Lagrange multipliers of the new active set \({\mathcal {A}}_{k+1}\) has to be determined.
3.2.2 Determination of stresses and stiffness contributions
With the updated Lagrange multipliers at hand, the update for the internal variables as well as the stresses and driving forces can be computed; see Table 1, steps 6 and 7. The Piola stress tensor  (20) is required for the finite element implementation chosen here and can be obtained from a transformation of the Mandel stresses as
(20) is required for the finite element implementation chosen here and can be obtained from a transformation of the Mandel stresses as

In the context of a finite element implementation, the total derivatives of the driving forces with respect to the field variables are required to be computed, see (23)-(26). Since a significant portion of the algorithm is computed in principal space, it is convenient to also split the derivatives into contributions computed in principal space and contributions computed in the Cartesian basis system. Following the algorithmic structure in [56], the spatial elasticity tensor  can be split into derivatives of the stress eigenvalues and the derivatives of the eigenvectors; see Table 3, step 1. The derivative of the stress eigenvalues with respect to the logarithmic strain eigenvalues is supplied in Appendix A.3. A transformation of the tangent operator contribution
can be split into derivatives of the stress eigenvalues and the derivatives of the eigenvectors; see Table 3, step 1. The derivative of the stress eigenvalues with respect to the logarithmic strain eigenvalues is supplied in Appendix A.3. A transformation of the tangent operator contribution  yields the derivative of the Piola stresses with respect to the deformation gradient; see Table 3, step 2. All derivatives of the stresses and driving forces which are required for the finite element implementation are summarised in Table 3, and further derivatives are specified in Appendix A.3.
yields the derivative of the Piola stresses with respect to the deformation gradient; see Table 3, step 2. All derivatives of the stresses and driving forces which are required for the finite element implementation are summarised in Table 3, and further derivatives are specified in Appendix A.3.
4 Basic model properties
This section illustrates the constitutive behaviour of the local ductile damage model by means of a homogeneous uniaxial deformation test. The influence of the material and model parameters is analysed in order to demonstrate basic model properties representing different material responses.
4.1 Homogeneous tension
An analysis of the implemented ductile damage model under homogeneous uniaxial tension loading is performed by prescribing a deformation in the form of

with  and where the stretch
and where the stretch  develops such that the stress is uniaxial in the direction of \(\varvec{e}\), i.e.
develops such that the stress is uniaxial in the direction of \(\varvec{e}\), i.e.  . The applied deformation is not increasing monotonously but rather it is interrupted at stretch values of \(1.1,\,1.15\) and 1.2 to simulate unloading behaviour. The exact load curve
. The applied deformation is not increasing monotonously but rather it is interrupted at stretch values of \(1.1,\,1.15\) and 1.2 to simulate unloading behaviour. The exact load curve  is depicted in Fig. 1. The gradient terms, and thus also the gradient-related parameters
is depicted in Fig. 1. The gradient terms, and thus also the gradient-related parameters  and
and  , are not active, since a homogeneous deformation is applied.
, are not active, since a homogeneous deformation is applied.
The influence of individual parameters is demonstrated by comparing the simulation responses of a reference parameter set with responses where the studied parameter is increased and decreased. For the reference parameter set, the material parameters are adopted from an early stage of parameter identification, see Sect. 5, and resemble the typical response of a ductile steel, see Table 4.
The variations in two parameters each are grouped together, and the response is illustrated in three figures (Figs. 2, 3 and 4), each depicting the stress–stretch response, the evolution of proportional hardening  and the evolution of the isotropic damage variable
and the evolution of the isotropic damage variable  . The stress–stretch response can be divided into three stages—the (very small) first stage shows an elastic response, the second stage is dominated by plastic behaviour and in the last stage degradation of the material takes place. For all parameter combinations (apart from one), plasticity and damage both continue to evolve throughout the subsequent loading. Although the plastic parameters—yield stress
. The stress–stretch response can be divided into three stages—the (very small) first stage shows an elastic response, the second stage is dominated by plastic behaviour and in the last stage degradation of the material takes place. For all parameter combinations (apart from one), plasticity and damage both continue to evolve throughout the subsequent loading. Although the plastic parameters—yield stress  , hardening modulus
, hardening modulus  and hardening exponent
and hardening exponent  —are common in the literature and have been extensively studied, the variation thereof is included here in order to demonstrate the non-intuitive influence upon the damage evolution. Increasing the yield stress (Fig. 2a, green line), hardening modulus (Fig. 2b, green line) and decreasing the hardening exponent (Fig. 3b, red line) all lead to slower evolution of plasticity and to a larger maximum of the elastic strains. Consequently, the stress is higher in the plasticity-dominated stage. However, this also leads to an increased damage driving force and accelerates the evolution of damage—a smaller plasticity-dominated stage is observed compared to the reference, and a more pronounced decline in stress is observed in the last stage. The opposite effect, i.e. plasticity evolves more strongly and the decline in stress is less pronounced, is observed if these parameters are varied such that plasticity evolves more.
—are common in the literature and have been extensively studied, the variation thereof is included here in order to demonstrate the non-intuitive influence upon the damage evolution. Increasing the yield stress (Fig. 2a, green line), hardening modulus (Fig. 2b, green line) and decreasing the hardening exponent (Fig. 3b, red line) all lead to slower evolution of plasticity and to a larger maximum of the elastic strains. Consequently, the stress is higher in the plasticity-dominated stage. However, this also leads to an increased damage driving force and accelerates the evolution of damage—a smaller plasticity-dominated stage is observed compared to the reference, and a more pronounced decline in stress is observed in the last stage. The opposite effect, i.e. plasticity evolves more strongly and the decline in stress is less pronounced, is observed if these parameters are varied such that plasticity evolves more.
Stress–stretch diagrams a and b, proportional hardening–stretch diagrams c and d and damage–stretch diagrams e and f. Influence of the initial yield limit  and the damage threshold
and the damage threshold  a, c and e as well as the hardening modulus
a, c and e as well as the hardening modulus  and the damage rate factor
and the damage rate factor  b, d and f on the material response under homogeneous tension
b, d and f on the material response under homogeneous tension
Stress–stretch diagrams a and b, proportional hardening–stretch diagrams c and d and damage–stretch diagrams e and f. Influence of the isochoric damage factor  and the effective stress factor
and the effective stress factor  a, c and e as well as the hardening exponent
a, c and e as well as the hardening exponent  and the damage threshold factor
and the damage threshold factor  b, d and f on the material response under homogeneous tension
b, d and f on the material response under homogeneous tension
Variation in the damage threshold  (Fig. 2a) and the damage rate factor
(Fig. 2a) and the damage rate factor  (Fig. 2b) leads to expected results. A higher threshold value and/or lower damage rate factor yields stiffer responses with less evolution of damage and more evolution of plasticity. Vice versa, stresses are lower and less plasticity evolution is observed. For a higher damage rate factor, damage accumulation is not necessarily higher compared to the reference set. Since the stiffness is influenced by a product of damage rate factor
(Fig. 2b) leads to expected results. A higher threshold value and/or lower damage rate factor yields stiffer responses with less evolution of damage and more evolution of plasticity. Vice versa, stresses are lower and less plasticity evolution is observed. For a higher damage rate factor, damage accumulation is not necessarily higher compared to the reference set. Since the stiffness is influenced by a product of damage rate factor  and damage variable
and damage variable  , however, the overall degradation of the elastic properties is higher. A much more diverse response is obtained by varying the damage influence factors
, however, the overall degradation of the elastic properties is higher. A much more diverse response is obtained by varying the damage influence factors  (Fig. 3). While the influence factor on the isochoric elastic energy
(Fig. 3). While the influence factor on the isochoric elastic energy  (Fig. 3a) exhibits a similar behaviour to the damage rate factor
(Fig. 3a) exhibits a similar behaviour to the damage rate factor  (Fig. 2b), the influence factor for the effective stress
(Fig. 2b), the influence factor for the effective stress  (Fig. 3a) has a significant impact on the overall response. Increasing the factor leads to a slightly stiffer response (cyan line). However, a decrease (orange line) leads to an abrupt drop in the stress response. At some point, the yield limit is higher than the effective stress, and evolution of plasticity stops. Instead, damage evolution strongly increases reaching a value ten times above the reference parameter set. The reason lies in the lower influence factor
(Fig. 3a) has a significant impact on the overall response. Increasing the factor leads to a slightly stiffer response (cyan line). However, a decrease (orange line) leads to an abrupt drop in the stress response. At some point, the yield limit is higher than the effective stress, and evolution of plasticity stops. Instead, damage evolution strongly increases reaching a value ten times above the reference parameter set. The reason lies in the lower influence factor  , which results in an insufficient compensation of damage in the effective stress. The influence factor in the damage potential
, which results in an insufficient compensation of damage in the effective stress. The influence factor in the damage potential  (Fig. 3b) mainly affects the transition from the plasticity-dominated stage into the final stage. At some point, the stress response and the accumulated damage coincide and the equivalent plastic strains only differ by a small amount. Figure 4 demonstrates the effect of the coupling factor
(Fig. 3b) mainly affects the transition from the plasticity-dominated stage into the final stage. At some point, the stress response and the accumulated damage coincide and the equivalent plastic strains only differ by a small amount. Figure 4 demonstrates the effect of the coupling factor  . Increasing the parameter
. Increasing the parameter  leads, as expected, to an increased evolution of damage, especially in the later stages of loading where plasticity has already been accumulated.
leads, as expected, to an increased evolution of damage, especially in the later stages of loading where plasticity has already been accumulated.
5 Parameter identification
The previously described ductile damage model shall now be employed to predict the behaviour of DP800 steel. To this end, a parameter identification is necessary, i.e. a numerical optimisation scheme. At this stage, a simplex algorithm is carried out to determine (optimal) parameters in terms of an objective function which evaluates how well simulation results and experimental data match based on a least squares criterion. This section describes how the required experimental data are obtained and how simulation and objective function are set up and gives details on the parameter identification approach.
5.1 Experimental data
For the parameter identification process, a tensile specimen of type A, see Fig. 5a, is chosen and subjected to tensile loading with three unloading stages. The specimens are cut with a water jet from DP800 sheets with a thickness of \(1.5\hbox {mm}\). In the tensile experiment, loading is applied by controlling the traverse displacement, see Fig. 6a. The experiment is captured by a camera, see Fig. 7a, which enables a determination of the inhomogeneous displacement field in a post-processing step. In addition, the camera is simultaneously used as an optical extensometer during the experiment, which allows a real-time measurement of the displacements \(u_\parallel \) in tensile direction and \(u_\perp \) perpendicular to the tensile direction in the centre of the specimen. The optical extensometer measures the average displacement on the edges of a \(10\hbox {mm}\) by \(2.6\hbox {mm}\) rectangle, which is positioned at the centre of the specimen and which has its longer side aligned with the tensile direction. The force is measured by a \(10\hbox {kN}\) load cell. All experiments were carried out with a micro-tensile machine from Kammrath & Weiß supporting a maximum load of \(10\hbox {kN}\). DIC (digital image correlation) is performed by means of the software Veddac 7.
Geometries of specimens A and B with dimensions. The actual specimens are measured optically revealing an average minimum width of \(B=3.85\hbox {mm}\) and an average radius of \(R=39.4\hbox {mm}\) for specimens of type A. The optical measurements of specimens of type B yield \(D=4.32\hbox {mm}\) for the diameter of the hole and \(W=7.8\hbox {mm}\) for the width
Figure 6b exhibits the load–displacement response of the tested specimens of type A. Overall, a response typical for dual-phase steels can be observed. The initially elastic behaviour smoothly transitions into a regime dominated by plasticity, before damage effects lead to softening and finally to failure. For seven different tests, the responses mostly coincide except that failure occurs at slightly different displacement–load levels. The point of unloading occurs at different optically measured displacements u between the different specimens. The reason is that unloading is controlled by the traverse displacement \(u_T\) and that the optically measured displacements (strongly) depend on the evolution of inelastic effects. The unloading response is important in order to be able to quantify the degradation of the elastic properties.
A degradation of elastic stiffness is measurable by using DIC. Consider only a narrow region in the centre of the specimen with initial length \(l_0=800\,\upmu \hbox {m}\), see Fig. 7b. Let l denote the current length, \(l_i\) the length of the region in fully unloaded state after ith reloading, A the current cross section and F the current force; then,
is a measure of the elastic stiffness during the ith reloading step. Since elastic strains are small compared to the plastic strains at the points considered for stiffness determination, the current cross section A is assumed to only depend on plastic strains. Thus, it is also reasonable to assume volume constancy, which renders the current cross section at the ith unloading point to be \(A_i = A_0\,l_0/l_i\). The result of the elastic stiffness analysis is depicted in Fig. 8. Both the average over all specimens and the values for specimen  show a monotonous decline in elastic stiffness. However, the measurement is not very reliable, as the large error bars indicate, and may only be used for qualitative conclusions.
show a monotonous decline in elastic stiffness. However, the measurement is not very reliable, as the large error bars indicate, and may only be used for qualitative conclusions.
a Load–displacement diagram for specimen  . Displacement \(u_{800}\) is determined from the region with \(800~\mu m\) width marked in Fig. 7b. The red lines indicate the determined stiffness. b Degradation of stiffness over (re-)loading steps in terms of normalised stiffness. The blue line corresponds to the stiffness determined for specimen
. Displacement \(u_{800}\) is determined from the region with \(800~\mu m\) width marked in Fig. 7b. The red lines indicate the determined stiffness. b Degradation of stiffness over (re-)loading steps in terms of normalised stiffness. The blue line corresponds to the stiffness determined for specimen  , while the red line (with error bars) is the average of specimens
, while the red line (with error bars) is the average of specimens  –
–
5.2 Simulation set-up
In order to successfully identify material parameters, it is vital to simulate the experiment as accurately as possible, whereby the specimen geometry and boundary conditions are of key importance. Boundary conditions can be applied most accurately by directly prescribing measured quantities, i.e. either the measured total reaction force or the displacement measured by the optical extensometer. Due to the underlying softening in the model, displacement-controlled loading is advantageous in order to be able to compute a response for too soft parameter combinations. Since the optical extensometer measures over a length of \(10\hbox {mm}\) in the centre of specimen, it is most convenient to restrict the simulation to this domain. Furthermore, to keep the numerical effort at a minimum, symmetry is used so that only a section measuring \(5\hbox {mm}\) needs to be discretised, see Fig. 9a. This domain is discretised with 4000 8-noded brick elements, enhanced by the so-called F-bar method [15], with three displacement degrees of freedom and one non-local damage degree of freedom at each node. Displacement field and non-local damage field are linearly interpolated.
The specimens are measured optically revealing an average minimum width of \(3.85\hbox {mm}\) and an average radius of \(39.4\hbox {mm}\) resulting in an initial cross section of \(A_0 = 5.755\hbox {mm}^2\), see Fig. 5a. The deviations from these average dimensions between different specimens are small (\(<20\,\mu \)m for the width). These measured dimensions are the basis for the discretised geometry.
5.3 Objective function
The implementation of the parameter identification closely follows the work in [51]. The goal of the objective function  is to quantify the difference between the response of the simulation and the physical specimen during the experiment. To this end, an objective function incorporating the reaction force and the displacement field is set up as
is to quantify the difference between the response of the simulation and the physical specimen during the experiment. To this end, an objective function incorporating the reaction force and the displacement field is set up as


where  are weighting factors and where
are weighting factors and where  is chosen. The reaction force is taken into account by the difference between the total measured reaction force of the experiment
is chosen. The reaction force is taken into account by the difference between the total measured reaction force of the experiment  and the total reaction force of the simulation
and the total reaction force of the simulation  in every time step. Directly comparing the displacement fields has the drawback of inherent rigid body motions in the measured displacement field. Thus, instead of using the displacement field directly, a strain-like quantity is employed for the evaluation of the objective function. By dividing the difference in the displacement of two neighbouring measurement points by their distance, a simple strain-like quantity
in every time step. Directly comparing the displacement fields has the drawback of inherent rigid body motions in the measured displacement field. Thus, instead of using the displacement field directly, a strain-like quantity is employed for the evaluation of the objective function. By dividing the difference in the displacement of two neighbouring measurement points by their distance, a simple strain-like quantity  is obtained, which is less sensitive to rigid body motions, cf. [51]. Since the displacement field in the experiment is evaluated at different measurement points than the finite element nodes of the simulation, it is necessary to interpolate the measured displacement field to the finite element nodes—a linear interpolation in time and space is performed.
is obtained, which is less sensitive to rigid body motions, cf. [51]. Since the displacement field in the experiment is evaluated at different measurement points than the finite element nodes of the simulation, it is necessary to interpolate the measured displacement field to the finite element nodes—a linear interpolation in time and space is performed.
5.4 Identified parameters
Immediately starting with the identification of all 15 parameters in the model at once requires a high numerical effort, since even an educated guess for the starting parameters may be significantly far from a numerical optimum. In addition, with this amount of parameters, the chosen experiment could possibly not yield enough information to uniquely identify all parameters. Before even beginning the identification process, some parameters can be excluded and can instead be arbitrarily set or determined manually. The penalty parameter  is kept constant as it just needs to be large enough in order to guarantee that the non-local damage variable
is kept constant as it just needs to be large enough in order to guarantee that the non-local damage variable  matches the local damage variable
matches the local damage variable  . If the penalty parameter
. If the penalty parameter  is chosen to be too large, numerical instabilities may arise. Previous studies have shown
is chosen to be too large, numerical instabilities may arise. Previous studies have shown  to be sufficient, see also Fig. 18b.
to be sufficient, see also Fig. 18b.
The influence factors  have been introduced in addition to the damage rate factor
have been introduced in addition to the damage rate factor  in order to be able to bound the difference between the different factors in the exponential damage functions, i.e. the influence factors are bounded by
in order to be able to bound the difference between the different factors in the exponential damage functions, i.e. the influence factors are bounded by  . Therefore, numerically unstable parameter combinations can be excluded from the optimisation process. The influence factor
. Therefore, numerically unstable parameter combinations can be excluded from the optimisation process. The influence factor  is chosen as
is chosen as  to prevent ambiguity between
to prevent ambiguity between  and
and  . The damage exponent
. The damage exponent  has a similar influence as does
has a similar influence as does  , so that
, so that  is chosen.
is chosen.
For the identification of the remaining 12 parameters, the numerical effort can be considerably reduced by splitting the problem into smaller subproblems. In this case, the distinction can be used between the elastic, plastic and damage stages in the response of the experiment in order to identify only the elastic, plastic or damage parameters, respectively. Since both plastic and damage stages are influenced by damage and plastic parameters, a final optimisation identifying plastic and damage parameters at once is carried out, where the parameters identified in the subproblems are chosen as starting values.
The elastic properties  and
and  can be determined directly from measurements. The Young’s modulus
can be determined directly from measurements. The Young’s modulus  is calculated with the help of measured forces and optically measured displacements in tension direction as well as with geometry information, whereas the Poisson ratio
is calculated with the help of measured forces and optically measured displacements in tension direction as well as with geometry information, whereas the Poisson ratio  is calculated with the ratio of the strains in the plane. Relations
is calculated with the ratio of the strains in the plane. Relations  and
and  result in
result in  and
and  .
.
The plastic stage is assumed to end at \(t=900\hbox {s}\) before the first unloading starts. At this early stage of loading, the damage portion barely has an influence and it is possible to identify a very good estimate, as exhibited by Fig. 10a, of the initial yield stress  , the hardening modulus
, the hardening modulus  and the hardening exponent
and the hardening exponent  . A table with the results from this and the following preliminary parameter identifications can be found in Appendix A.4. Since the plastic parameter identification includes a response free of softening, the loading in the underlying simulation can be controlled by force. By prescribing the experimentally measured force as boundary condition, only relative displacements in the objective function need to be taken into account, i.e.
. A table with the results from this and the following preliminary parameter identifications can be found in Appendix A.4. Since the plastic parameter identification includes a response free of softening, the loading in the underlying simulation can be controlled by force. By prescribing the experimentally measured force as boundary condition, only relative displacements in the objective function need to be taken into account, i.e.  and
and  . In other words, the force contribution in the goal function
. In other words, the force contribution in the goal function  is exactly satisfied.
is exactly satisfied.
On the basis of the identified plastic parameters, a parameter identification of only the most influential damage parameters (damage threshold  , damage rate factor
, damage rate factor  , effective stress factor
, effective stress factor  and regularisation parameter
and regularisation parameter  ) is carried out, see Fig. 10a for the corresponding load–displacement responses. Simulating the damage regime entails the inclusion of softening effects, and it is therefore beneficial to run the simulation controlled by displacement. Consequently, the objective function needs to take the force into account. In order to similarly weight the influence of displacement and force, both weights
) is carried out, see Fig. 10a for the corresponding load–displacement responses. Simulating the damage regime entails the inclusion of softening effects, and it is therefore beneficial to run the simulation controlled by displacement. Consequently, the objective function needs to take the force into account. In order to similarly weight the influence of displacement and force, both weights  and
and  are chosen such that the error in the objective function is scaled to have the unit of stress squared. To this end, the force is divided by cross section squared, and the relative displacements (strain-like quantities) are multiplied by Young’s modulus squared, i.e.
are chosen such that the error in the objective function is scaled to have the unit of stress squared. To this end, the force is divided by cross section squared, and the relative displacements (strain-like quantities) are multiplied by Young’s modulus squared, i.e.  and
and  . The factor 4 in
. The factor 4 in  is present due to symmetry, and the factor 0.7 in
is present due to symmetry, and the factor 0.7 in  has been determined empirically as yielding a subjectively good balance between matching force and displacement response simultaneously. These weighting factors are used in all following identifications.
has been determined empirically as yielding a subjectively good balance between matching force and displacement response simultaneously. These weighting factors are used in all following identifications.
Using the preliminary parameters as starting values, an identification (PI1) where all 12 parameters are to be determined by the simplex algorithm yields, after some restarts of the simplex, a good match with the experimental response, see Fig. 10. Based on this identification, other identifications with perturbed starting values are set up. (Most notable identifications are listed in Appendix A.5.) One of these identifications (PI4b) stands out from the others—the total objective function value is slightly lower when compared to PI1 but the identified parameters differ considerably, see Table 5. In particular, the regularisation parameter  is magnitudes higher in PI4b than in PI1, and damage threshold
is magnitudes higher in PI4b than in PI1, and damage threshold  and damage rate factor
and damage rate factor  also take much higher values. However, the effective stiffness degradation of both parameter sets is in fact very similar since the maximum value of the damage variable in the last load increment is much higher for PI1 (
also take much higher values. However, the effective stiffness degradation of both parameter sets is in fact very similar since the maximum value of the damage variable in the last load increment is much higher for PI1 ( ) than for PI4b (
) than for PI4b ( ). In the load–displacement diagram, Fig. 10, as well as in the contour plot of the damage function
). In the load–displacement diagram, Fig. 10, as well as in the contour plot of the damage function  , Fig. 13, the responses of both parameter sets are very similar, albeit distinguishable. A closer look at the error in relative displacement, as depicted in Figs. 11 and 12 , reveals no visible differences between both parameter sets. The relative displacements of the simulation match the experimentally determined relative displacement quite well for roughly the first
, Fig. 13, the responses of both parameter sets are very similar, albeit distinguishable. A closer look at the error in relative displacement, as depicted in Figs. 11 and 12 , reveals no visible differences between both parameter sets. The relative displacements of the simulation match the experimentally determined relative displacement quite well for roughly the first  of loading. Thereafter, relative displacements are higher in the simulation compared to the experimentally determined counterpart.
of loading. Thereafter, relative displacements are higher in the simulation compared to the experimentally determined counterpart.
Load–displacement diagram of the simulation response of selected parameter sets and experimental data. The experimental response is displayed as a blue continuous line and the identifications by means of square, X and circle. a Responses of the preliminary identifications compared to experiment  . b Responses of the final identifications PI1 and PI4b compared to experiment
. b Responses of the final identifications PI1 and PI4b compared to experiment 
From the identification point of view, i.e. considering the objective function, the parameter sets of PI1 and PI4b seem to match the experimental response equally well. However, several problems arise. Even if both parameter sets resulted in identical responses for the current boundary value problem, they would not (necessarily) result in identical responses of the material model for arbitrary boundary value problems; i.e. further experimental data, ideally experiments which activate different deformations modes, need to be taken into account in the future. Another problem stems from the correlation between parameters, e.g. between the parameters  and
and  . Damage variable
. Damage variable  always appears in combination with the parameter
always appears in combination with the parameter  with the exception of the contribution of the gradient of non-local damage variable
with the exception of the contribution of the gradient of non-local damage variable  . In fact, the quotient
. In fact, the quotient  yields approximately 22 for PI1 and 15 for PI4b—in contrast to the regularisation parameter
yields approximately 22 for PI1 and 15 for PI4b—in contrast to the regularisation parameter  having the values 0.54 and 379, suggesting a high correlation between both parameters. Further problems lie in the consideration of damage during parameter identification. Damage can only be distinguished from plasticity by means of elastic stiffness degradation in this framework, e.g. by elastic unloading. In the herein-considered experiment, damage is only implicitly taken into account via force and displacement measurements during unloading. It might be possible that different weighting of unloading and loading in the objective function—by choosing
having the values 0.54 and 379, suggesting a high correlation between both parameters. Further problems lie in the consideration of damage during parameter identification. Damage can only be distinguished from plasticity by means of elastic stiffness degradation in this framework, e.g. by elastic unloading. In the herein-considered experiment, damage is only implicitly taken into account via force and displacement measurements during unloading. It might be possible that different weighting of unloading and loading in the objective function—by choosing  accordingly — yields a parameter set which is able to predict the response of DP800 (or any other material) more precisely. An even more complex problem is the identifiability of the regularisation parameter
accordingly — yields a parameter set which is able to predict the response of DP800 (or any other material) more precisely. An even more complex problem is the identifiability of the regularisation parameter  , since further experiments, especially with specimens of much larger or smaller dimensions, are required. In spite of these open problems, the next section is a first approach to the validation of the parameter sets identified in this section.
, since further experiments, especially with specimens of much larger or smaller dimensions, are required. In spite of these open problems, the next section is a first approach to the validation of the parameter sets identified in this section.
Depiction of the relative displacement  of the first identified parameter set PI1. Contour plot of the squared absolute error of the relative displacement, i.e. objective function
of the first identified parameter set PI1. Contour plot of the squared absolute error of the relative displacement, i.e. objective function  , see (7172), at each node at \(t=3520\hbox {s}\) (left) and comparison of the evolution of the experimental and simulated relative displacements in x- and y-direction over time (right) for nodes P1, P2 and P3
, see (7172), at each node at \(t=3520\hbox {s}\) (left) and comparison of the evolution of the experimental and simulated relative displacements in x- and y-direction over time (right) for nodes P1, P2 and P3
Depiction of the relative displacement  of the last identified parameter set PI4b. Contour plot of the squared absolute error of the relative displacement, i.e. objective function
of the last identified parameter set PI4b. Contour plot of the squared absolute error of the relative displacement, i.e. objective function  , see (7172), at each node at \(t=3520\hbox {s}\) (left) and comparison of the evolution of the experimental and simulated relative displacements in x- and y-direction over time (right) for nodes P1, P2 and P3
, see (7172), at each node at \(t=3520\hbox {s}\) (left) and comparison of the evolution of the experimental and simulated relative displacements in x- and y-direction over time (right) for nodes P1, P2 and P3
Load–displacement diagrams with force in \(\hbox {N}\) over displacement in tensile direction in \(\mu \hbox {m}\). On the left side, experimental response of the tensile test of specimen B01 and the simulation response with parameters of PI1 and PI4b are displayed. The experimental response is displayed as a blue continuous line and the identifications by red squares and green x. The right load–displacement diagram shows the mesh dependence ( , red) and independence (
, red) and independence ( , blue) for parameter set PI1 by means of three different discretisations with 920, 3680 and 14720 elements. The zoom-in shows more clearly the difference in the responses for the different discretisations. The premature end of the simulations due to divergence is marked with a red ’x’
, blue) for parameter set PI1 by means of three different discretisations with 920, 3680 and 14720 elements. The zoom-in shows more clearly the difference in the responses for the different discretisations. The premature end of the simulations due to divergence is marked with a red ’x’
6 Towards validation
With two—apparently equally well fitting—parameter sets having been identified, cf. Table 5, the validation reveals the prediction capability of the material model together with the identified parameters. To this end, a second experiment is considered, featuring a tensile specimen with a hole (specimen B, see Fig. 5), see also Remark 5.
The tensile test is performed in the same way and with the same set-up as the tensile test of the notched tensile specimen (type A), as described in Sect. 5.1. The comparison of the experimental response with the simulation response reveals clearly visible differences between the responses of both parameter sets in the load–displacement diagram, see Fig. 14. Parameter set PI1 (red squares) shows overall good agreement with the experimental response, as the force is slightly underestimated in the beginning of the plastic stage. The other parameter set, PI4b (green x), overestimates the force response in the inelastic stage but is able to predict the unloading behaviour as well as parameter set PI1.
The comparison of the relative displacements confirms a better match between experimental and simulation responses for parameter set PI1, see Fig. 15, than for parameter set PI4b, see Fig. 16. The contour plots showing the squared error of relative displacement indicate only very few spots with relevant error levels for PI1. The red region on the boundary of the hole can be ignored as relative displacements are not computed correctly at that edge. The two red patches on the upper edge can probably be attributed to measurement errors from DIC. In the necking region, three points are marked and the evolution of relative displacements over time is plotted for these points in the right diagram of Fig. 15. For point P1, nearly perfectly matching simulation and experimental responses can be observed, while points P2 and P3 show small offsets between experimental and simulation responses. The offset for displacements in x-direction seems to slightly increase after each inelastic loading stage for both points. The displacements in y-direction match quite well in point P2, but for point P3 a constant offset is observed.
Qualitatively similar results are obtained for the second parameter set PI4b, see Fig. 16, but overall the error is larger as the error obtained for parameter set PI1. In the contour plot, the red patches occupy large domains and take higher values, especially around points P2 and P3 and to their right, indicating that probably the width of the localisation zone is predicted incorrectly in the simulation. This can be confirmed by the evolution of relative displacements over time. Displacements at point P1 are underestimated in the first 1000 seconds, but in the end, after 2000 seconds, they are overestimated, whereas at points P2 and P3, the underestimation of displacements constantly increases. The comparison of the damage evolution, see Fig. 17, reveals a higher localisation of damage evolution for the second parameter set PI4b.
Illustration of the relative displacement  of the first identified parameter set PI1. Contour plot of the squared absolute error of the relative displacement, i.e. objective function
of the first identified parameter set PI1. Contour plot of the squared absolute error of the relative displacement, i.e. objective function  , see (7172), at each node at \(t=2160\hbox {s}\) (left) and comparison of the evolution of the experimental and simulated relative displacements in x- and y-direction over time (right) for nodes P1, P2 and P3
, see (7172), at each node at \(t=2160\hbox {s}\) (left) and comparison of the evolution of the experimental and simulated relative displacements in x- and y-direction over time (right) for nodes P1, P2 and P3
Illustration of the relative displacement  of the last identified parameter set PI4b. Contour plot of the squared absolute error of the relative displacement, i.e. objective function
of the last identified parameter set PI4b. Contour plot of the squared absolute error of the relative displacement, i.e. objective function  , see (7172), at each node at \(t=2160\hbox {s}\) (left) and comparison of the evolution of the experimental and simulated relative displacements in x- and y-direction over time (right) for nodes P1, P2 and P3
, see (7172), at each node at \(t=2160\hbox {s}\) (left) and comparison of the evolution of the experimental and simulated relative displacements in x- and y-direction over time (right) for nodes P1, P2 and P3
Overall, the parameter set PI1 performs best and allows accurate predictions of the behaviour of DP800 steel. The mesh independence of this parameter set is proven in the right diagram of Fig. 14. An identical response is obtained for three different discretisations. Moreover, simulations with the same parameter set, but  and
and  (non-local damage field
(non-local damage field  is fixed at zero throughout the body) show a strong mesh dependence. The point where the total force starts to drop differs between the different discretisations. All simulations end prematurely (marked with an x in the figure), due to divergence in the global Newton–Raphson scheme of the FE method. Employing an arc-length method might allow the simulations to advance further—for the purpose of illustrating the mesh dependence though, the standard solution method is sufficient. The properly working micromorphic approach is depicted in Fig. 18. Substantially increasing the penalty parameter
is fixed at zero throughout the body) show a strong mesh dependence. The point where the total force starts to drop differs between the different discretisations. All simulations end prematurely (marked with an x in the figure), due to divergence in the global Newton–Raphson scheme of the FE method. Employing an arc-length method might allow the simulations to advance further—for the purpose of illustrating the mesh dependence though, the standard solution method is sufficient. The properly working micromorphic approach is depicted in Fig. 18. Substantially increasing the penalty parameter  leads to a quasi-identical distribution of the damage-related quantity
leads to a quasi-identical distribution of the damage-related quantity  . The absolute difference between local and non-local damage variables seems to be (inversely) proportional to the penalty parameter
. The absolute difference between local and non-local damage variables seems to be (inversely) proportional to the penalty parameter  ; i.e. the maximum difference for
; i.e. the maximum difference for  is
is  and for
and for  it is
it is  .
.
Remark 5
A proper validation requires a (sufficiently) distinct and more complex experiment in order to test a different deformation pattern than the one used for the identification. At the same time, the experiment must lie within the region which the model is able to predict; e.g. a pressure-dominated experiment can presumably not be correctly predicted with this model. The here-chosen tensile tests with a notched specimen and a specimen with a hole both are tension dominated but exhibit different localisation patterns.
7 Summary and outlook
The present contribution started with a brief summary of the finite element implementation of the gradient-enhanced damage formulation in finite strains. By making use of an additional field variable—denoted non-local damage—and by coupling it to a local damage variable, a regularised damage formulation could be achieved by taking gradients of the non-local damage field (instead of the local damage variable) into account. Therefore, gradients of the local damage variable—along with a cumbersome treatment of Karush–Kuhn–Tucker conditions on global finite element level—were avoided. Thus, the ductile damage model discussed thereafter could be solved on material point level. A von Mises finite strain plasticity formulation with nonlinear isotropic hardening was coupled in a multi-surface setting to a damage formulation in the spirit of Lemaitre. The well-known \([1-d]\) formulation was replaced by multiple exponential damage functions each weighting a different contribution. Most notably, the different weighting of volumetric and isochoric elastic energy contributions allowed the indirect control of the influence of triaxiality on damage evolution. Plasticity and damage evolution were coupled strongly by means of effective driving forces. The already-established concept of an effective stress governing evolution of plasticity was analogously applied to damage evolution; i.e. the damage driving force was divided by a term depending on the accumulated plastic strain. The resulting two-surface problem in determining the Lagrangian multipliers for damage and plasticity was solved by an active-set algorithm.
The adaptability of the material model to resemble material behaviour ranging from brittle to very ductile responses was demonstrated by homogeneous tension tests. For the presented material model, suitable material parameters for the prediction of the response of DP800 steel were identified by means of a parameter identification process. The parameter identification was based on a tensile test of a notched tensile specimen, where the reaction force was measured as well as the inhomogeneous displacement field determined by DIC. Based on these two data sources, two equally optimal parameter sets could be identified. The validation, based on an additional tensile test of a specimen with a hole, revealed that only one of the two identified parameter sets is able to predict the response from the experiment correctly. In summary, this contribution presented a regularised ductile damage model for finite strains, which, together with the identified material parameters, is able to accurately predict the response of DP800 steel.
Future work may possibly be carried out in two areas of research. The one area of research would be parameter identification where the theoretical flexibility, respectively adaptability, of the material model can be proven by identifying parameter sets for other materials, such as stainless steel. An analysis of damage evolution under different deformation types should be considered, e.g. shear- and compression-dominated experiments, multi-axial loading and more complex loading states. More importantly, the identifiability of the regularisation parameter as well as the applicability of an identified regularisation parameter on other boundary value problems, especially of much larger (or smaller) size, should be analysed. Recent works, see, e.g., [61, 65], suggested a non-constant regularisation parameter  , which could be worthwhile trying to combine with the modelling approach followed herein. This might improve the model’s capability capturing the drop in force close to failure. This drop may also be captured better if, during the parameter identification, the weighting factors
, which could be worthwhile trying to combine with the modelling approach followed herein. This might improve the model’s capability capturing the drop in force close to failure. This drop may also be captured better if, during the parameter identification, the weighting factors  corresponding to the last few load steps are increased. An indication that this is the case is given by the fact that, by not taking unloading in the identification into account, a more pronounced drop in force before failure is obtained. In addition, the initiation point of failure can be more confidently identified if the drop in total force before failure is captured more accurately.
corresponding to the last few load steps are increased. An indication that this is the case is given by the fact that, by not taking unloading in the identification into account, a more pronounced drop in force before failure is obtained. In addition, the initiation point of failure can be more confidently identified if the drop in total force before failure is captured more accurately.
The second area of research would comprise the improvement in the material model, e.g. by considering kinematic hardening. For applications in metal forming, it is important to include pressure insensitivity and/or the microcrack–closure–reopening effect in the damage evolution. The coupling between the evolution of damage and plasticity should be investigated further, especially regarding the influence of plasticity upon damage evolution introduced in this work. In view of the result of the parameter identification which cancelled the influence of hardening on the damage driving force, other choices for the function  could be analysed. Effects of anisotropy can certainly be considered, such as anisotropic damage and anisotropic plasticity as well as rate dependency or thermal effects.
could be analysed. Effects of anisotropy can certainly be considered, such as anisotropic damage and anisotropic plasticity as well as rate dependency or thermal effects.
Notes
From the modelling point of view, it is sufficient to introduce a single parameter in the exponential function, i.e.
 . In view of subsequent parameter identification, however, it is beneficial to split the parameter, see Sect. 5.4
. In view of subsequent parameter identification, however, it is beneficial to split the parameter, see Sect. 5.4
References
Voyiadjis, G.Z., Al-Rub, R K Abu, Voyiadjis, G .Z.: Gradient-enhanced coupled plasticity-anisotropic damage model for concrete fracture: computational aspects and applications. Int. J. Damage Mech. 18(2), 115–154 (2009)
Anderson, D., Butcher, C., Pathak, N., Worswick, M.J.: Failure parameter identification and validation for a dual-phase 780 steel sheet. Int. J. Solids Struct. 124, 89–107 (2017)
Anduquia-Restrepo, J., Narváez-Tovar, C., Rodríguez-Baracaldo, R.: Computational and numerical analysis of ductile damage evolution under a load-unload tensile test in dual-phase steel. Strojniski Vestnik/J. Mech. Eng. 64(5), 339–348 (2018)
Avril, S., Bonnet, M., Bretelle, A.-S., Grédiac, M., Hild, F., Ienny, P., Latourte, F., Lemosse, D., Pagano, S., Pagnacco, E., Pierron, F.: Overview of identification methods of mechanical parameters based on full-field measurements. Exp. Mech. 48(4), 381 (2008)
Balieu, R., Kringos, N.: A new thermodynamical framework for finite strain multiplicative elastoplasticity coupled to anisotropic damage. Int. J. Plast. 70, 126–150 (2015)
Bažant, Z.P., Belytschko, T.B., Chang, T.-P.: Continuum theory for strain-softening. J. Eng. Mech. 110(12), 1666–1692 (1984)
Bažant, Z.P., Pijaudier-Cabot, G.: Nonlocal continuum damage, localization instability and convergence. J. Appl. Mech. 55(2), 287–293 (1988)
Besson, J.: Continuum models of ductile fracture: a review. Int. J. Damage Mech 19(1), 3–52 (2010)
Betten, J.: Applications of tensor functions in continuum damage mechanics. Int. J. Damage Mech. 1(1), 47–59 (1992)
Brepols, T., Wulfinghoff, S., Reese, S.: Gradient-extended two-surface damage-plasticity: micromorphic formulation and numerical aspects. Int. J. Plast. 97(Supplement C), 64–106 (2017)
Brepols, T., Wulfinghoff, S., Reese, S.: A gradient-extended two-surface damage-plasticity model for large deformations. Int. J. Plast. 129, 102635 (2020)
Cao, T.-S., Mazière, M., Danas, K., Besson, J.: A model for ductile damage prediction at low stress triaxialities incorporating void shape change and void rotation. Int. J. Solids Struct. 63, 240–263 (2015)
Chaboche, J.-L.: Development of continuum damage mechanics for elastic solids sustaining anisotropic and unilateral damage. Int. J. Damage Mech. 2(4), 311–329 (1993)
De Borst, R., Sluys, L.J., Muhlhaus, H.-B., Pamin, J.: Fundamental issues in finite element analyses of localization of deformation. Eng. Comput. 10(2), 99–121 (1993)
de Souza Neto, E .A., Owen, D .R .J., Perić, D.: Computational Methods for Plasticity. Wiley, Chichester (2008)
Dimitrijevic, B.J., Hackl, K.: A method for gradient enhancement of continuum damage models. Technische Mechanik 28(1), 43–52 (2008)
Ekh, M., Menzel, A., Runesson, K., Steinmann, P.: Anisotropic damage with the MCR effect coupled to plasticity. Int. J. Eng. Sci. 41(13–14), 1535–1551 (2003)
Forest, S.: Micromorphic approach for gradient elasticity, viscoplasticity, and damage. J. Eng. Mech. 135(3), 117–131 (2009)
Guhr, F., Sprave, L., Barthold, F.-J., Menzel, A.: Computational shape optimisation for a gradient-enhanced continuum damage model. Comput. Mech. 65(4), 1105–1124 (2020)
Gurson, A.L.: Continuum theory of ductile rupture by void nucleation and growth: Part I-Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 99(1), 2–15 (1977)
Junker, P., Schwarz, S., Jantos, D.R., Hackl, K.: A fast and robust numerical treatment of a gradient-enhanced model for brittle damage. Int. J. Multiscale Comput. Eng. 17(2), 151–180 (2019)
Kachanov, L.: On time to rupture in creep conditions [in russian], izv. AN SSSR, OTN 8, 26–31 (1958)
Kattan, P.I., Voyiadjis, G.Z.: A coupled theory of damage mechanics and finite strain elasto-plasticity—I. Damage and elastic deformations. Int. J. Eng. Sci. 28(5), 421–435 (1990)
Kiefer, B., Waffenschmidt, T., Sprave, L., Menzel, A.: A gradient-enhanced damage model coupled to plasticity—multi-surface formulation and algorithmic concepts. Int. J. Damage Mech. 27(2), 253–295 (2018)
Krajcinovic, D.: Continuum models. In: Krajcinovic, D. (ed.) Damage Mechanics, Volume 41 of North-Holland Series in Applied Mathematics and Mechanics, chapter 4, pp. 415–602. North-Holland, Amsterdam (1996)
Kusche, C., Reclik, T., Freund, M., Al-Samman, Talal, Kerzel, U., Korte-Kerzel, S.: Large-area, high-resolution characterisation and classification of damage mechanisms in dual-phase steel using deep learning. PLoS One 14(5), e0216493 (2019)
Kusche, C.F., Dunlap, A., Pütz, F., Tian, Chunhua, Kirchlechner, C., Aretz, A., Schwedt, A., Al-Samman, Talal, Münstermann, S., Korte-Kerzel, S.: Efficient characterization tools for deformation-induced damage at different scales. Prod. Eng. Res. Devel. 14(1), 95–104 (2019)
Lämmer, H., Tsakmakis, Ch.: Discussion of coupled elastoplasticity and damage constitutive equations for small and finite deformations. Int. J. Plast. 16(5), 495–523 (2000)
Langenfeld, K., Mosler, J.: A micromorphic approach for gradient-enhanced anisotropic ductile damage. Comput. Methods Appl. Mech. Eng. 360, 112717 (2020)
Leckie, F.A., Onat, E.T.: Tensorial nature of damage measuring internal variables. In: Hult, J., Lemaitre, J. (eds.) Phys. Non-Linear. Struct. Anal., pp. 140–155. Springer, Berlin (1981)
Lemaitre, J.: A Continuous Damage Mechanics Model for Ductile Fracture. J. Eng. Mater. Technol. 107(1), 83–89 (1985)
Lemaitre, J.: A Course on Damage Mechanics. Springer, Berlin (1996)
Lemaitre, J., Dufailly, J.: Damage measurements. Eng. Fract. Mech. 28(5), 643–661 (1987)
Liebe, T., Menzel, A., Steinmann, P.: Theory and numerics of geometrically non-linear gradient plasticity. Int. J. Eng. Sci. 41(13–14), 1603–1629 (2003)
Liebe, T., Steinmann, P., Benallal, A.: Theoretical and computational aspects of a thermodynamically consistent framework for geometrically linear gradient damage. Comput. Methods Appl. Mech. Eng. 190(49–50), 6555–6576 (2001)
Ling, Chao, Forest, Samuel, Besson, Jacques, Tanguy, Benoît, Latourte, Felix: A reduced micromorphic single crystal plasticity model at finite deformations. application to strain localization and void growth in ductile metals. Int. J. Solids Struct. 134, 43–69 (2018)
Mahnken, R., Kuhl, E.: Parameter identification of gradient enhanced damage models with the finite element method. Eur. J. Mech. A. Solids 18(5), 819–835 (1999)
Mahnken, R., Stein, E.: Parameter identification for finite deformation elasto-plasticity in principal directions. Comput. Methods Appl. Mech. Eng. 147(1), 17–39 (1997)
Markiewicz, É., Langrand, B., Notta-Cuvier, D.: A review of characterisation and parameters identification of materials constitutive and damage models: from normalised direct approach to most advanced inverse problem resolution. Int. J. Impact Eng. 110, 371–381 (2017)
McVeigh, C., Vernerey, F., Liu, Wing Kam, Moran, B., Olson, G.: An interactive micro-void shear localization mechanism in high strength steels. J. Mech. Phys. Solids 55(2), 225–244 (2007)
Menzel, A., Steinmann, P.: A theoretical and computational framework for anisotropic continuum damage mechanics at large strains. Int. J. Solids Struct. 38(52), 9505–9523 (2001)
Menzel, A., Steinmann, P.: Geometrically non-linear anisotropic inelasticity based on fictitious configurations: application to the coupling of continuum damage and multiplicative elasto-plasticity. Int. J. Numer. Meth. Eng. 56(14), 2233–2266 (2003)
Murakami, S.: Mechanical modeling of material damage. J. Appl. Mech. 55(2), 280–286 (1988)
Murakami, S.: Continuum Damage Mechanics: A Continuum Mechanics Approach to the Analysis of Damage and Fracture (Solid Mechanics and Its Applications). Springer, Berlin (2012)
Nguyen, Tuan H .A., Bui, Tinh Quoc, Hirose, Sohichi: Smoothing gradient damage model with evolving anisotropic nonlocal interactions tailored to low-order finite elements. Comput. Methods Appl. Mech. Eng. 328, 498–541 (2018)
Nguyen, V.-D., Lani, F., Pardoen, T., Morelle, X.P., Noels, L.: A large strain hyperelastic viscoelastic-viscoplastic-damage constitutive model based on a multi-mechanism non-local damage continuum for amorphous glassy polymers. Int. J. Solids Struct. 96, 192–216 (2016)
Ostwald, R., Kuhl, E., Menzel, A.: On the implementation of finite deformation gradient-enhanced damage models. Comput. Mech. 64(Issue 3), 847–877 (2019)
Peerlings, R.H.J., de Borst, R., Brekelmans, W.A.M., de Vree, J.H.P., Spee, I.: Some observations on localisation in non-local and gradient damage models. Eur. J. Mech. A/Solids 15, 937–953 (1996)
Polindara, C., Waffenschmidt, T., Menzel, A.: A computational framework for modelling damage-induced softening in fibre-reinforced materials—application to balloon angioplasty. Int. J. Solids Struct. 118–119, 235–256 (2017)
Rabotnov, Y.N.: Creep problems in structural members, volume 7 of North-Holland Series in Applied Mathematics and Mechanics. North-Holland, Amsterdam, 1969. Trans. from the Russian
Rose, L., Menzel, A.: Optimisation based material parameter identification using full field displacement and temperature measurements. Mech. Mater. 145, 103292 (2020)
Rousselier, G.: Ductile fracture models and their potential in local approach of fracture. Nucl. Eng. Des. 105(1), 97–111 (1987)
Roux, E., Bouchard, P.-O.: On the interest of using full field measurements in ductile damage model calibration. Int. J. Solids Struct. 72, 50–62 (2015)
Sabnis, P.A., Forest, S., Cormier, J.: Microdamage modelling of crack initiation and propagation in FCC single crystals under complex loading conditions. Comput. Methods Appl. Mech. Eng. 312, 468–491 (2016)
Seupel, A., Hütter, G., Kuna, M.: An efficient FE-implementation of implicit gradient-enhanced damage models to simulate ductile failure. Eng. Fract. Mech. 199, 41–60 (2018)
Simo, J.C.: Numerical analysis and simulation of plasticity. In: Ciarlet, P.G., Lions, J.L. (eds.) Numerical Methods for Solids (Part 3) Numerical Methods for Fluids (Part 1). Handbook of Numerical Analysis, vol. VI, pp. 183–499. Elsevier, Amsterdam (1998)
Steinmann, P.: Formulation and computation of geometrically non-linear gradient damage. Int. J. Numer. Meth. Eng. 46(5), 757–779 (1999)
Steinmann, P., Stein, E.: A unifying treatise of variational principles for two types of micropolar continua. Acta Mech. 121(1–4), 215–232 (1997)
Triantafyllidis, N., Aifantis, E.C.: A gradient approach to localization of deformation. I. hyperelastic materials. J. Elast. 16(3), 225–237 (1986)
Tvergaard, V., Needleman, A.: Analysis of the cup-cone fracture in a round tensile bar. Acta Metall. 32(1), 157–169 (1984)
Vandoren, B., Simone, A.: Modeling and simulation of quasi-brittle failure with continuous anisotropic stress-based gradient-enhanced damage models. Comput. Methods Appl. Mech. Eng. 332, 644–685 (2018)
Waffenschmidt, T., Polindara, C., Menzel, A., Blanco, S.: A gradient-enhanced large-deformation continuum damage model for fibre-reinforced materials. Comput. Methods Appl. Mech. Eng. 268, 801–842 (2014)
Wcisło, B., Pamin, J., Kowalczyk-Gajewska, K.: Gradient-enhanced damage model for large deformations of elastic-plastic materials. Arch. Mech. 65(5), 407–428 (2013)
Wulfinghoff, S., Fassin, M., Reese, S.: A damage growth criterion for anisotropic damage models motivated from micromechanics. Int. J. Solids Struct. 121, 21–32 (2017)
Xu, Yanjie, Poh, Leong Hien: Localizing gradient-enhanced Rousselier model for ductile fracture. Int. J. Numer. Meth. Eng. 119(9), 826–851 (2019)
Zhang, Yi, Lorentz, E., Besson, J.: Ductile damage modelling with locking-free regularised gtn model. Int. J. Numer. Meth. Eng. 113(13), 1871–1903 (2018)
Zhu, Yazhi, Engelhardt, M.D.: A nonlocal triaxiality and shear dependent continuum damage model for finite strain elastoplasticity. Eur. J. Mech. A. Solids 71, 16–33 (2018)
Acknowledgements
Funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within the Collaborative Research Centre TRR 188 (Project number 278868966), Subproject C02, is gratefully acknowledged.
Funding
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Damage driving force and stress triaxiality
In Sect. 3, the damage driving force, introduced in (38), together with the particular choice of the free Helmholtz energy (33), results in

With the expressions for the volumetric and isochoric parts of the stresses

and with the definition of the stress triaxiality

the damage driving force  can be expressed in terms of stress triaxiality
can be expressed in terms of stress triaxiality  and
and  . Making use of
. Making use of  —only valid for the specific choice of the damage function (34)—one obtains
—only valid for the specific choice of the damage function (34)—one obtains

where  is assumed, see Sect. 5. This reformulation of damage driving force
is assumed, see Sect. 5. This reformulation of damage driving force  reveals the importance of the influence factor
reveals the importance of the influence factor  —the parameter
—the parameter  controls how stress triaxiality influences damage evolution.
controls how stress triaxiality influences damage evolution.
1.2 Jacobian for local Newton scheme
The Newton–Raphson scheme to determine the update for the Lagrange multipliers within the active-set algorithm, see Table 2, requires the entries





of the Jacobian  , cf. (64). The partial derivatives can be computed as
, cf. (64). The partial derivatives can be computed as





1.3 Derivatives in principal space
In this section of the appendix, all derivatives which are required for the computation of the consistent algorithmic tangent operator, see Table 3, are given. The specific structure only requires the derivatives of the eigenvalues. The eigenvalues are gathered in n-tuples and are denoted by \({\bar{\bullet }}\). The corresponding identity tensors are represented by  , an n-tuple with the value of all entries being identically 1, and by \({\text {diag}}(1)\), a diagonal \(n\times n\)-matrix with all diagonal entries being identically 1.
, an n-tuple with the value of all entries being identically 1, and by \({\text {diag}}(1)\), a diagonal \(n\times n\)-matrix with all diagonal entries being identically 1.
The increments of the Mandel stress tensor and the non-local damage driving force, i.e.


requires the tangent contributions





where the partial derivatives of the driving forces result in



Furthermore, the total derivatives of the internal variables—plastic strains  and isotropic damage
and isotropic damage  —are specified by
—are specified by




The occurring total derivatives of the Lagrange multipliers are not straightforward to determine. Utilisation of the implicit function theorem in the converged Newton–Raphson step leads to




1.4 Intermediate material parameter sets
The results of the parameter identification in Sect. 5 are based on multiple intermediate identifications. Initially, a subset of the parameters (plasticity-related parameters and damage-related parameters) have been identified, see Table 6. The first combined identification where the resulting parameters of the first identifications are used as starting values is listed as well.
1.5 Identifications with perturbed starting values
In Sect. 5, the results of two parameter identifications are analysed in more detail. They are chosen from multiple identifications where each has been started with different starting parameters, see Table 7. The identification PI4 initially yielded parameters very close to the (artificially) prescribed parameter bounds. The results of the restarts of this parameter identification with relaxed parameter bounds (denoted as PI4a and PI4b) are given in Table 8.
The load–displacement diagrams corresponding to the identified parameter sets can be found in Fig. 19.
Load–displacement diagram of the tensile test of specimen A-7 and the simulation response with parameters of the most notable parameter identifications. Force in \(\hbox {N}\) over optically measured displacement in tensile direction in \(\hbox {mm}\). The experimental response is displayed as a blue continuous line and the identifications by means of square, x and circle
1.6 Validation diagrams of additional parameter sets
For the sake of completeness, the load–displacement response of the validation example (specimen with a hole) for all identified parameter sets is given in Fig. 20.
Load–displacement diagram of the tensile test of specimen B-1 and the validation simulation response with parameters of the parameter identifications PI1 through PI4b. Force in \(\hbox {N}\) over optically measured displacement in tensile direction in \(\hbox {mm}\). The experimental response is displayed as a blue continuous line and the identifications by means of square, x and circle
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sprave, L., Menzel, A. A large strain gradient-enhanced ductile damage model: finite element formulation, experiment and parameter identification. Acta Mech 231, 5159–5192 (2020). https://doi.org/10.1007/s00707-020-02786-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-020-02786-5


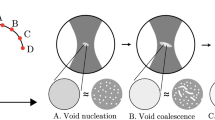


 over time t. The reduction in the stretch
over time t. The reduction in the stretch  at values 1.1, 1.15 and 1.2 results in a deformation-controlled unloading
at values 1.1, 1.15 and 1.2 results in a deformation-controlled unloading


 on the material response under homogeneous tension
on the material response under homogeneous tension


 before testing taken from the DIC camera. Red lines indicate the region with
before testing taken from the DIC camera. Red lines indicate the region with 





 on the undeformed configuration after the last load increment (
on the undeformed configuration after the last load increment (



 on the deformed configuration after the last load increment (
on the deformed configuration after the last load increment (
 on the undeformed configuration after the last load increment (
on the undeformed configuration after the last load increment ( for b
for b . In view of subsequent parameter identification, however, it is beneficial to split the parameter, see Sect.
. In view of subsequent parameter identification, however, it is beneficial to split the parameter, see Sect. 
