Abstract
Laminates made of metal—glass fiber-reinforced polymers—metal layers require material parameters for each constitutive model of the constituents. First, although parameter identification for metallic materials has been frequently discussed, the stepwise identification of material parameters in terms of uncertainties of previously determined parameters is investigated by the concept of error propagation. Second, the calibration of a model of orthotropy describing the large deformation behavior of the glass fiber-reinforced kernel layer is a challenging process, especially against the background of a reliable determination of the parameters. The main problem is related to the lack of available experiments. This issue is embedded in the concept of local identifiability. Thus, the article provides experiments to determine the parameters of both the steel as well as the glass fiber-reinforced polymers. Particularly for the latter issue, \(\mu \)-CT data is chosen to provide a representative volume element, where all deformation modes can be investigated. In this sense, a concept to determine all material parameters in a locally unique and reliable manner is studied. A linear error propagation concept provides the uncertainty of the resulting material parameters of the whole parameter set for the homogenized material. The entire parameter identification process is discussed thoroughly, and validation examples such as bending and deep drawing in metal forming processes, are provided to estimate the prediction accuracy. In this respect, the uncertainties found by parameter identification are applied to the prediction of finite element simulations of layered metal–composite–metal forming processes and error propagation is used to estimate the uncertainties of the simulations. In this contribution, we restrict ourselves to experiments at room temperature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Lightweight structures demand specific manufacturing technologies. One objective here is to obtain high structural stiffness under the constraint of a low structural weight. A particular concept of a lightweight planar sandwich structure is to compose the plates by a stiff surface coating material and a weak core layer material. Commonly, these laminated structures consist of a lightweight core (in the form of pure or a composite material) embedded between two thin and flat surface sheets. The thin sheets can be made of metals, reinforced composites, etc., whereas the core layer can be made of materials such as porous foams and polymers. Practical applications of these hybrid structures are commonly found in aerospace, railway, and automotive industries [46, 57, 100]. The manufacturing of sandwich structures itself is a challenging task. We refer to the works of Palkowski and Lange [73], Behrens et al. [11], and Grünewald et al. [30] on the discussion of manufacturing these layered structures. After the manufacturing step of the sandwiches, frequently they are deformed using, for example, bending or deep drawing processes, see [74] or [13]. At present, further extensive research is done in the area of various joining techniques between the core layer and the face sheets of sandwich structures, see [18].
Theoretical considerations of layered sandwich structures subjected to bending loads can be traced back to the works of Reissner [78], Alwan [2], and Azar [7]. The classical beam and plate theories are extended to incorporate the behavior of sandwich structures, see [1]. The development of these theories from linear (physically and geometrically) to nonlinear cases is possible with the help of numerical methods such as the finite element method (FEM). The full potential of sandwich structures is further exploited by subjecting them to complicated bending and deep drawing processes. Kim and Thomson [52] experimentally studied the formability of steel–polymer laminated structures. Parsa et al. [75], performed redrawing of components made of laminated stainless steel and aluminum materials and demonstrated the behavior using deep drawing and redrawing processes. Furthermore, Atrian and Fereshteh-Saniee [5] showed the effect of various process parameters on the deep drawing process of laminated metal sheets and validated FEM models with experimental results. Atrian and Panahi [6] investigated and also validated the effect of blank holder force on aluminum/polypropylene/steel sandwiches during deep drawing processes. In Harhash et al. [32, 33], the core layers are made of a PP/PE polymer compound (polypropylene–polyethylene) with steel as face sheets. In their investigations the sandwiches are subjected to bending and deep drawing processes. Klawonn et al. [53] presented a multi-scale simulation approach of the stretch forming test for a dual-phase steel. Hammarberg et al. [31] studied a ultrahigh-strength steel (UHSS) sandwich concept, intended for energy absorption, using FEM as well as homogenization of the perforated core using a stress-resultant based equivalent representation. Fischer et al. [26] investigated the quasi-structural mechanical properties of fiber metal laminates processed by thermoforming techniques.
In addition to the thin metallic layers in a sandwich, local reinforcements are inserted to increase the stiffness of the laminates, for example, at holes, riveted joints, etc., see [93] as well. One possibility for such an enhancement are fiber-reinforced composite materials for the core layer. For a 3D structural simulation of these composite materials, a constitutive model and appropriate material parameters are required. The generation of virtual experimental data or stochastic data using the microstructure for the identification of material parameters is discussed in the works of Mahnken [62]. Further literature on the stochastic data generation can be referred to the works of Rieger [82] and Nörenberg and Mahnken [71, 72]. The evaluation of consistent tangents for anisotropic materials using various homogenization techniques is explained in Doghri and Ouaar [23], Doghri and Friebel [22], Böhlke et al. [15], and Fritzen et al. [28] and the literature cited therein. Motevalli et al. [69] developed models of orthotropy using the concept of metric tensors. For the provided models, the material parameters need to be identified by experiments. Bargmann et al. [9] reviewed the state of the art representative volume element (RVE) generation techniques for heterogeneous materials. Görthofer et al. [29] used FFT-based computational techniques to investigate the sensitivity of the effective elastic properties entering the sheet metal compound (SMC) unit cell generator based on computational multi-scale strategy. Hofmann [47] performed tensile, shear, and bending experiments to identify the elastic material parameters using strain gauges. Li et al. [60] predicted the mechanical properties of orthotropic plain-weave composites with voids in the matrix material using unit cells at multi-scales. In the work of Schmidt et al. [86] the definition of the inverse problem for the two-scale parameter identification using \(\hbox {FE}^2\)-method is utilized. Applications of the composite materials for bending and deep drawing processes were also previously investigated. Hasebe and Sun [43] investigated the performance of sandwich panels with foam cores reinforced with composite laminates subjected to three point bending. Reyes and Kang [81] and Reyes and Gupta [80] investigated the formability characteristics of polypropylene-based fiber–metal sandwich structures. Davey et al. [20] developed an FE model to simulate the stamp forming of CF/PEEK sheets. Rajabi et al. [77] investigated the influence of four primary process variables for deep drawing and the effects of two types of composite cores (pure polypropylene and glass fiber-reinforced polypropylene) on the thermoplastic metal–composite structures.
In this work, a sandwich panel is manufactured using steel (heat-treated) as face sheets and woven glass fibers reinforcing a thermoplastic Polyamide-6 (GF-PA6) composite material as core material. A finite strain viscoplasticity model is drawn on to reproduce the principle structural behavior of the laminate in the forming process. Here, a slightly modified model of Lion [61], Tsakmakis and Willuweit [97] is chosen, see [21, 41] as well. For the case of composite material, a simple elasticity model incorporating orthotropy due to the presence of fibers is formulated on the basis of the invariant theory, see [49, 87, 88, 94], and the literature cited therein. For both models, the material parameters have to be determined by experimental data. The material parameter identification process of the steel model of viscoplasticity can be done on the basis of uniaxial tensile tests. Under the assumption of a homogeneous deformation within the center region of the specimen, the three-dimensional constitutive model is adapted to a uniaxial tensile problem. This is done using the tool discussed in Krämer et al. [55], and the concept of identifiability is discussed, [10, 12, 36]. For the GF-PA6 material, we combine analytical considerations with the numerical approach of using a representative volume element (RVE), which is obtained by a \(\mu \)-CT image. This data is chosen to provide a geometrical model, which is meshed by finite elements. In this case, the material behavior of the polymer matrix (PA6) and the glass fiber (and its mass content) must be known. Then, particular displacement loads are applied, and the resulting force data is chosen to determine the stress state by a homogenization technique. Based on a least-square approach using the residuum, i.e., the difference of the finite element response of the RVE and the homogenized orthotropic elastic response, the material parameters can be determined. On the basis of the identified parameters, several validation examples are discussed. First, the metal forming process of the pure steel (M) is considered. Second, the GF-PA6 model is studied, and third, the full M/GF-PA6/M laminate is investigated in a forming process. For this validation step, we are interested in the influence of uncertainties on the simulations arising from the material parameter identification. For this purpose, we draw on the concept of error propagation, which will indicate the influence of material parameters or their uncertainties on the finite element simulations.
The notation in use is defined in the following manner: geometrical vectors are symbolized by \(\vec {a} \), second-order tensors \(\mathrm {\mathbf {A}} \) by boldfaced Roman letters, and calligraphic letters \({\mathcal {A}}\) define fourth-order tensors. Furthermore, we introduce matrices at global level symbolized by boldfaced italic letters \({{{{{\varvec{\mathsf{{ A}}}}}}}}\) and matrices on local level (Gauss-point level) using boldfaced Roman letters \({{\mathbf {\mathsf{{A}}}}}\).
2 Experiments and manufacturing of sandwich laminates
In the following, we summarize the tests performed on a Zwick testing machine (\(10\,\hbox {kN}\) force gauge) at a predefined temperature of \(20\,^{\circ }\hbox {C}\) using a thermal chamber on heat-treated steel, pure semi-crystalline thermoplastic PA6 polymer (matrix material) and glass fiber reinforced in PA6 polymer (GF-PA6) composite material. The deformation (axial and lateral strains) quantities during the tensile testing are measured using a video extensometer, and ARAMIS system is used to measure the surface deformations during the shear testing (3D digital image correlation system ARAMIS of the company GOM, Brunswick, Germany). The experiments are required for both material parameter identification purposes as well as for validating the derived models. The geometry of the specimens (steel, pure PA6, GF-PA6) are shown in Fig. 1, and Table 1 contains the concerned geometrical data (d-thickness of the specimens). In the final part, a brief description of manufacturing the sandwich laminates is given.
2.1 Tensile testing of heat-treated steel
The steel sheets of deep drawing quality are heat-treated at \(440\,^{\circ }\hbox {C}\) for \(1\,\text {min}\) to enhance the adhesion properties, see [48]. The basic mechanical properties of steel are determined via tensile testing of specimens in rolling direction produced according to DIN 50114 standards. The geometry of the steel specimens used for tensile testing are as shown in Fig. 1a with the dimensions in Table 1. The tensile tests are carried out in the rolling direction, where we assume that the behavior is approximately isotropic. For identifying the material parameters of the viscoplasticity model representing the steel behavior, the constitutive modeling of the steel later on, tensile tests at four different displacement rates (\({\dot{u}}_{k+1} = 0.5 \times 10^{-k} {\,} \hbox {mm}\,\hbox {s}^{-1}\), \(k = 0,1,2,3\)) are performed. Here, the displacements of the specimens holders are controlled. The different displacement rates address the rate-dependent material properties.
Since we are interested in identifying the equilibrium stress state of the material under consideration, we follow the concept proposed in Haupt and Lion [44] where a multi-step relaxation test—similar to Fig. 2 but with five loading steps and holding times of \(t_h = 4 \,\hbox {h}\) (loading rate of \({\dot{u}}_3 = 0.5 \times 10^{-2} \,\hbox {mm}\,\hbox {s}^{-1}\)) is used. The termination points of the relaxation steps are considered to be the discrete equilibrium stress points which represent the rate-independent behavior of the material. Both experimental results are depicted in Fig. 6 (to avoid duplication of experimental findings and model response, the Figures are presented in the parameter identification Sections). Here, four repetitions were performed for each test, i.e., \(4 \times 5 = 20\) experiments were done, where axial and lateral information was measured.
2.2 Tensile testing of matrix material (PA6)
The uniaxial tensile experiments of pure PA6 are performed as follows. The specimens for the tensile testing are manufactured using an injection molding process according to DIN ISO 527-2 standards and are preconditioned at \(80\,^{{\circ }}\hbox {C}\) for \(72\,\hbox {h}\) to eliminate the moisture content. The geometrical data of the specimens are compiled in Fig. 1a with the values in Table 1. Again, a displacement-controlled multi-step relaxation process with a loading rate of \({\dot{u}}_3 = 0.5 \times 10^{-2} \, \hbox {mm}\,\hbox {s}^{-1}\) and holding times of \(t_h = 6\,\hbox {h}\) is used, see Fig. 2.
Since we are only interested in a linear elastic modeling of PA6, we restrict ourselves to the assumed linear elastic equilibrium stress part. The results of the experimental data—here, only the termination points of the multi-step relaxation test are shown—are summarized in Fig. 7.
2.3 Testing of composite material (GF-PA6)
The glass fiber reinforced in PA6 polymer (GF-PA6) composite material is directly obtained in the form of thin foils from the company bond laminates. The (electrically graded) E-glass fiber rovings have a Twill 2/2 fiber architecture according to DIN ISO 9354 standards. The composite material has a nominal fiber content of \(47\%\) by volume, and the overall density is \(1.80\,\hbox {g}\,\hbox {cm}^{-3}\). All the specimens are preconditioned at \(80\,^{\circ }\hbox {C}\) for \(72\,\text {h}\) to eliminate the moisture content.
2.3.1 Tensile testing of composite material (GF-PA6)
The tensile specimens are cut from the thin foils according to DIN ISO 527-4 standards. The geometry and dimensions of the tensile specimens used are shown in Fig. 1b and Table 1, respectively. A displacement-controlled multi-step relaxation test at a loading rate of \({\dot{u}}_3 = 0.5 \times 10^{-2} \, \hbox {mm}\,\hbox {s}^{-1}\) with inserted holding times of \(t_h = 3\,\text {h}\) is chosen, see Fig. 2. The tensile tests of specimens with \(\gamma =0^{\circ }\), see Fig. 1b, are drawn on for validating the fiber-reinforced composite material in Sect. 5.2.1.
2.3.2 Three-rail shear testing of composite material (GF-PA6)
Analogously, we performed shear tests at room temperature using the three-rail shear tool shown in Fig. 3a. Five displacement-controlled monotonous tests are carried out with a loading rate of \({\dot{u}}_3 = 0.5 \times 10^{-2} \, \hbox {mm}\,\hbox {s}^{-1}\). The surface deformations are measured using ARAMIS system, see Fig. 3b. The geometry and fiber directions of the specimens are as depicted in Fig. 1c, which are later drawn on for model validation purposes, see Sect. 5.2.2. The dimensions are assembled in Table 1.
2.4 Manufacturing of sandwich laminates
The multi-step manufacturing of the M/GF-PA6/M laminates takes place in a deep drawing press. The forming tool is modular and equipped with heating/cooling channels, which ensure, on the one hand, the melting of the thermoplastic PA6 in the composite material and, on the other hand, a defined cooling of the sandwich plates in one single step. The preparation steps are roughening, cleaning, and heat treating (\(440\,^{\circ }\hbox {C}\) for \(1\,\text {min}\)) the metallic layers, which enables a better adhesion to the polymer and the adhesive agent. The second step is the application of the adhesive agent, based on an amine-terminated copolyamide (SI Coating Nr: 310027), on the metallic surface. The core material—GF-PA6—is also cleaned using isopropanol to remove dust and organic impurities. Then, the composite is placed in between the metallic layers and placed in the preheated press. After a short holding time of \(30\,\hbox {s}\) in order to homogenize the temperature in the sandwich, the forming and bonding process starts where a load of \(70\,\hbox {kN}\) is applied, followed by compaction of the M/GF-PA6/M laminate. The last production step is the cooling of the sandwich plates to \(80\,^{\circ }\hbox {C}\) and removing the finished component. The results of the experimental data are shown in Fig. 11d.
3 Constitutive modeling
Since several materials are used in the laminates under consideration, a particular focus must be directed to each constitutive model. The metal layers are modeled using a von Mises-type viscoplasticity model although Lüders bands influence the post-elastic region, and the homogeneity of the deformation in the specimen, see Fig. 6. Since this behavior is difficult to model, we limit ourselves to a rather classical model. For further reading, we refer to Maziére and Forest [67], Ren et al. [79], and the references cited therein. The GF-PA6 composite core layer exhibits also a certain complexity the closer one looks. Thus, we assume a homogeneous distribution of the material for a first instance. Further, an anisotropic elastic response is assumed. Since we are only interested in modeling the undamaged material region, delamination, interface cracks, fracturing of the metal layers, and so forth, are not considered. The models are kept as simple as possible in view of the identifiability of the material parameters discussed later on.
3.1 Finite strain viscoplasticity model for heat-treated steel
The constitutive model for steel is followed according to [21, 61, 97], see for more details of the numerical treatment [41]. It is based on the multiplicative decomposition of the deformation gradient \(\mathrm {\mathbf {F}} = {{\,\mathrm{Grad}\,}}{{\varvec{\chi }}}_{\text {r}}(\vec {X} ,t)\) into an elastic and a viscous part, \(\mathrm {\mathbf {F}} = \hat{\mathrm {\mathbf {F}} }_{\text {e}} \mathrm {\mathbf {F}} _{\text {v}} \). Here, \(\vec {x} = {{\varvec{\chi }}}_{\text {r}}(\vec {X} ,t)\) represents motion of the material point \(\vec {X} \) having its placement at \(\vec {x} \) at time t. Further, the viscous part is decomposed into dissipative \(\mathrm {\mathbf {F}} _{\text {r}} \) and a storage part \(\tilde{\mathrm {\mathbf {F}} }_{\text {k}} \), \(\mathrm {\mathbf {F}} _{\text {v}} = \tilde{\mathrm {\mathbf {F}} }_{\text {k}} \mathrm {\mathbf {F}} _{\text {r}} \). Particular assumptions of the representation of the strain-energy function and the evaluation of the Clausius–Duhem inequality yield the constitutive model summarized in Table 2. All quantities are expressed relative to the reference configuration. \(\mathrm {\mathbf {C}} = {\mathrm {\mathbf {F}}}^{T} \mathrm {\mathbf {F}} \) defines the right Cauchy–Green tensor, whereas \(\mathrm {\mathbf {C}} _{\text {v}}= {\mathrm {\mathbf {F}}}^{T} _{\text {v}}\mathrm {\mathbf {F}} _{\text {v}}\) and \(\mathrm {\mathbf {C}} _{\text {r}}= {\mathrm {\mathbf {F}}}^{T} _{\text {r}}\mathrm {\mathbf {F}} _{\text {r}}\) represent the viscous and remaining right Cauchy–Green tensors, which are defined by the evolution equations (3) and (4) (flow rules). \(\tilde{\mathrm {\mathbf {T}} }= (\det \mathrm {\mathbf {F}} ) {\mathrm {\mathbf {F}}}^{-1} \mathrm {\mathbf {T}} {\mathrm {\mathbf {F}}}^{-T} \) is the second Piola–Kirchhoff tensor depending on the Cauchy stress tensor (true stresses) \(\mathrm {\mathbf {T}} \). \(\mathrm {\mathbf {Z}} \) can be interpreted as a backstress tensor. \(\mathrm {tr}\,\mathrm {\mathbf {A}} = a_k^{\; k}\) represents the trace operator of a second-order tensor \(\mathrm {\mathbf {A}} \). The model is of Armstrong–Frederick type, see [4], however, in a strain space formulation. The viscous behavior is attributed as Perzyna-type viscoplasticity, [76], where the “plastic multiplier” (6) depends on the yield function f, defined in Eq. (1), and the viscosity \(\eta \). \(\sigma _0\) serves only to non-dimensionalize the expression in the Macauley brackets.
Since we are interested in the material parameter identification process of the model later on, we summarize the material parameters of the model. In the elasticity relation (2), represented by a Neo-Hookean type model, we have the bulk modulus \(K_{\text {st}}= E_{\text {st}}/(3(1-2\nu _{\text {st}}))\) and shear modulus \(G_{\text {st}}= E_{\text {st}}/(2(1+\nu _{\text {st}}))\). Both can be expressed by Young’s modulus \(E_{\text {st}}\) and Poisson’s ratio \(\nu _{\text {st}}\). The uniaxial yield stress is denoted by \({\hat{k}}\) indicating that the model has no isotropic hardening part. The kinematic hardening behavior is controlled by the material parameters \(c_1\), \(c_2\), and \(\beta _{\text {st}}\). All viscous properties of the material response are assigned to the viscosity \(\eta \) and the viscosity exponent r. Although kinematic hardening rules were originally developed to model the Bauschinger effect, they are able to describe the nonlinear loading behavior as well.
3.2 Model of linear elasticity for PA6
Since the main response of the entire laminate is dominated by the response of the metal layers, we keep the models of the composite kernel layer as simple as possible. With regard to the modeling or parameter identification of the GF-PA6 composite, we need the modeling of the pure PA6. Therefore, a linear isotropic elastic behavior is assumed to be sufficient,
\(\hat{\mathrm {\mathbf {E}} } = \frac{1}{2} \left( {{\,\mathrm{grad}\,}}\vec {u} (\vec {x} ,t) + {{\,\mathrm{grad}\,}}^T \vec {u} (\vec {x} ,t) \right) \) is the linearized Green strain tensor, where \(\vec {u} \) represents the displacement field. \(\hat{\mathrm {\mathbf {E}} }^D = \hat{\mathrm {\mathbf {E}} } - (1/3) (\mathrm {tr}\,\hat{\mathrm {\mathbf {E}} }) \mathrm {\mathbf {I}} \) symbolizes the deviator of the strain tensor. In this model, \(E_{\text {m}}\) and \(\nu _{\text {m}}\) are the material parameters indicating Young’s modulus and Poisson’s ratio of the matrix material.
3.3 Model of orthotropy for composite modeling
The material response of the composite of a twill fabric behaves anisotropic. For the first instance, a model of finite strain hyperelasticity is drawn on for the special case of orthotropy. We assume two preferred directions \(\vec {a} _1\) and \(\vec {a} _2\), respectively. The material exhibits different responses in these preferred directions due to the weaving of the fabric. The fibers are orthogonal to each other, \(\vec {a} _1 \cdot \vec {a} _2 = 0\). According to [94] the strain-energy function is formulated by
There, a reduced system of invariants for an isotropic function is given by
\(\mathrm {\mathbf {E}} = 1/2 ({\mathrm {\mathbf {F}}}^{T} \mathrm {\mathbf {F}} - \mathrm {\mathbf {I}} )\) represents the Green–Lagrange strain tensor, whereas \(\mathrm {\mathbf {M}} _1 = \vec {a} _1 \otimes \vec {a} _1\) and \(\mathrm {\mathbf {M}} _2 = \vec {a} _2 \otimes \vec {a} _2\) symbolize the second-order structural tensors along the fiber directions \(\vec {a} _1\) and \(\vec {a} _2\). A dependence on \(\text {I}_3\) is not assumed (it vanishes in the following considerations). Since we are interested in a strain-energy which is quadratic in the strain measures, the terms
are assumed. The constitutive model implies the set of material parameters
containing 9 entries which have to be determined by particular experiments. The decomposition of the free energy function into “isotropic” and “anisotropic” parts leads to its corresponding decomposition of the second Piola–Kirchhoff stress tensor,
with the density in the reference configuration \(\rho _{\text {R}}\). Applying the Gateaux derivative yields
where we assign the density to the material parameters as it is common at this stage of derivation, e.g., \(\Lambda \leftarrow \rho _{\text {R}}\Lambda \). Since the stress–strain relation is linear in the strain state, we can rewrite Eq. (13) also in the form \(\tilde{\mathrm {\mathbf {T}} } = {\mathcal {C}} \mathrm {\mathbf {E}} \). This implies the fourth-order elasticity tensors for orthotropy
with
Here, \(\mathrm {\mathbf {I}} \) is the second-order identity tensor, and \({\mathcal {I}} = \left[ {\mathrm {\mathbf {I}} } \otimes {\mathrm {\mathbf {I}} } \right] ^{T_{23}} = \delta _{ik} \delta _{jl} \left( \vec {e} _i \otimes \vec {e} _j \otimes \vec {e} _k \otimes \vec {e} _l \right) \) symbolizes the fourth-order identity tensor, \(\mathrm {\mathbf {A}} = {\mathcal {I}} \mathrm {\mathbf {A}} \). The symbol \({\mathcal {A}}^{T_{23}}\) denotes the transposition of the second and third index of the fourth-order tensor \({\mathcal {A}}\), i.e., for \({\mathcal {A}} = a_{ijkl} \left( \vec {e} _i \otimes \vec {e} _j \otimes \vec {e} _k \otimes \vec {e} _l \right) \) we obtain \({\mathcal {A}}^{T_{23}} = a_{ikjl} \left( \vec {e} _i \otimes \vec {e} _j \otimes \vec {e} _k \otimes \vec {e} _l \right) \).
Two concluding remarks must be added. First, the second Piola–Kirchhoff stress tensors can be assumed to be identical to the stress tensor for the case of small strains, \(\tilde{\mathrm {\mathbf {T}} } \approx \mathrm {\mathbf {T}} \). Furthermore, the Green–Lagrange strain tensor \(\mathrm {\mathbf {E}} = 1/2 ({\mathrm {\mathbf {F}}}^{T} \mathrm {\mathbf {F}} - \mathrm {\mathbf {I}} )\) can be approximated by the strain tensor \(\hat{\mathrm {\mathbf {E}} } = \frac{1}{2} \left( {{\,\mathrm{grad}\,}}\vec {u} (\vec {x} ,t) + {{\,\mathrm{grad}\,}}^T \vec {u} (\vec {x} ,t) \right) \) for small strains, \(\mathrm {\mathbf {E}} \approx \hat{\mathrm {\mathbf {E}} }\). Later on, we consider these properties in the material parameter identification case. Second, it is common to look at the transition from the tensorial notation to matrix notation, commonly called Voigt notation, see [98]. The transition of the tensors in a matrix formulation in our application is presented in Hartmann and Kheiri Marghzar [40] (which is not exact the “Voigt idea”). In this case, we have
with \({{\mathbf {\mathsf{{T}}}}} {\, \in \mathbb {R}}^{6}\), \({{\mathbf {\mathsf{{E}}}}} {\, \in \mathbb {R}}^{6}\), and \({{\mathbf {\mathsf{{C}}}}} {\, \in \mathbb {R}}^{6 \times 6}\). If the fiber directions are chosen such that \(\vec {a} _1 = \vec {e} _1\) and \(\vec {a} _2 = \vec {e} _2\), then Eq. (20) can be written as
with \(\varphi _1 = \Lambda +2\mu +2\alpha _1 + 4 \mu _{1}+\beta _1\) and \(\varphi _2= \Lambda +2\mu +2\alpha _2 +4 \mu _{2}+\beta _2\).
With regard to analytical considerations in the material parameter identification process, it is sometimes useful to define or to use different sets of material parameters. The individual entries in the elasticity matrix \({{\mathbf {\mathsf{{C}}}}} \in {\mathbb {R}}^{6 \times 6}\) can also be represented by the material parameter set
or in terms of Young’s moduli, Poisson’s ratios, and shear moduli yielding the material parameter set
The inter-dependencies between the material parameter sets \(\varvec{\kappa }_{\text {SP}}\in {\mathbb {R}}^9\), \(\varvec{\kappa }_{\text {C}}\in {\mathbb {R}}^9\), and \(\varvec{\kappa }_{\text {S}}\in {\mathbb {R}}^9\) are summarized in Appendix B.
4 Parameter identification procedure
We follow the concept of nonlinear least-square optimization to adapt the constitutive models to the experimental data concerned. The numerical scheme is assumed to be a gradient-based method. In this case the square of the residual between all experimental information and the model concerned is minimized requiring the gradient of the model with respect to the material parameters. The result of the minimizer are the material parameters of the model under consideration. A major aspect, however, is connected with the study of how reliable the parameters are, which is discussed in more detail. In the following, general remarks with respect to the parameter identification are provided for both the model of finite strain viscoplasticity for steel as well as orthotropic elasticity for the reinforced composite kernel, which is distinguished in pure PA6 and the response of an representative volume element of the polymer composite.
4.1 General remarks on least-square identification
Under the assumption of homogeneous deformations, uniaxial tension or compression tests are one possibility to calibrate a model. This is done for the chosen steel. In this case, the parameter identification procedure is based on the reduction of the three-dimensional model to the uniaxial tensile case. Furthermore, the solution of a coupled system of differential-algebraic equations (DAE system) has to be calibrated at the steel data. Since this model type is similar to an overstress-type model, different subsets of parameters are determined at subsets of experimental information. Moreover, the type of parameter identification changes from algebraic equations to differential-algebraic equations. This is discussed in detail in Krämer et al. [55], Hartmann [35], which is based on considerations of Schittkowski [85].
An extension of the concept is given when the data is provided by full-field information such as it is the case for digital image correlation systems (DIC systems), see, for example, [95] for the background in DIC systems, and [3, 65] for combining DIC data and finite element simulations in the context of parameter identification. The data (displacements or strains) is spatially distributed, and accordingly, seemingly much more information can be provided. However, this does not mean that the material parameters are addressed by the experiments. This issue is linked to the theory of the identifiability of material parameters [10] and discussed in connection with questions of solid mechanics by Hartmann and Gilbert [36, 39], Hartmann et al. [38], Sewerin [91], and Hartmann and Gilbert [37].
One concept to identify material parameters is related to minimize the least-square problem
where \({{{{\varvec{\mathsf{{ d}}}}}}} {\, \in \mathbb {R}}^{{n_{\text {D}}}}\) represents the experimental data, vector, \({n_{\text {D}}}\) the total number of experimental data and \({{{{\varvec{\mathsf{{ s}}}}}}} {\, \in \mathbb {R}}^{{n_{\text {D}}}}\) the model response evaluated at the experimental data points (this implies a spatial and temporal interpolation of the data). The model response \({{{{\varvec{\mathsf{{ s}}}}}}}(\varvec{\kappa })\) depends on the material parameters \(\varvec{\kappa }{\, \in \mathbb {R}}^{{n_{\kappa }}}\). Of course, there might be inequality constraints for the parameters and weighting of the residuals \({{{{\varvec{\mathsf{{ r}}}}}}}(\varvec{\kappa }) = {{{{\varvec{\mathsf{{ s}}}}}}}(\varvec{\kappa }) - {{{{\varvec{\mathsf{{ d}}}}}}}\). The necessary condition of the minimum of Eq. (24) results in a system of nonlinear equations,
where
\({{{{{\varvec{\mathsf{{ D}}}}}}}} {\, \in \mathbb {R}}^{{n_{\text {D}}} \times {n_{\kappa }}}\) is the sensitivity matrix (Jacobian). In other words, we have to solve \({n_{\kappa }}\) equations, \({{{{\varvec{\mathsf{{ g}}}}}}}{\, \in \mathbb {R}}^{{n_{\kappa }}}\), if there are no additional constraints. There are many solvers treating the minimization problem, see, for example, [14, 58, 70, 85], which are programmed very stable so that results are—commonly—provided. However, the question about the local uniqueness and the reliability of the parameters, which stem from an inverse problem, has to be discussed. The first and essential step is to look at the model. Here, only those parts of the model are used, which can be determined by a special experiment. In the second step measures for the quality of the parameters and the local uniqueness of the identified parameters have to be checked. This process has also an influence in model development, because it is not uncommon that sophisticated models are over-parametrized, i.e., not all parameters can be determined by the available experiments (either the laboratory has no further testing devices, or it is definitely not possible to address the individual parameters uniquely). In conclusion, there might be deficiencies stemming from the model, for example, due to an over-parametrization, i.e., there do not exist any mechanical test and measuring devices or the experimental data is incomplete to address all material parameters. Furthermore, all experiments, i.e., the measuring devices and the specimens under consideration have inevitable uncertainties, see, for example, [96] for a detailed discussion. Finally, the inverse analysis can lead to multiple local minima, or locally infinite solutions. The latter is connected with the notion of local identifiability, see [10]. Thus, we draw on various measures indicating the reliability of the estimated parameters.
The first measure—apart from the \(R^2\)-value—of the identified material parameters \(\varvec{\kappa }^*\) is given by the confidence interval \(\Delta \varvec{\kappa }\). This value is based on the covariance matrix
where
represents the standard deviation, see, for example, [24], and
the Hessian matrix. An estimation of the Hessian is given by
(which is justified for a good fit, \(s_k(\varvec{\kappa }) - d_k \approx 0\)), with the sensitivity matrix (26). Now, the confidence interval is defined by
where
is calculated on the basis of the diagonal components of the covariance matrix (27). A further information is provided by the correlation matrix indicating whether the material parameters are linearly correlated,
Obviously, the diagonal terms are \(c_{ii} = 1\), and the off-diagonal elements represent the linear correlation between the parameters \(\kappa _i\) and \(\kappa _j\), \(|c_{ij}| \le 1\).
Identifiability is connected with the determinant of the Hessian (30). If it is zero, \(\det {{{{{\varvec{\mathsf{{ H}}}}}}}} = 0\), the parameters cannot be unique (locally). Alternatively, one can calculate the eigenvalues of the Hessian. If the smallest eigenvalue is (close to) zero, no unique solution can be found. This is connected with the notion of stability, [63, 64, 99]. There are two possibilities for evaluating this property. First, the Hessian, which is based on the underlying real experimental data, can be evaluated. The result strongly depends on the scattering of the data, and in some situations, it is not clear whether a small \(\det {{{{{\varvec{\mathsf{{ H}}}}}}}}\) results from the data or the over-parametrized model. Thus, the second possibility takes some more or less realistic material parameters, solves the direct problem and generates the so-called synthetic data. Then, this generated data is taken as “experimental input” for the identification process. The evaluation of the determinant of the Hessian provides an indicator whether the underlying test data principally address the material parameters. This is called re-identification in Hartmann and Gilbert [36, 37]. The aforementioned investigations will be considered in the following. The material parameters are identified using the tool developed in Krämer et al. [55].
Another aspect must be considered with respect to the error propagation of uncertainties on subsequent calculations. This is accounted for by means of the confidence interval \(\Delta \kappa _k\) of the underlying parameters using Gaussian error propagation, see [96]. A function \(F(\varvec{\kappa })\) with the estimated deviation \(\Delta \varvec{\kappa }\) yields the uncertainty
i.e., \(F \pm \delta F\). These expressions are evaluated at the best fit \(\varvec{\kappa }^*\). In particular, this concerns on the one hand identification approaches, which are carried out in several steps, and on the other hand the influence of parameter uncertainties on the results of both subsequent analytical calculations as well as finite element simulations based on them.
4.2 Parameter identification and model reduction for heat-treated steel
The process of parameter identification with regard to the finite strain viscoplasticity model for the steel can be treated by various approaches. Parameter identification investigations of such constitutive models and their stability or uniqueness can be found in Fossum [27], Ekh [25], Johansson et al. [50]. There, the correlation matrix is chosen as indicator of the quality of the material parameters based on two reasons: firstly, inadequate or insufficient experimental results, and, secondly, due to the complexity of the chosen model, see [63] as well. Ekh [25] performed the correlation analysis of the material parameters used in thermo-elastic-viscoplastic modeling of IN792 material where temperature-dependent step relaxation tests and creep tests are adopted for the parameter identification process. The resulting strong correlation between the material parameters was a priorily eliminated by fixing some of the parameters to zero and prescribing values to some of the material parameters (model reduction technique). The author finally concludes an improvement in the correlation values between the material parameters. Johansson et al. [50] suggested uniaxial stress-controlled, bi-axially stress-controlled or mixed controlled cyclic experiments to identify the material parameters of a hyperelasto-plasticity model in a single step. Here, some of the identified material parameters were strongly correlated with each other. To overcome this, some of the hardening parameters in the model were fixed and the remaining material parameters were re-identified. The strong correlation still existed even after the re-identification process. Kleuter et al. [54] tried to identify all the material parameters in a single step with tensile, relaxation, and multi-step relaxation test data on a flat specimen with a hole using PU D44 (polyurethane). This was described by a finite strain viscoelasticity model. Some of the material parameters were strongly correlated with each other for which the authors state the inability of the model to describe all the characteristics of the material and the contribution of errors (measurements and scattering) by the experiments.
In the following, several approaches are discussed. First, an estimate of the correlation between the parameters is used, which is independent of the measured data. It gives first information about the principal behavior of the material model at given process conditions. Second, all parameters are identified in a single step using the experimental data. This will lead to the essential result that the parameters describing the elastic range and the yield stress should be identified first. The identification of the elastic material parameters, their uncertainties and their error propagation to the calculation of subsequent parameters is discussed in Sect. 4.2.3. In a subsequent step, all parameters describing the inelastic behavior are considered. Here, it should be discussed which data of the uniaxial tensile test is necessary. In a following step, the modularity of the constitutive model is evaluated, since it is an overstress-type similar model [45, 56]. Further, a particular error propagation concept is proposed to see the influence of the “fixed” parameters from previous tests. Due to the strong correlation of the material parameters, a model reduction proves to be reasonable, i.e., not all parameters of the model are required to reproduce the response.
The quality of the parameters obtained is studied in detail and leads to conclusions of reducing the model. Furthermore, in stepwise identification concepts, the effect of uncertainties of previously identified material parameters on the subsequently determined parameters is considered with the help of Gaussian error propagation.
4.2.1 Estimation of correlation
Considering Eqs. (24)–(33), Eqs. (24)–(25) represent the optimization problem and Eqs. (27)–(33) represent evaluation quantities of optimization and are almost independent of the optimization problem. When evaluating the Hessian matrix according to Eq. (30), even an independence of the correlation matrix (33) from the experimental data can be observed. This implies that an evaluation of the correlation matrix is possible without using the measurement data. In contrast, the process control must be specified, since the material model represents an ordinary differential equation. Here, four rate-dependent processes with a stretch rate \({{\dot{\lambda }}}_k=0.4\times 10^{-k}\), \(k=1,\ldots ,4\) and a multi-step relaxation process, see Fig. 2, are chosen. Appendix A shows a first estimation of the material parameters of the model from Table 2, see Table 9. We use here four rate-dependent uniaxial tensile as well as the multi-step relaxation loading paths. Young’s modulus, Poisson’s ratio, and the yield stress are selected in advance. This then leaves five material parameters, three to describe the strain hardening model and two to describe the rate dependence and relaxation behavior. In the resulting correlation matrix
one can see, for example, a very strong correlation between \(c_2\) and \(\beta _{\text {st}}\) as well as between \(\eta \) and r. The signs then still indicate how the dependencies between material parameters look like. For example, \(\beta _{\text {st}}\) describes the saturation value of the kinematic hardening. If this becomes larger, the viscosity \(\eta \) must become smaller indicated by a negative sign. In the following, however, we will use all real measured data for the concrete evaluation and interpretation of the parameter identification. The aforementioned procedure, however, already gives a first trend of the correlations.
4.2.2 Single-step identification of material parameters
For the single-step identification of all the material parameters of the viscoplasticity model \(\varvec{\kappa }_{\text {st}}=\{ K_{\text {st}}, G_{\text {st}}, {\hat{k}}, c_1, c_2, \beta _{\text {st}}, \eta , r \}\) in Table 2 for steel, we use the collective data (axial stresses and lateral stretches) of uniaxial tensile experiments (rate-dependent and multi-step stress relaxation tensile tests). As discussed in Sect. 2.1 four repetitions for four rate-dependent and one multi-step relaxation path are incorporated. In this respect, axial and lateral information is taken into account, i.e., \(4\times 5\times 2= 40\) data files are considered. The material parameters obtained by this single-step identification process are shown in Table 3 (set A).
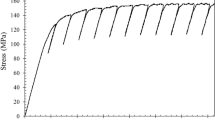
If these parameters are taken to generate the numerical test data, the re-identification step yields a determinant of the Hessian of \(\det {{{{{\varvec{\mathsf{{ H}}}}}}}} \approx 10^{-36}\). Thus, the experiments cannot address all the material parameters, although the optimization schemes yield parameters with seemingly reasonable results, see Fig. 4. Unfortunately, there are practical limitations to the type of experiments that could be performed on flat specimens to acquire the missing data. Even the evaluation of the determinant of the Hessian using all real data yields a value of \(\det {{{{{\varvec{\mathsf{{ H}}}}}}}} \le 10^{-60}\) indicating that also the scattered data cannot improve the missing data problem.
Results of single-step parameter identification for rate-dependent tests and multi-step relaxation test of heat-treated steel (fit is calculated using set A in Table 3)
The evaluation of the correlation matrix using Eq. (33),
shows that there are values larger than \(|c_{ij}| > 0.75\) indicating a strong linear correlation between the parameters. Obviously, there are correlations between the yield stress \({\hat{k}}\) and the hardening parameters \(c_1, c_2, \beta _{\text {st}}\) as well as the viscosity \(\eta \). The parameter \(c_1\), connected with the compressible behavior of the hardening model, correlates to \(c_2\) and \(\beta _{\text {st}}\). Further, a correlation between the hardening parameters \(c_2\) and \(\beta _{\text {st}}\) exists, and between the parameters describing the viscous behavior, \(\eta \) and r. Figs. 4a, b show the result of single-step identification procedure for rate-independent and rate-dependent parts of the model, respectively. Although there are these model deficiencies, an appropriate result is obtained.
The 1st Piola–Kirchhoff stress component in axial direction, \({T_{\text {R}}}_{xx}\), \(\mathrm {\mathbf {T}} _{\text {R}}= (\det \mathrm {\mathbf {F}} ) \mathrm {\mathbf {T}} {\mathrm {\mathbf {F}}}^{-T} \), is defined as the force divided by the undeformed cross section of the specimen (engineering stress). Here, the axial stretch is determined by the axial length L(t) divided by the original length \(L_0\), \(\lambda = L/L_0\), whereas the lateral stretch is defined by the relation of the lateral width B(t) to the initial width \(B_0\), \(\lambda _{\text {Q}}= B/B_0\). Both are given by the videoextensometer measurements.
A further indicator of problems in parameter identification is provided by the confidence interval (31)–(32). We start with the confidence intervals of identified material parameters. Some of the material parameters have a high relative error percentage. \(c_1\), \(\beta _{\text {st}}\), and \(\eta \) are more than questionable parameters requiring a different approach of identifying the parameters.
4.2.3 Elastic material parameters and yield stress
Due to the difficulty in local identifiability, large confidence intervals of some parameters and strong correlations between material parameters encountered in Sec. 4.2.2, we resort to identify the material parameters in stepwise manner exploiting the modular structure of the constitutive model. Since the constitutive model has the property of an overstress-type model, in a first step the viscosity is set to zero so that only the rate-independent part of the model is addressed. From the extensometer data, which is able to measure axial and lateral deformations, and the testing machine’s force gauge information, we determine in a classical manner Young’s modulus \(E_{\text {st}}\) and Poisson’s ratio \(\nu _{\text {st}}\), which is based on the elastic region of the four tensile tests using axial and lateral information, see Fig. 5a. These parameters and their confidence intervals are compiled in Table 3 (set B and C) as well as in Table 4 (set 1 to 3). From the identified parameters, we can calculate the bulk and shear modulus \(K_{\text {st}}= E_{\text {st}}/(3(1-2\nu _{\text {st}}))\) and \(G_{\text {st}}= E_{\text {st}}/(2(1+\nu _{\text {st}}))\).
With regard to the influence of the confidence interval of the elastic parameters \(E_{\text {st}}\) and \(\nu _{\text {st}}\) on the bulk (compression) and shear moduli \(K_{\text {st}}\) and \(G_{\text {st}}\), the Gaussian error propagation (34) is applied, see [96]. This estimation yields the confidence intervals depicted in Table 3 (set B and C) and Table 4 (set 1 to 3).
The determination of the yield stress \({\hat{k}}\) is much more critical. Since we have a steel with pronounced Lüders bands evolution, we define this parameter by hand-fitting to \({\hat{k}}=285\,\hbox {N}\,\hbox {mm}^{-2}\). The chosen yield stress \({\hat{k}}\) is given in Table 3 (set B and C) and Table 4 (set 1 to 3). In Sect. 4.2.7, the influence is discussed as well.
4.2.4 Two-step identification
First, it is assumed that the material parameters \(E_{\text {st}}\), \(\nu _{\text {st}}\), and \({\hat{k}}\) are given. In addition to these essential material parameters discussed in Sect. 4.2.3, the necessity of the nonlinear kinematic hardening parameters \((c_1, c_2, \beta _{\text {st}})\) and the parameters \((\eta ,r)\) to describe the rate-dependent material properties is examined in detail with respect to the given experimental data. There are two approaches. First, all material parameters describing the inelastic behavior are identified in one step, which is called the “two-step identification,” or, second, by exploiting the modular structure of the material model, which leads to additional identification steps. The two-step procedure is discussed first, whereas a three-step identification scheme is provided in Sect. 4.2.5.
In a first step, the experimental data with axial and lateral information of the four rate-dependent and the one multi-step stress relaxation paths with their individual repetitions are considered. This leads to the material parameters in Table 3 (set B, 2nd column). Obviously, the material parameters are very uncertain which the confidence intervals reveal. This is further supported by the determinant of the Hessian matrix (\(\det {{{{{\varvec{\mathsf{{ H}}}}}}}} \approx 2.9 \times 10^{-27}\)) and reflected in some strong correlations,
There are very strong correlations between \(c_1\) and \(\beta _{\text {st}}\), \(c_2\) and \(\beta _{\text {st}}\), as well as \(\eta \) and r. Thus, a more detailed investigation has to be provided.
4.2.5 Three-step identification and model reduction
In the following, the modularity of the constitutive model is exploited to minimize the correlations between the parameters. Thus, the termination points of multi-step relaxation tests are considered as data for addressing only the rate-independent part. Afterward, the parameters \(\eta \) and r can be studied at the rate-dependent loading paths. Furthermore, it will turn out that some of the parameters are not necessary due to the given data. This implies the step of model reduction.
Results of stepwise parameter identification for rate-dependent tests and multi-step relaxation test of heat-treated steel (fit is calculated using set 2 in Table 4)
All Material Parameters (Set 1) In order to determine the remaining parameters—apart from \((E_{\text {st}}, \nu _{\text {st}}, {\hat{k}})\)—of the equilibrium stress part of the model, \((c_1, c_2, \beta _{\text {st}})\), we draw on the termination points of relaxation, see Fig. 6a, which are estimated by the termination points of relaxation from a multi-step relaxation test. These are extrapolated by three exponential functions, see [66], leading to the hardening parameters \(\beta _{\text {st}}\), \(c_1\), and \(c_2\) shown in Table 4. For this step, the identification tool proposed in Krämer et al. [55] is chosen, where the viscosity \(\eta \) is set to zero, and the parameters \(K_{\text {st}}\), \(G_{\text {st}}\), and \({\hat{k}}\) are prescribed. Fig. 6a shows the result of parameter identification for the equilibrium stress part. The correlation matrix indicates a very strong correlation between some parameters,
In order to interpret the results, we study the model properties, particularly, the nonlinear hardening behavior of the extended Armstrong and Frederick model. \(c_1\) and \(c_2\) are related to an “elasticity relation,” where \(c_1\) can be interpreted as a “bulk modulus” and \(c_2\) as a “shear modulus.” In the original Armstrong and Frederick model for small strains, see [4], only \(c_2\) (deviatoric part) occurs. Due to the difficulty to separate—from the remaining lateral information—the inelastic part from the already identified elastic part, there is a moderate correlation between \(c_1\) and \(c_2\), but a large confidence interval in \(c_1\), see Table 4 (set 1). The Hessian \(\det {{{{{\varvec{\mathsf{{ H}}}}}}}} \approx 4.3 \times 10^{-2}\) shows identifiability, however, the confidence intervals of \(c_1\) and \(\beta _{\text {st}}\) are not acceptable. Thus, we set \(c_1\) to zero for a further investigation (first model reduction step). In this sense, the volumetric part of the kinematic hardening model is neglected (which obviously is hard to identify).
The remaining parameters are the viscosity \(\eta \) and the exponent r. For this purpose, both the four rate-dependent experiments and the multi-step relaxation experiments are considered for the parameter identification. Each test is performed four times where axial and lateral information are measured (thus, we have \(4 \times 5 \times 2 = 40\) data sets). \(\eta \) and r show a strong correlation as well,
and obviously the viscosity \(\eta \) is linearly correlated to r. The confidence intervals are around 20% of the original value implying not a really good identification, see the confidence interval in Table 4 (set 1). The determinant of the Hessian, \(\det {{{{{\varvec{\mathsf{{ H}}}}}}}} = 6.48 \times 10^{-7}\), indicates the sensitivity of identification as well. The reason for this may lie in the properties of the model. A derivation of analytical solutions even for the model equivalent for small deformations is not possible (neither for rate-dependent processes nor for a relaxation process). Further linearization approaches for a relaxation process index terms \(\eta ^{1/r}\), which may indicate the problems of confidence. Thus, we assume a constant exponent, \(r=1\), yielding a much more reliable viscosity \(\eta \) without loosing an essential quality of the fit.
Model Reduction Step (Set 2) In the following, only \(c_2\) of the deviatoric part and \(\beta _{\text {st}}\) are taken into consideration (set 2), which is similar to the classical Armstrong and Frederick model (only extended to large strains). The identification of \(c_2\) and \(\beta _{\text {st}}\) yields the correlation matrix
indicating that the parameters are linearly correlated (\(\det {{{{{\varvec{\mathsf{{ H}}}}}}}}\approx 6.6\times 10^{4}\) indicates identifiability). In Hartmann [34], and Krämer et al. [55] this is shown for the small strain case, where \(\beta _{\text {st}}\) is a linear function of \(c_2\). The parameter \(c_2\) is very stable and identifiable with a small confidence interval. However, \(\beta _{\text {st}}\) is not. The reason for this can be found in the fact that particularly \(\beta _{\text {st}}\) depends on the gradient behavior of the nonlinear kinematic hardening curve, and this is not strongly pronounced. Thus, \(\beta _{\text {st}}\) must be sensitive in this model for the given experimental data.
Alternatively, one could think of that the unloading behavior might be considered in the identification process as well. However, since only steel sheets are available and these immediately buckle laterally when unloaded, premature yielding in the compression zone (Bauschinger effect) cannot be considered. This could stabilize the identification of \(\beta _{\text {st}}\) but is experimentally really difficult, particularly, if lateral deformations are measured as well.
Further Modeling Reduction Step (Set 3) The previous investigation suggests to consider only a linear kinematic hardening model (we set \(c_1=0\) and \(\beta _{\text {st}}=0\)). This yields the parameters (set 3) in Table 4. Since \(\beta _{\text {st}}\) was very small, it has no essential influence. Fig. 6a shows the result of set 2 (rate-independent part of the model), which is very similar to the result of set 3. We can conclude that the quality measures of identification (confidence interval and identifiability) might help to obtain only the essential parts of complex constitutive models to represent the given experimental data.
The identification yields the curves in Fig. 6b. Furthermore, the determination of \(\eta \) for given \((c_2, \beta _{\text {st}})\) of set 2 and prescribed \(c_2\) for set 3 is not influenced, see Table 4, since the rate-independent part of the model is for both sets 2 and 3 very similar.
4.2.6 Two-step identification procedure for the reduced model
The question of identifying the material parameters for the reduced model \((c_2, \eta )\) follows immediately. Again, all measured data are used for identification, and in the first step, the elastic material parameters and the yield stress are identified, see Sect. 4.2.3. Based on this, the material parameters \(c_2\) and \(\eta \) are now determined in one step. This results in the material parameters \(c_2 = 588 \pm 89\,\hbox {N}\,\hbox {mm}^{-2}\) and \(\eta = 5871 \pm 244\,\hbox {s}^{-1}\). At this point it should already be mentioned that in Table 3 (set C) the additional uncertainties from the previously calculated values \((E_{\text {st}},\nu _{\text {st}},{\hat{k}})\) have already been determined by Gaussian error propagation, see Sect. 4.2.7. The determinant of the Hessian is moderate, \(\det {{{{{\varvec{\mathsf{{ H}}}}}}}} = 2.52\times 10^{-7}\), which holds for the correlation between \(c_2\) and \(\eta \) as well, \(C_{c_2 \eta } = 0.5245\). Thus, in principle a two-step identification is possible, but leads to different values than the three-step approach. However, the values are approximately within the uncertainty range calculated.
4.2.7 Propagation of uncertainties
In a more general view considering the stepwise approach of the parameter identification, the parameters identified from the previous step—and their relative uncertainties—have an impact on the uncertainty of the parameters yet to be identified. To estimate this propagation of uncertainty, we consider the Gaussian error propagation concept, see [96]. We assume that one parameter set \(\varvec{\kappa }^*{\, \in \mathbb {R}}^{{n_{\kappa ^*}}}\) has already been identified and the remaining parameters \(\varvec{\kappa }{\, \in \mathbb {R}}^{{n_{\kappa }}}\) have to be identified in the current step by solving Eq. (25). In this sense, the parameters \(\varvec{\kappa }= {\hat{\varvec{\kappa }}}(\varvec{\kappa }^*)\) need to be identified depending on the already known values \(\varvec{\kappa }^*\),
In terms of Gaussian error propagation to determine the uncertainty, see Eq. (34), we need the derivatives \(\mathrm d{\hat{\varvec{\kappa }}}/\mathrm d\varvec{\kappa }^*\), which we can determine in two ways. First, we apply the chain rule to Eq. (41) in the context of the implicit function theorem,
This is possible if the function \(\hat{{{{{\varvec{\mathsf{{ g}}}}}}}}\) is explicitly given as a program code. We must remember here that the model equations correspond to differential-algebraic equations. For this we refer to [35, 37, 85].
Alternatively, for the case of black-box solvers, the forward differential formula (or even central differences) is applicable,
or more general
Here, the column vector \({{{{\varvec{\mathsf{{ e}}}}}}}_j {\, \in \mathbb {R}}^{{n_{\kappa ^*}}}\) has only zero entries except at position j, which is 1. In this case the optimizer is called several times with varying input parameters \(\varvec{\kappa }^*\),
In addition to this estimated propagation of uncertainty, the confidence intervals of the material parameters evaluated using Eq.(31) in the current step is non-negligible. For this, Eq.(34) can be extended as
which is motivated by the discussion in Taylor [96, Sect. 3.5]. The first term results from the confidence interval of the current identification step, and the sum stems from the error propagation.
In the concrete stepwise identification here (set 3), the hardening parameter \(c_2\) is based on the previously determined elasticity parameters and the yield stress, \(K_{\text {st}}, G_{\text {st}}\), and \({\hat{k}}\). \(\Delta c_2\) is obtained by the identification step and is given in Table 5. The differentials are calculated on the basis of the second part in Eq. (46). The values are compiled in Table 5 in the 2nd to 4th column indicating that the yield stress shows the most uncertain contribution. \(\Delta K_{\text {st}}= \Delta K_{\text {st}}^*\) and \(\Delta G_{\text {st}}= \Delta G_{\text {st}}^*\) are given in Table 4, whereas \(\Delta {\hat{k}}\) is not known caused by the hand-fitting approach. If we assume \(\Delta {\hat{k}} \approx 15\,\hbox {N}\,\hbox {mm}^{-2}\)—which has a similar magnitude as the single-step identification uncertainty in Table 4–the aforementioned contributions in Table 5 to the resulting uncertainty \(\Delta c_2^* \approx 186\,\hbox {N}\,\hbox {mm}^{-2}\) are obtained. This value is shown in Table 4.
For the next step to determine the uncertainty of the viscosity \(\eta \), the values \(K_{\text {st}}, G_{\text {st}}, {\hat{k}}\), and \(c_2\) and their uncertainties are known. Again, \(\Delta \eta \) stems from the identification step, and the influences of the aforementioned parameters are assembled in Table 5 (columns 5 to 9). The resulting uncertainty for the viscosity is \(\Delta \eta ^* \approx 1130\,\hbox {s}^{-1}\), which can be seen in Table 4 under the column “set 3” indicated by the asterisk. Apart from larger values resulting from the bulk modulus \(K_{\text {st}}\) and the hardening parameter \(c_2\), the yield stress \({\hat{k}}\) has again the most influencing contribution to the uncertainty.
If one considers the uncertainty contribution from the parameters \((E_{\text {st}},\nu _{\text {st}},{\hat{k}})\) on the uncertainty of \((c_2,\eta )\) using the two-step identification procedure applied to the reduced model, see Sect. 4.2.6, the uncertainties of Table 6 are obtained. The uncertainties are approximately 34% for \(c_2\) and 15% for \(\eta \) which are smaller than those of the three-step identification scheme, see Table 4 (set 3). There, we have 40% and 30%. Thus, for \(c_2\) similar uncertainties are obtained, however, for \(\eta \) it is doubled using the three-step identification. The reason for the higher value is due to the additional uncertainty of the previously calculated value \(c_2\). Therefore, while the three-step strategy is seemingly more reasonable than the two-step approach for the material model at hand, it leads to larger uncertainties in parameter determination when considering the uncertainties created by previously determined parameters.
4.3 Parameter identification for PA6
The isotropic, linear elasticity model (7) for the pure PA6 material requires the determination of the two material parameters \(E_{\text {m}}\) and \(\nu _{m}\). Young’s modulus \(E_{\text {m}}\) is identified using the measured axial stress for prescribed multi-step displacement path (and measured strains using the videoextensometer). We consider strains up to \(2\%\). The Poisson number \(\nu _{\text {m}}\) is determined by evaluating the lateral strains. Again we draw on a multi-step relaxation path, see Fig. 2, i.e., the termination points of relaxation to generate the data points so that viscous properties are excluded. The identification procedure leads to a Young’s modulus and a Poisson number as summarized in Table 7. The response of the model in comparison with the experimental data is shown in Fig. 7. Both parameters are totally uncorrelated as shown in Hartmann and Gilbert [36], and the determinant of the Hessian is not equal zero. Again we calculate the bulk and shear modulus \(K_{\text {m}}\) and \(G_{\text {m}}\) on the basis of Young’s modulus and Poisson’s number and the uncertainty according to Eq. (34). All values show a reliable determination.
4.4 Parameter identification for the composite (orthotropy)
We are interested in applying the orthotropic elasticity relations (14) and (15), which has nine material parameters (parameter set of Spencer \(\varvec{\kappa }_{\text {SP}})\)). The composite is made of a woven fabric where the periodicity is approximately 16 mm. Since we are interested in the computation of metal forming processes, a homogenized constitutive model (anisotropic elasticity) is applied. Furthermore, we assume only moderate strains. Thus, we start with a model of small strains, and insert the material parameters into the finite strain model. The forming process yields large deflections but moderate strains so that this approach is assumed to be justified.
The unique identification of the whole set of nine material parameters is not a straight forward task using, for example, only DIC data, see the discussion in Hartmann et al. [38]. In a first step, we are interested to find out which kind of tests would be necessary to obtain unique parameters. Afterward, a representative volume element is chosen to evaluate specific deformation modes, where this procedure does not require a least-square approach.
4.4.1 Analytical consideration in orthotropic elasticity
In the following, we seek for an identification process to obtain the nine material parameters \(\varvec{\kappa }_{\text {SP}}\). According to [16] it is more simple to consider the material parameter set \(\varvec{\kappa }_{\text {S}}\) as defined in Eq. (23). For the relationships between the material parameter sets \(\varvec{\kappa }_{\text {S}}\) and \(\varvec{\kappa }_{\text {SP}}\) (as well as \(\varvec{\kappa }_{\text {C}}\)), see Appendix B. Here, we draw on the inverse relation of Eq. (20), see Eq. (63) with the compliance matrix \({{\mathbf {\mathsf{{S}}}}} = {{{\mathbf {\mathsf{{C}}}}}}^{-1}\) in Eq. (64). The parameter identification procedure proposed by Christensen [16] or Kaw [51], which is discussed in the following, seems to be simple. Unfortunately, it turns out that the implementation of the associated experiments and their evaluation is very difficult, and in some cases impossible. The subsequent relations are required for the numerical identification on the basis of representative volume elements as well, and, accordingly, are recapped.
-
(i)
Identification of \(E_{11}\) and \(\nu _{12}\): In order to identify the material parameters \(E_{11}\) and \(\nu _{12}\), we consider a tensile test of a composite specimen in \(\vec {e} _1\) direction (fiber directions: \(\vec {a} _1 = \vec {e} _1\) and \(\vec {a} _2 = \vec {e} _2\)). The axial strain \(\varepsilon _{11}\) is prescribed, and both the stress \(\sigma _{11}\) as well as the lateral strain \(\varepsilon _{22}\) are measured. This leads to the stress and strain states \({{\mathbf {\mathsf{{T}}}}} = \left\{ \sigma _{11},0,0,0,0,0 \right\} ^T\) and \({{\mathbf {\mathsf{{E}}}}} = \left\{ \varepsilon _{11}, \varepsilon _{22}, \varepsilon _{33}, 0 , 0 , 0 \right\} ^T\), respectively. The first two equations in Eq. (63) with the compliance matrix (64) lead to
$$\begin{aligned} \varepsilon _{11}&= \dfrac{\sigma _{11}}{E_{11}} \rightarrow E_{11} = \dfrac{\sigma _{11}}{\varepsilon _{11}}, \end{aligned}$$(47)$$\begin{aligned} \varepsilon _{22}&= -\nu _{12}\dfrac{\sigma _{11}}{E_{11}} = -\nu _{12}\varepsilon _{11} \rightarrow \nu _{12} = -\dfrac{\varepsilon _{22}}{\varepsilon _{11}}. \end{aligned}$$(48)This test can be carried out, and either DIC data or video extensometer information would be possible to be obtained. The Poisson number, however, is more uncertain than Young’s modulus.
-
(ii)
Identification of \(E_{22}\) and \(\nu _{21}\): To identify the material parameters \(E_{22}\) and \(\nu _{21}\), we consider a tensile test in \(\vec {e} _2\) direction (fiber directions \(\vec {a} _1 = \vec {e} _1\) and \(\vec {a} _2 = \vec {e} _2\)). The axial strain \(\varepsilon _{22}\) is prescribed, and the stresses \(\sigma _{22}\) along with the lateral strains \(\varepsilon _{11}\) are measured. This leads to the stress and strain states \({{\mathbf {\mathsf{{T}}}}} = \left\{ 0, \sigma _{22},0,0,0,0 \right\} ^T\) and \({{\mathbf {\mathsf{{E}}}}} = \left\{ \varepsilon _{11}, \varepsilon _{22}, \varepsilon _{33}, 0 , 0 , 0 \right\} ^T\), respectively. The first two equations in Eq. (63) using the compliance matrix (64) read
$$\begin{aligned} \varepsilon _{22}&= \dfrac{\sigma _{22}}{E_{22}} \rightarrow E_{22} = \dfrac{\sigma _{22}}{\varepsilon _{22}}, \end{aligned}$$(49)$$\begin{aligned} \varepsilon _{11}&= -\nu _{21}\dfrac{\sigma _{22}}{E_{22}} = -\nu _{21}\varepsilon _{22} \rightarrow \nu _{21} = -\dfrac{\varepsilon _{11}}{\varepsilon _{22}}. \end{aligned}$$(50)This test is very similar to the previous one and comparably simple.
-
(iii)
Identification of \(E_{33}\), \(\nu _{31}\), and \(\nu _{32}\): The third test is a laterally free compression test of a laminate plate. With this compression test, we have the stress and strain state \({{\mathbf {\mathsf{{T}}}}} = \left\{ 0,0,\sigma _{33},0,0,0 \right\} ^T\) and \({{\mathbf {\mathsf{{E}}}}} = \left\{ \varepsilon _{11}, \varepsilon _{22}, \varepsilon _{33},0,0,0 \right\} ^T\). The strain \(\varepsilon _{33}\) is prescribed leading to the measurement of stress \(\sigma _{33}\), and lateral strains \(\varepsilon _{11}\) and \(\varepsilon _{22}\). Since there is only a very thin gap between the testing machine’s holder in practice, this is a very challenging task—or more or less impracticable. The first three equations in Eq. (63) using the compliance matrix (64) yield
$$\begin{aligned} \varepsilon _{33}&= \dfrac{\sigma _{33}}{E_{33}} \rightarrow E_{33} = \dfrac{\sigma _{33}}{\varepsilon _{33}}, \end{aligned}$$(51)$$\begin{aligned} \varepsilon _{11}&= -\nu _{31}\dfrac{\sigma _{33}}{E_{33}} = -\nu _{31}\varepsilon _{33} \rightarrow \nu _{31} = -\dfrac{\varepsilon _{11}}{\varepsilon _{33}}, \end{aligned}$$(52)$$\begin{aligned} \varepsilon _{22}&= -\nu _{32}\dfrac{\sigma _{33}}{E_{33}} = -\nu _{32}\varepsilon _{33} \rightarrow \nu _{32} = -\dfrac{\varepsilon _{22}}{\varepsilon _{33}}. \end{aligned}$$(53)As discussed in Hartmann et al. [38], a compression experiment with lateral displacement constraints (this implies under the assumption of a homogeneous deformation \(\varepsilon _{11} = \varepsilon _{22} = 0\)) might be an alternative. However, the measured lateral stresses \(\sigma _{11}\) and \(\sigma _{22}\) are highly uncertain due to friction in the tool and the imperfections of the samples.
-
(iv)
Identification of \(\mu _{12}\): The material parameter \(\mu _{12}\) can be identified using a three-rail shear test, see, for example, [39] and the literature cited therein. The stress and strain state read \({{\mathbf {\mathsf{{T}}}}} = \left\{ 0,0,0,\tau _{12},0,0 \right\} ^T\) and \({{\mathbf {\mathsf{{E}}}}} = \left\{ 0, 0, 0, \gamma _{12} , 0 , 0 \right\} ^T\). From this the shear modulus
$$\begin{aligned} \gamma _{12}&= \dfrac{1}{\mu _{12}} \tau _{12} \rightarrow \mu _{12} = \dfrac{\tau _{12}}{\gamma _{12}} \end{aligned}$$(54)is obtained.
-
(v)
Identification of \(\mu _{23}\) and \(\mu _{31}\): Due to the restrictive thickness of the underlying orthotropic composite plates, the identification of the remaining shear moduli \(\mu _{23}\) and \(\mu _{31}\) is a challenging task as well. Semenov [89] proposed to identify the shear moduli from torsion experiments at flat specimens and circular tubes. However, torsion of flat specimens yields inhomogeneous deformations, and the preparation of tubelike composite specimens is very complicated. Alternatively, Hofmann [47] identified the inter-laminar shear moduli using short beam bending tests. One can think of lap shear test to determine \(\mu _{23}\), or \(\mu _{31}\). However, if we look at the periodicity of the specimen’s woven fabric in Fig. 8b, this is questionable caused by the internal inhomogeneity.
To conclude the topic of identification more comprehensively, some further relations are recapitulated or inequalities are included, which can possibly be included in the parameter identification. These inequalities, which are assembled in Appendix C, then serve either to stabilize the material parameter identification or to check their theoretical sense.
If the experiments could be performed, unique parameters can be expected. However, most of the mechanical experiments such as the compression test and the shear tests are difficult to be carried out due to measurement and accuracy issues essentially influencing the reliability of the parameters identified subsequently in the parameter identification concept. Thus, we provide “experimental test” indirectly as discussed in the following.
4.4.2 RVE/FEM approach (orthotropy)
We propose an alternative approach where a three-dimensional mesoscopic representative volume element (RVE) is generated using an actual \(\mu \)-CT of the composite material, see Fig. 8a. The raw \(8-\)bit image sequence obtained from the scan in tif-format is converted using the image processing open source software Fiji [84]. The data set consists of a stack of 2138 images each having a resolution of \(2940 \times 318\) pixels (318 pixels in thickness direction). At first, the images are calibrated to the real length (912 pixels = \(10\,\hbox {mm}\)). Then, suitable filters (Gauss 3D) and segmentation techniques based on the works of ([19, 90]) were tested and applied on the entire stack. As a final step, the important dimensions such as curvature of the fiber roving, major and minor diameters of the elliptical shaped roving of fibers in warp and weft directions are extracted and used to create the 3D geometry of the RVE in FE pre- and post-processor GiD, [17]. The properties of the composite material such as periodicity and fiber volume content are verified for the reconstructed RVE, see Fig. 8b. The regenerated RVE is modeled with 10-noded tetrahedral elements at a total of approximately 250000 elements, see Fig. 8c. The experimental procedures as explained in Sect. 4.4.1, i.e., the strain states are applied as displacement surface boundary conditions to the RVE, see Fig. 9. The individual constituents of the RVE are assigned with the material properties of glass fibers (Young’s modulus \(E_f = 78500\,\hbox {N}\,\hbox {mm}^{-2}\) and Poisson’s ratio \(\nu _f = 0.22\), see Table 10) and of PA6 polymer (\(E_m\) and \(\nu _m\)) as assembled in Table 7, i.e., the RVE simulations depends on the parameter set
There are several tasks which have to be followed. First, we have to determine the material parameter set \(\varvec{\kappa }_{\text {S}}\) according to the analytical expressions in Sect. 4.4.1. Since the parameter determination is based on the parameters \(\varvec{\kappa }_{\text {RFP}}\) by RVE simulations, we try to estimate the confidence intervals of \(\varvec{\kappa }_{\text {S}}\) based on the uncertainty data of set \(\varvec{\kappa }_{\text {RFP}}\). This is done using a linear error propagation concept, see [96]. Finally, we determine the parameters \(\varvec{\kappa }_{\text {SP}}\) and their confidence intervals for the sake of completeness.
To determine the material parameters of the entire composite described by the constitutive model of Sect. 3.3, we apply the displacement boundary conditions on the RVE in such a manner that we recreate the tensile tests in x- and y-direction (i.e., in \(\vec {e} _1\) and \(\vec {e} _2\) direction), the compression test with prescribed displacements on the upper surface in negative z-direction, and the three shear tests, see Fig. 9. First, we start with the determination of \(E_{11}\) according to Eq. (47) and apply the tensile displacement boundary conditions shown in Fig. 9a, where we assume \({\overline{u}}_x = \varepsilon _{11} L_x\) with the length \(L_x=16\,\hbox {mm}\) of the sample, see Fig. 8b. Then, we determine the stress state using the homogenization technique presented in Miehe and Koch [68], \({{\mathbf {\mathsf{{T}}}}} = (1/V) {{\mathbf {\mathsf{{D}}}}}_{\text {H}}\varvec{\lambda }\), where \({{\mathbf {\mathsf{{T}}}}}^T = \{\sigma _{11},\sigma _{22},\sigma _{33},\tau _{12},\tau _{23},\tau _{31}\}\) represents the homogenized stress vector, V the volume of the RVE, and \(\varvec{\lambda }{\, \in \mathbb {R}}^{{n_{\text {p}}}}\) is the nodal reaction force vector (Lagrange multiplier vector, see [42]). \({{\mathbf {\mathsf{{D}}}}}_{\text {H}}{\, \in \mathbb {R}}^{6 \times {n_{\text {p}}}}\) denotes the coordinate matrix containing the nodal coordinates assigned to the nodal reaction forces. \({n_{\text {p}}}\) is the number of prescribed nodal displacements. The axial stress \(\sigma _{11} = T_{1}(\varvec{\lambda }(\varvec{\kappa }_{\text {RFP}}))\) can be determined for given \(\varepsilon _{11}\) and depends on the material parameter set \(\varvec{\kappa }_{\text {RFP}}\) defined in Eq. (55).
With respect to the transverse strain determination \(\varepsilon _{11}\) required for the identification of \(\nu _{21}\), see loading conditions in Fig. 9b, the strain \(\varepsilon _{11}\) in Eq. (50) is calculated by averaging all resulting surface nodal displacements in x-direction at \(x=L_x\) by the width of the RVE,
\(L_x = 16\,\hbox {mm}\). N is the number of nodes on the surface \(x=L_x\). The displacements \(u_x^{J}\big |_{x=L_x} = {\tilde{u}}_x^J({{{{\varvec{\mathsf{{ u}}}}}}}(\varvec{\kappa }_{\text {RFP}}))\) depend on the material parameters \(\varvec{\kappa }_{\text {RFP}}\) as well. Similarly, the procedure is carried out for the relations (49)–(53) to determine \(E_{22}\), \(E_{33}\), \(\nu _{31}\), and \(\nu _{32}\). Thus, \(E_{11}\), \(E_{22}\) and \(E_{33}\) are obtained by the reaction force computation of the RVE, whereas \(\nu _{21}\), \(\nu _{31}\), and \(\nu _{32}\) are calculated by means of the lateral displacements.
For the determination of the shear moduli, we draw on, examplarily, Eq. (54). Here, \({\overline{u}}_{y}(x,y,L_z) = \gamma _{12} L_z\) is applied on the upper surface, see Fig. 9d. Again, the Lagrange multipliers (reaction forces) are evaluated, \(\tau _{12} = T_4(\varvec{\lambda }(\varvec{\kappa }_{\text {RFP}}))\), leading to \(\mu _{12} = T_4(\varvec{\lambda }(\varvec{\kappa }_{\text {RFP}})) L_z/{\overline{u}}_y(x,y,L_z)\). Similarly, the remaining shear moduli are calculated by the homogenization procedure. The identified material parameters \(\varvec{\kappa }_{\text {S}}\) are assembled in Table 8. Figure 8d shows exemplarily the von Mises stress distribution in the RVE subjected to tensile load in the x-direction.
Next, we are interested in the uncertainty of the parameter set \(\varvec{\kappa }_{\text {S}}\) resulting from the uncertainty of \(\varvec{\kappa }_{\text {RFP}}\). Obviously, the material parameters \(\varvec{\kappa }_{\text {S}}\) depend—by a subset of the Lagrange multipliers (reactions forces) and a subset of nodal displacements—on the parameters \(\varvec{\kappa }_{\text {RFP}}\), \(\varvec{\kappa }_{\text {S}}= {\hat{\varvec{\kappa }}}_{\text {S}}(\varvec{\lambda }(\varvec{\kappa }_{\text {RFP}}),{{{{\varvec{\mathsf{{ u}}}}}}}(\varvec{\kappa }_{\text {RFP}}))\). This dependence is given by the implicit system of linear equations (since we solve for linear elasticity),
where \(\overline{{{{{\varvec{\mathsf{{ p}}}}}}}} {\, \in \mathbb {R}}^{{n_{\text {u}}}}\) are the prescribed equivalent nodal forces, here they are zero, \(\overline{{{{{\varvec{\mathsf{{ p}}}}}}}}={{{{\varvec{\mathsf{{ 0}}}}}}}\), since only displacement-controlled processes are considered. \(\overline{{{{{\varvec{\mathsf{{ u}}}}}}}}{\, \in \mathbb {R}}^{{n_{\text {p}}}}\) are the prescribed and \({{{{\varvec{\mathsf{{ u}}}}}}}{\, \in \mathbb {R}}^{{n_{\text {u}}}}\) the unknown nodal displacements, see, for displacement control [42] and the literature cited therein. \({{{{{\varvec{\mathsf{{ K}}}}}}}}{\, \in \mathbb {R}}^{{n_{\text {u}}} \times {n_{\text {u}}}}\), \(\overline{{{{{{\varvec{\mathsf{{ K}}}}}}}}}{\, \in \mathbb {R}}^{{n_{\text {u}}} \times {n_{\text {p}}}}\), and \(\overline{\overline{{{{{{\varvec{\mathsf{{ K}}}}}}}}}}{\, \in \mathbb {R}}^{{n_{\text {p}}} \times {n_{\text {p}}}}\) are the stiffness matrices concerned.
Of course, there is a number of uncertainties in the entire procedure. First, the entire discretization (geometry, mesh fineness, element distortion, element formulation, homogenization technique, ...) might have an influence. This is so comprehensive that we only focus on linear error propagation of the material properties of the glass fibers and the matrix material. Conceptually, the subsequent presentation can also be extended to other influences. In the following, we assume that the material parameters \(\varvec{\kappa }_{\text {RFP}}\) in Eq. (55) and their uncertainties \(\Delta \varvec{\kappa }_{\text {RFP}}^T = \{\Delta E_m, \Delta \nu _m, \Delta E_{\text {f}}, \Delta \nu _{\text {f}}\}\) are known for the matrix material as well as the glass fibers used. For the uncertainty of the matrix material, we take the confidence interval provided in Table 7. The uncertainty of the glass fibers is more difficult since the manufacturer does not provide the information, and the determination, particularly, of the Poisson number is experimentally more than challenging. Thus, we make an estimation summarized in Appendix D. Using the standard deviation in Table 10 as uncertainty, the “confidence interval” of the parameter set \(\varvec{\kappa }_{\text {S}}\) is estimated in Table 8. This is done as follows: With respect to the linear error propagation concept in Eq. (34), we need the derivatives
The derivatives of the reaction forces and the nodal displacements are calculated by numerical differentiation (central differences),
with the vectors \(\overline{{{{{\varvec{\mathsf{{ e}}}}}}}}_j {\, \in \mathbb {R}}^{{n_{\kappa }}}\) (all entries are zero except for one having a 1 in row j). Examplarily, we have for the first test
with the unit vector \({{\mathbf {\mathsf{{e}}}}} _1{\, \in \mathbb {R}}^{6}\) having a one at entry one, all others are zero. All further derivatives are derived in a similar form.
Finally, we provide for completeness the parameter sets \(\varvec{\kappa }_{\text {C}}\) and \(\varvec{\kappa }_{\text {SP}}\), see Appendix B. Particularly, \(\varvec{\kappa }_{\text {SP}}\) of Eq. (12) is required for our validation examples, since the constitutive model is implemented using Spencer’s formulation. Additionally, the confidence intervals using the error propagation concept are compiled in Table 8 as well.
5 Validation examples
In the following, several validation examples are discussed. One goal is to see the influence of the parameters—obtained from homogeneous stress–strain states—onto inhomogeneous deformations. First, pure steel is studied in a stretch forming process. Second, tensile and shear tests of the reinforced composite material GF-PA6 are discussed to see the result of the RVE identification concept in comparison with real experiments. It is followed by shear test of the reinforced composite material GF-PA6, and finally, a stretch forming process of M/GF-PA6/M laminate is investigated, where two different core layer thicknesses are considered. In this last example, we also investigate the influence of the uncertainties of the material parameters, both those of steel and those of the composite, on the results of the finite element calculations.
5.1 Validation of pure heat-treated steel
The constitutive model of the heat-treated steel of Table 2 with the material parameters of Table 4 (set 2) is validated using a stretch forming process. In this type of forming technique, a blank made of heat-treated steel is deformed with a punch. The circular blank has a thickness of \(d=0.4\,\hbox {mm}\) and a diameter of \(D=200\,\hbox {mm}\). The blank is deformed using a hemispherical punch of radius \(R=50\,\hbox {mm}\) using an Erichsen testing machine. Due to the symmetry of the experimental setup only one quarter of the geometrical model is used. The blank is meshed with 20-noded hexahedral elements (C3D20) with 4 elements in the thickness direction. The blank is modeled with a total of 9400 elements. The punch, blank holder, and the die are formulated as discrete rigid bodies and meshed with R3D4 elements (die: 12717, holder: 10362 and punch: 6300), see Fig. 10a. The contact formulation “surface-to-surface” is chosen for the contact between the die–blank, holder–blank and punch–blank pairs. As the first step of the numerical simulation, the blank is rigidly clamped along the outer circumference using a holder force of \(F_{\text {BH}} = 100\,\hbox {kN}\). In the second step, the punch is pushed against the blank for a maximum displacement value of \({\overline{u}}_{\text {v}}= 36\,\hbox {mm}\) with a displacement rate of \(\dot{{\overline{u}}}_{\text {v}}= 1.37\,\hbox {mm}\,\hbox {s}^{-1}\). The simulations are performed with automatic load step incrementation (max. number of Newton iterations = 50, \(\Delta t_0 = 0.01\,\hbox {s}, \Delta t_{\text {min}}= 0.001\,\hbox {s}\), and \(\Delta t_{\text {max}}= 0.25\,\hbox {s}\)). The force–displacement response of the punch in Fig. 10b compares the experimental data (5 experiments) with numerical simulation, and it is a sufficient behavior. Due to the lack of information about the coefficient of static friction, the numerical simulation is performed for two values obtained from the literature, \(\mu _f=0.2\) and \(\mu _f=0.3\). Although the computation with a smaller friction coefficient is closer to the experiments, both simulations slightly overestimate the required punch force in the final deformation state. Figs. 10c, d show the deformation and von Mises stress state at the maximum load for the case of \(\mu _f=0.2\). However, the simulation matches the experimental course very well.
5.2 Validation of GF-PA6 composite
Next, the constitutive model of orthotropy representing the material behavior of glass fiber-reinforced PA6 is validated using a tensile and shear tests.
5.2.1 Tensile test
As explained in Sect. 2.3.1, here we draw on the in-house finite element program Tasafem. The orientation of fibers in the specimens is \(\gamma =0^{\circ }\), see Fig. 1b. Due to the symmetry of the experimental setup, only one-eighth of the geometry is used for FE simulations. The model is meshed with \(20-\)noded hexahedral elements with 5 elements in the thickness direction leading to a total of 8125 elements (composite material: 4875 elements and clamping area: 3250 elements). The specimens are elongated for a maximum prescribed displacement of \({\overline{u}}_x = 0.9\,\hbox {mm}\). Figure 11a shows the FE model, mesh and boundary conditions used for the validation of GF-PA6 composite material whereas Figs. 11b, c illustrate the deformation and von Mises stress state at the final step. Figure 11d refers to the comparison of the experimental data (3 experiments) with numerical simulation based on the values of axial force and axial displacement.
5.2.2 Three-rail shear test
To validate the concept of RVE parameter identification of GF-PA6 composite material, a shear test using a three-rail shear tool is chosen, see [92]. The experimental conditions are explained in Sect. 2.3.2. The geometry and fiber directions of the specimens are depicted in Fig. 1c, and the dimensions are assembled in Table 1. Figure 12 shows the comparison of shear stress response between the experimental data (5 experiments) with the analytical equation (54) and their respective uncertainties. The difference between the values at the later stages can be assigned to the increasing dominance of the corner effects in the experiments. This can be demonstrated meshing the region with finite elements (20-noded hexahedral elements, 5 elements in the thickness direction, horizontal 32 and vertical 80 elements in the optical free region). Analogously to the analytical considerations, the reaction forces in vertical direction are divided by the original cross section and the relative displacements (\({\overline{u}}_y=0.025\,\hbox {mm}\)) by the width to obtain the shear angle. The finite element result is shown in Fig. 12b indicating a softer behavior compared to the analytical considerations, which is a result of the known corner effect.
Comparison of shear stress versus shear strain response of experimental data (5 experiments) with analytical equation (54) and finite element solution—and their respective uncertainties
5.3 Validation of an M/GF-PA6/M sandwich structure
The entire geometrical models using the constitutive models developed for heat-treated steel and GF-PA6 composite are validated in form of an M/GF-PA6/M sandwich structure using a stretch forming process, see Fig. 10a, however, without exploiting any symmetry conditions as it was justified in Sect. 5.1. The manufacturing of the sandwich laminates is explained in Sect. 2.4. The punch, blank holder, and the die are formulated again as discrete rigid bodies and meshed with R3D4 elements (die: 3297, holder: 2669, and punch: 3465). The boundary conditions, contact formulations (friction coefficient \(\mu _f=0.2\)), and blank holder force remain the same as those of the validation example of heat-treated steel, see Sect. 5.1. The specimen has a diameter of \(D = 200\,\hbox {mm}\). The material parameters of the steel are given by set 3 in Table 4 and those of the composite core layer in Table 8 (3rd column). In the following, two configurations of the core layer are considered.
M/GF-PA6/M (0.4/0.5/0.4) In the first case, the GF-PA6 composite material has a thickness of \(d_{\text {c}}= 0.5\,\hbox {mm}\) and is bonded between the steel surface layers of thickness \(d_{\text {f}}= 0.4\,\hbox {mm}\). Thus, the overall thickness is \(d = 1.3\,\hbox {mm}\) (M/GF-PA6/M is (0.4/0.5/0.4)). The three-layered sandwich is meshed with 20-noded hexahedral elements (C3D20) with 4 elements in each layer in thickness direction. The sandwich is modeled with a total of 29472 elements (steel: 9824, GF-PA6: 9824). The punch indents with a maximum displacement of \({\overline{u}}_{\text {v}}= 8\,\hbox {mm}\) with a displacement rate of \(\dot{{\overline{u}}}_{\text {v}}= 1.31\,\hbox {mm}\,\hbox {s}^{-1}\). The simulation is performed with automatic load step incrementation (max. number of global Newton iterations \(n_{\text {max}}=50\), \(\Delta t_0 = 0.01\,\hbox {s}\), \(\Delta t_{\text {min}}= 0.001\,\hbox {s}\), and \(\Delta t_{\text {max}}= 0.25\,\hbox {s}\)).
Figure 13 shows the comparison of punch response and maximum principal strain distribution between the experimental data and numerical simulation in the stretch forming process of M/GF-PA6/M sandwich. The maximum principal strains are measured using the ARAMIS system on the bottom metallic layer of the sandwich on a path of \(30\,\hbox {mm}\) from the center in radial direction (\(\vec {e} _1\)-direction) of the sandwich at punch displacements of \({\overline{u}}_{\text {v}}= 4\,\hbox {mm}\) and \({\overline{u}}_{\text {v}}= 8\,\hbox {mm}\).
Instead of only showing the force–displacement curve (thick red line) in Fig. 13a, the confidence intervals of the finite element simulations are also calculated and displayed. The computation of the force’s confidence interval is done using the Gaussian error propagation concept,
where the derivatives are computed by forward differential formula applied to the finite element program Abaqus, see Eqs. (41)–(45). Since the confidence interval of the frictional coefficient is unknown, we assume \(\Delta \mu _f=0.05\). Here, \({n_{\kappa }}_{_{\text {st}}} = 5\) and \({n_{\kappa }}_{_{\text {RFP}}} = 9\) hold, i.e., to obtain the confidence interval using \(5+9+1=15\) parameters, 16 computations are required. In each load step, the sensitivities must be stored.
The punch force is slightly underestimated. The reasons must be related to uncertainties in the geometry in the experimental setup (punch, die, holder), the real thicknesses of the layers, and changes of the material properties due to the production process of the composite–metal laminate, the bonding behavior, etc.
Next, the maximum principal strain behavior is considered in Fig. 13b (here, F in Eq. (61) symbolizes the strain measure), where the data of the Aramis system is evaluated along a straight line starting at the center. This includes additional errors stemming from the DIC data. The simulation is really confident, since the uncertainty resulting from the error propagation is very small. On a closer look, this becomes clear, since with a thin disk loaded by the displacement-controlled punch, the strain that arises is an almost purely geometric effect. In other words, it is not really influenced by the material parameters.
This leads to the question, which uncertainty of which parameter has the largest influence on the calculation results. This is shown in Fig. 14. Here, the norms of the individual contributions are shown in Fig. 14a for the parameters characterizing the steel (and friction) and Fig. 14b for the composite. The elasticity parameters of the steel have an essential contribution at the beginning of the loading (the parameters characterizing the inelastic behavior are not active). Later, when the steel is already flowing, the influence of the uncertainties of the parameters of the composite becomes much larger. In addition, the hardening variable \(c_2\) is then also relevant. The influence of the friction uncertainty is not so dominant.
M/GF-PA6/M (0.4/2/0.4) In the second layer configuration, the thickness of the core material is increased to \(d_{\text {c}}= 2\,\hbox {mm}\) yielding an overall thickness of the sandwich of \(d = 2.8\,\hbox {mm}\), ((0.4/2/0.4); the volume fraction of the fibers is the same). The punch is pressed into the sandwich up to a maximum displacement of \({\overline{u}}_{\text {v}}= 5\,\hbox {mm}\) with a displacement rate of \(\dot{{\overline{u}}}_{\text {v}}= 1.19\,\hbox {mm}\,\hbox {s}^{-1}\). Due to the increased thickness, the core layer is meshed with 10 elements in the thickness direction which leads to a total of 44208 elements (steel: 9824, GF-PA6: 24560) in the sandwich. Figure 15a, b shows the comparison of the punch response and the maximum principal strain distribution between the experimental data and the numerical simulation. The maximum principal strains are measured again using the ARAMIS system at punch displacements of \({\overline{u}}_{\text {v}}= 2.5\,\hbox {mm}\) and \({\overline{u}}_{\text {v}}= 5\,\hbox {mm}\) at the same line as for the first testing configuration.
The responses of the finite element simulations are very satisfactory, where the confidence interval is shown again. For larger deformations, the stiffness of the simulations starts to become larger, which is due to the physically linear orthotropic elasticity for GF-PA6. This becomes stiffer for larger distortions, which can only be circumvented by using a nonlinear relationship or other strain measures (for example, Hencky strains). However, this is not the subject of the investigations here. The elongations tend to be well met, especially in the center of the sample, see Fig. 15b. Again, the uncertainties of the parameter have no essential influence on the strains, since they are mainly influenced by the geometrical influence of the sample and the punch. If we look again at the sensitivities of the error propagation concept, the hardening parameter \(c_2\) has an essential influence on the uncertainty in the force result, Fig. 16a.
Due to the thicker core layer, the influence of the uncertainties of the material parameters of orthotropic elasticity is now larger than in the simulation before, see Fig. 16b. In this sense, the sensitivities also give an indication of the load-bearing behavior of the laminate.
6 Conclusions
In this article the material parameter identification process to determine the material parameters of a finite strain viscoplasticity model and a model of orthotropic elasticity is provided for both the evaluation of quality measures of the parameters as well as the concept of identifiability. The viscoplasticity model is required to model the surface layers of an M/GF-PA6/M laminate, and the anisotropic hyperelasticity relation is chosen to represent the glass fiber-reinforced PA6 composite. It turns out that the chosen viscoplasticity model is over-parameterized with respect to the chosen experimental data so that some parameters are not necessary. This is indicated by the correlation matrix and the confidence interval. Thus, the evaluation of the quality measures has an essential influence on the choice of the model (in the remotest sense like model adaptivity or model reduction). Since it is common to apply stepwise parameter identification concepts, Gaussian error propagation is chosen to estimate the resulting confidence intervals of the parameters. The identification of the material parameters for the orthotropic elasticity relation is much more difficult, because, on the one hand, the identifiability must be guaranteed, and on the other hand, the available tests are not suitable to address all parameters. To avoid this, \(\mu \)-CT data have been used, which provide a representative volume element of the woven fabric embedded in the PA6 matrix material. This RVE was then used for parameter identification according to the concept of sequential parameter identification. For this purpose, the displacement boundary conditions of different tests are applied to the RVE, and by homogenization of the stresses, the parameters are determined. In other words, a mixture of analytical considerations and numerical treatment is required. Apart from the \(\mu \)-CT image, this procedure only requires the material properties of the matrix material and the fiber material itself. Additionally, we provide a concept to estimate the uncertainty of all nine material parameters resulting from the uncertainty of the matrix material and the glass fibers. The subsequent validation examples for the pure steel, the pure composite material, and also the sandwich show very good agreement in the force–displacement curves. Thus, this procedure seems to be sufficient to determine the parameter for each constituent of a complex laminate. The error propagation concept is applied to the entire finite element simulations of the M/GF-PA6/M laminates, where the influence of each individual uncertainty of a parameter on the finite element result is investigated. This is studied at two configurations, which make clear that additional uncertainties from the geometrical setting have to be considered as well. However, the study yields also the information about the influence of the parameters on the computations.
References
Allen, H.G.: Analysis and Design of Structural Sandwich Panels: The Commonwealth and International Library: Structures and Solid Body Mechanics Division. Elsevier (2013)
Alwan, A.: Large deflection of sandwich plates with orthotropic cores. AIAA J. 2(10), 1820–1822 (1964)
Andresen, K., Dannemeyer, S., Friebe, H., Mahnken, R., Ritter, R., Stein, E.: Parameteridentifikation für ein plastisches Stoffgesetz mit FE-Methoden und Rasterverfahren. Bauingenieur 71, 21–31 (1996)
Armstrong, P.J., Frederick, C.O.: A mathematical representation of the multiaxial Bauschinger effect. Technical Report General Electricity Generating Board, Report No.: RD/B/N731, Berceley Nuclear Laboratories (1966)
Atrian, A., Fereshteh-Saniee, F.: Deep drawing process of steel/brass laminated sheets. Compos.: Part B 47, 75–81 (2013)
Atrian, A., Panahi, H.: Experimental and finite element investigation on wrinkling behaviour in deep drawing process of al3105/polypropylene/steel304 sandwich sheets. Procedia Manuf. 15, 984–991 (2018)
Azar, J.: Bending theory for multilayer orthotropic sandwich plates. AIAA J. 6(11), 2166–2169 (1968)
AZO-Materials (2021). Azo materials: E-glass fibre. https://www.azom.com/properties.aspx?ArticleID=764. Last visited 2021 May 12
Bargmann, S., Klusemann, B., Markmann, J., Schnabel, J.E., Schneider, K., Soyarslan, C., Wilmers, J.: Generation of 3D representative volume elements for heterogeneous materials: a review. Progress Mater. Sci. 96, 322–384 (2018)
Beck, J.V., Arnold, K.J.: Parameter Estimation in Engineering and Science. Wiley, New York (1977)
Behrens, B.-A., Hübner, S., Neumann, A.: Forming sheets of metal and fibre-reinforced plastics to hybrid parts in one deep drawing process. Procedia Eng. 81, 1608–1613 (2014)
Beveridge, G.S.G., Schechter, R.S.: Optimization: Theory and Practice, 1st edn. McGraw-Hill Book Company, New York (1970)
Birman, V., Kardomateas, G.A.: Review of current trends in research and applications of sandwich structures. Compos. B Eng. 142, 221–240 (2018)
Björck, A.: Numerical Methods for Least Squares Problems. SIAM (Society for Industrial and Applied Mathematics), Philadelphia (1996)
Böhlke, T., Jöchen, K., Kraft, O., Löhe, D., Schulze, V.: Elastic properties of polycrystalline microcomponents. Mech. Mater. 42(1), 11–23 (2010)
Christensen, R.M.: Mechanics of Composite Materials. Dover Publication, Mineoly (2005)
Coll, A., Ribó, R., Pasenau, M., Escolano, E., Perez, J.S., Melendo, A., Monros, A., Gárate, J.: GiD v.14 User Manual (2018)
Contreiras, T.R., Pragana, J., Bragança, I., Silva, C., Alves, L.M., Martins, P.: Joining by forming of lightweight sandwich composite panels. Procedia Manuf. 29, 288–295 (2019)
Creveling, P.J., Whitacre, W.W., Czabaj, M.W.: A fiber-segmentation algorithm for composites imaged using x-ray microtomography: development and validation. Compos. A Appl. Sci. Manuf. 126, 105606 (2019)
Davey, S., Das, R., Cantwell, W.J., Kalyanasundaram, S.: Forming studies of carbon fibre composite sheets in dome forming processes. Compos. Struct. 97, 310–316 (2013)
Dettmer, W., Reese, S.: On the theoretical and numerical modelling of Armstrong–Frederick kinematic hardening in the finite strain regime. Comput. Methods Appl. Mech. Eng. 193, 87–116 (2004)
Doghri, I., Friebel, C.: Effective elasto-plastic properties of inclusion-reinforced composites. Study of shape, orientation and cyclic response. Mech. Mater. 37(1), 45–68 (2005)
Doghri, I., Ouaar, A.: Homogenization of two-phase elasto-plastic composite materials and structures: study of tangent operators, cyclic plasticity and numerical algorithms. Int. J. Solids Struct. 40(7), 1681–1712 (2003)
Draper, N.R., Smith, H.: Applied Regression Analysis, 3rd edn. Wiley, New York (1998)
Ekh, M.: Thermo-elastic-viscoplastic modeling of IN792. J. Mech. Behav. Mater. 12(6), 359–388 (2001)
Fischer, T., Grubenmann, M., Harhash, M., Hua, W., Heingärtner, J., Hora, P., Palkowski, H., Ziegmann, G.: Experimental and numerical investigations on the quasi-static structural properties of fibre metal laminates processed by thermoforming. Compos. Struct. 113418 (2020)
Fossum, A.F.: Parameter estimation for an internal variable model using nonlinear optimization and analytical/numerical response sensitivities. J. Eng. Mater. Technol. 119, 337–345 (1997)
Fritzen, F., Forest, S., Böhlke, T., Kondo, D., Kanit, T.: Computational homogenization of elasto-plastic porous metals. Int. J. Plast 29, 102–119 (2012)
Görthofer, J., Schneider, M., Ospald, F., Hrymak, A., Böhlke, T.: Computational homogenization of sheet molding compound composites based on high fidelity representative volume elements. Comput. Mater. Sci. 174, 109456 (2020)
Grünewald, J., Parlevliet, P., Altstädt, V.: Manufacturing of thermoplastic composite sandwich structures: a review of literature. J. Thermoplast. Compos. Mater. 30(4), 437–464 (2017)
Hammarberg, S., Larsson, S., Kajberg, J., Jonsén, P.: Numerical evaluation of lightweight ultra high strength steel sandwich for energy absorption. SN Appl. Sci. 2(11), 1–16 (2020)
Harhash, M., Gilbert, R.R., Hartmann, S., Palkowski, H.: Experimental characterization, analytical and numerical investigations of metal/polymer/metal sandwich composites - part 2: Free bending. Compos. Struct. 232(111421), 1–15 (2020)
Harhash, M., Gilbert, R.R., Palkowski, H., Hartmann, S.: Experimental characterization, analytical and numerical investigations of metal/polymer/metal sandwich composites - part 1: Deep drawing. Compos. Struct. 202, 1308–1321 (2018)
Hartmann, S.: Lösung von Randwertaufgaben der Elastoplastizität. Ein Finite-Elemente-Konzept für nichtlineare kinematische Verfestigung bei kleinen und finiten Verzerrungen. Doctoral thesis, Institute of Mechanics, University of Kassel. Report No. 1/1993 (1993)
Hartmann, S.: A remark on material parameter identification using finite elements based on constitutive models of evolutionary-type. Comput. Assist. Methods Eng. Sci. 24, 113–126 (2017)
Hartmann, S., Gilbert, R.R.: Identifiability of material parameters in solid mechanics. Arch. Appl. Mech. 88(1), 3–26 (2018)
Hartmann, S., Gilbert, R.R.: Material parameter identification using a least-square method applied to finite elements and experimental full-field information. Comput. Mech. 68(3), 633–650 (2021)
Hartmann, S., Gilbert, R.R., Kheiri Marghzar, A., Leistner, C., Dileep, P.K.: Material parameter identification of unidirectional fiber-reinforced composites. Arch. Appl. Mech. 91(2), 687–712 (2021)
Hartmann, S., Gilbert, R.R., Sguazzo, C.: Basic studies in biaxial tensile tests. GAMM-Mitteilungen 41, e201800004 (2018)
Hartmann, S., Kheiri Marghzar, A.: Modeling of fiber circumplacement around a hole using a streamline approach. Univ. J. Math. Appl. 1, 17–28 (2018)
Hartmann, S., Quint, K.J., Arnold, M.: On plastic incompressibility within time-adaptive finite elements combined with projection techniques. Comput. Methods Appl. Mech. Eng. 198, 178–193 (2008)
Hartmann, S., Quint, K.J., Hamkar, A.-W.: Displacement control in time-adaptive non-linear finite-element analysis. ZAMM J. Appl. Math. Mech. 88(5), 342–364 (2008)
Hasebe, R., Sun, C.: Performance of sandwich structures with composite reinforced core. J. Sandwich Struct. Mater. 2(1), 75–100 (2000)
Haupt, P., Lion, A.: Experimental identification and mathematical modeling of viscoplastic material behavior. Continuum Mech. Thermodyn. 7(1), 73–96 (1995)
Haupt, P., Lion, A.: Experimental identification and mathematical modelling of viscoplastic material behavior. J. Continuum Mech. Thermodyn. 7, 73–96 (1995)
Herrmann, A.S., Zahlen, P.C., Zuardy, I.: Sandwich structures technology in commercial aviation. In: Sandwich Structures 7: Advancing with Sandwich Structures and Materials, pp. 13–26. Springer (2005)
Hofmann, S.: Effect of interlaminar defects on the mechanical behaviour of carbon fibre reinforced silicon carbide. PhD thesis, DLR, Deutsches Zentrum für Luft-und Raumfahrt (2013)
Hua, W., Fischer, T., Harhash, M., Ziegmann, G., Palkowski, H.: Study on processing galvanized steel/PA6 sandwich composites by hot-pressing: Influence of interface properties and surface treatment on the adhesion strength. Compos. Struct. 236, 111779 (2020)
Itskov, M., Aksel, N.: A class of orthotropic and transversely isotropic hyperelastic constitutive models based on a polyconvex strain energy function. Int. J. Solids Struct. 41, 3833–3848 (2004)
Johansson, G., Ahlström, J., Ekh, M.: Parameter identification and modeling of large ratcheting strains in carbon steel. Comput. Struct. 84(15–16), 1002–1011 (2006)
Kaw, A.K.: Mechanics of Composite Materials, 2nd edn. CRC Press, Boca Raton (2006)
Kim, J.K., Thomson, P.: Forming behaviour of sheet steel laminate. J. Mater. Process. Technol. 22(1), 45–64 (1990)
Klawonn, A., Lanser, M., Uran, M., Rheinbach, O., Köhler, S., Schröder, J., Scheunemann, L., Brands, D., Balzani, D., Gandhi, A., et al.: Exasteel: towards a virtual laboratory for the multiscale simulation of dual-phase steel using high-performance computing. Softw. Exascale Comput.-SPPEXA 2016–2019(136), 351 (2020)
Kleuter, B., Menzel, A., Steinmann, P.: Generalized parameter identification for finite viscoelasticity. Comput. Methods Appl. Mech. Eng. 196, 3315–3334 (2007)
Krämer, S., Rothe, S., Hartmann, S.: Homogeneous stress-strain states computed by 3D-stress algorithms of FE-codes: application to material parameter identification. Eng. Comput. 31, 141–159 (2015)
Krempl, E.: Models of viscoplasticity. Some comments on equilibrium (back) stress and drag stress. Acta Mech. 69, 25–42 (1987)
Krzyżak, A., Mazur, M., Gajewski, M., Drozd, K., Komorek, A., Przybyłek, P.: Sandwich structured composites for aeronautics: methods of manufacturing affecting some mechanical properties. Int. J. Aerosp. Eng. 2016 (2016)
Lawson, C.L., Hanson, R.J.: Solving Least Squares Problems. Siam Society for Industrial and Applied Mathematics, Philadelphia (1995)
Lempriere, B.: Poisson’s ratio in orthotropic materials. AIAA J. 6(11), 2226–2227 (1968)
Li, H., Fan, X., Yan, C.: Prediction of orthotropic mechanical properties of plain-weave composites with matrix voids using unit cells at multi-scales. Polym. Int. 62(7), 1029–1037 (2013)
Lion, A.: Constitutive modelling in finite thermoviscoplasticity: a physical approach based on nonlinear rheological models. Int. J. Plast 16(5), 469–494 (2000)
Mahnken, R.: Identification of material parameters for constitutive equations. Int. J. Solids Struct. 2, 637–655 (2004)
Mahnken, R.: Identification of Material Parameters for Constitutive Equations, 2nd edn., pp. 1–21. Wiley (2017)
Mahnken, R., Stein, E.: Parameter identification for viscoplastic models based in analytical derivatives of a least-squares functional and stability investigations. Int. J. Plast 12, 451–479 (1996)
Mahnken, R., Stein, E.: A unified approach for parameter identification of inelastic material models in the frame of the finite element method. Comput. Methods Appl. Mech. Eng. 136, 225–258 (1996)
Martinez Page, M.A., Hartmann, S.: Experimental characterization, material modeling, identification and finite element simulation of the thermo-mechanical behavior of a zinc die-casting alloy. Int. J. Plast 101, 74–105 (2018)
Maziére, M., Forest, S.: Strain gradient plasticity modeling and finite element simulation of Lüders band formation and propagation. Continuum Mech. Thermodyn. 27, 83–104 (2015)
Miehe, C., Koch, A.: Computational micro-to-macro transitions of discretized microstructures undergoing small strains. Arch. Appl. Mech. 72(4–5), 300–317 (2002)
Motevalli, M., Uhlemann, J., Stranghöner, N., Balzani, D.: Geometrically nonlinear simulation of textile membrane structures based on orthotropic hyperelastic energy functions. Compos. Struct. 223, 110908 (2019)
Nocedal, J., Wright, S.J.: Numerical Optimization. Springer, New York (1999)
Nörenberg, N., Mahnken, R.: A stochastic model for parameter identification of adhesive materials. Arch. Appl. Mech. 83(3), 367–378 (2013)
Nörenberg, N., Mahnken, R.: Parameter identification for rubber materials with artificial spatially distributed data. Comput. Mech. 56(2), 353–370 (2015)
Palkowski, H., Lange, G.: Creation of tailored high-strength, hybrid sandwich structures. In: Advanced Materials Research, vol. 22, pp. 27–36. Trans Tech Publ (2007)
Palkowski, H., Sokolova, O.A., Carradò, A.: Sandwich materials. Encyclopedia of Automotive Engineering 1–17 (2014)
Parsa, M.H., Yamaguchi, K., Takakura, N.: Redrawing analysis of aluminum-stainless-steel laminated sheet using FEM simulations and experiments. Int. J. Mech. Sci. 43(10), 2331–2347 (2001)
Perzyna, P.: Fundamental problems in viscoplasticity. Adv. Appl. Mech. 9, 243–377 (1966)
Rajabi, A., Kadkhodayan, M., Manoochehri, M., Farjadfar, R.: Deep-drawing of thermoplastic metal-composite structures: experimental investigations, statistical analyses and finite element modeling. J. Mater. Process. Technol. 215, 159–170 (2015)
Reissner, E.: Finite deflections of sandwich plates. J. Aeronaut. Sci. 15(7), 435–440 (1948)
Ren, S., Morgeneyer, T., Mazière, M., Forest, S., Rousselier, G.: Effect of Lüders and Portevin-Le Chatelier localization bands on plasticity and fracture of notched steel specimens studied by DIC and FE simulations. Int. J. Plast 136, 102880 (2020)
Reyes, G., Gupta, S.: Manufacturing and mechanical properties of thermoplastic hybrid laminates based on dp500 steel. Compos. A Appl. Sci. Manuf. 40(2), 176–183 (2009)
Reyes, G., Kang, H.: Mechanical behavior of lightweight thermoplastic fiber-metal laminates. J. Mater. Process. Technol. 186(1–3), 284–290 (2007)
Rieger, A.: Zur Parameteridentifikation komplexer Materialmodelle auf der Basis realer und virtueller Testdaten. PhD thesis, Institute of Mechanics, University of Stuttgart (2005)
Rothe, S., Erbts, P., Düster, A., Hartmann, S.: Monolithic and partitioned coupling schemes for thermo-viscoplasticity. Comput. Methods Appl. Mech. Eng. 293, 375–410 (2015)
Schindelin, J., Arganda-Carreras, I., Frise, E., Kaynig, V., Longair, M., Pietzsch, T., Preibisch, S., Rueden, C., Saalfeld, S., Schmid, B., et al.: Fiji: an open-source platform for biological-image analysis. Nat. Methods 9(7), 676–682 (2012)
Schittkowski, K.: Numerical Data Fitting in Dynamical Systems. Kluwer Academic Publ, Dordrecht (2002)
Schmidt, U., Mergheim, J., Steinmann, P.: Identification of elastoplastic microscopic material parameters within a homogenization scheme. Int. J. Numer. Meth. Eng. 104(6), 391–407 (2015)
Schröder, J.: Theoretische und algorithmische Konzepte zur phänomenologischen Beschreibung anisotropen Materialverhaltens. Bericht i-1 1996, Universität Stuttgart (1996)
Schröder, J., Neff, P.: Invariant formulation of hyperelasticity transverse isotropy based on polyconvex free energy functions. Int. J. Solids Struct. 40, 401–445 (2003)
Semenov, P.: Determination of shear moduli of orthotropic materials from torsion tests. Polym. Mech. 2(1), 17–20 (1966)
Sencu, R., Yang, Z., Wang, Y., Withers, P., Rau, C., Parson, A., Soutis, C.: Generation of micro-scale finite element models from synchrotron x-ray ct images for multidirectional carbon fibre reinforced composites. Compos. A Appl. Sci. Manuf. 91, 85–95 (2016)
Sewerin, F.: On the local identifiability of constituent stress-strain laws for hyperelastic composite materials. Comput. Mech. 65, 853–876 (2020)
Sguazzo, C., Hartmann, S.: Tensile and shear experiments using polypropylene/polyethylene foils at different temperatures. Tech. Mech. 38, 166–190 (2018)
Sokolova, O.A., Carrado, A., Palkowski, H.: Metal-polymer-metal sandwiches with local metal reinforcements: A study on formability by deep drawing and bending. Compos. Struct. 94(1), 1–7 (2011)
Spencer, A.J.M.: Continuum Theory of the Mechanics of Fibre-Reinforced Composites, vol. 282. Springer, Berlin (1984)
Sutton, M.A., Orteu, J.-J., Schreyer, H.W.: Image Correlation for Shape, Motion and Deformation Measurements, 1st edn. Springer, New York (2009)
Taylor, J.R.: An Introduction to Error Analysis. University Science Books, California (1997)
Tsakmakis, C., Willuweit, A.: A comparative study of kinematic hardening rules at finite deformations. Int. J. Non-Linear Mech. 39(4), 539–554 (2004)
Vannucci, P.: Anisotropic elasticity, volume 85 of Lecture Notes in Applied and Computational Mechanics, 1st edn. Springer, Singapore (2018)
Vexler, B.: Adaptive finite element methods for parameter identification problems. PhD thesis, Ruprecht-Karls-Universität, Heidelberg, Germany (2004)
Wennberg, D.: Light-weighting methodology in rail vehicle design through introduction of load carrying sandwich panels. PhD thesis, KTH Royal Institute of Technology (2011)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We gratefully acknowledge the financial support provided by the German Research Foundation project, DFG HA 2024/19-1, PA 837/42-1, ZI 648/46-1. Furthermore, we would like to thank Rose Rogin Gilbert for helpful discussions in the parameter identification concepts, Jendrik-Alexander Tröger for helping with the FE simulations, and both Prof. Holger Steeb as well as Matthias Ruf, Institute of Applied Mechanics, University of Stuttgart (Germany) for providing us the \(\mu \)-CT data of the composite. Finally, we would like to thank Dr. Mohammed Harhash for helpful discussions. In addition, we would like to express a deep gratitude to the unknown reviewer who contributed to a significant improvement of the article.
Appendices
Appendix A: Rough estimation of the material parameters of the steel model
For a first estimation of the material parameters in Sect. 4.2.1, the following steps are carried out. First, a Young’s modulus and a Poisson’s number \(E_{\text {st}}=200\,000\,\hbox {N}\,\hbox {mm}^{-2}\) and \(\nu _{\text {st}}=0.3\) are chosen. This leads approximately to the bulk and shear moduli in Table 9. Next, the yield stress \({\hat{k}}\) is taken from Fig. 6a. For a rough estimation of the viscosity \(\eta \) and the exponent r the experience-based quantities in Table 9 are chosen. \(c_1\) and \(c_2\) are connected with a stored energy part since not all inelastic contributions dissipate into heat, see [41]. Since the deformations are not too large, the small strain case can be considered, see [83, Appendix A]. There, the strain energy \(\psi _k\), where \(c_X \hat{=} c_2 \hat{=} 2 {\hat{G}}\), can be interpreted as “shear modulus.” Thus, \(c_1\) is connected with a “bulk modulus.” Assuming nearly incompressibility, \({\hat{\nu }} = 0.49\), and a weak Young’s modulus \({\hat{E}} \approx 1000\,\hbox {N}\,\hbox {mm}^{-2}\) roughly yields \(c_1 = {\hat{K}} = {\hat{E}}/(3 (1-2{\hat{\nu }})) \approx 1.5\times 10^4\, \hbox {N}\,\hbox {mm}^{-2}\) and \(c_2 = 2 {\hat{G}} ={\hat{E}}/(1+{\hat{\nu }}) \approx 600\,\hbox {N}\,\hbox {mm}^{-2}\).
Using the Armstrong and Frederick ansatz (1D formulation) in arc-length represenation \(\xi (s) = c - b \xi (s)\) with the solution \(\xi (s) = c/b (1- \exp (-b s))\) one has the initial slope \(c_2 = c\) and \(c_2 \beta _{\text {st}}= b\), see [83, Appendix A]. This yields the saturation term \(c/b = 1/\beta _{\text {st}}\). The view in Fig. 6a leads to a stress increase from the yield stress \({\hat{k}}\) by about \(50\,\hbox {N}\,\hbox {mm}^{-2}\), i.e., \(\beta _{\text {st}}\approx 0.02\). Using the roughly estimated material parameters of Table 9 yields the correlation matrix (35).
Appendix B: Alternative representations of the elasticity matrices
There are mainly three possible representations of the elasticity matrix \({{\mathbf {\mathsf{{C}}}}}\) of the Voigt representation using the parameter set \(\varvec{\kappa }_{\text {SP}}\) (Spencer parameters; chosen in the computations using finite elements), \(\varvec{\kappa }_{\text {S}}\) (Young’s and shear modulus representation; chosen for analytical considerations and parameter identification purposes), and \(\varvec{\kappa }_{\text {C}}\) (formal parameters; are given to complete the representation). Since we have to switch between the representations between an implementation, the dependencies between the parameters are provided.
The elasticity matrix \({{\mathbf {\mathsf{{C}}}}}\) (21) can be rewritten in the following representation using the material parameter set \(\varvec{\kappa }_{\text {C}}\):
\({{\mathbf {\mathsf{{C}}}}}_u {\, \in \mathbb {R}}^{3 \times 3}\), \({{\mathbf {\mathsf{{C}}}}}_l{\, \in \mathbb {R}}^{3 \times 3}\). Another possibility for the matrix representation (20) is obtained from the compliance matrix \({{\mathbf {\mathsf{{S}}}}} {\, \in \mathbb {R}}^{6 \times 6}\),
with
\({{\mathbf {\mathsf{{S}}}}}_u {\, \in \mathbb {R}}^{3 \times 3}\), \({{\mathbf {\mathsf{{S}}}}}_l{\, \in \mathbb {R}}^{3 \times 3}\), \({{\mathbf {\mathsf{{C}}}}} = {{{\mathbf {\mathsf{{S}}}}}}^{-1}\), see [16]. This leads to
with
where
represents the determinant \(\det {{\mathbf {\mathsf{{S}}}}}_u\).
All material parameter sets \(\varvec{\kappa }_{\text {SP}}\) (Spencer’s model), \(\varvec{\kappa }_{\text {S}}\) (parameter set expressed by Young’s and shear moduli as well as Poisson numbers) and \(\varvec{\kappa }_{\text {C}}\) (the formal \(C_{ij}\)-stiffnesses) can be expressed by each other. The elaborate calculations yield the relations between the parameter sets, where we start with \(\varvec{\kappa }_{\text {S}}\) in dependence of \(\varvec{\kappa }_{\text {SP}}\) and \(\varvec{\kappa }_{\text {C}}\):
These expressions depend on the abbreviations:
The remaining shear moduli read
Alternatively, we can express Spencer’s model parameters \(\varvec{\kappa }_{\text {SP}}\) in dependence of \(\varvec{\kappa }_{\text {C}}\) and \(\varvec{\kappa }_{\text {S}}\):
Finally, we show the dependence of the set \(\varvec{\kappa }_{\text {C}}\) on \(\varvec{\kappa }_{\text {SP}}\) and \(\varvec{\kappa }_{\text {S}}\) for completeness:
Appendix C: Helpful inequalities for parameter identification in orthotropic elasticity
The 12 material constants in the compliance matrix as shown in Eq. (64) can be reduced to 9 independent parameters for the case of orthotropic materials using the symmetry condition, \({{\mathbf {\mathsf{{S}}}}} = {{\mathbf {\mathsf{{S}}}}}^T\), which implies
Thus, three reciprocal relations must be satisfied for an orthotropic material, i.e., the conditions
hold. In Sect. 4.4.2 an alternative way is followed based on evaluating a representative volume element (RVE) combined with the previous deformation states.
There might by also inequality constraints to stabilize the identification process. We summarize these relationships for completeness purposes only. According to [59], the sum of the work done by all stress components must be positive in order to show the formation of energy. This condition provides a thermodynamical constraint on the elastic constants, \(\kappa _s\). Formally, the constraint requires that the elasticity matrices must be positive definite. This mathematical condition can be augmented by the following physical argument. Evidently if only one normal component of stress is applied at a time, the corresponding strain is determined from that stress by the diagonal elements of the compliance matrix so that these must all be positive:
Similarly, under suitable constraints, deformation is possible in which only one extensional component of strain arises. Again, work is produced by the corresponding stress alone, and this is determined from the strain by the diagonal elements of the stiffness matrix. Therefore, these elements must be positive as well,
and
By the condition of symmetry of the compliances as applied to Poisson’s ratios in Eq. (89), it follows that the aforementioned inequalities (92) and (93) for Poisson’s ratios can be expressed as follows:
This condition shows that all three Poisson’s ratios cannot have large positive values at the same time, as their product must be less than one half.
Conditions (91)–(96) are chosen to check whether the identification scheme yields reasonable results.
Appendix D: Estimation of the standard deviation for a glass fiber
We assume that an upper and a lower value of a material parameter is given, \(\kappa _U\) and \(\kappa _L\), and that there is a normal distribution,
where \(\sigma _\kappa \) defines the standard deviation and \(\kappa _M\) the mean value, see Fig. 17. \(\sigma _\kappa \) and \(\kappa _M\) are assumed to be unknown. To provide an estimation of both quantities, we proceed as follows. We assume that the probability P within \(\kappa _L\) and \(\kappa _P\) is given,
\(\Delta \kappa = \kappa _M - \kappa _L\). In the calculations we choose \(P=0.9\), i.e., 90% of the values are within this region (gray region in Fig. 17). \(\kappa _M\) can be defined by \(\kappa _M = (\kappa _U + \kappa _L)/2\). Then, Eq. (98) represents a nonlinear function
with the solution \(p(\sigma _\kappa ) = 0\). This can be reformulated and expressed by the error function,
i.e.,
In AZO-Materials [8] minimum and maximum values are provided for Young’s modulus \(E_f\) and the Poisson number \(\nu _f\), i.e., we have the values in Table 10.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dileep, P.K., Hartmann, S., Hua, W. et al. Parameter estimation and its influence on layered metal–composite–metal plates simulation. Acta Mech 233, 2891–2929 (2022). https://doi.org/10.1007/s00707-022-03245-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-022-03245-z