1 Introduction

Already, von Humboldt (1845) (see also Hantel and Haimberger 2016) observed that all human sensory organs are needed to sense climate, and the sensation will always remain incomplete and it will be subjective. Similarly, human thermal comfort research in the middle of the twentieth century proposed as many as hundreds of factors that determine the outdoor thermal environment (Zhao et al. 2021). This view changed with the appearance of Fanger’s work (Fanger 1973). It was Fanger who selected the main environmental and human factors influencing the human thermal environment, which are as follows: air temperature, radiation, wind speed, air humidity, clothing thermal resistance, and activity. Fanger’s influence was huge (Zhao et al. 2021), as he converted the qualitative approach into a quantitative investigation and introduced the energy balance method–based treatment.

In the past decade, energy balance method–based treatments prevailed worldwide (Potchter et al. 2018) and many other methods, such as the device-based methods, algebraic or statistical methods, and methods serving special purposes (de Freitas and Grigorieva 2015), are underrepresented. Note, in this study, de Freitas and Grigorieva’s (2015) model type categorization is used. Among energy balance-based methods, physiological equivalent temperature (PET), universal thermal climate index (UTCI), and predicted mean vote (PMV) are the most popular indices. According to Staiger et al. (2019) and Matzarakis (2020), all three indices are suitable for the evaluation of climate from a human biometeorological point of view. Among the three indices mentioned, PET was used most frequently in the Carpathian region (e.g., Gulyás et al. 2006; Gulyás and Matzarakis 2009; Kántor et al. 2012; Bašarin et al. 2014, 2018). In these studies, the climate is analyzed in selected subregions of the Carpathian region.

Studies referring to the whole Carpathian region started to appear from 2020s (Ács et al. 2020a, 2020b). In these studies, the human thermal environment is considered in terms of clothing thermal resistance rcl and operative temperature To. The scheme is deterministic based on energy balance considerations (de Freitas and Grigorieva 2015). The parameter rcl depends on both To and metabolic heat flux density M. To expresses the heat load effect, which is triggered by all atmospheric variables (the most important: temperature, radiation, wind, humidity). M refers to a walking human in outdoor conditions whose speed is 1.1 ms−1. The model does not belong to the group of top models according to Staiger et al’s (2019) criteria characterizing a model’s suitability. In the work of Ács et al. (2021a), mean annual rcl values are statistically interconnected with the annual sum of potential evapotranspiration PE; this is how the first statistical rcl model was constructed. Both rcl and PE depend on the same atmospheric factors (radiation, air temperature, and wind); thus, it can be assumed that the statistical relationship between them might be strong. This was confirmed by Ács et al. (2021a). The analysis showed that rcl results depend also strongly on human body somatotype variations. The model, despite its shortcomings (climate and human-specific), can provide valuable extra human thermal climate information for Thornthwaite-type (Thornthwaite 1948) climate classification models like the Feddema model (Feddema 2005). The study of Ács et al. (2021a) can also be seen as a first attempt to link human and descriptive climate classification methods since generic climate classification models do not include human thermal climate information.

The statistical rcl model of Ács et al. (2021a) can be improved by the statistical interconnection of monthly and annual To values and monthly and annual sums of PE. To values obtained in such a way can be used for calculating rcl values as in deterministic models (Ács et al. 2020b, 2021b). The benefit of this replacement is twofold: fewer input data are required and the more lengthy and cumbersome calculation of To is avoided. The disadvantage is that the statistical interconnection of To and PE is climate-specific and limited in space and time. In addition, thermal load expressed in terms of rcl is characterized in terms of thermal sensation. The thermal load–thermal sensation relationship is determined for two individuals by the concurrent collection of weather and thermal sensation data. The thermal sensation–rcl point-cloud is also statistically treated.

According to the above, the aims of this study are as follows: (1) to present this new statistical-deterministic model, (2) to discuss the performance of the model, (3) to discuss individual thermal sensation–rcl relationships, and (4) to characterize the human thermal climate of the Carpathian region in terms of human heat load and thermal sensation on annual, seasonal and monthly time scales. The methods used are described in Section 2. The region and the locations of the cities where the collection of weather data is carried out and the thermal sensation observations are performed are presented in Section 3. The data used in the study are considered in Section 4. The results are presented and described in Section 5, the verification of the results in Section 5.1, the results characterizing the relationship between thermal sensation and thermal load in Section 5.2, and the human thermal climate results in Section 5.3. The suitability of the model is discussed in Section 6. The main conclusions are drawn in Section 7.

2 Methods

Three procedures are used: a scheme for characterizing environmental human thermal load, human thermal sensation observations, and lastly a data treatment method when the statistical link between thermal load and thermal sensation data is handled. Thermal load is characterized in terms of clothing thermal resistance. rcl estimates are made for both weather and climate data. When weather data are used, operative temperature is calculated deterministically (Ács et al. 2020b). In the case of climate data, operative temperature is calculated statistically as presented in the next section.

2.1 Determination of clothing thermal resistance

Clothing thermal resistance is simulated using clothed human body energy balance considerations (Ács et al. 2020b). It can be expressed as

$$r_{cl}=\rho\cdot c_p\cdot\frac{T_S-T_o}{M-\lambda E_{sd}-\lambda E_r-W}-r_{Hr},$$
(1)

where ρ is air density (kgm−3), cp is the specific heat at constant pressure (Jkg−10 C−1), TS is the skin temperature (°C), To is the operative temperature (°C), M is the metabolic heat flux density (Wm−2), λEsd is the latent heat flux density of dry skin (Wm−2), λEr is the respiratory latent heat flux density (Wm−2), W is the mechanical work flux density (Wm−2), and rHr is the combined resistance for expressing the thermal radiative (rR) and convective (rHa) heat exchanges (sm−1). These resistance terms can be expressed as

$$\frac{1}{{r}_{Hr}}= \frac{1}{{r}_{Ha}}+ \frac{1}{{r}_{R}},$$
(2)
$${r}_{Ha}\left[s{m}^{-1}\right]=7.4\cdot 41\cdot \sqrt[]{\frac{D}{{U}_{1.5}}},$$
(3)
$$\frac{1}{{r}_{R}} = \frac{4{\epsilon }_{cl}\sigma {T}_{a}^{3}}{\rho {c}_{p}},$$
(4)

where D (m) is the diameter of the cylindrical body with which the human body is approximated (Campbell and Norman 1998), U1.5 is airspeed relative to the human body at 1.5 m, εcl is the emissivity of clothing or skin (in this study, εcl = 1), σ is the Stefan-Boltzmann constant, and Ta is the air temperature (°C). U1.5 is calculated using wind speed at a height of 10 m and using a logarithmic wind profile supposing neutral thermal stability. As it may be seen, the scheme does not take into account the effect of the direction of a walking human compared to the direction of wind speed.

A human walking at a speed of 1.1 ms−1 is considered; the human is not sweating. The human’s total metabolic heat flux density is as follows,

$$M= {M}_{b}+ {M}_{w},$$
(5)

where Mb is the basal metabolic rate (W) and Mw is the metabolic rate (W) referring to walking. Mb is parameterized according to Mifflin et al. (1990) separately for men and women

$${M}_{b}^{male}\left[kcal\cdot {day}^{-1}\right]=9.99\cdot {M}_{bo}+6.25\cdot {L}_{bo}-4.92\cdot age+5,$$
(6)
$${M}_{b}^{female}\left[kcal\cdot {day}^{-1}\right]=9.99\cdot {M}_{bo}+6.25\cdot {L}_{bo}-4.92\cdot age-161,$$
(7)

where Mbo is body mass (kg), Lbo is body length (cm), and age is expressed in years. The human body surface A (m2) has to be estimated in order to express Mb in Wm−2, and for this, we use the well-known Dubois and Dubois (1915) formula,

$$A=0.2\cdot {M}_{bo}^{0.425}\cdot {\left(\frac{{L}_{bo}}{100}\right)}^{0.725}.$$
(8)

Mw is parameterized according to Weyand et al. (2010) as follows,

$${M}_{w}=1.1\cdot \frac{3.80\cdot {M}_{bo}\cdot {\left(\frac{{L}_{bo}}{100}\right)}^{-0.95}}{A}.$$
(9)

The coefficient 1.1 is added because of the chosen walking speed. The λEsd + λEr sum can be expressed as a percent of M (Campbell and Norman 1998), whilst W is parameterized according to Auliciems and Kalma (1979).

2.1.1 Estimation of operative temperature

Operative temperature is statistically evaluated using regression curves obtained by the statistical interconnection of To and PE on annual and monthly time scales. The regression curve equations refer to the CarpatClim dataset region for the period 1971–2000. Monthly estimates are performed only for vegetation period months from April to September. The equations linking To and PE are as follows,

Year

$${T}_{o}^{annual}= 0.03608\cdot {PE}^{annual}- 10.26.$$
(10)

Vegetation period months

$${T}_{o}^{April}= 0.0001\cdot {PE}_{April}^{3}- 0.0092\cdot {PE}_{April}^{2}+0.4179\cdot {PE}_{April}+0.6810,$$
(11)
$${T}_{o}^{May}= 0.0001\cdot {PE}_{May}^{3}- 0.0223\cdot {PE}_{May}^{2}+2.1093\cdot {PE}_{May}-54.3862,$$
(12)
$${T}_{o}^{June}= 0.0001\cdot {PE}_{June}^{3}- 0.0459\cdot {PE}_{June}^{2}+5.3414\cdot {PE}_{June}-190.6055,$$
(13)
$${T}_{o}^{July}= 0.0001\cdot {PE}_{July}^{3}- 0.0472\cdot {PE}_{July}^{2}+6.1240\cdot {PE}_{July}-246.8911,$$
(14)
$${T}_{o}^{August}= 0.0002\cdot {PE}_{August}^{3}- 0.0737\cdot {PE}_{August}^{2}+8.5701\cdot {PE}_{August}-315.4450,$$
(15)
$${T}_{o}^{September}= 0.0002\cdot {PE}_{September}^{3}- 0.0358\cdot {PE}_{September}^{2}+3.2006\cdot {PE}_{September}-82.9106.$$
(16)

Both indicators express thermal load; To is prevalent in human biometeorology, whilst PE is frequently used in environmental and hydrological surveys. Both To and PE depend upon the same meteorological variables; therefore, the statistical relationship between them is strong.

The To–PE point clouds together with regression curves for the year and for the month of July are presented in Figs. 1 and 2, respectively. As it can be seen, a linear and a third-order polynomial fitting is used linking To and PE.

Fig. 1
figure 1

Scatter chart of the annual mean of operative temperature as a function of the annual sum of potential evapotranspiration in the CarpatClim dataset region for the period 1971–2000

Full size image
Fig. 2
figure 2

Scatter chart of the July mean of operative temperature as a function of the July sum of potential temperature in the CarpatClim dataset region for the period 1971–2000

Full size image

2.1.2 Calculation of potential evapotranspiration

PE is calculated in the simplest way using only Ta and daylight length as inputs (McKenney and Rosenberg 1993). For the ith month (i = 1, …,12)

$${PE}_{i}=1.6\cdot \left(\frac{{L}_{i}}{12}\right)\cdot \left(\frac{{N}_{i}}{30}\right)\cdot {\left(\frac{{10\cdot T}_{ai}}{I}\right)}^{A},$$
(17)

where I is a heat index introduced by Thornthwaite (1948) as

$$I=\sum_{i=1}^{12}{t}_{i},$$
(18)
$$t_i=\left\{\begin{array}{lc}{(\frac{T_{ai}}5)}^{1.514},&if\;T_{ai}>0\\0,&if\;T_{ai}\leq0,\end{array}\right.$$
(19)
$$A=6.75\cdot {10}^{-7}\cdot {I}^{3}-7.71\cdot {10}^{-5}\cdot {I}^{2}+1.792\cdot {10}^{-2}\cdot I+0.49239.$$
(20)

Ni is the number of days in the ith month, Tai is the mean monthly air temperature [°C] of the ith month, and Li is the mean monthly daylight length [hours]. In our calculations, Li is estimated by calculating Li for the central day of the month (the 15th day in the month except for February) as follows,

$${L}_{i}=\frac{24}{180}\cdot \mathrm{arccos}\left[-tg\left(\varphi \right)\cdot tg\left({\delta }_{i}\right)\right]$$
(21)

where φ is latitude [0º] and δi is declination [0] on the central day of the ith month.

2.2 Determination of thermal sensation

Two individuals, a male and a female (their human state variables are presented in Table 1, see Section 4.3) served as the tools for the qualitative estimation of thermal state performing thermal sensation observations. Both individuals were asked to use the following thermal sensation type groups: very cold, cold, cool, neutral, slightly warm, warm, and very warm. Both persons are native in the region of the Hungarian lowland, where the climate can be characterized either as Cfb (C, warm temperate; f, no seasonality in the annual course of precipitation; b, warm summer) according to Köppen (1936), or as “cool and dry with extreme variations of temperature” according to Feddema (2005). During thermal sensing (usually lasting a minimum of 5 min), sweating or shivering did not occur and, of course, the observers were not aware of their vasodilation or vasoconstriction processes, not to mention other hidden thermoregulatory processes.

Table 1 Human state variables and metabolic heat flux densities of four persons (person 1, a male; person 2, a female; person 3, a representative Hungarian male; person 4, a representative Hungarian female)
Full size table

2.3 Thermal sensation and thermal load data treatment

Weather and thermal sensation data are collected concurrently, and the collected data then being filtered. First, the consistency between thermal load and thermal sensation data was checked. All those observations were removed where (a) positive clothing thermal resistance values were associated with the thermal sensation types “slightly warm” or “warm” and (b) negative clothing thermal resistance values were found. In the latter cases, the energy balance of the human body covered with clothing is not met because the sweating process is not simulated. Second, each thermal sensation group below the 5th and above the 95th percentiles of the associated To values was omitted. As mentioned, To is calculated deterministically (Ács et al. 2020b) taking into account all relevant weather elements (air temperature, radiation, wind speed, air humidity).

3 Region and locations

The CarpatClim dataset region is the region studied. The region together with the locations of the cities where the collection of weather and thermal sensation data is performed is presented in Fig. 3. This Central East European region is bounded by the 17° and 27°/44° and 50° longitude/latitude lines. It contains both lowlands and mountain areas with quite different climate types ranging either from Cfa (C, warm temperate; f, no seasonality in the annual course of precipitation; a, hot summer) to ET (tundra climate) according to Köppen (1936) or from “cool and dry with extreme variations of temperature” to “cold and saturated with medium variations of temperature and precipitation” according to Feddema (2005). The cities are located in the lowland region.

Fig. 3
figure 3

The region of the CarpatClim dataset and the locations (in red) of the cities where the collection of weather data is carried out and the thermal sensation observations are performed. The picture also contains basic elevation data and major geographical designations used in the study

Full size image

4 Data

Three types of data are used: climatic, weather, and human data. The main characteristics of each data type are separately considered.

4.1 Climatic data

Climatic data are taken from the CarpatClim dataset (Lakatos et al. 2013). The dataset is based on station observations. The number of stations taken into account depends upon the type of climatic element; it can vary between 300 and 1000 (Cheval et al. 2014). Among climatic data, we used the following: daily values of air temperature and wind speed at a height of 10 m. Daily data are quality controlled and homogenized by using the MASH (Multiple Analysis of Series for Homogenization) procedure (Szentimrey 1999). Monthly values are constructed from the daily values. The 30-year mean monthly values are calculated for the period 1971–2000. The spatial resolution of the data is 0.1° × 0.1°, which is equivalent to about 10 km × 10 km. Interpolation and gridding procedures are performed by using the MISH (meteorological interpolation based on surface homogenized data basis) method (Szentimrey and Bihari 2013).

4.2 Weather data

Weather data in cities are taken from the nearest automatic meteorological station operated either by the Hungarian Meteorological Service (HMS) or by a private company “Időkép.” The beeline distance between the automatic stations and the thermal sensation observation locations was in both cases shorter than 3 km. Air temperature, air humidity, wind speed, and atmospheric pressure are used from the measured data. Relative sunshine duration and cloudiness are estimated by observers.

Person 1 collected weather data in the period April 1, 2020–February 20, 2021. Observations are performed in the day and night as well under a large variety of weather conditions. In night-time periods (about 40% of the cases), air temperature ranged between − 11 and 28 °C, mostly still wind conditions prevailed, but there were also high average wind speeds of 4 and 7 ms−1. Relative air humidity varied between 40 and 100%. In daytime periods, global radiation and air temperature varied between 10 and 850 Wm−2 and between − 9 and 32 °C, respectively. Wind was in most cases moderate, between 2 and 3 ms−1, but, of course, there were also higher (average wind speed about 6–7 ms−1, gusts above 10 ms−1) and lower (under 1 ms−1) wind speed values. Relative air humidity varied between 20 and 100%.

Person 2 collected weather data in the period April 7, 2020–March 2, 2021. About two-thirds of the observations were carried out in anticyclonic weather conditions. The air pressure values vary between 993 and 1038 hPa. There was no precipitation at the time of the observations. In night-time periods (about 35% of the cases), the air temperature ranged between − 10 and 23 °C, while relative humidity varied between 40 and 100%. The average wind speed ranged between 0.1 and 6.7 ms−1. In daytime periods, air temperature values varied between − 9 and 34 °C while the relative humidity values were between 15 and 100%. The average wind speed varied from calm (0.1 ms−1) to high values (7.8 ms−1).

4.3 Human data

The human state variables used are as follows: body mass (the most important), body length, sex, and age. These personal data of four individuals together with calculated metabolic heat flux densities are presented in Table 1.

Data of persons 1 and 2 are used for determining the relationship between thermal sensation and thermal load. Metabolic heat flux densities of persons 3 and 4 are as close as possible to the metabolic heat flux densities of a representative Hungarian male and female, respectively (Zsákai et al. 2015; Bodzsár et al. 2016).

5 Results

Three result types are considered: (1) verification results, (2) thermal sensation–thermal load relationship results, and (3) results characterizing the human thermal climate of the region considered.

5.1 Verification results

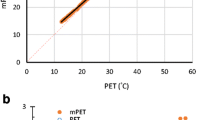
Verification results are constructed for persons 3 and 4 since their total energy flux densities are as close as possible to the total energy flux densities of an average Hungarian male and female, respectively. Figure 4 shows scatter plots between clothing thermal resistance values obtained by calculating operative temperature as a function of PE (statistical deterministic model) and by calculating operative temperature according to its definition (e.g., Ács et al. 2021b) (deterministic model).

Fig. 4
figure 4

Comparison of clothing thermal resistances obtained by calculating operative temperature by using statistical deterministic and deterministic procedures for a representative Hungarian male and female in the month of July (top) and in the year (bottom) in the CarpatClim dataset region for the period 1971–2000. Each point cloud contains a few thousand points

Full size image

The figure contains 4 scatter plots: for person 3 (representative Hungarian male) for the year and the month of July and the same for person 4 (representative Hungarian female). Straight lines at 45° are also plotted. It can be said that the agreement is good, especially for the year. For the annual estimate, there is a slight underestimation in the zones of higher rcl values (rcl is higher than 1.3 (clo), such cases are obviously in the mountainous areas). A similar underestimation in the zone of higher rcl values (rcl is higher than 0.3–0.4 (clo)) also exists for the month of July. This underestimation is somewhat larger as for the annual period. Note that the characteristics of the agreement are equally valid for male and female.

The agreement in terms of area distribution for the representative Hungarian male and female is presented in Figs. 5 and 6, respectively.

Fig. 5
figure 5

Area distribution of annual clothing resistance values obtained by calculating operative temperature by using deterministic (top, (a)) and by statistical deterministic (bottom, (b)) procedures for a representative Hungarian male in the CarpatClim dataset region for the period 1971–2000

Full size image
Fig. 6
figure 6

Area distribution of annual clothing resistance values obtained by calculating operative temperature by using deterministic (top, (a)) and by statistical deterministic (bottom, (b)) procedures for a representative Hungarian female in the CarpatClim dataset region for the period 1971–2000

Full size image

As we might have expected from Fig. 4, noticeable differences can be found only in mountainous areas, for example, in the Apuseni Mountains, Retezat Mountains, and Fagaras Mountains. The agreement in lowland areas is more noticeable than the agreement in mountainous areas.

5.2 Individual thermal sensation–thermal load relationships

Thermal sensation–thermal load relationships are determined for persons 1 and 2. Thermal load is expressed in terms of clothing thermal resistance. Note that the total energy flux densities of persons 1 and 2 are in the range of the total energy flux densities of persons 3 and 4, who represent the representative Hungarian male and female. These relationships are presented in Fig. 7.

Fig. 7
figure 7

The thermal sensation–clothing thermal resistance relationships for persons 1 and 2

Full size image

Person 1 is represented by triangles, whilst person 2 by circles. The rcl ranges registered for the thermal sensation categories used can be seen in Table 2.

Table 2 Clothing resistance ranges of persons 1 and 2 for different thermal sensation categories
Full size table

There are 236 and 242 points in total for persons 1 and 2, respectively. Each point represents a weather situation. Examining Figs. 7 and Table 2, two facts can be established: (1) the smallest inter-person deviations in rcl values are obtained for the thermal sensation types “neutral” and “cool.” The inter-person deviations in rcl values increase towards cold stresses. In our case, the largest deviations appeared in the thermal sensation category “very cold.” (2) In this case, discrete thermal sensation categories are used, at the same time, human thermal perception is continuous, and it is hard to separate it into different discrete types. Therefore, the adjacent thermal categories are not unequivocally separated by rcl values; there is a mixing between them regardless of the person. This mixing is unavoidable since human thermal perception depends strongly on a person’s psychological state, which increases the subjective nature of perception.

5.3 Human thermal climate

Human thermal climate characteristics will be separately considered for the time periods, year, the month of July, and for the vegetation period from April to September.

5.3.1 Year

Annual area distributions of clothing thermal resistance for the representative Hungarian male and female are presented in Figs. 5b and 6b, respectively. Both area distribution structures follow the area distribution structure of topography. The lowest rcl values (in red) are in southern lowland regions (Backa, Banat, Oltenia, Wallachian Plain). The rcl values in the Great Hungarian Plain are slightly larger with respect to the former lowland regions. In the hilly and foothills regions (e.g., Transdanubian Mountains, Transylvanian Plateau, eastern foothills of Carpathians), rcl values can even reach 1 (clo) (in green). The largest rcl values can be found in mountain regions, like Retezat, Fagaras, the Maramures Mountains, and the High Tatras. In these areas, rcl can vary between 1 and 1.8 (clo). Note that area distribution structures for male and female are very similar, although there is a slight shift between their rcl values. This is logical because their M values are different.

These thermal loads are perceived by humans 1 and 2 together as follows: a thermal load of 0.4–0.8 (clo) (in red) is perceived mostly as “neutral” or “cool,” but the perception “cold” may also occur, especially for persons whose M is lower than 135 Wm−2. For a slightly larger thermal load of 0.7–1.0 (clo) (in orange and green), only the perceptions “cool” and “cold” occur; of course, this depends on the person and their psychological state, which perception is represented to a greater extent. A thermal load of 1–1.8 (clo) (in blue) can be sensed as “cool,” “cold,” or “very cold.” Note that in these areas, the importance of personal differences on the evolution of thermal perception is much higher than in lowland and hilly regions. This means that in mountain regions, the same thermal load can be sensed either as “cool” or as “very cold” depending on the person and their psychological state.

5.3.2 July

The area distributions of clothing thermal resistance for the month of July for the representative Hungarian male and female are presented in Figs. 8 and 9, respectively.

Fig. 8
figure 8

Area distribution of July clothing thermal resistance values obtained by calculating operative temperature by using the statistical deterministic procedure for a representative Hungarian male in the CarpatClim dataset region for the period 1971–2000

Full size image
Fig. 9
figure 9

Area distribution of July clothing thermal resistance values obtained by calculating operative temperature by using a statistical deterministic procedure for a representative Hungarian female in the CarpatClim dataset region for the period 1971–2000

Full size image

In the month of July, the method is applicable only in mountain areas. In the mountains, rcl values can vary between 0 and 1.2 (clo). This thermal load is perceived by humans 1 and 2 as “neutral” or “cool.” As mentioned, the method is not applicable in lowland and hilly areas. Nevertheless, we can state that in these areas, the most common thermal perception types are “neutral” and “slightly warm.” Thus, in the month of July, the thermal perception type “neutral” is common in the Carpathian Basin.

5.3.3 The vegetation period from April to September

The area distributions of clothing thermal resistance for the 6-month period from April to September (hereinafter vegetation period) for a representative Hungarian male and female are presented in Figs. 10 and 11, respectively.

Fig. 10
figure 10

Area distribution of vegetation period clothing thermal resistance values obtained by calculating operative temperature by using the statistical deterministic procedure for a representative Hungarian male in the CarpatClim dataset region for the period 1971–2000

Full size image
Fig. 11
figure 11

Area distribution of vegetation period clothing thermal resistance values obtained by calculating operative temperature by using the statistical deterministic procedure for a representative Hungarian female in the CarpatClim dataset region for the period 1971–2000

Full size image

As in the previous case, the method is applicable only in mountain areas. rcl values can vary between 0 and 1.2 (clo), but very low (0–0.2 (clo)) rcl values are predominant. This is sensed as “neutral” by humans 1 and 2, but in higher areas, thermal perception types “cool” and “cold” may also occur. Area distributions obtained for man and woman are very similar, but the differences increase with increasing altitude. As mentioned, the method is not applicable in lowland and hilly areas. Note that the applicability of the method for man and woman differs unequivocally in the Podolian upland (top right corner in the figures). Note how common is the thermal perception type “neutral” in the mountains during the vegetation period.

6 Discussion

So far, mainly complex, energy balance–based models have been used for estimating human thermal load (e.g., Gagge et al. 1986; Mayer and Höppe 1987; Staiger et al. 2012; Jendritzky et al. 2012; Fiala et al. 2011; Blazejczyk et al. 2012). These types of models (mostly PET and UTCI models) have also been applied to the Carpathian Basin (e.g., Németh 2011; Kovács and Németh 2012; Kovács and Unger 2013). Most recently, human thermal load estimations in the Carpathian region are also made by applying a clothing index model (e.g., Ács et al. 2020a, 2020b). The PET, the UTCI, and the clothing index models are energy balance–based models (de Freitas and Grigorieva 2015), but they differ enormously in terms of model type and results. In such cases, it is especially difficult to compare and interpret the obtained results (Potchter et al. 2022). Regarding the model types, we can briefly say the following: PET and UTCI are working in a “forward mode”; that is, the skin temperature or clothing’s surface temperature is the variable to be calculated. The clothing index model is working in “backward mode”; that is, the skin temperature is known, and the thermal resistance of the clothing is the variable to be calculated. As a consequence of this difference in model structure, the clothing index model is much simpler than the UTCI or PET model. The clothing index model is an inverse Fanger model (Fanger 1970) analyzing a single-segment human body (Enescu 2019). The UTCI model contains 12 segments and 187 nodes, whilst PET has 1 segment and 2 nodes. The most popular model is PET. The UTCI applications are also not rare, but the clothing index models are the most rarely used ones. The UTCI and PET models can be successfully applied in both warm and cold climates. The clothing index model can only be successfully used in cool, cold climates. There are also big differences between the people in the models. In the UTCI and PET models, there is a “standardized human” (this human representing a group does not exist in reality), and in the clothing index model, there are individuals. These humans can be characterized in terms of worn or simulated clothing, activity, and thermal perception. In the UTCI and PET models, the thermal insulation value of the clothing is an input variable. In the UTCI model, the thermal insulation of clothing is estimated according to Havenith et al. (2012); in the PET model, its value is 0.9 clo. In the clothing index model, the thermal insulation of clothing is an output variable, which refers to a virtual clothing achieving the thermal equilibrium between the human body and the environment. There are also differences regarding human activity. In the PET model, there is a “standardized human” sitting indoors. In the UTCI and clothing index model, the human walks outdoors at a speed of 1.1 ms−1. Regarding the description of the human thermal sensation, the differences are very large. In the PET model, there is 9-point thermal sensation scale together with 9-point physiological stress level scale (Matzarakis and Mayer 1996). In the UTCI model, there is no thermal sensation scale at all, a 10-point scale is used for expressing thermal stress intensity (Bröde et al. 2012). In the clothing index model, a 7-point thermal perception scale is used, in which the designation of the categories is very similar to the one used in the ASHRAE 7-point scale (Enescu 2019).

The comparison of thermal loads obtained by different methods is only possible by comparing the thermal perceptions they cause. But a comparison of thermal sensations is difficult if the scales created for their characterization are different. The work of Potchter et al. (2022) deals with the analysis of these difficulties. In biometeorological research, and also in Potchter et al.’s (2022) work, the case of “thermal neutrality” has always been a very popular topic that has received much attention. Since Potchter et al. (2018, 2022) unequivocally showed that the amount of thermal load that characterizes “thermal neutrality” (comfort zone) depends on the type of climate, we will focus only on Köppen’s Cfb climate type, which is the prevailing climate type in the Hungarian lowland. In the case of “thermal neutrality,” PET is between 18 and 23 ℃ according to Matzarakis and Mayer (1996). A somewhat broader PET range (PET between 13 and 22.5 ℃) is obtained by Kovács et al. (2016). In the same case, clothing thermal resistance values change between 0 and 0.5–0.7 clo. The UTCI method uses thermal stress categories, not thermal perception categories. In the UTCI assessment scale, the stress category “no thermal stress” is the closest to “thermal neutrality.” During the occurrence of this category, the UTCI values are between 9 and 26 ℃. In our research (Ács et al. 2022), we were also convinced that in this interval of UTCI values, the thermal perception type “cool” was the most common, in addition to the fact that “neutral” and “cold” were also perceived. As we see, it is hard, almost impossible to be very precise in the comparison of different thermal load estimation methods because thermal perception scales also differ significantly. To overcome this difficulty, Potchter et al. (2022) proposes a biometeorological research protocol, where the statistical analysis of the observed data is a decisive methodological element. Note that in our research, data quality control and filtering of thermal load-thermal sensation data were also performed (Section 2.3).

In the science of modelling, it is extremely important to use the simplest models possible. The original rcl model (Ács et al. 2020b) is quite complex, not its human, rather its environmental physics part. The complexity of the environmental physics part can be reduced significantly by a simpler calculation of operative temperature. To is well correlated by both PE and Ta. Both relationships have their advantages and drawbacks. To is more similar to PE, than to Ta, since it depends upon radiation, air temperature, and wind speed like PE. However, PE is less usable in cold climates than Ta. Of course, the usage of PE increases the complexity of the model. We investigated both relationships, here only the To–PE statistical relationships are used and considered. The statistical approach is used not only for determining To but also for establishing the connection between thermal perception type and rcl. By establishing this link, the model is able to estimate not only individual human thermal load but also individual human thermal sensation, which is the ultimate goal of any human climate application. By using this latter statistical part of the model, we avoided the simulation of complex thermoregulation processes, such as sweating, shivering, vasodilation, and vasoconstriction. However, as we mentioned, persons 1 and 2 did not sweat or shiver at all during their observations. We agree with the opinion of Staiger et al. (2019) that human thermoregulation processes need to be simulated for human thermal comfort purposes; nevertheless, in our opinion, this complex model part can be ignored if the goal is to determine individual human thermal climate.

Of course, this first statistical deterministic model aiming at human thermal climate classification also has its drawbacks. Firstly, it is less applicable in warm climates; moreover, it is not applicable at all in the summer season of warm climates. The model would be applicable in the case of simulating the process of sweating. However, in a such model, thermal load is proportional not only to the clothing’s thermal resistance but also to the evaporative resistance of the skin (Parsons 2003). Extending the model in this way is one of our future tasks. Secondly, as a statistical model, it has also spatial–temporal limits to its application. Of course, it can be applied under similar geographical conditions, but the To–PE connection needs to be recalibrated in regions where annual PE is less than 450 mm∙year−1 and higher than 750 mm∙year−1. The model can also serve for establishing possible human thermal sensation type, especially for humans whose M while walking is around 130–145 Wm−2 and when the thermal load is moderate or less. Thermal sensation type is much less estimable with this model in more extreme climates and for humans whose M while walking is substantially different to 130–145 Wm−2. As mentioned, we can talk only about individual human thermal sensation types, but these individual thermal sensation types can be quite similar or even identical if the environmental and human conditions are not extreme.

Since we estimated To via PE, rcl is considered for the month of July, the vegetation period, and the year. In the month of July, in lowland and hilly areas, the model was not applicable. As mentioned, the reason is that the energy balance of the human body covered with clothing is not met. In mountains, besides thermal perception type “neutral,” “cool,” or even “cold” can also be sensed. These results are in accordance with the results obtained by deterministic models, which are more recent and simpler (Ács et al. 2020b), or more complex and based on a completely different treatment (e.g., Matzarakis and Gulyás 2006; Gulyás and Matzarakis 2009). In the vegetation period, the prevailing human sensation type is “cool.” Of course, the largest probability of perceiving thermal type “cold” is in the mountains, where rcl values can reach 1.2 (clo). Regarding annual perceptions, a relief-based configuration emerges. In lowlands, the dominant perception types are both “neutral” and “cool” depending on the person and their psychophysiological state; in hilly areas, it is more only “cool,” whilst in mountains, both “cool” and “cold” are common depending on the person and their psychophysiological state. In our treatments, thermal perceptions of persons 1 and 2 are equated with thermal perceptions of a representative Hungarian male and female (persons 3 and 4), respectively. Of course, we did so arbitrarily knowing that the difference between the M values of the persons is less than 15 Wm−2. As we have seen, there is a shift of 0.1–0.2 (clo) in the thermal load between Hungarian males and females. This is caused by the shift in their M values (the M of males is 147, whilst the M of females is 135 Wm−2). However, such a shift in the thermal perceptions between persons 1 and 2 was not registered, which is logical because the difference between their M values is small. It can be said, that sex difference seems to be not a determinant factor in the process of human thermal sensation, especially for moderate or lower thermal loads.

The model presented can be treated as an improved version of Ács et al.’s (2021a) statistical model for estimating rcl, since personal rcl values are simulated and not human groups like, for instance, ectomorphic and/or endomorphic humans. Moreover, here, thermal sensation type estimates are also presented. In summary, this method can be considered as a Feddema (2005) model version, which serves for representing human thermal climate since PE is converted into a personal rcl value, and the personal rcl value into a personal thermal perception type. Of course, Feddema’s (2005) “cool” and “cold” categories are not to be confused with the human perception types “cool” and “cold.” As we have already seen, Feddema’s category “cool” can be perceived either as “neutral or as “cool” or even as “cold” (see thermal sensation of person 2), and similarly, Feddema’s category “cold” either as “cold” or as “cool” or even as “very cold” depending on the person and their psychological state. The work of Ács et al. (2021a) showed that human thermal load depends on body shape. If human thermal perception also depended on body shape, it would be much easier to estimate individual human thermal perception categories. Of course, the hypothesis of human thermal perception–body shape link has to be checked, this is a task for the future.

7 Conclusion

The following main conclusions can be drawn: (1) a new statistical deterministic model is presented and validated for estimating human thermal load and sensation for individuals. (2) The model is not applicable in time periods with high thermal load. (3) The results of the model can be used as extra human information in the Feddema (2005) model. (4) The model can be applied outside the region considered, if new region-specific To–PE and human-specific thermal sensation-rcl statistical relationships are installed instead of those presented. (5) Human thermal sensation in the Carpathian region is governed by relief. In the Carpathian region’s lowland areas, the annual thermal sensation of the vast majority of people is mostly “neutral” or “cool,” in mountains mostly “cool” or “cold.” (6) There are thermal load differences between the sexes; however, these are not so large that thermal sensation differences between the sexes could be registered.