Creep Behavior and Associated Acoustic Characteristics of Heterogeneous Granite Containing a Single Pre-existing Flaw Using a Grain-Based Parallel-Bonded Stress Corrosion Model

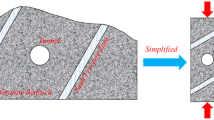
Abstract

Understanding the microcracking mechanisms and associated acoustic characteristics involved in the creep of heterogeneous granite at the grain scale is of high importance in practical engineering. To perform this task, a series of creep numerical simulations were conducted on granite with a single pre-existing open flaw using a grain-based parallel-bonded stress corrosion model. We investigated the effect of flaw inclination angle on the creep behavior and discussed the significance of microstructure. The results suggest that the axial strain, secondary creep strain rate and time-to-failure all depend strongly and nonlinearly on the flaw inclination angle. Creep failure is mainly induced by the initiation, propagation and coalescence of microcracks, and the dominant types are inter-grain tension cracks and intra-grain tension cracks. The b value, source types and distribution of acoustic emission events are associated with the flaw inclination angle and driving-stress ratio. Tensile sources account for the majority of the total number of acoustic emission sources, while shear and implosive acoustic emission sources are larger in magnitude. The model with higher heterogeneity creeps at a faster rate under the same applied constant axial stress. The higher number of acoustic emission events at each creep stage of such model indicates that the relatively heterogeneous microstructure provides more paths for the growth of microcracks during creep loading. As the heterogeneity increases, the secondary creep strain rate rises and the b value decreases. The position of the final macroscale shear band of pre-cracked granite is more affected by pre-existing flaw compared to its microstructure.

Highlights

• An extended grain-based parallel-bonded stress corrosion (GB-PSC) model was proposed to simulate the creep and associated acoustic behavior of granite.

• Voronoi tessellations to provide a more realistic representation of the microstructure of granite.

• Effects of open flaw inclination angle on creep behavior of pre-cracked granite were systematically investigated and the significance of microstructure were discussed.

• The acoustic emission characteristics of mineral boundaries and interiors during creep loading were obtained using the moment tensor analysis.

Appendices

Appendix A: Microcrack Types Generated in GBM

A microcrack can be categorized into two kinds in the perspective of granite at the grain scale (Guéguen and Boutéca 2004): (a) fractures propagating along grain boundaries are classified as inter-grain cracks; (b) fractures propagating through the mineral grains are classified as intra-grain cracks. As presented in Fig. 20, the GBM based on PFC2D can accurately simulate the initiation and propagation of inter-grain (Fig. 20a) and intra-grain (Fig. 20b) microcracks of granite.

Fig. 20

Microcrack initiation and propagation in GBM; a inter-grain and b intra-grain cracks (modified after Liu et al. 2021b; Li et al. 2018)

Appendix B: Parallel-Bonded Stress Corrosion (PSC) Model

The PSC model induces a damage rate ν to the parallel bond model based on the subcritical propagation rate of a mode I type tensile fracture (Potyondy 2007). The PSC model idealizes brittle rock as a cemented granular material and then removes the cement via a $\nu - \overline{\sigma }$ relationship. Tension force in the cement acts as a driving force. The corrosion damage rate ν can be stated as:

$$\nu = \left\{ {\begin{array}{*{20}l} {0, \, \overline{\sigma } < \overline{\sigma }_{a} } \hfill \\ { - \beta_{1} e^{{\beta_{2} ({{\overline{\sigma } } \mathord{\left/ {\vphantom {{\overline{\sigma } } {\overline{\sigma }_{c} }}} \right. \kern-0pt} {\overline{\sigma }_{c} }})}} , \, \overline{\sigma }_{a} \le \overline{\sigma } < \overline{\sigma }_{c} } \hfill \\ { - \infty , \, \overline{\sigma }_{c} \le \overline{\sigma } } \hfill \\ \end{array} } \right.,$$

(3)

where $\overline{\sigma }$, $\overline{\sigma }_{a}$, $\overline{\sigma }_{c}$ are the normal stress of parallel bond, micro-activation stress and normal tensile strength of the parallel bond, respectively. Material constants β₁ and β₂ change with the temperature and the chemical environment (Potyondy 2007).

The PSC model based on PFC2D is implemented in the following manner:

Step 1: Activate a wall-servo system to ensure that the particle assembly is under constant axial stress. Activate the PSC model and monitor the stress-corrosion time (creep loading time).

Step 2: Calculating the maximum normal tensile stress of each parallel bond contact. Based on Eqs. (4)–(7), estimating the time-to-failure (t_f) when the parallel bond will failure. Then divide the time t_f into n_c steps and therefore each the stress corrosion timestep is $\Delta t = t_{{\text{f}}} /n_{{\text{c}}}$. Note that the stress-corrosion rate ν of each parallel bond is determined by Eq. (3) and the diameter of the parallel bond $\overline{D}$ ($\overline{D} = 2\overline{R}$) before the stress corrosion is reduced by $\nu \Delta t$ to $\overline{D}^{^{\prime}}$.

$$t_{{\text{f}}} = \left\{ {\begin{array}{*{20}l} {0, \, \overline{\sigma } < \overline{\sigma }_{a} } \hfill \\ {\frac{{\overline{D} - \overline{D}^{\prime } }}{{\beta_{1} }}e^{{ - \beta_{2} \left( {{{\overline{\sigma } } \mathord{\left/ {\vphantom {{\overline{\sigma } } {\overline{\sigma }_{c} }}} \right. \kern-0pt} {\overline{\sigma }_{c} }}} \right)}} , \, \overline{\sigma }_{a} \le \overline{\sigma } < \overline{\sigma }_{c} } \hfill \\ \end{array} } \right.,$$

(4)

$$\overline{D}^{\prime } = \max \left\{ {\overline{\lambda }_{i} ,\beta_{\sigma } ,\beta_{\tau } } \right\}\overline{D} ,$$

(5)

$$\beta_{\sigma } = \frac{1}{{\overline{R} }}\left( {\frac{{ - \overline{F}^{n} \pm \sqrt {\left( {\overline{F}^{n} } \right)^{2} + 24\left| {\overline{M}^{s} } \right|\overline{\sigma }_{c} } }}{{4\overline{\sigma }_{c} }}} \right),$$

(6)

$$\beta_{\tau } = \frac{1}{{\overline{R} }}\left( {\frac{{\left| {\overline{F}^{s} } \right|}}{{2\overline{\tau }_{c} }}} \right),$$

(7)

where $\beta_{\sigma }$ and $\beta_{\tau }$ represent the radius reduction factor of a parallel bond computed using the section beam theory; $\overline{\tau }_{c}$ denotes the tangential shear strength of parallel bond; and $\overline{\lambda }_{i}$ represents radius coefficient.${\overline{\text{F}}}^{{\text{n}}}$, ${\overline{\text{F}}}^{{\text{s}}}$ are normal force and shear force at contacts.${\overline{\text{M}}}^{{\text{s}}}$ is the moment at contacts.

Step 3: After each ${\Delta t}$ is completed, rebalance the model until the maximum unbalance ratio is less than f_r.

Step 4: Cycling step (1)–(3) and stopping when: (a) for each parallel bond, $\overline{\sigma } < \overline{\sigma }_{a}$, suggesting that the time-to-failure of the model is infinite; (b) macroscopic failure occurs. Here, we consider n_c = 4, f_r = 1.0 × 10⁻⁴, and $\overline{\lambda }_{i} = 0.01$ in this work (Potyondy 2007).

Figure 21 shows the damage-rate relationships in the PSC model.

Fig. 21

Damage-rate relationships in the PSC model; a the stress corrosion process of the parallel bond; b damage-rate curve for the parallel bond diameter (modified after Potyondy 2007)

Appendix C: AE Simulation Based on the Moment Tensor Theory

When a parallel bond failure, the source particles bonded by the broken contact will shift and cause the surrounding parallel bond to deform (Hazzard and Young 2000). As a result of the bond failure, the force at the surrounding bonds will vary. Microcracks that are spatially and temporally near are treated as a single AE event in this study. The duration of each event is determined by assuming that a crack propagates at half the shear wave velocity of the rock model. Therefore, if a second crack forms within the source area of an ‘active’ crack, then the two cracks are considered part of the same AE event and the source area is expanded to encompass all of the source particles. In this way, events made up of multiple cracks can exist and more realistic magnitude distributions result. The following is the formula for calculating the AE moment tensor M (Hazzard and Young 2004):

$$M_{ij} { = }\sum {\Delta F_{i} R_{j} }$$

(8)

where $\Delta F_{i}$ is the ith part of a change in parallel bond contact force, and R_j is the distance between AE event centroid and contact point. The scalar moment M₀ determined as follows:

$$M_{0} = \left( {\frac{{\sum\nolimits_{j = 1}^{3} {m_{j}^{2} } }}{2}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$

(9)

where m_j is the jth eigenvalue of moment tensor M. The maximum value of the scalar moment M₀ is used to compute the magnitude M associated with the AE event:

$$M = \frac{2}{3}\log M_{0} { - }6$$

(10)

We assume the moment tensor is composed of isotropic and deviatoric components:

$${\mathbf{M}} = \frac{{tr\left( {\mathbf{M}} \right)}}{3}\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{ + }\left[ {\begin{array}{*{20}c} {m_{1}^{*} } & {} & {} \\ {} & {m_{2}^{*} } & {} \\ {} & {} & {m_{3}^{*} } \\ \end{array} } \right]$$

(11)

where tr(M) is the sum of eigenvalues and $m_{i}^{*}$ is deviatoric eigenvalues (i = 1, 2, 3).

Depending on their isotropic/deviatoric ratio R, the AE event are classified as “tensile,” “shear,” or “implosive” type. The isotropic/deviatoric ratio is given by (Feignier and Young 1992):

$$R = \frac{{{\text{tr}}\left( {\mathbf{M}} \right) \times 100\% }}{{\left| {{\text{tr}}\left( {\mathbf{M}} \right) + \sum {m_{i}^{*} } } \right|}}.$$

(12)

An AE event can by characterized as “tensile” (R > 30%), “shear” (− 30% ≤ R ≤ 30%), or “implosive” (R < − 30%) (Feignier and Young 1992).