Lithological Control on the Estimation of Uniaxial Compressive Strength by the P-Wave Velocity Using Supervised and Unsupervised Learning

Abstract

Uniaxial compressive strength (UCS) is the most fundamental physico–mechanical parameter used for any rock mass classification in geotechnical and geological engineering. However, determining UCS is a very tough, expensive, time consuming and destructive method and requires experienced workers. On the other hand, P-wave velocity (V_P) determination is cheap, precise, non-destructive and easy. There are many established relationships between UCS and V_P but mostly are low in range or proposed for multiple rock types of different origin. In this paper, the correlation of UCS with V_P has been assessed based on the rocks' lithology. The methodology used in this analysis was centred on the previous studies database, lithology-based data disintegration and data integration to establish lithology based simple regression (SR) equations. A total of 37 previous studies databases were processed, and 12 characteristic regression equations have been determined based on the lithology. The lithological control was also determined using the principal component analysis (PCA), which categorised the data into diverse rock types. Artificial neural network (ANN) has been used as a robust predictive tool to estimate the UCS using the V_P and rock type information.

1 Introduction

Uniaxial compressive strength (UCS) is the primary physico–mechanical parameter that is essentially required to assess the field conditions for any geotechnical or civil engineering constructions. Rock mass and other classification systems such as rock mass rating (RMR) proposed by Bieniawski (1973), slope mass rating (SMR) offered by Romana (1985), Q-slope offered by Bar and Barton (2017) etc. which are being used in various geotechnical, geological and civil purposes, fundamentally requires UCS as a primary physico-mechanical parameter. However, standards proposed by the International Society of Rock Mechanics (ISRM) (1979) and the American Society of Testing and Materials (ASTM) (2000) are very tough, time-consuming, expensive and destructive. Therefore, estimating the UCS using various indirect tests has become popular. UCS has been correlated with physical parameters such as density, porosity etc. and physico-mechanical parameters such as point load strength index (PLSI), rebound number (N_R), Brazilian tensile strength (BTS) and V_P. In the present study, the correlation of UCS with the V_P has been assessed based on the previous studies database. The V_P depends on the density and elastic properties of the material. The standards suggested by ASTM (2002) and ISRM (1978) for the determination of V_P is straightforward, easy, non-destructive, cheap and precise.

Many researchers have proposed a general regression for multiple types of rocks (Kahraman 2001; Karakus et al. 2005; Sharma and Singh 2008; Kilic and Teymen 2008; Sarkar et al. 2012; Karakul and Ulusay 2013; Teymen and Menguc 2020 etc.), whereas some researchers have proposed regression equations for single rock types (Tugrul and Zarif 1999; Yasar and Erdogan 2004; Chary et al. 2006; Vasconcelos et al. 2007; Minaeian and Ahangari 2011; Rahman et al. 2020 etc.). In this paper, an attempt has been made to propose a generalised regression equation based on the lithology and evaluate the statistical acceptance of regression equations proposed for particular rock types. A specific characteristic regression equation has been offered for each rock type (a total of 12) based on previous studies database.

Principal component analysis (PCA) and ANN are the most common unsupervised and supervised learning algorithm in machine learning, respectively. ANN is a modern predictive tool that many researchers have used, while PCA has been generally used for data-processing and classification or categorisation of the dataset. Sarkar et al. (2010) used ANN to predict the UCS and shear strength with three input parameters such as V_P, PLSI, slake durability index (SDI) and density for four different rock types. Sharma et al. (2017) compared the accuracy of adaptive neuro-fuzzy inference system, multiple regression analysis and ANN to predict the UCS using three input parameters (density, V_P and SDI). In this paper, PCA has been used to validate the lithological control on the estimation of UCS from the V_P by categorising the database into 12 rock types, whereas ANN has been trained to predict the UCS from V_P and rock type information using three different training function algorithms and the regression fit obtained from simple regression analysis have been compared with each other.

2 Previous Studies

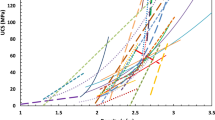
A plethora of research was conducted to estimate the UCS using the V_P (Table 1). Tugrul and Zarif (1999) proposed a regression equation to predict the UCS using V_P of 19 granitic rocks collected from different Turkey locations. Kahraman (2001) proposed a power correlation of UCS with the V_P of 27 different rock types, including sandstones, carbonates, tuffs etc., collected from different parts of Turkey. Yasar and Erdogan (2004) suggested a linear regression equation to predict the V_P using UCS, which was used for vice versa. They used 13 samples of carbonate rocks collected from different parts of Turkey. Karakus et al. (2005) used 9 samples of carbonate and igneous rocks to propose a multivariate linear regression to predict the Poisson’s ratio and Young’s modulus from N_R, V_P and porosity. Sousa et al. (2005) suggested a power correlation to estimate the UCS from V_P of 9 different granitic rocks procured from NE Portugal. Entwisle et al. (2005) suggested an exponential correlation equation to estimate the UCS from V_P of 171 samples of Volcanites procured from the UK NIREX off-site core characterisation programme. Chary et al. (2006) used sandstone samples from two different coalfields, namely SCCL and NLC, where they suggested regression equations separately for SCCL and NLC, to predict the UCS from V_P. Vasconcelos et al. (2007) used 19 samples to evaluate granites' behaviour in dry and saturated conditions. Kilic and Teymen (2008) proposed a power regression equation to predict the UCS of 19 samples of 10 different rock types using the V_P. Sharma and Singh (2008) suggested a common regression equation for 49 samples of 6 different rock types collected from India's different parts. Cobanoglu and Celik (2008) used cement mortar, limestone and sandstone core samples of different diameter and proposed a common correlation equation for all types of materials used based on sets of different diameters. Moradian and Behnia (2009) used 64 samples of marlstone, sandstone, and limestone to produce a common correlation between the samples' UCS and V_P. In contrast, Diamantis et al. (2009) suggested a linear regression equation for 32 serpentinite rocks from Central Greece. Torok and Vasarhelyi (2010) used 40 travertine samples from Hungary to study the influence of moisture and fabric on the rock's physico-mechanical properties. They also suggested a power regression equation to predict the UCS from V_P. The UCS and V_P database of Sarkar et al. (2010) with 40 samples of 4 rock types was also used in the study. Kurtulus et al. (2010) investigated the mechanical and physical properties of andesite rocks of Gokceada Island near Turkey mainland. A power correlation was offered by Yagiz (2011) for 3 types of rocks including mica-schist, travertine and carbonate. Kurtulus et al. (2012) investigated the physical and mechanical properties of serpentinites from NW Turkey. They proposed a linear regression between UCS and V_P along and across foliation planes with excellent R² values. The regression for across foliation tests was included for the present study. Minaeian and Ahangari (2011) proposed a linear regression equation to estimate the UCS of weak conglomerates using V_P. Sarkar et al. (2012) used 94 samples of 13 rock types from India and proposed a common correlation for all rock types. Babacan et al. (2012) suggested a linear regression equation between UCS and V_P for 15 samples of limestone. Karakul and Ulusay (2013) studied the variation in the physico-mechanical properties at varying degree of saturation and suggested a correlation equation to predict the physico-mechanical parameters from V_P. Azimian et al. (2013) studied 40 samples of marl from Iran and proposed a linear correlation between the UCS and V_P. Mishra and Basu (2013) suggested separate regression equations for granite, chlorite-schist and sandstone because they could not find a common correlation for all rock types used. Beiki et al. (2013) used genetic programming to estimate the UCS and elastic modulus of various carbonate rocks using V_P, porosity and density. Karaman and Kesimal (2015) correlated the N_R with the UCS and V_P of 46 rocks samples. Goh et al. (2014) investigated 77 Malaysian granite samples and suggested a power correlation between the UCS and V_P. Mohamad et al. (2014) suggested a common correlation equation for 3 types of rocks, including shale, old alluvium and iron pan. Goh et al. (2015) used 26 Malaysian schist samples and proposed a power correlation between UCS and V_P. Jamshidi et al. (2015) studied the effect of diameter size of the core specimen of 15 travertine rocks of Iran on the UCS and V_P and suggested a relation for 5 different diameter size. For the present study, the relationship of UCS and V_P for dry rock samples and 54 mm diameter size was considered. Kurtulus et al. (2015) used 96 samples of 3 rock types from Turkey and proposed correlations between V_P and different mechanical and physical properties. Selçuk and Nar (2016) used 42 samples of 8 rock types, and Kurtulus et al. (2016) used 32 samples of limestone to suggest a correlation equation between UCS and V_P. Awang et al. (2016) also proposed a correlation between UCS and V_P for shale rocks of Malaysia. Nespereira et al. (2019) used serpentinite rocks of NW Spain to propose a linear regression to predict the UCS from V_P. Teymen and Menguc (2020) used 93 samples of different rock types and suggested a common regression equation. Rahman et al. (2020) used Lower Gondwana sandstone and shale rocks and suggested separate regression equations for the 2 rock types, and recommended that each rock type follow a characteristic regression curve. The regression equations obtained by different researchers used in this study have been plotted and compared in Fig. 1, which is suggestive that there is no common and reliable regression equation that could be used for the prediction of UCS with the V_P. Hence, the study becomes very significant and important.

Table 1 Regression equations proposed by various researchers in previous studies

Fig. 1

Previous studies regression equations between UCS and V_P

3 Data Processing

3.1 Data Disintegration

The samples of different rock types used by various researchers in the previous studies were disintegrated on the basis of lithology irrespective of the proposed regression equation (Fig. 2). A total of 12 types of rocks have been identified using the previous studies database on the basis of lithology. A general overall trend, including all the rock types, have been proposed with a good R² value of 0.5657 and an exponential equation as follows (Eq. 1).

$${\text{UCS}} = 8.1469e^{{0.4506V_{P} }} .$$

(1)

Fig. 2

Data disintegration of the databases proposed by various researchers in the previous studies based on lithology

Many authors such as Kahraman (2001), Sharma and Singh (2008), Sarkar et al. (2012) etc., used multiple rock types and suggested an ordinary regression equation. Therefore, to propose a characteristic regression equation for a particular lithology, the method of data disintegration was used. For example, Kurtulus et al. (2015) used 96 samples of 3 rock types, including 10 samples of Kızderbent volcanic, 8 samples of Sopali arkose (T35-1), 36 samples of Korfez sandstone (T35-2), 20 samples of Derince sandstone (T35-3) and 22 samples of Akveren limestone. These rock types were disintegrated from the study and grouped as per the lithology under the heading of Volcanite (T35), Sandstone (T35-1, T35-2, T35-3) or Carbonate (T35).

3.2 Data Integration

In this section, all the lithology grouped after data disintegration has been analysed. The rock types shown in Fig. 3 (Group I: sandstone, carbonate, volcanite and granite) include $> \;100$ data points from the previous studies database. These rocks have been well studied in the past and suggest a characteristic regression trend-line with excellent R² values, while the rock types shown in Fig. 4 (Group II: shale, mica schist, ignimbrite and travertine) include $< \;100$ data points from the previous studies databases. The previous studies databases integrated on the basis of lithology suggested characteristic regression trend lines with excellent R² values. On the contrary, Group III rocks (conglomerate, slate/phyllite, chlorite schist and serpentinite) have not been well studied in the previous studies. These rocks belong to a grey area in the subject and are very difficult to prepare samples and test in the laboratory or field because of the presence of structural anisotropy. Hence, the rock types analysed and the regression proposed in Figs. 3 and 4 are more reliable and accurate than the group III rock types analysed in Fig. 5. Different lithology groups identified from data integration have been discussed below.

Fig. 3

Lithology based regression equations on predicting UCS from V_P obtained by integration of data published in previous studies; a sandstone, b carbonate, c volcanite, d plutonic rocks

Fig. 4

Lithology based regression equations on predicting UCS from V_P obtained by integration of data published in previous studies; a shale, b mica schist, c ignimbrite, d travertine

Fig. 5

Lithology based regression equations on predicting UCS from V_P obtained by integration of data published in previous studies; a conglomerate, b slate/phyllite, c chlorite schist, d serpentinite

3.2.1 Sandstone

A total of 14 previous studies database were used to obtain a characteristic regression equation for sandstone (Fig. 3a). An exponential curve has been proposed with a good R² value of 0.6627 (Eq. 2).

$${\text{UCS}} = 5.3211e^{{0.5745V_{P} }} .$$

(2)

Many previous studies database regressions are parallel or even overlapping with the proposed overall trend line. T11 and T21 have a similar regression line with a gradient much higher than the achieved overall trend line. T41, T35-3 and T13 are almost overlapping the overall trend-line. T39, T35-2 and T12 + T23 lie above the overall trend-line, which would predict a much higher value of UCS for corresponding V_P values. T8 and T35-1 lie below the overall trend-line. T7 shows an extraordinary regression which suggests drastic changes in UCS prediction within a very small range of V_P; hence the gradient of the regression is very steep.

3.2.2 Carbonate

The carbonates described in this section include limestone, marlstone, marble and dolomite rocks. The database used for carbonate rocks includes 15 previous studies (Fig. 3b). A power correlation equation (Eq. 2) has been suggested with a moderate R² value of 0.5613.

$${\text{UCS}} = 12.027V_{P}^{1.1592} .$$

(3)

T24, T29 and T35 are similar but show a steeper gradient than the overall trend line. T2, T3, and T13 regressions agree with the proposed overall trend line with slight deviations. T16 shows a parallel regression to the overall trend line but estimates much higher values of UCS for the corresponding V_P values while T4 and T22 lie below the overall trend line, which predicts underestimated values of UCS with a gentle slope gradient. T12, T18and T39 have very steep regression trend line and does not agree with the overall trend line with steep gradient regression slopes.

3.2.3 Volcanite

Volcanites are rocks that have solidified on the surface of the Earth. Rocks included in this section for analysis are dacite, andesite, basalt, rhyolite etc. A total of 10 previous studies database were used to suggest a characteristic regression equation for volcanites (Fig. 3c). For volcanites, two overall regression trend-lines have been suggested based on the inclusion of the T6 database. As the database is very large (database extraction problems due to overlapping data points), it has a greater influence on the proposed trend-line. The regression trend line without the T6 database (trend-A) shows an excellent R² value of 0.7683 (Eq. 4), while the overall trend with the T6 database (trend-B) shows a very small R² value of 0.4954 (Eq. 5).

$${\text{UCS}} = 12.241e^{{0.4611V_{P} }} ,$$

(4)

$${\text{UCS}} = 11.536e^{{0.4245V_{P} }} .$$

(5)

T29, T34 and T39 regression trend-lines agree with the overall trend-line (trend-A and trend-B). The T17 trend-line do not agree with the overall trend but lies within the field of the overall database. T11 and T21 databases lie parallel to the proposed overall regressions but predict higher values of UCS for the corresponding V_P values.

3.2.4 Plutonic Rocks

In Fig. 3d, all the previous studies database were observed to follow the proposed characteristic regression curve. The plutonic rock group mainly includes granites with other plutonic rocks of the T39 database such as diorite, granodiorite, gabbro, syenite etc. A total of 6 previous studies database were used to propose a characteristic power regression equation (Eq. 6) with an excellent R² value of 0.8103.

$${\text{UCS}} = 5.0952V_{P}^{1.8671} .$$

(6)

T1, T9, T30 and T39 database agrees with overall regression trend-line. In contrast, the T25 database lies in the general field of the overall trend-line. It depicts a steeper gradient regression slope that might underestimate or overestimate the UCS for granites with lower or higher V_P, respectively. The T5 database trend-line is parallel to the overall trend but predicts higher UCS values for the corresponding V_P values.

3.2.5 Shale

A power regression equation (Eq. 7) was proposed with an impeccable R² value of 0.8195. Out of 5 previous studies databases used for this rock group, 4 of the databases were observed to follow the general trend (Fig. 4a).

$$UCS = 4.9977V_{P}^{2.1718} .$$

(7)

The regression proposed by the database of T11 and T21 has a linear trend that predicts underestimated UCS values for higher V_P values if used beyond the proposed range. T31 and T40 have a polynomial and exponential regression trend, respectively, which agrees with the overall regression trend for shale rocks. T37 does not agree with the overall trend-line and estimates lower values of UCS for the corresponding V_P values with a gentler regression slope.

3.2.6 Mica Schist

Only 4 previous studies databases were used to propose the overall regression equation (Fig. 4b). An exponential curve has been suggested with an excellent R² value of 0.7946 (Eq. 8).

$${\text{UCS}} = 4.2616e^{{0.6487V_{P} }} .$$

(8)

T11 and T16 databases extend for a very low range of V_P and overlap each other. T32 database suggests a power regression trend-line that agrees with the overall regression, whereas T18 database regression predicts lower values of UCS for corresponding V_P values.

3.2.7 Ignimbrite

A total of 4 previous studies database were used to propose a characteristic regression equation for ignimbrite and tuff rocks (Fig. 4c). A linear regression equation (Eq. 9) with a good R² value of 0.5927 was suggested.

$${\text{UCS}} = 17.073V_{P} - 18.165.$$

(9)

T10, T23 and T39 databases lie parallel to the overall regression trend-line. T34 database suggested a trend-line with a gentler gradient than the overall trend-line. Therefore, predicting UCS using the T34 regression trend-line would give underestimated results for higher values of V_P.

3.2.8 Travertine

A total of 5 previous studies databases have been included, in which the majority of the data was incorporated from T15 and T33 databases. T15 database suggested a power regression that is parallel and close to the overall regression trend. T33 database suggested a linear regression that extends for the lower range of values and shows a slightly lower gradient, while the T18 database offers a linear regression with a higher slope than the overall trend of the proposed regression. Other studies (T10 and T39) have a very small database but lie in the field of the suggested regression. A power regression equation (Eq. 10) with an excellent R² value of 0.7568 was obtained for the overall database (Fig. 4d).

$${\text{UCS}} = 0.402V_{P}^{3.25} .$$

(10)

3.2.9 Conglomerate

Only T19 previous study database could be found to obtain the characteristic regression equation. A linear correlation equation (Eq. 11) was obtained with an excellent R² value of 0.9027 (Fig. 5a).

$${\text{UCS}} = 4.6139V_{P} + 1.0563.$$

(11)

3.2.10 Slate and Phyllite

A linear regression equation (Eq. 12) with an impeccable R² value of 0.9949 was obtained (Fig. 5b). Only 2 previous studies databases (T11 and T16) were incorporated to propose the characteristic regression equation.

$${\text{UCS}} = 18.866V_{P} - 32.023.$$

(12)

3.2.11 Chlorite Schist

Only the T26 database could be found to propose an exponential regression equation (Eq. 13) with a below-average R² value of 0.5184 (Fig. 5c).

$${\text{UCS}} = 0.3583e^{{0.8211V_{P} }} .$$

(13)

3.2.12 Serpentinite

T14 and T20 database proposed linear regression equations with excellent R² values of 0.81 and 0.92 for serpentinite rocks of Greece and Turkey, respectively. T38 database suggested a linear regression with a poor R² value of 0.29 to predict UCS from V_P for serpentinite rocks of Spain. The database from previous studies does not agree with each other. Hence, an unreliable exponential regression equation (Eq. 14) was obtained with a poor R² value of 0.1583 (Fig. 5d).

$${\text{UCS}} = 10.914e^{{0.3378V_{P} }} .$$

(14)

4 Results and Discussion

4.1 Simple Regression Analysis and Validation

In this paper, a simple bivariate regression analysis has been performed, and the best fit curve was evaluated to be linear $(y = mx + c$), power $(y = mx^{c}$) or exponential $(y = me^{x}$). Where $x$ is the independent variable, $y$ is the dependent variable, and $c$ is constant. The best-fit regression equation and R² values of the obtained 12 rock types under analysis have been shown in Table 2. The statistical credibility of the obtained regression equations was also analysed using the Student’s t test (Eq. 15).

$$\left| {\frac{{R\sqrt {n - 2} }}{{\sqrt {1 - R^{2} } }}} \right| \ge t_{{{\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/ {\vphantom {\alpha 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} .$$

(15)

Table 2 Statistical parameters and regression equations to predict UCS from V_P obtained for 12 rock types under study

The $t$ test is a statistical tool to differentiate between the means of two populations. The test was conducted for each regression equation with a confidence interval (CI) of 0.95, significance level $\left( \alpha \right)$ of 0.05 $\left( {CI + \alpha = 1.0} \right),$ degree of freedom $\left( {n {-} 2} \right),$ where n is the number of samples and R² is the coefficient of determination. The regression is accepted when the alternate hypothesis $\left( {H_{1} } \right)$ is accepted, and the null hypothesis $\left( {H_{0} } \right)$ is rejected. The $H_{1}$ is accepted and $H_{0}$ is rejected when the calculated $t$ value $\left( {t_{C} } \right)$ is greater than the tabulated $t$ value $\left( {t_{T} } \right).$

In Fig. 6, all the regression equations obtained from the database-disintegration and -integration methodology of the previous studies have been compared and analysed. It was surprising that shale rocks show the steepest trend-line gradient while conglomerate has the lowest trend-line slope as compared to other rock types. The sandstone regression has an intermediate slope between shale and conglomerate. Among these rocks, it was striking to see that the shale rocks which are composed of clay-sized particles, have the highest gradient, sandstone which is constituted of sand-sized particles, have intermediate gradient and conglomerate, which are composed of gravel-sized particles, shows the lowest gradient of the regression slope. Similarly, in igneous rocks, the volcanite rocks composed of fine-grained crystals have a higher regression gradient than the regression of the coarse-grained plutonic rocks.

Fig. 6

Lithology-based regressions for different rock types

Carbonate rocks show an intermediate gradient of the regression slope. Travertine rocks regression have a very steep gradient comparable to that of volcanite rock regression, but travertine rocks are confined to the high V_P region and estimated lower values of UCS than volcanite rock regression for corresponding V_P values. Ignimbrites, mica schist and sandstone have a similar regression gradient, but the ignimbrites extend for very small V_P values while mica-schist extends to very high V_P values. The slate/phyllite regression line extends for intermediate values of V_P with a slope gradient similar to that of sandstone and serpentinite. The chlorite schist and serpentinite rocks regressions have a similar gradient, but serpentinite regression yields higher UCS values at lower V_P values.

4.2 Principal Component Analysis (PCA)

Principal Component Analysis (PCA) is the most commonly used unsupervised learning algorithm in machine learning. It is a linear transformation method that transforms n-dimensional space to another space with a reduced number of dimensions with minimal loss of information. This technique processes high-dimensional data and uses the dependencies between the variables to represent it in a more amenable and low-dimensional form. In this paper, a classification approach has been used to identify the regressions to predict the UCS from the V_P on the basis of lithology (Fig. 7). Here, PCA has been particularly used as a classification tool and not as a predictive tool. In a similar manner, Mahmoudi et al. (2020) used PCA to study the spread rate of COVID-19 in different countries and compared them.

Fig. 7

PCA analysis to classify the rocks based on lithology

The PCA projects the multi-dimensional data onto an orthogonal coordinate system so that the variability is maximum along with the first component (PC1) axis. A data matrix is first defined as follows (Eq. 16).

$$X_{D} = \left( {\begin{array}{*{20}c} {\overrightarrow{{d_{1} }} _{} } \\ {\overrightarrow{{d_{2} }} _{} } \\ \vdots \\ {\overrightarrow{{d_{n} }} _{} } \\ \end{array} } \right),$$

(16)

where $\overrightarrow{{{d_{i} }}}$ is the row vector which consists of $m$ values from the ith observation. To generate a modified data matrix $X$ with data vectors $\overrightarrow{{{d_{l} }}} ^{\prime }$, where $l = 1, 2, \ldots , n$ and column-wise zero mean, we first subtract the $1 \times m$ vector $\overrightarrow{{\mu }}$ containing the mean of each column of $X_{D}$ from each of the rows of $X_{D}$ for transformation to the principal components. The PCA builds an orthogonal set of vectors $\overrightarrow{{{w_{k} }}}$ with $k = 1, 2, \ldots , m$ in such a way that $\overrightarrow{{{w_{1} }}}$ maximises the variance of the data vector projections $t_{l}^{\left( 1 \right)} = \overrightarrow{{{d_{l} }}} ^{\prime } \cdot \overrightarrow{{{w_{1} }}}$. The obtained data vector projection is called the first principal component scores. Similarly, the second principal component (PC2) is projected orthogonally to the $\overrightarrow{{{w_{1} }}}$ in the $m - 1$ dimensional subspace and so on. This operation is equivalent to maximising

$$\mathop \sum \limits_{l = 1}^{n} \left( {\overrightarrow{{{d_{l} }}} ^{\prime } \cdot \overrightarrow{{w}} } \right)^{2} = \overrightarrow{{w}}^{T} X^{T} X\overrightarrow{{w}}$$

(17)

Subject to $\overrightarrow{{w}}^{T} \overrightarrow{{w}}$ = 1. Introducing Lagrange multipliers and varying with respect to $\overrightarrow{{w}}$ yields

$$X^{T} X\overrightarrow{{{w_{i} }}} = \lambda_{i} \overrightarrow{{{w_{i} }}} ,$$

(18)

where $\lambda_{i}$ is the eigenvalue that quantify the variance of the corresponding scores. For the present study, V_P has been considered as the PC1 and UCS as the PC2. The two-dimensional $\left( m \right)$ scatter plot has been reduced or transformed into an $m - 1$ dimension plot. Hence, the dimensionality of the dataset has been reduced while the variance was maximised, as shown in Fig. 7.

4.3 Artificial Neural Network (ANN)

ANN is an artificial soft computing technology that has been extensively used in recent years. It offers a highly accurate predictive or modelling tool that mimics the function of a biological brain. It has information processing features such as non-linearity, noise tolerance, parallelism and learning-generalisation, which makes it better than other predictive methods. For the present study, the Neural Fitting App of MATLAB^© was used. The structure of an ANN consists of a three-layer system (input-hidden-output) called the multi-layer perceptron model (Fig. 8). All three in-built training functions were used and compared with each other. Levenberg–Marquardt (LM) algorithm (trainlm) is a typically fast algorithm that requires more memory and less time to compute; Bayesian regularization (BR) algorithm (trainbr) generally is a slow processing algorithm that requires less memory but more time but can result in a good generalisation of some noisy and challenging dataset. In comparison, the scaled conjugate gradient (SCG) algorithm (trainscg) requires less memory, and the training automatically stops when the generalisation stops improving. These three training functions were used to train the ANN model with three hidden layers (logarithmic sigmoid transfer function), V_P and rock-type as input layers and UCS as a target/output layer (tangent sigmoid transfer function). The network was trained for each rock type with its corresponding database. The best validation performance and regressions for different training functions of ANN have been shown in Fig. 9.

Fig. 8

A general ANN structure for the present study

Fig. 9

Showing the best validation performance and regression plot for different ANN models

4.4 Comparative Analysis

The results obtained from the regression and ANN model assessed on the basis of lithology were compared in the scatter plot for the measured and estimated UCS shown in Fig. 10. To analyse the predictive capacity of the model, the measured and estimated UCS values were drawn according to the x:y line (1:1). All the plots for different rock types were observed to show data points close to the x:y line (except for schist and serpentinite rocks), indicating that the proposed regression and ANN models on the basis of lithology are statistically acceptable.

Fig. 10

Plots of estimated versus measured values for different rock types including simple regression and best ANN model; a sandstone, b carbonate, c volcanite, d plutonic rocks, e shale, f mica schist, g ignimbrite, h travertine, i conglomerate, j slate and phyllite, k chlorite schist and l serpentinite

The developed ANN models from different training functions were able to predict the UCS for different rock types very efficiently. The efficiency of the predictive ANN models was assessed by comparing the calculated Chi-squared ($\chi^{2}$) values for the SR and the ANN models (Table 3). The Chi-squared values have been calculated using Eq. 19 as follows.

$$\chi^{2} = \sum\nolimits_{i = 1}^{k} {\frac{{\left( {O_{i} - E_{i} } \right)^{2} }}{{E_{i} }},}$$

(19)

where O is the observed value, and E is the estimated value for the ith sample, and k is the total number of samples. The above equation was used to quantify the difference between the observed and estimated values using simple regression (O-SR) and different ANN models (O-BR, O-LM, and O-SCG). Note that the equation was not used for hypothesis testing. Depending on the lowest $\chi^{2}$ value, the ANN model was chosen to be plotted in the 1:1 plot for that particular rock. The BR-ANN model was selected for carbonate, volcanite, plutonic rocks, shale, mica schist and chlorite schist. Similarly, LM-ANN model was selected for sandstone, ignimbrite, travertine and slate/phyllite rocks, while the SCG-ANN model was selected for conglomerate and serpentinite rocks.

Table 3 Chi-squared values for different predictive models

5 Conclusion

This study was aimed to establish a characteristic regression equation between UCS and V_P for 12 rock types identified from the previous studies. It was observed that there was no general regression equation that could be used to predict the UCS from V_P with high precision for multiple rock types. Hence, a separate characteristic regression equation was proposed for each rock type under study. It was observed that each rock type has its own characteristic regression curve, which could be used to predict the UCS from V_P easily and precisely. Shale, sandstone and conglomerate exhibit characteristic regression curves, which could be attributed to the constituent grain-size particles. Similarly, the regression curve of plutonic rocks, which are coarse-grained rocks, predict lower values of UCS than volcanite, which are fine-grained rocks for corresponding values of V_P. Therefore, it must be concluded that a common regression equation cannot be used to predict the UCS from V_P for multiple rock types.

The regression equations for four rock types in group I, namely, sandstone, carbonate. volcanite, and plutonic rocks have been rigorously studied, while rocks of group II such as shale, mica schist ignimbrite and travertine exhibit characteristic regressions but require more study. The group III rocks (conglomerate, slate/phyllite, chlorite schist and serpentinite) have not been studied well in the past because of sample preparation and testing constraints due to structural anisotropy.

The lithological control for the studied relationship in this paper has also been validated using PCA, which validated the relationship based on the rock type. The proposed regression equations for 12 rock types have been statistically tested using the x:y (1:1) scatter plots and Student’s t test, where the ${H}_{0}$ was rejected and ${H}_{1}$ was accepted in all the cases. The ANN models generated using three different training function algorithms (BR, LM and SCG) have been compared with each other and the simple regression curves using the $\chi^{2}$ method. The BR algorithm was able to generalise the dataset better than LM and SCG algorithms.