Abstract
We prove existence of infinitely many solutions \(u \in H^1_r({\mathbb {R}}^N)\) for the nonlinear Choquard equation
where \(N\ge 3\), \(\alpha \in (0,N)\), \(I_\alpha (x) := \frac{{\varGamma }(\frac{N-\alpha }{2})}{{\varGamma }(\frac{\alpha }{2}) \pi ^{N/2} 2^\alpha } \frac{1}{|x|^{N- \alpha }}\), \(x \in {\mathbb {R}}^N \setminus \{0\}\) is the Riesz potential, and F is an almost optimal subcritical nonlinearity, assumed odd or even. We analyze the two cases: \(\mu \) is a fixed positive constant or \(\mu \) is unknown and the \(L^2\)-norm of the solution is prescribed, i.e. \(\int _{{\mathbb {R}}^N} |u|^2 =m>0\). Since the presence of the nonlocality prevents to apply the classical approach, introduced by Berestycki and Lions (Arch Ration Mech Anal 82(4):347–375, 1983), we implement a new construction of multidimensional odd paths, where some estimates for the Riesz potential play an essential role, and we find a nonlocal counterpart of their multiplicity results. In particular we extend the existence results due to Moroz and Van Schaftingen (Trans Am Math Soc 367(9):6557–6579, 2015).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Given a nonlinearity \(F \in C^1({\mathbb {R}},{\mathbb {R}})\) and set \(f:=F'\), we are interested to seek for multiple solutions \(u \in H^1_r({\mathbb {R}}^N)\) of the nonlocal equation
where \(N\ge 3\), \(\alpha \in (0,N)\) and \(I_\alpha :\, {\mathbb {R}}^N\setminus \{ 0\}\rightarrow {\mathbb {R}}\) is the Riesz potential defined by
here \(H^1_r({\mathbb {R}}^N)\) denotes the space of radially symmetric Sobolev functions.
We aim to analyze the two cases: \(\mu \) is a fixed positive constant or \(\mu \) is unknown and the mass of the solution, described by its \(L^2\)-norm, is prescribed.
In literature the semilinear Eq. (1.1) with nonlocal source has several physical motivations and it is usually called nonlinear Choquard equation.
In 1954 the Eq. (1.1) with \(N=3\), \(\alpha =2\) and \(F(s)={1\over 2}|s|^2\), that is
was elaborated by Pekar in [40] to describe the quantum theory of a polaron at rest. Successively, in 1976 it was arisen in the work [28] suggested by Choquard on the modeling of an electron trapped in its own hole, in a certain approximation to Hartree-Fock theory of one-component plasma (see also [16, 17, 49]).
In 1996 the Eq. (1.2) was derived by Penrose in his discussion on the self-gravitational collapse of a quantum mechanical wave-function [36, 42,43,44] (see also [51, 52]) and in that context it is referred as Schrödinger-Newton system.
Finally we notice that if u is a solution of (1.2), then the wave function
is a solitary wave of the time-dependent Hartree equation [20]
thus (1.2) represents the stationary nonlinear Hartree equation.
In literature the study of standing waves of (1.3) has been pursed in two main directions, which opened two different challenging research fields.
A first topic regards the search for solutions of (1.2) with a prescribed frequency \(\mu \) and free mass, the so-called unconstrained problem. The second line of investigation of the problem (1.3) consists of prescribing the mass \(m >0\) of u, thus conserved by \(\psi \) in time
and letting the frequency \(\mu \) to be free. Such problem is usually said constrained.
For the unconstrained problem, the first investigations for existence and symmetry of the solutions to (1.2) go back to the works of Lieb [29], Lions [32] and Menzala [34] and also to [7, 36, 49] by means of ordinary differential equations techniques. We mention also the recent papers by Lenzmann [26] and by Winter and Wei [54] about the nondegeneracy of the unique radial solution of (1.2).
Recently Moroz and Van Schaftingen considered the special model
and they proved in [37, Theorem 1] that (1.5) has solutions if and only if
(see also [3, 33, 39]). Moreover in [37] they showed that all positive groundstates of (1.5) are radially symmetric and monotone decreasing about some point and derived the decay asymptotics at infinity of such groundstates (see [8] for \(p \ge 2\)). Furthermore, in [18, 19, 47] the authors study, for some values of p and \(\alpha \), least energy nodal solutions, odd with respect to a hyperplane; see also [8, 14, 53, 55, 56] for other results on sign-changing solutions with various symmetries and saddle type solutions.
Recently in [38] Moroz and Van Schaftingen considered the problem (1.1) when F is a Berestycki-Lions type function under the following general assumptions:
-
(F1)
\(F \in C^1({\mathbb {R}}, {\mathbb {R}})\);
-
(F2)
there exists \(C >0\) such that for every \(s \in {\mathbb {R}}\),
$$\begin{aligned} |s f(s)| \le C \big (|s|^{\frac{N + \alpha }{N}} + |s|^{\frac{N + \alpha }{N-2}}\big ); \end{aligned}$$ -
(F3)
$$\begin{aligned}\lim _{s \rightarrow 0} \frac{F(s)}{|s|^{\frac{N+ \alpha }{N}}} =0, \quad \lim _{ s \rightarrow + \infty } \frac{F(s)}{|s|^{\frac{N+ \alpha }{N-2}}} =0; \end{aligned}$$
-
(F4)
 , that is, there exists \(s_0 \in {\mathbb {R}}\), \(s_0 \ne 0\) such that \(F(s_0) \ne 0\).
, that is, there exists \(s_0 \in {\mathbb {R}}\), \(s_0 \ne 0\) such that \(F(s_0) \ne 0\).
In [38, Theorem 1], they proved the existence of a ground state solution \(u \in H^1({\mathbb {R}}^N)\) of (1.1) and in [38, Theorem 4] they showed that, if F satisfies (F1), (F2) and, in addition, f is odd and has constant sign on \((0, \infty )\), then every ground state of (1.1) has constant sign and it is radially symmetric with respect to some point in \({\mathbb {R}}^N\).
To our knowledge it is still an open problem the existence of infinitely many radially symmetric solutions for the nonlinear Choquard Eq. (1.1) under the optimal assumptions (F1)–(F4) and symmetric conditions on the nonlocal source term \((I_\alpha *F(u))f(u)\). We note that this term is odd if F is even or odd. This issue requires the implementation of new ideas since the approach due to Berestycki and Lions [5], dealing with scalar field equations with odd local nonlinearities, can not be directly adapted in presence of a nonlocal source, both if F is even or odd.
Concerning the constrained problem, we remark that it has a significant relevance in physics, not only for the quantum probability normalization, but also because the mass may also have specific meanings, such as the power supply in nonlinear optics, or the total number of atoms in Bose-Einstein condensation. Moreover, the investigation of constrained problems can give a better insight of the dynamical properties, as the orbital stability of solutions of (1.3). In a local framework the seminal contribution to the study of the constrained problem is due to Stuart [48] and Cazenave and Lions [6].
The existence of multiple radial standing wave solutions to (1.3) with prescribed \(L^2\)-norm has been faced by Lions in [31] and for the nonlinear Choquard Eq. (1.5) it has been obtained by Ye [57] (see also [11] for the planar logarithmic Choquard equation). We remark that all these multiplicity results deal with odd power nonlinearities f (see also [27] for odd powers-sum type functions). More recently, the first and the third author [12] obtained existence of a solution to
assuming that F satisfies (F1), (F4) and it is \(L^2\)-subcritical, namely
-
(CF2)
there exists \(C >0\) such that for every \(s \in {\mathbb {R}}\),
$$\begin{aligned} |s f(s)| \le C \big (|s|^{\frac{N + \alpha }{N}} + |s|^{\frac{N + \alpha +2 }{N}}\big ); \end{aligned}$$ -
(CF3)
$$\begin{aligned}\lim _{s \rightarrow 0} \frac{F(s)}{|s|^{\frac{N+ \alpha }{N}}} =0, \quad \lim _{ s \rightarrow + \infty } \frac{F(s)}{|s|^{\frac{N+ \alpha +2}{N}}} =0. \end{aligned}$$
The existence result in [12] relies on a new approach, based on a Lagrangian formulation of the problem.
As regards the problem of multiplicity, recently Bartsch et al. [2] obtained the existence of infinitely many solutions of (1.7), assuming that f is an odd function which satisfies monotonicity and Ambrosetti–Rabinowitz conditions [1]. We highlight that the restriction on odd functions is not just a matter of symmetry of the functional, but it is related also to some sign restriction on the function f. The authors in [2] rely on mountain pass and concentration-compactness arguments, together with the use of a stretched functional, i.e. a functional in an augmented space which takes into consideration scaling properties and the Pohozaev identity.
It remains open the challenging problem of the existence of infinitely many solutions for the constrained nonlinear Choquard Eq. (1.7) under optimal assumptions on the nonlinearity f, when monotonicity and Ambrosetti-Rabinowitz type conditions do not hold or f is not odd.
In the present paper we will give an affirmative answer to both the unconstrained and constrained problems when F satisfies the general Berestycki–Lions type assumptions (F1)–(F4) and (F1)–(CF2)–(CF3)–(F4) respectively, together with the symmetric condition
-
(F5)
F is odd or even.
We begin to notice that despite [12], where existence is investigated, to gain multiplicity the symmetry of the function F plays a crucial role. In particular, we assume F to be odd or even, which guarantees the evenness of the energy functional associated to (1.1). We emphasize that the possibility to assume both the symmetries on F is a particular feature of the nonlocal source. Indeed, in the source-local case [5, 9, 22], the nonlinear term is usually assumed odd in order to get the symmetry of the functional. We mention the recent paper [15] where the existence of a single nonradial solution to (1.1) is obtained under the condition (F5).
We start our analysis by the constrained case, which appears, as usual, more delicate. By virtue of [41], radially symmetric solutions to (1.7) can be characterized as critical points of the \(C^1\)-functional \(\mathcal {L}: H^1_r({\mathbb {R}}^N) \rightarrow {\mathbb {R}}\)
constrained on the sphere
A possible approach to problem (1.7) is to minimize \(\mathcal {L}\) on the sphere \(\mathcal {S}_m\), whenever the functional is here bounded. Nevertheless, in the spirit of [12], for the general class of nonlinearities related to [4, 25, 38], considered in this paper, we introduce a Lagrangian formulation of the nonlocal problem (1.7) and we extend a new approach introduced by Hirata and the third author [22] for the local case. One advantage of this method is that it can be suitably adapted to derive multiplicity results of normalized solutions in several different frameworks (see [9] for a fractional scalar field equation).
Namely, writing \({\mathbb {R}}_+:=(0, +\infty )\), a solution \((\mu ,u)\in {\mathbb {R}}_+ \times H^1_r({\mathbb {R}}^N)\) of (1.7) corresponds to a critical point of the functional \(\mathcal {I}^m: {\mathbb {R}}_+ \times H^1_r({\mathbb {R}}^N)\rightarrow {\mathbb {R}}\) defined by
We seek for critical points \((\mu ,u) \in {\mathbb {R}}_+ \times H^1_r({\mathbb {R}}^N)\) of \(\mathcal {I}^m\), namely weak solutions of \(\partial _u \mathcal {I}^m(\mu , u)=0\) and \(\partial _{\mu } \mathcal {I}^m(\mu , u)=0\).
Inspired by the Pohozaev’s identity, we introduce the Pohozaev’s functional \(\mathcal {P}:{\mathbb {R}}_+ \times H^1_r({\mathbb {R}}^N) \rightarrow {\mathbb {R}}\) by setting
and the Pohozaev level set
We note that \(\{(\mu ,0)|\, \mu \in {\mathbb {R}}_+\}\subset { int}\,{\varOmega }\) and thus

where the interior and the boundary are taken with respect to the topology of \({\mathbb {R}}_+ \times H^1_r({\mathbb {R}}^N)\). Therefore \((\mu , u) \in \partial {\varOmega }\) if and only if  satisfies the Pohozaev’s identity \(\mathcal {P}(\mu , u)=0\). We recognize a mountain pass structure [1] for the functional \(\mathcal {I}^m\) in \({\mathbb {R}}_+\times H_r^1({\mathbb {R}}^N)\), where the mountain is given by \(\partial {\varOmega }\). We call \(\partial {\varOmega }\) a Pohozaev mountain for \(\mathcal {I}^m\). We emphasize that under assumptions (F1)-(F2), if \(u \in H^1_r({\mathbb {R}}^N)\) solves \(\partial _u \mathcal {I}^m(\mu , u)=0\) with \(\mu \in {\mathbb {R}}_+\) fixed, then \(\mathcal {P}(\mu , u)=0\).
satisfies the Pohozaev’s identity \(\mathcal {P}(\mu , u)=0\). We recognize a mountain pass structure [1] for the functional \(\mathcal {I}^m\) in \({\mathbb {R}}_+\times H_r^1({\mathbb {R}}^N)\), where the mountain is given by \(\partial {\varOmega }\). We call \(\partial {\varOmega }\) a Pohozaev mountain for \(\mathcal {I}^m\). We emphasize that under assumptions (F1)-(F2), if \(u \in H^1_r({\mathbb {R}}^N)\) solves \(\partial _u \mathcal {I}^m(\mu , u)=0\) with \(\mu \in {\mathbb {R}}_+\) fixed, then \(\mathcal {P}(\mu , u)=0\).
Using a variant of the Palais-Smale condition [22, 23], which takes into account the Pohozaev’s identity, we will prove a deformation theorem which enables us to apply minimax arguments in the product space \({\mathbb {R}}_+ \times H^1_r({\mathbb {R}}^N)\). We will prove the existence of multiple \(L^2\)-normalized solutions detecting minimax structures in such product space.
We state our main results.
Theorem 1
Suppose \(N\ge 3\), \(\alpha \in (0, N)\) and (F1)-(CF2)-(CF3)-(F4)-(F5).
-
(i)
For any \(k \in {\mathbb {N}}\) there exists \(m_k \ge 0\) such that for every \(m > m_k\), the problem (1.7) has at least k pairs of nontrivial, distinct, radially symmetric solutions.
-
(ii)
Assume in addition an \(L^2\)-subcritical growth also at zero, i.e.
-
(CF4)
$$\begin{aligned} \lim _{s \rightarrow 0} \frac{|F(s)|}{|s|^{\frac{N+ \alpha +2}{N}}} = + \infty ; \end{aligned}$$
additionally, if F is odd, assume that \(|F(s)|\) is non-decreasing in \([0,\delta _0]\) for some \(\delta _0>0\).
Then \(m_k=0\) for each \(k \in {\mathbb {N}}\), that is for any \(m >0\) the problem (1.7) has countably many pairs of solutions \((\mu _n, u_n)_{n \in {\mathbb {N}}}\) satisfying \({\mathcal {L}}(u_n) <0\), \(n \in {\mathbb {N}}\). Moreover we have
$$\begin{aligned} {\mathcal {L}}(u_n) \rightarrow 0 \quad \hbox {as } n \rightarrow + \infty . \end{aligned}$$ -
(CF4)
We point out that a key point of our argument is the construction of multidimensional odd paths, which appears delicate in the case of nonlocal nonlinearities, especially when f is even. Differently from [9, 22], the classical argument given by [5] cannot be applied directly in the context of nonlinear Choquard equations because of the presence of a nonlocal source, and we need to implement a new approach to gain the existence of an admissible odd path. To this aim we proceed by finding suitable annuli: using characteristic functions corresponding to the annuli, we construct our multidimensional odd paths. Here interactions between these characteristic functions produced by the Riesz potential play a crucial role, in particular the index \(\alpha \) is related to the strength of interaction and the case \(\alpha \in (0,1]\) reveals to be more delicate. We use sharp estimates for the Riesz potential obtained by Thim [50] in an essential way.
We notice that Theorem 1 improves the multiplicity result found in [2] for \(L^2\)-subcritical odd nonlinearities f under stronger assumptions.
Remark 1
We point out that, for F odd, the monotonicity near the origin in (CF4) can be slightly weakened, with no change in the proof, with the following condition:
-
For some \(\delta _0>0\), F has a constant sign in \((0,\delta _0]\) and
$$\begin{aligned} \sup _{s \in (0, \delta _0],\, h\in [0,1]} \frac{F(s h)}{F(s)}=:M < +\infty . \end{aligned}$$(1.8)
In particular, when \(|F(s)|\) is non-decreasing, we have \(M=1\). As a nontrivial example one can consider \(\beta \in (\frac{N+\alpha }{N}, \frac{N+\alpha +2}{N})\) and F oscillating near zero between \(|s|^{\beta }\) and \(2|s|^{\beta }\), so that \(M\le 2\); for instance the odd extension of
If instead F oscillates (not strictly) between \(|s|^{\beta _1}\) and \(|s|^{\beta _2}\), with \(\frac{N+\alpha }{N}< \beta _1< \beta _2 < \frac{N+\alpha +2}{N}\), then \(M=+\infty \); thus for instance the odd extension of
is not included in (1.8).
Remark 2
We highlight that we assume a priori the positivity of the Lagrange multiplier \(\mu \). As a matter of fact, this condition seems to be quite natural: one can indeed prove that if u is a minimum of \(\mathcal {L}\) constrained on \(\mathcal {S}_m\), and its energy is negative (that is, \(\mathcal {L}(u)<0\)), then a posteriori the corresponding Lagrange multiplier \(\mu \) is strictly positive (see [12]). This is actually the case of our paper: see Remark 7. In addition, from a physical point of view, in the study of standing waves the multiplier \(\mu \) describes the frequency of the particle, and thus it is positive; moreover, this prescribed sign is characteristic also of chemical potentials in the description of ideal gases, see [30, 45].
As a further byproduct of the construction of multidimensional odd paths we gain the existence of infinitely many solutions for the unconstrained problem. More precisely, defined the \(C^1\)-functional \(\mathcal {J}_{\mu }: H^1_r({\mathbb {R}}^N) \rightarrow {\mathbb {R}}\) by setting
we will establish the following result.
Theorem 2
Suppose \(N\ge 3\), \(\alpha \in (0, N)\) and \(\mu >0\) fixed. Assume that (F1)–(F5) hold. Then there exist countably many radial solutions \((u_n)_{n \in {\mathbb {N}}}\) of the nonlinear Choquard Eq. (1.1). Moreover we have
Our multiplicity result is the counterpart of what done in [5] for the local case with odd nonlinearities and extend the existence result in [38], due to Moroz and Van Schaftingen.
Remark 3
Noticed that (F2)-(F3) are weaker than (CF2)-(CF3), we point out that in both cases we work in a subcritical setting: the exponent \(2^m_{\alpha }:=\frac{N+ \alpha +2}{N}\) in condition (CF2)-(CF3) appears as a mass (or \(L^2\)) critical exponent for the Choquard equations, and it is strictly smaller than the Hardy-Littlewood-Sobolev upper-critical exponent \(2^*_{\alpha }:= \frac{N+\alpha }{N-2}\) appearing in (F2)-(F3). In both cases, as a peculiar feature of nonlocal sources (see [38]), we need also a lower-critical exponent \(2^{\#}_{\alpha }:= \frac{N+\alpha }{N}\). Different qualitative phenomena are related to sub and super \(L^2\)-critical cases: for instance, the sub or super \(L^2\)-criticality of the exponent influences the boundedness of the functional \(\mathcal {J}\) on \(\mathcal {S}_m\), and also the lifespan and the stability of the solutions in the time-dependent Choquard equation (see [6]).
The paper is organized as follows. Section 2 is dedicated to recalls and notations. In Sect. 3 we derive a Palais–Smale–Pohozaev condition and introduce an augmented functional which will be used in Sect. 3.3 to gain a deformation lemma. In Sect. 4 we first give some insights on the minimax geometry of the unconstrained case, building a multidimensional odd path and studying the behavior of the symmetric mountain pass values according to variable values of \(\mu \). Afterwards, we detect a mountain pass structure, built on the Pohozaev’s mountain, for the constrained case. We study in addition suitable minimax values defined through the tool of the genus, and in Sect. 4.5 we prove the main Theorem 1. Section 4.6 is devoted for Proofs of Lemma 1 and 2, which give essential interaction estimates for non-local term. Finally in Sect. 5 we deal with the unconstrained case by proving Theorem 2.
2 Functional setting
In what follows we use the notation:
and set
moreover we briefly denote by q the lower-critical exponent \(2^{\#}_{\alpha }\) and by p the \(L^2\)-critical exponent \(2^m_{\alpha }\), i.e.
We recall the following generalized Hardy-Littlewood-Sobolev inequality [29].
Proposition 1
Let r, \(s \in (1,+\infty )\) such that \(\frac{1}{r} - \frac{1}{s} = \frac{\alpha }{N}\), then the map
is continuous. In particular, if r, \(t \in (1, +\infty )\) verify \(\frac{1}{r} + \frac{1}{t} = \frac{N+\alpha }{N}\), then there exists a constant \(C=C(N,\alpha ,r,t)>0\) such that
for all \(g\in L^r({\mathbb {R}}^N)\) and \(h\in L^t({\mathbb {R}}^N)\).
For technical reasons we write, from now on,
We consider the functional \(\mathcal {I}^m : {\mathbb {R}}\times H^1_r({\mathbb {R}}^N) \rightarrow {\mathbb {R}}\) defined by
where we set
Using Proposition 1 and (F1)–(F2), we notice that \(\mathcal {D}\) is continuous on \(L^2({\mathbb {R}}^N) \cap L^{2^*}({\mathbb {R}}^N)\), where \(2^*= \frac{2N}{N-2}\) is the Sobolev critical exponent, and thus continuous on \(H^1_r({\mathbb {R}}^N)\); notice that if we assume (CF2), then \(\mathcal {D}\) is continuous also on \(L^2({\mathbb {R}}^N) \cap L^{2 + \frac{4}{N+\alpha }}({\mathbb {R}}^N)\). Moreover, it is easy to see that \(\mathcal {I}^m \in C^1({\mathbb {R}}\times H^1_r({\mathbb {R}}^N), {\mathbb {R}})\).
To deal with the unconstrained problem, we further define the \(C^1\)-functional \(\mathcal {J}:{\mathbb {R}}\times H^1_r({\mathbb {R}}^N) \rightarrow {\mathbb {R}}\) by setting
It is immediate that, for any \((\lambda , u) \in {\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\),
For a fixed \(\lambda \in {\mathbb {R}}\), u is critical point of \(\mathcal {J}(\lambda , \cdot )\) if and only if u solves
in this paper by solution we will always mean weak solution. If (F1)–(F2) hold, by [38, Theorems 2 and 3] we have that each solution u of (2.3) belongs to \(W^{2,2}_{loc}({\mathbb {R}}^N)\) and it satisfies the Pohozaev’s identity
Inspired by this relation, we also introduce the Pohozaev’s functional \(\mathcal {P}:{\mathbb {R}}\times H^1_r({\mathbb {R}}^N) \rightarrow {\mathbb {R}}\) by setting
We consider the action of \({\mathbb {Z}}_2\) on \({\mathbb {R}}^n\), \(n \in {\mathbb {N}}^*\), and on \({\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\), given by
We notice that, under the assumption (F5), \(\mathcal {I}^m\), \(\mathcal {J}\) and \(\mathcal {P}\) are invariant under this action, i.e. they are even in u:
In addition, we observe by the Principle of Symmetric Criticality of Palais [41] that every critical point of \(\mathcal {I}^m\) (resp. \(\mathcal {J}\)) restricted to \({\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\) is actually a critical point of \(\mathcal {I}^m\) (resp. \(\mathcal {J}\)) on the whole \({\mathbb {R}}\times H^1({\mathbb {R}}^N)\). This observation justifies our restriction onto the radial setting. Finally, we denote by \(P_2: {\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\rightarrow H^1_r({\mathbb {R}}^N)\) the projection on the second component.
Remark 4
We observe that, by substituting F with \(-F\), there is no loss of generality in assuming
in (F4) and
in (CF4), together with F non-decreasing when it is odd. Thus, for the remaining of the paper we assume this positivity on the right-hand side of zero.
3 Palais-Smale-Pohozaev condition and deformation theory
3.1 Palais-Smale-Pohozaev condition
For every \(b \in {\mathbb {R}}\) we set
As already observed, under (F1)-(F2) we have that \(\mathcal {P}(\lambda , u)=0\) for each \((\lambda , u) \in K_b^m\). We notice also that, assuming (F5), \(K_b^m\) is invariant under the following \({\mathbb {Z}}_2\)-action, that is
Under our assumptions on F, it seems difficult to verify the standard Palais-Smale condition for the functional \(\mathcal {I}^m\). Therefore we cannot recognize that \(K_b^m\) is compact.
Inspired by [13, 22, 23], we introduce the Palais-Smale-Pohozaev condition, which is a weaker compactness condition than the standard Palais-Smale one. Such condition takes into account the scaling properties of \(\mathcal {I}^m\) through the Pohozaev’s functional \(\mathcal {P}\). Using this new condition we will show that \(K_b^m\) is compact when \(b<0\).
Definition 1
For \(b \in {\mathbb {R}}\), we say that \((\lambda _n, u_n) \subset {\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\) is a Palais-Smale-Pohozaev sequence for \(\mathcal {I}^m\) at level b (shortly a \((PSP)_b\) sequence) if
We say that \(\mathcal {I}^m\) satisfies the Palais-Smale-Pohozaev condition at level b (shortly the \((PSP)_b\) condition) if every \((PSP)_b\) sequence has a strongly convergent subsequence in \({\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\).
We show now the following result.
Proposition 2
Assume (F1)-(CF2)-(CF3) and let \(b <0\). Then \(\mathcal {I}^m\) satisfies the \((PSP)_b\) condition.
Proof
Let \(b <0\) and let \((\lambda _n, u_n) \subset {\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\) be a \((PSP)_b\) sequence, i.e. satisfying (3.1)–(3.4). First we note that by (3.2) we obtain
Step 1: \(\lambda _n\) is bounded from below and \(\Vert u_n \Vert _2^2 \rightarrow m\) as \(n \rightarrow + \infty \).
We have by (3.4), (3.1) and (3.5)
Here we used (3.5). From the above identity, we derive boundedness of \(\lambda _n\) from below, since \(b <0\). This result joined to (3.5) finally gives \(\Vert u_n\Vert _2^2\rightarrow m\).
Step 2: \(\lambda _n\) and \(\Vert \nabla u_n \Vert _2^2\) are bounded.
Since, by (3.3), \(\varepsilon _n := \Vert \partial _u \mathcal {I}^m(\lambda _n, u_n)\Vert _{(H_r^1({\mathbb {R}}^N))^*}\rightarrow 0\), we have
We observe that by \(\mathrm{(CF3)}\) for \(\delta >0\) fixed, there exists \(C_\delta >0\) such that
where we recall \(p=\frac{N+ \alpha +2}{N}\) and \(q=\frac{N+\alpha }{N}\). Thus
Therefore by \(\mathrm{(CF2)}\), Proposition 1 and Young’s inequality we have
and thus, by the Gagliardo-Nirenberg inequality,
Since by Step 1 \(\Vert u_n\Vert _2^2=m+o(1)\), we have
For \(\delta \) small enough, we have the boundedness of \(e^{\lambda _n}\) and \(\Vert \nabla u_n\Vert _2\). Hence \(\lambda _n\) can not go to \(+\infty \) and thus by Step 1 we infer that \(\lambda _n\) is bounded.
Step 3: \(\lambda _n\) and \( u_n \) strongly converge.
By Steps 1-2, the sequence \((\lambda _n, u_n)\) is bounded in \({\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\) and thus after extracting a subsequence, denoted in the same way, we may assume that \(\lambda _n \rightarrow \lambda _0\) and \(u_n \rightharpoonup u_0\) weakly in \(H^1_r({\mathbb {R}}^N)\) for some \((\lambda _0, u_0) \in {\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\). Taking into account the assumptions (F1)–(F3) and the compact embedding of \(H^1_r({\mathbb {R}}^N)\) in \(L^r({\mathbb {R}}^N)\) for \(r \in (2, 2^*)\), we have
and
Thus we derive that \(\langle \partial _u \mathcal {I}^m(\lambda _n, u_n), u_n \rangle \rightarrow 0\) and \(\langle \partial _u \mathcal {I}^m(\lambda _n, u_n), u_0 \rangle \rightarrow 0\), and hence
which implies \(u_n \rightarrow u_0\) strongly in \(H^1_r({\mathbb {R}}^N)\). \(\square \)
As a straightforward consequence we obtain the following result.
Corollary 1
Assume (F1)-(CF2)-(CF3) and let \(b <0\). Then \(K_b^m \cap ({\mathbb {R}}\times \{0\}) = \emptyset \) and \(K_b^m\) is compact.
Remark 5
We emphasize that the \((PSP)_b\) condition does not hold at level \(b=0\). Indeed we can consider a \((PSP)_0\) unbounded sequence \((\lambda _n, 0)\) with \(\lambda _n \rightarrow - \infty \).
3.2 An augmented functional
Following [21, 22, 24] we define
and introduce the augmented functional \(\mathcal {H}^m: M\rightarrow {\mathbb {R}}\)
By the scaling properties of \(\mathcal {I}^m\) we can recognize that
for all \((\theta , \lambda ,u ) \in M\), and thus
We point out that, considered the action of \({\mathbb {Z}}_2\) on M
and assumed (F5), it results that \(\mathcal {H}^m\) is \({\mathbb {Z}}_2\)-invariant, i.e. it is even in u:
Introducing a metric on M by
for any \((\alpha , \nu , h) \in T_{(\theta ,\lambda ,u)} M \equiv {\mathbb {R}}\times {\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\), we regard M as a Hilbert manifold. We also denote the dual norm on \(T^*_{(\theta ,\lambda ,u)}M\) by \(\Vert \cdot \Vert _{(\theta ,\lambda , u), *}\), and observe that both \(\Vert \cdot \Vert _{(\theta , \lambda , u)}\) and \(\Vert \cdot \Vert _{(\theta , \lambda , u),*}\) actually depend only on \(\theta \).
Denote now
the gradient with respect to all the variables; a direct computation shows that
for any \((\theta , \lambda , u)\in M\) and \((\alpha , \nu , h) \in T_{(\theta , \lambda , u)}M\), and thus we obtain
We furthermore define
the set of critical points of \(\mathcal {H}^m\) at level b, and we deduce
Finally we introduce the standard distance between two points as the infimum of the lengths of the curves connecting the two points, namely
As a consequence of Proposition 2 we obtain the following.
Proposition 3
Assume (F1)–(CF2)–(CF3) and let \(b <0\). Then \(\mathcal {H}^m\) satisfies the following Palais–Smale-type condition \((\widetilde{PSP})_b\). That is, for each sequence \((\theta _n, \lambda _n, u_n)\subset M\) such that
as \(n \rightarrow +\infty \), we have, up to a subsequence,
Proof
See [9, Proposition 4.6]. \(\square \)
We notice that the \((\widetilde{PSP})_b\) condition is different from the standard Palais-Smale condition and it ensures the compactness after a suitable scaling. We also highlight that, if \({{\tilde{K}}}_b^m\ne \emptyset \), then \({{\tilde{K}}}_b^m\) is not compact (see (3.8)).
3.3 Deformation theory
We write, for \(b \in {\mathbb {R}}\)
We state the following result.
Proposition 4
Assume (F1)-(CF2)-(CF3). Let \(b<0\), and let \(\mathcal {O}\) be a neighborhood of \(K_b^m\) with respect to the standard distance of \({\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\). Let \(\bar{\varepsilon }>0\), then there exist \(\varepsilon \in (0,\bar{\varepsilon })\) and \(\eta : [0,1]\times ({\mathbb {R}}\times H^1_r({\mathbb {R}}^N))\rightarrow {\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\) continuous such that
-
1.
\(\eta (0, \cdot ,\cdot )=id_{{\mathbb {R}}\times H^1_r({\mathbb {R}}^N)}\);
-
2.
\(\eta \) fixes \([\mathcal {I}^m\le b-\bar{\varepsilon }]\), that is, \(\eta (t, \cdot ,\cdot )=id_{[\mathcal {I}^m\le b-\bar{\varepsilon }]}\) for all \(t \in [0,1]\);
-
3.
\(\mathcal {I}^m\) is non-increasing along \(\eta \), and in particular \(\mathcal {I}^m(\eta (t,\cdot , \cdot ))\le \mathcal {I}^m(\cdot , \cdot )\) for all \(t \in [0,1]\);
-
4.
if \(K_b^m= \emptyset \), then \(\eta (1, [\mathcal {I}^m\le b+\varepsilon ])\subset [\mathcal {I}^m\le b-\varepsilon ]\);
-
5.
if \(K_b^m\ne \emptyset \), then
$$\begin{aligned} \eta (1,[\mathcal {I}^m\le b+\varepsilon ]\setminus \mathcal {O}) \subset [\mathcal {I}^m\le b-\varepsilon ] \end{aligned}$$and
$$\begin{aligned} \eta (1, [\mathcal {I}^m\le b+\varepsilon ]) \subset [\mathcal {I}^m\le b-\varepsilon ]\cup \mathcal {O}; \end{aligned}$$ -
6.
if (F5) holds, then \(\eta (t, \cdot ,\cdot )\) is \({\mathbb {Z}}_2\)-equivariant, i.e. for \(\eta =(\eta _1, \eta _2)\) we have \(\eta _1\) even and \(\eta _2\) odd in u.
To prove this, we work first on the functional \(\mathcal {H}\), for which we obtained a \((\widetilde{PSP})\) condition.
Proposition 5
Assume (F1)-(CF2)-(CF3). Let \(b<0\), and let \(\tilde{\mathcal {O}}\) be a neighborhood of \({\tilde{K}}_b^m\) with respect to \({\mathrm{dist}}_M\). Let \(\bar{\varepsilon }>0\), then there exist \(\varepsilon \in (0,\bar{\varepsilon })\) and \(\tilde{\eta }: [0,1]\times M\rightarrow M\) continuous such that
-
1.
\(\tilde{\eta }(0, \cdot ,\cdot ,\cdot )=id_M\);
-
2.
\(\tilde{\eta }\) fixes \([\mathcal {H}^m \le b-\bar{\varepsilon }]_M\), that is \(\tilde{\eta }(t, \cdot ,\cdot ,\cdot )=id_{[\mathcal {H}^m \le b-\bar{\varepsilon }]_M}\) for all \(t\in [0,1]\);
-
3.
\(\mathcal {H}^m\) is non-increasing along \(\tilde{\eta }\), and in particular \(\mathcal {H}^m(\tilde{\eta }(t,\cdot ,\cdot , \cdot ))\le \mathcal {H}^m(\cdot , \cdot , \cdot )\) for all \(t\in [0,1]\);
-
4.
if \({\tilde{K}}_b^m= \emptyset \), then \(\tilde{\eta }(1, [\mathcal {H}^m \le b+\varepsilon ]_M)\subset [\mathcal {H}^m \le b-\varepsilon ]_M\);
-
5.
if \({\tilde{K}}_b^m \ne \emptyset \), then
$$\begin{aligned} \tilde{\eta }(1,[\mathcal {H}^m \le b+\varepsilon ]_M\setminus \tilde{\mathcal {O}}) \subset [\mathcal {H}^m \le b-\varepsilon ]_M \end{aligned}$$and
$$\begin{aligned} \tilde{\eta }(1,[\mathcal {H}^m \le b+\varepsilon ]_M) \subset [\mathcal {H}^m \le b-\varepsilon ]_M\cup \tilde{\mathcal {O}}; \end{aligned}$$ -
6.
if (F5) holds, then \(\tilde{\eta }(t, \cdot ,\cdot )\) is \({\mathbb {Z}}_2\)-equivariant, i.e. for \(\tilde{\eta }=(\tilde{\eta }_0,\tilde{\eta }_1,\tilde{\eta }_2)\) we have \(\tilde{\eta }_0\), \(\tilde{\eta }_1\) even and \(\tilde{\eta }_2\) odd in u.
Proof of Proposition 5
Under \((\widetilde{PSP})_b\), we observe that for any \(b<0\) there exists \(\varepsilon \), \(\delta \), \(\nu >0\) such that
for \((\theta ,\lambda ,u)\in M\) satisfying \(\mathcal {H}^m(\theta ,\lambda ,u)\in [b-\varepsilon ,b+\varepsilon ]\) and \({\mathrm{dist}}_M((\theta ,\lambda ,u), {\widetilde{K}}_b^m) \ge \delta \). We can prove Proposition 5 in a standard way. See e.g. [9, Theorem 7.2]. \(\square \)
Proof of Proposition 4
We introduce the following notation:
which are a kind of rescaling projection and immersion. Observe that
By means of these operators we are able to prove that neighborhoods of \({\tilde{K}}_b^m\) are brought to neighborhoods of \(K_b^m\). Moreover, for a deformation \(\tilde{\eta }\) obtained in Proposition 5, define
It is now a straightforward computation showing that \(\eta \) satisfies the requests of Proposition 4; we refer to [9, 13, 22, 23] for details. \(\square \)
We notice that the found deformation \(\eta \) does not generally satisfy other classical properties of deformations, such as semigroup property; see [22] for some comments.
4 Minimax methods
4.1 Construction of multidimensional odd paths
In this section we study geometry of
for a fixed \(\lambda \in {\mathbb {R}}\). We introduce a sequence of minimax values \(a_n(\lambda )\), \(n=1,2,\cdots \). These values play important roles to find multiple solutions for the constrained problem, i.e. for a Proof of Theorem 1, and those for the unconstrained problem, i.e. for a Proof of Theorem 2.
For \(n\in {\mathbb {N}}^*\) and \(\lambda \in {\mathbb {R}}\) we introduce the set of paths
and the minimax values
For \(n\ge 2\) the nonemptiness of \({\varGamma }_n(\lambda )\) has to be checked; for \(n=1\) we refer to [38, claim 1 of Proposition 2.1]. Classically, in the local framework this fact was proved in [5] by constructing inductively piecewise affine paths. This construction does not fit the nonlocality interaction given by the Choquard term, thus we need another approach.
Proposition 6
Assume (F1)–(F4). Let \(n \in {\mathbb {N}}^*\) and \(\lambda \in {\mathbb {R}}\). Then \({\varGamma }_n(\lambda )\ne \emptyset \), thus \(a_n(\lambda )\) is well defined. Moreover, \(a_n(\lambda )>0\) and it is increasing with respect to \(\lambda \) and n.
To deal with this proof we need a deep understanding of the Riesz potential on radial functions, and we rely on a result by [50, Theorem 1]. See also [35, Lemma 6.3] and references therein.
Theorem 3
([50]). Let \(u\in H_r^1({\mathbb {R}}^N)\) be radial and \(\alpha \in (0, N)\). Then \(I_{\alpha }*u\) is radial and
where \(F_\alpha \) is positive and it satisfies for some constants \(C_{N,0}\), \(C_{N,\infty }\), \(C_{N,\alpha }>0\),
and
with
For a Proof of Proposition 6, we prepare some notation and some estimates. We set
for any \(R\gg h >0\). We have the following key estimates.
Lemma 1
It results as \(h\rightarrow 0\)
Here we write \(f\sim g\) if there exist constants \(C_1\), \(C_2>0\) independent of h such that
We postpone a Proof of Lemma 1 and give it in Sect. 4.6.
We show how to use it to build a continuous odd map in \(L^2({\mathbb {R}}^N) \cap L^{2^*}({\mathbb {R}}^N)\); by a regularization argument, we will obtain a map in \({\varGamma }_n(\lambda )\).
By scaling, we have
For \(R\ge 2\), we set
Then we have
where \(C_{01}\), \(C_{02}>0\) are independent of \(R\ge 2\). We check (4.4) only for \(\alpha =1\). We have
Next we compute the interaction effect between \(\chi (R^i,h_{R^i};\cdot )\) and \(\chi (R^j,h_{R^j};\cdot )\) with \(i, j \in {\mathbb {N}}\), \(i\ne j\) and \(R\gg 1\).
Lemma 2
For \(i<j\) we have
We postpone the Proof of Lemma 2 and we will give it in Sect. 4.6.
Proof of Proposition 6
For \(s_0>0\) with \(F(s_0)>0\), which is given in (F4) or (CF4), we will construct a path \(\gamma \in {\varGamma }_n(\lambda )\) such that
Step 1: Construction of an odd path in \(L^r\).
For \(n\ge 2\) (for \(n=1\) the construction is simpler), we consider the polyhedron
and we recall that \({\varSigma }\) is homeomorphic to \(\partial D_n\). For a large \(R\gg 1\), which we will choose later, we define
where \(r \in [1, +\infty ]\). Here we regard \(\chi (R^i,0;x)\equiv 0\). For \(s_0>0\) with \(F(s_0)>0\), which is given in (F4) or (CF4), we have
We note that
-
(i)
For any \(t=(t_1,\cdots ,t_n)\in {\varSigma }\), there exists at least one \(t_k\) such that \(|t_k|=1\).
-
(ii)
By Lemma 1,
$$\begin{aligned} F(\pm s_0)^2 \int \!\!\!\!\int _{{\mathbb {R}}^N\times {\mathbb {R}}^N}I_\alpha (x-y) \chi (R^k,h_{R^k};x)\chi (R^k,h_{R^k};y) \,dxdy \ge C_0. \end{aligned}$$ -
(iii)
By (i) and (ii),
$$\begin{aligned} \sum _{i=1}^n F(\pm s_0)^2 \int \!\!\!\!\int _{{\mathbb {R}}^N\times {\mathbb {R}}^N}I_\alpha (x-y) \chi (R^i,h_{R^i};x)\chi (R^i,h_{R^i};y) \,dxdy \ge C_0. \end{aligned}$$ -
(iv)
If \(i\ne j\), by Lemma 2,
$$\begin{aligned} \int \!\!\!\!\int _{{\mathbb {R}}^N\times {\mathbb {R}}^N}I_\alpha (x-y)\chi (R^i,h_{R^i};x) \chi (R^j,h_{R^j};x)\,dxdy \rightarrow 0 \quad \hbox {as}\ R\rightarrow \infty . \end{aligned}$$
By (i)–(iv), we have for sufficiently large \(R\gg 1\),
In what follows we fix \(R\gg 1\) so that (4.5) holds.
Step 2: Construction of an odd path in \(H_r^1\).
For \(0\le h\ll R\) and \(\varepsilon >0\), we set
Here we regard
We note that
We set
We note that for \(\varepsilon >0\), \(\gamma _{\varepsilon ,R}(t):{\varSigma }\rightarrow H_r^1({\mathbb {R}}^N)\) is continuous and by (4.5) and the continuity of \(\mathcal {D}\) on \(L^2({\mathbb {R}}^N) \cap L^{2^*}({\mathbb {R}}^N)\), we have for \(\varepsilon >0\) small
Since
we have for large \(\theta \gg 1\)
Regarding \(D_n=\{ st \mid s\in [0,1], \, t\in {\varSigma }\}\) and extending \(s_0\gamma _{\varepsilon ,{R}}(t)(\cdot /\theta )\) to \(D_n\) by
finally we obtain a path \({\widetilde{\gamma }}\in {\varGamma }_n(\lambda )\).
Step 3: Conclusion. What remains to prove is the monotonicity and positivity of \(a_n(\lambda )\). Since \(D_n\subset D_{n+1}\), we may regard for \(\gamma \in {\varGamma }_{n+1}(\lambda )\),
Thus we have \(a_n(\lambda )\le a_{n+1}(\lambda )\). Since \(\mathcal {J}(\lambda ,u)\) is monotone in \(\lambda \), we also have the monotonicity with respect to \(\lambda \).
The positivity of \(a_1(\lambda )\) is essentially obtained in [38] (see also [12]). Thus
\(\square \)
Remark 6
We notice that the construction of an odd map in \(L^r\) gets much easier when F is an even function. Indeed there is no negative contribution given by the mixed interactions. We give only an outline of the proof, highlighting that in this case we do not need to use the fine Theorem 3 given by [50].
Define for every \(i=1,\dots n\) and \(s\in [0,1]\) the annuli
For every \(t=(t_1, \dots , t_n) \in {\varSigma }\) we have that \(A_1(t_1), \dots , A_n(t_n)\) are disjoint. Moreover, if \(t_i=0\), then \({\mathrm{meas}}(A_i(t_i))=0\). Thus we define a continuous, odd map by
Since F is even, we obtain
where C does not depend on the specific t. The regularization to a \(H^1_r\)-path can be done as in the general case (or by mollification), as well as the extension to \(D_n\).
We highlight that this construction can be adapted also to the local case, and thus it gives a simplified construction of a multidimensional path in the setting of Berestycki and Lions [5].
4.2 Asymptotic of symmetric mountain pass values
We end this section with some key estimates on the asymptotic behavior of \(a_n(\lambda )\) as \(\lambda \rightarrow \pm \infty \).
Proposition 7
Assume (F1)–(F4) and let \(n \in {\mathbb {N}}^*\).
-
(i)
If (CF3) holds, then \(\lim _{\lambda \rightarrow +\infty } \frac{a_n(\lambda )}{e^{\lambda }}=+\infty \).
-
(ii)
If (CF4) holds, then \(\lim _{\lambda \rightarrow -\infty } \frac{a_n(\lambda )}{e^{\lambda }}=0\).
Proof of (i) of Proposition 7
We write \(q={\frac{N+\alpha }{N}}\), \(p={\frac{N+\alpha +2}{N}}\) and \(\mu =e^{\lambda }\) (and consequently adapt the notations) for the sake of simplicity.
Since \(a_n(\mu )\ge a_1(\mu )\) for each \(n \in {\mathbb {N}}^*\), it is sufficient to show the claim for \(n=1\). By \(\mathrm{(CF3)}\), for any \(\delta >0\) there exists \(C_\delta >0\) such that
For \(v\in H^1_r({\mathbb {R}}^N)\), setting \(u_s:=s^{N/2}v(s \cdot )\), we have
where we write for \(\delta >0\) and \(A\ge 0\),
We also denote by \(b(\delta ,A)\) the MP value of \(\mathcal {J}_{\delta ,A}\). Taking into account the continuity and monotonicity property of \(b(\delta ,A)\) with respect of each variable \(\delta \) and A and observing that \(\mathcal {J}_{\delta ,A}\) satisfies the (PS) condition, we have
Thus, from (4.7) we have that
Setting \(s:=\sqrt{\mu }\), we obtain
and thus \( {\frac{a_1(\mu )}{\mu }} \ge b(\delta , C_\delta \mu ^{-1/2})\), which implies
Since \(\delta >0\) is arbitrary, we gain
\(\square \)
We deal now with the proof of (ii) of Proposition 7. We highlight that, when F is even, the proof can be simplified (see [12]).
We start noticing that, by (CF4) and Remark 4, for some \(\delta _0>0\)
which implies
-
(i)
when F is even, \(F(s)>0\) for all \(s\in [-\delta _0,\delta _0]\setminus \{ 0\}\);
-
(ii)
when F is odd, \(F(s)<0\) for all \(s\in [-\delta _0,0)\).
By (CF4), we also note that there exists \(L_s>0\) with \(L_s\rightarrow \infty \) as \(s\rightarrow 0^+\) such that
First we observe that the path \(\gamma _{R,\varepsilon }:\, {\varSigma }\rightarrow H_r^1({\mathbb {R}}^N)\), defined in (4.6), has the following property.
Lemma 3
There exists a constant \(A>0\) independent of \(s\in (0,\delta _0]\) such that
Here o(1) is a quantity which goes to 0 as \(\varepsilon \rightarrow 0\) uniformly in \(t\in {\varSigma }\) and \(s\in (0,\delta _0]\).
Proof
We prove Lemma 3 in 2 steps.
Step 1: For \(t\in {\varSigma }\), set
Then for sufficiently large \(R>0\), we have
This fact follows from (4.4) and Lemma 2. We fix \(R\gg 1\) so that (4.9) holds.
Step 2: \(\mathcal {D}(s\gamma _{R,\varepsilon }(t)) \ge {1\over 2}F(s)^2 A\) as \(\varepsilon \rightarrow 0\).
We note that for \(\varepsilon >0\) small
Thus we have
We consider cases \(i=j\) and \(i\ne j\) separately.
First we focus on the case \(i=j\). For both of even and odd F
where we used the positivity of F and the monotonicity of the integral. Next we consider the case \(i\ne j\) for even F. Since \(F(s)\ge 0\) for \(s\in [-\delta _0,\delta _0]\),
Finally we consider the case \(i\ne j\) for odd F. Since \(|F(s)|=F(|s|)\) for \(s\in [-\delta _0,\delta _0]\)
Setting \(C_i(t,\varepsilon ):=\big \{x \mid {\mathrm{dist}}(x,A(R^i,|t_i|h_{R^i}))\in (0,\varepsilon )\big \}\), we have

Thus for \(r\in {[1,\infty )}\) and \(s \in (0,\delta ]\)
Here we use the fact that \(\max _{h\in [0,1]} {F(hs)\over F(s)} \le 1\), which follows from the local monotonicity assumption in (CF4). We note that (4.14) implies, exploiting again the local monotonicity
Thus, it follows from (4.10)–(4.12) and (4.16) that
This concludes the proof. \(\square \)
Proof of (ii) of Proposition 7
For \(s_0\in (0,\delta _0]\) and \(\mu >0\), we consider a path
We have
Thus for \(\mu \) small
which implies \(s_0\gamma _{R,\varepsilon }(t)(\cdot /\mu ^{-\frac{1}{2}}) \in {\varGamma }_n(\lambda )\). Moreover by (4.8)
where
Thus we have
Since \(C_{s_0}\rightarrow 0\) as \(s_0\rightarrow 0\), we have (ii) of Proposition 7. \(\square \)
4.3 The Pohozaev mountain
We consider the Pohozaev level set
We notice that, under the assumption (F5), \({\varOmega }\) is symmetric with respect to the axis \(\{(\lambda ,0) \mid \lambda \in {\mathbb {R}}\}\), that is,
We start showing the following property.
Lemma 4
We have
Proof
Since \(\mathcal {D}(u)=o(\Vert u\Vert _{H^1}^2)\) as \(u \rightarrow 0\), the conclusion follows from the definition of \(\mathcal {P}(\lambda ,u)\). \(\square \)
By (4.17) we detect the Pohozaev’s mountain

We observe that \(\partial {\varOmega } \ne \emptyset \), for instance by [38, Theorems 1 and 3].
Proposition 8
Assume (F1)–(F4). We have the following properties.
-
(i)
\(\mathcal {J}(\lambda ,u)\ge 0\) for all \((\lambda ,u)\in {\varOmega }\).
-
(ii)
\(\mathcal {J}(\lambda ,u)\ge a_1(\lambda )>0\) for all \((\lambda ,u)\in \partial {\varOmega }\).
-
(iii)
Assume (CF3). For any \(m>0\), we set
$$\begin{aligned} E^m:= \inf _{(\lambda ,u)\in \partial {\varOmega }}\mathcal {I}^m(\lambda ,u), \quad \text { and } \quad B^m:=\inf _{\lambda \in {\mathbb {R}}} \left( a_1(\lambda ) -\frac{e^\lambda }{2}m \right) . \end{aligned}$$Then \(E^m \ge B^m >-\infty \). In particular \(B^m \in {\mathbb {R}}\) and
$$\begin{aligned} \mathcal {I}^m(\lambda ,u) \ge B^m \quad \hbox {for every}\ (\lambda ,u)\in \partial {\varOmega }. \end{aligned}$$
Proof
We notice that for all \((\lambda ,u)\in {\varOmega }\)
and thus (i) follows. Point (ii) follows from the fact that for each \(\lambda \) the mountain pass level \(a_1(\lambda )\) coincides with the ground state energy level (see [38, Sect. 4.2], and [10, Proposition 2] for details). Focus on (iii): the fact that \(E^m \ge B^m\) is a direct consequence of (ii), while the fact that \(B^m >-\infty \) comes from Proposition 7 (i). \(\square \)
From now on we assume (CF3) to give sense to the quantity \(B^m\). In view of Proposition 8 (iii), we set for \(m>0\) and \(n\in {\mathbb {N}}^*\)
and
we point out that asking \({\varTheta }=({\varTheta }_1, {\varTheta }_2) \in {\varGamma }^m_n\) to be \({\mathbb {Z}}_2\)-equivariant means that \({\varTheta }_1\) is even and \({\varTheta }_2\) is odd, and in particular \({\varTheta }_2(0)=0\) which implies \({\varTheta }(0) \in {\varOmega }\).
Proposition 9
Assume (F1)-(F2)-(CF3)-(F4)-(F5). We have the following properties.
-
(i)
For any \(m>0\) and \(n \in {\mathbb {N}}^*\), we have \({\varGamma }_n^m\ne \emptyset \) and
$$\begin{aligned} b_n^m\le a_n(\lambda ) - e^{\lambda } \frac{m}{2}, \end{aligned}$$(4.18)for each \(\lambda \in {\mathbb {R}}\). Moreover, \(b_n^m\) increases with respect to n.
-
(ii)
For any \(k\in {\mathbb {N}}^*\) there exists \(m_k\ge 0\), namely given by
$$\begin{aligned} m_k:= 2\inf _{\lambda \in {\mathbb {R}}}\frac{a_k(\lambda )}{e^{\lambda }}, \end{aligned}$$(4.19)such that for \(m>m_k\)
$$\begin{aligned} b_n^m < 0 \quad \text {for}\ n=1,2,\dots , k. \end{aligned}$$Moreover, \(m_k\) is increasing with respect to k.
-
(iii)
If (CF4) holds, then \(m_k=0\) for each \(k \in {\mathbb {N}}^*\). That is, for each \(m>0\) we have
$$\begin{aligned} b_n^m < 0 \quad \text {for all}\ n\in {\mathbb {N}}^*. \end{aligned}$$
Proof
For given \(\lambda \in {\mathbb {R}}\) and \(\zeta \in {\varGamma }_n(\lambda )\), we will find a \(\psi \in {\varGamma }_n^m\) such that
so that we have
and, passing to the infimum over \({\varGamma }_n(\lambda )\), we gain (4.18).
To find \(\psi \in {\varGamma }_n^m\) with (4.20), observe that, by definition of \({\varGamma }_n(\lambda )\) and compactness of \(\zeta (\partial D_n)\), there exists \(C>0\) such that \(\mathcal {D}(\zeta (\xi ))\ge C >0\) for \(\xi \in \partial D_n\). Thus, we have \(\mathcal {I}^m(\lambda , \zeta (\xi )(\cdot /L)) \rightarrow - \infty \) and \(\mathcal {P}(\lambda , \zeta (\xi )(\cdot /L))\rightarrow -\infty \) as \(L \rightarrow +\infty \), uniformly for \(\xi \in \partial D_n\). Thus, for \(L\gg 1\) we obtain, for every \(\xi \in \partial D_n\),
We also note that \(\mathcal {I}^m(\lambda + L,0)=-{\frac{e^{\lambda + L}}{ 2}}m \rightarrow -\infty \) as \(L\rightarrow +\infty \). Thus, for \(L\gg 1\), we find that the path \(\psi : D_n \rightarrow {\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\)
satisfies \(\psi (0)=(\lambda +L, 0)\in {\mathbb {R}}\times \{0\}\), \(\mathcal {I}^m(\psi (0))\le B^m-1\) and \(\mathcal {I}^m(\psi (\xi ))\le B^m-1\) for \(\xi \in \partial D_n\). Thus, by (4.21), we obtain \(\psi \in {\varGamma }^m_n\) and (4.20) holds.
The monotonicity of \(b_n^m\) with respect to n is a consequence of the definition. Point (ii) follows from (4.18) and (iii) follows from Proposition 7 (ii). \(\square \)
As a corollary to Proposition 9, we have the following result.
Corollary 2
For any \(m>0\), we have \(B^m= E^m = b^m_1\), i.e. the first minimax value \(b_1^m\) equals the Pohozaev minimum \(E^m\) on the product space.
Proof
Since any path in \({\varGamma }^m_n\) passes through \(\partial {\varOmega }\), we have \(b^m_n \ge E^m \ge B^m\) for each n. On the other hand, passing to the infimum (4.18) we obtain \(b_1^m \le B^m\) and thus the claim. \(\square \)
By Propositions 2 and 4, \(\mathcal {I}^m\) satisfies the \((PSP)_b\) condition for \(b<0\) and the deformation lemma holds. Let \(m_k\ge 0\) be a number given in Proposition 9. For \(m>m_k\) we can see that \(b_n^m<0\) for \(n=1,2,\cdots , k\) are critical values of \(\mathcal {I}^m\). If \(b_n^m\) are different, we can see the multiplicity of solutions. To deal with the case \(b_n^m=b_{n'}^m\) for some \(n\ne n'\), we need another family of minimax methods, which we consider in the following section.
4.4 Existence of multiple critical points
Let us define now new minimax families which enable us to find multiple solutions. We use an idea from [46], in which the genus theory is developed effectively in a general setting, where \({\mathbb {Z}}_2\)-action \({\mathbb {Z}}_2\times X\rightarrow X\); \((\pm 1, u)\mapsto \pm u\) is considered in a general Banach space X. The genus theory is applied for our \({\mathbb {Z}}_2\)-action in [22].
We recall the genus of a closed symmetric set \(A\subset X\) with  . We write \({\mathrm{genus}}(A)=n\) if n is the least integer \(n \in {\mathbb {N}}\) such that there exists a continuous odd map \(\beta : A \rightarrow {\mathbb {R}}^n \setminus \{0\}\); if such n does not exists, we set \({\mathrm{genus}}(A):=+\infty \).
. We write \({\mathrm{genus}}(A)=n\) if n is the least integer \(n \in {\mathbb {N}}\) such that there exists a continuous odd map \(\beta : A \rightarrow {\mathbb {R}}^n \setminus \{0\}\); if such n does not exists, we set \({\mathrm{genus}}(A):=+\infty \).
For each \(n\in {\mathbb {N}}^*\), define
and
We notice that \(\left\{ {\varTheta }(D_n)\right\} _{{\varTheta } \in {\varGamma }^m_n} \subset {\varLambda }^m_n\). In the following lemma, we observe that \({\varLambda }_n^m\) and \(c_n^m\) inherits the properties of \({\varGamma }_n^m\) and \(b_n^m\) and they enjoy an extra property (v).
Proposition 10
Assume (F1)-(F2)-(CF3)-(F4). Let \(n \in {\mathbb {N}}^*\) and \(m>0\). Then
-
(i)
\({\varLambda }_n^m \ne \emptyset \).
-
(ii)
\({\varLambda }_{n+1}^m\subset {\varLambda }_n^m\), and thus \(c_n^m\le c_{n+1}^m\).
-
(iii)
\(c_n^m\le b_n^m\).
-
(iv)
\(B^m = E^m \le c_1^m\).
-
(v)
Let \(A\in {\varLambda }_n^m\) and \(Z\subset {\mathbb {R}}\times H^1_r({\mathbb {R}}^N)\) be \({\mathbb {Z}}_2\)-invariant, closed, and such that \(0 \notin \overline{P_2(Z)}\) and \({\mathrm{genus}}(\overline{P_2(Z)})\le i<n\). Then \(\overline{A\setminus Z} \in {\varLambda }_{n-i}^m\).
Proof
The proof is essentially given in [22] and [9, Proposition 7.7]. In particular, (iv) follows from the fact that
\(\square \)
4.5 Proof of Theorem 1
Fix \(n\in {\mathbb {N}}^*\) and let \({\varLambda }_n^m\) and \(c_n^m\) satisfying the properties of Proposition 10. We build now multiple solutions.
Proposition 11
Assume (F1)–(CF2)–(CF3)–(F4)–(F5). Fix \(k\in {\mathbb {N}}^*\) and assume \(m>m_k\) (see (4.19)). Then
are critical values of \(\mathcal {I}^m\). Moreover
-
(i)
If, for some \(q\in {\mathbb {N}}^*\),
$$\begin{aligned} c_n^m< c_{n+1}^m< \dots< c_{n+q}^m<0 \end{aligned}$$then we have \(q+1\) different nonzero critical values, and thus \(q+1\) different pairs of nontrivial solutions of (1.7);
-
(ii)
If instead, for some \(q\in {\mathbb {N}}^*\),
$$\begin{aligned} c_n^m = c_{n+1}^m = \dots = c_{n+q}^m =:b <0 \end{aligned}$$(4.22)then
$$\begin{aligned} {\mathrm{genus}}(P_2(K_b^m))\ge q+1 \end{aligned}$$(4.23)and thus \(\# P_2(K_b^m)=+\infty \), which means that we have infinite different solutions of (1.7).
Summing up, we have at least k different pairs of nontrivial solutions of (1.7).
Proof
Since the \((PSP)_b\) condition holds for \(b<0\) by Proposition 2, we can develop deformation theory given in Proposition 5. We can also observe that the minimax classes \({\varLambda }_n^m\) are stable under the deformation. Thus Proposition 11 follows from Proposition 10. See [9, Theorem 7.8] for details. \(\square \)
Proof of Theorem 1
Theorem 1 follows from Proposition 11 easily. See also [9, Theorem 1.4]. \(\square \)
Remark 7
It is shown in [12] that the first solution corresponding to \(b_1^m\) is also a ground state, that is, it attains a minimum on the \(L^2\)-sphere \(\mathcal {S}_m\).
4.6 Proofs of Lemmas 1 and 2
Here we give Proof of Lemmas 1 and 2.
Proof of Lemma 1
We apply Theorem 3 to \(u(|x|)=\chi (1,h;|x|)\). In particular, by (4.1) we have
First we note that
We consider the following three cases separately:
(i) When \(\alpha \in (1,N)\) we may assume \(F({r\over \rho })\sim C_{N,\alpha }>0\). Thus
(ii) When \(\alpha =1\)
Thus
We set
Then
Thus for some C, \(C'>0\)
We compute
Similarly we have
from which we obtain
(iii) When \(\alpha \in (0,1)\)
Thus
Since
we have as in (4.24)
This completes the proof. \(\square \)
Proof of Lemma 2
Since \({{\mathrm{supp}}}\chi (R,h_R; \cdot )=\big \{x\in {\mathbb {R}}^N \mid |x|\in [R-h_R,R+h_R]\big \}\) we have
Thus
Here
Thus
When \(\alpha \in (1,N)\), we have by the definition of \(h_R\)
When \(\alpha =1\), we obtain
When \(\alpha \in (0,1)\),
This concludes the proof. \(\square \)
5 Unconstrained problem
In this section we sketch how to obtain infinitely many radial solutions for the unconstrained problem (1.1) and give a proof of Theorem 2. Here we assume (F1)–(F5). We fix \(\lambda \in {\mathbb {R}}\) and write \(\mu =e^\lambda \); omitting \(\lambda \), we denote \(\mathcal {J}(\cdot ):=\mathcal {J}(\lambda , \cdot ): H^1_r({\mathbb {R}}^N) \rightarrow {\mathbb {R}}\), i.e.
Similarly we write \(\mathcal {P}(\cdot ):=\mathcal {P}(\lambda , \cdot )\). For every \(b \in {\mathbb {R}}\) we set
We have the following result.
Proposition 12
Assume (F1)–(F3) and let \(b \in {\mathbb {R}}\). Then \(\mathcal {J}\) satisfies the Palais-Smale-Pohozaev condition at level b (shortly \((PSP)_b\)), that is every sequence \((u_n) \subset H^1_r({\mathbb {R}}^N)\) satisfying
admits a strongly convergent subsequence in \(H^1_r({\mathbb {R}}^N)\). In particular, \(K_b(\lambda )\) is compact in \(H_r^1({\mathbb {R}}^N)\).
Proof
First observe that, by (5.2) and (5.4) we obtain
We observe that \(b\ge 0\) and the boundedness of \(u_n\) in \(H_r^1({\mathbb {R}}^N)\). Thus by (F2)–(F3), \(\mathcal {D}'(u_n)\) has a strongly convergent subsequence in \((H_r^1({\mathbb {R}}^N))^*\) and by (5.3), \(u_n\) has a strongly convergent subsequence in \(H_r^1({\mathbb {R}}^N)\). \(\square \)
Set \( [\mathcal {J}\le b] := \{ u\in H_r^1({\mathbb {R}}^N) \mid \mathcal {J}_{\lambda }(u) \le b\}\). Following the arguments of Sects. 3.2 and 3.3, we prove the following deformation result by means of an augmented functional. See also [12, 13].
Proposition 13
Assume (F1)–(F3). Let \(b\in {\mathbb {R}}\) and let \(\mathcal {O}\) be a neighborhood of \(K_b(\lambda )\). Let \(\bar{\varepsilon }>0\), then there exist \(\varepsilon \in (0,\bar{\varepsilon })\) and \(\eta : [0,1]\times H^1_r({\mathbb {R}}^N)\rightarrow H^1_r({\mathbb {R}}^N)\) continuous such that
-
1.
\(\eta (0, \cdot )=id_{H^1_r({\mathbb {R}}^N)}\);
-
2.
\(\eta \) fixes \([\mathcal {J}\le b-\bar{\varepsilon }]\), that is, \(\eta (t, u)=u\) for all \(t \in [0,1]\) and \(\mathcal {J}(u)\le b\);
-
3.
\(\mathcal {J}\) is non-increasing along \(\eta \), and in particular \(\mathcal {J}(\eta (t,\cdot ))\le \mathcal {J}(\cdot )\) for all \(t \in [0,1]\);
-
4.
if \(K_b= \emptyset \), then \(\eta (1, [\mathcal {J}\le b+\varepsilon ])\subset [\mathcal {J}\le b-\varepsilon ]\);
-
5.
if \(K_b\ne \emptyset \), then
$$\begin{aligned} \eta (1,[\mathcal {J}\le b+\varepsilon ]\setminus \mathcal {O}) \subset [\mathcal {J}\le b-\varepsilon ] \end{aligned}$$and
$$\begin{aligned} \eta (1, [\mathcal {J}\le b+\varepsilon ]) \subset [\mathcal {J}\le b-\varepsilon ]\cup \mathcal {O}; \end{aligned}$$ -
6.
if (F5) holds, then \(\eta (t, \cdot )\) is \({\mathbb {Z}}_2\)-equivariant, i.e. it is odd.
As in Sect. 4.4, for any \(n \in {\mathbb {N}}^*\) we define \({\varGamma }_n:={\varGamma }_n(\lambda )\). We note that \({\varGamma }_n\ne \emptyset \) is shown in Proposition 6. Now our Theorem 2 can be obtained through the arguments given in [46]. Here we just give the definition of another minimax classes \({\varLambda }_n^m\), which ensures the multiplicity of solutions. We set for \(n\in {\mathbb {N}}^*\)
and
Then we have \(\{ \gamma (D_n)|\, \gamma \in {\varGamma }_n\}\subset {\varLambda }_n\) and we can also see that
Moreover we have the following result.
Proposition 14
Assume (F1)–(F5). Let \(n \in {\mathbb {N}}^*\) and \(m>0\). Then
-
(i)
\({\varLambda }_n \ne \emptyset \) and \(c_n\le c_{n+1}\).
-
(ii)
Let \(A\in {\varLambda }_n\) and \(Z\subset H^1_r({\mathbb {R}}^N)\) be \({\mathbb {Z}}_2\)-invariant, closed, and such that \(0 \notin {\overline{Z}}\) and \({\mathrm{genus}}({\overline{Z}})\le i<n\). Then \(\overline{A\setminus Z} \in {\varLambda }_{n-i}\).
-
(iii)
\(c_n\) is a critical value of \(\mathcal {J}\). Moreover
$$\begin{aligned} c_n\rightarrow +\infty \quad \hbox {as}\ n\rightarrow +\infty . \end{aligned}$$In particular, \(\mathcal {J}\) has an unbounded sequence of critical values.
Proof
Using Proposition 13, the proof can be given along the lines in [46]. See also [13]. \(\square \)
Proof of Theorem 2
Availability of data and material
Not applicable.
References
Ambrosetti, A., Rabinowitz, P.H.: Dual variational methods in critical point theory and applications. J. Funct. Anal. 14(4), 349–381 (1973)
Bartsch, T., Liu, Y., Liu, Z.: Normalized solutions for a class of nonlinear Choquard equations. SN Partial Differ. Equ. Appl. 1(34), 25 (2020)
Battaglia, L., Van Schaftingen, J.: Groundstates of the Choquard equations with a sign-changing self-interaction potential. Z. Angew. Math. Phys. 69(86), 16 (2018)
Berestycki, H., Lions, P.-L.: Nonlinear scalar field equations I: existence of a ground state. Arch. Ration. Mech. Anal. 82(4), 313–345 (1983)
Berestycki, H., Lions, P.-L.: Nonlinear scalar field equations II: existence of infinitely many solutions. Arch. Ration. Mech. Anal. 82(4), 347–375 (1983)
Cazenave, T., Lions, P.-L.: Orbital stability of standing waves for some nonlinear Schrödinger equations. Comm. Math. Phys. 85(4), 549–561 (1982)
Choquard, P., Stubbe, J., Vuffray, M.: Stationary solutions of the Schrödinger-Newton model - an ODE approach. Differential Integral Equations 21(7–8), 665–679 (2008)
Cingolani, S., Clapp, M., Secchi, S.: Multiple solutions to a magnetic nonlinear Choquard equation. Z. Angew. Math. Phys. 63(2), 233–248 (2012)
Cingolani, S., Gallo, M., Tanaka, K.: Normalized solutions for fractional nonlinear scalar field equation via Lagrangian formulation. Nonlinearity 34(6), 4017–4056 (2021)
Cingolani, S., Gallo, M., Tanaka, K.: Symmetric ground states for doubly nonlocal equations with mass constraint. Symmetry 13(7), article ID 1199, pp. 17 (2021)
Cingolani, S., Jeanjean, L.: Stationary solutions with prescribed \(L^2\)-norm for the planar Schrödinger-Poisson system. SIAM J. Math. Anal. 51(4), 3533–3568 (2019)
Cingolani, S., Tanaka, K.: Ground state solutions for the nonlinear Choquard equation with prescribed mass, In: Ferone, V., Kawakami, T., Salani, P., Takahashi F. (eds) "Geometric Properties for Parabolic and Elliptic PDE’s". Springer INdAM Series 47, Cortona 2019, pp. 23–41 (2021)
Cingolani, S., Tanaka, K.: Deformation argument under PSP condition and applications. Anal. Theory Appl. 37(2), 191–208 (2021)
Clapp, M., Salazar, D.: Positive and sign changing solutions to a nonlinear Choquard equation. J. Math. Anal. Appl. 407(1), 1–15 (2013)
D’Avenia, P., Mederski, J., Pomponio, A.: Nonlinear scalar field equation with competing nonlocal terms. Nonlinearity 34(8), 5687–5707 (2021)
Fröhlich, J., Lenzmann, E.: Mean-field limit of quantum Bose gases and nonlinear Hartree equation. In: Sémin. Équ. Dériv. Partielles, École Polytech., Palaiseau, talk no. 18, pp. 26 (2004)
Fröhlich, J., Tsai, T.-P., Yau, H.-T.: On the point-particle (Newtonian) limit of the non-linear Hartree equation. Comm. Math. Phys. 225(2), 223–274 (2002)
Ghimenti, M., Moroz, V., Van Schaftingen, J.: Least action nodal solutions for the quadratic Choquard equation. Proc. Am. Math. Soc. 145(2), 737–747 (2017)
Ghimenti, M., Van Schaftingen, J.: Nodal solutions for the Choquard equation. J. Funct. Anal. 271(1), 107–135 (2016)
Hartree, D.: The wave mechanics of an atom with a non-Coulomb central field. Part I. Theory and methods. Math. Proc. Cambridge Philos. Soc. 24(1), 89–110 (1928)
Hirata, J., Ikoma, N., Tanaka, K.: Nonlinear scalar field equations in \({{\mathbb{R}}}^N\): mountain pass and symmetric mountain pass approaches. Topol. Methods Nonlinear Anal. 35(2), 253–276 (2010)
Hirata, J., Tanaka, K.: Nonlinear scalar field equations with \(L^2\) constraint: mountain pass and symmetric mountain pass approaches. Adv. Nonlinear Stud. 19(2), 263–290 (2019)
Ikoma, N., Tanaka, K.: A note on deformation argument for \(L^2\)-normalized solutions of nonlinear Schrödinger equations and systems. Adv. Differ. Equ. 24(11–12), 609–646 (2019)
Jeanjean, L.: Existence of solutions with prescribed norm for semilinear elliptic equations. Nonlinear Anal. 28(10), 1633–1659 (1997)
Jeanjean, L., Tanaka, K.: A remark on least energy solutions in \({{\mathbb{R}}}^N\). Proc. Am. Math. Soc. 131(8), 2399–2408 (2003)
Lenzmann, E.: Uniqueness of ground states for pseudorelativistic Hartree equations. Anal. PDE 2(1), 1–27 (2009)
Li, G.-B., Ye, H.-Y.: The existence of positive solutions with prescribed \(L^2\)-norm for nonlinear Choquard equations. J. Math. Phys. 55(12), 1–19 (2014)
Lieb, E.H.: Existence and uniqueness of the minimizing solution of Choquard’s nonlinear equation. Stud. Appl. Math. 57(2), 93–105 (1977)
Lieb, E.H.: Sharp constants in the Hardy–Littlewood–Sobolev and related inequalities. Ann. Math. 118(2), 349–374 (1983)
Lieb, E.H., Seiringer, R., Solovej, J.P., Yngvason, J.: The mathematics of the Bose gas and its condensation. In: Oberwolfach Seminars 34, Birkäuser Basel (2005)
Lions, P.-L.: The Choquard equation and related questions. Nonlinear Anal. 4(6), 1063–1073 (1980)
Lions, P.-L.: Symétrie et compacité dans les espaces de Sobolev. J. Funct. Anal. 49(3), 315–334 (1982)
Ma, L., Zhao, L.: Classification of positive solitary solutions of the nonlinear Choquard equation. Arch. Ration. Mech. Anal. 195(2), 455–467 (2010)
Menzala, P.: On regular solutions of a nonlinear equation of Choquard’s type. Proc. Roy. Soc. Edinburgh Sect. A 86(3–4), 291–301 (1980)
Mercuri, C., Moroz, V., Van Schaftingen, J.: Groundstates and radial solutions to nonlinear Schrödinger-Poisson-Slater equations at the critical frequency. Calc. Var. Partial Differ. Equ. 55(146), 58 (2016)
Moroz, I.M., Penrose, R., Tod, P.: Spherically-symmetric solutions of the Schrödinger–Newton equations, topology of the Universe Conference (Cleveland, OH, 1997). Classical Quantum Gravity 15(9), 2733–2742 (1998)
Moroz, V., Van Schaftingen, J.: Groundstates of nonlinear Choquard equations: existence, qualitative properties and decay asymptotics. J. Funct. Anal. 265(2), 153–184 (2013)
Moroz, V., Van Schaftingen, J.: Existence of groundstates for a class of nonlinear Choquard equations. Trans. Am. Math. Soc. 367(9), 6557–6579 (2015)
Moroz, V., Van Schaftingen, J.: A guide to the Choquard equation. J. Fixed Point Theory Appl. 19(1), 773–813 (2017)
Pekar, S.: Untersuchung über die elektronentheorie der kristalle. Akademie Verlag, Berlin (1954)
Palais, R.S.: The principle of symmetric criticality. Comm. Math. Phys. 69(1), 19–30 (1979)
Penrose, R.: On gravity’s role in quantum state reduction. Gen. Relativity Gravitation 28(5), 581–600 (1996)
Penrose, R.: Quantum computation, entanglement and state reduction. Philos. Trans. Roy. Soc. A 356(1743), 1927–1939 (1998)
Penrose, R.: The Road to Reality. A Complete Guide to the Laws of the Universe. Alfred A. Knopf Inc., New York (2005)
Pitaevskii, L., Stringari, S.: Bose-Einstein Condensation. Oxford University Press, USA (2003)
Rabinowitz, P.H.: Minimax methods in critical point theory with applications to differential equations. CBMS Reg. Conf. Ser. Math. 65, Amer. Math. Soc., Providence (1986)
Ruiz, D., Van Schaftingen, J.: Odd symmetry of least energy nodal solutions for the Choquard equation. J. Differ. Equ. 264(2), 1231–1262 (2018)
Stuart, C.: Bifurcation from the continuous spectrum in the \(L^2\)-theory of elliptic equations on \({{\mathbb{R}}}^n\). In: Recent Methods in Nonlinear Analysis and Applications, Liguori (Naples) (1980) pp. 231–300
Stuart, C.: Existence theory for the Hartree equation. Arch. Ration. Mech. Anal. 51, 60–69 (1973)
Thim, J.: Asymptotics and inversion of Riesz potentials through decomposition in radial and spherical parts. Ann. Mat. 195(2), 232–241 (2015)
Tod, P.: The ground state energy of the Schrödinger–Newton equation. Phys. Lett. A 280(4), 173–176 (2001)
Tod, P., Moroz, I.M.: An analytical approach to the Schrödinger–Newton equations. Nonlinearity 12(2), 201–216 (1999)
Wang, Z.-Q., Xia, J.: Saddle solutions for the Choquard equation II. Nonlinear Anal. 201, 25 (2020)
Wei, J., Winter, M.: Strongly interacting bumps for the Schrödinger–Newton equation. J. Math. Phys. 50(1), 23 (2009)
Weth, T.: Spectral and variational characterizations of solutions to semilinear eigenvalue problems. Dissertation, Johannes Gutenberg-Universität, Mainz (2001)
Xia, J., Wang, Z.-Q.: Saddle solutions for the Choquard equation. Calc. Var. Partial Differ. Equ. 58(3), 30 (2019)
Ye, H.: Mass minimizers and concentration for nonlinear Choquard equations in \({{\mathbb{R}}}^N\). Topol. Methods Nonlinear Anal. 48(2), 393–417 (2016)
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
The first and second authors are supported by MIUR-PRIN project “Qualitative and quantitative aspects of nonlinear PDEs” (2017JPCAPN_005), and partially supported by GNAMPA-INdAM. The third author is supported in part by Grant-in-Aid for Scientific Research (19H00644, 18KK0073, 17H02855, 16K13771) of Japan Society for the Promotion of Science.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest/Competing interests
The authors declare that they have no conflict of interest.
Code availability
Not applicable.
Additional information
Communicated by P. H. Rabinowitz.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cingolani, S., Gallo, M. & Tanaka, K. Multiple solutions for the nonlinear Choquard equation with even or odd nonlinearities. Calc. Var. 61, 68 (2022). https://doi.org/10.1007/s00526-021-02182-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-021-02182-4
Keywords
- Nonlinear Choquard equation
- Nonlocal source
- Riesz potential
- Even and odd nonlinearities
- Multidimensional odd paths
- Radially symmetric solutions
- Normalized solutions
- Lagrange multiplier
- Pohozaev’s identity



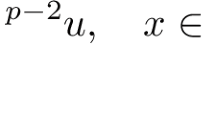
 , that is, there exists
, that is, there exists