Very high order discontinuous Galerkin method in elliptic problems

Abstract

The paper deals with high-order discontinuous Galerkin (DG) method with the approximation order that exceeds 20 and reaches 100 and even 1000 with respect to one-dimensional case. To achieve such a high order solution, the DG method with finite difference method has to be applied. The basis functions of this method are high-order orthogonal Legendre or Chebyshev polynomials. These polynomials are defined in one-dimensional space (1D), but they can be easily adapted to two-dimensional space (2D) by cross products. There are no nodes in the elements and the degrees of freedom are coefficients of linear combination of basis functions. In this sort of analysis the reference elements are needed, so the transformations of the reference element into the real one are needed as well as the transformations connected with the mesh skeleton. Due to orthogonality of the basis functions, the obtained matrices are sparse even for finite elements with more than thousands degrees of freedom. In consequence, the truncation errors are limited and very high-order analysis can be performed. The paper is illustrated with a set of benchmark examples of 1D and 2D for the elliptic problems. The example presents the great effectiveness of the method that can shorten the length of calculation over hundreds times.

1 Introduction

In scientific literature the discontinuous Galerkin (DG) methods or the finite elements method are called high-order when polynomial order p is greater than 2, but is not greater than 10, e.g. in the DG method [11, 23, 24, 29, 31, 35, 43] and in the finite element method [5, 8, 16, 20, 26, 27]. This paper exploits the version the discontinuous Galerkin method where the continuity and boundary conditions are enforced by the finite difference rule. Thus, the method is called the discontinuous Galerkin method with finite difference rules (DGFD) [23, 25]. In this work the polynomial order in finite elements exceeds $p=10$ and reaches $p=101$ in two-dimensional (2D) and even $p=1001$ in one-dimensional (1D) boundary value problems. The hp-mesh refinement is also tackled in this work. The mesh refinement techniques are still one of the mainstream of scientific research since it is used for automatic mesh adaptation, e.g. [10, 15, 38, 40, 48, 49] This paper reveals that it is very easy to combine very high-order finite elements with low-order elements in conforming and non-conforming meshes, so the hp-adaptivity may be very easy to perform in the DGFD method.

The discontinuous Galerkin method was proposed in the seventies of the previous century in [42] and constant development of the method has been observed since the time, see [9, 13, 19, 34, 44] and its application to many problems, such as analysing plates and shell [17, 36], elastic wave propagation [6, 7] or fluid floats [3, 32]. The present paper constitutes another step towards developing the DG method, with particular attention to the DGFD method. In this research the results from the DGFD method are compared with those obtained by the standard discontinuous Galerkin (SDG), where the SDG method is the interior penalty DG method [1]. In both DGFD and SDG methods the orthogonal polynomials as basis functions are applied. For the sake of clarity the scalar elliptic problem is chosen to be analysed in order to present the properties of the DGFD method with very high order elements. However, the presented techniques may be directly extended to other kinds of problems. A typical example of the scalar elliptic problem is heat transport with Fourier’s law, which is explored in this work.

In the high-order FEM and DG method the approximations in finite elements are constructed mainly by Lagrangian polynomials, e.g. [2, 30]. This approach can give correct results providing that the approximation order does not exceed $p=10$. For higher orders $p>10$ the level of truncation errors becomes so high that they strongly disturb the final solutions. Therefore it is impossible to use approximation higher than $p=10$ in these methods. This work presents the remedy for high level truncation error which involves the application of orthogonal basis functions in the finite elements. The orthogonal basis functions applied in this paper are Legendre or Chebyshev polynomials. These polynomials are orthogonal or orthogonal with weight, but in order to take advantage of the orthogonality properties the functions have to be applied in $[-1,\,1]$ and $[-1,\,1]\times [-1,\,1]$ domains in 1D and 2D, respectively.

There exist a method called p-FEM [46] or p-version FEM [45], which uses hierarchical approximation in finite elements. In this method higher polynomials are accommodated to the low order approximation using a hierarchical procedure. Quite arbitrary polynomials may be used to enrich the approximation, so relatively often the Legendre polynomials are chosen e.g. [8, 18, 21]. The hierarchical approximation with Legendre polynomials enables to achieve high order elements, however they do not exceed $p=10$, anyway.

The idea of applying the orthogonal basis functions in DG method is not new and reaches early 2000th, e.g. [28] and the idea has been further developed by other researchers [4, 12, 19, 37, 47]. Other techniques for orthogonal basis functions are based on Gram–Schmidt orthogonalization procedure as in [33, 41]. In the mentioned works the applications of orthogonal basis functions are motivated by mass matrices which are diagonal or at least block diagonal in such cases, and the approximation orders have not exceeded 10, anyway. The present work considers the elliptic problem in which no mass matrix appears. On the other hand, neither the Legendre nor Chebyshev basis functions does not result in diagonal stiffness matrix. The motivation for orthogonal polynomials as basis functions is different. The usage of such basis functions can effectively reduce truncation errors, so that a very high-order piece-wise approximate solution can be achieved. In consequence, the method gives a solution of high-accuracy on a coarse mesh. The main novelty of this paper is connected with the application of approximation orders that are much higher than in existing literature. To reach the goal not only orthogonal polynomials need to be used, but also other techniques need to be applied, which in details are presented in this paper. The critical point in DG methods are the compatibility conditions on the mesh skeleton and boundary conditions on Dirichlet outer boundary. In the SDG method the Nitsche’s method is applied to enforce both the inter-element continuity and the Dirichlet conditions. However, for higher-order basis functions the SDG method stops to be stable. It is shown in this work that the DGFD method is numerically stable even for an approximation order greater than 100.

In the FEM and DG methods a finite elements mesh plays two roles: firstly, it discretizes the domain geometry and secondly, it performs the appropriate calculations to solve the regarded problem. Therefore, the mesh density is a resultant of the domain complexity (e.g. along curved boundaries) and the complexity of the considered problem (e.g. the mesh is denser in places with high gradients). The domain and solution complexities can be separated from each other as shown in [22]. It means that the approximate solution can be obtained in the simple reference domain that is meshed independently on the real domain shape. This work presents the example in which the problem is defined on a quarter of annuls domain but is solved on a square domain discretized by four quadrilateral high-ordered finite elements.

In a case when non-rectangular finite elements are used in the mesh the transformed to appropriate reference element needs to be performed. The transformations are the same as in the isoparametric elements; for details see e.g. [51]. However, in the DGFD method the integrals along the mesh skeleton and along the outer Dirichlet boundary have to be taken additionally into account for such transformations. The details of how to deal with such transformations in the DGFD method are presented in this paper. In consequence, a very high-ordered and numerically stable approximate solution of the considered problem can be obtained on both structured and unstructured meshes. The application of very high-ordered orthogonal polynomial functions in the DGFD method with the transformation into the reference element in 1D and 2D is presented in this paper.

This paper is the continuation of Author’s research on the DG methods presented in the following papers [22,23,24,25] but it goes a step forward. In this paper the Legendre and Chebyshev polynomials are, for the first time, applied to the DGFD method on structured and unstructured meshes. In consequence the approximation orders in finite elements may exceed $p=10$ for square reference elements. Additionally, the calculations on the reference elements for DGFD method is presented in this work. In the DGFD method the main difficulty connected with reference elements lays in the fact that the compatibility conditions on the mesh skeleton are based on the relations constructed in the narrow vicinity of the skeleton. Thus, the transformations from the reference finite element into the real one, is not as obvious as in the SDG method, for example. The detailed description of such a transformation is presented in this work.

The structure of this paper enables a description of the DGFD method with orthogonal basis functions. The method is presented by means of a scalar elliptic problem which has a clear physical interpretation of heat transport that is introduced in Sect. 2, where the weak form of the considered problem is prepared for the DGFD method. Section 3 describes the details connected with the approximations upon finite elements including the orthogonal basis functions in 1D and 2D spaces. This section is concluded with the linear system of equations. In the case when 2D non-rectangular finite elements are applied in the mesh, the transformation to the reference square finite element is needed. The details of this transformation in the DGFD method are presented in Sect. 4. Some information connected with numerical integration is provided in Sect. 5. The high-order DGFD method is illustrated by 1D and 2D examples in Sect. 6. The paper is finished with some conclusions.

2 Problem formulation

This paper considers the two-dimensional domain $V$ with outer boundary $S$. In the domain the following second order boundary value problem, which is understood as a conductivity heat transport problem, is formulated

$$\begin{aligned} \begin{aligned}&\hbox {div}\,{\mathbf {q}}-{r}= 0,\quad {\mathbf {q}}= - \lambda \nabla t\quad {\text {in }} V\\&t= \hat{t}\quad {\text {on }}S_t,\quad {\mathbf {q}}\cdot {\mathbf {n}}=\hat{h} \quad {\text {on }}S_q \end{aligned} \end{aligned}$$

(1)

where ${\mathbf {q}}$ is the heat flux vector, r the heat source density, $\lambda$ is the heat conductivity parameter for a thermally isotropic material, $\hat{t}$ and $\hat{h}$ are prescribed values of temperature and heat flux, respectively, $S_t$ and $S_q$ are the parts of the $S$ where the temperature $\hat{t}$ and heat flux $\hat{h}$ are prescribed, respectively, and ${\mathbf {n}}$ is the unit vector normal to the outer boundary. The heat flux vector is related to the temperature field with the application of the Fourier’s law included in (1)$_2$.

The formulation of the DGFD method starts with a weak form of the analysed problem shown in Eq. (1),

$$\begin{aligned} \int \limits _{V}{v}\hbox {div}\,{\mathbf {q}}\,\mathrm {d}V- \int \limits _{V}{v}{r}\,\mathrm {d}V=0,\quad \forall \, {v}\end{aligned}$$

(2)

where ${v}$ is the test function.

The considered problem is solved using a finite element mesh by means of the weak Galerkin formulation where the approximation on the mesh skeleton is non-continuous. The method is known as Discontinuous Galerkin method. In spite of the fact, that the basic problem in Eq. (1) is continuous, in the subsequent analysis the discontinuities on $S_{s}$ need to be taken in to account.

Due to the discontinuities in the approximation, two operators need to be defined: the jump operator $[\![\bullet ]\!]$ and the mid-value operator $\left\langle \bullet \right\rangle$ on $S_{s}$, which are defined in this work as follows

$$\begin{aligned} \begin{aligned}&[\![f]\!] = \lim _{\epsilon \rightarrow 0} \, [\![f]\!]_{\epsilon },\quad \left\langle f \right\rangle = \lim _{\epsilon \rightarrow 0} \left\langle f \right\rangle _{\epsilon } \end{aligned} \end{aligned}$$

(3)

where the jump and mean values at distance $\epsilon$ are as follows

$$\begin{aligned}{}[\![f]\!]_{\epsilon }&= f(\mathbf x + \epsilon \, {\mathbf {n}}^{s}) - f(\mathbf x - \epsilon \, {\mathbf {n}}^{s}),\nonumber \\ \left\langle f \right\rangle _{\epsilon }&= 0.5\,\Bigl ( f(\mathbf x + \epsilon \, {\mathbf {n}}^{s}) + f(\mathbf x - \epsilon \, {\mathbf {n}}^{s}) \Bigr ) \end{aligned}$$

(4)

where ${\mathbf {n}}^{s}$ is the unit vector normal to $S_{s}$.

It is a well known property that the jump of superposition of the two functions can be expressed as follows

$$\begin{aligned}{}[\![f g]\!] = [\![f]\!]\left\langle g \right\rangle + \left\langle f \right\rangle [\![g]\!] \end{aligned}$$

(5)

When integration by parts is performed on the first component in Eq. (2) and the boundary condition in Eq. (1)$_4$ is taken into account, the following equation is obtained

$$\begin{aligned}&\int \limits _{S_{q}} {v}\hat{h} \,\mathrm {d}S+\int \limits _{S_{t}} {v}{\mathbf {q}}\cdot {\mathbf {n}}\,\mathrm {d}S-\int \limits _{V}\nabla {v}\cdot {\mathbf {q}}\,\mathrm {d}V+\int \limits _{S_{s}} [\![{v}{\mathbf {q}}]\!] \cdot {\mathbf {n}}^{s}\,\mathrm {d}S\nonumber \\&\quad -\int \limits _{V}{v}{r}\,\mathrm {d}V= 0 \;.\end{aligned}$$

(6)

The heat flux on $S_{s}$ in the mesh skeleton normal direction is set to zero since there is no heat source on the skeleton. It means, on the other hand, that the heat flux is continuous in the ${\mathbf {n}}^{s}$ direction

$$\begin{aligned}{}[\![{\mathbf {q}}]\!] \cdot {\mathbf {n}}^{s}=0 \quad \Rightarrow \quad \left\langle {\mathbf {q}} \right\rangle \cdot {\mathbf {n}}^{s}= {\mathbf {q}} \cdot {\mathbf {n}}^{s}\quad \text {on }\,S_{s}\end{aligned}$$

(7)

Fig. 1

Graphical illustration of Eqs. (9) (a) and (10) (b). Derivatives of $t$ on $S_{s}$ and $S_t$ are taken from the red curve

When the relations from the Eqs. (5) and (7) and the Fourier’s law are transposed to the Eq. (6), it is changed as follows:

$$\begin{aligned}&\int \limits _{S_{q}}{v}\,\hat{h}\,\mathrm {d}S-\int \limits _{S_{t}}\lambda \, {v}\,\nabla t\cdot {\mathbf {n}}\,\mathrm {d}S+\int \limits _{S_{s}} \lambda \, [\![{v}]\!]\,\nabla t\cdot {\mathbf {n}}^{s}\,\mathrm {d}S\nonumber \\&\quad +\int \limits _{V}\lambda \, \nabla {v}\cdot \nabla t\,\mathrm {d}V-\int \limits _{V}{v}\,{r}\,\mathrm {d}V= 0 \end{aligned}$$

(8)

In some of the integrals in Eq. (8) the temperature gradient vectors on the outer boundary and on the skeleton have to be evaluated. Following the procedures presented in [23, 25], they are approximated by the four order finite difference rules

$$\begin{aligned} \nabla t\cdot {\mathbf {n}}^{s}&= \frac{3}{2}\cdot \frac{[\![t]\!]_{d}}{2d} -\frac{1}{2} \cdot \left\langle \nabla t \right\rangle _{d}\cdot {\mathbf {n}}^{s}\quad \text {on }\,S_{s}\end{aligned}$$

(9)

$$\begin{aligned} \nabla t\cdot {\mathbf {n}}&= 6 \cdot \frac{\hat{t} - t(\mathbf x_{2d)}}{2d} - 4\nabla _nt(\mathbf x_d)- \nabla _nt(\mathbf x_{2d} ) \quad \text {on }\,S_t\end{aligned}$$

(10)

where $\mathbf x_d= \mathbf x - d\, {\mathbf {n}}$, $\mathbf x_{2d} = \mathbf x - 2\,d\, {\mathbf {n}}$ and $\nabla _nt= \nabla t\cdot {\mathbf {n}}$. The finite difference rules are based on the distance parameter $d$. The parameter is very small in relation to the neighbouring finite elements and can be easily estimated in the way presented in [24]. The graphical interpretation of Eqs. (9) and (10) for 1D case are shown in Fig. 1.

Equation (8) can be written as equality of bilinear and linear forms

$$\begin{aligned} A(t,{v}) = F({v})\,,\quad \forall {v}\end{aligned}$$

(11)

where both the trial $t$ and test ${v}$ functions belong to the so called broken Sobolev space:

$$\begin{aligned}&t,\, {v}\in H^1(V,V_h)\nonumber \\ {}&\quad = \left\{ w \in L^2(V);\, w\Bigl |_{V^e} \in H^1(V^e)\, \forall \, V^e \in V_h \right\} \end{aligned}$$

(12)

where $V_h$ represents the sets of disjoint finite elements that covers the whole domain $V$.

The definitions of bilinear and linear forms in Eq. (11) are defined as follows:

$$\begin{aligned} A(t,{v})&= \int \limits _{V}\lambda \nabla {v}\cdot \nabla t\,\mathrm {d}V+ \frac{3}{4} \int \limits _{S_{s}}\frac{\lambda }{d}\, [\![{v}]\!] [\![t]\!]_{d} \,\mathrm {d}S\nonumber \\&\quad - \frac{1}{2}\int \limits _{S_{s}}\lambda [\![{v}]\!] \,{\mathbf {n}}^{s}\cdot \left\langle \nabla t \right\rangle _{d}\,\mathrm {d}S+3\int \limits _{S_{t}}\frac{\lambda }{d} {v}t(\mathbf x_{2d}) \,\mathrm {d}S\nonumber \\&\quad +4\int \limits _{S_{t}}\lambda {v}\nabla _nt(\mathbf x_{d})\,\mathrm {d}S+\int \limits _{S_{t}}\lambda {v}\nabla _nt(\mathbf x_{2d})\,\mathrm {d}S\end{aligned}$$

(13)

$$\begin{aligned} F({v})&=\int \limits _{V}{v}\, {r}\,\mathrm {d}V- \int \limits _{S_{q}}{v}\,\hat{h}\,\mathrm {d}S+3\int \limits _{S_{t}}\frac{\lambda }{d}\, {v}\hat{t} \,\mathrm {d}S\end{aligned}$$

(14)

3 Approximation

The approximation in the e-th single finite element is constructed with the help of the local basis functions and the local degrees of freedom

$$\begin{aligned} t^e\left(\mathbf x\right) = \sum _{i=1}^{n_e} b_i^e\left(\mathbf x\right) \check{t}_i^e = \mathbf {b}^e \,{\check{\mathbf {t}}}^e,\quad \text {for}\quad \mathbf x\in V^e \end{aligned}$$

(15)

where $\mathbf {b}^e$ and $\check{t}_i^e$ are the vectors of the local basis functions and local degrees of freedom for the e-th element, respectively. The ’local degrees of freedom’ indicate degrees of freedom connected with the single finite element and ’local basis functions’ means that the basis functions are defined in the local coordinates connected with the element and their support is limited to the element. The choice of the local basis functions for each cell is quite arbitrary and depends on the problem considered. However, the polynomial basis functions are widely used since they generally provide correct results for a wide class of problems. In the Author’s previous papers [22, 23, 25] the polynomial basis functions have been constructed as monomials, defined in the cell local coordinates scaled to the sizes of the cells, i.e.:

$$\begin{aligned} x^e=\frac{x-x_m^e}{0.5\,h^e_{x}}\,,\quad y^e=\frac{y-y_m^e}{0.5\,h^e_{y}} \end{aligned}$$

(16)

where the point $(x_m^e, y_m^e)$ is a centre of gravity of the e-th element cell and $h^e_{x}$, $h^e_{y}$ are the characteristic lengths of the e-th cell in the x and y directions, respectively.

In this paper the orthogonal Legendre and Chebyshev polynomials basis functions are applied as basis functions. The Legendre polynomials are orthogonal without weight and Chebyszev functions are orthogonal with weight $\frac{1}{\sqrt{1-x^2}}$, in both of the case the orthogonality are preserved in the interval [1, 1]. For more details see for example [14].

For 1D the recursive definition of Legendre functions is as follows

$$\begin{aligned} P_0(\xi )&=1,\quad P_1(\xi )=\xi ,\nonumber \\ P_{n+1}(\xi )&= \bigl ((2 n + 1)\cdot \xi \cdot P_{n}(\xi ) - n\cdot P_{n-1}(\xi ) \bigr )/(n+1) \end{aligned}$$

(17)

and the definition of the Chebyshev functions is

$$\begin{aligned} T_0(\xi )&= 1,\quad T_1(\xi ) = \xi ,\nonumber \\ T_{n+1}(\xi )&= 2\cdot \xi \cdot T_{n}(\xi ) - T_{n-1}(\xi ) \end{aligned}$$

(18)

The vectors of basis functions for the Legendre basis functions in 2D are then defined as follows

$$\begin{aligned} \begin{aligned}&\text {for } p=1{:}\quad \mathbf {b}^e=\mathbf {b}_1^e\\ {}&\quad =\begin{bmatrix} 1&P_1(x^e)&P_1(y^e) \end{bmatrix}\\&\text {for } p=2{:}\quad \mathbf {b}^e=\mathbf {b}_2^e\\ {}&\quad =\begin{bmatrix} \mathbf {b}_1^e&P_1(x^e) P_1(y^e)&P_2(x^e)&P_2(y^e) \end{bmatrix}\\&\text {for } p=3{:}\quad \mathbf {b}^e=\mathbf {b}_3^e\\ {}&\quad =\begin{bmatrix} \mathbf {b}_2^e&P_3(x^e)&P_2(x^e) P_1(y^e)&P_1(x^e) P_2(y^e)&P_3(y^e) \end{bmatrix}\\&\text {for } p=4{:}\quad \mathbf {b}^e=\mathbf {b}_4^e\\ {}&\quad =\begin{bmatrix} \mathbf {b}_3^e&P_4(x^e)&P_3(x^e) P_1(y^e)&P_2(x^e) P_2(y^e)&P_1(x^e) P_3(y^e)&P_4(y^e) \end{bmatrix}\\&\text {and so on.} \end{aligned} \end{aligned}$$

(19)

The vectors of basis functions for the Chebyshev polynomials are constructed in the same manner as in Eq. 19.

In the 2D DGFD method finite element mesh may consists of finite elements of a quite arbitrary shape. For example, they may be triangle, quadrilateral, pentagon or of any other shape as shown in [25]. In the DGFE method the vector of basis functions may consist of Legendre or Chebyshev polynomials as well as monomials. However, when very high-order approximation is going to be achieved the orthogonal basis functions as well as reference elements have to be applied in the calculations. In 1D a single finite element is just a segment and due to local transformation in Eq. (16) each segment is transformed to $[-1,1]$ reference segment. On the other hand, a quadrilateral finite element has to be transformed to the square $[-1,1]\times [-1,1]$ reference element. For rectangular finite elements the simple transformation as shown in Eq. (16), is sufficient. In the case when the element cell is quadrilateral but not rectangular an easy transformation to the reference square can be performed, as shown in Sect. 4.

Equation (15) presents the approximation for one element cell. It can be rewritten as an approximation for the whole domain

$$\begin{aligned} t= {\varvec{\Phi }}{\check{\mathbf {t}}},\quad \text {in } V\end{aligned}$$

(20)

where ${\varvec{\Phi }}$ is the global approximation matrix and ${\check{\mathbf {t}}}$ is the global vector of degrees of freedom.

The jumps and mid-values are approximated using the same vector of degrees of freedom, i.e.

$$\begin{aligned}&[\![t]\!] = [\![{\varvec{\Phi }}]\!]{\check{\mathbf {t}}},\quad \left\langle t \right\rangle = \left\langle {\varvec{\Phi }} \right\rangle {\check{\mathbf {t}}}\quad \text {on } S_{s}\end{aligned}$$

(21)

In the same way the approximation of the jump and mean values at distance $\epsilon$ from $S_{s}$ is defined

$$\begin{aligned}&[\![t]\!]_{\epsilon } = [\![{\varvec{\Phi }}]\!]_{\epsilon } {\check{\mathbf {t}}},\quad \left\langle t \right\rangle _{\epsilon } = \left\langle {\varvec{\Phi }} \right\rangle _{\epsilon } {\check{\mathbf {t}}}\end{aligned}$$

(22)

In this paper the Galerkin formulation is regarded, thus the same approximations as in the Eqs. (20), (21) and (22) are applied to the test function ${v}$.

When the approximations from the Eqs. (20), (21) and (22) are substituted to the weak form Eq. (11), the linear system of equations is obtained

$$\begin{aligned} \mathbf K {\check{\mathbf {t}}}&= \mathbf F \end{aligned}$$

(23)

$$\begin{aligned} \mathbf K&= \int \limits _{V}\lambda \,\mathbf B^{\mathrm {T}}\mathbf B\,\mathrm {d}V+ \frac{3}{4}\int \limits _{S_{s}} \frac{\lambda }{d} [\![{\varvec{\Phi }}]\!]^{\mathrm {T}}[\![{\varvec{\Phi }}]\!]_{d} \,\mathrm {d}S\nonumber \\&\quad - \frac{1}{2} \int \limits _{S_{s}} \lambda [\![{\varvec{\Phi }}]\!]^{\mathrm {T}}{{\mathbf {n}}^{s}}^{\mathrm {T}}\left\langle \mathbf B \right\rangle _{d} \,\mathrm {d}S+3\int \limits _{S_{t}} \frac{\lambda }{d}\, {\varvec{\Phi }}^{\mathrm {T}}{\varvec{\Phi }}(\mathbf x_{2d}) \,\mathrm {d}S\nonumber \\&\quad +4\int \limits _{S_{t}} \lambda \, {\varvec{\Phi }}^{\mathrm {T}}\mathbf B_n (\mathbf x_d)\,\mathrm {d}S+\int \limits _{S_{t}} \lambda \, {\varvec{\Phi }}^{\mathrm {T}}\mathbf B_n (\mathbf x_{2d})\,\mathrm {d}S\nonumber \\ \mathbf F&= \int \limits _{V}{\varvec{\Phi }}^{\mathrm {T}}{r}\,\mathrm {d}V- \int \limits _{S_{q}} {\varvec{\Phi }}^{\mathrm {T}}\hat{h} \,\mathrm {d}S+ 3 \int \limits _{S_{t}} \frac{\lambda }{d} {\varvec{\Phi }}^{\mathrm {T}}\hat{t} \,\mathrm {d}S\end{aligned}$$

(24)

where $\mathbf B= \nabla {\varvec{\Phi }}$ and $\mathbf B_n=\nabla _n{\varvec{\Phi }}$.

4 Finite element transformation

For the Legendre and Chebyshev functions the transformation into the square reference element is required. In the 1D case the transformation is easily obtained by the Eq. (16) where only one coordinate $x$ is considered. For the two-dimensional case the same transformation technique can be used providing that the finite element is of rectangular shape. Otherwise, other transformation methods have to be applied.

In this section transformation techniques for quadrilateral elements to the square reference element are analysed. Although, such kind of transformations for the finite element method where the isoparametric finite elements are used can be found in literature, see [50], here the compatibility condition on the mesh skeleton and Dirichlet boundary conditions have to be additionally taken into account in such a transformation. In this paper the transformation is based on the first degree polynomials, whereas the element with a very high-order approximation can be defined on it.

Fig. 2

Transformation of square reference finite element into real quadrilateral e-th finite element

The real finite element is defined in the $(\mathbf x )$ global coordinates, whereas the reference finite element is defined on $\left(\varvec{\xi }\right)$ coordinates. The transformation between these two coordinate systems can be derived for the e-th element, i.e. $\mathbf x=\mathbf x(\varvec{\xi },e)$. The transformation of the reference element into the real one is illustrated in Fig. 2. The coordinates vectors $\mathbf x$ and $\varvec{\xi }$ are defined in this paper in two-dimensional spaces as

$$\begin{aligned} \mathbf x= \begin{bmatrix} x\\ y\end{bmatrix},\quad \varvec{\xi }= \begin{bmatrix} \xi \\ \eta \end{bmatrix} \end{aligned}$$

(25)

The transformation of reference element into the real one has the form of first order polynomial for both of the coordinates

$$\begin{aligned} x(\varvec{\xi },e)&= a^e_x+ b^e_x\,\xi + c^e_x\,\eta + d^e_x\,\xi \eta \end{aligned}$$

(26)

$$\begin{aligned} y(\varvec{\xi },e)&= a^e_y+ b^e_y\,\xi + c^e_y\,\eta + d^e_y\,\xi \eta \end{aligned}$$

(27)

where $a^e_x$, $b^e_x$, $c^e_x$, $d^e_x$, $a^e_y$, $b^e_y$, $c^e_y$, $d^e_y$ are the transformation coefficients for the e-th element for $x$ and $y$ coordinates, respectively.

Integration along outer boundary and along the mesh skeleton requires the transformation Jacobian which is based on the Nanson’s formula [39], that describes the relation of the infinitesimally small boundaries in the real and reference configurations

$$\begin{aligned} {J_F^n}^e({\mathbf {n}}) = \frac{\,\mathrm {d}S^e}{\,\mathrm {d}\varGamma ^e} = J_F^e ||{\mathbf G^e}^{\mathrm {T}}{\mathbf {n}}|| \end{aligned}$$

(28)

In order to apply the calculations to the reference element, the definitions presented in Eqs. (13) and (14) have to be rewritten so that, the sums over all elements, skeleton segments and outer boundary segments are implicitly applied. Finally, the two definitions are rewritten so that they are expressed on the reference finite element

$$\begin{aligned} A(t,{v})&= \sum _{e=1}^{Ne}\int \limits _{\varOmega ^e}\nabla _{\varvec{\xi }} V^{\mathrm {T}}\varvec{\varLambda }^e \nabla _{\varvec{\xi }} T\,\mathrm {d}\varOmega ^e\nonumber \\&\quad + \sum _{i=1}^{Ns} \Biggl ( \frac{3}{4} \int \limits _{\varGamma _s^i} \frac{\lambda }{d}\, [\![\![V]\!]\!]^i [\![\![T]\!]\!]^i_d{J_F^n}^{e(i)}_s \,\mathrm {d}\varGamma _s^i\nonumber \\&\quad - \frac{1}{2} \int \limits _{\varGamma _s^i} \lambda [\![\![V]\!]\!]^i \,{\mathbf {n}}^{s}\cdot \left\langle \left\langle \mathbf G^{\mathrm {T}}\nabla _{\varvec{\xi }}T \right\rangle \right\rangle ^i_d{J_F^n}^{e(i)}_s \,\mathrm {d}\varGamma _s^i \Biggr )\nonumber \\&\quad +\sum _{j=1}^{Nt} \Biggl (3\int \limits _{\varGamma _t^j}\frac{\lambda }{d} VT(\varvec{\xi }_{2d}) {J_F^n}^{e(j)}_t \,\mathrm {d}\varGamma _t^j\nonumber \\&\quad +4\int \limits _{\varGamma _t^j} \lambda V\nabla _nT(\varvec{\xi }_{d}) {J_F^n}^{e(j)}_t \,\mathrm {d}\varGamma _t^j\nonumber \\&\quad +\int \limits _{\varGamma _t^j} \lambda V\nabla _nT(\varvec{\xi }_{2d}) {J_F^n}^{e(j)}_t \,\mathrm {d}\varGamma _t^j \Biggr ) \end{aligned}$$

(29)

$$\begin{aligned} F({v})&= \sum _{e=1}^{Ne} \int \limits _{\varOmega ^e}V\, RJ_F^e \,\mathrm {d}\varOmega ^e- \sum _{i=1}^{Nq}\int \limits _{\varGamma _q^i} V\,\hat{H} {J_F^n}^{e(i)}_q({\mathbf {n}}) \,\mathrm {d}\varGamma _q^i\nonumber \\&\quad + \sum _{j=1}^{Nt} 3 \int \limits _{\varGamma _t^j} \frac{\lambda }{d}\, V\hat{T} {J_F^n}^{e(j)}_t({\mathbf {n}}) \,\mathrm {d}\varGamma _t^j \end{aligned}$$

(30)

where Ns is the number of the skeleton segments; Nt, Nq are the numbers of outer boundary segments for Dirichlet and Neumann boundary conditions, respectively; $T$ is the temperature on the reference element; $\varvec{\varLambda }^e = \lambda J_F^e\mathbf G^e{\mathbf G^{e{\mathrm {T}}}}^{\mathrm {T}},\quad \text {in } \varOmega ^e$; $\mathbf G= \frac{\partial \varvec{\xi }}{\partial \mathbf x}, \quad J_F^e = 1/\det (\mathbf G^e)\quad \text {in } \varOmega ^e$; $\varvec{\xi }_d = \varvec{\xi }- d\mathbf G^e{\mathbf {n}}, \quad \text {on } \varGamma ^i \text { or } \varGamma _{s}^i$ where e is the element number aligned to a particular boundary segment; $[\![\![V]\!]\!]^i = V^{e(i+)} - V^{e(i-)}, \qquad \text {on } \varGamma _{s}$; $[\![\![T]\!]\!]_d^i = T^{e(i+)}(-\varvec{\xi }_d) - T^{e(i-)}(\varvec{\xi }_d), \quad \text {on } \varGamma _{s}$; $V^{e(i+)}$ is the value of the function on the element on the right side of the i-th skeleton segment; $T^{e(i-)}(\varvec{\xi }_d)$ is the value of the function on the element on the left side of the ith skeleton segment with distance $d$; $\left\langle \left\langle \mathbf G^{\mathrm {T}}\nabla _{\varvec{\xi }}T \right\rangle \right\rangle ^i_d= 0.5 \cdot \left( {\mathbf G^{e(i+)}}^{\mathrm {T}}\nabla _{\varvec{\xi }}T^{e(i+)}\Bigr |_{-\varvec{\xi }_d} + {\mathbf G^{e(i-)}}^{\mathrm {T}}\nabla _{\varvec{\xi }}T^{e(i-)}\Bigr |_{\varvec{\xi }_d} \right)$; ${J_F^n}^{e(i)}_q = {J_F^n}^e({\mathbf {n}})$ where e is the element number belonging to i-th segment of the outer boundary $S_q^i$; ${J_F^n}^{e(j)}_t= {J_F^n}^e({\mathbf {n}})$ where e is the element number belonging to j-th segment of the outer boundary $S_t^j$; ${J_F^n}^{e(i)}_s = {J_F^n}^e({\mathbf {n}}^{s})$ where e is number of one of two elements belonging to i-th segment of the skeleton $S_{s}^i$.

The test function and the temperature on the reference element in Eqs. (29) and (30) are approximated using Legendre or Chebyshev basis as shown in Sect. 3. In such an approach high accuracy of high ordered finite elements may be achieved.

5 Integration

The orthogonal basis functions in two-dimensional case, presented in Eq. (19), require square $[-1,\,1] \times [-1,\,1]$ reference finite element to exploit their orthogonality. The integration over the square element has to be performed using the Gauss rule inherited from one-dimensional integration, i.e.

$$\begin{aligned} \int \limits _{-1}^1\int \limits _{-1}^1 f(\xi , \eta ) \,\mathrm {d}\xi \,\mathrm {d}\eta \approx \sum _{i=1}^{N_g} \sum _{j=1}^{N_g} w_i w_j f(\theta _i, \theta _j) \end{aligned}$$

(31)

where $N_g$ is the number of integration points in 1D, $\theta _i$ are 1D integration points and $w_i$ are the 1D integration weights. In consequence, in the square domain the number of integration points is equal to $N_g^2$.

In this paper the points $\theta _i$ are Gauss–Legendre integration points, which have been applied to monomial basis functions as well as to Legendre and Chebyshev basis functions. In spite of Gauss–Legendre points, there were no differences in the examples provided for Legenedre and Chebyshev basis functions. The results were the same even for high-order polynomials.

The integration order has to be adjusted to the approximation degree in the finite elements. It should be noted that in the first integral in Eq. (24) the integrand is a matrix that consists of the first derivatives of basis functions. It means that elements of the matrix are polynomials which are up to $2(p-1)$ degree. And for instance, when the approximation degree is 101 then one needs to integrate the polynomial of 200 degree, and so on. A similar situation occurs in the case of other integrals.

6 Examples

This section is devoted to presenting a set of examples in 1D and 2D. The approximate solutions with high-ordered approximations converge rapidly. Thus, it is quite easy for them to reach the machine precision limit connected with the floating point truncations in the software calculations framework. All the examples have been prepared in the Matlab environment for which the machine epsilon is $\textit{eps}=2.2204\hbox {e}{-}16$, meaning the distance from 1.0 to the next larger double-precision number. In other words, any number in Matlab is stored with about 15 digits of precision. As a result it is not possible to approximate any function with $L_2$ error lower than about $1\hbox {e}{-}12$ (providing that the values of the function are bounded by 1 and $-1$).

A simple test in Matlab can be performed in order to indicate the level of accuracy in numeric calculations. In the test the randomly generated set of equations is solved and then the accuracy is checked, as shown below:

The level of error for $N=10$ is $\textit{err}=4.27\hbox {e}{-}15$, for $N=100$ the error is about $\textit{err}=2.62\hbox {e}{-}13$, for $N=1000$ the error level is $\textit{err}=1.95\hbox {e}{-}11$ and for $N=10000$ the error is about $\textit{err}=3.16\hbox {e}{-}09$.

As such rudimentary tests reveal, the truncation errors may strongly affect final results. Depending on the problem under consideration the highest accuracy that can be obtained is $1\hbox {e}{-}11$ and sometimes it is about $1\hbox {e}{-}9$ or even higher. The effects are illustrated by the example results since at certain level of the error occurrence the approximate solution stops converging.

In Sect. 6.1 the one-dimensional benchmark example is considered. In this example the DGFD method is compared with the FEM as well as with the SDG method. Also the convergence analysis is performed for all the methods to show how they deal with very high-orders approximations. The two-dimensional benchmark examples are presented in Sect. 6.2 in which the DGFD method with very high-ordered finite elements is analysed. The example in the following Sect. 6.3 deals with the domain with curved boundaries. In the last example in Sect. 6.4 the a priori hp mesh refinement is shown. In this refinement the mesh is non-conforming and very high-ordered finite elements are combined with low-ordered elements.

Fig. 3

Exact solution for 1D example, $n=51$

Fig. 4

Example 1: convergence of DGFD approximate solution in $L_2$ norm (a) and $H_1$ semi-norm (b), $n=51$

6.1 Benchmark 1D example

In this section the following one-dimensional boundary problem is considered

$$\begin{aligned} -\Delta t&= f(x),\quad x \in [0,1]\nonumber \\ t(0)&=\hat{t}, \quad t'(1)=\hat{h} \end{aligned}$$

(32)

The function f(x) is taken from the exact solution of the problem that is assumed to be as follows

$$\begin{aligned} t(x)=\cos \left( n \pi x \right) \cdot \exp \left( -\alpha \cdot (\beta - x)^2 \right) \end{aligned}$$

(33)

with $n=51$ $\alpha =12$ and $\beta =0.4$. The function strongly oscillates and has 51 local extrema and, moreover, its gradients are quite high, which is presented in Fig. 3. The right hand side function and both kinds of the boundary conditions in Eq. (32) are taken from the exact solution.

Fig. 5

Example 1: convergence of FEM approximate solution in $L_2$ norm (a) and $H_1$ semi-norm (b), $n=51$

Fig. 6

Example 1: times of calculations (in seconds) for DGFD method and FEM, $n=51$. a DGFD, b FEM

The problem has been solved by the DGFD method with application of Chebyshev and Legendre basis functions. The results for those two basis functions are almost the same, therefore the results for Chebyshev functions are presented. Firstly, the convergence analysis of the DGDF method for various approximation order p was performed. In the analysis the errors in $L_2$ norm and $H_1$ semi-norms have been considered, which can be seen in Fig. 4. The same convergence analysis has been prepared for FEM, see Fig. 5. It can be noticed that the DGFD method is stable for low order as well as for high order approximations. For $p=40$ the convergence curve is very steep which means a high rate of convergence. On the other hand, the finite element method fails for orders greater than 11. For $p=15$, FEM stops to converge due to a high level of truncation errors. During the convergence analysis the time of calculations have been measured. Figure 6 shows the time of calculation in seconds with respect to error in $L_2$ error for both DGFD method and FEM. These diagrams show how much time it takes to reach a particular level of accuracy. It can be noticed that the higher order is applied, the less time it takes to obtain the demanded level of error. For example, for $p=1$ DGFD method needs over 15 mins to reach error $10^{-6}$, but only half a second for $p=40$ to obtain error level $10^{-12}$. The same tendency is observed for FEM, but due to fact that in FEM the approximation order is limited the method cannot be as effective as the DGFD method.

Fig. 7

Example 1: $L_2$ errors in relation to approximation degrees p for various discretizations, $p=2,4,6,9,12,17,25,50,71,100$. a Results for discretization with 2 elements, b results for discretization with 5 elements, c results for discretization with 10 elements, d results for discretization with 20 elements

Subsequently, for the comparison reasons the problem under consideration has been solved by means of approaches: the SDG method, the FEM and the DGFD method. In this case the SDG method has been also applied with the Chebyshev basis function. For the DGFD method both monomial and the Chebyshev basis functions has been used. In FEM the standard Lagrange functions are used. In conclusion, the solution of this problem has been solved by the following approaches:

• DGFD with Chebyshev functions (DGFD_C)

• DGFD with monomial functions (DGFD_M)

• SDG with Chebyshev functions (SDG_C)

• FEM

The domain $[0\, 1]$ has been discretized by two, five, ten and twenty regular finite elements. The calculations have been performed for approximation order p which is equal to 2, 4, 6, 9, 12, 17, 25, 50, 71 and 100. The results are presented in Fig. 7 where the of $L_2$ norms are shown in relation to p in logarithmic scales for various discretizations. Figure 7a shows the results for the two-element discretization. In this case only approximate solutions for DGFD_C and SDG_C for higher approximations give sensible results. The two other methods have failed. In a case of with five elements, Fig. 7b, the FEM and DGFD_M methods have not given satisfactory results. However, the approximate solution for the DGFD_C and SDG_C methods leads to quite low error levels for higher approximation degrees, i.e. $p>25$. When the domain is discretized with ten finite elements, Fig. 7c, all four methods give the same results for approximation up to $p=12$. For higher orders the error of the DGFD_M method is on the same level while in FEM the error is even higher due to truncation errors. For the DGFD_C and SDG_C methods the errors are much lower for higher orders, but the error of the DGFD_C method is almost two orders lower. Quite similar effects can be observed for denser discretization by 20 elements. FEM gives the worst results for higher orders since the method is completely numerically unstable for $p>12$. Now the DGFD_C is over two three orders lower in comparison to SDG_C.

It is shown in the example that the Chebyshev and Legendre functions can be used as basis functions for the discontinuous Galerkin method. For lower ordered approximations the results are the same as for the FEM or SDG method with monomial or orthogonal basis functions. For higher approximations when p is greater than twenty the Lagrange functions or monomial basis fail due to the great level of truncation errors. The remedy for this is the usage of orthogonal polynomials. For Chebyshev and Legendre basis functions, it is seen that the truncation errors do not dominate the final results. It is also evident here that the DGFD method gives much better results in comparison to the SDG method.

Fig. 8

Exact solution for 1D example, $n=6000$

The extension of the example provides the calculations for even higher approximation degrees. It can be concluded from the results presented in Fig. 7 that the DGFD_C method is stable and gives the best results in comparison to SDG_C and other methods. That is the reason for choosing the DGFD_C method for further analysis. In order to present the behaviour of the method for higher than hundred approximation orders another version of the problem in Eq. (32) is presented. Now $n=6000$ is considered which means that in the $[0\,1]$ domain the function has 6000 local extrema and so strongly oscillates. The gradients in this function are extremely high and even reach $t'=\pm 1.5e4$. The function is shown in Fig. 8, but the oscillations are so dense that the function line cannot be distinguished.

Table 1 The results for the example 1 with $n=6000$

Table 2 The results for the example 1 with $n=6000$

The example has been solved using various numbers of finite elements and approximation orders. It should be noted that for $p=101$ the polynomials of order up to 200 have to be integrated; see the first integral in definition $\mathbf K$ in Eq. (24). Similarly, for $p=1001$ a polynomial of two thousand degree has to be integrated. In spite of the fact that extremely high ordered polynomials are integrated the final results are satisfactory. In each case the Gauss integration order has been adopted adequately to the approximation order. For example, in the case of $p=$ 1001 over 12 thousands integration points have been applied. The results are presented in Tables 1 and 2 where errors in $L_2$ norm as well as in $H_1$ seminorm are shown. In Table 1 the results are presented under the assumptions that approximately the same number of degrees of freedom are in the meshes for various p. It can be noticed that the accuracy increases with the approximation order p. It shows that the higher order the better results can be achieved. Similar effect, but in other form, is presented in Table 2. In this case the numbers of degrees have been set, so that to achieve the same level of accuracy, namely the value of error in L$_2$ norm about $1\hbox {e}{-}7$. For the case $p=1001$ such accuracy can be achieved using about 12,000 #dof. When p decreases the #dof increases. In consequence, for $p=2$ 1.2 millions #dof have to be used to reach $1\hbox {e}{-}7$ error level. Anyway, for $p=2$ we need to use over 100 times more #dof in comparison than for $p=1001$. Other effect can now be noticed connected with derivatives. In spite of the fact that the error levels in $L_2$ norm are comparable to the qualities of derivatives for lower order solution, they are much worse in comparison to such high-ordered solutions. Summing up, very high-order elements give very good results for relatively small number of degrees of freedom in comparison to lower-order elements. It also means that the very high-order elements are computationally much effective, since for the coarse mesh the elements give a high-quality solution. In Tables 1 and 2 the numbers of integration points (#ip) have been shown. For the 1D problem the #ip consists of the integration points that are inside finite elements plus those between finite elements plus other two on the two ends of the domain. In the 1D problem the #dof and #ip are approximately the same.

Fig. 9

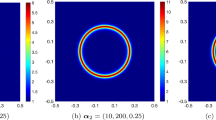
Maps of function $t(x,y)$ in Eq. (35) for various values of r. a $r=5$, b $r=10$, c $r=30$, d $r=100$

Fig. 10

Meshes used in polynomial benchmark example. a Structured $2\times 2$, b unstructured $2\times 2$, c structured $10\times 10$, d unstructured $10\times 10$

6.2 Benchmark 2D examples

In this section the two-dimensional benchmark tests are considered. The conclusion that can be drawn from the previous section is that the DGFD method with orthogonal basis function gives the best results in comparison to other tested methods. Therefore, for the sake of clarity, in this section mainly the results for the DGFD method with Chebyshev basis functions are presented. However, in the first example in this section the results from the DGFD and SDG methods are compared where the Legendre polynomials as basis functions are chosen.

The benchmark tests are based on the following boundary problem

$$\begin{aligned} -\Delta t= f(x,y) \end{aligned}$$

(34)

The problem is defined on the square domain $[-1,\,1] \times [-1,\,1]$. The boundary conditions and the right hand side function f(x, y) are derived from the exact solution $t(x,y)$. The exact solution is high order polynomial, exponential or trigonometrical function in Sects. 6.2.1–6.2.3, respectively.

Table 3 The results for 2D polynomial benchmark example on structured $2\times 2$ mesh

Table 4 The results for 2D polynomial benchmark example on unstructured $2\times 2$ mesh

Table 5 The results for 2D polynomial benchmark example on structured $10\times 10$ mesh

Table 6 The results for 2D polynomial benchmark example on unstructured $10\times 10$ mesh

6.2.1 Polynomial example

The boundary value problem from the Eq. (34) is used for testing both DGFD and SDG methods using polynomial benchmark polynomial problem. It is assumed that the exact solution is polynomial of order r defined as follows:

$$\begin{aligned} t(x,y) = \sum _{i=0}^{i=r} \sum _{j=0}^{j=i} a_{ij} T_{j}(x) T_{i-j}(y) \end{aligned}$$

(35)

where $a_{ij} \in (-1, 1)$ are randomly generated coefficients. The right-hand side function is taken directly from the (35) as well as the Dirichlet conditions which are set all around the outer boundary. The maps of the function defined in Eq. (35) for various values of r are shown in Fig. 9. It can be noticed that the function is variable in the domain, especially for higher values of r, and so the gradients are very high.

The problem has been solved using DGFD and SDG in which the Legendre polynomials as basis function have been used. The calculations employed the structured and unstructured meshes that consisted of 4 or 100 finite elements which are shown Fig. 10. The elements in the unstructured meshes are strongly distorted to check the influence of the transformation to the final results. The orders of basis function have been set so that to achieve as good results as possible. In the regarded problem the exact solution is polynomial, so the exact solution should be recovered by the two methods when the polynomial basis functions of appropriate order are applied. For the structured meshes the orders of finite elements have been set the same as the polynomial order in Eq. (35), i.e. $p=r$. For unstructured meshes the transformations to the reference elements need to be applied as described in Sect. 4. Thus, higher order elements need to be used for exact solution recovery, and it has been revealed that for unstructured meshes the exact solution has been obtained when $p=2r$. In this example both DGFD and SDG methods are tested to check how they cope with compatibility and boundary conditions for both structured and unstructured meshes.

For the structured $2\times 2$ mesh the problem has been solved for the range polynomial order r from 2 up to 100, while for the unstructured $2\times 2$ mesh r has been set from 2 up to 40. In the case of the structured $10\times 10$ mesh the maximum value of r has been 30 and 15 for the unstructured $10\times 10$ mesh. In the calculations the reciprocal condition numbers (rcond function in Matlab) for the numerical matrices have been checked. For a well-conditioned matrix rcond is close to 1.0, while for an ill-conditioned matrix the function gives the value close to zero. When $\texttt {rcond}<1\hbox {e}{-}20$ it means that the matrix is almost singular. The result of the analysis has been shown in Tables 3, 4, 5 and 6.

The DGFD method is able to reproduce the exact solution for low as well as for high order polynomials. The errors that are shown in Tables 3, 4, 5 and 6 for the DGFD method come from the machine precision epsilon, mentioned in Sect. 6. It can be noticed that for $p>50$ the influences of the truncation errors on the final results are increasingly more evident. However, for the DGFD method the levels of errors are very small even for very high order approximations in structured, as well as in unstructured meshes. The SDG method, on the other hand, cannot recover the exact solution and the errors are over five orders smaller in comparison to those obtained by the DGFD method. For a very high order approximation the SDG method fails since it cannot give a solution with acceptable error level. The rcond level for the SDG method is very low since it is smaller than $1\hbox {e}{-}9$ for low and high values of p in both kinds of the meshes considered. The value rcond for the DGFD method is usually greater than $1\hbox {e}{-}7$. It means, in other words, that the main matrix in the DGFD method is well-conditioned while such matrix in the SDG method is rather ill-conditioned. Such conclusions are true for both structured and unstructured meshes, which means that the approach proposed in the DGFD method is well established and is suitable to cope well with very high order approximation. The values of rcond for unstructured meshes are lower in comparison to those in structured meshes, which means that the transformation procedure affects the orthogonality properties of the basis functions. But in the DGFD the influence is not dominant and a very high approximation can be applied for not-rectangular finite elements. Tables 3, 4, 5 and 6 present the numbers of integration points, which are approximately twice the #dof. It confirms the computational efficiency of the very high-order DGFD method.

In the DGFD method the fluxes on the mesh skeleton are approximated by the fourth order finite difference rule. The similar approach is used to apply Dirichlet boundary conditions. These approximations are performed in the small distance $d$ from the skeleton or the outer boundary, see Eqs. (9) and (10). In the calculations the $d$ is much smaller that the sizes of the adjacent cells, which is why the fourth order is enough for such approximations for low as well as high values of p. It has been shown in this example that the DGFD method with fourth order finite difference rules for fluxes on the skeleton and the outer boundary can recover exact solutions when very high-order elements are used. The DGFD method is more stable and gives much better results in comparison to the SDG method.

6.2.2 Exponential example

This section considers the problem from Eq. (34), for which the boundary conditions and right-hand side function is taken from the following exponential exact solution (see Fig. 11):

$$\begin{aligned} t(x,y) = \exp \Bigl (-5 \cdot \left( x-y \right) ^2 - 5 x^2 \Bigr ) \end{aligned}$$

(36)

So, the right-hand side function is:

$$\begin{aligned} f(x,y)&= \left( - 50x^2 + 60xy - 20y^2 + 3\right) \nonumber \\&\quad \cdot \exp \Bigl (-5 \cdot \left( x-y \right) ^2 - 5 x^2 \Bigr ) \end{aligned}$$

(37)

Fig. 11

The exact solution for the 2D exponential example in $[-1,\, 1] \times [-1,\,1]$ domain

Table 7 The results for the 2D exponential example

The problem has been solved three times on regular quadrilateral meshes for $p=6,\, 11,\,31$. The densities of the meshes have been set so that to obtain error value about $1\hbox {e}{-}9$ in $L_2$ norm. The results are shown in Table 7 with the time of calculations. It can be noticed that when using lower order elements a denser mesh needs to be applied, so that the number of degrees of freedom increases. This leads, on the other hand, to time consuming calculations, which in this case took in Author’s program an hour and a half. The same problem but solved on the mesh with very high-order elements required a much smaller number of degrees of freedom and it was a matter of seconds to get a high quality solution. It shows once again a great computational effectiveness of the DGFD method with very high-order elements.

6.2.3 Trigonometrical example

Once again the problem from Eq. (34) is considered, but in this case the boundary conditions and the right hand side function f(x, y) are derived from the exact solution $t(x,y)$, that is:

$$\begin{aligned} t(x,y)= x^2\,y + \sin (0.5\,n\,\pi \,x) \cdot \sin (0.5\,n\,\pi \,y) \;.\end{aligned}$$

(38)

and the right-hand side function is:

$$\begin{aligned}&f(x,y)\nonumber \\ {}&\quad = -(2\,y - 2\,(0.5\,n\,\pi )^2\,\sin (0.5\,n\,\pi \,x)\cdot \sin (0.5\,n\,\pi \,x)) \end{aligned}$$

(39)

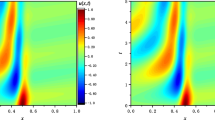
The parameter n defines the number of local extrema in x or y directions. In the example presented here the parameter n has been set to 32, which means that in the considered domain $[-1,\, 1] \times [-1 ,\, 1]$ there are 1024 local extrema. The exact solution of the problem is depicted in Fig. 12 in the square domain $[-1,\, 1] \times [-1 ,\, 1]$ for $n=32$. It can be noticed that the function strongly fluctuates and so has quite big gradients.

Fig. 12

Exact solution for the 2D trigonometrical example in $[-1,\, 1] \times [-1 ,\, 1]$ domain, $n=32$

The results are shown in the form of convergence of approximate solutions in $L_2$ error measure in relation to the number of degrees of freedom in the mesh. The calculations have been performed for structured and unstructured meshes with quadrilateral elements. For structured meshes all elements are squares, so the trivial transformation to the reference element is needed. In the unstructured meshes the quadrilateral elements are strongly deformed, so the correctness of of the transformation presented in Sect. 4 may be verified. Examples of the structured and unstructured meshes are presented in Fig. 10. The unstructured meshes have been generated from the appropriate structured meshes by randomly generated shifts of the vertices of the elements. In consequence, the unstructured meshes consist of quadrilateral elements which are strongly distorted.

The convergence curves for approximation orders $p=10,\, 15,\, 35$ are shown in Fig. 13 where the results obtained on structured and unstructured meshes are put side by side. For the structured meshes the convergence curves, Fig. 13a, are almost straight lines and the convergence rates are typical for discrete methods. On the other hand, the convergence curves for unstructured meshes, Fig. 13b, fluctuate and it is hard to set the convergence rates. However, it can be seen from the general tendencies that the methods converge to the exact solution, but with smaller rates in comparison to the structured mesh. The DGFD method on the unstructured mesh can give satisfactorily good results where their quality depends on the level of distortions of the quadrilateral elements.

Fig. 13

Convergence rates in 2D trigonometrical example. a Structured mesh, b unstructured mesh

6.3 Example in the reference domain

This example examines the domain that has a shape of a quarter of annulus; see Fig. 14a. The domain is defined by the outer $R=2$ and the inner $r=1$ radii. In order to solve such a problem by FEM, a dense finite element mesh has to be generated so that the mesh can reproduce geometry with adequate accuracy. On the other hand, if we want to use a high ordered DGFD approach, the best results are obtained for the coarse mesh, but the coarse mesh does not strictly cover the considered domain which has curved boundaries. The remedy for such a situation is the analysis in the reference domain, as presented in [22]. The reference domain can be a domain with an arbitrary shape. To make it simple, the square reference domain is chosen $[-1, 1] \times [-1,1]$. On the square domain four-element and hundred-element quadrilateral meshes, structured and unstructured, have been set, the same which are shown in Fig. 10. Subsequently, the results calculated in the reference domain are then transformed into the real domain.

Fig. 14

Quarter of annulus example: domain geometry and exact solution. a Quarter of annulus domain, $r=1$, $R=2$, b exact solution

In this example the problem considered is defined in Eqs. (34), (38) and (39), and with $n=32$, but in the domain which is shown in Fig. 14a. The exact solution of the problem is shown in Fig. 14b. The algorithm for the analysis in the reference domain requires a mathematical transformation between the two domains. In this example the transformation from the reference domain into the real domain, generated in [22], is as follows:

$$\begin{aligned} x(\xi ,\eta )&= 1.635 \eta + 0.2555\xi ^2 -0.104\xi ^2\eta -0.1281x^3\nonumber \\&\quad +1.0607\sin \left( \frac{\pi }{4} \xi \right) +1.0607\cos \left( \frac{\pi }{4} \xi \right) \nonumber \\&\quad -1.6318\sin \left( \frac{\pi }{4} \eta \right) \nonumber \\ y(\xi ,\eta )&= 1.635 \eta - 0.2555\xi ^2 -0.104\xi ^2\eta -0.1281x^3\nonumber \\&\quad -1.0607\sin \left( \frac{\pi }{4} \xi \right) +1.0607\cos \left( \frac{\pi }{4} \xi \right) \nonumber \\&\quad -1.6318\sin \left( \frac{\pi }{4} \eta \right) \end{aligned}$$

(40)

The calculations have been performed for the order $p=80$ (3321 #dof in element) on four-element meshes and $p=30$ (396 #dof in element) on hundred-element meshes. The results are presented in the form of error maps in the real domain in Figs. 15 and 16 for $p=80$ and $p=30$, respectively. As it can be noticed the domain representation in the calculations was strict due to the domain transformation. The error levels are much smaller for structured meshes in comparison to those from the unstructured mesh, regardless of the approximation order. The error levels for $p=80$ are quite small for the structured mesh, in spite of the fact that there are only four elements and 13,284 #dof in the mesh.

Fig. 15

Maps of errors of approximate solution with $p=80$, #dof $=$ 13,284 on quarter of annulus domain. a Structured mesh, Fig. 10a, b unstructured mesh, Fig. 10b

Fig. 16

Maps of errors of approximate solution with $p=30$, #dof $=$ 49,600 on quarter of annulus domain. a Structured mesh, Fig. 10c, b unstructured mesh, Fig. 10d

In this example the convergence analysis has been performed for the same meshes and approximation orders as presented in Sect. 6.2.3. It can be seen in Fig. 17a that the transformation to the reference domain slightly influences the convergence rates, since the rates are a little bit smaller. In the case of the unstructured mesh, Fig. 17b, the convergence curves fluctuate in a similar manner as in Fig. 13b, but they converge to the exact solution.

Fig. 17

Convergence rate in reference domain example. a Structured mesh, b unstructured mesh

6.4 Example with hp mesh refinement

In the last example the domain with a rectangular hole inside is considered. In Fig. 18 the geometry of the regarded domain and boundary conditions are presented, while Fig. 19 reveals the solution of the problem which has been obtained using overkilled mesh. All the data in this example are dimensionless. It can be observed that there are heat flux concentrations at the hole vertices. The values of the components of the heat flux vector go to infinity at the vertices, hence the maps in the Fig. 19b and c are limited to the value 100.

Fig. 18

Domain with rectangular domain, dimensions and boundary conditions, $\lambda =1$

Fig. 19

Domain with hole example: overkilled solution of the problem. a Map of temperature t, b map of heat flux $q_x$, c map of heat flux $q_y$

Two meshes which have been a priori hp refined have been used to solve the problem. The refined meshes are shown in Fig. 20a and b for the first case and for the second case in Fig. 21a and b. It can be noticed that in both cases the meshes are non-conforming, but this is not a problem for the DGFD method. In case 1 the orders of finite elements that are in the close neighbourhood to the hole vertexes are $p=30$. The orders of farther elements are $p=15$ and the ones for the following elements $p=10$. The rest of the elements are of order $p=3$. The details are shown in Fig. 20b. In case 2 the most of the elements are of order $p=3$ but those close to the hole vertexes are of order $p=30$. It means that in the case 2 very high-ordered finite elements are set side by side to low-ordered finite elements. The results for these two cases are presented in the form of maps of heat fluxes $q_x$ and $q_y$: Fig. 20c and d for case 1 and in Fig. 21c and d for case 2. It can be seen in these results that in spite of the fact that both meshes are nonconforming and very high-ordered finite elements are combined with low-ordered finite elements the final results are continuous and of high-quality.

Fig. 20

Domain with hole example: approximate solution for hp refined mesh, case 1. a Nonconforming mesh, b orders p in elements, c map of flux $q_x$, d map of flux $q_y$

Fig. 21

Domain with hole example: approximate solution for hp refined mesh, case 2. a Nonconforming mesh, b orders p in elements, c map of flux $q_x$, d map of flux $q_y$

7 Conclusions

This paper presented the version of the DG method called DGFD method with very high-order elements. This approach made it possible to obtain high-order piecewise polynomial solution for polynomial order up to $p=101$ in 2D and $p=1001$ in 1D. Such high order solutions have been achieved by combining few techniques in one method, i.e.:

• 1. the discontinuous approximation upon finite elements is used,

• 2. the finite difference rules for compatibility conditions on the mesh skeleton and on the Dirichlet boundary are applied

• 3. the Chebyshev or Legendre polynomials are used as a basis functions in finite elements,

• 4. the orthogonality of the basis functions is obtained only in reference elements, so the transformations from the reference element to the real elements are employed,

• 5. the appropriate order of Gauss–Legendre quadrature is applied on the reference element.

In this method there are no shape functions nor nodes in finite elements. The degrees of freedom in a single finite element are just coefficients of linear combination of basis functions. The number of degrees of freedom in element (#edof) is strictly connected with the approximation order p. It can be easily shown that in 1D $\#\text {edof} = p+1$ and in 2D $\#\text {edof} = 0.5\cdot \left( (p-1)^2+p-1\right)$. For example in 2D for $p=101$ the $\#\text {edof}$ is 5253, and so on. On the other hand, due to the fact that the DG method is based on weak formulation we need to integrate polynomials up to the order of $2(p-1)$. So in consequence, when the approximating polynomial order is $p=1001$, the polynomials have to be integrated up to two thousand order, which in this paper has been done for the 1D example. The compatibility conditions based on finite difference rules are so effective that is possible to put side by side a very high-ordered element with a low-ordered element and the results remain continuous. The high computational efficiency of the proposed approach was proven. A high-quality approximate solution was obtained in quite a short time when a very high-order approximation was applied. The solution of similar quality but for low-order approximation can last even several dozens times longer.

It has been shown that in the DGFD method the orders of finite elements are unlimited from the practical point of view. Due to the rapid convergence rates on the meshes with very high-order elements the solution easily reaches the machine precision limits. The elements with $p>100$ are not justified from the application point of view, but it has been shown in this paper that it is feasible to use them. In 1D elements the number of degrees of freedom is almost the same as the elements order. While for 2D finite element the #dof goes up with the square power, i.e. second order finite elements keep 6 #dof while hundred order element has over five thousands #dof. Thus the p or h type mesh refinement, in situation when the mesh consists of very high-order elements, may cause significant increase of #dof in the mesh. On the other hand in the DGFD method the very high-order elements can be easily combined with low-order elements, as shown in one of the examples. Keeping in mind the fact that the orders of elements are practically unlimited, a balance between mesh density and element orders should be found to reveal the optimal combination, therefore further research is needed on the subject.

The main aim of this paper was to present the new method and illustrate it with a series of benchmark examples. The application of the very high-order DGFD method to other kinds of problems is a matter of further research.