An analysis of a discontinuous spectral element method for elastic wave propagation in a heterogeneous material

Abstract

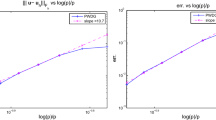
The numerical dispersion and dissipation properties of a discontinuous spectral element method are investigated in the context of elastic waves in one dimensional periodic heterogeneous materials. Their frequency dependence and elastic band characteristics are studied. Dispersion relations representing both pass band and stop band structures are derived and used to assess the accuracy of the numerical results. A high-order discontinuous spectral Galerkin method is used to calculate the complex dispersion relations in heterogeneous materials. Floquet–Bloch theory is used to derive the elastic band structure. The accuracy of the dispersion relation is investigated with respect to the spectral polynomial orders for three different cases of materials. Numerical investigations illustrate a spectral convergence in numerical accuracy with respect to the polynomial order based on the elastic band structure and a discontinuous jump of the maximum resolvable frequency within the pass bands resulting in a step-like increase of it with respect to the polynomial order.

Appendix

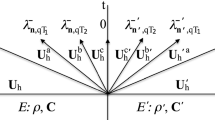
We derive the numerical dispersion relation of DSEM scheme chosen to simulate the elastic wave propagation through homogeneous materials in this study. Equation (12) can be expressed in the matrix form

$$\begin{aligned} \frac{\delta }{2}\mathbf{Q}\frac{\partial \mathbf{C}^{n}}{\partial t}+\mathbf{N}_{-1} \mathbf{C}^{n-1}+\mathbf{N}_0 \mathbf{C}^{n}+\mathbf{N}_1 \mathbf{C}^{n+1}=0, \end{aligned}$$

(41)

where $\mathbf{C}^{n} =[{\mathbf{C}_{0}^{n}} ,{\mathbf{C}_{1}^{n}} ,\ldots ,\mathbf{C}_{\mathrm{p}}^{n} ]^{\mathrm{T}}$. Here, $\mathbf{A}_{\mathrm{L}}^{n-1} =\mathbf{A}_{\mathrm{L}}^n$ and $\mathbf{A}_\mathrm{R}^{n+1} =\mathbf{A}_\mathrm{R}^n$ since the medium is homogeneous. If the element is uniform in one dimension, then we can seek solutions of the form

$$\begin{aligned} \mathbf{C}^{n}={\tilde{\mathbf{C}}}\hbox {e}^{\mathrm{j}(\omega t-kn\delta )}, \end{aligned}$$

(42)

where ${\tilde{\mathbf{C}}}$ is a complex vector of dimension $[\hbox {N}\times (\hbox {p}+1)]$. The substitution of Eq. (42) into (41) gives an algebraic system for ${\tilde{\mathbf{C}}}$

$$\begin{aligned} \left( \frac{\hbox {j}\omega \delta }{2}\mathbf{Q}+\hbox {e}^{\mathrm{j}k\delta }\mathbf{N}_{-1} +\mathbf{N}_0 +\hbox {e}^{-\mathrm{j}k\delta }\mathbf{N}_1 \right) {\tilde{\mathbf{C}}}=0. \end{aligned}$$

(43)

If we define the non-dimensional wave number and frequency as $\tilde{k}=k\delta$ and $\tilde{\omega }=\omega \delta /c$ where $c=\sqrt{K/\rho }$, Eq. (43) has a non-trivial solution when the determinant of the following matrix is zero, which leads to the numerical dispersion relation given by

$$\begin{aligned} \det \bigg (\frac{\hbox {j}c\tilde{\omega }}{2}\mathbf{Q}+\hbox {e}^{\mathrm{j}\tilde{k}}\mathbf{N}_{-1} +\mathbf{N}_0 +\hbox {e}^{-\mathrm{j}\tilde{k}}\mathbf{N}_1 \bigg )=0, \end{aligned}$$

(44)

where

$$\begin{aligned}&\{Q\}_{lm} =\mathbf{I}\int _{-1}^1 {L_l (\xi )L_m (\xi )\hbox {d}\xi } , \nonumber \\&\{N_0 \}_{lm} =\mathbf{A}_\mathrm{L}^n L_l (1)L_m (1)\nonumber \\&\quad -\mathbf{A}_\mathrm{R}^n L_l (-1)L_m (-1) -\mathbf{A}^{n}\int _{-1}^1 {L_m (\xi ) \frac{\partial L_l (\xi )}{\partial \xi }\hbox {d}\xi ,} \nonumber \\&\{N_{-1} \}_{lm} =-\mathbf{A}_\mathrm{L}^n L_m (1)L_l (-1),\nonumber \\&\{N_1 \}_{lm} =\mathbf{A}_\mathrm{R}^n L_m (-1)L_l (1), \nonumber \\&\quad \hbox { where }l,m=0,1,\ldots ,\hbox {p}. \end{aligned}$$

(45)