The effect of photosynthesis time scales on microalgae productivity

Abstract

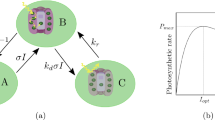
Microalgae are often seen as a potential biofuel producer. In order to predict achievable productivities in the so called raceway culturing system, the dynamics of photosynthesis has to be taken into account. In particular, the dynamical effect of inhibition by an excess of light (photoinhibition) must be represented. We propose a model considering both photosynthesis and growth dynamics. This model involves three different time scales. We study the response of this model to fluctuating light with different frequencies by slow/fast approximations. Therefore, we identify three different regimes for which a simplified expression for the model can be derived. These expressions give a hint on productivity improvement which can be expected by stimulating photosynthesis with a faster hydrodynamics.

Appendix A: analytical derivation

A1. Low frequency signal

Equation (11) is taken as an expression for the productivity of the photosynthetic system and the mean value during one period is taken. The domain of the integral can be restricted to the light phase of the cycle only, since during the dark phase B = 0.

$$\bar{B}_{\text{slow}} = \frac{1}{2T} \int\limits_T B \text{d}t$$

(36)

By replacing A by 1 − B − C, and assuming that A rests in its equilibrium while C is periodically oscillating:

$$B = \tau \sigma I A$$

(37)

we get:

$$\bar{B}_{\text{slow}} = \frac{1}{2}\frac{\tau \sigma I_0}{1 + \tau \sigma I_0} \left( 1- \frac{1}{T}\int\limits_T C \text{d}t \right)$$

(38)

Analogously, the differential equation for C can be reformulated

$$\dot{C} = -\left(k_\text{d} \tau \frac{(\sigma I_0)^2}{1+ \tau \sigma I_0} +k_\text{r}\right) C + \frac{(\sigma I_0)^2}{1+ \tau \sigma I_0}$$

(39)

This equation can be easily solved. C ₀ is determined by applying the periodic boarder condition. Several simplification steps lead to the following expression for the integral:

$$\int\limits_T C \text{d}t= \frac{C_0 - \delta(I)}{\epsilon}(1-\gamma(I) + \delta(I) T)$$

(40)

Using expression Eq. (38), we get expression Eq. (18).

A2. High frequency signal

Under the precondition that the periodicity of the signal is short, we already showed that the dynamics of C is negligible. In contrast, the transition process of A and B has to be taken into account. The expression for the mean growth rate has to account for the entire period, since B ≥ 0 during the dark phase. The expression for the growth rate turns to:

$$\bar{B}_{\text{fast}} = \frac{1}{2 T} \left( \int\limits_0^T B \text{d}t + \int\limits_T^{2T} B \text{d}t \right)$$

(41)

The first integral being during the light period and the second during the dark period. To solve the integrals, an expression for A(t) has to be determined from the differential equation. By assumption that C is a constant value and with periodical boarder conditions, Eq. (13) can be solved with the result:

$$A( t) = \left(A_0 + \frac{1-C}{1+ I_0 \sigma \tau}\right) e^{(-\frac{ t}{\tau}-I_0 \sigma \xi t)} - \frac{1-C}{1+ I_0 \sigma \tau},{ \quad{\text{for}} } \;t\in [0,T]$$

(42)

$$A( t) = \left(A_T + 1-C e^{(-\frac{t-T}{\tau})}\right) - 1-C,\quad{ \text{for} } \;t \in [T,2T]$$

(43)

With Eqs. (42) and (13), periodical boarder conditions and the assumption $\dot{C} = 0$, a value for C can be determined to:

$$C= \frac{k_\text{d}(\sigma I)^2}{2Tk_\text{r}} \frac{T\eta - T\theta}{\eta ^2 +\frac{k_\text{d}(\sigma I)^2}{2Tk_\text{r}}\left(T \eta - T\theta \right)}$$

(44)

with the expressions:

$$\eta = \frac{1}{\tau} + \sigma I_0, \quad\theta = \frac{(1-\alpha_0)(1-\alpha_\text{I})}{T(1-\alpha_0\alpha_\text{I})}, \quad\alpha_\text{I} = e^{-\left(\frac{1}{\tau} +\sigma I_0\right)T}, \quad\alpha_0 = e^{-\frac{T}{\tau} }$$

(45)

Knowing the value of C, the integrals in Eq. (41) can be resolved and B can be formulated as:

$$\bar{B}_{\text{fast}} = \frac{\sigma I_0}{2}\frac{\eta-\theta+\tau \delta \theta}{\eta ^2 + \frac{k_\text{d}(\sigma I)^2}{2 k_\text{r}}(\eta - \theta)}$$

(46)

A3. Proof of monotony

Low frequency

It can be shown, that the function:

$$\Phi(x, a, b) = \frac{(1-e^{-ax})(1-e^{-bx})}{x(1-e^{-(a+b)x})}$$

(47)

is strictly monotonic decreasing in x and it holds $\Phi(x,a,b) >0$ for a > 0, b > 0, x > 0.

Further, $\bar{B}_{\text{slow}}(I,T)$ can be defined as follows:

$$\bar{B}_{\text{slow}}(I,T) = \left( 1 + \frac{\delta(I)}{k_{\text{r}}} \Phi(T, k_{\text{r}}, \chi )\right) \cdot \bar{B}_{\text{SS}}/2$$

(48)

with $\chi = k_\text{r} + k_\text{d} \frac{(\sigma I)^2}{1+ \tau \sigma I}$, consequently, $\bar{B}_{\text{slow}}$ is strictly monotonic decreasing in T.

High frequency

$\bar{B}_{\text{fast}}$ can be written as:

$$\bar{B}_{\text{fast}} = \frac{\sigma I_0}{2}\frac{\eta-\Phi(1/ \tau , \eta , T)+\tau \eta \Phi(1/ \tau , \eta , T)}{\eta ^2 + \frac{k_{\text{d}}(\sigma I)^2}{2 k_{\text{r}}}(\eta - \Phi(1/ \tau , \eta , T))}$$

(49)

Derivation with respect to T yields:

$$\frac{\partial \bar{B}_{\text{fast}}}{\partial T} = \frac{\eta ^2 ( \frac{k_{\text{d}} \sigma I ^2}{2 k_{\text{r}}} + \sigma I \tau )}{\left(\eta ^2 + \frac{k_{\text{d}}(\sigma I)^2)^2}{2 k_{\text{r}}}(\eta - \Phi(1/ \tau , \kappa , T))\right)^2} \cdot \frac{\partial \Phi ( 1/ \tau, \eta , T)}{\partial T}$$

(50)

Taking into account the parameters, it is clear that the fraction is positive. With the property $\frac{\partial \Phi ( 1/ \tau, \eta , T)}{\partial T} < 0$, it is shown that $\bar{B}_{\text{fast}}$ is strictly monotonic decreasing with respect to T.