Abstract
We study a new integrable probabilistic system, defined in terms of a stochastic colored vertex model on a square lattice. The main distinctive feature of our model is a new family of parameters attached to diagonals rather than to rows or columns, like in other similar models. Because of these new parameters the previously known results about vertex models cannot be directly applied, but nevertheless the integrability remains, and we prove explicit integral expressions for q-deformed moments of the (colored) height functions of the model. Following known techniques our model can be interpreted as a q-discretization of the Beta polymer model from (Probab Theory Relat Fields 167(3):1057–1116 (2017). arXiv:1503.04117) with a new family of parameters, also attached to diagonals. To demonstrate how integrability with respect to the new diagonal parameters works, we extend the known results about Tracy–Widom large-scale fluctuations of the Beta polymer model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Overview
During the last decades a new conjectural universality law has been actively researched under the name KPZ universality, originating from [31]. Unfortunately, despite the significant breakthroughs made in recent years we are still unable to prove or sometimes even formulate the desired universality statements. However, for some exceptional models one can directly verify the large-scale properties expected from the KPZ class models by finding explicit expressions describing the precise behavior of natural observables. Such expressions come from intricate algebraic or combinatorial properties, usually referred to as integrability, and various recent examples of large-scale analysis of integrable models can be found in [1, 3,4,5,6,7, 17, 25, 26, 36, 44,45,46] and references therein.
We focus on two integrable models, namely, the q-Hahn vertex model and the directed Beta polymer model. The former model was introduced in [38] (see also [22, 24] for alternative descriptions) and it belongs to the family of stochastic solvable vertex models, which are of a particular interest for the following twofold reason. On one hand, vertex models have a rich algebraic integrability structure coming from the celebrated Yang–Baxter equation for \({\mathcal {R}}\)-matrix of the underlying quantum groups. In particular, this allows to find explicit integral expressions for q-deformed moments of naturally defined height functions, cf [7, 12, 16, 21]. On the other hand, the stochastic vertex models can be degenerated to numerous other integrable models, including ASEP, q-Hahn and q-boson particle systems, and the mentioned directed Beta polymer model, cf. [11, 16, 24]. During this transition the explicit integral expressions for the vertex models reduce to expressions describing natural observables of the other models, which allow to explicitly study various properties. In this way integrability of a number of probabilistic systems can be inferred from the Yang–Baxter integrability of the vertex models.
The directed Beta polymer was originally introduced in [4] using two equivalent descriptions: it can either be viewed as a polymer model with Beta distributed weights or as a random walk in a random time-dependent Beta environment. This dual description already distinguished the Beta polymer model among the other integrable discrete polymers, namely, log-Gamma [39], strict-weak [25, 36] and inverse-Beta [41] polymers, which cannot be readily interpreted as random walks in random environments (RWRE). Moreover, there is a whole cluster of integrable models obtainable as degenerations of the Beta polymer, this cluster includes strict-weak polymer, uniform sticky Brownian motions [17, 28, 33], Bernoulli-Exponential directed first passage percolation [4] as well as other percolation models. Going in the other direction, the Beta polymer itself can be obtained as a \(q\rightarrow 1\) limit of the q-Hahn vertex model, and this connection is closely related to the approach used originally in [4] to obtain integrability and asymptotics.Footnote 1 Overall, these numerous connections to other models give rise to a lot of interesting properties and conjectures, making Beta polymer a popular object in recent research, cf. [9, 17, 18, 32].
The present work is devoted to a new layer of integrability of the q-Hahn vertex model, which has remained unnoticed until now. Namely, we find a new family of parameters, which are attached to the diagonals of the square lattice defining the model and which can be added to the model without breaking the integrability. To capture the most general situation containing the new parameters we introduce diagonally inhomogeneous colored q-Hahn vertex model, and the first main result of this work is the proof of integral expressions for the q-deformed moments of the colored height functions of this model. Such explicit expressions justify our claims about integrability and encapsulate the behavior of the model in a form suitable for subsequent analysis. As a direct application, we demonstrate that the shift-invariance property from [11, 27] holds for our model, indicating that a broad class of symmetries is compatible with the additional parameters.
Existence of such integrable parameters attached to diagonals was surprising to us, and it is so far unique for the solvable vertex models: integrability is usually justified by the Yang–Baxter equation, which is well-suited only for the parameters attached to rows and columns of the model, but other parameters are typically incompatible with the Yang–Baxter equation. Accordingly, all other known solvable vertex models only have parameters attached to rows or columns. The q-Hahn model itself was known to have families of natural integrable column and row parameters coming from fusion of the six-vertex model, however, that construction did not indicate existence of the diagonal parameters in any way. Moreover, to the best of our knowledge the new diagonally inhomogeneous q-Hahn model cannot be obtained from any other model via known procedures. We believe that this is one of the reasons why the integrability with respect to diagonals has been hidden.
As an immediate consequence of our first result, we are able to degenerate the diagonal integrability to the Beta polymer model, finding an integrable inhomogeneous extension containing three families of parameters, attached to columns, rows and diagonals. Previously, only Beta polymer models inhomogeneous along two directions at most were known to be integrable. Moreover, to the best of our knowledge, this is the first integrable example of a directed polymer model inhomogeneous in three directions (there exist several related models with two families of parameters, studied in [5, 23, 42]). We expect that a lot of currently known properties of the Beta polymer can be extended to our inhomogeneous version, moreover, some new properties might emerge based on the new extension. To reinforce this claim, as the second main result of this work we find the Tracy–Widom asymptotics for the inhomogeneous model, extending one of the original results about the Beta polymer from [4].
Below we briefly describe the models and our results.
1.2 Main results: integral expressions for the diagonally inhomogeneous q-Hahn model
Let \(q\in (0,1)\) and \((\mu _0, \mu _1, \mu _2, \dots )\), \((\kappa _1, \kappa _2, \dots )\), \((\lambda _1,\lambda _2,\dots )\) be real parameters satisfying
The colored diagonally inhomogeneous q-Hahn vertex model consists of a random ensemble of colored up-right paths in a positive quadrant \({\mathbb {Z}}_{\ge 0}^2\), with colors labeled by positive integers. The paths are sampled according to the following procedure:
-
All paths start from the left boundary of the model \(\{0\}\times {\mathbb {Z}}_{\ge 1}\), with \(b_j\) paths of color j starting at (0, j). The numbers \(b_j\) are independent and distributed according to
$$\begin{aligned} \mathbb P(b_j=b)=(\kappa _j/\mu _0)^b\frac{(\lambda _j/\kappa _j;q)_b}{(q;q)_b}\frac{(\kappa _j/\mu _0;q)_\infty }{(\lambda _j/\mu _0;q)_\infty }, \qquad b\in {\mathbb {Z}}_{\ge 0}. \end{aligned}$$ -
The remaining configuration is sampled sequentially and independently around each integer point (i, j), starting from the bottom and going along the rows. At each integer point all paths coming from the left turn upwards, while the paths coming from below might turn right following the probabilities

where \(\varvec{A}=(A_1, A_2, \dots )\) is a finite integer sequence with \(A_c\) equal to the number of paths of color c entering from below, \(\varvec{B},\varvec{C},\varvec{D}\) similarly encode the colors of paths along the left, top and the right edges respectively, and we set \(|\varvec{A}|=A_1+A_2+\cdots , |\varvec{D}|=D_1+D_2+\cdots \).
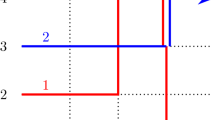
The name for the model comes from the probabilities above: one can notice that, for a specific choice of parameters, the probabilities resemble the orthogonality weights of the q-Hahn polynomials. On the other hand, the probabilities depend on the parameters \(\mu _i,\kappa _j,\lambda _{j-i}\) attached to columns \(i=const\), rows \(j=const\) or diagonals \(j-i=const\) respectively, hence we call the model inhomogeneous, see Fig. 1 for a schematic description of the parameters. Finally, the diagonal parameters make our model unique among the other vertex models, hence inhomogeneity in this direction is emphasized.
The configurations of our model can be described in terms of colored height functions \(h_{\ge c}^{(x,y)}\), which are assigned to the facets \((x,y)\in \left( {\mathbb {Z}}+\frac{1}{2}\right) ^2\) formed by rows and columns and count the number of paths of color \(\ge c\) passing below the facet, as depicted on Fig. 1. We consider the following observable: for collections
and a permutation \(\tau \in S_k\) set \(\tau .{\mathbf {c}}=(c_{\tau ^{-1}(1)}, c_{\tau ^{-1}(2)}, \dots , c_{\tau ^{-1}(k)})\) and
Theorem 1.1
(Theorem 4.2 in the text) With the notation above we have
where the positively oriented contours \(\varGamma _b\) are chosen to enclose \(\mu _i^{-1}\) and \(q\varGamma _a\) for \(a<b\), with other singularities being outside of the contours, and \(T_{\tau }\) denotes the polynomial representation of the Hecke algebra generated by the Demazure-Lusztig operators
The proof is based on the idea which has already appeared in [12]: we show that both sides of (1.1) satisfy the same discrete recurrence relations, called local relations. However, the required local relations and our way of proving them are novel: we use Yang–Baxter equations for this purpose, directly connecting the existence of local relations with the integrability of vertex models. Surprisingly, one of the needed equations is the recently discovered deformed Yang–Baxter equation from [13], which has appeared in the context of spin q-Whittaker functions.
Theorem 1.1 and the recurrence relations based on the Yang–Baxter equations indicate that our model is integrable, however, they do not clearly explain where the integrability and the diagonal parameters come from. To partially remedy this, let us briefly outline a more constructive approach to Theorem 1.1, which however does not work in full generality. The main idea comes from [16, 21]: By definition, the average of an observable \({\mathcal {O}}\) can be written as
It turns out that for certain observables \({\mathcal {O}}\) similar to \({\mathcal {Q}}_{\ge \tau .{\mathbf {c}}}^{({\mathbf {x}},{\mathbf {y}})}\) one can relate both \(\mathcal O(\lambda )\) and \({\mathbb {P}}[\lambda ]\) to spin deformations of Hall–Littlewood or q-Whittaker symmetric functions, which are constructed using higher spin six-vertex model (cf. [15, 16, 19]) or q-Hahn model (cf. [13, 20, 35]). In this situation to compute \({\mathbb {E}}\left[ {\mathcal {O}}\right] \) one can first find a suitable Cauchy-type summation identity, which identifies the sum above with a single evaluation of a higher-spin symmetric function, and then find an integral expression for the latter.
For this constructive approach to work, one needs Cauchy-type summation identities and integral expressions for higher-spin functions, which in the context of vertex models are usually found with a “zipper”-argument based on a suitable Yang–Baxter equation. Unfortunately, we do not know how to do it for our model in full generality. However we can find suitable Yang–Baxter equations in two situations: In the previously known case when all parameters \(\lambda _d\) attached to diagonals are equal this was done in [16, 21] using Yang–Baxter equations coming from the colored six vertex-model. In the other case, when all column parameters \(\mu _i\) are equal and we ignore the colors of the model, the integral expression can be constructed using the deformed Yang–Baxter equation from [13], which has an additional degree of freedom giving rise to the diagonal parameters. The exact form of our model and Theorem 1.1 were initially heuristically conjectured by taking superposition of these two cases.
1.3 Main results: limit theorem for inhomogeneous Beta polymer
Consider a lattice on the plane formed by the edges \((i,j)\rightarrow (i+1,j+1)\) and \((i,j)\rightarrow (i,j+1)\) for \((i,j)\in \mathbb Z_{\ge 0}^2\) such that \(j\ge i\). Let \({\widetilde{\sigma }}_i,{\widetilde{\rho }}_j,{\widetilde{\omega }}_d\) be a family of real parameters attached to columns \(i=const\), rows \(j=const\) and diagonals \(j-i=const\) respectively and satisfying
To each edge we assign a weight in the following way: for each integer point (i, j) we first independently sample a random variable \(\eta _{i,j}\sim {{\,\mathrm{Beta}\,}}({\widetilde{\sigma }}_i-{\widetilde{\rho }}_j, {\widetilde{\rho }}_j-{\widetilde{\omega }}_{j-i})\) using the Beta distribution
and then we set
The delayed Beta polymer partition function \({\mathfrak {Z}}_{x,y}^{(r)}\) is defined as
where the sum is over all directed lattice paths \(\pi \) from (0, r) to (x, y), and \(f(\pi )=\min \{i\mid \pi _{i+1}-\pi _i=(0,1)\}\), so the path starts accumulating its weight with a delay, waiting until the first vertical step, see Fig. 2.
The partition function \({\mathfrak {Z}}_{x,y}^{(r)}\) also has an alternative description, in terms of a random walk in a random environment (RWRE). Fix x, y and let \(\eta _{i,j}\sim {{\,\mathrm{Beta}\,}}({\widetilde{\sigma }}_i-{\widetilde{\rho }}_j, {\widetilde{\rho }}_j-{\widetilde{\omega }}_{j-i})\) be the random variables as in the polymer description above. Then, conditionally on the random environment \(\{\eta _{i,j}\}_{i,j}\), we consider a random walk \(X_t\) on \({\mathbb {Z}}\), starting at \(X_0=2x-y\) and doing independent \(\pm 1\) steps with probabilities
where we use \(\mathsf P\) to denote the probability space of the random walk, conditioned on the environment \(\{\eta _{i,j}\}_{i,j}\). With this setup, we have \({\mathfrak {Z}}_{x,y}^{(r)}=\mathsf{P}(X_{y-r}\ge -r)\), which can be checked as in [4].Footnote 2 Note that in the RWRE description the parameters \({\widetilde{\sigma }}_i,{\widetilde{\rho }}_j,{\widetilde{\omega }}_d\) are attached to the lines \(t-X={const}\), \(t=const\) and \(t+X=const\) respectively.
Under a \(q\rightarrow 1\) limit the diagonally inhomogeneous q-Hahn model converges to the inhomogeneous Beta polymer, and the expression from Theorem 1.1 produces an explicit integral expression for the moments:
where the contour \({\mathcal {S}}_b\) surrounds \({\widetilde{\sigma }}_i\) and \({\mathcal {S}}_a+1\) for \(a<b\). Such integral expressions are well-suited for asymptotic analysis and the standard workflow consists of first obtaining a Fredholm determinant expression for the Laplace transform of \({\mathfrak {Z}}^{(r)}_{x,y}\) (which is analytic since \({\mathfrak {Z}}^{(r)}_{x,y}\in (0,1)\) almost surely) and then performing a steep descent analysis. Below we list our results.
Consider the large scale limit of \({\mathfrak {Z}}^{(0)}_{\lfloor {xt} \rfloor ,\lfloor {yt} \rfloor }\) when the parameters \({\widetilde{\sigma }}_i,{\widetilde{\rho }}_j,{\widetilde{\omega }}_d\) have finite number of possible values \(\sigma _i, \rho _j, \omega _d\) repeated with frequencies \(\alpha _i,\beta _j,\gamma _d\). For example, when \(\gamma _1=\gamma _2=\frac{1}{2}\) we assume that half of the diagonals have parameter \({\widetilde{\omega }}_d=\omega _1\) while the other half has parameter \(\omega _2\); see Sect. 8 for a precise description of the model. We conjecture (Conjecture 8.2 in the text) that the following limit relation holds:
where the slope \(x/y\in (0, \frac{\sum \beta _i\rho _i-\sum \gamma _i\omega _i}{\sum \alpha _i\sigma _i-\sum \gamma _i\omega _i})\) is fixed,Footnote 3\(F_{GUE}(s)\) denotes the GUE Tracy–Widom distribution [43] and the constants I, c are defined in an implicit way involving an auxiliary parameter \(\theta \in (\max _i\sigma _i, \infty )\) and polygamma functions \(\varPsi _k\):
Under assumptions dictated by purely technical reasons we are also able to partially verify our conjecture:
Theorem 1.2
(Theorem 8.4 in the text) When \(\theta \in (0,\frac{1}{2})\) and
we have
with the notation specified above.
In other words, we are able to partially verify the conjectural limit statement for the model having only diagonal parameters \(\omega _d<-1\), with Beta distributions \({{\,\mathrm{Beta}\,}}(1, -1-\omega _d)\). Note that even in the homogeneous case our result is more general than the analogous one from [4], where the full proof is given only for the model with \({{\,\mathrm{Beta}\,}}(1,1)\) distributions.
Shortly after this paper has been written, a more general limit result for the homogeneous Beta polymer has appeared in [37], and it covers the model with \({{\,\mathrm{Beta}\,}}(\alpha ,\beta )\) distributions for arbitrary \(\alpha ,\beta \in {\mathbb {R}}_{>0}\). It would be interesting to see in what generality the methods and results from [37] can be transferred to the inhomogeneous model.
1.4 Layout of the paper
Sections 2–5 are devoted to the integrability of the q-Hahn vertex model with diagonal parameters: In Sect. 2 we describe the needed background on vertex models and Yang–Baxter equations, which is immediately used in Sect. 3 to establish local recurrence relations for the q-Hahn model. In Sect. 4 we define the q-Hahn vertex model and prove one of the central results of this work, Theorem 4.2, using relations from the previous section. Section 5 is a brief overview of the shift-invariance property for the vertex models, which can be established using Theorem 4.2. Then we pass to the Beta polymer side of the work, starting with Sect. 6 where we describe the transition from the q-Hahn vertex model to the Beta polymer model, and continuing with Sect. 7 where we use integral expressions coming from Theorem 4.2 to write a Fredholm determinant expression for the Laplace transform of the polymer partition function. Finally, Sect. 8 is devoted to the large-scale analysis of the inhomogeneous Beta polymer model, with the results stated in Conjecture 8.2 and Theorem 8.4.
1.5 Notation
Throughout the work we follow the following standard notation. For \(k\in {\mathbb {Z}}_{>0}\) the symmetric group of rank k consists of permutations of k elements and is denoted by \(S_k\). For a permutation \(\pi \in S_k\) its length is denoted by \(l(\pi )\) and is defined as the number of pairs (i, j) such that \(i<j\) and \(\pi (i)>\pi (j)\). A partition \(\lambda \) is a finite integer sequence \(\lambda _1\ge \lambda _2\ge \cdots \ge \lambda _l>0\), with \(l=l(\lambda )\) being called the length of \(\lambda \). If \(\lambda _1+\cdots +\lambda _{l(\lambda )}=n\) we write \(\lambda \vdash n\). The part multiplicities \(m_k(\lambda )\) are defined by \(m_k(\lambda )=\#\{i\mid \lambda _i=k\}\).
For any \(n\in {\mathbb {Z}}\) the q-Pochhammer symbol is defined as
In particular, \((x;q)_0:=1\). We also set \((x;q)_\infty :=\prod _{i=1}^{\infty }(1-xq^{i-1})\). For \(n,m\ge 0\) the q-binomial coefficient \(\left( {\begin{array}{c}n\\ m\end{array}}\right) _q\) is given by
With the assumption \(|q|<1\), all expressions above make sense both numerically and formally in the space of power series in q.
For a pair of parameters \((\alpha ,\beta )\in {\mathbb {R}}_{\ge 0}^2\) the Beta distribution is defined by the following density function with respect to the Lebesgue measure:
where \(\varGamma (z)\) is the Gamma function. We use \({{\,\mathrm{Beta}\,}}(\alpha ,\beta )\) to denote a Beta-distributed random variable with the corresponding parameters.
For a trace-class operator K over \(L^2(X)\) we use \(\det (I+K)_{L^{2}(X)}\) to denote its Fredholm determinant. The only operators K considered in this work are integral operators of the form
where K(x, y) is called the kernel of K. In this case the Fredholm determinant is given explicitly by
We often use Fredholm determinants over complex integration contours, so for a contour \({\mathcal {C}}\subset {\mathbb {C}}\) we let \(L^2({\mathcal {C}})\) denote the space of functions on \({\mathcal {C}}\) with the complex valued integration measure \(\frac{dz}{2\pi {\mathbf {i}}}\).
The Tracy–Widom GUE cumulative distribution function \(F_{GUE}(r)\) is defined by
where \({{\,\mathrm{Ai}\,}}(z)\) is the Airy function and the integration contours in the last expression do not intersect and go to infinity along the prescribed directions.
2 Vertex models and Yang–Baxter equation
The focus of this section is the Yang–Baxter equation, which can be seen as the fundamental reason for integrability of the models presented in this work. More precisely, here we introduce our notation for vertex models, describe vertex weights and provide known forms and consequences of the Yang–Baxter equation.
2.1 Vertex configurations and weights
Vertex models are described in terms of vertices, which we graphically represent as intersections of oriented lines. Segments of the lines separated by the vertices are called edges, so each vertex has a pair of incoming edges and a pair of outgoing edges. A configuration of a vertex is an assignment of four labels to the adjacent edges. Finally, to each vertex configuration we assign a vertex weight, depending on these four labels.
Configurations of our models are labeled by compositions assigned to the edges, that is, by n-tuples of nonnegative integers \(\varvec{A}=(A_1,A_2, \dots , A_n)\in {\mathbb {Z}}_{\ge 0}^n\). We often present configurations as ensembles of oriented colored lattice paths directed along the edges, with colors labeled by integers \(1, 2, \dots , n\).Footnote 4 The two descriptions are identified by encoding the colors of paths occupying a single edge by a composition \(\varvec{A}=(A_1, \dots , A_n)\), where \(A_i\) is the number of paths with color i.
Throughout the text we use the following notation regarding compositions. For a composition \(\varvec{A}=(A_1, \dots , A_n)\) we set \(|\varvec{A}|:=A_1+A_2+\cdots +A_n\). More generally, for integers \(1\le i,j\le n\) let
Finally, given a composition \(\varvec{A}\) we can define an ordered \(|\varvec{A}|\)-tuple of integers \(1^{A_1}2^{A_2}\dots n^{A_n}\) which consists of 1 repeated \(A_1\) times, followed by \(A_2\) copies of 2, \(A_3\) copies of 3 and so on.
The main family of vertex weights used in this work is the family of q-HahnFootnote 5 vertex weights, denoted in one of the following ways

and given explicitly by
Here \(\varvec{A}=(A_1, \dots , A_n), \varvec{B}=(B_1, \dots , B_n), \varvec{C}=(C_1, \dots , C_n), \varvec{D}=(D_1, \dots , D_n)\) are compositions, q is a globally fixed quantization parameter and s, t are spin parameters. Note that the weights \(W_{t,s}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\) vanish unless the following conservation law holds:
Moreover, the weights \(W_{t,s}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\) vanish unless \(\varvec{A}\ge \varvec{D}\), that is, \(A_i\ge D_i\) for all i. Moreover, the weights \(W_{t,s}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\) do not depend on \(\varvec{B}\) and \(\varvec{C}\) as long as the conservation law (2.4) holds.
Another family of vertex weights used in this work consists of higher spin six-vertex weights and is denoted by

where j, l are integers from [0, n] and \(\varvec{I},\varvec{K}\) are compositions. To keep consistency with the edge labelling by compositions, we can interpret integers j, l as compositions \(\varvec{J},\varvec{L}\) satisfying \(|\varvec{J}|,|\varvec{L}|\le 1\): if \(j=0\) set \(\varvec{J}={\mathbf {e}}^0={\mathbf {0}}=(0, \dots , 0)\), while for \(j\ne 0\) set \(\varvec{J}\) equal to the standard basis vector \({\mathbf {e}}^j\in {\mathbb {Z}}^n\):

The values of the weights \(w_{z;s}\) are summarized in the table below:

where i, j are integers from [1, n] satisfying \(i<j\), \(\varvec{I}=(I_1, \dots , I_n)\) is a composition and all unlisted weights are assumed to be 0 since they violate the conservation law. The parameter q is the same quantization parameter as in the q-Hahn weights, while the parameters z and s are spectral and spin parameters respectively.
Both vertex weights \(W_{t,s}\) and \(w_{z;s}\) are particular cases of more general weights \(\mathcal W_{z}^{\mathsf{N},\mathsf{M}}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\),Footnote 6 which are defined for compositions satisfying
and are given explicitly by
where the sum is over compositions \(\varvec{P}=(P_1, \dots , P_n)\) such that \(P_i\le \min (B_i, C_i)\) and we set
The weights \(W_{t,s}\) and \(w_{u;s}\) are recovered using the following specializations:

where we use the rational dependence of the weights \({\mathcal {W}}_{z}^{\mathsf{N},\mathsf{M}}\) on \(q^{-\mathsf{N}}\) and \(q^{-\mathsf{M}}\) to perform analytic continuations, replacing \(q^{-\mathsf{N}}\) and \(q^{-\mathsf{M}}\) by \(t^2\) and \(s^2\) respectively.
Though it is not needed for our purposes, let us briefly elaborate on the origins of these weights. The weights \(\mathcal W_{z}^{\mathsf{N},\mathsf{M}}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\) originate from the quantum group \(U_q(\widehat{\mathfrak {sl}}_{n+1})\) and can be seen as the matrix coefficients of a renormalized \({\mathcal {R}}\)-matrix acting on symmetric tensor representations, see [30]. The explicit expression (2.8) was obtained in [14] using methods of three-dimensional solvability. See [19, Appendix C] for a condensed summary of the properties of \({\mathcal {W}}_{z}^{\mathsf{N},\mathsf{M}}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\) relevant for the current work. The colored higher spin six-vertex weights are coefficients of the \({\mathcal {R}}\)-matrix above when one of the representations is the standard representation, and these weights are related to a spin deformation of the non-symmetric Hall–Littlewood polynomials, see [19] and Remark 3.8. The q-Hahn weights are not as well-understood as the other weights; we limit ourselves to stating that in one-color case they are related to spin deformations of the q-Whittaker symmetric functions, see [13, 20, 35].
2.2 Yang–Baxter equations
The vertex weights described above are distinguished by an algebraic relation called the Yang–Baxter equation. In the most general situation relevant to this work the Yang–Baxter equation is given in [19, Appendix C]:
where both sums are taken over arbitrary triples of compositions \(\varvec{K}_1, \varvec{K}_2, \varvec{K}_3\). Note that both sums are actually finite due to the non-negativity of compositions and the conservation law.
Setting \(x=y=z\) and using specialization (2.9) we obtain the Yang–Baxter equation for the weights \(W_{t,s}\):
Throughout the text we usually write such equations using graphical notation. For instance, (2.11) is represented by the following diagrammatic equation:

More precisely, the diagrams like the above one denote partition functions of the corresponding models. That is, given such a diagram with a fixed labelling of the boundary edges and an assignment of vertex weights to the vertices, the corresponding partition function is defined by taking the sum of products of vertex weights over all possible configurations of the internal edges.
Another instance of the Yang–Baxter equation is obtained by setting \(\mathsf{N}=1, y=z=1\) in (2.10) and applying (2.9). The result is graphically represented by

Note that we again use diagrams to write the equation, but this time the lines have different thickness. Throughout the text we follow the following convention: thick edges can be labelled by any compositions, while thin edges are labeled by compositions \(\varvec{I}\) with \(|\varvec{I}|\le 1\).
In [13] it was shown that the Yang Baxter equations involving the weights \(W_{t,s}\) can be sometimes deformed by adding an additional parameter to the equation in a nontrivial way. More precisely, the following deformed Yang–Baxter equations hold:

where \(\eta \) in both cases is the added deformation parameter.
Since the context of [13] required only one-colored models, the deformed Yang–Baxter equations were only proved in that case, while for the colored situation the proofs can be repeated verbatim. However, for the completeness sake, we provide the proofs for the colored setting in “Appendix A” of the arXiv version of this paper.
2.3 Stochasticity
Apart from the Yang–Baxter equation the vertex weights \(W_{t,s}\) and \(w_{z;s}\) satisfy another property, namely, they are stochastic: the sum of vertex weights with the same valid incoming configuration is equal to 1. In other words, the following identities hold

where for the first identity \(\varvec{A},\varvec{B}\) are arbitrary compositions, and for the second one \(\varvec{I}\) is an arbitrary composition and \(j\in [0, n]\).
The importance of the stochasticity comes from the probabilistic interpretation of the vertex models, where the stochastic weights can be used to define a stochastic sampling rule for an outgoing configuration of a vertex given an incoming one. We postpone the detailed discussion of this construction until Sect. 4.
There are several ways to establish relations (2.16), (2.17). One option is to verify everything by a direct computation, which can be readily performed for the weights \(w_{z;s}\), but gets more involved for the weights \(W_{t,s}\). Another approach is to use the general weights \({\mathcal {W}}_{z}^{\mathsf{N},\mathsf{M}}\), which turn out to be stochastic as well:
where \(\varvec{A},\varvec{B}\) are arbitrary compositions satisfying the constraints (2.7). The latter fact can be derived, for example, from the fusion construction of the weights \({\mathcal {W}}_{z}^{\mathsf{N},\mathsf{M}}\), see [11, Appendix].
Finally, for the weights \(W_{t,s}\) one can use the Yang–Baxter equation to prove (2.16). This approach is described in Sect. 3, where a more general local relation is considered.
2.4 Exchange relations and Hecke algebras
Given a vertex model, it is usual to consider row-to-row transfer matrices. For a fixed L let \(V_L\) denote an infinite dimensional vector space with basis enumerated by L-tuples of compositions. We denote the elements of this basis by \(|\varvec{I}_1, \dots , \varvec{I}_L\rangle \) and we let \(\langle \varvec{I}_1, \dots , \varvec{I}_L|\in V_L^*\) denote the elements of the basis dual to \(\{|\varvec{I}_1, \dots , \varvec{I}_L\rangle \}_{\varvec{I}_1, \dots , \varvec{I}_L}\).
For a fixed pair of families \(\varXi =(\xi _1, \dots , \xi _L)\in \mathbb R^L,\mathsf{S}=(s_1, \dots , s_L)\in {\mathbb {R}}^L\), define operators \({\mathcal {C}}_i(u\mid \varXi ,\mathsf{S})\) on \(V_L\) by

where \(1\le i\le n\) and the partition function on the right-hand side consists of L vertices with the weights \(w_{u\xi _1;s_1}, w_{u\xi _2;s_2}, \dots , w_{u\xi _L, s_L}\). For any \(1\le i<j\le n\) the operators \({\mathcal {C}}_i,{\mathcal {C}}_j\) satisfy the following commutation relations:
All these relations can be proved using the Yang–Baxter equation, namely, set \(\mathsf{N}=\mathsf{M}=1\) in (2.10) and apply a zipper-like argument to move a vertex with weights \({\mathcal {W}}^{1,1}_{u/v}\) between a pair of rows. The exact argument is given in [19, Theorem 3.2.2].Footnote 7
For the purposes of this work we only need the commutation relation (2.20), which we rewrite as
where \(T^{(w_1,w_2)}\) is an operator acting on rational functions in \(w_1,w_2\) by
Operators \(T^{(w_1,w_2)}\) are closely related to the polynomial representation of the Hecke algebra via Demazure-Lusztig operators. The Hecke algebra \({\mathcal {H}}_k\) is a \({\mathbb {C}}\)-algebra with basis \(\{T_\pi \}_{\pi \in S_k}\) enumerated by permutations \(\pi \in S_k\) and satisfying the following defining relations
where \(T_i=T_{\sigma _i}\) denote the basis elements corresponding to the simple transpositions \(\sigma _i\) exchanging i and \(i+1\). Note that the elements \(T_i\) generate \({\mathcal {H}}_k\), and thus we can define a representation of \({\mathcal {H}}_k\) on the rational functions in \(w_1, \dots , w_k\) by setting
where \({\mathfrak {s}}_i\) denotes the operator exchanging the variables \(w_i\) and \(w_{i+1}\).Footnote 8 Note that these operators preserve polynomials in \(w_1, \dots , w_k\), hence for any rational function f in \(w_1,\dots , w_k\) the function \(T_\pi f\) is well defined on the domain of f, that is, \(T_\pi f\) does not have any additional singularities compared to f.
3 Local relations
In this section we use the Yang–Baxter equation to derive two recurrence relations: the first relation captures the local behavior of q-moments of the colored height functions, defined in the next section, while the other relation compares rational function of certain form. While the underlying objects behind these relations are different, surprisingly, the relations themselves turn out to be identical. This observation will play a central role in the proof of one of the main results of this work, namely Theorem 4.2.
3.1 Ordered permutations
Both local relations in this section can be described in terms of order-preserving length p subsequences of a generic sequence \({\mathbf {c}}=(c_1, c_2, \dots , c_r)\), which can be naturally encoded by subsets \({\mathcal {I}}=\{i_1, i_2, \dots , i_p\}\subset \{1, 2, \dots , r\}\):
But for our purposes it is more convenient to encode such subsequences using permutations. Recall that the action of the symmetric group on sequences is defined by
Then any subsequence of \({\mathbf {c}}\) can be constructed as
for a permutation \(\pi \) satisfying
This leads us to the following definitions.
A permutation \(\pi \) is called [a, b]-ordered if
More generally, a permutation \(\pi \) is \([a_1,b_1]\times [a_2,b_2]\)-ordered if it is simultaneously \([a_1,b_1]\)-ordered and \([a_2,b_2]\)-ordered. With this notation the following can be readily verified:
Lemma 3.1
There is a one-to-one correspondence between integer subsets \(\{i_1, \dots , i_p\}\subset [1,r]\) and \([1,p]\times [p+1,r]\)-ordered permutations \(\pi \) determined by setting \(\pi ^{-1}(a)=i_a\) for \(1\le a\le p\), where we have ordered \(i_1<i_2<\cdots <i_p\). Moreover, for a \([1,p]\times [p+1,r]\)-ordered permutation \(\pi \) we have
\(\square \)
So, each order-preserving length p subsequence of \({\mathbf {c}}=(c_1, \dots , c_r)\) can be uniquely described as \(\pi .{\mathbf {c}}[1,p]\) for a \([1,p]\times [p+1, r]\)-ordered permutation \(\pi \).Footnote 9 We denote the set of such permutations by \(S^{p\mid r-p}\).
3.2 Local relation: q-moments
The first local relation describes the local behavior of a certain observable of the weights \(W_{s,t}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\), which are treated as a stochastic sampling rule for compositions \((\varvec{C},\varvec{D})\) given \((\varvec{A},\varvec{B})\).
Proposition 3.2
For any compositions \(\varvec{A},\varvec{B}, \varvec{R}\in {\mathbb {Z}}_{\ge 0}^{n}\) we have
where the sum in the right-hand side is over compositions \(\varvec{P}=(P_1, \dots , P_n)\) such that \(P_i\le R_i\).
The proof of Proposition 3.2 will be given shortly, but first we want to explain the probabilisitic interpretation of (3.1). For a sequence \({\mathbf {c}}=(c_1, c_2, \dots , c_r)\) and a composition \(\varvec{A}=(A_1,\dots , A_n)\) define
where we use the notation \(A_{[i,j]}\) from (2.1). Since the weights \(W_{t,s}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\) are stochastic we can define a (complex-valued) probability measure on configurations of the outgoing edges \((\varvec{C},\varvec{D})\) conditioned on a given fixed incoming configuration \((\varvec{A},\varvec{B})\). We denote this probability measure as
and let \({\mathbb {E}}_{t,s}\) denote the expectation with respect to this probability measure.
Corollary 3.3
For a sequence \({\mathbf {c}}=(c_1, \dots , c_r)\) such that
and arbitrary compositions \(\varvec{A},\varvec{B}\) the following relation holds
where the sum is over subsets \({\mathcal {I}}\subset \{1, 2, \dots , r\}\), \(l({\mathcal {I}})\) denotes the number of elements in \({\mathcal {I}}\) and
Equivalently,
where the sum is over all \([1,p]\times [p+1, r]\)-ordered permutations and
Reduction of Corollary 3.3 to Proposition 3.2
The second part follows at once from Lemma 3.1. So we focus on the first part.
Let \({\mathbf {c}}=1^{R_1}2^{R_2}\dots n^{R_n}\) for a composition \(\varvec{R}=(R_1,\dots , R_n)\) with \(|\varvec{R}|=r\), so that
Then for any composition \(\varvec{D}\) we have
Similarly, if \({\mathbf {c}}[{\mathcal {I}}]=1^{P_1}2^{P_2}\dots n^{P_n}\) for a composition \(\varvec{P}\), then \({\mathcal {Q}}_{\ge {\mathbf {c}}[\mathcal I]}(\varvec{A})=q^{\sum _{i\le j}P_iA_j}\). Thus, (3.3) is equivalent to
Note that \(P_i=\left| {\mathcal {I}}\cap \left\{ R_{[1,i-1]}+1,\dots ,R_{[1,i]}\right\} \right| \), so to reduce Corollary 3.3 to Proposition 3.2 it is enough to show for any compositions \(\varvec{P}\le \varvec{R}\) that
The latter relation readily follows from the standard expression for the q-binomial coefficients, cf. [29, Theorem 6.1]:
applied for \(1\le k\le n\) to the decomposition \(\mathcal I={\mathcal {I}}_1\sqcup {\mathcal {I}}_2\sqcup \cdots \sqcup {\mathcal {I}}_n\), with \({\mathcal {I}}_k:={\mathcal {I}}\cap \left\{ R_{[1,k-1]}+1,\dots , R_{[1,k]}\right\} \). \(\square \)
Proof of Proposition 3.2
The main idea is to see the relation (3.1) as a particular instance of the Yang–Baxter equation. We start with the Yang–Baxter equation (2.12) with the following parameters and boundary conditions

where \(t,s,\varvec{A},\varvec{B},\varvec{R}\) are the same as in (3.1), while \(\varepsilon \) is an arbitrary parameter and \(\varvec{X},\varvec{Y}\) are arbitrary compositions satisfying
The next step is to take \(\varepsilon \rightarrow 0\) and to analytically continue the labels of the vertical edges. Namely, consider the following vertex weights:

where \(\varvec{\alpha }=(\alpha _1, \dots , \alpha _n)\in \mathbb C^n\) and \(\varvec{\beta }=(\beta _1, \dots , \beta _n)\in {\mathbb {C}}^n\) are analytically continued compositions and we use the notation \(\varvec{\alpha }q^{\varvec{I}}=(\alpha _1q^{I_1}, \dots , \alpha _nq^{I_n})\). The weights \({\widetilde{W}}_t\) are obtained from the weights \(W_{t,\varepsilon }\) by taking \(\varepsilon \rightarrow 0\) and performing analytic continuation: using (2.3) one can readily verify that

Note that the weight \({\widetilde{W}}_{t}(\varvec{\alpha },\varvec{J};\varvec{\alpha }q^{\varvec{J}-\varvec{L}},\varvec{L})\) is a polynomial in \(\alpha _1, \alpha _2, \dots , \alpha _n\), with the highest degree termFootnote 10 having an explicit expression
Multiplying both sides of (3.5) by \(\varepsilon ^{-2|\varvec{R}|}\), taking \(\varepsilon =0\) and applying (3.6) we obtain

for any \(\varvec{\alpha }=(q^{X_1}, q^{X_2}, \dots , q^{X_n})\), where \(\varvec{X}=(X_1, \dots , X_n)\) is a composition satisfying \(\varvec{X}+\varvec{R}-\varvec{A}-\varvec{B}\ge 0\). Note that we have explicitly indicated the summations over internal edges in both sides of (3.8), specifying the internal labels. In particular, both sides are clearly finite sums of polynomial functions in \(\alpha _1, \dots , \alpha _n\) over \({\mathbb {C}}(q,s,t)\), hence the equality for \(\varvec{\alpha }=q^{\varvec{X}}\) can be continued to any \(\varvec{\alpha }=(\alpha _1, \dots , \alpha _n)\in {\mathbb {C}}^n\).
Having established (3.8) for arbitrary \(\varvec{\alpha }\), we can now set \(\varvec{\alpha }=(\alpha , \alpha , \dots , \alpha )\), that is, all \(\alpha _i\) are equal to a single variable \(\alpha \). Then both sides of (3.8) become polynomials in \(\alpha \) of degree \(nR_1+(n-1)R_2+\cdots + R_n\). Taking the highest degree coefficients using (3.7) we get
which is equivalent to (3.1) after elementary algebraic manipulations. \(\square \)
Remark 3.4
We have not used (2.16) during the proof of Proposition 3.2, so one can use the Yang–Baxter equation (2.12) to show that the weights \(W_{t,s}\) are stochastic.
Remark 3.5
The local relation above also holds for more general weights \({\mathcal {W}}^{\mathsf{N},\mathsf{M}}_{z}\) from (2.8), with the analogue of Proposition 3.2 having the following form:
Using the same methods as in Sect. 4 below, this identity can be written in a form similar to (4.15), describing the local behavior of the height functions around a vertex with weights \({\mathcal {W}}^{\mathsf{N},\mathsf{M}}_{z}\). Since (3.9) is not used in the present work we omit its proof, but the identity from Proposition 3.2 constitutes the majority of that proof: plugging the explicit expression (2.8) into the left-hand side of (3.9) one obtains a double summation which can be taken in the order allowing two subsequent applications of Proposition 3.2, readily leading to the right-hand side of (3.9) after algebraic manipulations.
Remark 3.6
For the six-vertex model the recurrence relation analogous to Corollary 3.3 can be found, in increasing generality, in [10,11,12] (in the former two the relation is called the four point relation). We note that the local relation for the q-Hahn model from the current work does not directly follows from those earlier results, and vice versa, the local relations for the six-vertex model cannot be obtained as degenerations of Corollary 3.3.
3.3 Local relation: rational functions
Now we turn to the second relation, which considers certain rational functions in \(w_1, \dots , w_r\). Recall that the action of the Hecke algebra \({\mathcal {H}}_r\) on the rational functions in \(w_1, \dots , w_r\) is generated by
Proposition 3.7
For any integer \(r\in {\mathbb {Z}}_{\ge 0}\) and any complex parameters \(t,s,\lambda \) such that \(s^2\ne q^{-n}\) for any \(n\in \mathbb Z_{\ge 0}\) the following equality of rational functions in \(w_1, \dots , w_r\) holds
where the sum is taken over \([1,p]\times [p+1, r]\)-ordered permutations \(\tau \), that is, permutations satisfying
Proof
The main idea of the proof is to take two columns of vertices with weights \(w_{u;s}\), find an explicit expression for their partition function using exchange relations and then apply the deformed Yang–Baxter equation (2.15) to exchange the columns. The resulting identity turns out to be equivalent to the claim. Throughout the proof we use additional complex parameters \(x,y,\varepsilon \) and we fix a composition \(\varvec{1}^r=(1, 1, \dots , 1)\in {\mathbb {Z}}^r\).
We start with defining the two-column functions mentioned above. For any composition \(\varvec{P}\le \varvec{1}^r\) define
where we set
and \({\mathcal {C}}_i\) are the row operators (2.18). Alternatively, we can depict these functions as

where the diagram consists of 2r vertices with the weights \(w_{z,t}\) from (2.5). The vertex at the intersection of row i and the first column has the spectral and spin parameters \(\left( \frac{\lambda w_{r-i+1}}{xs}; \frac{s}{x}\right) \), while the parameters of the other vertex in the same row are \(\left( \frac{\lambda w_{r-i+1}}{y\epsilon }; \frac{\epsilon }{y}\right) \).
Now we want to use the exchange relations to obtain an explicit expression for \(f_{\varvec{1}^r-\varvec{P}\mid \varvec{P}}\). Since x, y are fixed in this part of an argument, for now we write \(\varXi ,\mathsf{S}\) instead of \(\varXi _{x,y}, \mathsf{S}_{x,y}\). The exchange relation (2.22) implies that
for any permutation \(\pi \) such that \(l(\pi )<l(\pi \sigma _i)\), where \(\sigma _i\) is the transposition exchanging i and \(i+1\). The index \(r-i\) of the inverse Hecke algebra operator comes from the fact that w are ordered in the reverse order compared to \({\mathcal {C}}\). Iterating the identity above for a reduced expression \(\tau =\sigma _{i_1}\dots \sigma _{i_l}\) we obtain
where \({\widetilde{\tau }}\) is the image of \(\tau \) under the automorphism of \(S_r\) sending \(\sigma _i\) to \(\sigma _{r-i}\).
For now we focus on the partition function in the right-hand side of (3.10), namely

It turns out that the partition function above can be explicitly computed for a certain choice of \(\tau \). Namely, for a composition \(\varvec{P}\le \varvec{1}^r\) let \(\tau _{\varvec{P}}\in S_r\) be the unique permutation satisfying
In other words, \(\tau _{\varvec{P}}\) is the minimal permutation such that \(\tau ^{-1}_{\varvec{P}}(r-|\varvec{P}|+1), \dots , \tau ^{-1}_{\varvec{P}}(r)\) are the colors present in \(\varvec{P}\). Then for \(\tau =\tau _{\varvec{P}}\) the partition function (3.11) has only one configuration with non-vanishing contribution: the path of color \(\tau ^{-1}_{\varvec{P}}(i)\) for \(1\le i\le r-|\varvec{P}|\) enters at row i and immediately goes upwards, exiting through the first column, while the path of color \(\tau ^{-1}_{\varvec{P}}(i)\) for \(r-|\varvec{P}|< i\le r\) enters at row i, crosses the first column and exits through the second one. Since each horizontal edge can be occupied by at most one path, this is the unique possible configuration. Computing the vertex weights for this configuration gives
where we set \(p:=|\varvec{P}|\) and we use the definition of \(\tau _{\varvec{P}}\) to deduce
Plugging the expression above for the “frozen” partition function into (3.10) we get
The next step is based on the deformed Yang Baxter equation (2.15), used in the following form:

Here the tilted vertices have the weights \(W_{\epsilon /x,\epsilon /y}\), while the other vertices have w-weights with indicated parameters. Introducing a new operator \({\mathcal {R}}\) with coefficients
we can rewrite (3.12) as
Using this exchange relation, we obtain
where in the last equation we have explicitly evaluated the action of \({\mathcal {R}}\) on \(\langle \varvec{1}^r, \varvec{0}|\). Plugging the explicit expressions for the functions \(f_{\varvec{1}^r-\varvec{P}|\varvec{\varvec{P}}}\) gives
The remainder of the proof consists of algebraic manipulations bringing the identity above to the desired form. First, we set \(x=t\) and \(y=1\). Then, recalling the discussion from Sect. 3.1, the summation over \(\varvec{P}\le \varvec{1}^r\) is equivalent to the summation over subsets \({\mathcal {I}}\subset \{1,2,\dots ,r\}\), which is in turn equivalent to the summation over pairs \((p,\pi )\), where \(p\le r\) and \(\pi \in S^{r-p|p}\). Moreover, tracing back these equivalences, one can readily see that \(\varvec{P}\) corresponds to the pair \((|\varvec{P}|, \tau _{\varvec{P}})\), so we get
The claim follows since the action of the Hecke algebra commutes with the multiplication by \(\prod _{i=1}^r(1-\lambda t^{-2} w_i)^{-1}\) and \(\tau \in S^{r-p\mid p}\) if and only if \({\widetilde{\tau }}\in S^{p\mid r-p}\). \(\square \)
Remark 3.8
The functions \(f_{\varvec{1}^r-\varvec{P}|\varvec{P}}\) used throughout the proof of Proposition 3.7 are particular cases of the non-symmetric spin Hall–Littlewood functions introduced in [19]. The first part of the proof partially reproduces the exchange relations from [19, Section 5], while the second part can be interpreted as a new recurrence relation based on the deformed Yang–Baxter relation.
4 q-moments of height function
In this section we describe and prove the first main result of this work, namely, the integral expression for q-moments of the colored height functions of the colored diagonally inhomogeneous q-Hahn vertex model.
4.1 The model
As noted before, the weights \(W_{t,s}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\) are stochastic, so they can be used to interpret a vertex as a random sampling of an outgoing configuration given an incoming one. Now we extend this sampling construction by considering a grid of vertices with a certain choice of the spin parameters of the weights \(W_{t,s}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\). Then, given an incoming boundary conditions, we can sample a random configuration of the grid, that is, an assignment of a random composition to each lattice edge. Let us describe the construction in more detail.
Fix the number of colors n and consider a square grid of size \(N\times N\). We identify the grid with the subset of \(\mathbb Z_{\ge 0}^2\) formed by intersections of N rows \(\mathbb Z\times \{j\}\) directed to the right and N columns \(\mathbb Z\times \{i\}\) directed upwards, where \(1\le i,j\le N\). We treat this grid as a vertex model with vertices (i, j) for \(i,j\in [1,N]\), vertical edges \((i, j)\rightarrow (i,j+1)\) for \(i\in [1,N], j\in [0,N]\) and horizontal edges \((i, j)\rightarrow (i+1,j)\) for \(i\in [0,N], j\in [1,N]\). A configuration \(\varSigma \) of the model is an assignment of compositions to the edges listed above. We use \(\varvec{A}^{(i,j)}\) (resp. \(\varvec{B}^{(i,j)}\)) to denote the composition of the vertical (resp. horizontal) edge starting at (i, j).
Assume that we are given \(q\in (0,1)\), a composition \(\varvec{I}\) such that \(|\varvec{I}|=N\) and three families of real parameters \((\mu _0, \mu _1, \mu _2, \dots )\), \((\kappa _1, \kappa _2, \dots )\), \((\dots ,\lambda _{-1},\lambda _0,\lambda _1,\lambda _2,\dots )\) satisfying
We construct a random configuration \(\varSigma \) of the model according to the following sampling procedure:
-
The compositions \(\varvec{A}^{(i,0)}\) of all the bottom incoming vertical edges \((i,0)\rightarrow (i,1)\) are set to \(\varvec{0}\).
-
To construct compositions of the incoming left horizontal edges we first sample a collection of independent random nonnegative integers \((b_1, b_2, \dots , b_N)\) with distributions
$$\begin{aligned} \mathbb P(b_j=b)=(\kappa _j/\mu _0)^b\frac{(\lambda _j/\kappa _j;q)_b}{(q;q)_b}\frac{(\kappa _j/\mu _0;q)_\infty }{(\lambda _j/\mu _0;q)_\infty }, \qquad b\in {\mathbb {Z}}_{\ge 0}. \end{aligned}$$(4.2)Then the composition \(\varvec{B}^{(0,j)}\) of the jth incoming horizontal edge \((0,j)\rightarrow (1,j)\) has the form \(\varvec{B}^{(0,j)}=(0,\dots , 0, b_j, 0,\dots , 0)\), where all positions but \(B_c^{(0,j)}=b_j\) are equal to 0. The non-vanishing color c is determined as the unique color satisfying \(I_{[1,c-1]}<j\le I_{[1,c]}\). In other words, the left incoming edges of the first \(I_1\) rows have color 1, the next \(I_2\) rows have color 2 and so on.
-
The compositions of the remaining edges are sampled sequentially in \(N^2\) steps, which correspond to the vertices (i, j) of the model and are performed in lexicographical order with respect to (i, j), starting from the vertex (1, 1).
-
At each step we have a vertex (i, j) with already sampled compositions \(\varvec{A}^{(i,j-1)}\) and \(\varvec{B}^{(i-1,j)}\) of the incoming edges \((i,j-1)\rightarrow (i,j)\) and \((i-1,j)\rightarrow (i,j)\), due to the order of the steps. Then we treat the vertex weights \(W_{\sqrt{\lambda _{j-i}/\kappa _j},\sqrt{\lambda _{j-i}/\mu _i}}\) as probabilities for a stochastic sampling algorithm, transforming the incoming compositions into the outgoing ones \(\varvec{A}^{(i,j)},\varvec{B}^{(i,j)}\):
$$\begin{aligned}&{\mathbb {P}}(\varvec{A}^{(i,j)}=\varvec{C}, \varvec{B}^{(i,j)}=\varvec{D}\mid \varvec{A}^{(i,j-1)}=\varvec{A}, \varvec{B}^{(i-1,j)}=\varvec{B})=W_{\sqrt{\frac{\lambda _{j-i}}{\kappa _j}}, \sqrt{\frac{\lambda _{j-i}}{\mu _i}}}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\nonumber \\&\quad =\mathbb {1}_{\varvec{A}+\varvec{B}=\varvec{C}+\varvec{D}}\ (\kappa _j/\mu _i)^{|\varvec{D}|}\frac{(\kappa _j/\mu _i;q)_{|\varvec{A}|-|\varvec{D}|}(\lambda _{j-i}/\kappa _j;q)_{|\varvec{D}|}}{(\lambda _{j-i}/\mu _i;q)_{|\varvec{A}|}}q^{\sum _{i<j}D_i(A_j-D_j)}\prod _{i=1}^n\left( {\begin{array}{c}A_i\\ D_i\end{array}}\right) _q.\nonumber \\ \end{aligned}$$(4.3)
Note that all the probabilities are nonnegative for \(q\in (0,1)\) and \(\mu _i,\kappa _j,\lambda _{d}\) satisfying (4.1). Since the weights at vertex (i, j) depend on \(\sigma _i, \kappa _j\) and \(\lambda _{j-i}\), we treat these parameters as attached to column \(i=const\), row \(j=const\) and diagonal \(j-i=const\) respectively, see Fig. 3 for a depiction of the parameters of the weights in the model.
In the description of the model we have also used that (4.2) gives a well-defined probability distribution. This follows from the identity
which can be proved by setting \(y=q^{-n}, n\in {\mathbb {Z}}_{\ge 0}\) and reducing the claim to the q-binomial theorem.
Finally, note that the vertex sampling is trivial outside of the region \(i<j\): since the weight \(W_{t,s}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\) vanishes unless \(\varvec{A}\ge \varvec{D}\), a vertex (i, j) with the incoming bottom configuration \(\varvec{A}^{(i,j-1)}=\varvec{0}\) is forced to have a deterministic sampling with \(\varvec{B}^{(i,j)}=\varvec{0}\) and \(\varvec{A}^{(i,j)}=\varvec{B}^{(i-1,j)}\), that is, the top outgoing configuration is equal to the left incoming one. These rules force all vertices (i, j) with \(i>j\) to have edge labels \(\varvec{0}\) around them, while the sampling at the vertices (i, i) is deterministic. In particular, the model does not depend on the parameters \(\{\lambda _{d}\}_{d\le 0}\), thus we can freely omit them from now on.
Remark 4.1
The q-Hahn model described in this section originates from the work [13], where the one-colored case of this model was used to construct inhomogeneous spin q-Whittaker functions. Existence of an integrable vertex model with diagonal parameters not attached to its lines is surprising: usually integrability is caused by the Yang–Baxter equation, where parameters are attached to the lines of the model. Actually, the q-Hahn model without diagonal parameters was already known and it was previously obtained from the six-vertex model directly via fusion, see [16, 20].
However, the ordinary q-Hahn model without diagonal parameters was in a certain sense “incomplete”, which was indicated in [20]. Namely, the q-Hahn model can be used to construct spin q-Whittaker functions, which are dual in the sense of the dual Cauchy identity to the spin Hall–Littlewood functions, constructed using higher spin six-vertex model. The latter functions have a natural inhomogeneous version, coming from a model with three families of parameters (one family is attached to rows and two families are attached to columns of the higher spin six-vertex model), but the corresponding inhomogeneous version of the spin q-Whittaker functions turned out to be unreachable using the ordinary q-Hahn model. This was remedied with the discovery of the deformed Yang–Baxter equations in [13], which have naturally led to the vertex model construction for the inhomogeneous spin q-Whittaker functions featuring the additional diagonal parameters.
4.2 The colored height functions and the formula for q-moments
The vertex model just introduced has a collection of natural observables, called colored height functions. We denote them by \(h_{\ge c}^{(x,y)}(\varSigma )\), where \(\varSigma \) is a configuration of the model, \(c\in [1,n]\) is an integer representing a color and \((x,y)\in \left( {\mathbb {Z}}_{\ge 0}+\frac{1}{2}\right) ^2\) is a point treated as a facet of the grid between columns \(x\pm \frac{1}{2}\) and rows \(y\pm \frac{1}{2}\).
Informally, the height function \(h_{\ge c}^{(x,y)}\) indicates the number of paths of color \(\ge c\) passing below (x, y). More precisely, for a given fixed configuration \(\varSigma \) we define the corresponding height functions following two local rules:
-
If \(\varvec{A}^{(x-\frac{1}{2},y-\frac{1}{2})}\) denotes the label of the vertical edge \((x-\frac{1}{2},y-\frac{1}{2})\rightarrow (x-\frac{1}{2}, y+\frac{1}{2})\) then
$$\begin{aligned} h^{(x-1,y)}_{\ge c}(\varSigma )=h^{(x,y)}_{\ge c}(\varSigma ) + A_{[c, n]}^{(x-\frac{1}{2},y-\frac{1}{2})}. \end{aligned}$$(4.5) -
If \(\varvec{B}^{(x-\frac{1}{2},y+\frac{1}{2})}\) denotes the label of the horizontal edge \((x-\frac{1}{2},y+\frac{1}{2})\rightarrow (x+\frac{1}{2}, y+\frac{1}{2})\) then
$$\begin{aligned} h^{(x,y +1)}_{\ge c}(\varSigma )=h^{(x,y)}_{\ge c}(\varSigma ) + B_{[c, n]}^{(x-\frac{1}{2},y+\frac{1}{2})}. \end{aligned}$$(4.6)
Due to the conservation law around each vertex, these local rules give a well-defined height function \(h^{(x,y)}_{\ge c}(\varSigma )\), see Fig. 3. The resulting height functions are unique up to a global additive shift; we fix the normalization by requiring
for any color \(c\in [1,n]\) and configuration \(\varSigma \).
To simplify expressions in the following sections we also introduce the following notation for the multi-point height function: for a sequence of colors \({\mathbf {c}}=(c_1, \dots , c_k)\), a pair of sequences of half integers \({\mathbf {x}}=(x_1, \dots , x_k), {\mathbf {y}}=(y_1, \dots , y_k)\) and a configuration \(\varSigma \) we set
4.3 The integral expression for q-moments
The main result of this section expresses a certain observable of the q-Hahn model as a nested contour integral. The observable in question is denoted by \({\mathcal {Q}}_{\ge \tau .{\mathbf {c}}}^{({\mathbf {x}},{\mathbf {y}})}(\varSigma )\) and for a configuration of the model \(\varSigma \), an ordered sequence of colors \({\mathbf {c}}=(c_1, \dots , c_k)\), a permutation \(\tau \in S_k\) and a pair of sequences of half integers \({\mathbf {x}}=(x_1, \dots , x_k), {\mathbf {y}}=(y_1, \dots , y_k)\) it is defined by
where we follow the notation
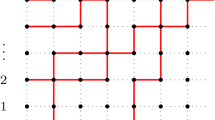
To formulate the result we also need to specify integration contours. They are denoted by \(\varGamma _1, \varGamma _2, \dots , \varGamma _k\) and are assumed to satisfy the following conditions:
-
Every contour \(\varGamma _a\) is a union of simple positively oriented closed contours in \({\mathbb {C}}\);
-
The points from \(\{\mu ^{-1}_i\}_{i\ge 0}\) and \(\{\kappa ^{-1}_j\}_{j\ge 1}\) are inside every contour \(\varGamma _a\), while 0 and the points from \(\{\lambda ^{-1}_d\}_{d\ge 1}\) are outside of the contours;
-
For any \(a<b\) the contour \(\varGamma _b\) encircles both contours \(\varGamma _a\) and \(q\varGamma _a\). Here \(q\varGamma _a\) denotes the contour obtained by multiplying all points of \(\varGamma _a\) by q.
See Fig. 4 for a possible configuration of the contours. Note that the conditions on the parameters (4.1) guarantee the existence of such contours.
Theorem 4.2
Let \(\varSigma \) be a random configuration of the q-Hahn model with the weights defined by parameters \(\{\mu _i\}_{i\ge 0}\), \(\{\kappa _j\}_{j\ge 1}\), \(\{\lambda _d\}_{d\ge 1}\) and the left boundary condition given by a composition \(\varvec{I}\) as in Sect. 4.1. Then for any sequences \({\mathbf {c}}=(c_1, \dots , c_k)\), \({\mathbf {x}}=(x_1, \dots , x_k)\) and \({\mathbf {y}}=(y_1, \dots , y_k)\) satisfying
and for any permutation \(\tau \in S_k\) the following holds:
where the integration contours \(\varGamma _a\) are specified before the theorem, \(T_\tau \) denotes the action of the Hecke algebra defined by (2.23) and the integers \(l_a\) are defined by \(l_a=I_{[1,c_a-1]}\).
The proof of the theorem occupies the remainder of the section, but before it we explain how Theorem 4.2 simplifies in the one-colored case, when \(n=1\). Then all colors in \({\mathbf {c}}\) are equal to 1, the colors of the incoming left boundary edges are defined by \(\varvec{I}=(N)\) and the operators \(T_\tau \) act on a constant 1, multiplying it by \(q^{l(\tau )}\). Since the only nontrivial height function in the color-blind case is \(h_{\ge 1}\), we omit \({\mathbf {c}}\) and write just \({\mathcal {Q}}^{{\mathcal {A}},{\mathcal {B}}}(\varSigma )\) instead of \({\mathcal {Q}}^{{\mathcal {A}},{\mathcal {B}}}_{\ge (1,\dots , 1)}(\varSigma )\) in the one-colored case:
Corollary 4.3
Let \(\varSigma \) be a random configuration sampled from the one-colored q-Hahn model with parameters \(\{\mu _i\}_{i\ge 0}, \{\kappa _j\}_{j\ge 1}, \{\lambda _d\}_{d\ge 1}\). Then for any sequences \({\mathbf {x}}=(x_1, \dots , x_k)\) and \({\mathbf {y}}=(y_1, \dots , y_k)\) satisfying
the following holds:
where the integration contours \(\varGamma _a\) are simple positively oriented curves satisfying
-
The points from \(\{\mu ^{-1}_i\}_{i\ge 0}\) are inside every contour \(\varGamma _a\), while 0 and the points from \(\{\lambda ^{-1}_d\}_{d\ge 1}\) are outside of the contours;
-
For any \(a<b\) the contour \(\varGamma _b\) encircles both contours \(\varGamma _a\) and \(q\varGamma _a\).
Note that, contrary to the colored case, in the one-colored situation the integrand has no singularities at \(\kappa _j^{-1}\), so we need no restrictions on the positions of \(\kappa ^{-1}_j\) with respect to the contours \(\varGamma _a\).
Remark 4.4
When all parameters \(\{\lambda _d\}_{d\ge 1}\) are equal and there is no inhomogeneity assigned to diagonals, the q-Hahn model can be obtained from the colored higher-spin six-vertex model using stochastic fusion. In this case Theorem 4.2 can be obtained from analogous integral expressions for the q-moments of the higher-spin model: for one-color case this was done in [16], while the colored situation is covered by [12, 21]. But it seems that the general case with arbitrary parameters \(\{\lambda _d\}_{d\ge 1}\) cannot be reached with fusion.
4.4 Explicit integral computations
The proof of Theorem 4.2 consists of two ingredients: explicit computations of the contour integrals in certain degenerate cases, and recurrence relations given in Sect. 3. Here we focus on the former.
We fix the contours \(\varGamma _a\) as in the theorem, and let \({\mathbf {w}}=(w_1, \dots , w_k)\) denote the collection of the integration variables. We need the following fact describing the operators adjoint to \(T_\tau \) with respect to the scalar product
Proposition 4.5
([19]) Assume that \(F(w_1, \dots , w_k)=F({\mathbf {w}})\) and \(G(w_1, \dots , w_k)=G({\mathbf {w}})\) are rational functions having only singularities of the form \(w_a=\mu _i^{-1}\), \(w_a=\kappa _j^{-1}\) or \(w_a=\lambda _d^{-1}\). Then for any permutation \(\tau \) the following relation holds:
or, equivalently,
Proof
The complete proof is given in [19, Proposition 8.1.3], see also [12, Proposition 4.1]. The main idea is to prove that the generators \(T_i\) are self-adjoint, which is enough since \(T_i\) generate the Hecke algebra \({\mathcal {H}}_k\). Each \(T_i\) is a sum of a multiplication by a constant and \(\frac{w_{i+1}-qw_i}{w_{i+1}-w_i}{\mathfrak {s}}_i\). The former is clearly self-adjoint, while for the latter note that the multiplication by \(\frac{w_{i+1}-qw_i}{w_{i+1}-w_i}\) removes the singularity of the integrand at \(w_{i+1}=qw_i\), allowing to exchange the contours \(\varGamma _i\) and \(\varGamma _{i+1}\) without changing the integral. Performing a change of variables swapping \(w_i\) and \(w_{i+1}\), one can see that \(\frac{w_{i+1}-qw_i}{w_{i+1}-w_i}{\mathfrak {s}}_i\) is also self-adjoint. \(\square \)
The next statement describes the situation when one of the integrals can be easily computed, reducing the number of integration variables by one. In the context of Theorem 4.2 we will use this computation when \(x_k=y_k\) and the integral has no residue at \(w_k=\lambda _d^{-1}\) for any d, see Step 2 in Sect. 4.5.
Proposition 4.6
Assume that \(f_1, \dots , f_k\) and \(g_1, \dots , g_k\) are rational functions in one variable satisfying
-
For every \(a\in [1,k]\) the function \(f_k(w)g_a(w)\) is holomorphic outside of \(\varGamma _k\);
-
For every \(a\in [1,k]\) the poles of \(f_a(w)\) and \(g_a(w)\) are inside of \(\{\mu _i^{-1}\}_{i\ge 0}\cup \{\kappa _j^{-1}\}_{j\ge 1}\cup \{\lambda _d^{-1}\}_{d\ge 1}\);
-
For every \(a\in [1,k]\) we have \(f_a(0)=g_a(0)=1\).
Then
where \(\rho =\sigma _{k-1}\sigma _{k-2}\dots \sigma _{\tau (k)}\) is the cycle sending \(\tau (k), \tau (k)+1, \dots , k\) to \(\tau (k)+1, \tau (k)+2, \dots , k, \tau (k)\) respectively, while leaving other elements intact, and the permutation \(\tau '\) is defined by \(\tau '=\rho ^{-1}\tau \).
Proof
The proof is similar to [12, Lemma 4.2.1]. Note that \(T_{\tau }=T_{\rho }T_{\tau '}\), so by Proposition 4.5 the left-hand side can be rewritten as
Now we are taking the integral with respect to \(w_k\) by computing its residues outside of \(\varGamma _k\). Note that \(\tau '(k)=k\), hence
By the conditions of the claim the function
is holomorphic with respect to \(w_k\) outside of \(\varGamma _k\), so the only non-vanishing residue of the integrand in (4.10) outside of \(\varGamma _k\) is the residue at \(w_k=0\). Computing it, we obtain

To finish the proof, note that for any function \(G({\mathbf {w}})\) nonsingular at \(w_{a}=0\) for every a we have

where \(\sigma _i\) is a simple transposition acting on the variables \({\mathbf {w}}\) by permutation. A straightforward induction yields

\(\square \)
Another integral we need to explicitly compute by taking residues is the right-hand side of (4.7) when \(x_1=\cdots =x_k=\frac{1}{2}\). For convenience, set \(p_i:=y_i-\frac{1}{2}\) and recall that \(l_a\) corresponds to the position of the color \(c_a\) on the left boundary.
Proposition 4.7
Fix \(N>0\). For any integer sequences \(l_1, l_2, \dots , l_k\) and \(p_1, p_2, \dots , p_k\) such that
and any permutation \(\tau \) we have
where for every integer \(j\in [1, N]\) we set
that is, \(r_j\) is the number of intervals \([l_{\tau ^{-1}(a)}+1, p_a]\) containing j.
Proof
The proof is by induction on k and N, where at each step we either reduce k or N by 1, keeping \(N,k\ge 0\). The base case \(k=0\) is trivial.
Assume that \(k> 0\) and let \({\mathbf {l}}=(l_1, \dots , l_k)\) and \({\mathbf {p}}=(p_1, \dots , p_k)\). Set
We have three cases:
Case 1: \(l_k<N\) and \(p_1<N\): Then for any a we have \(l_a, p_a<N\), so \(r_N=0\), \(N>0\) and we can freely reduce N by 1 without changing the claim.
Case 2: \(l_k=N\): Here we can compute the integral with respect to \(w_k\) by applying Proposition 4.6 for the functions
Since \(l_k=N\ge p_a\) for any a, after the multiplication by \(f_k(w)\) the poles of \(g_a(w)\) at \(w=\lambda _j^{-1}\) vanish, so the function \(f_k(w)g_a(w)\) has no nonzero residues outside of \(\varGamma _k\) and Proposition 4.6 implies that
where the permutation \({\tau }'\) as defined by \(\tau =\rho \tau '\) for the same cycle \(\rho \) as in Proposition 4.6 and
Hence, the right-hand sides of (4.11) for the triples \(({\mathbf {l}}, {\mathbf {p}}, \tau )\) and \(({{\mathbf {l}}}', {\mathbf{p}}', {\tau }')\) coincide.
At the same time, the families of intervals \(\{[l_{\tau ^{-1}(a)}+1, p_a]\}_{a\in [1,k]}\) and \(\{[l_{{\tau }'^{-1}(a)}+1, {p}_{\rho (a)}]\}_{a\in [1,k-1]}\) differ only by the empty interval \([l_k+1, p_{\tau (k)}]\), implying that the left-hand sides of the claim for \(({{{\mathbf {l}}}},{{\mathbf {p}}},{\tau })\) and \(({{{\mathbf {l}}}}', {{\mathbf {p}}}', {\tau }')\) coincide as well. Thus, we can reduce k by 1 and the induction step hold.
Case 3: \(l_k<N\) and \(N=p_1=p_2=\cdots =p_r>p_{r-1}\): To tackle this case we start computing the integrals with respect to \(w_1, \dots , w_r\), taking residues inside \(\varGamma _1, \dots , \varGamma _r\). Note that possible simple poles at \(w_1=\kappa ^{-1}_j, \dots , w_r=\kappa ^{-1}_j\) coming from \(F^{{\mathbf {l}}}({\mathbf {w}})\) are cancelled by \(\prod _{a=1}^r\prod _{j=1}^N(1-\kappa _jw_a)\) from \(G^{\mathbf{p}}({\mathbf {w}})\), so all non-vanishing residues inside \(\varGamma _1, \dots , \varGamma _r\) come from the singularities of
Taking into account the geometry of the contours, the integral with respect to \(w_1\) has only one residue inside \(\varGamma _1\), which is at \(w_1=\mu _0^{-1}\). Computing this residue for the expression above, we obtain

Hence, after taking the residue at \(w_1=\mu _0^{-1}\), the integral with respect to \(w_2\) again has only one non-vanishing residue inside \(\varGamma _2\), this time at \(w_2=q\mu ^{-1}_0\). Continuing this argument, we see that the only non-vanishing contribution in the computation of the right-hand side of (4.11) comes from the residue at \(w_1=\mu _0^{-1}, w_2=q\mu _0^{-1}, \dots , w_r=q^{r-1}\mu _0^{-1}\). Note that

where \({{\mathbf {p}}}'=(p_1-1, p_2-1, \dots , p_r-1, p_{r+1}, \dots , p_k)\). Hence
At the same time, note that \(r_N=r\) for the triple of data \(({{\mathbf {l}}}, {\mathbf {p}}, \tau )\), while the numbers \(r_i\) for \(i<N\) are the same for both triples \(({{\mathbf {l}}}, {\mathbf {p}}, \tau )\) and \(({\mathbf {l}}, {\mathbf {p}}', \tau )\). So, factoring out the term \(\frac{(\kappa _N/\mu _0;q)_r}{(\lambda _N/\mu _0;q)_r}\), we reduce the claim for \(({{\mathbf {l}}}, {\mathbf {p}}, \tau )\) to the claim for \(({{\mathbf {l}}}, {\mathbf {p}}', \tau )\), and the latter one allows to freely reduce N by 1, finishing the step of induction. \(\square \)
4.5 Proof of Theorem 4.2
The main idea of the proof is to use induction, applying the local relations from Sect. 3 to reduce the coordinates \({\mathbf {x}}\) and \({\mathbf {y}}\). This process has to eventually reach either the case \(x_k=y_k\), when we can use Proposition 4.6 to reduce k, or the case \(x_1=x_2=\cdots =x_{k}=\frac{1}{2}\), in which the claim holds by Proposition 4.7. Throughout the whole argument the parameters of the model, the contours \(\varGamma _a\) and the sequence \({\mathbf {c}}\) are fixed.
Step 1. Fix \({\mathbf {x}},{\mathbf {y}},\tau \) as in the claim and assume that \(\frac{1}{2}<x_k<y_k\). In this main step we use the local relations to show that the claim for \(({\mathbf {x}},{\mathbf {y}},\tau )\) follows from the claims for \(({\mathbf {x}}',{\mathbf {y}}',\tau ')\) with smaller coordinates \(x'_a\le x_a, y'_b\le y_b\), \({\mathbf {y}}'\ne {\mathbf {y}}\).
More precisely, we start by finding integers \(m\in {\mathbb {Z}}_{\ge 0}, r\in {\mathbb {Z}}_{>0}\) such that
where \(m+r\le k\) and if \(m=0\) or \(m+r=k\) we omit inequalities involving \(x_0,y_0\) or \(x_{k+1}, y_{k+1}\) respectively. In other words, m is chosen in a way that all points \((x_a,y_a)\) are either equal to the point \((x_{m+1},y_{m+1})\), strictly below it or strictly to the left of it, while r is the number of the points equal to \((x_{m+1},y_{m+1})\). To show existence of such m, r one can take m equal to the maximal index such that \(x_m<x_{k}\) (if \(x_1=x_k\) take \(m=0\)) while r is the maximal index such that \(y_{m+r}=y_{m+1}\). For any \(a\le b\) let \({\mathbf {e}}^{[a,b]}\in {\mathbb {Z}}^k\) denote the vector with 1 entries at positions \(a, a+1, \dots , b\), and 0s elsewhere:
It turns out that the claim for \({\mathbf {x}},{\mathbf {y}}\) and arbitrary \(\tau \) follows from the claims for \({\mathbf {x}}-{\mathbf {e}}^{[m+1,m+p]}, {\mathbf {y}}-{\mathbf {e}}^{[m+1,m+r]}\) with \(p=0, \dots , r\). To show it we proceed in three sub-steps: first we simplify the permutation \(\tau \) and then apply the local relation to both sides of (4.7).
Step 1.1. For now we want to show that it is enough to consider permutations \(\tau \) which are \([m+1, m+r]\)-ordered:
For the left-hand side of (4.7) note that for any permutation \(\rho \in S_{[m+1,m+r]}\) permuting only numbers \(m+1, \dots , m+r\) we have
thus the left-hand side depends only on the right coset of \(\tau \) in \(S_{[m+1,m+r]}\backslash S_{k}\). On the other hand, we can rewrite the right-hand side of (4.7) as
where
Note that \(F^{{\mathbf {x}},{\mathbf {y}}}({\mathbf {w}})\) is symmetric in \(w_{m+1}, w_{m+2},\dots , w_{m+r}\), hence for any \(\rho \in S_{[m+1, m+r]}\) we have
since \(T_i f(w_i, w_{i+1})=qf(w_i, w_{i+1})\) for any f symmetric in \(w_{i},w_{i+1}\). Multiplying (4.13) on the left by \(T_{\tau _{min}}^{-1}\) for a minimal permutation \(\tau _{min}\) of a coset in \(S_{[m+1,m+r]}\backslash S_{k}\), one can readily see that the right-hand side of (4.7) also depends only on the left coset of \(\tau \), rather than \(\tau \) itself. So, we can assume that \(\tau \) is a minimal representative of a left coset in \(S_{[m+1,m+r]}\backslash S_{k}\), or, equivalently, \(\tau \) is \([m+1, m+r]\)-ordered.
Step 1.2. Now, assuming that \(\tau \) is \([m+1, m+r]\)-ordered, we want to apply an appropriate local relation to the left-hand side of (4.7). Let \(v=(x_{m+1}-\frac{1}{2},y_{m+1}-\frac{1}{2})\) denote the vertex immediately to the south-west of the facet \((x,y):=(x_{m+1}, y_{m+1})=\cdots =(x_{m+r}, y_{m+r})\). It has vertex weights \(W_{\sqrt{\lambda /\kappa },\sqrt{\lambda /\mu }}\), where
Now we want to change the order in which we perform the sampling of the model: first we sample the outgoing configurations for the vertices (i, j) either below v or to the left of v, obtaining a configuration \(\varSigma _{\swarrow v}\), and then we sample the remaining configuration \(\varSigma \). Since all our samplings are independent, their order does not matter as long as each vertex is sampled after the vertices directly below and to the left of it, so the resulting configuration is distributed in the same way as in the initial model. But note that \(\varSigma _{\swarrow v}\) determines the value of the height functions at the facets \((x_{a}, y_{a})\) for \(a\le m\), because they are to the left of v, and at the facets \((x_{a}, y_{a})\) for \(m+r< a\) because they are below v.
At the same time, the height functions at (x, y) are determined only by \(\varSigma _{\swarrow v}\) and the labels of the edges around v, which are determined by the sampling at v. Let \((\varvec{A},\varvec{B})\) denote the compositions of the incoming bottom and left edges of v, determined by \(\varSigma _{\swarrow _v}\), and let \((\varvec{C}, \varvec{D})\) denote the compositions of the outgoing top and right edges of v. Then the local rule (4.6) from the definition of the height functions implies that
and hence
where we use the notation \({\mathcal {Q}}_{\ge {\mathbf {c}}}(\varvec{D})\) from (3.2) and we set
Taking expectations we obtain
Now we can apply Corollary 3.3 to the conditional expectation inside to get
where the second sum is over \([m+1, m+p]\times [m+p+1, m+r]\)-ordered permutations of \(m+1, \dots , m+r\). For the same reasons as in Step 1.1, for any such permutation \(\rho \) we have \({\mathcal {Q}}_{\ge \tau .{\mathbf {c}}}^{{\mathbf {x}},{\mathbf {y}}-{\mathbf {e}}^{[m+1, m+r]}}={\mathcal {Q}}_{\ge \rho \tau .{\mathbf {c}}}^{{\mathbf {x}},{\mathbf {y}}-{\mathbf {e}}^{[m+1, m+r]}}\) and using the definition of the height function in a way similar to (4.14) we have
So the local relation from Corollary 3.3 gives the following relation on the left-hand side of (4.7):
Step 1.3. Continuing with the same setup, we now want to apply the other local relation to the right-hand side of (4.7). Using the notation from Step 1.1, namely (4.12), we rewrite the right-hand side as
Note that
so we can apply Proposition 3.7 with \(t=\sqrt{\lambda /\kappa }, s=\sqrt{\lambda /\mu }\) to obtain
Since \(F^{{\mathbf {x}},{\mathbf {y}}-{\mathbf {e}}^{[m+1,m+r]}}({\mathbf {w}})\) is symmetric in \(w_{m+1}, \dots , w_{m+r}\) and
we get
Let \({\mathcal {I}}^{{\mathbf {x}},{\mathbf {y}}}_{\tau }\) denote the right-hand side of (4.7). Then, the application of the local relation above gives
which looks identical to the analogous relation for the left-hand side (4.15). Thus, the identity (4.7) for \(({\mathbf {x}},{\mathbf {y}},\tau )\) follows from \(({\mathbf {x}}-{\mathbf {e}}^{[m+1,m+p]},{\mathbf {y}}-{\mathbf {e}}^{[m+1, m+r]}, \rho \tau )\) for various \(p\in [0,r]\) and \(\rho \in S_{[m+1, m+r]}^{p | r-p}\).
Step 2. Applying Step 1 we can reduce the coordinates \({\mathbf {x}},{\mathbf {y}}\) until either \(x_1=\cdots =x_k=\frac{1}{2}\) or \(x_k=y_k\). Here we deal with the latter case, assuming that \(x_k=y_k\) and showing that in this situation we can reduce k by 1 and replace the data \(({\mathbf {x}},{\mathbf {y}},{\mathbf {c}},\tau )\) by
where \(\rho \) is the cycle sending \(\tau ^{-1}(k), \tau ^{-1}(k)+1, \dots , k\) to \(\tau ^{-1}(k)+1, \dots , k, \tau ^{-1}(k)\) respectively.
For the left-hand side of (4.7) note that for any color c we have
due to the behavior of the model: all edges adjacent to vertices (i, j) for \(i>j\) have compositions \(\varvec{0}\). This means that we can freely remove this height function from \({\mathcal {Q}}_{\ge \tau .{\mathbf {c}}}^{{\mathbf {x}},{\mathbf {y}}}\), obtaining
for any possible configuration \(\varSigma \). Taking expectation we conclude that the left-hand sides for \(({\mathbf {x}},{\mathbf {y}},{\mathbf {c}},\tau )\) and \(({\mathbf {x}}',{\mathbf {y}}',{\mathbf {c}}',\tau ')\) are equal.
For the right-hand side of (4.7) we are going to apply Proposition 4.6. Set
Since \(x_k=y_k\), the function \(f_k(w)\) has no singularities outside of \(\varGamma _k\), as well as the functions \(g_a(w)\) for any \(a\in [1,k]\). Thus, the conditions of Proposition 4.6 hold and we have
where \(\rho \) and \(\tau '\) are exactly the permutations defined above. Plugging back the expressions for \(f_a, g_a\), we get the right-hand side of (4.7) for \(({\mathbf {x}}',{\mathbf {y}}',\tau ',{\mathbf {c}}')\), as desired.
Step 3. Repeating Steps 1 and 2, at some point we either reach \(k=0\), when the claim is trivial, or the situation when \(x_1=x_2=\cdots =x_k=\frac{1}{2}\). In the latter case Proposition 4.7 implies that the right-hand side of (4.7) is equal to
At the same time, recall that the compositions of the incoming edges are mono-colored, and the color of the incoming edge on row j is \(\ge c_{\tau ^{-1}(a)}\) if and only if \(j> l_{{\tau ^{-1}(a)}}\). Recall that \(b_j=|\varvec{B}^{(0,j)}|\) denote the random integers used to define the compositions at the left boundary and distributed according to (4.2), so we get for \({\mathbf {x}}=\left( \frac{1}{2},\dots , \frac{1}{2}\right) \)
which is equal to the value of the right-hand side, concluding the base case. Note that for the last identity we have used (4.4). \(\square \)
5 Shift invariance
In this section we show how the integral expressions from Theorem 4.2 lead to certain symmetries of the diagonally inhomogeneous q-Hahn model, which are similar to the shift-invariance symmetries of the stochastic colored six-vertex model from [11] and [27]. Our argument is identical to [12, Section 7].
To state the result we need a finer description of the height functions. For simplicity, consider a q-Hahn vertex model with incoming colors along the left boundary defined by \(\varvec{I}=(1,1,1,\dots )\), that is, in the incoming boundary composition at row j only \(j\hbox {th}\) entry is nonzero. Then, for each color c we can define a cutoff point \((\frac{1}{2}, c-\frac{1}{2})\), which separates the rows with the incoming colors on the left \(\ge c\) and \(<c\). Since such cutoff points uniquely determine the corresponding colors, instead of using a color c and a point (x, y) to identify a colored height function \(h^{(x,y)}_{\ge c}\) we can equivalently use a pair of points \((\frac{1}{2}, c-\frac{1}{2})\) and (x, y). It turns out that the latter pair of points plays an important role in visualizing the behavior of the height function.
For a color \(c\in {\mathbb {Z}}_{\ge 1}\) and a point \((x,y)\in \left( \mathbb Z_{\ge 0}+\frac{1}{2}\right) ^2\) such that \(y-x\ge c\) define the following integer intervals:
Here [a, b] denotes an integer interval \(a, a+1, \dots , b\). In other words, \({{\,\mathrm{Row}\,}},{{\,\mathrm{Col}\,}},{{\,\mathrm{Diag}\,}}\) are exactly the labels of the rows, columnsFootnote 11 and diagonals passing between the points \((\frac{1}{2}, c-\frac{1}{2})\) and (x, y), possibly containing (x, y) but avoiding \((\frac{1}{2}, c-\frac{1}{2})\). The additional constraint \(y-x\ge c\) listed above is not restrictive, since \(h_{\ge c}^{(x,y)}\equiv 0\) for \(y-x<c\).
We start with the informal statement of the shift-invariance symmetry, which is rigorously described in Proposition 5.1. Given a vector of height functions \(\left( h_{\ge c_1}^{(x_{\tau (1)}, y_{\tau (1)})},\dots , h_{\ge c_k}^{(x_{\tau (k)}, y_{\tau (k)})}\right) \) with \(x_a,y_a, c_a\) ordered as before in Theorem 4.2, the joint k-dimensional distribution is determined solely by
-
The collections of parameters attached to the rows \({{\,\mathrm{Row}\,}}_{\ge c_a}^{(x_{\tau (a)},y_{\tau (a)})}\), columns \({{\,\mathrm{Col}\,}}_{\ge c_a}^{(x_{\tau (a)},y_{\tau (a)})}\) and diagonals \({{\,\mathrm{Diag}\,}}_{\ge c_a}^{(x_{\tau (a)},y_{\tau (a)})}\), corresponding to the height functions,
-
The relative order \(\tau \) of evaluation and cutoff points of the height functions.
The data in the first part corresponds to the one-dimensional distributions of \(h^{(x,y)}_{\ge c}\), which are determined by the listed parameters in view of Theorem 4.2. Since the one-dimensional distributions are determined by the joint k-dimensional distributions, one can expect this data to be necessary. On the contrary, the second part corresponds to the relative position of the height functions with respect to each other on the plane, and this data is not a priori contained in the joint distribution. Moreover, we actually expect it to be redundant, see Remark 5.2.
An example of the shift invariance: by Proposition 5.1 the joint distribution of the height functions \((h_{\ge 1}^{(3/2,9/2)}, h^{(3/2,9/2)}_{\ge 3})\) on the left is equal to the joint distribution of \(({{\widetilde{h}}}_{\ge 1}^{(3/2,9/2)}, {{\widetilde{h}}}^{(3/2,5/2)}_{\ge 1})\) on the right. Here the two models have the same row, column and diagonal parameters, but with different orderings corresponding to \(\psi _{{{\,\mathrm{Row}\,}}}, \psi _{{{\,\mathrm{Col}\,}}}, \psi _{{{\,\mathrm{Diag}\,}}}\). To illustrate assumptions of Proposition 5.1, note that for \(h^{(3/2,9/2)}_{\ge 3}\) on the left we have rows \({{\,\mathrm{Row}\,}}^{(3/2,9/2)}_{\ge 3}=\{3,4\}\) with the parameters \(\{\kappa _3,\kappa _4\}\), while for \(\widetilde{h}^{(3/2,5/2)}_{\ge 1}\) on the right \({{\,\mathrm{Row}\,}}^{(3/2,5/2)}_{\ge 1}=\{1,2\}\) with the same parameters \(\{\kappa _3,\kappa _4\}\)
Proposition 5.1
Let \(\{\mu _i\}_{i\ge 0}\), \(\{\kappa _j\}_{j\ge 1}\), \(\{\lambda _d\}_{d\ge 1}\) be parameters of a q-Hahn model, and let \({\mathbf {c}}=(c_1, \dots , c_k)\), \({\mathbf {x}}=(x_1, \dots , x_k)\) and \({\mathbf {y}}=(y_1, \dots , y_k)\) be sequences satisfying
Additionally, let \(\tau \in S_k\) be a permutation such that \(y_{\tau (a)}-x_{\tau (a)}\ge c_{a}\). Similarly, let \(\{{\widetilde{\mu }}_i\}_{i\ge 0}\), \(\{{\widetilde{\kappa }}_j\}_{j\ge 1}\), \(\{{\widetilde{\lambda }}_d\}_{d\ge 1}\), \({\widetilde{{\mathbf {c}}}}=({\widetilde{c}}_1, \dots , {\widetilde{c}}_k)\), \({\widetilde{{\mathbf {x}}}}=({\widetilde{x}}_1, \dots , {\widetilde{x}}_k)\), \({\widetilde{{\mathbf {y}}}}=({\widetilde{y}}_1, \dots , {\widetilde{y}}_k)\) and \({\widetilde{\tau }}=\tau \) be another collection of data satisfying identical constraints, which we treat as another q-Hahn model.
Assume that there exist bijections \(\psi _{{{\,\mathrm{Row}\,}}}, \psi _{{{\,\mathrm{Diag}\,}}}:{\mathbb {Z}}_{\ge 1}\rightarrow {\mathbb {Z}}_{\ge 1}, \psi _{{{\,\mathrm{Col}\,}}}:{\mathbb {Z}}_{\ge 0}\rightarrow {\mathbb {Z}}_{\ge 0}\) satisfying
for any \(a=1, \dots , k\) and
for any \(i\ge 0, j\ge 1, d\ge 1\). Then the following random vectors are equal in finite-dimensional distributions:
where h and \({\widetilde{h}}\) denote the height functions of the two q-Hahn models.
See Fig. 5 for an example of the setup of Proposition 5.1. We are not going to give a complete proof of Proposition 5.1, since it is identical to the proof of [12, Theorem 7.1]. Below we just outline the main steps of that argument.
Sketch of the proof
The proof is based on the following observation: the joint k-dimensional distribution of a random vector \((h_1, \dots , h_k)\) of nonnegative real numbers is completely determined by the q-moments \({\mathbb {E}}\left[ q^{a_1h_1+\cdots +a_kh_k}\right] \) for \(a_1, \dots , a_k\in {\mathbb {Z}}_{\ge 0}\). Repeating in the statement of Proposition 5.1 the first height function for \(a_1\) times, the next height function for \(a_2\) times and so on, one readily see that it is enough to prove
where \({\widetilde{{\mathbb {E}}}}\) denotes expectation in the second model. Applying Theorem 4.2 to both sides, the problem is reduced to matching the right-hand sides of the integral expression (4.7).
To match integral expressions, we expand the operator \(T_\tau \) as a linear combination of the permutation operators acting on the variables \({\mathbf {w}}\):
where \(Z_{\tau }^\rho ({\mathbf {w}})\) are rational functions in \({\mathbf {w}}\) and the inequality \(\rho \preceq \tau \) is taken with respect to the strong Bruhat order, see [12, Proposition 3.1]. Then, to match the integral expressions, it is enough to prove for any \(\rho \preceq \tau \) that
When \(\rho =\tau \) both sides of (5.1) are equal by the assumptions of the claim: for the left-hand side the factors in the product over a can be rewritten as
where \({\overline{\rho }}=\rho ^{-1}\), and the statement of Proposition 5.1 essentially just tells that the expression above is equal to the analogous expression for the right-hand side of (5.1) when \(\rho =\tau \).
For general \(\rho \) one can closely follow the proof of [12, Lemma 7.1.3] and show that for any \(\rho \preceq \tau \) one of the following situations holds:
-
For some a we have \(y_{\rho (a)}-x_{\rho (a)}< c_{\rho (a)}\) and \({\widetilde{y}}_{\rho (a)}-{\widetilde{x}}_{\rho (a)}<{\widetilde{c}}_{\rho (a)}\), that is, the corresponding height functions \(h^{(x_{\rho (a)}, y_{\rho (a)})}_{\ge c_a}\) and \({\widetilde{h}}^{({\widetilde{x}}_{\rho (a)}, {\widetilde{y}}_{\rho (a)})}_{\ge {\widetilde{c}}_a}\) are degenerate and equal to 0. Then both sides of (5.1) have no nonzero residues with respect to \(w_a\) outside of the integration contours, and hence vanish.
-
For every a we have \(y_{\rho (a)}-x_{\rho (a)}\ge c_{\rho (a)}\) and \({\widetilde{y}}_{\rho (a)}-{\widetilde{x}}_{\rho (a)}\ge {\widetilde{c}}_{\rho (a)}\). Then one can verify that the conditions of Proposition 5.1 still hold when \(\tau \) is replaced by \(\rho \) and, in particular, the expressions of the form (5.2) match for \(\rho \) as well.
\(\square \)
Remark 5.2
This section is based on [12, Section 7], where the shift-invariance for the stochastic colored six-vertex model is derived directly from the integral expressions for the q-moments of the height functions. The shift-invariance for the six-vertex model was initially introduced in [11] and in full generality it was proved in [27], where flip symmetries were used as a basic block for all other symmetries. Moreover, it was shown in [27] that the relative position of the height functions, encoded by \(\tau \) in our notation, is irrelevant and joint distributions of height functions are determined solely by their one-dimensional distributions. Since we don’t know how the q-Hahn model with diagonal parameters can be constructed from the six-vertex model, the more general invariance result from [27] cannot be applied to our model, but we suspect it to be true.
6 Reduction to Beta polymer
In this section we follow [11] in order to reduce the results from Sect. 4 to the Beta polymer model. See also [12, 21] for similar arguments.
6.1 Continuous model
As before, we treat q-Hahn vertex model from Sect. 4 as a sequence of independent stochastic samplings corresponding to the vertices, depending on the parameters \(\mu _i, \kappa _j,\lambda _d\). We slightly simplify the model by assuming that the incoming colors from the left are different and are encoded by the composition \(\varvec{I}=(1,1,1,\dots )\). We consider the following limit regime:
where \(\sigma _i, \rho _j,\omega _d\) are new real parameters satisfying
It turns out that the limiting model in this regime is described in terms of the Beta distribution. Below we present without proofs the exact description, referring to [11] for the general case, and to [4] for the one-colored case.
Proposition 6.1
In the regime (6.1) the random variable \(\exp (-\varepsilon b_j)\) for \(b_j\) distributed as in (4.2) converges weakly as \(\varepsilon \rightarrow 0\) to \({{\,\mathrm{Beta}\,}}(\sigma _0-\rho _j, \rho _j-\omega _j)\).
Proof
See [11, Proposition 6.16] or [4, Lemma 2.3].
Proposition 6.2
The stochastic sampling rule for \((\varvec{C},\varvec{D})\) given \((\varvec{A},\varvec{B})\) defined by the vertex weights \(W_{\sqrt{\lambda _{j-i}/\kappa _j},\sqrt{\lambda _{j-i}/\mu _i}}(\varvec{A},\varvec{B};\varvec{C},\varvec{D})\) weakly converges in the limit regime
to the following sampling procedure for the outgoing masses \({\varvec{\gamma }}=(\gamma _1, \dots , \gamma _n)\) and \({\varvec{\delta }}=(\delta _1, \dots , \delta _n)\) given the incoming masses \({\varvec{\alpha }}=(\alpha _1, \dots , \alpha _n)\) and \({\varvec{\beta }}=(\beta _1, \dots , \beta _n)\): We take a Beta-distributed random variable \(\eta \sim {{\,\mathrm{Beta}\,}}(\sigma _i-\rho _j,\rho _j-\omega _{j-i})\) and define \(\delta _k\), \(0\le \delta _k\le \alpha _k\), for all k through
where we set \(\delta _{\ge k}=\sum _{l\ge k}\delta _l\) and \(\alpha _{\ge k}=\sum _{l\ge k}\alpha _l\). The remaining masses \(\gamma _k\) are defined by
so the conservation law holds for each color.
Proof
See [11, Corollary 6.21]. For \(n=1\) this is also proved in [4, Lemma 2.4].
The two statements above result in the following model, serving as the limit under (6.1) of the inhomogeneous q-Hahn vertex model and depending on the parameters \(\sigma _i, \rho _j, \omega _d\):
-
Each lattice edge of the positive quadrant \({\mathbb {Z}}_{\ge 1}^2\) has a random real-valued vector \({\varvec{u}}=(u_1, u_2, u_3, \dots )\) attached to it. Coordinate \(u_i\ge 0\) is interpreted as the mass of color i;
-
To sample a configuration of the model we first sample independent Beta-distributed variables \(\eta _{i,j}\sim {{\,\mathrm{Beta}\,}}(\sigma _i-\rho _j, \rho _j-\omega _{j-i})\) for all \( i\ge 0, j\ge 1\);
-
For the edges entering the quadrant from below all masses are set to 0;
-
For the edge entering the quadrant at row j only the mass \(u_j\) is non-zero and it is equal to \(-\ln (\eta _{0,j})\);
-
Given the incoming masses of colors \({\varvec{\alpha }},{\varvec{\beta }}\) entering into a vertex (i, j) from the bottom and from the left, the outgoing masses \({\varvec{\gamma }}, {\varvec{\delta }}\) exiting the vertex to the top and to the right are defined through
$$\begin{aligned}&\exp (-\delta _{\ge k})=\exp (-\alpha _{\ge k})+(1-\exp (-\alpha _{\ge k}))\eta _{i,j}, \qquad k=1,2,\dots ,\\&\gamma _k=\alpha _k+\beta _k-\delta _k,\qquad k=1,2,\dots , \end{aligned}$$where \(\delta _{\ge k}=\sum _{l\ge k}\delta _l\) and \(\alpha _{\ge k}=\sum _{l\ge k}\alpha _l\).
-
This definition implies that only colors \(\le j\) pass through vertex (i, j), guaranteeing that at any vertex we are working only with finite sequences of masses.
We can define the colored height functions \({\widetilde{h}}_{\ge c}^{(x,y)}\) of the continuous model in the same manner as for the q-Hahn model: we set \({\widetilde{h}}_{\ge c}^{(x,\frac{1}{2})}=0\) and
-
If the vertical edge \((x-\frac{1}{2},y-\frac{1}{2})\rightarrow (x-\frac{1}{2}, y+\frac{1}{2})\) has masses \({\varvec{u}}=(u_1, u_2,\dots )\), then
$$\begin{aligned} {\widetilde{h}}^{(x-1,y)}_{\ge c}={\widetilde{h}}^{(x,y)}_{\ge c} + u_{\ge c}. \end{aligned}$$ -
If the horizontal edge \((x-\frac{1}{2},y+\frac{1}{2})\rightarrow (x+\frac{1}{2}, y+\frac{1}{2})\) has masses \({\varvec{u}}=(u_1, u_2, \dots )\), then
$$\begin{aligned} {\widetilde{h}}^{(x,y +1)}_{\ge c}={\widetilde{h}}^{(x,y)}_{\ge c} + u_{\ge c}. \end{aligned}$$
The following generalization of [11, Corollary 6.22] straightforwardly follows from the statements above and clarifies in what sense the continuous model is the limit of the q-Hahn model.
Corollary 6.3
Let \(h^{(x,y)}_{\ge c}[\varepsilon ]\) denote the height function of the q-Hahn model in the regime (6.1). Then in finite-dimensional distributions
6.2 Beta polymer
Fix the same collection of parameters \(\{\sigma _i, \rho _j, \omega _{d}\}\) as before. For \((x,y)\in {\mathbb {Z}}^2_{\ge 0}\)Footnote 12 and \(r\in {\mathbb {Z}}_{\ge 0}\) such that \(r\le y-x\) define the delayed inhomogeneous Beta polymer partition function \({\mathfrak {Z}}_{x,y}^{(r)}\) as follows:
-
Let \(\{\eta _{i,j}\}_{i\ge 0, j\ge 0}\) be a collection of independent Beta distributed variables
$$\begin{aligned} \eta _{i,j}\sim {{\,\mathrm{Beta}\,}}(\sigma _i-\rho _j, \rho _j-\omega _{j-i}); \end{aligned}$$ -
For all \(t,r\ge 0\) set
$$\begin{aligned} {\mathfrak {Z}}_{t,r+t}^{(r)}\equiv 1,\qquad {\mathfrak {Z}}_{0, r+t}^{(r)}=\eta _{0,r+1}\eta _{0,r+2}\dots \eta _{0,r+t}; \end{aligned}$$ -
For general \((x,y)\in {\mathbb {Z}}^2_{\ge 1}\) such that \(x>y+r\) the partition function \({\mathfrak {Z}}^{(r)}_{x,y}\) is defined by the recurrence relation
$$\begin{aligned} {\mathfrak {Z}}^{(r)}_{x,y}=\eta _{x,y}{\mathfrak {Z}}^{(r)}_{x,y-1}+(1-\eta _{x,y}){\mathfrak {Z}}^{(r)}_{x-1,y-1}. \end{aligned}$$
The model just described is an inhomogeneous generalization of the Beta polymer model from [4], with three families of the parameters. See Sect. 1 for a graphical description of \({\mathfrak {Z}}^{(r)}_{x,y}\).
It turns out that the continuous vertex model described earlier can be identified with the delayed inhomogeneous Beta polymer model, in the way identical to the homogeneous situation [11]: repeating the proof of [11, Proposition 7.1] verbatim one can verify that for \((x,y)\in {\mathbb {Z}}^2_{\ge 0}\) the height functions \({\widetilde{h}}_{\ge c}^{(x+\frac{1}{2},y+\frac{1}{2})}\) of the continuous vertex model as random variables can be defined by the recurrence relation
and the initial conditions
for exactly the same choice of \(\eta _{i,j}\). Comparing the recurrence relations and initial conditions for \({\widetilde{h}}_{\ge c}^{(x+\frac{1}{2},y+\frac{1}{2})}\) and \({\mathfrak {Z}}_{x,y}^{(r)}\) one obtains
Corollary 6.4
The finite dimensional distributions of
coincide with the finite dimensional distributions of
As a result of the discussion in this section, we have realized the Beta polymer partition functions as certain limits of the height functions of the q-Hahn model. Thus, Theorem 4.2 can be used to obtain an integral expression for the joint moments of the partitions functions \(\{{\mathfrak {Z}}_{i,j}^{(r)}\}\). To formulate the result, consider a degenerated representation \( t_\tau \) of the Hecke algebra, acting on functions in \(v_1, \dots , v_k\) and defined by the generators
Proposition 6.5
For any sequences \((r_1, \dots , r_k)\), \((x_1, \dots , x_k)\) and \((y_1, \dots , y_k)\) satisfying
and for any permutation \(\tau \in S_k\) the following holds:
where the integration contours \({\mathcal {S}}_a\) encircle the points \(\{\sigma _i\}_{i}\) and \(\{\rho _j\}_j\) as well as the contours \({\mathcal {S}}_b, {\mathcal {S}}_b+1\) for any \(b<a\), while the points \(\{\omega _d\}_d\) are outside of the contours. Here \({\mathcal {S}}_b+1\) denotes the contour \({\mathcal {S}}_b\) shifted to the right by 1.
Proof
We take the limit (6.1) in the integral expression from Theorem 4.2, applied to the height functions \(h^{(x_a+\frac{1}{2}, y_a+\frac{1}{2})}_{\ge r_{\tau ^{-1}(a)}+1}\) and assuming \(\varvec{I}=(1,1,\dots )\). Set
For the left-hand side of (4.7) we can apply Corollaries 6.3 and 6.4 to obtain
since the finite-dimensional distributions of \(q^{h^{(x+\frac{1}{2},y+\frac{1}{2})}_{\ge r+1}}=\exp (-\varepsilon h^{(x+\frac{1}{2},y+\frac{1}{2})}_{\ge r+1})\) converge to the finite-dimensional distributions of \(\exp (-{\widetilde{h}}_{\ge r+1}^{(x+\frac{1}{2},y+\frac{1}{2})})\sim {\mathfrak {Z}}^{(r)}_{x,y}\) as \(\varepsilon \rightarrow 0\).
For the right-hand side of (4.7) we perform a change of coordinates \(w_a=1-\varepsilon v_a\). One can readily see that for fixed contours \({\mathcal {S}}_1, \dots , {\mathcal {S}}_k\) satisfying the conditions of the claim and a sufficiently small \(\varepsilon \) the contours \(1-\varepsilon {\mathcal {S}}_a\) satisfy the conditions for the contours \(\varGamma _a\), and so in the right-hand side after a change of contours we have an integral over fixed compact contours, with integrand depending on \(\varepsilon \). Point-wise we have
One can readily check that the integrand is uniformly bounded for fixed contours \({\mathcal {S}}_a\) and sufficiently small \(\varepsilon \), so by dominated convergence the claim follows. \(\square \)
As a particular case of Proposition 6.5, we have an integral expression for the moments of a single partition function \({\mathfrak {Z}}^{(r)}_{x,y}\) of the inhomogeneous Beta polymer. Note that, up to a shift of parameters, one dimensional distributions of \({\mathfrak {Z}}^{(r)}_{x,y}\) depend only on x and \(y-r\) (this is the vector between end points of paths inside the polymer), so without loss of generality we can set \(r=0\) and consider the moments of \({\mathfrak {Z}}_{x,y}:={\mathfrak {Z}}^{(0)}_{x,y}\):
Corollary 6.6
For any \((x,y)\in {\mathbb {Z}}_{\ge 0}^2\) such that \(y\ge x\) and any \(k\in {\mathbb {Z}}_{\ge 0}\) we have
where the integration contours \({\mathcal {S}}_a\) encircle \(\sigma _i\), leave \(\omega _d\) outside and \({\mathcal {S}}_b\) encircles both \(\mathcal S_a\) and \({\mathcal {S}}_a+1\) for \(a<b\).
7 Laplace transform for inhomogeneous Beta polymer partition function
From now on we focus on the partition function \({\mathfrak {Z}}_{x,y}={\mathfrak {Z}}_{x,y}^{(0)}\) of the inhomogeneous Beta polymer, with parameters \(\sigma _i, \rho _j, \omega _d\). Our goal is Theorem 8.4, which partially establishes the Tracy–Widom large-scale behavior and which is proved in next section. Our result generalizes the corresponding result from [4], moreover, our proof follows the same outline: in this section we find a suitable expression for the Laplace transform of \({\mathfrak {Z}}_{x,y}\) in terms of a Fredholm determinant, which is asymptotically analyzed in next section to establish the limit theorem.
Our starting point is the integral expression (6.4) for the moments of \({\mathfrak {Z}}_{x,y}\). Fix x, y and the parameters of the model \(\sigma _i, \rho _j,\omega _d\), and assume that
Since our aim is an integral expression for the Laplace transform of \({\mathfrak {Z}}_{x,y}\) which involves all the moments, it is convenient to replace the integration over shifted contours \({\mathcal {S}}_1, \dots , {\mathcal {S}}_k\) in (6.4) by an integration over a single contour \({\mathcal {C}}\). This is done with the help of the following statement:
Proposition 7.1
Suppose that contours \({\mathcal {S}}_1, \dots , {\mathcal {S}}_k\) and a rational function f(v) satisfy
-
The contours \(S_a\) are positively-oriented simple closed curves in \({\mathbb {C}}\);
-
For any \(a<b\) the contour \({\mathcal {S}}_b\) encircles both contours \({\mathcal {S}}_a\) and \({\mathcal {S}}_a+1\);
-
The contour \({\mathcal {S}}_1+1\) is completely outside of \({\mathcal {S}}_1\);
-
All the poles of the function f(v) are either in the interior of \({\mathcal {S}}_1\) or in the exterior of \({\mathcal {S}}_k\).
Then
where the sum in the right-hand side is over partitions \(\lambda \) of k, \(l(\lambda )\) denotes the number of nonzero parts of \(\lambda \) and \(m_i\) denotes the number of parts of \(\lambda \) equal to i.
Rough idea of the proof
The statement above follows a type of deduction called contour shift argument. The main idea is to shrink the contours \(\mathcal S_2, \dots , {\mathcal {S}}_k\) in the left-hand side to the smallest contour \({\mathcal {S}}_1\), picking up the residues at \(v_b=v_a+1\) for \(b>a\). Due to the conditions on the function f and the contours, all non-zero residues along this deformation come from the poles of \(\prod _{a<b}\frac{v_b-v_a}{v_b-v_a-1}\), and a careful bookkeeping produces the right-hand side.
A detailed explanation of the full argument can be found in [2, Proposition 3.2.1] and [8, Proposition 7.4], where more general q-deformed versions of the argument are presented. To adopt those claims to our setting one have to repeat the argument similar to the proof of Proposition 6.5, see [2, Proposition 6.2.7] and [4, Proposition 3.6]. \(\square \)
Let
and choose \({\mathcal {C}}={\mathcal {S}}_1\) to be a sufficiently small contour around the points \(\sigma _i\) such that the shifted contour \({\mathcal {C}}+1\) and the points \(\omega _d\) are completely outside of \({\mathcal {C}}\). Such contour exists due to the conditions (6.2), (7.1).
Corollary 7.2
With the notation above, we have
Proof
Direct application of (7.2).
Now we want to take a sum over k in (7.3) to obtain the Laplace transform. But to resolve possible convergence issues we need to estimate the integrand for large \(\lambda \). Set
where \(\varGamma (z)\) is the gamma function. Then
Lemma 7.3
For a fixed \(\delta >0\) and any \(z\in {\mathbb {C}}\) such that \(\arg (z-\sigma )\in [-\pi +\delta ;\pi -\delta ]\) we have as \(z\rightarrow \infty \)
where \(\varDelta =\sum _{i=0}^x\sigma _i-\sum _{j=1}^y\rho _j+\sum _{d=1}^{y-x}\omega _d\).
Proof
We use the following useful asymptotic expansion from [34][(1), (4), pp. 31–32], valid uniformly for \(\arg (z)\in [-\pi +\delta /2;\pi -\delta /2]\) and \(|z|\rightarrow \infty \)
and, more generally, for a fixed \(a\in {\mathbb {C}}\) and sufficiently large z such that \(\arg (z)\in [-\pi +\delta /2;\pi -\delta /2]\)
Here \(\ln \) denotes the principal branch of the natural logarithm. Plugging this expression into the definition of g(z) we get
implying the claim. \(\square \)
Proposition 7.4
For any \(u\in {\mathbb {C}}\) we have
where \(\det (I+K)\) denotes the Fredholm determinant of K, and \(\widetilde{K_u}\) is the integral operator with the kernel
Proof
The proof essentially repeats [2, Proposition 3.2.8]. First we rewrite (7.3) as
and then change the summation over partitions to a summation over arbitrary sequences, absorbing the multinomial coefficient:
Now we want to take the sum over k, but we need to be careful about possible convergence issues. For the left-hand side we have \(|{\mathfrak {Z}}_{x,y}|\le 1\) almost surely, so the sum converges absolutely for any u and by dominated convergence gives the Laplace transform:
For the right-hand side we can use the conditions on the parameters \(\sigma _i, \rho _j,\omega _d\) and on the compact contour \({\mathcal {C}}\) to give a uniform in \((v,v',n)\in {\mathcal {C}}\times {\mathcal {C}}\times {\mathbb {Z}}_{\ge 1}\) upper-bound
At the same time, by Lemma 7.3 we have
where \(\varDelta =\sum _{i=0}^x\sigma _i-\sum _{j=1}^y\rho _j+\sum _{d=1}^{y-x}\omega _d\) and the constants of \(O\left( n^{-1}\right) \) can be chosen independently of \(v\in {\mathcal {C}}\), since \({\mathcal {C}}\) is bounded. Hence for some constants \(\varLambda _2,\varepsilon >0\) and any \(n\in {\mathbb {Z}}_{\ge 1}\) we have
Gathering all pieces, we obtain
and hence, by Hadamard’s inequality,
where \(\xi >0\) is the length of the contour \({\mathcal {C}}\). Since
for any \(u\in {\mathbb {C}}\), the right-hand side of (7.6) absolutely converges. \(\square \)
So, we have obtained an expression for the Laplace transform in terms of a Fredholm determinant over \(L^2({\mathbb {Z}}_{\ge 1}\times {\mathcal {C}})\). But the summation over \({\mathbb {Z}}_{\ge 1}\) is inconvenient for the asymptotical analysis, so we replace it by another integration using Mellin-Barnes integral formula. To proceed we add another assumption, namely, we assume that there exists a vertical line \({\mathcal {L}}=\{z \mid {{\,\mathrm{Re}\,}}[z]=h\}\) for some h such that the contours \({\mathcal {C}}\) and \({\mathcal {C}}+1\) are separated by \({\mathcal {L}}\). Note that this is still possible because of (7.1).
Proposition 7.5
For any \(u\in {\mathbb {C}}\) such that \(\arg (-u)\in \left( -\frac{\pi }{2};\frac{\pi }{2}\right) \) we have
where \({\mathcal {L}}\) is a vertical line \(\{z\mid {{\,\mathrm{Re}\,}}[z]=h\}\) directed upwards and for \((-u)^{z-v}=e^{(z-v)\ln (-u)}\) we use the principal branch of the natural logarithm.
Proof
The statement and the proof are similar to [4, Lemma 3.7], but our restrictions on u are different.
Since the contour \({\mathcal {C}}\) is compact, there exists \(N_0\in \mathbb Z_{>0}\) such that the contour \({\mathcal {C}}\) is entirely inside the rectangle formed by the lines \({\mathcal {L}}, {\mathcal {L}}-1, {\mathbb {R}}+N_0{\mathbf {i}}, {\mathbb {R}}-N_0{\mathbf {i}}\). For \(N>N_0\) let \({\mathcal {H}}_N\) denote the rectangle formed by the lines \({\mathcal {L}}\), \({\mathcal {L}}+N\), \(\mathbb R+N{\mathbf {i}}, {\mathbb {R}}-N{\mathbf {i}}\), oriented clockwise. Then the integral
has nonzero residues only at the poles of \(\frac{\pi }{\sin (\pi (z-v))}\), since all the residues of \(\frac{g(v)}{g(z)}\) are to the left of the line \({\mathcal {L}}\). Computing the residues at \(z=v+n\) for \(n=1,\dots , N\) we get
Now we want to take \(N\rightarrow \infty \) in both sides. For the left-hand side, using the same upper-bound on \(K(v,n;v'n')\) as in Proposition 7.4, we have
so the absolute convergence holds for any \(u\in {\mathbb {C}}\).
For the right-hand side we need to show that the integral along the symmetric difference of \({\mathcal {L}}\) and \({\mathcal {H}}_N\) converges to 0. This symmetric difference \({\mathcal {D}}_N\) consists of the line segments sequentially connecting the points \(h-\infty {\mathbf {i}}, h-N{\mathbf {i}}, h+N-N{\mathbf {i}}, h+N+N{\mathbf {i}}, h+N{\mathbf {i}}, h+\infty {\mathbf {i}}\).
Clearly, \(\frac{1}{z-v'}\) for \(z\in {\mathcal {D}}_N\) can be bounded uniformly in N, while \(\frac{\pi }{\sin (\pi (z-v))}\) decays exponentially in \({{\,\mathrm{Im}\,}}[z]\):
where \(\varLambda _3\) does not depend on N. To bound \(\frac{1}{g(z)}\) we use Lemma 7.3 to get
for a constant \(\varLambda _4\) and \(z\in {\mathcal {D}}_N\) for sufficiently large N. Finally, due to the condition on u, we have
for some \(\delta >0\). Combining everything together we see that for some constant \(\varLambda _5>0\) the integrand is bounded by
which is enough to conclude that the integral over \({\mathcal {D}}_N\) tends to 0. \(\square \)
Proposition 7.6
For any \(u\in {\mathbb {C}}\) such that \(\arg (-u)\in (-\frac{\pi }{2};\frac{\pi }{2})\) we have
where the integral operator \({K_u}\) is defined by the kernel
Here \({\mathcal {C}}\) is a sufficiently small contour containing \(\sigma _i\) for all i, and \({\mathcal {L}}\) is a vertical line separating \({\mathcal {C}}\) and \({\mathcal {C}}+1\).
Proof
From Proposition 7.4 we have
Due to the dominated convergence, which is valid since the contour \({\mathcal {C}}\) is compact and we have an integrable converging upper-bound (7.7), we can exchange the second summation and the integration. Since \({\widetilde{K}}_u(v, n; v', n')\) does not depend on \(n'\), we can use use the same absolute upper-bound (7.7) and multi-linearity of the determinant with respect to rows to get
Then the claim follows from Proposition 7.5. \(\square \)
8 Limit theorem
This section is devoted to the partial result about the Tracy–Widom large-scale limit of the partition function \({\mathfrak {Z}}_{x,y}\) of the inhomogeneous Beta polymer model, when \(x,y\rightarrow \infty \) at a constant ratio and the parameters of the model have finite number of values repeated with certain frequencies. Our approach follows [4]: we perform a steepest descent analysis of the Fredholm determinant from Proposition 7.6.
8.1 Overview
Fix k and consider three families of parameters \(\{\sigma _1,\dots , \sigma _k\}, \{\rho _1,\dots , \rho _k\}\) and \(\{\omega _1, \dots , \omega _k\}\). Let \(\{\alpha _1, \dots , \alpha _k\}\), \(\{\beta _1, \dots , \beta _k\}, \{\gamma _1, \dots , \gamma _k\}\) be collections of corresponding “frequencies" satisfying
For a fixed slope x/y we consider the partition function \({\mathfrak {Z}}_{\lfloor {xt}\rfloor ,\lfloor {yt}\rfloor }\) as \(t\rightarrow \infty \), where parameters of the model \(\{{\widetilde{\sigma }}_0, \dots , {\widetilde{\sigma }}_{\lfloor {xt}\rfloor }\}\), \(\{{\widetilde{\rho }}_1, \dots , {\widetilde{\rho }}_{\lfloor {yt}\rfloor }\}\), \(\{{\widetilde{\omega }}_1, \dots , {\widetilde{\omega }}_{\lfloor {yt}\rfloor -\lfloor {xt}\rfloor }\}\)Footnote 13 are defined in the following way: For the column parameters, exactly \(\alpha _i^{[t]} xt \) out of \(\lfloor xt\rfloor +1\) parameters \({{\widetilde{\sigma }}}_i\) are equal to \(\sigma _i\), where \(\alpha _i^{[t]}\) is a sequence satisfying
Similarly, the row parameters \(\rho _j\) and the diagonal parameters \(\omega _d\) are repeated for \(\beta _j^{[t]}yt\) and \(\gamma ^{[t]}_d(y-x)t\) times respectively, where
Motivated by the homogeneous setting [4] we are looking for a result of the form
where \(F_{GUE}(p)\) is the GUE Tracy–Widom distribution [43]. A probabilistic interpretation, which one can find more natural, is given by identification of \({\mathfrak {Z}}_{\lfloor {xt} \rfloor ,\lfloor {yt} \rfloor }\) with the distribution of a random walk in a random Beta environment. From this point of view, we are looking at large deviations of the random walk, studying fluctuations of a random rate function (depending on the random environment) from the expected limit I(x/y) depending on the slope. See [4] for more details.
To prove a limit relation (8.1) it is enough to set \(u^{[t]}=-\exp (tI-t^{1/3}cr)\) and show that
because, by [2, Lemma 4.1.39]Footnote 14 we have
given that the limit is a continuous distribution function. So, the problem is reduced to studying the Laplace transform, which by Proposition 7.6 has an expression in terms of a Fredholm determinant. The latter can be analyzed using the steepest descent method: rewrite the kernel \(K_{u^{[t]}}\) as
where
As \(t\rightarrow \infty \) the function \(h^{[t]}(z)\) converges to the function
which, for the right choice of I, has a second order critical point \(\theta \) depending on the slope y/x in a nontrivial way. However, the dependence of the slope x/y on \(\theta \) can be easily described, suggesting the following parametrization by \(\theta \in (\max _i\sigma _i,\infty )\):
where \(\varPsi (z)\) denotes the digamma function and \(\varPsi _k(z)\) denotes the kth polygamma function:
Proposition 8.1
(1) The function \(x(\theta )/y(\theta )\) is increasing in \(\theta \in (\max _i \sigma _i, \infty )\), with the limit values
(2) \(c(\theta )\) can be chosen to be positive.
Proposition 8.1 is proved in “Appendix B” of the arXiv version of this paper.
With this parametrization we have \(h(z)-h(\theta )=\frac{c^3}{3}(z-\theta )^3 +O((z-\theta )^4)\) for z close to \(\theta \), and the general philosophy of the steepest descent method suggests that asymptotical behavior of the Fredholm determinant is dominated by its behavior in a small neighborhood of \(\theta \), which, after certain manipulation, can be shown to produce \(F_{GUE}(r)\).
Conjecture 8.2
For any \(\theta \in (\max (\sigma ), \infty )\) we have
with \(x=x(\theta ), y=y(\theta ), I=I(\theta ), c=c(\theta )\) defined above in terms of \(\theta \).
Unfortunately, the general case turns out to be technically challenging, and we do not pursue it here. In this section we prove Conjecture 8.2 for parameters \(\sigma _i,\rho _i,\omega _i,\theta \) satisfying the following restrictions:
Assumption 8.3
We assume that
-
All \(\sigma _i\) are equal to 0, while all \(\rho _i\) are equal to \(-1\):
$$\begin{aligned} \sigma _1=\sigma _2=\cdots =\sigma _k=0,\qquad \rho _1=\rho _2=\cdots =\rho _k=-1. \end{aligned}$$ -
\(\theta \in \left( 0, \frac{1}{2}\right) \).
Theorem 8.4
Under Assumption 8.3 we have
Remark 8.5
Theorem 8.4 generalizes [4, Theorem 5.2] by adding a degree of freedom corresponding to the diagonal parameters \(\omega _i\), while in [4] they were additionally assumed to be equal to \(-2\). Returning to the Beta polymer model, Theorem 8.4 corresponds to the model with Beta distributions \({{\,\mathrm{Beta}\,}}(1,-{\widetilde{\omega }}-1)\) with parameters \({\widetilde{\omega }}<-1\) constant along the diagonals and having finitely many possible values \(\omega _1, \dots , \omega _k\).
The restrictions from Assumption 8.3 come from two technical difficulties. Namely, to justify the steepest descent argument one needs to
-
Find contours \({\mathcal {C}}_\theta ,{\mathcal {L}}_\theta \) passing through \(\theta \) and satisfying \({{\,\mathrm{Re}\,}}[h(z)-h(v)]\le 0\) for \(z\in {\mathcal {L}}_\theta , v\in {\mathcal {C}}_\theta \), with equality only if \(v=z=\theta \);
-
Prove that one can deform the initial contours \({\mathcal {C}},{\mathcal {L}}\) to \({\mathcal {C}}_\theta ,{\mathcal {L}}_\theta \) without changing the limit of the Fredholm determinant.
For the first step a suitable descent contour \({\mathcal {L}}_{\theta }\) for \({{\,\mathrm{Re}\,}}[h(z)]\) valid for any parameters \(\sigma _i,\rho _i,\omega _i\) was found in [4] and it is given by a vertical line passing through \(\theta \). At the same time, finding a descent contour for \(-{{\,\mathrm{Re}\,}}[h(v)]\) is much more involved for general parameters: we know how to find it only if \(\sigma _i-\rho _j=1\) for any i, j and \(\theta -\max _i\sigma _i<1\), forcing the first part of Assumption 8.3.Footnote 15 Under these restrictions another contour from [4] turns out to be sufficient, we denote it by \({\mathcal {C}}_\theta \) and it is equal to a circle around 0 of radius \(\theta \). However, numerical computations and related results suggest that a descent contour for \(-{{\,\mathrm{Re}\,}}[h(v)]\) should exist in general: see [17] for an example of a significantly more involved argument used to lift the analogous assumption in a different but related setting.
The second step is complicated by potential singularities of the Fredholm determinant along the deformation of \({\mathcal {C}}, {\mathcal {L}}\) to \({\mathcal {C}}_\theta ,{\mathcal {L}}_\theta \). One can hope to estimate the residues at these singularities and show that their contribution asymptotically vanishes, but the required argument is technically challenging. The second part of Assumption 8.3 allows us to avoid this issue, since for \(\theta <\frac{1}{2}\) the contours can be deformed without crossing any singularities of the relevant integrands.
The remainder of Sect. 8 is devoted to the proof of Theorem 8.4. As clarified above, it is enough to prove
where \(u^{[t]}=-\exp (tI-t^{1/3}cr)\). The proof is structured as follows: first we describe the needed properties of the function h(z), as well as specify estimates on convergence of \(h^{(t)}(z)\) to h(z). Then we prove various bounds on the kernel \(K_u\) from Proposition 7.6. Finally, to prove Theorem 8.4 we reduce the computation of the limit to a small neighborhood of \(\theta \), perform a change of variables to get rid of lower degree terms and use standard algebraic manipulations to establish (8.3).
8.2 h-functions and descent contours
Here we list the needed properties of the functions h(z) and \(h^{[t]}(z)\), which are defined by
with x, y, I defined in terms of \(\theta \) as before.
We start with the properties of h(z). Define the contour \({\mathcal {L}}_\theta \) as a vertical line passing through \(\theta \), oriented upwards:
Under Assumption 8.3 we also define the contour
oriented counter-clockwise. See Fig. 6 for a depiction of the contours.
The proofs of the following three statements are technical and are omitted from this text, they can be found in “Appendix B” of the arXiv version of this paper. The first statement does not require Assumption 8.3.
Proposition 8.6
\({\mathcal {L}}_\theta \) is a steep descent contour for \({{\,\mathrm{Re}\,}}[h(z)]\), that is, \({{\,\mathrm{Re}\,}}[h(\theta +bi)]\) decreases for positive b and increases for negative b.
Proposition 8.7
Under Assumption 8.3\({\mathcal {C}}_\theta \) is a steep descent contour for \(-{{\,\mathrm{Re}\,}}[h(z)]\), that is, \(-{{\,\mathrm{Re}\,}}[h(\theta e^{\phi {\mathbf {i}}})]\) decreases for \(\phi >0\) and increases for \(\phi <0\).
Proposition 8.8
Suppose that Assumption 8.3 is satisfied. Let \(\psi (\varepsilon )=\arg (v_{\varepsilon }-\theta )\), where \(v_{\varepsilon }\) is the intersection point of \({\mathcal {C}}_\theta \) with the circle of radius \(\varepsilon \) around \(\theta \) satisfying \({{\,\mathrm{Im}\,}}[v_{\varepsilon }]>0\). Then for sufficiently small \(\varepsilon \) there exists a constant b such that
Let us briefly sketch the main idea of the omitted proofs of Propositions 8.6–8.8. It turns out that the function h(z) is a convex combination of the analogous functions for the homogeneous model, namely
where
This allows one to reduce the problem to the homogeneous case and analyze the functions h(z) in a way similar to [4, Section 5]. See “Appendix B” of the arXiv version for more details.
The next statement reiterates the fact that \(\theta \) is a critical point of h(z).
Lemma 8.9
For z in a neighborhood of \(\theta \) we have
where c is given by (8.2). Moreover, \(c>0\).
Proof
Readily follows by considering the Taylor expansion of h(z), taking derivatives and using the definitions of \(x(\theta ), y(\theta ), I(\theta )\) and \(c(\theta )\). The positivity of c follows from Proposition 8.1. \(\square \)
Finally, we need the following statements regarding the convergence of \(h^{[t]}(z)\) to h(z) in various situations.
Lemma 8.10
Assume that a sequence of points \(z_t\in {\mathbb {C}}\) converges to \(\theta \) in a way that \(h^{[t]}(z_t)\) is well defined for all \(t>0\). Then
assuming that the right-hand side exists.
Proof
Note that
Since \(\alpha ^{[t]}_i-\alpha _i=O(1/t)\) and \(\ln \varGamma (z-\sigma _i)\) is continuous around \(\theta \), we have
Taking sum over i and repeating the same argument for \(\beta _i,\beta _i^{[t]},\rho _i\) and \(\gamma _i,\gamma _i^{[t]},\omega _i\) we obtain
which implies the claim. \(\square \)
Lemma 8.11
Let \(K\subset {\mathbb {C}}\) be a compact subset not containing any of the parameters \(\sigma _i,\rho _i,\omega _i\). Then for any \(z\in K\) and \(t>0\) we have
for some constant \(\varLambda >0\) depending only on the compact set K but not on t.
Proof
Following the lines of the proof of Lemma 8.10, since \(\alpha ^{[t]}_i-\alpha _i=O(1/t), \beta ^{[t]}_i-\beta _i=O(1/t), \gamma ^{[t]}_i-\gamma _i=O(1/t)\) there exists a constant \(\varLambda _1>0\) such that
At the same time, since K is bounded away from \(\sigma _i,\rho _i,\omega _i\), there exists another constant \(\varLambda _2>0\) such that
Combining these upper bounds concludes the proof. \(\square \)
Lemma 8.12
For sufficiently large z such that \(\arg (z)\in [-\pi +\delta ,\pi -\delta ]\) for a fixed \(\delta \) we have
where the constants of \(O(z^{-1})\) can be chosen independently of t, and \(\varDelta ^{[t]}\) is given by
Note that, due to our conventions on \(\alpha _i^{[t]}, \beta _i^{[t]}\) and \(\gamma _i^{[t]}\), we have a uniform in t bound \(|\varDelta ^{[t]}|<\varLambda \) for a constant \(\varLambda >0\) independent of t.
Proof
By taking logarithm the claim can be rephrased as
Now we can use the asymptotic expansion for Gamma function, used before in Lemma 7.3: with the same restrictions on z as in the claim and any fixed \(a\in {\mathbb {C}}\) we have
Recall that \(\sum _{i=1}^k\alpha _i=\sum _{i=1}^k\beta _i=\sum _{i=1}^k\gamma _i=1\), while for \(\alpha ^{[t]}_i,\beta ^{[t]}_i,\gamma ^{[t]}_i\) we have
with 1 in the first equality coming from having \(\lfloor {xt} \rfloor +1\) column parameters \(\{{\widetilde{\sigma }}_i\}_{i=0,\dots , \lfloor {xt} \rfloor }\). Thus
Combining the identity above with the asymptotic expansion for the Gamma function, we obtain
where \(\varLambda _1\) is the same constant as in the proof of Lemma 8.11. Applying the asymptotic expansion for the Gamma function to the right-hand side implies the claim. \(\square \)
8.3 Kernel estimates
Recall that the substitution of \(u=-\exp (tI-t^{1/3}cr)\) into the integral kernel from Proposition 7.6 leads to the following kernel:
For \(v,v'=\theta \) we interpret the integral above using its principal value as the contour \({\mathcal {L}}_\theta \) passes to the right of \(\theta \). In other words, we slightly deform the contour \({\mathcal {L}}_\theta \) to an upwards oriented contour \({\mathcal {L}}_\theta ^{[t]}\) consisting of vertical lines \(\{\theta \pm Y{\mathbf {i}}\mid Y\in [t^{-1/3},\infty )\}\) and a semicircle \(\{\theta +t^{-1/3}e^{\phi {\mathbf {i}}}\mid \phi \in [-\pi ,\pi ]\}\), see Fig. 6.
The aim of this section is to give asymptotical bounds on behavior of the kernel. We use the following notation. For \(\varepsilon >0\) let \({\mathcal {L}}_{\theta ,\varepsilon }^{[t]}\) and \({\mathcal {C}}_{\theta ,\varepsilon }\) denote the parts of the contours \({\mathcal {L}}_{\theta }^{[t]}\) and \({\mathcal {C}}_\theta \) contained inside the \(\varepsilon \)-neighborhood of \(\theta \). Define the kernel \(K_{\varepsilon }^{[t]}\) by
Finally, define \({\mathcal {K}}(\varepsilon )={\mathcal {D}}_\varepsilon \cup {\mathcal {A}}_\varepsilon \cup ({\mathcal {C}}_\theta \backslash {\mathcal {C}}_{\theta ,\varepsilon })\) as a contour consisting of the upward-oriented wedge
a part of the contour \({\mathcal {C}}_\theta \) outside of the \(\varepsilon \)-neighborhood of \(\theta \), which we denote as \({\mathcal {C}}_{\theta ,\ge \varepsilon }\), and a couple of upward-oriented arcs
where \(\psi (\varepsilon )\) is chosen so that the result is connected. See Fig. 7 for a depiction of the contour \({\mathcal {K}}(\varepsilon )\).
For the following statements we fix \(\varepsilon >0\).
Lemma 8.13
Let \(v,v'\in {\mathcal {K}}(\varepsilon )\) be a pair of points such that \({{\,\mathrm{Re}\,}}[h(v)-h(\theta )]\ge b\) for some fixed \(b\ge 0\). Then for \(t>\varepsilon ^{-3}\) we have
where the constants \(\varLambda , a>0\) depend only on \(\varepsilon \) and the parameters of the model.
Lemma 8.14
Let \(v,v'\in {\mathcal {K}}(\varepsilon )\) be a pair of points such that \({{\,\mathrm{Re}\,}}[h(v)-h(\theta )]\ge b\) for a fixed \(b\ge 0\). Then for \(t>\varepsilon ^{-3}\) we have
where \(\varLambda >0\) is a constant depending only on \(\varepsilon \) and b, but not on \(v,v'\). In particular, if \(b> 0\) we also have
for some other constant \(\varLambda '>0\) depending on \(\varepsilon \) and b.
Proof of Lemma 8.13
The assumption \(t>\varepsilon ^{-3}\) is needed only to ensure that the semicircle of \({\mathcal {L}}^{[t]}_\theta \) is inside the \(\varepsilon \) neighborhood. Then we need to bound the integral
taken over two vertical lines \(\{\theta \pm Y{\mathbf {i}}|Y>\varepsilon \}\). We denote this contour by \({\mathcal {L}}_{\theta ,\ge \varepsilon }\)
Note that the contour \({\mathcal {K}}(\varepsilon )\) is bounded away from \({\mathcal {L}}_{\theta ,\ge \varepsilon }+n\) for any \(n\in {\mathbb {Z}}\), hence we have
where \(\varLambda _1>0\) is a constant depending only on \(\varepsilon \) but not on \(v,v'\). So it is enough to give a sufficiently strong upper-bound on \(|\exp (t(h^{[t]}(z)-h^{[t]}(v))-crt^{1/3}(z-v))|\). Due to the steep descent from Proposition 8.6, for some constant \(a>0\) we have
But the kernel \(K^{[t]}\) is defined in terms of \(h^{[t]}(z)\) rather than h(z) and to proceed we have to split the problem in two parts, with |z| large and z compactly supported.
Since \({\mathcal {K}}(\varepsilon )\) is compact, by Proposition 8.11 we have
where the constant \(\varLambda _3>1\) does not depend on v. On the other hand, by Lemma 8.12 and the asymptotical expansion for the Gamma function (7.4), for sufficiently large \(M>\varepsilon \) independent of \(t,\varepsilon \) we have
Recall that \(\varDelta ^{[t]}\) is uniformly bounded, so set \(\varDelta =\inf _{t}\varDelta ^{[t]}>-\infty \). Then, assuming \(M>1\), for some constant \(\varLambda _2'\) and any \(z\in {\mathcal {L}}_\theta , |z|>M, v\in {\mathcal {K}}(\varepsilon )\) we obtain
where we have used that \(|z^z|>|z|^\theta e^{-\frac{\pi }{2}|{{\,\mathrm{Im}\,}}[z]|}\) and \(|z|<\theta +|{{\,\mathrm{Im}\,}}(z)|\) for \(z\in {\mathcal {L}}_\theta \).
At the same time, having fixed M from the previous part, for \(z\in {\mathcal {L}}_{\theta ,\ge \varepsilon }, |z|<M\) we can again apply Lemma 8.11 to get
for \(\varLambda _4>1\). Hence, for some constant \(\varLambda _2''>0\) depending only on \(\varepsilon ,M\) we have
Setting \(\varLambda _2=\max (\varLambda _2',\varLambda _2'')\) and gathering all the pieces together, we get
where \(\varLambda _1,\varLambda _2\) depend only on \(\varepsilon \), but not on \(v,v',t\). \(\square \)
Proof of Lemma 8.14
By Lemma 8.13 it is enough to prove that
To bound the integral \(K_{\varepsilon }^{[t]}(v,v')\) we deform the integration contour \({\mathcal {L}}^{[t]}_{\theta ,\varepsilon }\) further, changing it to the contour \({\mathcal {P}}\) consisting of the line segments \({\mathcal {P}}_1=\{\theta +Y{\mathbf {i}}\mid y\in [-\varepsilon , -\delta t^{-\frac{1}{3}}]\cup [\delta t^{-\frac{1}{3}},\varepsilon ]\}\), and the semicircle \({\mathcal {P}}_2=\{\theta + \delta t^{-1/3}e^{\phi {\mathbf {i}}}\mid \phi \in [-\pi /2,\pi /2]\}\), where the parameter \(\delta >0\) possibly depends on \(\varepsilon \) and is chosen small enough so that \({\mathcal {K}}(\varepsilon )\) is bounded away from \({\mathcal {P}}+n\) uniformly in \(t>1\) for \(n\ne 0\).Footnote 16 Then there exists a constant \(\varLambda _1\) depending only on \(\varepsilon ,\delta \), such that
which implies, due to the geometry of \({\mathcal {K}}(\varepsilon )\), existence of uniform in \(v,v',t\) constants \(\varLambda _{1,{\mathcal {P}}_1}\) and \(\varLambda _{1,{\mathcal {P}}_2}\) such that
To bound the exponential term in the integrand of \(K^{[t]}_{\varepsilon }\) we use Lemma 8.11, obtaining
for a constant \(\varLambda _2\) depending only on \(\varepsilon \). Since \({{\,\mathrm{Re}\,}}[v]<\theta \) and \({{\,\mathrm{Re}\,}}[h(v)-h(\theta )]\ge b\), for any t we have
To finish the upper-bounds we have to consider the contours \({\mathcal {P}}_1\) and \({\mathcal {P}}_2\) separately, starting with \({\mathcal {P}}_1\). Since \({\mathcal {L}}_\theta \) is a steep descent contour for \({{\,\mathrm{Re}\,}}[h(z)]\) by Proposition 8.6, for \(z\in \theta +{\mathbb {R}}{\mathbf {i}}\) we have
Then the whole integral is bounded as follows:
for some constant \(\varLambda _3\) depending only on \(\varepsilon \).
To upper-bound the part taken over \({\mathcal {P}}_2\) we use the Taylor expansion, finding a constant \(\varXi >0\) such that
Plugging \(z=\theta +\delta t^{-1/3}e^{i\phi }\) we get
where \(\varLambda _4\) is a constant depending on \(\varepsilon \). Gathering the bounds above and using that the length of \({\mathcal {P}}_2\) is equal to \(\pi t^{-1/3}\) we get
The claim follows by combining the bounds for \({\mathcal {P}}_1\) and \({\mathcal {P}}_2\), . \(\square \)
8.4 Proof of Theorem 8.4
Recall that, in view of Proposition 7.6, it is enough to prove
where we use the notation from the previous subsection.
Step 1. First we show that the limit is dominated by the behavior in a neighborhood of \(\theta \). Namely, in this step we show that for sufficiently small fixed \(\varepsilon >0\) we have
where \({\mathcal {D}}_\varepsilon =\{\theta +Re^{\pm 2\pi {\mathbf {i}}/3}\mid R\in [0,\varepsilon ]\}\).
It is more convenient to proceed in two steps, reducing first the contour \({\mathcal {C}}_\theta \) to \({\mathcal {D}}_\varepsilon \) and then the kernel \(K^{[t]}\) to \(K_{\varepsilon }^{[t]}\). Note that we can deform \({\mathcal {C}}_\theta \) to \({\mathcal {K}}(\varepsilon )={\mathcal {D}}_\varepsilon \cup {\mathcal {A}}_\varepsilon \cup ({\mathcal {C}}_\theta \backslash {\mathcal {C}}_{\theta ,\varepsilon })\) without changing the value of the determinant. Since \(\mathcal C_\theta \) is a steep descent contour for \(-{{\,\mathrm{Re}\,}}[h(z)]\), for each \(\varepsilon \) there exists a constant \(b_1>0\) such that
At the same time, by Proposition 8.8, for sufficiently small \(\varepsilon \) there exists a constant \(b_2>0\) (depending on \(\varepsilon \)) such that
Thus, for sufficiently small fixed \(\varepsilon \) there exists \(b>0\) such that
Hence we can apply Lemma 8.14, obtaining a constant \(\varLambda _1\) such that
Note that the difference of Fredholm determinants \(\det (I+K^{[t]})_{L^2(\mathcal C_\theta )}-\det (I+K^{[t]})_{L^2({\mathcal {D}}_\varepsilon )}\) is equal to \(\sum _{l\ge 0}\frac{B_l}{l!}\), where \(B_l\) are integrals of \(\det [K(v_i,v_j)]_{i,j=1}^l\) taken over the difference \({\mathcal {K}}(\varepsilon )^l\backslash {\mathcal {D}}^l_\varepsilon \). Since each point in this difference has at least one of \(v_i\) not in \({\mathcal {D}}_\varepsilon \), by (8.5), Lemma 8.14 and Hadamard’s bound we get
Summing over l, we obtain
where \(\varLambda _3\) is a constant depending only on \(\varLambda _1,\varLambda _2\), and to get the last inequality we use \(\frac{l^{l/2+1}}{l!}\le \frac{2^{(l/2+1)}l}{\lfloor {l/2} \rfloor !}\) and apply the Taylor expansion of the exponent separately to odd and even values of l.
The argument replacing \(K^{[t]}\) by \(K_{\varepsilon }^{[t]}\) is identical and relies on Lemma 8.13. We have
and using multi-linearity of determinants and Lemmas 8.13 and 8.14 we have the following upper-bound for some constants \(\varLambda _3,a>0\)
which is enough to give an absolutely convergent upper-bound.
So, we have reduced Theorem 8.4 to proving
Step 2. After getting rid of the global parts of the integration contours, in this step we take the needed limit by scaling the neighborhood of \(\theta \) by \(t^{1/3}\).
For now, fix \(\varepsilon >0\) which is sufficiently small so that the argument in the previous step works, but otherwise arbitrary. We would like to perform the following change of coordinates in the Fredholm determinant \(\det (I+K^{[t]}_{\varepsilon })_{L^2({\mathcal {D}}_\varepsilon )}\) and the kernel \(K_{\varepsilon }^{[t]}\):
This leads to
with the contour \(\widetilde{{\mathcal D}}=\{|R|e^{{{\,\mathrm{sign}\,}}(R)2\pi {\mathbf {i}}/3}\mid R\in [-\infty , \infty ]\}\) and the kernel
To take the limit as \(t\rightarrow \infty \) we start with the point-wise convergence of the kernel \({\widetilde{K}}^{[t]}_{\varepsilon }({\widetilde{v}}, {\widetilde{v}}')\). Let \(\widetilde{{\mathcal {L}}}^{[t]}_{\varepsilon }\) be the contour consisting of vertical lines \(\{\pm Y{\mathbf {i}}\mid Y\in [1, \varepsilon t^{1/3}]\}\) and a semicircle \(\{e^{\phi {\mathbf {i}}}\mid \phi \in [-\pi ,\pi ]\}\), oriented so that the imaginary part increases. Also, let \(\widetilde{{\mathcal {L}}}\) denote the limiting contour with the vertical lines \(\{\pm Y{\mathbf {i}}\mid Y\in [1, \infty ]\}\) and the same semicircle. Then
Clearly
where for the two equalities we have sequentially used Lemmas 8.9 and 8.10. So the integrand converges to
Now we need to give integrable upper-bounds. Note that \({{\,\mathrm{Re}\,}}\left[ t\left( h^{[t]}(\theta +t^{-1/3}{\widetilde{z}})-h^{[t]}(\theta )\right) \right] \) is unifromly bounded for \(z\in {\widetilde{{\mathcal {L}}}}\): by Lemma 8.11 it is enough to consider \({{\,\mathrm{Re}\,}}\left[ t\left( h(\theta +t^{-1/3}{\widetilde{z}})-h(\theta )\right) \right] \) and for \(|{\widetilde{z}}|>1\) we can use the steep descent of \({\mathcal {L}}_\theta \), while for \({\widetilde{z}}\) on the semicircle this follows from the Taylor expansion of h(z) from Lemma 8.9. So for some constant \(\varLambda _1>0\) we have:
Due to the quadratic decay we can apply dominated convergence, obtaining
To finish we need to justify commutation of the Fredholm determinant and the limit above. To do it, we again use dominated convergence with an absolutely summable upper-bound on the Fredholm determinant. Note that for \({\widetilde{v}}\in \widetilde{{\mathcal {D}}}\) such that \(|{\widetilde{v}}|<\varepsilon t^{1/3}\) we have
for some \(\varLambda _2>0\). By Taylor expansion, there exists an independent of \(\varepsilon \) constant \(\varXi \) such that
Then for any \(\varepsilon <1\) we get
Recall that for the whole argument \(\varepsilon \) was an arbitrary sufficiently small number, so we can reduce it even further to get \(\frac{c^3}{3}-\varepsilon \varXi =b>0\). Combining the bound above with (8.6) we get
for some \(\varLambda _3>0\), which combined with Hadamard’s bound is sufficient for an integrable and absolutely summable upper-bound on the kernel of the Fredholm determinant. Hence
with the kernel \({\widetilde{K}}_\infty \) defined in (8.7).
Step 3. To finish the proof we need to show that the Fredholm determinant in the right-hand side is indeed equal to \(F_{GUE}\), which can be done by standard manipulations. Rescaling \({\widetilde{v}},{\widetilde{z}}\) by c we can assume that
Since the integrand has quadratic decay, we can deform the contour \(\widetilde{{\mathcal {L}}}\) to a contour going from \(\infty e^{-i\pi /3}\) to \(\infty e^{i\pi /3}\) with \({{\,\mathrm{Re}\,}}[{\widetilde{z}}]>0\). Now we can apply the same argument as in [6, Lemma 8.6]: For any \({\widetilde{z}}\) such that \({{\,\mathrm{Re}\,}}[{\widetilde{z}}]>0\) we use
to write \({\widetilde{K}}_\infty =-AB\), where A, B are operators with kernels
Then
where \(K_{{{\,\mathrm{Ai}\,}}}(\lambda ,\mu )\) is the Airy kernel. Since AB and BA are trace-class operators we have \(\det (I-AB)=\det (I-BA)\), cf. [40], so we finally get
\(\square \)
Notes
The q-Hahn vertex model is closely related to the q-Hahn TASEP, which was originally used to establish the integrability of the Beta polymer model.
One way to check it is to identify the polymer paths contributing to \({\mathfrak {Z}}_{x,y}^{(r)}\) with trajectories \((X_t,t)\) of the random walk reaching the half-line \(X_t\ge r, X_t+t=y-2r\), using the change of coordinates \((i,j)=(\frac{X+y-t}{2}, y-t)\).
The range for the slope looks more natural in the RWRE description: \(\frac{\sum \beta _i\rho _i-\sum \gamma _i\omega _i}{\sum \alpha _i\sigma _i-\sum \gamma _i\omega _i}\) corresponds to the average drift of the walk, and we are looking at fluctuations at non-typical velocities. See [4] for more details about the RWRE interpretation of the model.
The color 0 is commonly reserved for the absence of a path.
In the case \(n=1\) the vertex weights (2.3) reproduce the orthogonality weights for the q-Hahn polynomials, hence the name.
To avoid possible confusion with the weights \(W_{t,s}\), we refrain from using any graphical notation for the weights \({\mathcal {W}}^{\mathsf{N},\mathsf{M}}_z\).
Throughout the text the Hecke algebra appears only via this faithful representation, so identification of the basis elements \(T_\pi \) with the operators \(T_\pi \) should not cause confusion.
Though we do not use this terminology, \([1,p]\times [p+1,r]\)-ordered permutations are commonly called \((p,r-p)\)-shuffles.
The degree of a monomial \(\alpha _1^{l_1}\dots \alpha _n^{l_n}\) is \(l_1+\cdots +l_n\).
With the exception of the artificially added 0th column.
From now on x, y will usually be integers, rather than half-integers as before.
In earlier sections \(\sigma _i, \rho _j,\omega _d\) were used to denote the parameters of individual columns, rows and diagonals. To lighten the expressions in this section it is convenient for us to change the notation by using \({\widetilde{\sigma }}_i,{\widetilde{\rho }}_j,{\widetilde{\omega }}_d\) for individual parameters while \(\sigma _i, \rho _j,\omega _d\) denote their possible values; this abuse of notation should not cause confusion.
Following the notation of [2, Lemma 4.1.39], we need to set \(f(x)=e^{-e^{xct^{1/3}}}\).
To simplify the assumptions we have also used the invariance of the model under simultaneous additive shifts of all the parameters \(\sigma _i,\rho _i,\omega _i\).
Basically, we reduce the semicircle part of \({\mathcal {L}}^{[t]}_{\theta ,\varepsilon }\) avoiding additional singularities of \(\frac{1}{\sin (\pi (z-v))}\). More precisely, we want \({\mathcal {K}}(\varepsilon )\) to be between \({\mathcal {P}}-1\) and \({\mathcal {P}}\).
References
Amir, G., Corwin, I., Quastel, J.: Probability distribution of the free energy of the continuum directed random polymer in 1+1 dimensions. Commun. Pure Appl. Math. 64, 466–537 (2011). arXiv:1003.0443
Borodin, A., Corwin, I.: Macdonald processes. Probab. Theory Relat. Fields 158, 225–400 (2014). arXiv:1111.4408
Barraquand, G., Corwin, I.: The \(q\)-Hahn asymmetric exclusion process. Ann. Appl. Probab. 26(4), 2304–2356 (2016). arXiv:1501.03445
Barraquand, G., Corwin, I.: Random walk in Beta-distributed random environment. Probab. Theory Relat. Fields 167(3), 1057–1116 (2017). arXiv:1503.04117
Barraquand, G., Corwin, I., Dimitrov, E.: Fluctuations of the log-gamma polymer free energy with general parameters and slopes (2020). arXiv:2012.12316
Borodin, A., Corwin, I., Ferrari, P.: Free energy fluctuations for directed polymers in random media in 1+1 dimension. Commun. Pure Appl. Math. 67(7), 1129–1214 (2014). arXiv:1204.1024
Borodin, A., Corwin, I., Gorin, V.: Stochastic six-vertex model. Duke Math. J. 165(3), 563–624 (2016). arXiv:1407.6729
Borodin, A., Corwin, I., Petrov, L., Sasamoto, T.: Spectral theory for the q-Boson particle system. Compos. Math. 151, 1–67 (2015). arXiv:1308.3475
Barraquand, G., Le Doussal, P.: Moderate deviations for diffusion in time dependent random media. J. Phys. A Math. Theor. 53, 215002 (2020). arXiv:1912.11085
Borodin, A., Gorin, V.: A stochastic telegraph equation from the six-vertex model. Ann. Probab. 47(6), 4137–4194 (2019). arXiv:1803.09137
Borodin, A., Gorin, V., Wheeler, M.: Shift-invariance for vertex models and polymers (2019). arXiv:1912.02957
Bufetov, A., Korotkikh, S.: Observables of stochastic colored vertex models and local relation (2020). arXiv:2011.11426
Borodin, A., Korotkikh, S.: Inhomogeneous spin \(q\)-Whittaker polynomials (2021). arXiv:2104.01415
Bosnjak, G., Mangazeev, V.: Construction of \(R\)-matrices for symmetric tensor representations related to \(U_q(\widehat{sl_n})\). J. Phys. A Math. Theor. 49, 495204 (2016). arXiv:1607.07968
Borodin, A.: On a family of symmetric rational functions. Adv. Math. 306, 973–1018 (2017). arXiv:1410.0976
Borodin, A., Petrov, L.: Higher spin six vertex model and symmetric rational functions. Sel. Math. New Ser. 24, 751–874 (2018). arXiv:1601.05770
Barraquand, G., Rychnovsky, M.: Large deviations for sticky Brownian motions. Electron. J. Probab. 25(119), 1–52 (2020). arXiv:1905.10280
Balázs, M., Rassoul-Agha, F., Seppäläinen, T.: Large deviations and wandering exponent for random walk in a dynamic beta environment. Ann. Probab. 47(4), 2186–2229 (2019). arXiv:1801.08070
Borodin, A., Wheeler, M.: Coloured stochastic vertex models and their spectral theory (2018). arXiv:1808.01866
Borodin, A., Wheeler, M.: Spin \(q\)-Whittaker polynomials. Adv. Math. 376, 107449 (2021). arXiv:1701.06292
Borodin, A., Wheeler, M.: Observables of coloured stochastic vertex models and their polymer limits. Prob. Math. Phys. 1, 205–265 (2020). arXiv:2001.04913
Corwin, I.: The q-Hahn Boson process and q-Hahn TASEP. Intern. Math. Res. Not. 2015(14), 5577–5603 (2015). arXiv:1401.3321
Corwin, I., O’Connell, N., Seppäläinen, T., Zygouras, N.: Tropical combinatorics and Whittaker functions. Duke Math. J. 163(3), 513–563 (2014). arXiv:1110.3489
Corwin, I., Petrov, L.: Stochastic higher spin vertex models on the line. Commun. Math. Phys. 343(2), 651–700 (2016). arXiv:1502.07374
Corwin, I., Seppäläinen, T., Shen, H.: The strict-weak lattice polymer. J. Stat. Phys. 160, 1027–1053 (2015). arXiv:1409.1794
Ferrari, P., Veto, B.: Tracy-Widom asymptotics for q-TASEP. Ann. Inst. Henri Poincaré Probab. Stat. 51(4), 1465–1485 (2015). arXiv:1310.2515
Galashin, P.: Symmetries of stochastic colored vertex models (2020). arXiv:2003.06330
Howitt, C., Warren, J.: Consistent families of Brownian motions and stochastic flows of kernels. Ann. Probab. 37(4), 1237–1272 (2009). arXiv:math/0611292
Kac, V., Cheung, P.: Quantum Calculus. Springer, New York (2002)
Kuniba, A., Mangazeev, V., Maruyama, S., Okado, M.: Stochastic \(R\) matrix for \(U_q(\widehat{sl_n})\). Nucl. Phys. B 913, 248–277 (2016). arXiv:1604.08304
Kardar, K., Parisi, G., Zhang, Y.Z.: Dynamic scaling of growing interfaces. Phys. Rev. Lett. 56, 889–892 (1986)
Le Doussal, P., Thiery, T.: Diffusion in time-dependent random media and the Kardar–Parisi–Zhang equation. Phys. Rev. E 96, 010102 (2017). arXiv:1705.05159
Le Jan, Y., Lemaire, S.: Products of Beta matrices and sticky flows. Probab. Theory Relat. Fields 130, 109–134 (2004). arXiv:math/0307106
Luke, Y.: The Special Functions and Their Approximations, vol. I. Academic Press, New York (1969)
Mucciconi, M., Petrov, L.: Spin q-Whittaker polynomials and deformed quantum Toda (2020). arXiv:2003.14260
O’Connell, N., Ortmann, J.: Tracy-Widom asymptotics for a random polymer model with gamma-distributed weights. Electron. J. Probab. 20, 1–18 (2015). arXiv:1408.5326
Oviedo, G., Panizo, G., Ramirez, A.: Second order fluctuations of large deviations for perturbed random walks. arXiv:2108.02877 (2021)
Povolotsky, A.M.: On the integrability of zero-range chipping models with factorized steady states. J. Phys. A Math. Theor. 46, 465205 (2013). arXiv:1308.3250
Seppäläinen, T.: Scaling for a one-dimensional directed polymer with boundary conditions. Ann. Probab. 40(1), 19–73 (2012). arXiv:0911.2446
Simon, B.: Trace Ideals and Their Applications, 2nd edn. American Mathematical Society, Providence (2000)
Thiery, T., Le Doussal, P.: On integrable directed polymer models on the square lattice. J. Phys. A Math. Theor. 48, 465001 (2015). arXiv:1506.05006
Talyigás, Z., Vető, B.: Borodin-Pèchè fluctuations of the free energy in directed random polymer models. J. Theor. Probab. 33(3), 1426–1444 (2020). arXiv:1809.09869
Tracy, C., Widom, H.: Level-spacing distributions and the Airy kernel. Commun. Math. Phys. 159, 151–174 (1994). arXiv:hep-th/9211141
Tracy, C., Widom, H.: Integral formulas for the asymmetric simple exclusion process. Commun. Math. Phys. 279(3), 815–844 (2008). arXiv:0704.2633
Tracy, C., Widom, H.: A Fredholm determinant representation in ASEP. J. Stat. Phys. 132(2), 291–300 (2008). arXiv:0804.1379
Tracy, C., Widom, H.: Asymptotics in ASEP with step initial condition. Commun. Math. Phys. 290(1), 129–154 (2009). arXiv:0807.1713
Acknowledgements
The author is grateful to Alexei Borodin for numerous helpful comments about the work. The author would also like to thank Guillaume Barraquand and Ivan Corwin for their clarifications regarding the work [4].
Funding
Open Access funding provided by the MIT Libraries.
Author information
Authors and Affiliations
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Korotkikh, S. Hidden diagonal integrability of q-Hahn vertex model and Beta polymer model. Probab. Theory Relat. Fields 184, 493–570 (2022). https://doi.org/10.1007/s00440-022-01117-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-022-01117-0