A study of non-uniform imperfect contact in shear wave propagation in a magneto-electro-elastic laminated periodic structure

Abstract

The present study deals with shear wave propagation in a fully coupled Magneto-Electro-Elastic (MEE) multi-laminated periodic structure having non-uniform and imperfect interfaces. As a solution methodology, we applied a more general low-frequency dynamic asymptotic homogenization technique where the solution will be single-frequency dependent and the obtained results generalize those published in Chaki and Bravo-Castillero (Compos Struct 322:117410, 2023b) where the perfect contact case was studied. Effective homogenized dispersive equations of motion in second- and fourth-order approximations, also known as “Good” Boussinesq equations in elastic case, are derived. Local problems, closed-form expression of dispersion equations in second and fourth-order approximations and closed-form solutions of first and second local problems in second-order approximation for tri-laminated MEE periodic structure have been obtained and also validated for elastic laminates with imperfect contact case and MEE laminates with perfect contact case. The effect of non-uniform and imperfect contact, angle of incidence, unit cell size, volume fraction and ME-coupling on the wave propagation is illustrated through dispersion graphs. The effect of non-uniform and imperfect contact on dispersion curve serves as the highlight of the present work.

1 Introduction

Due to the coupling effect and the ability to transform energy from one form, viz. mechanical, electric and magnetic energy to another form, the magneto-electro-elastic (MEE) composites have gained huge attention. These composites are made of piezoelectric (PE) and piezomagnetic (PM) materials exhibiting a magnetoelectric effect which is absent in individual PE and PM constituents. MEE composites hold numerous applications in smart sensors and actuators, ultrasonic devices, non-destructive testing (NDT), energy harvesters, detectors. The constitutive equations of MEE composites are derived from classical continuum mechanics combined with Maxwell’s electromagnetic theory [1, 22, 27, 42] in quasi-static approximation. A detailed derivation and description of magneto-electro-elastic materials can be found in the books of [6] and [29] and also in the review of [46].

MEE composites which hold numerous applications in magnetic field sensors, tunable devices, actuators, transformers/gyrators, information storage devices, and energy harvesters are comprised of a layered structure. Hence, understanding the static and dynamic behavior of MEE laminates has become an important research topic in recent years. As for some early works on MEE composites, [28] and [7] studied magnetoelectric effect in composites with piezoelectric and piezomagnetic phases. Later on, the exact solutions for MEE laminates in cylindrical bending was derived by [33]. [32] also studied the free vibrations of simply supported and multilayered magneto-electro-elastic plates. [25] studied lattice vibration of metamaterial structure by constructing piezoelectric–piezomagnetic multilayer which simultaneously produce negative permeability and permittivity. Later on, [53] studied coupled phonon polaritons in an MEE superlattice composed of piezoelectric (PSL) and piezomagnetic (PMSL) superlattice. A finite element formulation for large deflection of multilayered magneto-electro-elastic plates was given by [3]. [50] analyzed natural characteristics of MEE multilayered plate using analytical and finite element method. Later, [52] performed semi-analytical analysis of static and dynamic responses for laminated MEE plates. [19] studied multiple crossing points of Lamb wave propagating in a magneto-electro-elastic composite plate. [31] has given a review on orthogonal polynomial methods for modeling elastodynamic wave propagation in elastic, piezoelectric and magneto-electro-elastic composites. Recently, [15] studied the effect of non-perfect and locally perturbed interface on anti-plane surface wave in a magneto-electro-elastic layered structure. The aforementioned works show evidence of the importance of the theoretical development in layered/laminated composite models which motivates the present work.

In recent times, homogenization techniques have become an efficient tool to study heterogeneous composites which exhibit non-classical properties and hold enormous applications from aerospace engineering to medical devices. In the literature, many homogenization techniques can be found which provide an equivalent homogenized system of the heterogeneous composite and explicit formulas to obtain the effective properties of the homogenized system. In order to analyze and design materials and devices with ME coupling, it is important to determine the distribution of the physical fields within these hetero-structures and homogenization schemes play a crucial role for evaluating the effective properties. One of the most popular explicit formula to compute the effective properties was given by [24] for MEE composites where Mori-Tanaka method was used. [48] also derived the effective properties for fibrous composites having piezoelectric and piezomagnetic phases. [23] applied two-scale homogenization to study porous magneto-electric two-phase composites. In several monographs and articles [5, 30, 34, 35, 37, 38, 40, 45], the asymptotic homogenization method (AHM) is acknowledged as an efficient tool to calculate the effective properties for small-scale heterogeneous composites. Several works from the literature can be cited in the vicinity of MEE composites for static case. The multiphase magneto-electro-thermo-elastic materials with periodic inclusions of finite dimensions were studied by [2] using asymptotic homogenization method. [8] gave explicit formula to derive effective stiffness, electric and magnetic coefficients of MEE multi-laminated composite using asymptotic homogenization. [41] on using asymptotic homogenization analyzed thermo-magneto-electro-elastic periodic laminates. [11] applied asymptotic homogenization to study thermo-magneto-electro-elastic multilaminated composites with imperfect contact. [12] calculated the effective thermo-piezoelectric properties of porous ceramics using asymptotic homogenization and FEM for energy-harvesting applications. [49] studied the size effects of mechanical metamaterials using second-order asymptotic homogenization method.

Imperfect bonding between two layers of composites arises due to microdefects, aging of glue at the joint of two solids and other form of damages. Although imperfect contacts are random in reality, such imperfect contact of non-deterministic nature certainly cannot be studied neither through mathematical analysis nor through simulations and the same also goes for the case of non-periodic imperfectness pattern in a periodic structure. To calculate the effective properties of periodic composites, it is necessary to consider an appropriate interface model. Hence, due to mathematical simplicity, deterministic imperfectness are considered by several researchers at the interfaces of the finite number of laminates of a unit cell which repeats periodically. Such periodic imperfect contact is not new and several research papers are available in the literature, viz. [39, 11, 20, 44]. Non-uniform imperfect bonding where the imperfect bonding is not uniform throughout the interface has also been studied through deterministic approach. Recently, [13] studied effective properties of thermo-magneto-electro-elastic laminated composite with non-uniform imperfect contact through asymptotic homogenization. A similar idea has been adopted in the present manuscript.

The effect of heterogeneities in waveguides becomes more dominant for dynamic cases, especially when the traveling wavelength is comparable to the size of the material’s heterogeneities, successive wave reflections, refractions and dispersion phenomena occur. A dispersive system for wave propagation in periodic heterogeneous media was derived by [17] considering multiscale AHM. In this work, they have obtained a “bad" Boussinesq equation by applying AHM with temporal and spatial scaling. They had to reformulate the equation into “good" Boussinesq equation using approximation which was a major setback. The multi-scale AHM was also applied to coupled thermo-viscoelastic problem by [51]. Both [36] and [4] studied wave propagation in fiber-reinforced periodic composite using AHM. A non-local dispersive model was first suggested by [47] and later, [18] proposed a high-frequency asymptotic homogenization method for periodic media. An emphasis is given to work of [9] who studied shear wave propagation in laminated triclinic periodic laminated structure by proposing a dynamic asymptotic homogenization and later the study was extended for imperfect bonding case [10]. The mathematical as well as numerical results obtained in the present work will be validated with [10] for elastic case. Recently, [16] studied anti-plane wave in a MEE laminated periodic composite structure with perfect contact using dynamic asymptotic homogenization method. The present paper is a generalization of the work of [16] by considering non-uniform imperfect contact in MEE laminated composite which is a more realistic scenario. The effect of non-uniform imperfect contact on shear wave propagation in MEE laminated composite periodic structure has not yet been studied through dynamic asymptotic homogenization.

In this work, a low-frequency generalized dynamic asymptotic homogenization is proposed to study shear wave propagation in an MEE laminated composite periodic structure with non-uniform imperfect interface. The homogenization method is based on [5] and on recently published work of [16] where along with field variables, asymptotic expansion of the frequency is also considered. Local problems are derived using dynamic asymptotic homogenization method. Effective dispersive systems in second and fourth-order approximation are derived directly using dynamic asymptotic homogenization which represent the “good" Boussinesq equation in elastic case. Closed form expressions of the dispersion relations in second and fourth-order approximation and solution of first and second local problem in second-order approximation for tri-laminated MEE composite are obtained. Numerical results are obtained for tri-laminated MEE composite periodic structure in second-order approximation where various parameters affecting the dispersion curve have been examined. The obtained results have been validated with [16] for perfect contact and [9, 10] for elastic case. In particular, the effect of non-uniform imperfect bonding is the highlight of the present study.

2 Formulation of the problem

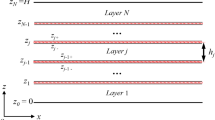
A magneto-electro-elastic (MEE) laminated periodic configuration is considered with unit volume $\Omega =(0,1)^3 \subset {\mathbb {R}}^3$ having boundary $\partial \Omega =\partial _1 \Omega \cup \partial _2 \Omega$ where $\partial _1 \Omega$ and $\partial _2 \Omega$ are disjoint boundary set. The unit volume $\Omega$ is considered to be constructed by N identical sets of p laminae that are stacked along $x_1$-direction depicted in Fig. 1. Here, Y represents local cell which is a set of p laminae that repeats. $\Gamma ^{\varepsilon }$ represents the set of all interphases in $\Omega$, whereas $\Gamma$ represents the set of all interphases in Y. $\theta _q (q=1, 2,\ldots , p)$ represents the points in Y where the interphases intersect the $y=\frac{x_1}{\varepsilon }$ axis. $\varepsilon =1/N\ll 1$ is a small perturbation parameter. Here the contact of the laminates are considered to be non-uniform and imperfect whose mass-spring idealization is also depicted in Fig. 1.

Fig. 1

Magneto-electro-elastic laminate stacked periodically in the $x_1$-direction along with its unit local cell and mass-spring idealization of non-uniform imperfect bonding

The following MEE coefficients and fields in compact form are considered [41]:

$$\begin{aligned} M_{jl}^{\varepsilon }=\begin{pmatrix} c_{ijkl}^{\varepsilon } &{} e_{jil}^{\varepsilon } &{} q_{jil}^{\varepsilon } \\ e_{jkl}^{\varepsilon } &{} -\kappa _{jl}^{\varepsilon } &{} -\alpha _{jl}^{\varepsilon }\\ q_{jkl}^{\varepsilon } &{} -\alpha _{jl}^{\varepsilon } &{} -\mu _{jl}^{\varepsilon } \end{pmatrix},\,\,\,\, \Sigma _j^{\varepsilon }=\begin{pmatrix} \sigma _{ij}^{\varepsilon }\\ D_j^{\varepsilon }\\ B_j^{\varepsilon } \end{pmatrix},\,\,\,\, U^{\varepsilon }=\begin{pmatrix} u_{k}^{\varepsilon }\\ \phi ^{\varepsilon }\\ \psi ^{\varepsilon } \end{pmatrix}, \end{aligned}$$

where $i,j,k,l=1,2,3$, $M_{jl}^{\varepsilon }$ is a matrix containing material coefficients where $c_{ijkl}^{\varepsilon }$ is a stiffness tensor, $e_{lij}^{\varepsilon }$ is piezoelectric coefficient, $\kappa _{jl}^{\varepsilon }$ is dielectric permittivity, $q_{lij}^{\varepsilon }$ is piezomagnetic coefficient, $\mu _{jl}^{\varepsilon }$ is magnetic permeability, $\alpha _{jl}^{\varepsilon }$ is magnetoelectric coefficient. $\Sigma _j^{\varepsilon }$ is a column matrix where $\sigma _{ij}^{\varepsilon }$ represents mechanical stress, $D_j^{\varepsilon }$ represents electric displacement, $B_j^{\varepsilon }$ represents magnetic induction, $U^{\varepsilon }$ is also a column matrix which includes displacement vector $u_{k}^{\varepsilon }$, electric potential $\phi ^{\varepsilon }$ and magnetic potential $\psi ^{\varepsilon }$. $\rho ^{\varepsilon }$ represents density. The local MEE coefficients are rapidly oscillating $\varepsilon Y$-periodic functions of $x_1$, i.e., $c_{ijkl}^{\varepsilon }({\textbf{x}})=c_{ijkl}\left( \frac{x_1}{\varepsilon } \right)$ and so on.

It is to be noted that in quasi-static approximation, the MEE material obeys the Maxwell’s equations as $\nabla \times {\textbf{E}}^\varepsilon =0$, $\nabla \times {\textbf{H}}^\varepsilon =0$, $\nabla \cdot {\textbf{B}}^\varepsilon =0$, $\nabla \cdot {\textbf{D}}^\varepsilon =0$ along with the Navier’s equation of motion as $\sigma _{ij,i}^\varepsilon =\rho ^\varepsilon \ddot{u}_{i}^\varepsilon$. The relation between electric field vector and electric potential is considered as $E_i^\varepsilon =-\phi _{,i}^\varepsilon$, whereas the relation between magnetic field vector and magnetic potential is considered as $H_i^\varepsilon =-\psi _{,i}^\varepsilon$ where both $\phi ^\varepsilon$ and $\psi ^\varepsilon$ are scalar electric and magnetic potentials which are considered under the quasi-static approximation. A detailed derivation of the constitutive equation for MEE material can be found in the book chapter of “Electromagnetics in Deformable Solids" by G.A. Maugin given in the book of [29] and also in the book of [6].

Since, the moduli satisfy ellipticity condition, there exists a constant $\chi >0$ such that for every ${\textbf{x}}\in \Omega {\setminus } \Gamma ^{\varepsilon }$, we have the following inequalities

$$\begin{aligned} c_{ijkl}^{\varepsilon }\,a_{ij}a_{kl}\ge \chi a_{ij}a_{ij}\hspace{0.5cm}\text{ and }\hspace{0.5cm} \left( E_{ij}({\textbf{x}})X_j,X_i \right) \ge \chi \left( X_i,X_i\right) , \end{aligned}$$

where $E_{ij}=\begin{pmatrix} \kappa _{jl}^{\varepsilon } &{} \alpha _{jl}^{\varepsilon }\\ \alpha _{jl}^{\varepsilon } &{} \mu _{jl}^{\varepsilon } \end{pmatrix}$, $a_{ij}$ being a matrix and $X_i\in {\mathbb {R}}^2$.

The constitutive equation for MEE material can be written as

$$\begin{aligned} \Sigma _j^{\varepsilon }({\textbf{x}})=M_{jl}^{\varepsilon }({\textbf{x}})\frac{\partial U^{\varepsilon }}{\partial x_l}({\textbf{x}}) \end{aligned}$$

(1)

and in absence of body force, the equation of motion is

$$\begin{aligned} \frac{\partial }{\partial x_j}\left( M_{jl}^{\varepsilon } \frac{\partial }{\partial x_l} U^{\varepsilon }\right) ={\mathcal {P}}^{\varepsilon }\frac{\partial U^{\varepsilon }}{\partial t^2}, \end{aligned}$$

(2)

where ${\mathcal {P}}^{\varepsilon }=\begin{pmatrix} \rho ^{\varepsilon } &{} 0 &{} 0\\ 0&{} 0&{} 0\\ 0&{} 0&{} 0 \end{pmatrix}$.

Now, we consider low-frequency shear wave propagation in a MEE laminated periodic composite. The shear wave propagation is considered to be of low frequency since the wavelength of propagating waves must be larger than the characteristic lengthscale of the microstructure. Due to shear wave being an anti-plane wave, we consider the domain $\Omega ^{\varepsilon }=\varepsilon Y\times (0,1)$ where $Y=\big \{y\in {\mathbb {R}}\; |\; y\in (0,1)\big \}.$

Hence, the boundary value problem becomes

$$\begin{aligned} \frac{\partial }{\partial x_j}\left( M_{jl}^{\varepsilon } \frac{\partial }{\partial x_l} U^{\varepsilon }\right) ={\mathcal {P}}^{\varepsilon }\frac{\partial ^2 U^{\varepsilon }}{\partial t^2},\hspace{1cm} {\textbf{x}}\in \Omega ^{\varepsilon }\setminus \Gamma ^{\varepsilon } \end{aligned}$$

(3)

with non-uniform imperfect interface condition

$$\begin{aligned} \Sigma _j^{\varepsilon } n_j = K^\varepsilon [[ U^{\varepsilon }({\textbf{x}}) ]], \hspace{0.5cm} \text{ and } \hspace{0.5cm} [[ \Sigma _j^{\varepsilon } ]] n_j =0, \hspace{1cm} {\textbf{x}}\in \Gamma ^{\varepsilon } \end{aligned}$$

(4)

and the boundary condition

$$\begin{aligned} U^{\varepsilon } = 0,\hspace{0.5cm} {\textbf{x}}\in \partial _1 \Omega ^{\varepsilon }\hspace{0.5cm} \text{ and } \hspace{0.5cm} \Sigma _j^{\varepsilon } n_j = F,\hspace{0.5cm} {\textbf{x}}\in \partial _2 \Omega ^{\varepsilon }, \end{aligned}$$

(5)

where $n_j$ is the unit normal, $M_{jl}^{\varepsilon }=M_{jl}(y)$ and $K^\varepsilon =\varepsilon ^{-1}K^{(q)}\left( x_2,x_3\right)$, where $K^{(q)}\left( x_2,x_3\right)$ is a $5\times 5$ matrix valued function of $\Gamma ^\varepsilon \in {\mathbb {R}}^3$ taking different values for each $x_1=\varepsilon (\theta _q+i), \; i=0,1,\ldots ,N-1$, such that

$$\begin{aligned} K^{(q)}\left( x_2,x_3\right) = \begin{pmatrix} K_1^{(q)}\left( x_2,x_3\right) &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} K_2^{(q)}\left( x_2,x_3\right) &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} K_3^{(q)}\left( x_2,x_3\right) &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -E^{(q)}\left( x_2,x_3\right) &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -M^{(q)}\left( x_2,x_3\right) \\ \end{pmatrix}, \end{aligned}$$

where $K_l^{(q)}\left( x_2,x_3\right) , E^{(q)}\left( x_2,x_3\right) , M^{(q)}\left( x_2,x_3\right)$ are Y-periodic positive functions corresponding to the stiffness tensor, dielectric permittivity and magnetic permeability being positive definite. A similar imperfect condition has also been adopted in [13] and [26] where the normal component of the mechanical traction, electric displacement and magnetic flux are proportional to the jump of mechanical displacements, electric and magnetic static potentials, respectively, and the proportionality factors are Y-periodic functions and inversely proportional to its width.

Fig. 2

a Non-uniform imperfect contact between two layers and mass-spring model interpretation of b uniform imperfect contact and c non-uniform imperfect contact

A mass-spring model interpretation of the uniform and non-uniform imperfect contact is depicted in Fig. 2 where in Fig. 2b, the stiffness of the springs are equal representing uniform imperfect contact, whereas in Fig. 2c, the stiffness of the springs is different representing non-uniform imperfect contact.

On considering time-harmonic solutions, we obtain

$$\begin{aligned} u_3^{\varepsilon }(x_1,x_2,t)&= W^{\varepsilon }(x_1,x_2)T(t),\,\, \phi ^{\varepsilon }(x_1,x_2,t) = \Phi ^{\varepsilon }(x_1,x_2)T(t),\nonumber \\ \psi ^{\varepsilon }(x_1,x_2,t)&= \Psi ^{\varepsilon }(x_1,x_2)T(t), \end{aligned}$$

(6)

where $T(t)=e^{i\omega t}$ and hence, the equation of motion becomes

$$\begin{aligned}{} & {} \frac{\partial }{\partial x_j}\left( M_{jl}^{\varepsilon } \frac{\partial }{\partial x_l} U^{\varepsilon }\right) =-\omega ^2 {\mathcal {P}}^{\varepsilon } U^{\varepsilon }, \hspace{0.5cm} {\textbf{x}}\in \Omega ^{\varepsilon }\setminus \Gamma ^{\varepsilon } \end{aligned}$$

(7)

$$\begin{aligned}{} & {} T^{\prime \prime }(t)+\omega ^2 T(t)=0,\hspace{0.5cm} t>0 \end{aligned}$$

(8)

where $\omega ^2\equiv \omega ^2(\varepsilon )$ and Eq.(8) is an identity.

3 Asymptotic homogenization

We first consider the regular asymptotic expansion of the frequency and field variables as

$$\begin{aligned}&\omega =\omega _0 +\varepsilon \omega _{1}+\varepsilon ^2 \omega _{2}+\varepsilon ^3 \omega _{3}+\varepsilon ^4 \omega _{4}+{\mathcal {O}}(\varepsilon ^5),\\&\quad U({\textbf{x}},{y})={\hat{U}}^{(0)}({\textbf{x}}) + \varepsilon U^{({1})}({\textbf{x}},{y})+ \varepsilon ^{2} U^{({2})}({\textbf{x}},{y}) + \varepsilon ^{3} U^{({3})}({\textbf{x}},{y}) + \varepsilon ^{4} U^{({4})}({\textbf{x}},{y}) +{\mathcal {O}}(\varepsilon ^5),\\&\quad \omega ^2={\bar{\omega }}_{0}+ \varepsilon {\bar{\omega }}_{1}+ \varepsilon ^2 {\bar{\omega }}_{2}+ \varepsilon ^3 {\bar{\omega }}_{3}+ \varepsilon ^4 {\bar{\omega }}_{4}+{\mathcal {O}}(\varepsilon ^5), \end{aligned}$$

where ${\bar{\omega }}_n=\sum _{k=0}^n \omega _k\omega _{n-k}.$

Due to the fast variable y, we also have $\frac{\partial }{\partial x_i}\equiv \frac{\partial }{\partial x_i}+\varepsilon ^{-1}\frac{\partial }{\partial y}$. Imposing the expansions in Eq. (7) and equating the terms of the order $\varepsilon ^{-2}, \varepsilon ^{-1}, \varepsilon ^{0}, \varepsilon ^{1}$ and $\varepsilon ^{2}$ to zero, we obtain the following

$$\begin{aligned}&\varepsilon ^{n}:\hspace{0.3cm} L_{yy}U^{(n+2)}=-L_{yx}U^{(n+1)}-L_{xy}U^{(n+1)}-L_{xx}U^{(n)} -{\mathcal {P}}({y})\sum _{k=0}^n{\bar{\omega }}_k U^{(n-k)}, \end{aligned}$$

(9)

for $n=-1,0,1,2$, along with boundary conditions (4) and (5) where $L_{\alpha \beta }=\frac{\partial }{\partial \alpha _i}\left( M_{ij} \frac{\partial }{\partial \beta _j} \right)$ with $\alpha , \beta \in \{x,y\}$.

A necessary and sufficient condition for the existence of Y-periodic solutions $U({\textbf{x}},{y})$ of the system can be found in the lemma provided in the Appendix of [13] where the periodic solution is unique up to an additive constant.

Hence, the solutions of the equations of (9) exist for the order of $\varepsilon ^n, n=-1,0,1,2$ and can be represented in the form as

$$\begin{aligned} U^{(1)}({\textbf{x}},y)&=N_k(y)\frac{\partial {\hat{U}}^{(0)}({\textbf{x}})}{\partial x_k}+{\hat{U}}^{(1)}({\textbf{x}}), \end{aligned}$$

(10)

$$\begin{aligned} U^{(2)}({\textbf{x}},{y})&=N_{jk}({y})\frac{\partial ^2 {\hat{U}}^{(0)} ({\textbf{x}})}{\partial x_j \partial x_k}+N_{k}({y})\frac{\partial {\hat{U}}^{(1)} ({\textbf{x}})}{\partial x_k}+{\hat{U}}^{(2)}({\textbf{x}}), \end{aligned}$$

(11)

$$\begin{aligned} U^{(3)}({\textbf{x}},{y})&=N_{jkl}({y})\frac{\partial ^3 {\hat{U}}^{(0)} ({\textbf{x}})}{\partial x_j \partial x_k \partial x_l}+N_{jk}({y})\frac{\partial ^2 {\hat{U}}^{(1)} ({\textbf{x}})}{\partial x_j \partial x_k}+N_{k}({y})\frac{\partial {\hat{U}}^{(2)} ({\textbf{x}})}{\partial x_k}+{\hat{U}}^{(3)}({\textbf{x}}), \end{aligned}$$

(12)

$$\begin{aligned} U^{(4)}({\textbf{x}},{y})&=N_{jk_1k_2l}({y})\frac{\partial ^4 {\hat{U}}^{(0)} ({\textbf{x}})}{\partial x_j \partial x_{k_1}\partial x_{k_2} \partial x_l}+N_{jkl}({y})\frac{\partial ^3 {\hat{U}}^{(1)} ({\textbf{x}})}{\partial x_j \partial x_{k_1} \partial x_l}+N_{jk}({y})\frac{\partial ^2 {\hat{U}}^{(2)} ({\textbf{x}})}{\partial x_j \partial x_{k_1}}\nonumber \\&\quad +N_{k}({y})\frac{\partial {\hat{U}}^{(3)} ({\textbf{x}})}{\partial x_{k_1}}+{\hat{U}}^{(4)}({\textbf{x}}), \end{aligned}$$

(13)

where the local functions $N_k({y})$, $N_{jkl}({y})$, $N_{jkl}({y})$, $N_{jk_1k_2l}({y})$ are, respectively, $1-$periodic solutions of the following local problems

$$\begin{aligned}{} & {} \left. \begin{array}{ll} &{}{\mathcal {O}}(\varepsilon ^{-1}):\hspace{0.5cm} L N_k(y)=-\frac{\textrm{d} (M_{1k})}{\textrm{d} y},\hspace{0.3cm} y\in Y \setminus \Gamma ,\\ &{}\hspace{1cm} M_{11}\frac{\textrm{d} N_k }{\textrm{d}y} +M_{1k}=K^{(q)} [[ N_k ]],\,\, [[ M_{11}\frac{\textrm{d}N_k}{\textrm{d}y} +M_{1k} ]] =0, \,\, \,\, y =\theta _q. \end{array} \right\} \end{aligned}$$

(14)

$$\begin{aligned}{} & {} \left. \begin{array}{ll} &{}{\mathcal {O}}(\varepsilon ^{0}):\hspace{0.1cm}L N_{jk}(y)=- \frac{\textrm{d}}{\textrm{d}y}\left( M_{lj}N_k(y)\right) - M_{j1}\frac{d N_k}{\textrm{d}y}-M_{jk}+\frac{\rho (y)}{\hat{\rho }}{\hat{M}}_{jk},\hspace{0.2cm} y\in Y\setminus \Gamma \\ &{}\hspace{1cm} M_{11}\frac{\textrm{d}N_{jk}}{\textrm{d}y} +M_{1j}N_k = K^{(q)}[[ N_{jk}]],\,\, [[ M_{11}\frac{\textrm{d}N_{jk}}{\textrm{d}y} +M_{1j}N_k ]] =0,\hspace{0.3cm}\,\,\, y =\theta _q. \end{array} \right\} \nonumber \\ \end{aligned}$$

(15)

$$\begin{aligned}{} & {} \left. \begin{array}{ll} &{}{\mathcal {O}}(\varepsilon ^{1}):\hspace{0.1cm} L N_{jkl}(y)=-\frac{\textrm{d}}{\textrm{d}y}\left( M_{1l}N_{jk}\right) - M_{l1}\frac{d N_{jk}}{d y}-M_{jl}N_k+\frac{\rho (y)}{\hat{\rho }}{\hat{M}}_{jl}N_k,\hspace{0.1cm} y\in Y\setminus \Gamma \\ &{}\hspace{1cm}M_{11}\frac{\textrm{d}N_{jkl}}{\textrm{d}y} +M_{1l}N_{jk}=K^{(q)}[[ N_{jkl}]],\,\,[[ M_{11}\frac{\textrm{d}N_{jkl}}{\textrm{d}y} +M_{1l}N_{jk} ]] =0,\hspace{0.3cm}\,\,\, y =\theta _q. \end{array} \right\} \nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned}{} & {} \left. \begin{array}{ll} &{}{\mathcal {O}}(\varepsilon ^{2}):\hspace{0.5cm} L N_{jk_1k_2l}(y)=-\frac{\textrm{d}}{\textrm{d} y}\left( M_{1k_2}N_{jk_1l}\right) -M_{k_21}\frac{\textrm{d}N_{jk_1l}}{d y}-M_{k_2l}N_{jk_1} \\ &{} \hspace{3cm}\,+\frac{\rho (y)}{\hat{\rho }}{\hat{M}}_{k_2 l}N_{jk_1} +\frac{\rho (y)}{\hat{\rho }}{\hat{M}}_{jk_1k_2l},\hspace{0.5cm} y\in Y\setminus \Gamma \\ &{}\hspace{1cm} M_{11}\frac{\textrm{d}N_{jk_1k_2l}}{\textrm{d}y} +M_{1k_2}N_{jk_1l}=K^{(q)}[[ N_{jk_1k_2l}]],\,\,\,\,\\ &{} \hspace{3cm}\,\,\,\, [[ M_{11}\frac{\textrm{d}N_{jk_1k_2l}}{\textrm{d}y} +M_{1k_2}N_{jk_1l} ]] =0,\hspace{0.3cm} y =\theta _q. \end{array} \right\} \end{aligned}$$

(17)

Here, Equations (14)-(17) represent corresponding “first”, “second”, “third” and “fourth” local problems and the operator $L \equiv \frac{\textrm{d}}{\textrm{d}y}\left( M_{11}\frac{\textrm{d}}{\textrm{d}y}\right)$.

The existence of local function which has a unique Y-periodic solution up to an additive constant, such that $\left\langle N_\Xi \right\rangle =0$, $\Xi =k, jk, jkl, jk_1k_2l$, is proven in the Lemma given in [13]. Using the necessary and sufficient condition for the solvability of the system in the class of $Y-$periodic functions in y, we now obtain the following homogenized equations

$$\begin{aligned}&{\mathcal {O}}(\varepsilon ^{0}): {\hat{M}}_{jk_1} \frac{\partial ^2 {\hat{U}}^{(0)}}{\partial x_j \partial x_{k_1}}+\omega _0^2\hat{{\mathcal {P}}}{\hat{U}}^{(0)}=0,\\&\quad {\mathcal {O}}(\varepsilon ^{1}): {\hat{M}}_{j{k_1}} \frac{\partial ^2 {\hat{U}}^{(1)}}{\partial x_j \partial x_{k_1} }+{\omega }_0^2\hat{{\mathcal {P}}}{\hat{U}}^{(1)}=0, \,\,\, \text{ and } \,\,\, {\hat{M}}_{jk_1l} =0\,\,\,\text{ with } \,\,\, {\omega }_1=0,\\&\quad {\mathcal {O}}(\varepsilon ^{2}): {\hat{M}}_{j{k_1}}\frac{\partial ^2 {\hat{U}}^{(2)}}{\partial x_j \partial x_{k_1}}+{\omega }_0^2\hat{{\mathcal {P}}}{\hat{U}}^{(2)}=0, \, {\hat{M}}_{jk_1k_2l}\frac{\partial ^4 {\hat{U}}^{(0)}}{\partial x_j \partial x_{k_1}\partial x_{k_2}\partial x_{l}}+{\bar{\omega }}_2 \hat{{\mathcal {P}}} {\hat{U}}^{(0)}=0\\&\qquad \text{ with }\,\,\,\,\omega _2=-\frac{\omega _0^3}{2} {\hat{M}}_{jk_1k_2l} {\hat{M}}_{jk_1}^{-1} \hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1}, \end{aligned}$$

where

$$\begin{aligned} {\hat{M}}_{jk}&=\left\langle M_{j1}\frac{\textrm{d}N_k}{\textrm{d}y}+M_{jk} \right\rangle , \,\,{\hat{M}}_{jkl}= \left\langle M_{l1}\frac{\partial N_{jk}}{\partial y}+M_{jl}N_k-\frac{\rho (y)}{\hat{\rho }}{\hat{M}}_{jl}N_k \right\rangle ,\\ {\hat{M}}_{jk_1k_2l}&=\left\langle M_{k_21}\frac{\partial N_{jk_1l}}{\partial y}+M_{k_2l}N_{jk_1}-\frac{\rho ({y})}{\hat{\rho }}{\hat{M}}_{k_2 l}N_{jk_1} \right\rangle . \end{aligned}$$

Here, the null average is defined as $\left\langle (\bullet )\right\rangle =\int _0^1 (\bullet ) dy$.

3.1 Effective dispersive system

3.1.1 Second-order approximation

Under the second-order approximation, we assume the field vector as

$$\begin{aligned} U({\textbf{x}},t,\varepsilon )=T(t)\left( U^{(0)}({\textbf{x}},{y})+\varepsilon U^{(1)}({\textbf{x}},{y})+\varepsilon ^2 U^{(2)}({\textbf{x}},{y})\right) . \end{aligned}$$

(18)

The null average of Eq.(18) is

$$\begin{aligned} {\hat{U}}({\textbf{x}},t)=\left\langle U({\textbf{x}},t,\varepsilon )\right\rangle =T(t)\left( {\hat{U}}^{(0)}({\textbf{x}},{y})+\varepsilon {\hat{U}}^{(1)}({\textbf{x}},{y})+\varepsilon ^2 {\hat{U}}^{(2)}({\textbf{x}},{y})\right) . \end{aligned}$$

(19)

Now, using Eq.(8), we obtain the following

$$\begin{aligned} \hat{{\mathcal {P}}}\frac{\partial ^2 {\hat{U}}({\textbf{x}},t) }{\partial t^2}=\hat{{\mathcal {P}}} {\hat{U}}({\textbf{x}},{y})\frac{\partial ^2 T}{\partial t^2}= -\hat{{\mathcal {P}}} \omega ^2 {\hat{U}}({\textbf{x}},{y}) T(t). \end{aligned}$$

(20)

On using the expansions $\omega =\omega _0+\varepsilon \omega _1+\varepsilon ^2\omega _2$ and $\omega ^2={\bar{\omega }}_0+\varepsilon {\bar{\omega }}_1+\varepsilon ^2{\bar{\omega }}_2$ along with $\omega _1=0$ and ${\bar{\omega }}_1=0$, we obtain

$$\begin{aligned} \hat{{\mathcal {P}}} \omega ^2 {\hat{U}}({\textbf{x}},{y}) T(t)&=\hat{{\mathcal {P}}}\left( \omega _0+\varepsilon ^2\omega _2 \right) ^2 {\hat{U}}({\textbf{x}},{y}) T(t)\nonumber \\&=\hat{{\mathcal {P}}}\omega _0^2 {\hat{U}} T + \varepsilon ^2 \hat{{\mathcal {P}}}(2 \omega _0\omega _2){\hat{U}} T + \varepsilon ^4 \hat{{\mathcal {P}}} \omega _2^2{\hat{U}} T \nonumber \\&=\hat{{\mathcal {P}}}\omega _0^2 {\hat{U}} T + 2 \varepsilon ^2 \hat{{\mathcal {P}}}\omega _2 (\omega _0+2\varepsilon ^2\omega _2){\hat{U}} T -3 \varepsilon ^4 \hat{{\mathcal {P}}} \omega _2^2{\hat{U}} T \nonumber \\&=\hat{{\mathcal {P}}}\omega _0^2 {\hat{U}} T + 2 \varepsilon ^2 \hat{{\mathcal {P}}}\frac{\omega _2}{\omega _0} (\omega _0^2+2\varepsilon ^2\omega _0\omega _2){\hat{U}} T -3 \varepsilon ^4 \hat{{\mathcal {P}}} \omega _2^2{\hat{U}} T \nonumber \\&=\hat{{\mathcal {P}}}\omega _0^2 {\hat{U}} T + 2 \varepsilon ^2 \hat{{\mathcal {P}}}\frac{\omega _2}{\omega _0} ({\bar{\omega }}_0+\varepsilon {\bar{\omega }}_1+\varepsilon ^2{\bar{\omega }}_2){\hat{U}} T -3 \varepsilon ^4 \hat{{\mathcal {P}}} \omega _2^2{\hat{U}} T \nonumber \\&=\hat{{\mathcal {P}}} \omega _0^2 {\hat{U}} T +2\varepsilon ^2 \hat{{\mathcal {P}}} \frac{\omega _2}{\omega _0}\omega ^2 {\hat{U}} T-3\varepsilon ^4\hat{{\mathcal {P}}} \omega _2 {\hat{U}} T. \end{aligned}$$

(21)

On neglecting higher order terms, i.e., ${\mathcal {O}}(\varepsilon ^4)$ and putting the expression of $\omega _2$, we derive

$$\begin{aligned} \hat{{\mathcal {P}}} \omega ^2 {\hat{U}}({\textbf{x}},{y}) T(t) = \hat{{\mathcal {P}}} \omega _0^2 {\hat{U}}({\textbf{x}},{y}) T(t) -\varepsilon ^2\omega ^2\omega _0^2 \eta ^* \hat{{\mathcal {P}}} {\hat{U}}({\textbf{x}},{y}) T(t), \end{aligned}$$

(22)

where $\eta ^*={\hat{M}}_{jk_1k_2l} {\hat{M}}_{jk_1}^{-1} \hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1}$.

From the local problems up to $O(\varepsilon ^2)$, we have

$$\begin{aligned} {\hat{M}}_{jk_1} \frac{\partial ^2 {\hat{U}}({\textbf{x}},{y})}{\partial x_j \partial x_{k_1}}+\omega _0^2\hat{{\mathcal {P}}}{\hat{U}}({\textbf{x}},{y})=0, \end{aligned}$$

(23)

where ${\hat{U}}({\textbf{x}},{y})={\hat{U}}^{(0)}({\textbf{x}},{y})+\varepsilon {\hat{U}}^{(1)}({\textbf{x}},{y})+\varepsilon ^2 {\hat{U}}^{(2)}({\textbf{x}},{y})$.

Now, on using $\omega ^2 T=-\frac{\partial ^2 T}{\partial t^2}$ from the identity (8) and using Eq.(23) in Eq.(22), we obtain

$$\begin{aligned} \hat{{\mathcal {P}}}\frac{\partial ^2 {\hat{U}}({\textbf{x}},t) }{\partial t^2}={\hat{M}}_{jk_1} \frac{\partial ^2 {\hat{U}}({\textbf{x}},t) }{\partial x_j \partial x_{k_1}}+\varepsilon ^2 \eta ^* {\hat{M}}_{jk_1} \frac{\partial ^4 {\hat{U}}({\textbf{x}},t) }{\partial x_j \partial x_{k_1} \partial t^2}. \end{aligned}$$

(24)

Eq. (24) is an effective homogenized dispersive equation of motion in second-order approximation. A similar expression has been obtained in [16] for MEE laminated composite with perfect contact, in [9] for triclinic medium with perfect contact and also in [10] for triclinic medium with imperfect contact.

It is to be noted that Eq.(24) represents “good" Boussinesq equation in elastic case. In [17], a “bad" Boussinesq equation was derived using AHM and then it was reformulated into “good" Boussinesq equation by approximation. However, by the generalized dynamic asymptotic homogenization method, the “good" Boussinesq equation can be directly achieved. This shows that the proposed technique is much more powerful. Equation similar to (24) arise in fluid dynamics of shallow water theory and crystal-lattice theory.

3.1.2 Fourth-order approximation

For fourth-order approximation, we consider the following

$$\begin{aligned} {\hat{U}}({\textbf{x}},t)=\left\langle U({\textbf{x}},t,\varepsilon )\right\rangle =T(t)\left( {\hat{U}}^{(0)}+\varepsilon {\hat{U}}^{(1)}+\varepsilon ^2 {\hat{U}}^{(2)}+\varepsilon ^3 {\hat{U}}^{(3)}+\varepsilon ^4 {\hat{U}}^{(4)}\right) . \end{aligned}$$

(25)

On proceeding in similar fashion as in Sect. 3.1.1, Eq. (20) will be the same for the fourth-order approximation. On using the expansions: $\omega =\omega _0+\varepsilon \omega _1+\varepsilon ^2\omega _2+\varepsilon ^3\omega _3+\varepsilon ^4\omega _4$ and $\omega ^2={\bar{\omega }}_0+\varepsilon {\bar{\omega }}_1+\varepsilon ^2{\bar{\omega }}_2+\varepsilon ^3{\bar{\omega }}_3+\varepsilon ^4{\bar{\omega }}_4$ along with $\omega _1=\omega _3=0$, ${\bar{\omega }}_1={\bar{\omega }}_3=0$ and ${\bar{\omega }}_2=2\omega _0\omega _2$, ${\bar{\omega }}_4=2\omega _0\omega _4+\omega _2^2$, we obtain

$$\begin{aligned} \hat{{\mathcal {P}}} \omega ^2 {\hat{U}}({\textbf{x}},{y}) T(t)&=\hat{{\mathcal {P}}}\left( \omega _0+\varepsilon ^2\omega _2+\varepsilon ^4\omega _4 \right) ^2 {\hat{U}}({\textbf{x}},{y}) T(t)\nonumber \\&=\hat{{\mathcal {P}}}\omega _0^2 {\hat{U}} T + \varepsilon ^2 \hat{{\mathcal {P}}}\left[ 2 \omega _0\omega _2+\varepsilon ^2 (2\omega _0\omega _4+\omega _2^2)+\varepsilon ^4 (2\omega _2\omega _4)+\varepsilon ^6\omega _4^2 \right] {\hat{U}} T \nonumber \\&=\hat{{\mathcal {P}}}\omega _0^2 {\hat{U}} T + 2\varepsilon ^2 \hat{{\mathcal {P}}} \frac{\omega _2}{\omega _0}\left[ \omega _0^2+\varepsilon ^2 (2\omega _0\omega _2)+\varepsilon ^4 (2\omega _0\omega _4+\omega _2^2) \right] {\hat{U}} T \nonumber \\&\quad + 2\varepsilon ^4 \hat{{\mathcal {P}}} \frac{\omega _4}{\omega _0}\left[ \omega _0^2+\varepsilon ^2 (2\omega _0\omega _2)+\varepsilon ^4 (2\omega _0\omega _4+\omega _2^2) \right] {\hat{U}} T -3 \varepsilon ^4 \hat{{\mathcal {P}}} \omega _2^2 {\hat{U}} T \nonumber \\&\quad - 2\varepsilon ^6 \hat{{\mathcal {P}}} \left( 3\omega _4\omega _2+\frac{\omega _2^3}{\omega _0} \right) {\hat{U}} T-\varepsilon ^8 \hat{{\mathcal {P}}}\left( 3\omega _4^2+2\omega _4\frac{\omega _2^2}{\omega _0}\right) {\hat{U}} T \nonumber \\&=\hat{{\mathcal {P}}}\omega _0^2 {\hat{U}} T + 2\varepsilon ^2 \hat{{\mathcal {P}}} \frac{\omega _2}{\omega _0}\omega ^2 {\hat{U}} T + 2\varepsilon ^4 \hat{{\mathcal {P}}} \frac{\omega _4}{\omega _0}\omega ^2 {\hat{U}} T \nonumber \\&\quad -3\varepsilon ^4 \hat{{\mathcal {P}}}\frac{\omega _2^2}{\omega _0^2} \left[ \omega _0^2+\varepsilon ^2 (2\omega _0\omega _2)+\varepsilon ^4 (2\omega _0\omega _4+\omega _2^2) \right] {\hat{U}} T+{\mathcal {O}}(\varepsilon ^6)\nonumber \\&=\hat{{\mathcal {P}}}\omega _0^2 {\hat{U}} T + 2\varepsilon ^2 \hat{{\mathcal {P}}} \frac{\omega _2}{\omega _0}\omega ^2 {\hat{U}} T + 2\varepsilon ^4 \hat{{\mathcal {P}}} \frac{\omega _4}{\omega _0}\omega ^2 {\hat{U}} T -3\varepsilon ^4 \hat{{\mathcal {P}}}\frac{\omega _2^2}{\omega _0^2}\omega ^2 {\hat{U}} T +{\mathcal {O}}(\varepsilon ^6) \nonumber \\ \end{aligned}$$

(26)

In order to find the expression of $\omega _4$, we need to derive “fifth" and “sixth" local problems, i.e.,

$$\begin{aligned}{} & {} \left. \begin{array}{ll} &{}{\mathcal {O}}(\varepsilon ^{3}):\hspace{0.5cm} L N_{jk_1k_2k_3l}=- \frac{\textrm{d}}{\textrm{d}y}\left( M_{1k_3}N_{jk_1k_2l} \right) - M_{k_31}\frac{d N_{jk_1k_2l} }{\textrm{d}y}- M_{k_2k_3}N_{jk_1l} \\ &{} \hspace{3cm}\,+\frac{\rho (y)}{\hat{\rho }}{\hat{M}}_{k_2k_3}N_{jk_1l} +\frac{\rho (y)}{\hat{\rho }}{\hat{M}}_{jk_2k_3l}N_{k_1},\hspace{0.5cm} y\in Y\setminus \Gamma \\ &{}\hspace{1cm} M_{11}\frac{\partial N_{jk_1k_2k_3l}}{\partial y} +M_{1k_3}N_{jk_1k_2l}=K^{(q)}[[ N_{jk_1k_2k_3l}]],\,\,\,\,\\ &{} \hspace{3cm}\,\,\,\, [[ M_{11}\frac{\partial N_{jk_1k_2k_3l}}{\partial y} +M_{1k_3}N_{jk_1k_2l} ]] =0,\hspace{0.3cm} y =\theta _q, \end{array} \right\} \end{aligned}$$

(27)

$$\begin{aligned}{} & {} \left. \begin{array}{ll} &{}{\mathcal {O}}(\varepsilon ^{4}):\hspace{0.5cm} L N_{jk_1k_2k_3k_4l}=- \frac{\partial }{\partial y}\left( M_{1k_4}N_{jk_1k_2k_3l}\right) - M_{k_41}\frac{\partial N_{jk_1k_2k_3l}}{\partial y} \\ &{} \hspace{3cm}\,- M_{k_3k_4}N_{jk_1k_2l}+\frac{\rho }{\hat{\rho }}{\hat{M}}_{k_3 k_4}N_{jk_1k_2l} +\frac{\rho }{\hat{\rho }}{\hat{M}}_{k_2k_3 k_4l} N_{jk_1}\\ &{} \hspace{3cm}\,+\frac{\rho }{\hat{\rho }}{\hat{M}}_{jk_1k_2k_3 k_4l},\hspace{3cm} y\in Y\setminus \Gamma \\ &{}\hspace{1cm} M_{11}\frac{\partial N_{jk_1k_2k_3k_4l}}{\partial y} +M_{1k_4}N_{jk_1k_2k_3l}=K^{(q)}[[ N_{jk_1k_2k_3k_4l}]],\,\,\,\,\\ &{} \hspace{3cm}\,\,\,\, [[M_{11}\frac{\partial N_{jk_1k_2k_3k_4l}}{\partial y} +M_{1k_4}N_{jk_1k_2k_3l} ]] =0,\hspace{0.3cm} y =\theta _q, \end{array} \right\} \end{aligned}$$

(28)

along with homogenized systems

$$\begin{aligned} {\mathcal {O}}(\varepsilon ^{4}): {\hat{M}}_{jk_1}\frac{\partial ^2 {\hat{U}}^{(3)}}{\partial x_j \partial x_{k_1}}+ {\omega }_0^2{\mathcal {P}}{\hat{U}}^{(3)}=0,\hspace{0.5cm} {\hat{M}}_{jk_1k_2k_3l}=0,\hspace{0.5cm}\omega _3=0, \end{aligned}$$

(29)

$$\begin{aligned} \left. \begin{array}{ll} &{}{\mathcal {O}}(\varepsilon ^{4}): {\hat{M}}_{jk_1}\frac{\partial ^2 {\hat{U}}^{(4)}}{\partial x_j \partial x_{k_1}}+ {\omega }_0^2\hat{{\mathcal {P}}}{\hat{U}}^{(4)} =0, \,\,\, \text{ and } \\ &{}\hspace{1cm}{\hat{M}}_{jk_1k_2k_3k_4l}\frac{\partial ^6 {\hat{U}}^{(0)}}{\partial x_j \partial x_{k_1}\partial x_{k_2}\partial x_{k_3}\partial x_{k_4}\partial x_{l}} +{\bar{\omega }}_4 \hat{{\mathcal {P}}} {\hat{U}}^{(0)}=0 \\ &{}\hspace{1cm}\text{ and }\,\,\,\omega _4=-\frac{\omega _2^2}{2\omega _0} + \frac{\omega _0^5}{2} {\hat{M}}_{jk_1k_2k_3k_4l} {\hat{M}}_{jk_1}^{-1}\hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1}\hat{{\mathcal {P}}}{\hat{M}}_{k_3k4}^{-1}, \end{array} \right\} \end{aligned}$$

(30)

where ${\hat{M}}_{jk_1k_2k_3l}=\left\langle M_{k_31}\frac{\partial N_{jk_1k_2l}}{\partial y}+M_{k_2k_3}N_{jk_1l}-\frac{\rho }{\hat{\rho }}{\hat{M}}_{k_2 k_3}N_{jk_1l}-\frac{\rho }{\hat{\rho }}{\hat{M}}_{jk_2k_3l}N_{k_1} \right\rangle$ and ${\hat{M}}_{jk_1k_2k_3k_4l}=\left\langle M_{k_41}\frac{\partial N_{jk_1k_2k_3l}}{\partial y}+M_{k_3k_4}N_{jk_1k_2l}-\frac{\rho }{\hat{\rho }}{\hat{M}}_{k_3 k_4}N_{jk_1k_2l} -\frac{\rho }{\hat{\rho }}{\hat{M}}_{k_2k_3 k_4l}N_{jk_1} \right\rangle$.

For further simplification, we consider

$$\begin{aligned} \omega _2&=-\frac{\omega _0^3}{2} {\hat{M}}_{jk_1k_2l} {\hat{M}}_{jk_1}^{-1} \hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1}=-\frac{\omega _0^3}{2}\eta ^* ,\\ \omega _4&=-\frac{\omega _2^2}{2\omega _0} + \frac{\omega _0^5}{2} {\hat{M}}_{jk_1k_2k_3k_4l} {\hat{M}}_{jk_1}^{-1}\hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1}\hat{{\mathcal {P}}}{\hat{M}}_{k_3k4}^{-1}=-\frac{\omega _0^5}{2}\eta ^{**}, \end{aligned}$$

where $\eta ^*={\hat{M}}_{jk_1k_2l} {\hat{M}}_{jk_1}^{-1} \hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1}$, $\eta ^{**}=\frac{(\eta ^*)^2}{4}+\eta _0$ and $\eta _0={\hat{M}}_{jk_1k_2k_3k_4l} {\hat{M}}_{jk_1}^{-1}\hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1}\hat{{\mathcal {P}}}{\hat{M}}_{k_3k4}^{-1}$.

Now, on putting the above expressions of $\omega _2$ and $\omega _4$ in Eq. (26), neglecting $O(\varepsilon ^6)$ and using (23), (30) and (8), we obtain

$$\begin{aligned} \hat{{\mathcal {P}}}\frac{\partial ^2 {\hat{U}}({\textbf{x}},t) }{\partial t^2}&={\hat{M}}_{jk_1} \frac{\partial ^2 {\hat{U}}({\textbf{x}},t) }{\partial x_j \partial x_{k_1}}+\varepsilon ^2 \eta ^* {\hat{M}}_{jk_1} \frac{\partial ^4 {\hat{U}}({\textbf{x}},t) }{\partial x_j \partial x_{k_1} \partial t^2}\nonumber \\&\quad -\varepsilon ^4 {\tilde{\eta }} ({\hat{M}}_{jk_1}^{-1} \hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1} )^{-1} \frac{\partial ^6 {\hat{U}}({\textbf{x}},t) }{\partial x_j \partial x_{k_1}\partial x_{k_2} \partial x_{l} \partial t^2}, \end{aligned}$$

(31)

where ${\tilde{\eta }} =\eta ^{**}-\frac{3}{4}(\eta ^*)^2$.

4 Dispersion relation

4.1 For zero-order homogenized system

From the homogenized system obtained for $O(\varepsilon ^0)$ and using Eq. (20), we deduce

$$\begin{aligned} {\hat{M}}_{jk_1} \frac{\partial ^2 {\hat{U}}({\textbf{x}},t) }{\partial x_j \partial x_{k_1}}=\hat{{\mathcal {P}}}\frac{\partial ^2 {\hat{U}}({\textbf{x}},t) }{\partial t^2}. \end{aligned}$$

(32)

In order to derive the dispersion equation, we consider a harmonic solution of Eq.(32) as

$$\begin{aligned} {\hat{U}}({\textbf{x}},t)={\mathcal {U}}e^{i(k_jx_j-\omega t)}, \end{aligned}$$

(33)

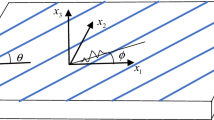
where ${\mathcal {U}}$ is amplitude, and $k_1=k \sin \theta$ and $k_2=k \cos \theta$ are the propagation vector components with k being the wave number.

On putting the considered harmonic solution in Eq.(32), we obtain

$$\begin{aligned} -\left( {\hat{M}}_{11} k^2 \sin ^2 \theta +{\hat{M}}_{12}k^2\sin 2\theta +{\hat{M}}_{22}k^2 \cos ^2 \theta \right) {\mathcal {U}}+\hat{{\mathcal {P}}}\omega ^2{\mathcal {U}}=0, \end{aligned}$$

(34)

where ${\hat{M}}_{jk}=\left\langle M_{jk}\right\rangle -\left\langle M_{j1}(M_{11})^{-1}M_{1k}\right\rangle +\left\langle M_{j1}(M_{11})^{-1} \right\rangle \left[ \sum _{q=1}^P((K^{(q)})^{-1}+\left\langle M_{11}^{-1}\right\rangle \right] ^{-1}$ $\left\langle (M_{11})^{-1}M_{1k}\right\rangle$, i.e., ${\hat{M}}_{11}=\left( \sum _{q=1}^P((K^{(q)})^{-1}+\left\langle M_{11}^{-1} \right\rangle \right) ^{-1}$, ${\hat{M}}_{12}=0$ and ${\hat{M}}_{22}=\left\langle M_{22} \right\rangle$.

In order to obtain non-trivial solution of (34), we must have

$$\begin{aligned}&\begin{vmatrix} -\left( {\hat{c}}_{55}\sin ^2\theta +{\hat{c}}_{44}\cos ^2\theta \right) k^2+\hat{\rho }\omega ^2&-\left( {\hat{e}}_{15}\sin ^2\theta +{\hat{e}}_{24}\cos ^2\theta \right) k^2&-\left( {\hat{q}}_{15}\sin ^2\theta +{\hat{q}}_{24}\cos ^2\theta \right) k^2\\ -\left( {\hat{e}}_{15}\sin ^2\theta +{\hat{e}}_{24}\cos ^2\theta \right) k^2&\left( \hat{\kappa }_{11}\sin ^2\theta +\hat{\kappa }_{22}\cos ^2\theta \right) k^2&\left( \hat{\alpha }_{11}\sin ^2\theta +\hat{\alpha }_{22}\cos ^2\theta \right) k^2\\ -\left( {\hat{q}}_{15}\sin ^2\theta +{\hat{q}}_{24}\cos ^2\theta \right) k^2&\left( \hat{\alpha }_{11}\sin ^2\theta +\hat{\alpha }_{22}\cos ^2\theta \right) k^2&\left( \hat{\mu }_{11}\sin ^2\theta +\hat{\mu }_{22}\cos ^2\theta \right) k^2 \end{vmatrix}=0, \end{aligned}$$

(35)

which provides the effective phase velocity as

$$\begin{aligned} c_0^2&=\frac{\left( {\hat{c}}_{55}\sin ^2\theta +{\hat{c}}_{44}\cos ^2\theta \right) }{\hat{\rho }}\nonumber \\&\quad +\frac{\begin{array}{ll} &{} \left( {\hat{e}}_{15}\sin ^2\theta +{\hat{e}}_{24}\cos ^2\theta \right) ^2\left( \hat{\mu }_{11}\sin ^2\theta +\hat{\mu }_{22}\cos ^2\theta \right) -2\left( {\hat{e}}_{15}\sin ^2\theta +{\hat{e}}_{24}\cos ^2\theta \right) \left( \hat{\alpha }_{11}\sin ^2\theta +\hat{\alpha }_{22}\cos ^2\theta \right) \\ {} &{}\hspace{0.5cm}\times \left( {\hat{q}}_{15}\sin ^2\theta +{\hat{q}}_{24}\cos ^2\theta \right) +\left( \hat{\kappa }_{11}\sin ^2\theta +\hat{\kappa }_{22}\cos ^2\theta \right) \left( {\hat{q}}_{15}\sin ^2\theta +{\hat{q}}_{24}\cos ^2\theta \right) ^2 \end{array}}{\hat{\rho } \left[ \left( \hat{\kappa }_{11}\sin ^2\theta +\hat{\kappa }_{22}\cos ^2\theta \right) \left( \hat{\mu }_{11}\sin ^2\theta +\hat{\mu }_{22}\cos ^2\theta \right) -\left( \hat{\alpha }_{11}\sin ^2\theta +\hat{\alpha }_{22}\cos ^2\theta \right) ^2\right] }. \end{aligned}$$

(36)

Here, Eq.(36) is clearly non-dispersive system independent of wave number.

4.2 For second-order effective dispersive system

Now, on applying the harmonic solution to Eq.(24), we obtain

$$\begin{aligned} \left[ \left( I-\varepsilon ^2\eta ^* \omega ^2 \right) \left( {\hat{M}}_{11} k^2 \sin ^2 \theta +{\hat{M}}_{12}k^2\sin 2\theta +{\hat{M}}_{22}k^2 \cos ^2 \theta \right) -\hat{{\mathcal {P}}}\omega ^2\right] {\mathcal {U}}=0. \end{aligned}$$

(37)

Again, in order to obtain non-trivial solution, we must have the following

$$\begin{aligned} \text{ Det }\left[ \left( I-\varepsilon ^2\eta ^* \omega ^2 \right) \left( {\hat{M}}_{11} k^2 \sin ^2 \theta +{\hat{M}}_{12}k^2\sin 2\theta +{\hat{M}}_{22}k^2 \cos ^2 \theta \right) -\hat{{\mathcal {P}}}\omega ^2\right] =0, \end{aligned}$$

(38)

which represents the dispersion equation for the homogenized system that depends on wave number. Equation(38) is a generalization of the dispersion equation that has been obtained in [16] for MEE laminated composite with perfect contact, in [9] for triclinic medium with perfect contact and in [10] for triclinic medium with imperfect contact.

4.3 For fourth-order effective dispersive system

On applying the harmonic solution to Eq.(31) and using ${\hat{M}}_{12}=0$, we obtain

$$\begin{aligned}&\bigg [\left( I-\varepsilon ^2\eta ^* \omega ^2 \right) \left( {\hat{M}}_{11} k^2 \sin ^2 \theta +{\hat{M}}_{12}k^2\sin 2\theta +{\hat{M}}_{22}k^2 \cos ^2 \theta \right) \nonumber \\&\quad -\varepsilon ^4{\tilde{\eta }} \omega ^2 \Big \{({\hat{M}}_{11}^{-1} \hat{{\mathcal {P}}}{\hat{M}}_{11}^{-1})^{-1} k^4 \sin ^4 \theta +(({\hat{M}}_{11}^{-1} \hat{{\mathcal {P}}}{\hat{M}}_{22}^{-1})^{-1}+({\hat{M}}_{22}^{-1} \hat{{\mathcal {P}}}{\hat{M}}_{11}^{-1})^{-1}) k^4 \sin ^2 \theta \cos ^2 \theta \nonumber \\&\quad +({\hat{M}}_{22}^{-1} \hat{{\mathcal {P}}}{\hat{M}}_{22}^{-1})^{-1} k^4 \cos ^4 \theta \Big \} -\hat{{\mathcal {P}}}\omega ^2\bigg ]{\mathcal {U}}=0. \end{aligned}$$

(39)

Hence, the fourth-order dispersion equation is obtained as

$$\begin{aligned}&\text{ Det }\bigg [\left( I-\varepsilon ^2\eta ^* \omega ^2 \right) \left( {\hat{M}}_{11} k^2 \sin ^2 \theta +{\hat{M}}_{12}k^2\sin 2\theta +{\hat{M}}_{22}k^2 \cos ^2 \theta \right) \nonumber \\&\quad -\varepsilon ^4{\tilde{\eta }} \omega ^2 \Big \{({\hat{M}}_{11}^{-1} \hat{{\mathcal {P}}}{\hat{M}}_{11}^{-1})^{-1} k^4 \sin ^4 \theta +(({\hat{M}}_{11}^{-1} \hat{{\mathcal {P}}}{\hat{M}}_{22}^{-1})^{-1}+({\hat{M}}_{22}^{-1} \hat{{\mathcal {P}}}{\hat{M}}_{11}^{-1})^{-1}) k^4 \sin ^2 \theta \cos ^2 \theta \nonumber \\&+({\hat{M}}_{22}^{-1} \hat{{\mathcal {P}}}{\hat{M}}_{22}^{-1})^{-1} k^4 \cos ^4 \theta \Big \} -\hat{{\mathcal {P}}}\omega ^2\bigg ]=0. \end{aligned}$$

(40)

The dispersion equation (40) is certainly a new equation which has not been derived before. This equation analytically shows more dispersive nature of the dynamic system. It is also to be noted that in case of ${\tilde{\eta }}=0$, Eq.(40) reduces to Eq.(38) and for $\eta ^*=0$, Eq.(40) reduces to Eq.(35) which also validates our results.

5 Numerical results and discussion

In order to obtain numerical results, we consider a tri-laminated composite structure, i.e., $(0,1)=(0,\theta _1)\cup (\theta _1,\theta _2)\cup (\theta _2,1)$ where the shear wave is incident at an angle $\theta$ to the laminate and obeys dispersion equation (38) in second-order approximation. For the PE and PM phases, BaTiO$_3$ and CoFe$_2$O$_4$ are considered, respectively, for which the corresponding data are taken into account [21, 43] (Table 1):

Table 1 Material properties of BaTiO$_3$ and CoFe$_2$O$_4$

Fig. 3

Dispersion curves showing variation of frequency against wave-number for BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ MEE laminated composite for a distinct values of mechanical imperfect bonding parameter $(K_3)$; b distinct values of electric imperfect bonding parameter (E); and c distinct values of magnetic imperfect bonding parameter (M)

Fig. 4

a 3-layered composite unit cell with non-uniform imperfect contact and physical interpretation of b non-uniform contact function $K_3(x_2,x_3)$ and c non-uniform contact function $K_3^*(x_2,x_3)$

Fig. 5

a 2-D function plot of $K_3(x_2, x_3)$ against $x_2$-axis; b 3-D dispersion plot for distinct function values of $K_3$; c 2-D function plot of $K_3^*(x_2, x_3)$ against $x_2$-axis; d 3-D dispersion plot for distinct function values of $K_3^*$

Fig. 6

Dispersion curves showing variation of frequency against wave-number for BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ MEE laminated composite a with mechanical, electrical and magnetic imperfect contact and b with mechanical, electrical and magnetic perfect contact for distinct sizes of unit cell

Fig. 7

Dispersion curves showing variation of frequency against wave-number for BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ MEE laminated composite a with mechanical, electrical and magnetic imperfect contact and b with mechanical, electrical and magnetic perfect contact for distinct values of angle of incidence ($\theta$) of harmonic wave

Fig. 8

Dispersion curves showing variation of frequency against wave-number for BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ MEE laminated composite a with mechanical, electrical and magnetic imperfect contact and b with mechanical, electrical and magnetic perfect contact for distinct values of volume fractions

Fig. 9

Dispersion curves showing variation of frequency against wave-number for a BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ MEE laminated composite case and b BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ elastic laminated composite and epoxy/glass/epoxy laminated composite case with mechanical, electrical and magnetic imperfect contact

Fig. 10

Dispersion curves showing variation of frequency against wave-number for a MEE composite, electro-elastic composite, magneto-elastic composite and elastic laminates with imperfect contact (I.C.) and perfect contact (P.C.); b magnification of dispersion curves at certain range for I.C. case; c magnification of dispersion curves at certain range for P.C. case; and d dispersion curves for distinct types of MEE laminated composite with mechanical, electrical and magnetic imperfect contact

Fig. 11

Variation of effective magnetoelectric coefficient $(\hat{\alpha }_{11})$ against a mechanical imperfect bonding parameter ($K_3$); b electrical imperfect bonding parameter (E); and c magnetic imperfect bonding parameter (M)

For the numerical computation, we consider 3-layered laminated composite BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ (or B/C/B) MEE periodic structure with harmonic wave propagation perpendicular ($\theta =90^\circ$) to the layer. Moreover, for the numerical computation, we consider $\varepsilon =0.06$ and $K_3=10$ GPa, $E=10$ C$^2$N$^{-1}$m$^{-2}$, $M=10$ NA$^{-1}$.

Figure 3 shows the effect of mechanical, electrical and magnetic imperfect contact on the dispersion curves for BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ MEE laminated composite. It is to be noted that $K_3=\infty$ represents mechanical perfect interface; $E=\infty$ represents electric perfect interface; and $M=\infty$ represents magnetic perfect interface. Figure 3a reveals as the mechanical imperfect bonding parameter ($K_3$) increase, the frequency decreases. Figure 3b shows the electric imperfect bonding (E) has very small but increasing effect on dispersion curve, whereas Fig. 3c depicts that the magnetic imperfect bonding (M) has very small but decreasing effect as compared to $K_3$. Hence, the effect of $K_3$ dominates over other two on dispersion curve making the system more dispersive.

Now, in order to analyze a deterministic non-uniformity of the mechanical imperfect contact, we consider the following smooth functions:

$$\begin{aligned} K_3(x_2,x_3)&=\left[ \left( 10^3-10\right) \left( -\cos (2\pi x_2)+1\right) +10\right] \text{ GPa }, \end{aligned}$$

(41)

$$\begin{aligned} K_3^*(x_2,x_3)&=\left[ \left( 10^3-10\right) \left( -\sin (\pi x_2)+1\right) +10\right] \text{ GPa }, \end{aligned}$$

(42)

The physical interpretation of the two functions is depicted in Fig. 4. Figure 4b represents imperfect contact near the edges and perfect contact in the middle along $x_2$-axis, whereas Fig. 4c represents perfect contact near the edges and imperfect contact in the middle along $x_2$-axis.

It is to be noted that non-uniform condition has been analyzed only for mechanical imperfect contact, since it is already reported in Fig. 3 that the mechanical imperfect parameter has dominating effect over electric and magnetic ones. Further mechanical imperfect parameter $K_3(x_2,x_3)$ is a function of both $x_2$ and $x_3$, however, due to simplicity, we set $x_3$ to be fixed and analyze two different functions (41) and (42).

The non-uniform functions (41) and (42) have been studied as in Fig. 5. The function $K_3(x_2,x_3)$ is plotted in Fig. 5a whose physical interpretation is that along $x_2$-direction, the mechanical bonding becomes perfect at the middle $(x_2=0.5)$ of the interface, whereas at the edges $(x_2=0,1)$, the contact is strongly imperfect, i.e., both the laminates start moving freely. Keeping the function values of $K_3$ obtained for $x_2=(0,1)$ in the 3$^{rd}$ axis, a 3D plot is drawn in Fig. 5(b) for the dispersion curve in order to show the effect of non-uniformity of mechanical imperfect contact. The frequency curve tends to increase with the increasing values of $K_3$ and attains maximum due to perfect contact condition, whereas as the value of $K_3$ starts to decrease, the frequency curve also decreases due to presence of imperfect bonding.

On the other hand, the function $K_3^*(x_2,x_3)$ in (42) is plotted in Fig. 5c whose physical interpretation is that along $x_2$-direction, the mechanical imperfect bonding becomes perfect at the edges $(x_2=0,1)$ and at the middle $(x_2=0.5)$ of the interface, the contact is strongly imperfect. Figure 5d also shows proportional relation between frequency and imperfect bonding, i.e., the frequency curve tends to decrease from high frequency with the decreasing values of $K_3^*$ and as the value of $K_3^*$ starts to increase, the frequency curve also increases. Figure  5b, d both shows that the non-uniformity of the mechanical imperfect contact has significant effect on the dispersion curve.

In order to show the effect of the sizes of unit cells of laminated composite on the dispersion curve, Fig. 6 has been drawn. Figure 6a, b shows the variation of frequency for BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ MEE laminated composite in case of mechanical, electrical and magnetic imperfect contact and in case of mechanical, electrical and magnetic perfect contact, respectively. It is to be noted that $\varepsilon =0$ represents the case of non-dispersive curve ($c=c_0$) and as the size of 3-laminae unit cell increases, the system becomes more dispersive. In particular, the frequency curves are much higher in case of perfect contact as compared imperfect one. The effect of unit cell size for perfect contact case in MEE laminated composite has already been studied in [16] which validates the graphs.

Figure 7a, b illustrates the effect of angle of incidence ($\theta$) of harmonic wave on the dispersion curve for BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ MEE laminated composite for imperfect and perfect contact, respectively. It is concluded from Fig. 7a that the dispersion curve is minimum when harmonic wave travels perpendicular ($\theta =90^\circ$) to composite layer, whereas it is maximum when it travels parallel ($\theta =0^\circ$) to the layer. The effect of angle of incidence of wave in case of imperfect interface is found to be small. However, in case of BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ MEE laminated composite with perfect contact, the dispersion curve is maximum when shear wave travels perpendicular to composite layer, whereas it is minimum when it travels parallel to the lamina. A similar result has been found in [16] for perfect contact and also in [9] for elastic case.

In order to study the effect of volume fraction in a 3-laminae unit cell of BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ MEE laminated composite periodic structure, Fig. 8a, b has been drawn for imperfect and perfect contact cases, respectively. It is to be noted that $\theta _1=0$ and $\theta _2=1$ represent monolithic CoFe$_2$O$_4$ unit cell, whereas $\theta _1=\theta _2=0.5$ represents monolithic BaTiO$_3$ unit cell. It is observed that for Fig. 8a, the system becomes non-dispersive in both monolithic cases of BaTiO$_3$ unit cell and CoFe$_2$O$_4$ unit cell and as the volume fraction of BaTiO$_3$ increases, the frequency curve decreases and the system becomes more dispersive. On the other hand, in Fig. 8b for perfect contact, the dispersion curves reveal that the system becomes non-dispersive only in monolithic case of CoFe$_2$O$_4$ unit cell and as the volume fraction of BaTiO$_3$ increases, the frequency curve decreases and the system becomes more dispersive. A similar result has also been obtained in [16] for perfect contact case.

Figure 9 represents a comparison between MEE case with mechanical, electrical and magnetic imperfect interface and elastic case with mechanical imperfect interface only. In Fig. 9a, the black curve represents the non-dispersion curve, whereas the red curve represents the dispersion curve for BaTiO$_3$/ CoFe$_2$O$_4$/ BaTiO$_3$ MEE laminated composite periodic structure with mechanical, electrical and magnetic imperfect interface. In Fig. 9b, the green curve and yellow curve represent dispersion curve and non-dispersion curve for 3-layered BaTiO$_3$/ CoFe$_2$O$_4$/ BaTiO$_3$ elastic laminated composite periodic structure (in absence of electro-magnetic properties) with mechanical imperfect interface, whereas the blue curve and the magenta curve represent dispersion curve and non-dispersion curve for 3-layered epoxy/glass/epoxy (or E/G/E) laminated periodic structure with mechanical imperfect interface only. For Glass material in E/G/E case, we consider $E_1=76$ Gpa and $\rho _1=2500$ Kg/m$^3$ and for epoxy resin, $E_2=3$ Gpa and $\rho _2=1300$ Kg/m$^3$ [14]. A similar dispersion curve (with phase velocity) for glass/epoxy biphasic elastic model with mechanical imperfect bonding can also be found in [10]. On comparison, it has been found that the frequency curves are higher in case of elastic periodic structure with mechanical imperfect interface as compared to MEE case with mechanical, electrical and magnetic imperfect interface, hence, MEE imperfect interface makes the system more dispersive. In particular, the frequency curves are lower in case of BaTiO$_3$/CoFe$_2$O$_4$/BaTiO$_3$ elastic laminated structure with imperfect contact as compared to the case of Epoxy/Glass/Epoxy (or E/G/E) laminated structure with imperfect contact.

In Fig. 10a, the black curve represents MEE composite with mechanical ($K_3$), electric (E) and magnetic (M) imperfect contact; green curve represents MEE composite with perfect contact; red curve represents electro-elastic composite with mechanical ($K_3$) and electric (E) imperfect contact; magenta curve represents electro-elastic composite with perfect contact; blue curve represents magneto-elastic composite with mechanical ($K_3$) and magnetic (M) imperfect contact; cyan curve represents magneto-elastic composite with perfect contact; dark yellow curve represents only elastic laminated composite with mechanical ($K_3$) imperfect contact; and light yellow curve represents elastic laminated composite with mechanical perfect contact. Figure 10b, c shows the magnification of the dispersion curves at different ranges. The dispersion curves reveal the relation between MEE-composite and imperfect bonding at distinct frequencies. The MEE-composite tends to decrease the dispersion curve making the system more dispersive when the system has imperfect interfaces as compared to the case when it has perfect interfaces at any finite frequency. For the case of imperfect bonding at low frequency, the difference between the dispersion curve for elastic composite with mechanical imperfect bonding (dark-yellow curve) and MEE composite with mechanical, electrical and magnetic imperfect bonding (black curve) can be observed which signifies that the MEE composite decreases the dispersion curve significantly at low frequency in the presence of imperfect bonding. On the other hand, the difference between the dispersion curves of elastic case (light yellow curve) and MEE coupled case (green curve) for perfect bonding can only be visible at higher frequency which signifies that the MEE composite also decreases the dispersion curve at higher frequency in the presence of perfect bonding, but not as significantly as compared to the case of imperfect bonding. Moreover, magneto-elastic composite and electro-elastic composite also show similar effect on dispersion curves in the presence and absence of imperfect bonding at any finite frequency. The case of electro-elastic composite makes the system more dispersive as compared to the case of MEE-composite and the case of magneto-elastic composite makes the system more dispersive as compared to case of electro-elastic composite. In conclusion, the MEE-composite, electro-elastic composite and magneto-elastic composite decrease the dispersion curve, i.e., make the system more dispersive and the effect is substantial in case of imperfect bonding as compared to the case of perfect bonding.

In Fig. 10d, the black curve represents the dispersion curve for the effective magneto-electro-elastic properties of the BaTiO$_3$/ CoFe$_2$O$_4$/ BaTiO$_3$ (B/C/B) MEE laminated composite periodic structure with imperfect interface obtained by the dynamic asymptotic homogenization method; the red curve represents the dispersion curve for the effective magneto-electro-elastic properties of the COMP10/COMP90/COMP10 composite (COMP10=10% BaTiO3 and COMP90=90% BaTiO3) with imperfect interface whose data are provided in Table 1 of [15] where the effective properties have been calculated using closed-form expressions given in [24]; the blue curve represents dispersion curve for the BaTiO3 monolithic structure with imperfect interface; and the magenta curve represents dispersion curve for the CoFe$_2$O$_4$ monolithic structure with imperfect interface. The blue and magenta curves tend to become non-dispersive. It has been found that in case of BaTiO$_3$/ CoFe$_2$O$_4$/ BaTiO$_3$ (B/C/B) MEE laminated composite periodic structure with imperfect interface, the dispersion curve is minimum as compared to other composite cases. This implies that the present dynamic asymptotic homogenization method makes the system more dispersive than the other cases which numerically validates the aim of the present work.

In order to show the effect of imperfect bonding on magneto-electric (ME)-coupling, Figure 11a–c is plotted showing the variation of effective magnetoelectric coefficient $\hat{\alpha }_{11}$ against mechanical, electrical and magnetic imperfect bonding ($K_3, E, M$). It is to be noted that $\hat{\alpha }_{22}=0$. In the horizontal axis of Fig. 11a–c, the imperfect bonding parameters are varied from very low to high values such that it achieves imperfect bonding to perfect bonding case. In Fig. 3, it has been already shown that the effect of mechanical imperfect bonding $K_3$ on dispersion curve dominates as compared to the effects of the electrical (E) and magnetic (M) imperfect bonding. A similar observation is also found in Fig. 11a–c where the effect of $K_3$ dominates on $\hat{\alpha }_{11}$ as compared to the other two. As the imperfect bonding parametric value increases, $\hat{\alpha }_{11}$ decreases which implies that the mechanical, electrical and magnetic imperfect bonding weaken the ME-coupling. This result also coincides with the results obtained by [11] and [13] for imperfect bonding in static case.

6 Conclusion

The present study provides a mathematical framework for the analysis of shear wave propagation phenomena in magneto-electro-elastic laminated periodic composite structure with non-uniform imperfect interfaces by proposing a dynamic asymptotic homogenized model. The present study is considered under low-frequency regime, i.e., the wavelength of propagating waves is much larger than the characteristic lengthscale of the microstructure. Regular asymptotic expansion of the frequency is considered instead of temporal scale. The local problems satisfying necessary and sufficient condition for the existence of 1-periodic solutions; closed-form expressions of the dispersion equation in second- and fourth-order approximation; and closed-form solutions of the first and second local problems in second-order approximation are derived explicitly for multi-laminated MEE composites with a unit periodic cell having any finite number of layers with mechanical, electrical and magnetic imperfect interfaces. Mathematical results are validated with those reported for perfect contact in [16] and also for the purely elastic case in [9] having perfect contact and in [10] having imperfect contact for second-order approximation. It is also pointed out that the obtained homogenized dispersive system is a “good" Boussinesq equation in elastic case. In [17], a “bad" Boussinesq equation was derived using AHM and then it was reformulated into “good" Boussinesq equation by approximation. However, by the proposed dynamic asymptotic homogenization method, the “good" Boussinesq equation can be directly achieved. This shows that the proposed technique is much more powerful. The procedure followed here, which is based on [5] and on recently published work of [16], allows a better understanding of the approximation model.

The dispersion phenomena for MEE periodic structure with tri-laminated unit cell having non-uniform imperfect interfaces have been studied for various parameters, such as mechanical, electrical and magnetic imperfect bonding, size of unit cell, angle of incidence of harmonic wave, volume fractions of the composites. It is concluded from the numerical results that the presence of imperfect bonding makes the system more dispersive. The effect of mechanical imperfect bonding dominates over the electric and magnetic one. The presence of non-uniformity in the imperfect bonding also strongly affect the dispersion curve. The system also becomes more dispersive when the size of the unit cell increases for MEE periodic structure in both perfect and imperfect contact cases. The angle of incidence of wave has an decreasing effect on the frequency curve in case of imperfect interface, whereas it has an increasing effect in case of perfect interface which is an interesting phenomena, although the effect of angle of incidence of wave in case of imperfect interface is very small. It is also concluded that in presence of imperfect interfaces, the system becomes more dispersive when the composite structure is non-monolithic. The magneto-electro-elastic composite along with mechanical, electrical and magnetic imperfect interface makes the system more dispersive as compared to elastic one with mechanical imperfect interface. In particular, electro-elastic composite makes the system more dispersive as compared to MEE-composite, whereas the magneto-elastic composite makes the system more dispersive as compared to electro-elastic composite. The effect is found to be substantial in case of imperfect bonding as compared to the case of perfect bonding. A comparison between the dispersion curve for effective dispersion equation of MEE case obtained by dynamic homogenization method and dispersion curve for MEE case with effective material constants obtained by approximate method of [24] shows that the present model is more dispersive and provides better approximation. Further, ME-coupling is also studied and it is found that it gets weakened as the imperfect bonding increases.

The consequence of the study bestows a theoretical framework that can be employed for surface acoustic wave or Rayleigh wave or Lamb wave at any angle of incidence in a piezoelectric or piezomagnetic or simply elastic multi-laminated composite with any finite number of laminates in the unit cell with any deterministic non-uniform imperfect interfacial function. The theoretical model provides control over the parameters and material constituents to achieve desired effective property and a framework to design and analyze smart systems. All these parametric effects provide a reference to consider while designing smart systems (ME-SAW devices) or studying structural health monitoring (SHM) system and NDTs where surface acoustic waves or Rayleigh waves or Lamb waves at certain angle of incidence are needed to propagate in a fully coupled MEE multi-laminated periodic structure where the interfaces may not have perfect contact. Considering the type of wave propagation, boundary condition and non-uniform imperfect interfacial function, the homogenized effective dispersive equation can be analytically derived using the proposed model and can be directly used for analysis.

Appendices

Solution of first and second local problems

1.1 Solution of first local problem

From the first local problem, in case of p-layered MEE composite structure, we obtain

$$\begin{aligned} \frac{d }{\textrm{d}y}\left( M_{11}\frac{\textrm{d}N_k(y)}{\textrm{d}y}\right) =-\frac{d (M_{1k})}{\textrm{d}y},\hspace{0.3cm} \,\,\,\, \text{ in }\,\,\,\, y\in (0,1)\setminus \Gamma , \end{aligned}$$

(A.1)

with non-uniform imperfect interface condition

$$\begin{aligned} M_{11}\frac{\textrm{d}N_k(y)}{\textrm{d}y} +M_{1k}=K^{(q)}[[ N_k(y)]],\,\,\, [[ M_{11}\frac{\textrm{d}N_k(y)}{\textrm{d}y} +M_{1k} ]] =0,\hspace{0.3cm} y = \theta _q, \end{aligned}$$

(A.2)

where $(0,1)=(0,\theta _1)\cup (\theta _1,\theta _2)\cup \cdots \cup (\theta _p,1)$ represents the p-laminae with repetition.

On integrating Eq.(A.1) for each $y\in \left( \theta _s,\theta _{s+1} \right)$ with $s=0,1,\ldots ,p$, we obtain

$$\begin{aligned} M_{11}\frac{\textrm{d}N_k(y)}{\textrm{d}y}+ M_{1k}=A_{k}^{(j)}, \end{aligned}$$

(A.3)

where $A_{k}^{(j)}$ is the integration constant for each interval $(\theta _j,\theta _{j+1})$.

Now, for p-laminated structure, from stress continuity (A.2)$_2$, we have $A_{k}^{(0)}=A_{k}^{(1)}=\cdots =A_{k}^{(p)}\equiv A_{k}$ (on assumption).

Hence, Eq.(A.3) becomes

$$\begin{aligned} M_{11}\frac{\textrm{d}N_k(y)}{\textrm{d}y}+ M_{1k}=A_{k}, \end{aligned}$$

(A.4)

from which we obtain

$$\begin{aligned} \frac{\textrm{d}N_k(y)}{\textrm{d}y}= M_{11}^{-1}A_{k}-M_{11}^{-1}M_{1k}. \end{aligned}$$

(A.5)

On taking average of the above, we obtain

$$\begin{aligned} \left\langle \frac{\textrm{d}N_k(y)}{\textrm{d}y}\right\rangle&= \int _0^{\theta _1^-}\frac{d N_k(y)}{\textrm{d}y} dy+\int _{\theta _1^+}^{\theta _2^-}\frac{\textrm{d}N_k(y)}{\textrm{d}y} dy + \cdots + \int _{\theta _{p}^+}^{1}\frac{\textrm{d}N_k(y)}{\textrm{d}y} dy \\&= \left\langle M_{11}^{-1}\right\rangle A_{k}-\left\langle M_{11}^{-1}M_{1k}\right\rangle . \end{aligned}$$

On simplification, we derive the relation

$$\begin{aligned} -\sum _{q=1}^p[[ N_k ]] \vert _{y=\theta _q} =\left\langle M_{11}^{-1}\right\rangle A_{k}-\left\langle M_{11}^{-1}M_{1k}\right\rangle . \end{aligned}$$

(A.6)

Using (A.2)$_1$ and (A.4) in (A.6), we obtain

$$\begin{aligned} A_{k}=\left\langle M_{11}^{-1} \right\rangle _K^{-1}\left\langle M_{11}^{-1}M_{1k} \right\rangle , \end{aligned}$$

(A.7)

where $\left\langle M_{11}^{-1} \right\rangle _K^{-1}=\left( \sum _{q=1}^p (K^{(q)})^{-1} +\left\langle M_{11}^{-1} \right\rangle \right) ^{-1}$ with $I=\begin{pmatrix} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}1 \end{pmatrix}$.

Now, for each $y\in (\theta _{s},\theta _{s+1})$, integrating (A.5) from 0 to y, we get

$$\begin{aligned} N_k(y)-N_{k}(0)=B_{k}(y), \end{aligned}$$

(A.8)

where $B_{k}(y)=\sum _{q=1}^{s} (K^{(q)})^{-1} A_{k}+\int _0^y\left( M_{11}^{-1}A_k-M_{11}^{-1}M_{1k} \right) d\xi$.

On taking average of Eq.(A.8) and using $\left\langle N_k\right\rangle =0$ for uniqueness, we obtain

$$\begin{aligned} N_k(y)=B_{k}(y)-\left\langle B_{k}(y)\right\rangle . \end{aligned}$$

(A.9)

For a tri-layered periodic structure $(0,1)=(0,\theta _1)\cup (\theta _1,\theta _2) \cup (\theta _2,1)$, we consider

$$\begin{aligned} M_{jk}= \left\{ \begin{array}{ll} &{}M_{jk}^{(0)},\,\,\, \text{ for } \,\,\, y\in (0,\theta _1),\\ &{}M_{jk}^{(1)},\,\,\, \text{ for } \,\,\, y\in (\theta _1,\theta _2),\\ &{}M_{jk}^{(0)},\,\,\, \text{ for } \,\,\, y\in (\theta _2,1), \end{array} \right. \end{aligned}$$

(A.10)

for which, on using interface condition and considering $K^{(1)}=K^{(2)}=K$, we obtain

$$\begin{aligned} N_1(y)= \left\{ \begin{array}{ll} &{} \left[ (M_{11}^{(0)})^{-1}\left\langle M_{11}^{-1}\right\rangle ^{-1} -I\right] y-\left\langle B_{k}(y)\right\rangle ,\,\,\, \text{ for } \,\,\, y\in (0,\theta _1),\\ &{}\left[ K^{-1}+\left( (M_{11}^{(0)})^{-1}-(M_{11}^{(1)})^{-1}\right) \theta _1+(M_{11}^{(1)})^{-1}y \right] \left( K^{-1} +\left\langle M_{11}^{-1} \right\rangle \right) ^{-1}\\ &{}\hspace{6cm}-Iy -\left\langle B_{k}(y)\right\rangle ,\,\,\, \text{ for } \,\,\, y\in (\theta _1,\theta _2),\\ &{}\left[ 2K^{-1}+\left( (M_{11}^{(1)})^{-1}-(M_{11}^{(0)})^{-1}\right) (\theta _2-\theta _1)+(M_{11}^{(0)})^{-1}y \right] \left( 2K^{-1} +\left\langle M_{11}^{-1} \right\rangle \right) ^{-1}\\ &{}\hspace{6cm}-Iy-\left\langle B_{k}(y)\right\rangle ,\,\,\, \text{ for } \,\,\, y\in (\theta _2,1), \end{array} \right. \end{aligned}$$

(A.11)

along with $N_2(y)=0$ and $N_3(y)=0$, where

$$\begin{aligned} \left\langle B_k\right\rangle&=2K^{-1}\left[ 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right] ^{-1} +\left( (M_{11}^{(0)})^{-1}\left\langle M_{11}^{-1}\right\rangle ^{-1}-I\right) \frac{\theta _1^2}{2} +\left( (M_{11}^{(0)})^{-1}\left\langle M_{11}^{-1}\right\rangle ^{-1}-I\right) \nonumber \\&\quad \times \theta _1(\theta _2-\theta _1) +\left( (M_{11}^{(1)})^{-1}\left( K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1}-I\right) \left( \frac{\theta _2^2}{2}-\frac{\theta _1^2}{2}-\theta _1(\theta _2-\theta _1)\right) \nonumber \\&\quad +\left( (M_{11}^{(0)})^{-1}\left\langle M_{11}^{-1}\right\rangle ^{-1}-I\right) \theta _1(1-\theta _2) +\left( (M_{11}^{(1)})^{-1}\left( K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1}-I\right) (\theta _2-\theta _1)(1-\theta _2)\nonumber \\&\quad +\left( (M_{11}^{(0)})^{-1}\left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1}-I\right) \left( \frac{1}{2}-\frac{\theta _2^2}{2}-\theta _2(1-\theta _2)\right) . \end{aligned}$$

1.2 Solution of second local problem

From the second local problem, in case of p-layered MEE composite structure, we obtain

$$\begin{aligned} L N_{jk}(y)=- \frac{\textrm{d}}{\textrm{d}y}\left( M_{1j}N_k(y)\right) - M_{j1}\frac{d N_k}{\textrm{d}y}-M_{jk}+\frac{\rho (y)}{\hat{\rho }}{\hat{M}}_{jk},\hspace{0.5cm} y\in (0,1)\setminus \Gamma \end{aligned}$$

(A.12)

with non-uniform imperfect interface condition

$$\begin{aligned} M_{11}\frac{\textrm{d}N_{jk}(y)}{\textrm{d}y} +M_{lj}N_k=K^{(q)}[[ N_{jk}]],\,\,\, [[ M_{11}\frac{\textrm{d}N_{jk}(y)}{\textrm{d}y} +M_{lj}N_k ]] =0,\hspace{0.3cm} y = \theta _q. \end{aligned}$$

(A.13)

On using Eq.(A.4) and (A.7), Eq.(A.12) becomes

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}y}\left[ M_{11}\frac{\textrm{d}}{\textrm{d}y}N_{jk}+M_{1j}N_k \right] =-R_{jk}-M_{jk}+\frac{\rho }{\hat{\rho }}{\hat{M}}_{jk}, \end{aligned}$$

(A.14)

where $R_{jk}=M_{j1}M_{11}^{-1}\left\langle M_{11}^{-1}\right\rangle _K^{-1}\left\langle M_{11}^{-1}M_{1k}\right\rangle -M_{j1}M_{11}^{-1}M_{1k}$.

On integrating Eq.(A.14) from 0 to y for each $y\in \left( \theta _{s},\theta _{s+1} \right)$, we obtain

$$\begin{aligned}&\int _{0^+}^{\theta _1^-}\frac{\textrm{d}}{\textrm{d}y}\left[ M_{11}\frac{\textrm{d}}{\textrm{d}y}N_{jk}+M_{1j}N_k \right] d\xi +\int _{\theta _1^+}^{\theta _2^-}\frac{\textrm{d}}{\textrm{d}y}\left[ M_{11}\frac{\textrm{d}}{\textrm{d}y}N_{jk}+M_{1j}N_k \right] d\xi \nonumber \\&\quad +\cdots +\int _{\theta _{s}}^y\frac{\textrm{d}}{\textrm{d}y}\left[ M_{11}\frac{\textrm{d}}{\textrm{d}y}N_{jk}+M_{1j}N_k \right] d\xi =Q_{jk}, \end{aligned}$$

(A.15)

where $Q_{jk}=\int _0^y\left( -R_{jk}-M_{jk}+\frac{\rho }{\hat{\rho }}{\hat{M}}_{jk}\right) d\xi$.

Now, using interface condition (A.2)$_2$, we derive

$$\begin{aligned} \left[ M_{11}\frac{\textrm{d}}{\textrm{d}y}N_{jk}+M_{1j}N_k \right] _{\xi =y}=Q_{jk}+A_{jk}, \end{aligned}$$

(A.16)

where $A_{jk}=\left[ M_{11}\frac{\textrm{d}}{\textrm{d}y}N_{jk}+M_{1j}N_k \right] _{\xi =0^+}$.

From Eq.(A.16), we obtain

$$\begin{aligned} \frac{\textrm{d}N_{jk}(y)}{\textrm{d}y}=M_{11}^{-1}Q_{jk}+M_{11}^{-1}A_{jk}-M_{11}^{-1}M_{1j}N_k. \end{aligned}$$

(A.17)

Now, on taking average and using the condition (A.13)$_1$, we obtain

$$\begin{aligned} -\sum _{q=1}^{p}\left( K^{(q)}\right) ^{-1}\left[ M_{11}\frac{\textrm{d}}{\textrm{d}y}N_{jk}+M_{1j}N_k \right] _{\xi =\theta _q}=\left\langle M_{11}^{-1}\right\rangle A_{jk}+\left\langle M_{11}^{-1}Q_{jk}-M_{11}^{-1}M_{1j}N_k\right\rangle . \end{aligned}$$

(A.18)

In view of interface condition (A.13)$_2$, we have

$$\begin{aligned} \left[ M_{11}\frac{\textrm{d}}{\textrm{d}y}N_{jk}+M_{1j}N_k \right] _{y=\theta _1}=\left[ M_{11}\frac{\textrm{d}}{\textrm{d}y}N_{jk}+M_{1j}N_k \right] _{y=\theta _2}=\cdots =\left[ M_{11}\frac{\textrm{d}}{\textrm{d}y}N_{jk}+M_{1j}N_k \right] _{y=\theta _{p}} \end{aligned}$$

and in view of (A.16), we obtain $\left[ M_{11}\frac{\textrm{d}}{\textrm{d}y}N_{jk}+M_{1j}N_k \right] _{y=\theta _1}=Q_{jk}(\theta _1)+A_{jk}$.

Hence, from (A.18), we derive

$$\begin{aligned} A_{jk}=-\left\langle M_{11}^{-1}\right\rangle _K^{-1}\left[ \sum _{q=1}^{p}\left( K^{(q)}\right) ^{-1}Q_{jk}(\theta _1)+\left\langle M_{11}^{-1} Q_{jk}(y)\right\rangle -\left\langle M_{11}^{-1}M_{1j}N_k(y) \right\rangle \right] . \end{aligned}$$

(A.19)

Now, integrating Eq.(A.17) from 0 to y for each $y\in \left( \theta _{s},\theta _{s+1} \right)$ and using interface condition (A.13)$_1$, we obtain

$$\begin{aligned} N_{jk}(y)-N_{jk}(0)=B_{jk}(y), \end{aligned}$$

(A.20)

where

$$\begin{aligned} B_{jk}(y)=\sum _{q=1}^{s}\left( K^{(q)}\right) ^{-1}\left( Q_{jk}(\theta _1)+A_{jk}\right) + \int _0^y \left[ M_{11}^{-1}Q_{jk}(y)+M_{11}^{-1}A_{jk}-M_{11}^{-1}M_{1j}N_k \right] d\eta . \end{aligned}$$

On taking average of Eq.(A.20) and using the uniqueness condition $\left\langle N_{jk} \right\rangle =0$, we obtain

$$\begin{aligned} N_{jk}(y)=B_{jk}(y)-\left\langle B_{jk}(y) \right\rangle . \end{aligned}$$

(A.21)

For the 3-layered structure given in Eq.(A.10) and considering $K^{(1)}=K^{(2)}=K$, we calculate the following

$$\begin{aligned} B_{11}(y)= \left\{ \begin{array}{ll} &{}(M_{11}^{(0)})^{-1}\left[ -\left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{11}\right] \frac{y^2}{2} + (M_{11}^{(0)})^{-1} A_{11} \\ &{}\hspace{1cm} - \left[ (M_{11}^{(0)})^{-1} \left\langle M_{11}^{-1}\right\rangle ^{-1} - I \right] \frac{y^2}{2}+\left\langle B_k\right\rangle y,\,\,\hspace{1cm} \text{ for } \,\, y\in (0,\theta _1),\\ &{} (M_{11}^{(0)})^{-1} \left[ -\left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{11}\right] \frac{\theta _1^2}{2} + (M_{11}^{(0)})^{-1} A_{11} \theta _1\\ &{}\hspace{1cm} - \left[ (M_{11}^{(0)})^{-1} \left\langle M_{11}^{-1}\right\rangle ^{-1} - I \right] \frac{\theta _1^2}{2}+\left\langle B_k\right\rangle \theta _1\\ &{}\hspace{1cm} + (M_{11}^{(1)})^{-1} \left\{ \left( \frac{\rho ^{(0)}-\rho ^{(1)}}{\hat{\rho }} \right) {\hat{M}}_{11}\theta _1 (y-\theta _1)\right. \\ &{}\hspace{1cm}\left. +\left[ -\left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1} +\frac{\rho ^{(1)}}{\hat{\rho }}{\hat{M}}_{11}\right] \left( \frac{y^2}{2}-\frac{\theta _1^2}{2}\right) \right\} \\ &{}\hspace{1cm} + (M_{11}^{(1)})^{-1} A_{11}(y-\theta _1)- \left\{ \left[ K^{-1}(y-\theta _1)+\left( (M_{11}^{(0)})^{-1}-(M_{11}^{(1)})^{-1}\right) \right. \right. \\ &{}\hspace{1cm} \left. \left. \times \theta _1(y-\theta _1)+(M_{11}^{(1)})^{-1}\left( \frac{y^2}{2}-\frac{\theta _1^2}{2}\right) \right] \left( K^{-1} +\left\langle M_{11}^{-1} \right\rangle \right) ^{-1}\right. \\ &{}\hspace{1cm} \left. -I\left( \frac{y^2}{2}-\frac{\theta _1^2}{2}\right) -\left\langle B_{k}(y)\right\rangle (y-\theta _1) \right\} ,\,\,\, \hspace{2cm}\text{ for }\,\, y\in (\theta _1,\theta _2),\\ &{} (M_{11}^{(0)})^{-1} \left[ -\left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{11}\right] \frac{\theta _1^2}{2} + (M_{11}^{(0)})^{-1} A_{11} \theta _1 \\ &{}\hspace{1cm}- \left[ (M_{11}^{(0)})^{-1} \left\langle M_{11}^{-1}\right\rangle ^{-1} - I \right] \frac{\theta _1^2}{2}+\left\langle B_k\right\rangle \theta _1\\ &{}\hspace{1cm} + (M_{11}^{(1)})^{-1} \left\{ \left( \frac{\rho ^{(0)}-\rho ^{(1)}}{\hat{\rho }} \right) {\hat{M}}_{11}\theta _1 (\theta _2-\theta _1)\right. \\ &{}\hspace{1cm}\left. +\left[ -\left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1} +\frac{\rho ^{(1)}}{\hat{\rho }}{\hat{M}}_{11}\right] \left( \frac{\theta _2^2}{2}-\frac{\theta _1^2}{2}\right) \right\} \\ &{} \hspace{1cm} + (M_{11}^{(1)})^{-1} A_{11}(\theta _2-\theta _1)+ (M_{11}^{(0)})^{-1} \left\{ \left( \frac{\rho ^{(1)}-\rho ^{(0)}}{\hat{\rho }} \right) {\hat{M}}_{11} (\theta _2-\theta _1)(y-\theta _2)\right. \\ &{}\hspace{1cm}\left. +\left[ -\left\langle M_{11}^{-1}\right\rangle ^{-1} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{11} \right] \left( \frac{y^2}{2}-\frac{\theta _2^2}{2}\right) \right\} + (M_{11}^{(0)})^{-1} A_{11}(y-\theta _2) \\ &{}\hspace{1cm}- \left\{ \left[ K^{-1}(\theta _2-\theta _1)+\left( (M_{11}^{(0)})^{-1}-(M_{11}^{(1)})^{-1}\right) \theta _1(\theta _2-\theta _1)\right. \right. \\ &{}\hspace{1cm} \left. +(M_{11}^{(1)})^{-1}\left( \frac{\theta _2^2}{2}-\frac{\theta _1^2}{2}\right) \right] \left( K^{-1} +\left\langle M_{11}^{-1} \right\rangle \right) ^{-1} -I\left( \frac{\theta _2^2}{2}-\frac{\theta _1^2}{2}\right) \\ &{}\hspace{1cm}\left. -\left\langle B_{k}(y)\right\rangle (\theta _2-\theta _1) \right\} - \left\{ \left[ 2K^{-1}(y-\theta _2)+\left( (M_{11}^{(1)})^{-1}-(M_{11}^{(0)})^{-1}\right) \right. \right. \\ &{}\hspace{1cm}\left. \times (\theta _2-\theta _1)(y-\theta _2) +(M_{11}^{(0)})^{-1}\left( \frac{y^2}{2}-\frac{\theta _2^2}{2}\right) \right] \left( 2K^{-1} +\left\langle M_{11}^{-1} \right\rangle \right) ^{-1}\\ &{}\hspace{1cm} \left. -I\left( \frac{y^2}{2}-\frac{\theta _2^2}{2}\right) -\left\langle B_{k}(y)\right\rangle (y-\theta _2)\right\} ,\,\,\, \hspace{3cm} \text{ for }\,\, y\in (\theta _2,1)\\ \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} B_{jj}(y)= \left\{ \begin{array}{ll} &{}(M_{11}^{(0)})^{-1} \left[ -M_{jj}^{(0)} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{jj}\right] \frac{y^2}{2} + (M_{11}^{(0)})^{-1} A_{jj}, \hspace{2cm}\,\,\, \text{ for } \,\,\, y\in (0,\theta _1),\\ &{}(M_{11}^{(0)})^{-1} \left[ -M_{jj}^{(0)} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{jj}\right] \frac{\theta _1^2}{2} + (M_{11}^{(0)})^{-1} A_{jj}\theta _1\\ &{}\hspace{1cm}+ (M_{11}^{(1)})^{-1}\left\{ \left( \frac{\rho ^{(0)}-\rho ^{(1)}}{\hat{\rho }}\right) {\hat{M}}_{jj} \theta _1(y-\theta _1)\right. \\ &{}\hspace{1cm}\left. +\left[ - M_{jj}^{(1)} +\frac{\rho ^{(1)}}{\hat{\rho }}{\hat{M}}_{jj}\right] \left( \frac{y^2}{2}-\frac{\theta _1^2}{2}\right) \right\} + (M_{11}^{(1)})^{-1} A_{jj}(y-\theta _1), \,\, \text{ for } \,\,\, y\in (\theta _1,\theta _2),\\ &{}(M_{11}^{(0)})^{-1} \left[ -M_{jj}^{(0)} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{jj}\right] \frac{\theta _1^2}{2} + (M_{11}^{(0)})^{-1} A_{jj}\theta _1\\ &{}\hspace{1cm}+ (M_{11}^{(1)})^{-1}\left\{ \left( \frac{\rho ^{(0)}-\rho ^{(1)}}{\hat{\rho }}\right) {\hat{M}}_{jj} \theta _1(\theta _2-\theta _1) +\left[ - M_{jj}^{(1)} +\frac{\rho ^{(1)}}{\hat{\rho }}{\hat{M}}_{jj}\right] \left( \frac{\theta _2^2}{2}-\frac{\theta _1^2}{2}\right) \right\} \\ &{}\hspace{1cm}+ (M_{11}^{(1)})^{-1} A_{jj}(\theta _2-\theta _1)+ (M_{11}^{(0)})^{-1}\left\{ \left( \frac{\rho ^{(1)}-\rho ^{(0)}}{\hat{\rho }}\right) {\hat{M}}_{jj}(\theta _2-\theta _1)(y-\theta _2) \right. \\ &{}\hspace{1cm}\left. +\left[ - M_{jj}^{(0)} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{jj}\right] \left( \frac{y^2}{2}-\frac{\theta _2^2}{2}\right) \right\} + (M_{11}^{(0)})^{-1} A_{jj}(y-\theta _2), \,\, \text{ for } \,\,\, y\in (\theta _2,1), \end{array} \right. \end{aligned}$$

when $j=k=2$ or 3 and $B_{jk}=0$ for $j\ne k$.

$$\begin{aligned} A_{11}&= -\left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1}\left[ 2K^{-1}\left( -\left( 2K^{-1}+\left\langle M_{11}^{-1} \right\rangle \right) ^{-1}+\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{11} \right) \theta _1\right. \\&\quad \left. +(M_{11}^{(0)})^{-1}\left\{ -\left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1} + \frac{\rho ^{(0)}}{\hat{\rho }} {\hat{M}}_{11} \right\} \frac{\theta _1^2}{2}+ (M_{11}^{(1)})^{-1}\right. \\&\quad \times \left\{ \left( \frac{\rho ^{(0)}-\rho ^{(1)}}{\hat{\rho }} \right) {\hat{M}}_{11}\theta _1 (\theta _2-\theta _1)+\left[ -\left\langle M_{11}^{-1}\right\rangle ^{-1} + \frac{\rho ^{(1)}}{\hat{\rho }} {\hat{M}}_{11} \right] \left( \frac{\theta _2^2}{2}-\frac{\theta _1^2}{2} \right) \right\} \\&\quad + (M_{11}^{(0)})^{-1} \left\{ \left( \frac{\rho ^{(1)}-\rho ^{(0)}}{\hat{\rho }} \right) {\hat{M}}_{11} (\theta _2-\theta _1)(1-\theta _2) \right. \\&\quad \left. \left. +\left[ -\left\langle M_{11}^{-1}\right\rangle ^{-1} + \frac{\rho ^{(0)}}{\hat{\rho }} {\hat{M}}_{11} \right] \left( \frac{1}{2}-\frac{\theta _2^2}{2} \right) \right\} \right] ,\\ A_{22}&= -\left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1}\left[ 2K^{-1}\left( -M_{22}^{(0)} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{22}\right) \theta _1\right. \\&\quad +(M_{11}^{(0)})^{-1}\left\{ -M_{22}^{(0)} + \frac{\rho ^{(0)}}{\hat{\rho }} {\hat{M}}_{22} \right\} \frac{\theta _1^2}{2} + (M_{11}^{(1)})^{-1} \left\{ \left( \frac{\rho ^{(0)}-\rho ^{(1)}}{\hat{\rho }} \right) {\hat{M}}_{22}\right. \\&\quad \left. \times \theta _1 (\theta _2-\theta _1) +\left[ -M_{22}^{(1)} + \frac{\rho ^{(1)}}{\hat{\rho }} {\hat{M}}_{22} \right] \left( \frac{\theta _2^2}{2}-\frac{\theta _1^2}{2} \right) \right\} + (M_{11}^{(0)})^{-1} \\&\quad \left. \times \left\{ \left( \frac{\rho ^{(1)}-\rho ^{(0)}}{\hat{\rho }} \right) {\hat{M}}_{22} (\theta _2-\theta _1)(1-\theta _2) +\left[ -M_{22}^{(0)} + \frac{\rho ^{(0)}}{\hat{\rho }} {\hat{M}}_{22} \right] \left( \frac{1}{2}-\frac{\theta _2^2}{2} \right) \right\} \right] \end{aligned}$$

and

$$\begin{aligned} A_{33}&= -\left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1}\left[ 2K^{-1}\left( -M_{33}^{(0)} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{33}\right) \theta _1\right. \\&\quad +(M_{11}^{(0)})^{-1}\left\{ -M_{33}^{(0)} + \frac{\rho ^{(0)}}{\hat{\rho }} {\hat{M}}_{33} \right\} \frac{\theta _1^2}{2}+ (M_{11}^{(1)})^{-1} \left\{ \left( \frac{\rho ^{(0)}-\rho ^{(1)}}{\hat{\rho }} \right) {\hat{M}}_{33}\theta _1 (\theta _2-\theta _1)\right. \\&\quad \left. +\left[ -M_{33}^{(1)} + \frac{\rho ^{(1)}}{\hat{\rho }} {\hat{M}}_{33} \right] \left( \frac{\theta _2^2}{2}-\frac{\theta _1^2}{2} \right) \right\} \left. + (M_{11}^{(0)})^{-1} \left\{ \left( \frac{\rho ^{(1)}-\rho ^{(0)}}{\hat{\rho }} \right) \right. \right. \\&\quad \left. \left. \times {\hat{M}}_{33} (\theta _2-\theta _1)(1-\theta _2) +\left[ -M_{33}^{(0)} + \frac{\rho ^{(0)}}{\hat{\rho }} {\hat{M}}_{33} \right] \left( \frac{1}{2}-\frac{\theta _2^2}{2} \right) \right\} \right] , \end{aligned}$$

$$\begin{aligned} Q_{11}(y)= \left\{ \begin{array}{ll} &{} \left[ -\left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{11}\right] y,\,\,\hspace{2cm} \text{ for } \,\,\, y\in (0,\theta _1),\\ &{}\left( \frac{\rho ^{(0)}-\rho ^{(1)}}{\hat{\rho }}\right) {\hat{M}}_{11} \theta _1+\left[ - \left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1} +\frac{\rho ^{(1)}}{\hat{\rho }}{\hat{M}}_{11}\right] y,\, \, \text{ for } \,\,\, y\in (\theta _1,\theta _2),\\ &{}\left( \frac{\rho ^{(1)}-\rho ^{(0)}}{\hat{\rho }}\right) {\hat{M}}_{11} (\theta _2-\theta _1)+\left[ - \left( 2K^{-1}+\left\langle M_{11}^{-1}\right\rangle \right) ^{-1} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{11}\right] y, \\ &{}\hspace{8cm} \text{ for } \,\,\, y\in (\theta _2,1), \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} Q_{jj}(y)= \left\{ \begin{array}{ll} &{} \left[ -M_{jj}^{(0)} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{jj}\right] y,\,\,\hspace{4cm} \text{ for } \,\,\, y\in (0,\theta _1),\\ &{}\left( \frac{\rho ^{(0)}-\rho ^{(1)}}{\hat{\rho }}\right) {\hat{M}}_{jj} \theta _1+\left[ - M_{jj}^{(1)} +\frac{\rho ^{(1)}}{\hat{\rho }}{\hat{M}}_{jj}\right] y,\,\,\hspace{1cm} \text{ for } \,\,\, y\in (\theta _1,\theta _2),\\ &{}\left( \frac{\rho ^{(1)}-\rho ^{(0)}}{\hat{\rho }}\right) {\hat{M}}_{jj} (\theta _2-\theta _1)+\left[ - M_{jj}^{(0)} +\frac{\rho ^{(0)}}{\hat{\rho }}{\hat{M}}_{jj}\right] y,\,\,\hspace{0.5cm} \text{ for } \,\,\, y\in (\theta _2,1), \end{array} \right. \end{aligned}$$

when $j=k=2$ or 3. and $Q_{jk}=0$ for $j\ne k$.

Derivation of closed-form expression of $\eta ^*$

For $O(\varepsilon ^2)$, we consider

$$\begin{aligned} \eta ^*={\hat{M}}_{jk_1k_2l} {\hat{M}}_{jk_1}^{-1} \hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1} =\left\langle M_{k_21}\frac{d N_{jk_1l}}{d y}+M_{k_2l}N_{jk_1}-\frac{\rho ({y})}{\hat{\rho }}{\hat{M}}_{k_2 l}N_{jk_1} \right\rangle {\hat{M}}_{jk_1}^{-1} \hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1}. \end{aligned}$$

(B.22)

Considering the third local problem with multiplication by $N_k$ and taking null average, we obtain

$$\begin{aligned} \left\langle N_k\left[ \frac{\textrm{d}}{\textrm{d}y}\left( M_{11}\frac{\textrm{d}N_{jk_1l}}{\textrm{d}y} + M_{1l}N_{jk_1}\right) \right] \right\rangle = -\left\langle N_i\left( M_{l1}\frac{\textrm{d}N_{jk_1}}{\textrm{d}y}+M_{jl}N_{k_1}-\frac{\rho ({y})}{\hat{\rho }}{\hat{M}}_{jl}N_{k_1} \right) \right\rangle . \end{aligned}$$

(B.23)

On integrating by parts the left hand side, we obtain

$$\begin{aligned} \left\langle M_{11}\frac{\textrm{d}N_{jk_1l}}{\textrm{d}y}+M_{1l}N_{jk_1}\right\rangle&= -\left\langle N_i\left( M_{l1}\frac{\textrm{d}N_{jk_1}}{d y}+M_{jl}N_{k_1}-\frac{\rho ({y})}{\hat{\rho }}{\hat{M}}_{jl}N_{k_1} \right) \right\rangle \nonumber \\&\quad - \left\langle \left( M_{11}^{-1}M_{1k_2}M_{1l} - M_{11}^{-1}A_{1k_2} M_{1l} -M_{k_2l} \right) N_{jk_1}\right\rangle . \end{aligned}$$

(B.24)

Now, we note that

$$\begin{aligned} \left\langle \frac{\rho }{\hat{\rho }}{\hat{M}}_{k_2 l}N_{jk_1} \right\rangle = -\left\langle R {\hat{M}}_{k_2 l} \frac{\textrm{d}N_{jk_1}}{\textrm{d}y} \right\rangle , \end{aligned}$$

(B.25)

where $R=\int _0^y \left( \frac{\rho (y)}{\hat{\rho }} -1 \right) d\xi$.

On the other hand, using (B.24) and (B.25), we obtain the expression of $\eta ^*$ as

$$\begin{aligned} \eta ^*&=\left[ \left\langle R {\hat{M}}_{k_2 l} \frac{\textrm{d}N_{jk_1}}{\textrm{d}y} \right\rangle -\left\langle N_i\left( M_{l1}\frac{\textrm{d}N_{jk_1}}{d y}+M_{jl}N_{k_1}-\frac{\rho }{\hat{\rho }}{\hat{M}}_{jl}N_{k_1} \right) \right\rangle \right. \nonumber \\&\quad \left. - \left\langle \left( M_{11}^{-1}M_{1k_2}M_{1l} - M_{11}^{-1}A_{1k_2} M_{1l} -M_{k_2l} \right) N_{jk_1}\right\rangle \right] {\hat{M}}_{jk_1}^{-1} \hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1}. \end{aligned}$$

(B.26)

Using Eq.(A.12), we obtain the closed-form expression of Eq.(B.26) as follows:

$$\begin{aligned} \eta ^*&=\left[ \left\langle R {\hat{M}}_{k_2 l} M_{11}^{-1}Q_{jk_1} \right\rangle + \left\langle R {\hat{M}}_{k_2 l} M_{11}^{-1}A_{jk_1} \right\rangle - \left\langle R {\hat{M}}_{k_2 l} M_{11}^{-1}M_{1j}N_{k_1} \right\rangle -\left\langle N_i M_{l1} M_{11}^{-1}Q_{jk_1} \right\rangle \right. \nonumber \\&\quad \left. -\left\langle N_i M_{l1} M_{11}^{-1}A_{jk_1} \right\rangle +\left\langle N_i M_{l1} M_{11}^{-1}M_{1j}N_{k_1} \right\rangle -\left\langle N_i M_{jl}N_{k_1}\right\rangle +\left\langle N_i \frac{\rho }{\hat{\rho }}{\hat{M}}_{jl}N_{k_1} \right\rangle \right. \nonumber \\&\quad \left. - \left\langle \left( M_{11}^{-1}M_{1k_2}M_{1l} - M_{11}^{-1}A_{1k_2} M_{1l} -M_{k_2l} \right) N_{jk_1}\right\rangle \right] {\hat{M}}_{jk_1}^{-1} \hat{{\mathcal {P}}} {\hat{M}}_{k_2l}^{-1}. \end{aligned}$$

(B.27)